7 класс. Геометрия. Атанасян. Учебник. Ответы к стр. 10
Начальные геометрические сведения
Луч и угол
Луч. Угол
Ответы к стр. 10
8. Проведите прямую, отметьте на ней точки A и B и на отрезке АВ отметьте точку С. а) Среди лучей AB, BC, CA, AC и BA назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
а) Совпадающие лучи (имеют начало в одной точке и одно направление): АС и АВ, ВС и ВА;
б) Луч СВ.
9. Начертите три неразвёрнутых угла и обозначьте их так: ∠AOB, ∠hk, ∠M.
∠AOB, ∠hk, ∠M.
10. Начертите два развёрнутых угла и обозначьте их буквами.
∠AСB, ∠bα или ∠C.
11. Начертите три луча h, k и I с общим началом. Назовите все углы, образованные данными лучами.
Начертите три луча h, k и I с общим началом. Назовите все углы, образованные данными лучами.
∠hk, ∠kl и ∠hl.
12. Начертите неразвёрнутый угол hk. Отметьте две точки внутри этого угла, две точки вне этого угла и две точки на сторонах угла.
Точки A и B лежат внутри ∠hk, точки N и M лежат вне ∠hk, точки C и D лежат на сторонах ∠hk.
13. Начертите неразвёрнутый угол. Отметьте точки А, B, М и N так, чтобы все точки отрезка AB лежали внутри угла, а все точки отрезка MN лежали вне угла.
Точки А и В отрезка АВ лежат внутри ∠
14. Начертите неразвёрнутый угол АОВ и проведите: а) луч ОС, который делит угол АОВ на два угла; б) луч OD, который не делит угол АОС на два угла.
15. Сколько неразвёрнутых углов образуется при пересечении двух прямых?
При пересечении двух прямых (k и h) образуется четыре (1, 2, 3, 4) неразвёрнутых углов.
16. Какие из точек, изображённых на рисунке 17, лежат внутри угла hk, а какие — вне этого угла?
Точки М и А лежат внутри ∠hk, точки С и N лежат вне ∠hk.
17. Какие из лучей, изображенных на рисунке 18, делят угол АОВ на два угла?
Луч делит угол на два угла, если он:
1) исходит из вершины угла;
2) проходит внутри угла.
Луч l делит угол АOВ на два угла, так как он исходит из вершины угла АOВ и проходит внутри угла АOВ.
Луч h делит угол АOВ на два угла, так как он исходит из вершины угла АOВ и проходит внутри угла АOВ.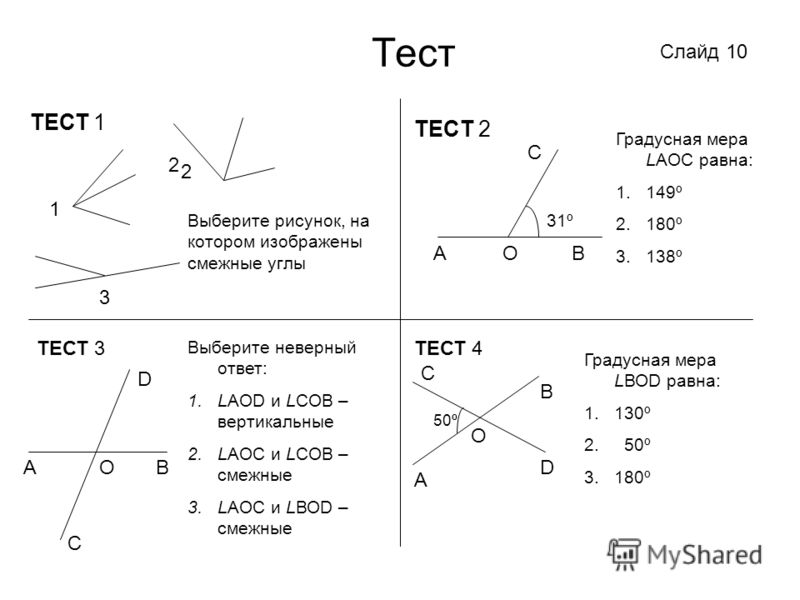
Луч k не делит угол АOВ на два угла, так как он исходит из вершины угла АOВ, но не проходит внутри угла АOВ.
Лучи l и h лежат внутри ∠АОВ и каждый луч делит этот угол на два угла.
ГДЗ. Ответы по геометрии. 7 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Геометрия. 7 класс
supportМерзляк 5 класс — § 11. Угол. Обозначение углов
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какую фигуру называют углом? — Углом называют фигуру, образованную двумя лучами, имеющими общее начало.
2. Какие два угла называют равными? — Два угла называют равными, если они совпадают при наложении.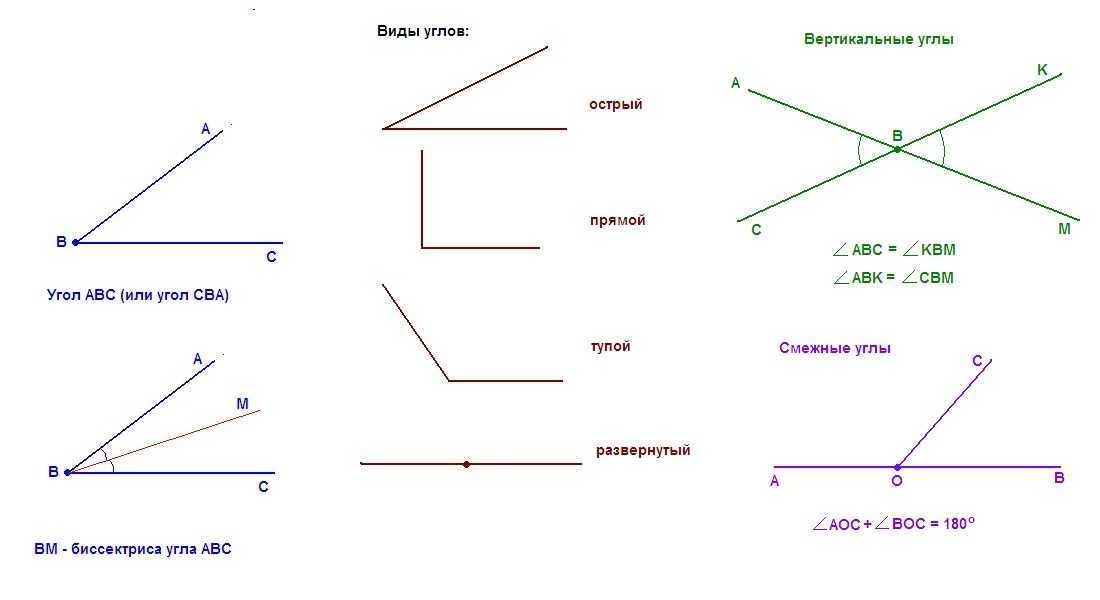
3. Как называют луч, который делит угол на два равных угла? — биссектриса.
Комментарий: Запомнить это сложное слово поможет шутка: «Биссектриса — это крыса, которая бегает по углам и делит угол пополам».
Решаем устно
1. Каких чисел не хватает в цепочке вычислений?
2. Решите уравнение:
3. Корнем каких из следующих уравнений является число 5:
1) 2х — 3 = 7, если х = 5, то:
2 • 5 — 3 = 7
10 — 3 = 7
7 = 7 — верно, значит число 5 является корнем уравнения 2х — 3 = 7.
2) х + 20 = 20 + х, если х = 5, то:
5 + 20 = 20 + 5
25 = 25 — верно, значит число 5 является корнем уравнения х + 20 = 20 + х.
3) 36 — 3х = 20, если х = 5, то:
36 — 3 • 5 = 20
36 — 15 = 20
21 ≠ 20 — неверно, значит число 5 не является корнем уравнения 36 — 3х = 20.
4) х • х • х + 25 = 150, если х = 5, то:
25 • 5 + 25 = 150
125 + 25 = 150
150 = 150 — верно, значит число 5 является корнем уравнения х • х • х + 25 = 150.

5) 0 • х = 10, если х = 5, то:
0 • 5 = 10
0 = 10 — неверно, значит число 5 не является корнем уравнения 0 • х = 10.
6) х + 12 = 22 — х, если х = 5, то:
5 + 12 = 22 — 5
17 = 17 — верно, значит число 5 является корнем уравнения 36 — 3х = 20.
Ответ: число 5 является корнем уравнений № 1, 2, 4, 6.
4. У Пети и Миши было поровну конфет. Петя отдал Мише 8 конфет. На сколько конфет у Миши стало больше, чем у Пети?
Пусть изначально у Пети и у Миши было по х конфет. Тогда после обмена стало:
- у Пети х — 8 конфет
- у Миши х + 8 конфет
Сравним, на сколько конфет у Миши стало больше, чем у Пети:
8 + 8 = 16 (конфет) — у Миши больше, чем у Пети.
Ответ: на 16 конфет.
Упражнения
281. Как можно обозначить угол, изображённый на рисунке 73?
Данный угол можно обозначить как: ∠K, ∠MKN, ∠NKM.
282. На каком из рисунков 74, а, б, в луч ОК является биссектрисой угла АОВ?
Луч ОК является биссектрисой угла АОВ на рисунке 74 б.
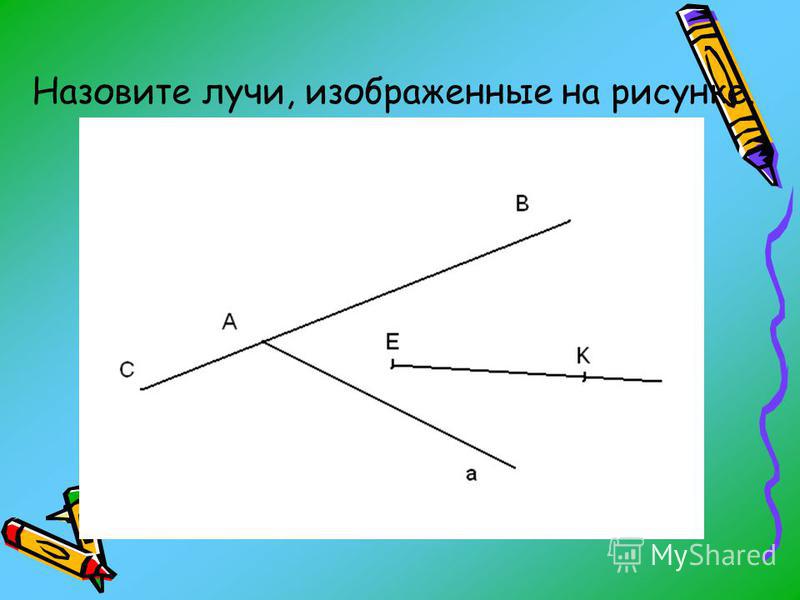
283. Назовите все углы, изображённые на рисунке 75.
На рисунке изображено 3 угла:
- ∠BAE (можно обозначить как ∠EAB)
- ∠EAM (можно обозначить как ∠MAE)
- ∠BAM (можно обозначить как ∠MAB)
284. Запишите все углы, изображённые на рисунке 76.
На рисунке изображено 3 угла:
- ∠OTC (можно обозначить как ∠CTO)
- ∠CTF (можно обозначить как ∠FTC)
- ∠OTF (можно обозначить как ∠FTO)
285. Какие из лучей, изображённых на рисунке 77, пересекают сторону угла ВОС?
Сторону угла ВОС пересекают лучи AK, ST.
286. Какие из лучей, изображённых на рисунке 78, пересекают сторону угла ВОС?
Сторону угла ВОС пересекают лучи RP, FE.
287. Начертите ∠MNE и проведите лучи NA и NC между его сторонами. Запишите все образовавшиеся углы.
На рисунке образовалось 6 углов:
- ∠MNA (можно обозначить как ANM)
- ∠MNC (можно обозначить как CNM)
- ∠MNE (можно обозначить как ENM)
- ∠ANC (можно обозначить как CNA)
- ∠ANE (можно обозначить как ENA)
- ∠CNE (можно обозначить как ENC)
288.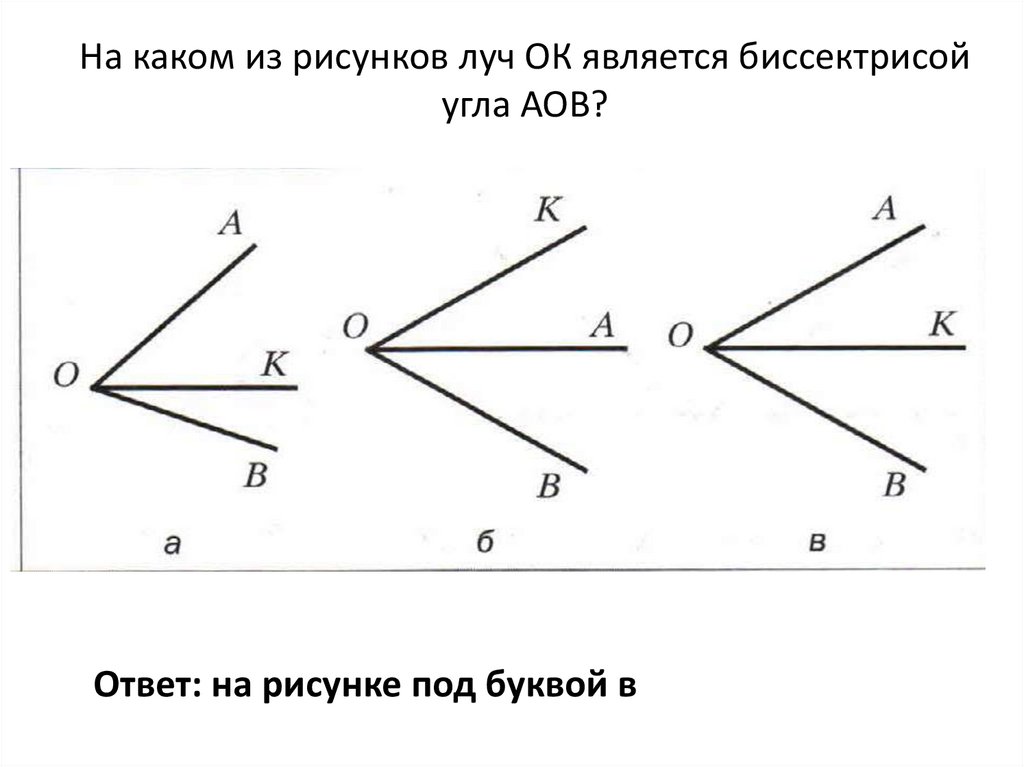
На рисунке изображены следующие равные углы:
- ∠ABE = ∠СВF или ∠EBA = ∠FBC
- ∠ABF = ∠CBE или ∠FBA = ∠EBC
289. На рисунке 80 ∠AOB = ∠DOE, ∠BOC = ∠COD. Есть ли ещё на этом рисунке равные углы?
На рисунке изображены следующие равные углы:
- ∠AOB = ∠DOE или ∠BOA = ∠EOD
- ∠BOC = ∠COD или ∠COB = ∠DOC
- ∠AOC = ∠EOC или ∠COA = ∠COE
- ∠AOD = ∠EOB или ∠DOA = ∠BOE
290. На рисунке 81 углы FOK и МОЕ равны. Какие ещё углы, изображённые на этом рисунке, равны?
На рисунке изображены следующие равные углы:
- ∠FOK = ∠MOE или ∠KOF = ∠EOM
- ∠FOM = ∠EOK или ∠MOF = ∠KOE
Упражнения для повторения
291. Составьте числовое выражение и найдите его значение:
- произведение суммы чисел 18 и 20 и числа 8: (18 + 20) • 8 = 38 • 8 = 304
- частное от деления разности чисел 128 и 29 на число 11: (128 — 29) : 11 = 99 : 11 = 9
- частное от деления произведения чисел 15 и 6 на их разность: (15 • 6) : (15 — 6) = 90 : 9 = 10
292. Решите уравнение:
Решите уравнение:
293. На ХХП зимних Олимпийских играх, состоявшихся в 2014 г. в городе Сочи, олимпийская сборная России завоевала 33 медали. Наши спортсмены получили 24 золотых и серебряных медали, а золотых и бронзовых — 22. Сколько медалей каждого вида завоевала на этой Олимпиаде наша сборная?
1) 33 — 22 = 11 (шт.) — медалей — серебряные.
2) 24 — 11 = 13 (шт.) — медалей — золотые.
3) 22 — 13 = 9 (шт.) — медалей — бронзовые.
Ответ: 13 золотых медалей, 11 серебряных медалей и 9 бронзовых медалей.
294. Учащиеся пятых классов ехали на двух автобусах на экскурсию. Когда из одного автобуса, в котором было 42 учащихся, восемь учащихся перешли во второй автобус, то в обоих автобусах учащихся стало поровну. Сколько учащихся было во втором автобусе сначала?
Пусть во втором автобусе сначала было х учащихся. Тогда, после того перешло 8 учащихся из первого автобуса, во втором автобусе стало (х + 8) учащихся.
Мы знаем, что в первом автобусе сначала было 42 учащихся, а после перехода осталось (42 — 8) учащихся — столько же, сколько стало во втором автобусе после перехода.
Составим уравнение:
х + 8 = 42 — 8
х + 8 = 34
х = 34 — 8
х = 26
Значит сначала в первом автобусе было 26 учащихся.
Ответ: 26 учащихся.
Задача от мудрой совы
295. На озере начали распускаться кувшинки. Каждый день количество кувшинок возрастало вдвое. На двадцатый день кувшинками заросла вся поверхность озера. На какой день половина озера была покрыта кувшинками?
Мы знаем, что каждый день количество кувшинок становилось вдвое больше (удваивалось), значит в предыдущий день в озере была половина кувшинок, но сравнению в последующим днём. То есть если на 20-й день озеро полностью заросло кувшинками, то половина от этого числа была в предыдущий день — 19-й.
Ответ: на 19- день.
- Ответы к учебнику для 5 класса.
А. Г. Мерзляк
- Переход на главную страницу сайта
Учебник по физике: Диаграммы лучей — Вогнутые зеркала
Темой этого раздела было то, что мы видим объект, потому что свет от объекта попадает в наши глаза, когда мы смотрим на объект вдоль линии. Точно так же мы видим изображение объекта, потому что свет от объекта отражается от зеркала и попадает в наши глаза, когда мы смотрим на изображение объекта. Исходя из этих двух основных предпосылок, мы определили положение изображения как место в пространстве, от которого исходит свет. Лучевые диаграммы были ценным инструментом для определения пути света от объекта к зеркалу и к нашим глазам. В этом разделе урока 3 мы исследуем метод рисования диаграмм лучей для объектов, расположенных в разных местах перед вогнутым зеркалом.
Чтобы нарисовать эти диаграммы, нам придется вспомнить два правила отражения для вогнутых зеркал:
- Любой падающий луч, идущий параллельно главной оси на пути к зеркалу, при отражении пройдет через точку фокуса.

- Любой падающий луч, проходящий через фокальную точку на пути к зеркалу, после отражения будет двигаться параллельно главной оси.
Ранее в этом уроке была показана следующая диаграмма, иллюстрирующая путь света от объекта к зеркалу и к глазу.
На этой диаграмме изображены пять падающих лучей и соответствующие им отраженные лучи. Каждый луч пересекается в месте изображения, а затем расходится к глазу наблюдателя. Каждый наблюдатель будет наблюдать одно и то же место на изображении, и каждый световой луч будет подчиняться закону отражения. Тем не менее, для определения местоположения изображения потребуются только два из этих лучей, поскольку для нахождения точки пересечения требуется только два луча. Из пяти нарисованных падающих лучей два соответствуют падающим лучам, описанным нашими двумя правилами отражения для вогнутых зеркал. Поскольку это самая простая и предсказуемая пара лучей для рисования, именно эти два луча будут использоваться в оставшейся части этого урока.
Пошаговый метод построения лучевых диаграмм
Ниже описан метод построения лучевых диаграмм для вогнутого зеркала. Метод применяется к задаче рисования диаграммы луча для объекта, расположенного на за центром кривизны (С) вогнутого зеркала. Тем не менее, тот же метод работает для рисования диаграммы лучей для любого местоположения объекта.
1. Выберите точку в верхней части объекта и нарисуйте два падающих луча, идущих к зеркалу.
Используя линейку, точно нарисуйте один луч так, чтобы он проходил точно через точку фокуса на пути к зеркалу. Нарисуйте второй луч так, чтобы он шел точно параллельно главной оси. Поместите наконечники стрел на лучи, чтобы указать направление их движения.
2. Как только эти падающие лучи попадут на зеркало, отразите их в соответствии с двумя правилами отражения для вогнутых зеркал.
Луч, проходящий через фокальную точку на пути к зеркалу, отразится и пойдет параллельно главной оси.Используйте линейку, чтобы точно нарисовать его путь. Луч, который шел параллельно главной оси на пути к зеркалу, отразится и пройдет через фокальную точку. Поместите наконечники стрел на лучи, чтобы указать направление их движения. Продлите лучи за точку их пересечения.
3. Отметьте изображение верхней части объекта.
Точка изображения верхней части объекта — это точка пересечения двух отраженных лучей. Если бы вы провели третью пару падающих и отраженных лучей, то через эту точку прошел бы и третий отраженный луч. Это просто точка, в которой весь свет от вершины объекта будет пересекаться при отражении от зеркала. Конечно, остальная часть объекта тоже имеет изображение, и его можно найти, применив те же три шага к другой выбранной точке. (См. примечание ниже.)
4. Повторите процесс для нижней части объекта.
Целью лучевой диаграммы является определение местоположения, размера, ориентации и типа изображения, формируемого вогнутым зеркалом.Как правило, для этого требуется определить, где находится изображение верхнего и нижнего пределов объекта, а затем отследить все изображение. После выполнения первых трех шагов было найдено только положение изображения верхнего экстремума объекта. Таким образом, процесс необходимо повторить для точки на дне объекта. Если низ предмета лежит на главной оси (как в этом примере), то изображение этой точки также будет лежать на главной оси и находиться на том же расстоянии от зеркала, что и изображение верха предмета. . На этом этапе можно заполнить все изображение.
Некоторым учащимся трудно понять, как можно вывести все изображение объекта после определения одной точки на изображении. Если объект выровнен по вертикали (например, объект со стрелкой, используемый в приведенном ниже примере), то процесс прост. Изображение представляет собой просто вертикальную линию. Теоретически необходимо выбрать каждую точку на объекте и нарисовать отдельную лучевую диаграмму, чтобы определить положение изображения этой точки. Для этого потребуется много диаграмм лучей, как показано ниже.
Для этого потребуется много диаграмм лучей, как показано ниже.
К счастью, ярлык существует. Если объект представляет собой вертикальную линию, то изображение также является вертикальной линией. Для наших целей мы будем иметь дело только с более простыми ситуациями, в которых объект представляет собой вертикальную линию, нижняя часть которой расположена на главной оси. Для таких упрощенных ситуаций изображение представляет собой вертикальную линию с нижним концом, расположенным на главной оси.
Приведенная выше лучевая диаграмма показывает, что когда объект находится в позиции за центром кривизны, изображение расположено в положении между центром кривизны и фокальной точкой. Кроме того, изображение перевернуто, уменьшено в размере (меньше объекта) и реально. Это тип информации, которую мы хотим получить из лучевой диаграммы. Эти характеристики изображения будут более подробно обсуждаться в следующем разделе Урока 3.
После того, как метод рисования диаграмм лучей будет отработан пару раз, он станет таким же естественным, как дыхание. Каждая диаграмма дает определенную информацию об изображении. На двух приведенных ниже диаграммах показано, как определить местоположение, размер, ориентацию и тип изображения для ситуаций, когда объект расположен в центре кривизны и когда объект расположен между центром кривизны и фокальной точкой.
Каждая диаграмма дает определенную информацию об изображении. На двух приведенных ниже диаграммах показано, как определить местоположение, размер, ориентацию и тип изображения для ситуаций, когда объект расположен в центре кривизны и когда объект расположен между центром кривизны и фокальной точкой.
Следует отметить, что процесс построения лучевой диаграммы одинаков вне зависимости от того, где находится объект. Хотя результат диаграммы лучей (расположение изображения, размер, ориентация и тип) отличается, одни и те же два луча всегда рисуются . Два правила отражения применяются для определения места, где все отраженные лучи расходятся (что для реальных изображений также является местом пересечения отраженных лучей).
В трех вышеописанных случаях — когда объект находится за точкой С, когда объект находится в точке С и когда объект находится между С и F — световые лучи сходятся в точку после отражаясь от зеркала. В таких случаях формируется действительное изображение . Как обсуждалось ранее, реальное изображение формируется всякий раз, когда отраженный свет проходит через место изображения. В то время как плоские зеркала всегда создают мнимые изображения, вогнутые зеркала способны создавать как реальные, так и мнимые изображения. Как показано выше, реальные изображения получаются, когда объект находится на расстоянии, превышающем одно фокусное расстояние от зеркала. А мнимое изображение формируется, если объект расположен менее чем на одно фокусное расстояние от вогнутого зеркала. Чтобы понять, почему это так, можно использовать лучевую диаграмму.
В таких случаях формируется действительное изображение . Как обсуждалось ранее, реальное изображение формируется всякий раз, когда отраженный свет проходит через место изображения. В то время как плоские зеркала всегда создают мнимые изображения, вогнутые зеркала способны создавать как реальные, так и мнимые изображения. Как показано выше, реальные изображения получаются, когда объект находится на расстоянии, превышающем одно фокусное расстояние от зеркала. А мнимое изображение формируется, если объект расположен менее чем на одно фокусное расстояние от вогнутого зеркала. Чтобы понять, почему это так, можно использовать лучевую диаграмму.
Смотри! Преподаватель физики обсуждает природу реального изображения, используя демонстрацию физики phun. Лучевая диаграмма для формирования виртуального изображения
Лучевая диаграмма для случая, в котором находится объект перед фокус показан на диаграмме справа.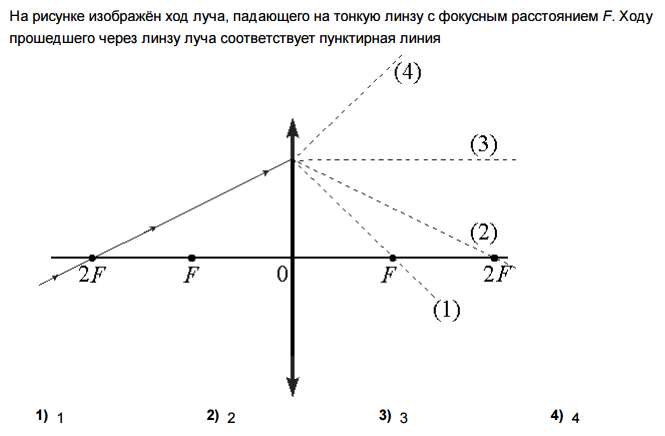 Обратите внимание, что в этом случае световые лучи после отражения от зеркала расходятся. Когда световые лучи расходятся после отражения, формируется мнимое изображение. Как и в случае с плоскими зеркалами, местоположение изображения можно найти, проследив все отраженные лучи назад, пока они не пересекутся. Каждому наблюдателю казалось бы, что отраженные лучи расходятся от этой точки. Таким образом, точка пересечения протяженных отраженных лучей является точкой изображения. Поскольку свет на самом деле не проходит через эту точку (свет никогда не проходит за зеркалом), изображение называется виртуальным изображением. Обратите внимание, что когда объект находится в положении перед фокальной точкой , его изображение прямое и увеличенное, расположенное по другую сторону зеркала. На самом деле одно обобщение, которое можно сделать обо всех виртуальных изображениях, создаваемых зеркалами (как плоскими, так и криволинейными), состоит в том, что они всегда вертикальны и всегда расположены по другую сторону зеркала.
Обратите внимание, что в этом случае световые лучи после отражения от зеркала расходятся. Когда световые лучи расходятся после отражения, формируется мнимое изображение. Как и в случае с плоскими зеркалами, местоположение изображения можно найти, проследив все отраженные лучи назад, пока они не пересекутся. Каждому наблюдателю казалось бы, что отраженные лучи расходятся от этой точки. Таким образом, точка пересечения протяженных отраженных лучей является точкой изображения. Поскольку свет на самом деле не проходит через эту точку (свет никогда не проходит за зеркалом), изображение называется виртуальным изображением. Обратите внимание, что когда объект находится в положении перед фокальной точкой , его изображение прямое и увеличенное, расположенное по другую сторону зеркала. На самом деле одно обобщение, которое можно сделать обо всех виртуальных изображениях, создаваемых зеркалами (как плоскими, так и криволинейными), состоит в том, что они всегда вертикальны и всегда расположены по другую сторону зеркала.
До сих пор мы видели на диаграммах лучей, что реальное изображение создается, когда объект расположен на расстоянии более одного фокусного расстояния от вогнутого зеркала; а мнимое изображение формируется, когда объект находится на расстоянии менее одного фокусного расстояния от вогнутого зеркала (т. е. перед F ). Но что происходит, когда объект находится в точке F? То есть какой тип изображения образуется, когда предмет находится ровно в одном фокусном расстоянии от вогнутого зеркала? Конечно, лучевая диаграмма всегда является одним из инструментов, помогающих найти ответ на такой вопрос. Однако, когда для этого случая используется лучевая диаграмма, возникает немедленная трудность. Падающий луч, начинающийся с верхнего края объекта и проходящий через фокальную точку, не достигает зеркала. Таким образом, для определения точки пересечения всех отраженных лучей необходимо использовать другой падающий луч. Любой падающий луч света будет работать, пока он встречается с зеркалом. Вспомним, что единственная причина, по которой мы использовали две имеющиеся у нас, заключается в том, что их удобно и легко рисовать. На приведенной ниже диаграмме показаны два падающих луча и соответствующие им отраженные лучи.
Любой падающий луч света будет работать, пока он встречается с зеркалом. Вспомним, что единственная причина, по которой мы использовали две имеющиеся у нас, заключается в том, что их удобно и легко рисовать. На приведенной ниже диаграмме показаны два падающих луча и соответствующие им отраженные лучи.
В случае объекта, находящегося в фокусе (F), световые лучи не сходятся и не расходятся после отражения от зеркала. Как показано на диаграмме выше, отраженные лучи движутся параллельно друг другу. Впоследствии световые лучи не будут сходиться на стороне зеркала объекта, чтобы сформировать реальное изображение; они также не могут быть расширены назад на противоположной стороне зеркала, чтобы пересечься и сформировать мнимое изображение. Так как же следует интерпретировать результаты лучевой диаграммы? Ответ: изображения нет!! Удивительно, но когда объект находится в фокусе, в пространстве нет точки, в которой наблюдатель мог бы видеть, из которой все отраженные лучи кажутся расходящимися.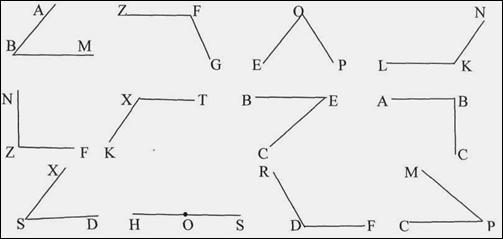 Изображение не формируется, когда предмет находится в фокусе вогнутого зеркала.
Изображение не формируется, когда предмет находится в фокусе вогнутого зеркала.
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения Optics Bench или нашего интерактивного приложения Name That Image. Вы можете найти это в разделе Physics Interactives на нашем сайте. Интерактивная скамья Optics Bench предоставляет учащимся интерактивную среду для изучения формирования изображений линзами и зеркалами. Интерактивное приложение Name That Image Interactive предлагает учащимся интенсивную умственную тренировку по распознаванию характеристик изображения для любого заданного местоположения объекта перед изогнутым зеркалом.
Посетите: Интерактивная скамья Optics Bench || Назовите это изображение Interactive
На приведенном ниже рисунке показаны два световых луча, исходящих из верхней части объекта и падающих на зеркало. Опишите, как можно нарисовать отраженные лучи для этих световых лучей, фактически не используя транспортир и закон отражения.
Следующий раздел:
Перейти к следующему уроку:
Лучи, показанные на рисунке, считаем параксиальными. Изображение виртуального точечного объекта O, образованного линзой LL, равно
CENGAGE PHYSICS-GEOMETRICAL OPTICS-Single Correct
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro and dekho sari videos bina kisi ad ki рукаават ке!
Обновлено на: 27-06-2022
Текстовое решение
A
Виртуальный
C
Расположен ниже Основной оси
D
Расположенный слева от Lens
. правильный ответ а., в., г.
правильный ответ а., в., г.
Решение
Ответ
Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.
Похожие видео
Изображение I формируется точечным объектом O с помощью линзы, оптическая ось которой AB, как показано на рисунке. а) Укажите, выпуклая это линза или вогнутая? б) Нарисуйте лучевую диаграмму, чтобы определить местонахождение линзы и ее фокуса.
10968399
Текст Решение
Объект помещен перед вогнутой линзой. Мнимое изображение предмета формируется с той же стороны линзы, что и предмет, но ближе к линзе. Будут ли лучи, формирующие это изображение, снова преломляться на линзе, образуя второе изображение?
11311373
выпуклая линза формирует мнимое изображение предмета. Каково положение объекта?
12014184
किसी लेन्स में आभासी प्रतिबिम्ब वस्तु के स्ष लेन्स के ओ ओर बनता है?
94980557
Выпуклая линза формирует мнимое изображение предмета, помещенного ………… .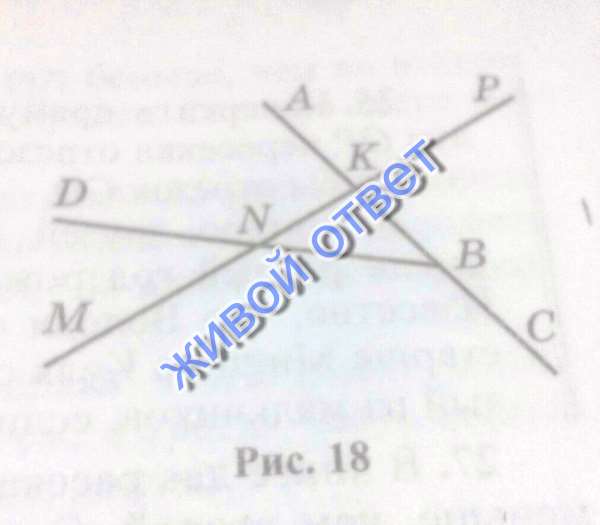
96609425
Линза, формирующая реальное или мнимое изображение в зависимости от положения объекта.
96609713
Выпуклая линза формирует мнимое изображение предмета, помещенного…….. .
116057086
Текст Решение
Выпуклая линза формирует мнимое изображение предмета, расположенного ………….
119555370
Выпуклая линза формирует мнимое изображение предмета, помещенного ………… .
119573656
Выпуклая линза формирует мнимое изображение, если объект _______
203454354
Рассмотрим расположение тонких линз, как показано на рисунке. Объект O находится на расстоянии mR от системы тонких линз. От линзовой системы на неизвестном расстоянии расположено плоское зеркало, так как показано, при каком значении m изображение О и предмета О будут совпадать друг с другом. Считаем приближение параксиальных лучей справедливым.
204300627
Выпуклая линза формирует мнимое изображение предмета. Каково положение объекта?
642692221
Изображение I формируется точечным объектом O с помощью линзы, оптическая ось которой AB, как показано на рисунке.

 А. Г. Мерзляк
А. Г. Мерзляк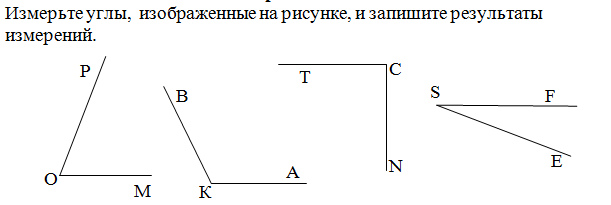
 Используйте линейку, чтобы точно нарисовать его путь. Луч, который шел параллельно главной оси на пути к зеркалу, отразится и пройдет через фокальную точку. Поместите наконечники стрел на лучи, чтобы указать направление их движения. Продлите лучи за точку их пересечения.
Используйте линейку, чтобы точно нарисовать его путь. Луч, который шел параллельно главной оси на пути к зеркалу, отразится и пройдет через фокальную точку. Поместите наконечники стрел на лучи, чтобы указать направление их движения. Продлите лучи за точку их пересечения. Как правило, для этого требуется определить, где находится изображение верхнего и нижнего пределов объекта, а затем отследить все изображение. После выполнения первых трех шагов было найдено только положение изображения верхнего экстремума объекта. Таким образом, процесс необходимо повторить для точки на дне объекта. Если низ предмета лежит на главной оси (как в этом примере), то изображение этой точки также будет лежать на главной оси и находиться на том же расстоянии от зеркала, что и изображение верха предмета. . На этом этапе можно заполнить все изображение.
Как правило, для этого требуется определить, где находится изображение верхнего и нижнего пределов объекта, а затем отследить все изображение. После выполнения первых трех шагов было найдено только положение изображения верхнего экстремума объекта. Таким образом, процесс необходимо повторить для точки на дне объекта. Если низ предмета лежит на главной оси (как в этом примере), то изображение этой точки также будет лежать на главной оси и находиться на том же расстоянии от зеркала, что и изображение верха предмета. . На этом этапе можно заполнить все изображение.
Leave A Comment