Какая точка лежит на прямой проходящей через точки: Уравнение прямой

Уравнение прямой

Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x + B y + C = 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = k x + b

где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

k = tg φ

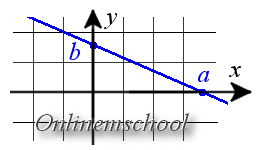
Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки M(x₁, y₁) и N(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂, то уравнение прямой можно найти, используя следующую формулу

x — x1	=	y — y1
x2 — x1		y2 — y1

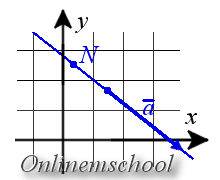
Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x₀y = m t + y₀

где N(x₀, y₀) — координаты точки лежащей на прямой, a = {l, m} — координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки N(x₀, y₀) лежащей на прямой и направляющего вектора a = {l; m} (l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Пример 1. Найти уравнение прямой проходящей через две точки M(1, 7) и N(2, 3).

Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки

x — 12 — 1 = y — 73 — 7

Упростив это уравнение получим

каноническое уравнение прямой

x — 11 = y — 7-4

Выразим y через x и получим уравнение прямой с угловым коэффициентом

y — 7 = -4(x — 1)

y = -4x + 11

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 — 1; 3 — 7} = {1; -4}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = -4t + 7

Пример 2. Найти уравнение прямой проходящей через две точки M(1, 3) и N(2, 3).

Решение. Так как M_y — N_y = 0, то невозможно записать уравнение прямой проходящей через две точки.

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 — 1; 3 — 3} = {1; 0}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = 3

Уравнение прямой в пространстве

Уравнение прямой, проходящей через две различные точки в пространстве

Если прямая проходит через две точки M(x₁, y₁, z₁) и N(x₂, y₂, z₂), такие что x₁ ≠ x₂, y₁ ≠ y₂ и z₁ ≠ z₂, то уравнение прямой можно найти используя следующую формулу

x — x1	=	y — y1	=	z — z1
x2 — x1		y2 — y1		z2 — z1

Параметрическое уравнение прямой в пространстве

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t + x0
	y = m t + y0
	z = n t + z0

где (x₀, y₀, z₀) — координаты точки лежащей на прямой, {l; m; n} — координаты направляющего вектора прямой.

Каноническое уравнение прямой в пространстве

Если известны координаты точки M(x₀, y₀, z₀) лежащей на прямой и направляющего вектора n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x — x0	=	y — y0	=	z — z0
l		m		n

Прямая как линия пересечения двух плоскостей

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

	A1x + B1y + C1z + D1 = 0
	A2x + B2y + C2z + D2 = 0

при условии, что не имеет место равенство

A1	=	B1	=	C1	.
A2		B2		C2

Аналитическая геометрия в пространстве (Лекция №19)

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

Под углом

между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

Условие параллельности двух плоскостей.

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

1. Составить уравнение плоскости, проходящей через точку

   M(-2; 1; 4) параллельно плоскости 3x+2y-7z+8=0.

   Уравнение плоскости будем искать в виде Ax+By+Cz+D=0. Из условия параллельности плоскостей следует, что: . Поэтому можно положить A=3, B=2, C=-7. Поэтому уравнение плоскости принимает вид3x+2y-7z+D=0.

   Кроме того, так какMÎ α, то-6+2-28+D=0, D=32.

   Итак, искомое уравнение 3x+2y-7z+32=0.

2. Составить уравнение плоскости, проходящей через точки M₁(1; 1; 1), M₂(0; 1; –1) перпендикулярно плоскости x+y+z=0.

   Так как M₁Î α, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0.

   Далее, так как M₂Î α, то подставив координаты точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0.

   Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0.

   Выразим коэффициенты Aи Bчерез C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0.

   Окончательно получаем -2x+y+z=0.

3. Составить уравнение плоскости, проходящей через точку M(-2; 3; 6) перпендикулярно плоскостям 2x+3y-2z-4=0 и 3x+5y+z=0.

   Так как MÎ α, то A(x+2)+B(x-3)+C(z-6)=0.

   По условию задачи , поэтому

   Итак уравнение плоскости принимает вид 13(

   x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М₁ и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М₁(x₁, y₁, z₁), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t, что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М₁ и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Пусть М₁(x₁, y₁, z₁) – точка, лежащая на прямой l, и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t. Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox. Тогда направляющий вектор прямой перпендикулярен Ox, следовательно, m=0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t, получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz.

Примеры.

1. Составить канонические и параметрические уравнения прямой, проходящей через точку М₁(1;0;-2) параллельно вектору .

   Канонические уравнения: .

   Параметрические уравнения:

2. Составить уравнения прямой, проходящей через две точки М₁(-2;1;3), М₂(-1;3;0).

   Составим канонические уравнения прямой. Для этого найдем направляющий вектор . Тогда l: .

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z= 0:

Решив эту систему, найдем точку M₁(1;2;0).

Аналогично, полагая y= 0, получим точку пересечения прямой с плоскостью xOz:

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М₁ на прямой и направляющий вектор прямой.

Координаты точки М₁ получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y= 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l: .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

.

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l₁ параллельна l₂ тогда и только тогда, когда параллелен .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Примеры.

1. Найти угол между прямыми и .

2. Найти уравнения прямой проходящей через точку М₁(1;2;3) параллельно прямой l₁:

   Поскольку искомая прямая l параллельна l₁, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l₁.

3. Составить уравнения прямой, проходящей через точку М₁(-4;0;2) и перпендикулярной прямым: и .

   Направляющий вектор прямой l можно найти как векторное произведение векторов и :

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Рассмотрим векторы и . Если угол между ними острый, то он будет , где φ – угол между прямой и плоскостью. Тогда .

Если угол между векторами и тупой, то он равен . Следовательно . Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим .

Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. .

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.

Примеры.

1. Написать уравнение плоскости, проходящей через точку М₁(2;-3;4) параллельно прямым и .

   Так как M₁Î α, то уравнение плоскости будем искать в виде

   .

   Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений

   Отсюда

   Итак, или .

2. Найти угол между прямой и плоскостью .

   Направляющий вектор прямой . Нормальный вектор плоскости . Следовательно,

3. Найдите точку, симметричную данной М(0;-3;-2) относительно прямой .

   Составим уравнение плоскости α перпендикулярной l. MÎ α, . Следовательно, или .

   Найдём точку пересечения прямой l и α:

   Итак, N(0.5;-0.5;0.5). Пусть искомая точка М₁ имеет координаты М₁(x,y,z). Тогда очевидно равенство векторов , т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5). Откуда x=1, y=2, z=3 или М₁(1;2;3)..

Точка пересечения прямой и плоскости онлайн

С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Точка пересечения прямой и плоскости − теория, примеры и решения

1. Точка пересечения плоскости и прямой, заданной в каноническом виде

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L₁:

,

(1)

и плоскость α:

где M₁(x₁, y₁, z₁) − точка, лежащая на прямой L₁, q₁={m₁, p₁, l₁} − направляющий вектор прямой L₁, а n={A,B,C} − нормальный вектор плоскости α.

Найти точку пересечения прямой L₁ и плоскости α (Рис.1).

Запишем уравнение (1) в виде системы двух линейных уравнений:

Сделаем перекрестное умножение в уравнениях (3) и (4):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:

Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L₁ и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L₁ лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L₁ и плоскости α.

Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же

2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L₁ в параметрическом виде:

и плоскость α:

где M₁(x₁, y₁, z₁) − точка, лежащая на прямой L₁, q₁={m₁, p₁, l₁} − направляющий вектор прямой L₁, а n={A,B,C} − нормальный вектор плоскости α.

Задачу нахождения нахождения точки пересечения прямых L₁ и плоскости α можно решить разными методами.

Метод 1. Приведем уравнения прямой L₁ к каноническому виду.

Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:

Так как левые части уравнений (10) равны, то можем записать:

Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.

Метод 2. Для нахождения точки пересечения прямой L₁ и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):

Откроем скобки и найдем t:

Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L₁ лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.

Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L₁ и плоскости α подставим полученное значение t из (14) в (8).

3. Примеры нахождения точки пересечения прямой и плоскости.

Пример 1. Найти точку пересечения прямой L₁:

и плоскости α:

Представим уравнение (15) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (17) и (18):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Упростим:

Для нахождения точки пересечения прямой L₁ и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):

Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:

Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:

Второй этап. Обратный ход Гаусса.

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Запишем решение:

Ответ. Точка пересечения прямой L₁ и плоскости α имеет следующие координаты:

Пример 2. Найти точку пересечения прямой L₁:

и плоскости α:

Представим уравнение (22) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (24) и (25):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Упростим:

Для нахождения точки пересечения прямой L₁ и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):

Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:

Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:

Из расширенной матрицы восстановим систему линейных уравнений:

Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L₁ и плоскость α не пересекаются, т.е. они параллельны.

Ответ. Прямая L₁ и плоскость α параллельны, т.е. не имеют общую точку.

Пример 3. Найти точку пересечения прямой в параметрическом виде L₁:

и плоскости α:

Решение. Для нахождения точки пересечения прямой L₁ и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):

Откроем скобки:

Упростив уравнение, получим:

Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L₁ удовлетворяет уравнению плоскости α. Следовательно прямая L₁ лежит на плоскости α.

Ответ. Прямая L₁ лежит на плоскости α.

Уравнение прямой на плоскости. Примеры решения типовых задач. Часть 2

Задача № 1. При каких значениях m и n прямая (m-3n-2)x+(2m+4n-1)y-3m+n-2=0 отсекает на оси Ox отрезок, равный 3 ед. масштаба, а на оси Oy отрезок, равный (-2).
Задача № 2. Через точку М (2;-1) провести прямую параллельно прямой 2x+3y=0.
Решение. Угловой коэффициент искомой прямой согласно условию параллельности должен быть равным угловому коэффициенту данной прямой: y=-2/3, k=-2/3.

Рис.1

Составим уравнение искомой прямой по формуле: y-y₁= k(x—x₁)
у+1=-2/3(х—2), Зу+3=—2х+4, 2х+3у—1=0.
Эту задачу можно решать и так.
Так как искомая прямая должна быть параллельна данной прямой, то A/2=B/3, или A:В=2:3.
Уравнение прямой будем искать в виде: 2х+Зy+С=0. С определим из условия, что прямая проходит через точку М (2; —1): 2·2+3·(-1)+c=0, c=3-4=-1, с=-1.
Следовательно, уравнение прямой будет 2х+3у-1=0.
Ответ: 2х+3у-1=0.
Решения этих двух задач подробно объясняются в следующем видео:

Задача № 3. Составить уравнения сторон треугольника, для которого точки А(—1; 2), В(3;-1) и С(0; 4) являются серединами сторон.
Решение этой задачи подробно изложено в следующем видео

Задача № 4.По какой линии должна двигаться точка, начальное положение которой определено координатами (3; 8), чтобы кратчайшим путем дойти до прямой х—2у — 2 = 0? В какой точке она достигнет этой прямой и как велик будет пройденный путь?
Решение этой задачи подробно изложено в следующем видео

Задача № 5. Точка М (-4; 5) является вершиной квадрата, диагональ которого лежит на прямой 7x-y+8=0. Составить уравнения сторон и второй диагонали этого квадрата.
Решение этой задачи подробно изложено в следующем видео

Задача № 6.

Алгоритм

— Как проверить, лежит ли точка на линии между двумя другими точками

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

,

java — поиск максимального количества точек, лежащих на одной прямой в двухмерной плоскости

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

Загрузка…

2. Авторизоваться зарегистрироваться

.

Как найти уравнение прямой, которая проходит через точку пересечения прямых 7x — 3y — 19 = 0 и 3x + 2y + 5 = 0, при условии, что прямая параллельна прямой с уравнением y = 2x +1?

Геометрия

Наука

• Анатомия и физиология
• астрономия
• астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия
• физика

математический

• Алгебра
• Исчисление
• Геометрия
• Prealgebra
• тригонометрия и алгебра
• Статистика

.