Зависимость плотности от температуры
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого числа.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Правда, вода является исключением из этого правила, её плотность при затвердевании уменьшается.
Отношение П. двух веществ при определённых стандартных физических условиях называется относительной П.: для жидких и твёрдых веществ она обычно определяется по отношению к П. дистиллированной воды при 4 °С, для газов — по отношению к П. сухого воздуха или водорода принормальных условиях.
Единицей П. в СИ является кг/м3, в СГС системе единиц г/см3. На практике пользуются также внесистемными единицами П.: г/л, т/м3 и др.
Для
измерения П. веществ
применяют плотномеры, пикнометры, ареометры,
гидростатическое взвешивание (см. Мора
весы).
Др. методы определения П. основаны на
связи П. с параметрами состояния вещества
или с зависимостью протекающих в веществе
процессов от его П. Так, плотность идеального
газа может
быть вычислена по уравнению
состояния r
= pm/RT,
где р
—давление газа, m — его молекулярная
масса (мольная
масса), R — газовая
постоянная
Диапазон значений П. природных тел и сред исключительно широк. Так, П. межзвёздной среды не превышает 10-21кг/м3, средняя П. Солнца составляет 1410 кг/м3, Земли — 5520 кг/м3,наибольшая П. металлов — 22 500 кг/м3(осмий), П. вещества атомных ядер — 1017кг/м3, наконец, П. нейтронных звёзд может, по-видимому, достигать 1020
Манометр — это механический измерительный прибор, конструктивно представляющий собой стальной или пластиковый циферблат с пружиной в виде трубки, предназначенный для измерения давления жидких и газообразных веществ.
В механических манометрах измеряемое давление с помощью чувствительного элемента преобразуется в механическое перемещение, вызывающее механическое отклонение стрелок или других деталей механизмов отсчета, записи результата измерений, а также устройств сигнализации и стабилизации давлений в системах контролируемого объекта. В качестве чувствительных элементов механических манометров применяются трубчатые пружины, гармониковые (сильфонные) и плоские мембраны и другие измерительные механизмы, в которых под действием давления вызываются упругие деформации или упругости специальных пружин.
По точности все механические манометры делятся на: технические, контрольные и образцовые. Технические манометры имеют классы точности 1,5; 2,5; 4; контрольные 0,5; 1,0; образцовые 0,16; 0,45.
Манометрические трубчатые пружины представляют собой пустотелые трубки овального или иного сечения, изогнутые по дуге окружности, по винтовой или спиральной линиям и имеющие один или несколько витков. В обычной конструкции, которая наиболее часто применяется на практике, используются одновитковые пружины. Принципиальная и структурная схемы манометра с одновитковой трубчатой пружиной представлены на рис.2.
Рис.2. Механический манометр и его характеристики
К штуцеру 1 припаян конец манометрической пружины 5. Второй запаянный конец К шарнирно связан тягой 3 с рычагом зубчатого сектора 4. Зубья сектора сцеплены с ведомым зубчатым колесом 6, которое насажено на ось 7 стрелки 9. Для устранения колебаний стрелки из-за зазоров между зубьями зубчатой передачи применяют спиральную пружину 2, концы которой связаны с корпусом и осью 7. Под стрелкой находится неподвижная шкала.
Под действием разности давлений внутри и снаружитрубчатая пружина меняет форму своего сечения, в результате чего ее запаянный конецК перемещается пропорционально действующей разности давлений .
Структурная схема механического манометра (рис.2,б) состоит из трех линейных звеньев I, II, III, статические характеристики которых представлены графиками ,и, где– перемещение свободного конца трубчатой пружины,– начальный центральный угол трубчатой пружины. Благодаря линейности всех звеньев общая статическая характеристикаманометра линейна и шкала равномерна. Входной величиной звенаI является измеряемое давление , а выходной – перемещениесвободного (запаянного) конца манометрической пружины5. Тяга 3 с рычагом зубчатого сектора 4 образует второе звено. Входной величиной звена II является , а выходной – угловое отклонение конца манометрической пружины. Входной величиной звенаIII (звено III — это зубчатый сектор, сцепленный с ведомым зубчатым колесом 6) служит угловое отклонение , а выходной – угловое отклонение стрелки9 от нулевой отметки шкалы 8.
Механические манометры применяют для измерений в области низкого вакуума. В деформационных манометрах упругий элемент, связанный с индикатором, прогибается под действием разницы измеряемого и эталонного давлений (атмосфера или высокий вакуум). В сильфонных промышленных манометрах серии ВС-7 измеряемое давление вызывает перемещение сильфона, передающееся самописцу. Эти приборы имеют линейную шкалу до 760 тор и точность показаний 1,6%.
Список использованной литературы:
studfiles.net
Зависимость плотности газа от температуры, стр.4
Зависимость плотности газа от температуры
Что происходит с плотностью некоторой массы газа, если температура повышается, а давление остается неизменным?
Вспомним, что плотность равна массе тела, деленной на объем. Так как масса газа постоянна, то при нагревании плотность газа уменьшается вот столько раз, во сколько увеличился объем.
Как мы знаем, объем газа прямо пропорционален абсолютной температуре, если давление остается постоянным. Следовательно,
(9)
Объединенный закон газового состояния
Мы рассматривали случаи, когда одна из трех величин, характеризующих состояние газа (давление, температура и объем), не изменяется. Мы видели, что если температура постоянна, то давление и объем связаны друг с другом законом Бойля— Мариотта; если объем постоянен, то давление и температура связаны законом Шарля; если постоянно давление, то объем и температура связаны законом Гей-Люссака. Установим связь между давлением, объемом и температурой некоторой массы газа, если
Пусть
начальные объем, давление и абсолютная
температура некоторой массы газа равны
V1,
P1 и
Т1, конечные — V2,
P2 и T2 — Можно представить себе, что переход
от начального к конечному состоянию
произошел в два этапа. Пусть, например,
сначала изменился объем газа от V1
до V2, причем температура Т1, осталась без изменения. Получившееся
при этом давление газа обозначим Pср..
Затем изменилась температура от Т
Закон Бойля — Мариотта
Р1V1t1
PcpV2T1
Закон Шарля
PcpV2T1
P2V2T2
Пименяя, к первому переходу закон Бойля-Мариотта запишем
или
Применяя ко второму переходу закон Шарля, можно написать
Перемножив эти равенства почленно и сокращая на Pcp получим:
(10)
Итак, произведение объема некоторой массы, газа на его давление пропорционально абсолютной температуре газа. Это и есть объединенный закон газового состояния или уравнение состояния газа.
Закон Дальтона
До сих пор мы говорили о давлении какого-нибудь одного газа — кислорода, водорода и т. п. Но в природе и в технике мы очень часто имеем дело со смесью нескольких газов. Самый важный пример этого — воздух, являющийся смесью азота, кислорода, аргона, углекислого газа и других газов. От чего зависит давление смеси газов?
Поместим в колбу кусок вещества, химически связывающего кислород из воздуха (например, фосфор), и быстро закроем колбу пробкой с трубкой. присоединенной к ртутному манометру. Через некоторое время весь кислород воздуха соединится с фосфором. Мы увидим, что манометр покажет меньшее давление, чем до удаления кислорода. Значит, присутствие кислорода в воздухе увеличивает его давление.
Точное исследование давления смеси газов было впервые произведено английским химиком Джоном Дальтоном (1766—1844) в 1809 г. Давление, которое имел бы каждый из газов, составляющих смесь, если бы удалить остальные газы из объема, занимаемого смесью, называют парциальным давлением этого газа. Дальтон нашел, что давление смеси газов равно сумме парциальных давлений их (закон Дальтона). Заметим, что к сильно сжатым газам закон Дальтона неприменим, так же как и закон Бойля — Мариотта.
Как истолковать закон Дальтона с точки зрения молекулярной теории, скажу немного далее.
Плотности газов
Плотность газа является одной из важнейших характеристик его свойств. Говоря о плотности газа, обычно имеют в виду его плотность при нормальных условиях (т. е. при температуре 0° С и давлении 760 мм рт. ст.). Кроме того, часто пользуются относительной плотностью газа, под которой подразумевают отношение плотности данного газа к плотности воздуха при тех же условиях. Легко видеть, что относительная плотность газа не зависит от условий, в которых он находится, так как согласно законам газового состояния объемы всех газов меняются при изменениях давления и температуры одинаково.
Плотности некоторых газов
Газ Плотность при нормальных условиях в г/л или в кг/м3Отношение к плотности воздуха Отношение к плотности водорода Молекулярный или атомный вес
Воздух 1,293
0,0899 1,25 1,43 1,977 0,179 1
0,0695 0,967 1.11 1,53 0,139 14,5
1 14 16 22 2 29 (средний)
Водород (Н2) 0,0899 0,0695 1 2
Азот (N2) 1,25 0,967 14 28
Кислород (О2) 1,43 1,11 16 32
Углекислый газ (СО2) 1,977 1,53 22 44
Гелий (Не) 0,179 0,139 2 4
Определение плотности газа можно осуществить так. Взвесим колбу с краном дважды: один раз откачав из нее по возможности полностью воздух, другой раз наполнив колбу исследуемым газом до давления, которое должно быть известно. Разделив разность весов на объем колбы, который надо определить предварительно, найдем плотность газа при данных условиях. Затем, пользуясь уравнением состояния газов, легко найдем плотность газа при нормальных условиях dн. Действительно, положим в формуле (10) Р2=Рн, V2=Vн, Т2=Тн и, умножив числитель и знаменатель
формулы на массу газа m, получим:
Отсюда, принимая во внимание,(m/v1)=d1, и (m/v)=dннаходим:
Результаты измерений плотности некоторых газов приведены в таблице выше.
Последние два столбца указывают на пропорциональность между плотностью газа и его молекулярным весом (в случае гелия — атомным весом).
topref.ru
Плотность газов и паров: таблица при различных температурах
Плотность газов и паров при нормальных условиях
В таблице приведена плотность газов и паров при нормальных условиях – температуре 0°С и нормальном атмосферном давлении (760 мм. рт. ст.). Для некоторых газов, например газа стибина, плотность дана при температуре 15°С и давлении 754 мм. рт. ст.
Значение плотности газов в таблице указано в размерности кг/м3 для следующих газов и паров: азот N2, аммиак NH3, аргон Ar, ацетилен C2H2, бор фтористый BF3, бутан C4H10, водород: бромистый HBr, йодистый HI, мышьяковистый H3As, селенистый H2Se, сернистый H2S, теллуристый H2Te, фосфористый H3P, хлористый HCl, воздух, гелий He, германия тетрагидрид GeH4, диметиламин (CH3)2NH, дифтордихлорметан CF2Cl2, дициан C2N2, закись азота N2O, кислород O2, кремний фтористый SiF4, гексагидрид Si2H6, тетрагидрид SiH4, криптон Kr, ксенон Xe, метан CH4, метиленхлорид CH3Cl, метиламин CH5N, метиловый эфир C2H6O, метилфторид CH3F, метилхлорид CH3Cl, мышьяк фтористый AsF5, неон Ne, нитрозил фтористый NOF и хлористый NOCl, озон O3, окись азота NO, пропан C3H8, пропилен C3H6, радон Rn, двуокись серы SO2 и гексафторид серы SF2, силан диметил SiH2(CH3)2, метил SiH3CH3, хлористый SIH3Cl, трифтористый SiHF3, стибин SbH3, сульфурил фтористый SO2F2, триметиламин (CH3)3N, триметилбор (CH3)3B, двуокись углерода CO2, окись углерода CO, сероокись COS, фосфор фтористый PF2, оксифторид POF3, пентафторид PF5, фтор F2, фторокись азота NO2, двуокись хлора ClO2, окись хлора Cl2O, хлорокись азота NO2Cl, этан C2H6, этилен C2H4, окись азота NO.
Плотность газов вычисляется, как отношение молярной массы газа к его молярному объему, который при 0°С и давлении 1 атм. равен 22,4 л/моль.
Следует отметить, что самым легким газом является водород — плотность этого газа при нормальных условиях равна 0,0899 кг/м3. Для удобства восприятия плотность газов приводят именно к плотности водорода, используя при этом относительную плотность по водороду. Например, относительная плотность газа азота N2 по водороду равна 13,9.
Наибольшую плотность имеет газ радон. Этот радиоактивный газ имеет плотность при нормальных условиях 9,73 кг/м3, а его относительная плотность по водороду составляет величину 108,2.
Необходимо отметить, что при увеличении давления газов и паров, их плотность увеличивается пропорционально.
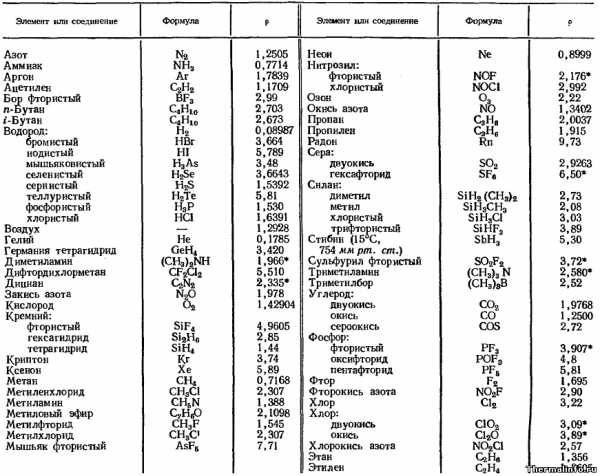
Примечание: Для газов и паров, рядом со значением плотности которых, присутствует символ *, ее величина в таблице приведена при температуре 20°С.
Из анализа данных, представленных в таблице, видно, что плотность рассмотренных газов находится в диапазоне от 0,089 до 9,73 кг/м3.
Плотность газов в жидком и твердом состояниях при различных температурах
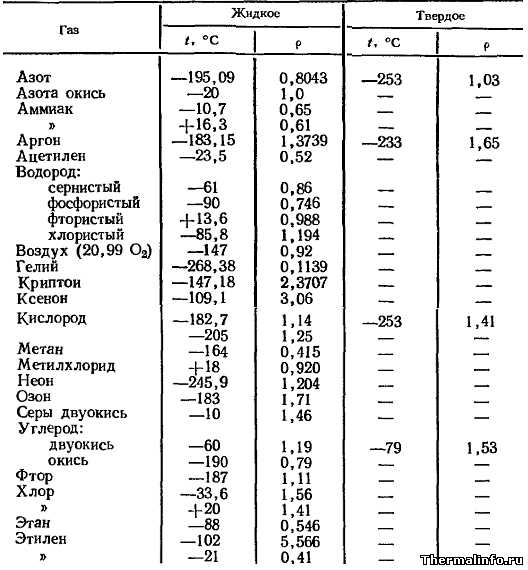
Значения плотности газов и паров в жидком и твердом состояниях приведены в таблице в зависимости от температуры при нормальном атмосферном давлении. Величина плотности газов указана в основном при низких температурах (в интервале от -268 до 20°С), при которых они находятся в жидком, или твердом состояниях.
При низких температурах плотность некоторых газов сравнима с плотностью металлов. К плотным (тяжелым) газам в жидком состоянии можно отнести такие газы, как этилен, криптон (плотность 2371 кг/м3) и ксенон (плотность 3060 кг/м3). Например, плотность газа этилена при температуре -102°С имеет значение 5566 кг/м3, что почти в полтора раза больше плотности алюминия. При этом этилен находится в жидком состоянии.
Газы в твердом состоянии имеют плотность немногим больше, чем в жидком. Твердое состояние газа достигается при более низкой температуре.
Например, углекислый газ находится в виде жидкости при температуре -60°С (при атмосферном давлении), но уже при -79°С становиться твердым и имеет плотность 1530 кг/м3.
Плотность газов в таблице дана в т/м3и приведена для следующих газов: азот N2, окись азота NO, аммиак NH3, аргон Ar, ацетилен C2H2, водород: сернистый H2S, фосфористый H3P, фтористый HF, хлористый HCl, воздух, гелий He, криптон Kr, ксенон Xe, кислород O2, метан CH4, метилхлорид CH3Cl, неон Ne, озон O3, сера двуокись SO2, углерод: двуокись CO2, окись CO, фтор F2, хлор Cl2, этан C2H6, этилен C2H4.
 Источник:
Источник:
Таблицы физических величин. Справочник. Под ред. акад. И.К. Кикоина. М.: Атомиздат, 1976. — 1008 с.
thermalinfo.ru
Решение. Плотность газа зависит от температуры следующим образом
Задача 1. Определить удельный вес γ1 дымовых газов при температуре t1 = (950 + N) 0С, если плотность их при нормальных физических условиях ρ0 = 1,295 кг/м3. Давление считать постоянным, а газы идеальными.Дано: t1 = (950 + N) = (950 + 2) = 952 0С,
ρ0 = 1,295 кг/м3
γ1 = ?
Решение.
Плотность газа зависит от температуры следующим образом:
где ρt и ρ0 – плотность газа соответственно при новой температуре Т и при начальной температуре. В нашем случае Т = 952ºС, Т0 = 20 ºС или 273,15 ºК.
Удельный вес дымовых газов при данной температуре составит:
Ответ: γ1 = 2,75 кг/м3
Задача 2. Трубопровод внутренним диаметром dв = 207 мм, длиной l = (100 + N) м, подготовленный к гидравлическому испытанию, заполнен водой при атмосферном давлении (р1 = ра). Какое количество воды необходимо дополнительно подать в трубопровод при повышении давления в нем до р2 = (5 + 0,1N) МПа по манометру. Изотермический коэффициент сжимаемости воды принять равным βр = 0,5∙10-9 м2/Н. Деформацией трубопровода пренебречь.
Дано: dв = 207 мм, l = (100 + N) = (100 + 2) = 102 м,
р2 = (5 + 0,1N) = (5 + 0,1∙2) = 5,2 МПа, βр = 0,5∙10-9 м2/Н,
р1 = ра
∆W = ?
Решение.
Определим вместимость трубопровода по формуле:
Объем воды ∆W, необходимый для подачи в трубопровод для повышения давления найдем из соотношения для коэффициента сжимаемости:
,
∆W – изменение объема W, соответствующее изменению давления на величину ∆р.
Ответ: ∆W = 0,008 м3
Задача 3. В вертикальном цилиндрическом резервуаре диаметром D = (10 + 0,1N) м хранится (500 + N) т нефти, плотность которой при температуре t0 = 0ºC равна ρ0 = 850 кг/м3. Определить колебания уровня нефти в резервуаре при изменении температуры нефти от t0 = 0ºC до t = (10 + N) ºC. Расширение стенок резервуара не учитывать. Коэффициент температурного расширения нефти принять равным βt= 0,00072 ºС-1.
Дано: D = (10 + 0,1N) = (10 + 0,1∙2) = 10,2 м,
m = (500 + N) = (500 + 2) = 502 т = 502000 кг,
t0 = 0ºC, t = (10 + 2) = 12 ºC, βt= 0,00072 ºС-1
∆h = ?
Решение.
Объем резервуара, заполненный нефтью, рассчитывается по формуле:
где h — высота уровня нефти в резервуаре, м;
D – диаметр резервуара, м.
Объем нефти в резервуаре при t0 = 0ºC:
Изменение уровня нефти при температурном расширении составит:
где объем воды ∆W найден из соотношения для коэффициента температурного расширения:
,
∆W – изменение объема W, соответствующее изменению температуры на величину ∆t.
Ответ: ∆h = 0,06 м
Задача 4. Поршень 1 гидравлического пресса имеет диаметр d = (0,08 + N∙10-3) м. Сила Р1 = (30 + 0,1N) кгс, действующая на поршень 1, создает усилие на поршне 2 Р2 = (750 + 0,1N) кгс. Определить диаметр D поршня 2. Коэффициент полезного действия η пресса принять равным 0,85.
Дано: d = (0,08 + N∙10-3) = (0,08 + 2∙10-3) = 0,082 м,
Р1 = (30 + 0,1N) = (30 + 0,1∙2) = 30,2 кгс = 302 Н,
Р2 = (750 + 0,1N) = (750 + 0,1∙2) = 750,2 кгс = 7502 Н,
η = 0,85.
D = ?
Решение.
В соответствии с законом Паскаля, прикладывая к меньшему поршню силу Р1, мы создаем в жидкости давление р = Р1/S1 (S1 – площадь поршня диаметром d), которое передается и большому поршню, вызывая силу Р2 = р∙S2, р = Р2/S2. Так как давление одинаковое, то приравнивая правые части с учетом КПД получаем следующую зависимость:
Выражаем D:
Ответ: D = 0,443 м
Задача 5. Определить плотность ρtплавающего в воде тела, имеющего форму прямоугольного параллелепипеда, высота которого h = (0,4 + 0,01N) м, если тело выступает над водой на расстоянии y = (0,15 + 0,01N) м. Температуру воды принять равной tв = (5 + N) ºС.
Дано: h = (0,4 + 0,01N) = (0,4 + 0,01∙2) = 0,42 м,
y = (0,15 + 0,01N) = (0,15 + 0,01∙2) = 0,17 м,
tв = (5 + N) = (5 + 2) = 7 ºС
ρt = ?
Решение.
По закону Архимеда можем записать равенство:
где Рв – выталкивающая сила, действующая на тело.
G – вес тела. Выталкивающую силу можем записать выражением:
,
где х – длина прямоугольного параллелепипеда;
V1 – объем погруженной части тела.
Вес тела:
,
где V – объем тела.
Плотность воды при данной температуре определяем по справочнику [1], ρв = 999 кг/м3
Ответ: ρt = 595 кг/м3
Задача 6. В открытые сообщающиеся сосуды налиты жидкости разной плотности. Определить высоты h1 и h2, м, если известно, что разность уровней свободных поверхностей в сосудах h = (0,5 + 0,1N) м. Плотности жидкостей равны: ρ1 = (770 + N) кг/м3; ρ2 = (1000 + N) кг/м3
Дано: h = (0,5 + 0,1N) = (0,5 + 0,1∙2) = 0,7 м,
ρ1 = (770 + N) = (770 + 2) = 772 кг/м3;
ρ2 = (1000 + N) = (1000 + 2) = 1002 кг/м3
h1 = ? h2 = ?
Решение.
Запишем уравнение равновесия по отношению к плоскости раздела 0-0:
Откуда
h2 = h1 – h = 3,04 — 0,7 = 2,34 м
Ответ: h1 = 3,04 м, h2 = 2,34 м
Задача 7. Определить тягу ∆р, Па через дымовую трубу высотой Н = (50 + 3N) м, если плотность дымовых газов ρг = 0,65 кг/м3, а температура наружного воздуха составляет tв = (-30 + N) ºС. Давление в трубе принять равным атмосферному (рат), а сечение трубы постоянным.
Дано: Н = (50 + 3N) = (50 + 3∙2) = 56 м,
ρг = 0,65 кг/м3, tв = (-30 + N) = (-30 + 2) = -28ºС
∆р = ?
Решение.
Давление в топке на уровне 2-2 запишется следующим выражением:
где ртр – давление, создаваемое дымовыми газами, удаляемыми через трубу;
рат – атмосферное давление на уровне 1-1
Давление перед входом в топку на уровне 2-2:
где рвозд — давление создаваемое столбом воздуха высотой Н.
,
где ρвозд – плотность воздуха при данной температуре. Плотность воздуха определим по формуле:
где ρt и ρ0 – плотность газа соответственно при новой температуре Т и при начальной температуре. В нашем случае Т = -28ºС = 265 ºК, Т0 = 20 ºС = 293 ºК, ρ0 = 1,295 кг/м3.
Перепад давлений ∆р:
Ответ: ∆р = 483,4 Па
skachate.ru
Плотность — Зависимость плотности от температуры
Химия — Плотность — Зависимость плотности от температуры
28 февраля 2011Оглавление:
1. Плотность
2. Виды плотности и единицы измерения
3. Зависимость плотности от температуры
4. Плотности астрономических объектов
5. Плотности некоторых газов
6. Измерение плотности
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведет себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого числа.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Правда, вода является исключением из этого правила, её плотность при затвердевании уменьшается.
Диапазон плотностей в природе
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда .
- Плотность межзвёздной среды ~10÷10 кг/м³.
- Средняя плотность Солнца примерно в 1,5 раза выше плотности воды, равной 1000 кг/м³.
- Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
- Cредняя плотность Земли равна 5520 кг/м³.
- Жидкий водород при атмосферном давлении имеет плотность 70 кг/м³.
- Жидкий гелий при атмосферном давлении 130 кг/м³.
- Вода 1000 кг/м³.
- Гранит 2600 кг/м³
- Железо 7874 кг/м³.
- Наибольшую плотность среди металлов имеет осмий.
- Плотность атомных ядер ≈2·10 кг/м³.
- Плотность белых карликов 10—10 кг/м³
- Плотность нейтронных звёзд имеет порядок 10÷10 кг/м³.
- Теоретическую верхнюю границу плотности по представлениям современной физики представляет планковская плотность ≈ 5,1×10 кг/м³, хотя может быть, эта верхняя граница, хотя скорее всего действительно является оценкой сверху, но возможно, очень сильно завышенной.
Просмотров: 6840
| Полярные вещества |
4108.ru
Плотность зависимость от температуры — Справочник химика 21
Плотность нефтепродуктов уменьшается с повышением темпера туры. Зависимость относительной плотности от температуры определяется по формуле, предложенной Д. И. Менделеевым [c.10]Плотность, в практике нефтепереработки принято иметь дело с относительной плотностью. Относительная плотность — это безразмерная величина, численно равная отнощению массы нефтепродукта при температуре определения к массе чистой воды при 4°С, взятой в том же объеме. В отличие от плотности относительным удельным весом называется отношение веса нефтепродукта при температуре определения к весу чистой воды при 4 °С в том же объеме. При одной и той же температуре плотность и удельный вес численно равны, так как вес вещества пропорционален его массе. В СССР принято определять плотность р при 20°С. Так как зависимость плотности нефтепродуктов от температуры имеет линейный характер, то, зная плотность при температуре I, можно найти по формуле [c.43]
Индекс корреляции является важным показателем сажевого сырья. Он выражает зависимость между плотностью и температурой кипения для углеводородов различных рядов. Для расчета индекса корреляции выведена формула [c.201]
Товарная уксусная кислота обычно представляет собой водный раствор, плотность и температура застывания которого меняются специфическим образом в зависимости от концентрации (рис. 1). Это необходимо учитывать при хранении, транспортировании и добавлении СНзСООН к закачиваемому раствору. [c.10]Газообразные жидкости имеют меньшую плотность по сравнению с капельными, при этом имеется сильная зависимость плотности от температуры и давления. [c.27]
Содержание в нефтях смолисто-асфальтеновых веществ Сел и парафинов Сп можно рассчитать в зависимости от коксуемости (К), плотности и температуры застывания нефти [27] [c.37]
Поэтому устройство и эксплуатация факельных трубопроводов должны осуществляться в соответствии с правилами техники безопасности для трубопроводов горючих, токсичных и сжиженных газов. Кроме того, при проектировании, строительстве и эксплуатации газопроводов необходимо руководствоваться строительными нормами и правилами (СНиП) и другими обязательными нормами п правилами. В зависимости от конкретных условий следует учитывать некоторые особенности обеспечения герметичности факельных трубопроводов. Несмотря на то, что сбрасываемые газы различаются по составу и параметрам и расход их колеблется в широких пределах, допустимая скорость их должна обеспечиваться. Поэтому при расчетах диаметров цеховых и общезаводских (межцеховых) трубопроводов и других элементов факельных установок должны учитываться максимальное (аварийное) и постоянное количество сбрасываемого на сжигание газа, его состав, плотность, давление, температура, молекулярная масса, теплота сгорания, длительность периода максимального сброса и др. [c.213]
Плотность нефти и нефтепродуктов существенно зависит от-температуры и давления окружающей среды. Для большинства нефтеиродуктов, особенно в небольших интервалах температур, зависимость плотности от температуры имеет линейный. характер и в общем случае выражается уравнением [c.23]
Равновесие в двухфазной системе жидкая вода — лед характеризуется кривой ОВ, выражающей зависимость температуры замерзания воды от давления. Следует обратить внимание, что в отличие от большинства других веществ для воды в известных пределах повышение давления вызывает понижение температуры ее замерзания. Это объясняется тем, что плотность льда меньше плотности воды, а повышение давления всегда способствует образованию той фазы, которая обладает меньшим объемом, т. е. большей плотностью (принцип смещения равновесий см. 87). [c.249]
Характеристический фактор К определяет химическую природу нефтепродукта, его парафинистость. Определяется в зависимости от двух параметров — плотности и температуры кипения, величина которых зависит от состава нефтепродуктов. Для парафини-стых нефтепродуктов 12,5-4-13, для нафтено-ароматических /(=104-11, для ароматизированных /С 10 и менее, для крекинг-бензина К 11,5- 11,8. Применяется характеристический фактор для корреляции при расчете физико-химических свойств нефтепродуктов. Характеристический фактор определяют по формуле [c.8]
С понижением температуры работоспособность кислотных аккумуляторов значительно ухудшается, во-первых, из-за возрастания их внутреннего сопротивления, во-вторых, в результате замед
www.chem21.info
Зависимость давления газа от температуры
Начнем с выяснения зависимости давления газа от температуры при условии неизменного объема определенной массы газа. Эти исследования были впервые произведены в 1787 г. Шарлем. Можно воспроизвести эти опыты в Упрощенном виде, нагревая газ в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки.
Пренебрежем ничтожным увеличением объема колбы при нагревании и незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, можно считать объем газа неизменным. Подогревая «воду в сосуде, окружающем колбу, будем отмечать температуру газа по термометру, а соответствующее давление — по манометру. Наполнив сосуд тающим, льдом, измерим давление соответствующее температуре 0°С.
Опыты подобного рода показали следующее:
1. Приращение давления некоторой массы газа при нагревании на 1° составляет определенную часть того давления, которое имела данная масса газа при температуре 0°С. Если давление при 0°С обозначить через Р, то.приращение давления газа при нагревании на 1°С.
При нагревании на т градусов приращение давления будет в т раз больше, т. е. приращение давления пропорционально приращению температуры.
2. Величина , показывающая, на какую часть давления при 0°С увеличивается давление газа при нагревании на 1°, имеет одно и то же значение(точнее, почти одно и то же) для всех газов,, а именно(1/273)град-1. Величину называют термическим, коэффициентом давления. Таким образом, термический коэффициент давления для всех газов имеет одно и то же значение, равное (1/273)град-1.
Давление некоторой массы газа при нагревании на 1° в неизменном объеме увеличивается на (1/273) часть давления при 0°С .(закон Шарля).
Следует иметь, однако, в виду, что температурный коэффициент давления газа, полученный при измерении температуры по ртутному термометру, не в точности одинаков для разных температур: закон Шарля выполняется только приближенно, хотя и с очень большой степенью точности.
www.apxu.ru

Leave A Comment