Окружность, вписанная в правильный треугольник
Определение и формулы окружности, вписанной в правильный треугольник
Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
В любой треугольник можно вписать окружность, причем, только одну.
Если окружность вписана в правильный треугольник (в тот, у которого все стороны равны между собой), то ее радиус вычисляется по формуле
где – площадь треугольника, а – его полупериметр; или его можно выразить через сторону следующим образом:
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Вписанный и описанный треугольник — материалы для подготовки к ЕГЭ по Математике
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным
В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
,
где — полупериметр,
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
Ответ: .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
Ответ: .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Правильный (равносторонний) треугольник. Определение, свойства

Равносторонний (правильный) треугольник – треугольник, у которого все стороны равны.
Свойства
1. Все углы правильного треугольника равны между собой и равны 60˚.
 2. Связь между радиусом
2. Связь между радиусом  вписанной окружности правильного треугольника и его стороной
вписанной окружности правильного треугольника и его стороной  :
: 
3. Связь между радиусом  описанной окружности около правильного треугольника и его стороной
описанной окружности около правильного треугольника и его стороной  :
:  .
.
4. Радиусы вписанной 
 окружностей связаны следующим образом:
окружностей связаны следующим образом: 
5. Высота 
 и медиана
и медиана  выражаются через сторону треугольника
выражаются через сторону треугольника  следующим образом:
следующим образом: 
6. Площадь правильного треугольника со стороной
правильного треугольника со стороной  вычисляется по формуле:
вычисляется по формуле: 
Думаю, вам будет полезна таблица формул для треугольника.
Построение правильных многоугольников — Техническое черчение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
|
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника. |
Треугольник. Формулы и свойства треугольников.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
 Остроугольный треугольник — все углы треугольника острые.
Остроугольный треугольник — все углы треугольника острые.
 Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
 Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
По числу равных сторон
 Разносторонний треугольник — все три стороны не равны.
Разносторонний треугольник — все три стороны не равны.
 Равнобедренный треугольник — две стороны равны.
Равнобедренный треугольник — две стороны равны.
 Равносторонним треугольник или правильный треугольник — все три стороны равны.
Равносторонним треугольник или правильный треугольник — все три стороны равны.
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
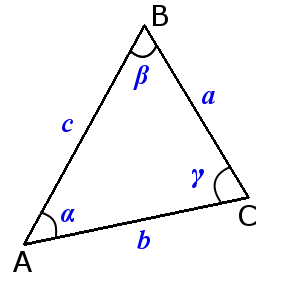
Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианыa = 23√2(mb2 + mc2) — ma2
b = 23√2(ma2 + mc2) — mb2
c = 23√2(ma2 + mb2) — mc2
Медианы треугольника
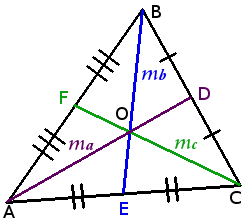
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD = BOOE = COOF = 21
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b2
mc = 12√2a2+2b2-c2
Биссектрисы треугольника
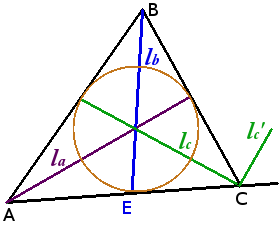
Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, —
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB = ECBC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc‘ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√bcp(p — a)b + c
lb = 2√acp(p — b)a + c
lc = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
Высоты треугольника
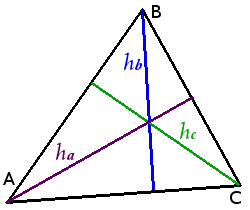
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc = 1a:1b:1c = (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:ha = bc2R
hb = ac2R
hc = ab2R
Окружность вписанная в треугольник
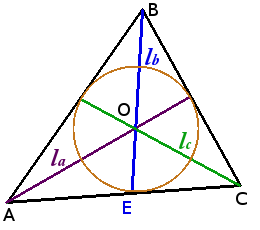
Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:Окружность описанная вокруг треугольника
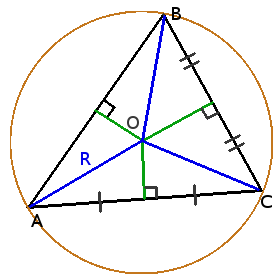
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.rR = 4 sinα2 sinβ2 sinγ2 = cos α + cos β + cos γ — 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2.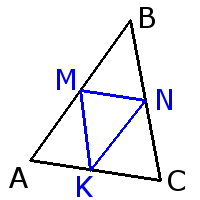 Средняя линия треугольника параллельна основанию и равна его половине.
Средняя линия треугольника параллельна основанию и равна его половине.MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольникаS∆MBN = 14 S∆ABC
S∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника
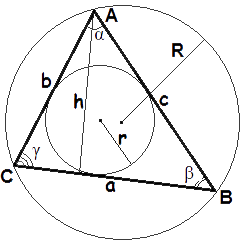
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 12a · ha
S = 12b · hb
S = 12c · hc - Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p = a + b + c2 — полупериметр треугльника. - Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 12a · b · sin γ
S = 12b · c · sin α
S = 12a · c · sin β - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Определение. Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Подобие треугольников
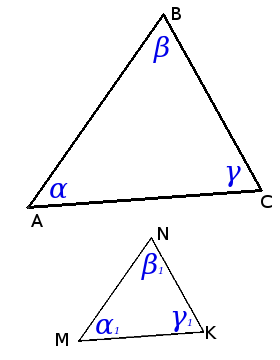 Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k — коэффициент подобияПризнаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны. Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:S∆АВСS∆MNK = k2
Задачи на комбинацию окружности и треугольника
 Продолжаем решать простейшие геометрические задачки.
Продолжаем решать простейшие геометрические задачки.
Разбираем Задачи №6 ЕГЭ по математике.
Сегодня работаем с окружностью, вписанной в треугольник и описанной около треугольника.
Вы можете пройти автотренинг «Планиметрия»
В категорию «Задачи №6» входят также задачи следующих типов + показать
Окружность, вписанная в треугольник
Задача 1.
Площадь треугольника равна 800, а радиус вписанной окружности равен 16. Найдите периметр этого треугольника.

Решение: + показать
Задача 2.
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 66.

Решение: + показать Радиус вписанной окружности в правильный треугольник Итак, Ответ: 22.  – есть
– есть  высоты (
высоты ( ), так в правильном треугольнике высоты совпадают с медианами, а медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
), так в правильном треугольнике высоты совпадают с медианами, а медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Задача 3.
Сторона правильного треугольника равна  . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.

Решение: + показать
Задача 4.
В треугольнике ABC  . Найдите радиус вписанной окружности.
. Найдите радиус вписанной окружности.

Решение: + показать Найдем гипотенузу по т. Пифагора: Найдем площадь и периметр треугольника, чтобы воспользоваться затем формулой Тогда Ответ: 1. 

 :
:



Задача 5.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 11. Найдите гипотенузу c этого треугольника. В ответе укажите  .
.

Решение: + показать
Задача 6.
Боковые стороны равнобедренного треугольника равны 181, основание равно 38. Найдите радиус вписанной окружности.

Решение: + показать
Задача 7.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Решение: + показать
Задача 8.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 18, 33. Найдите периметр данного треугольника.

Решение: + показать
Окружность, описанная около треугольника
Задача 1.
Найдите радиус окружности, описанной около прямоугольного треугольника  , если стороны квадратных клеток равны 1.
, если стороны квадратных клеток равны 1.

Решение: + показать
Задача 2.
Боковые стороны равнобедренного треугольника равны 50, основание равно 60. Найдите радиус описанной окружности этого треугольника.

Решение: + показать Воспользуемся следующей формулой: Площадь будем искать по формуле Герона: Тогда Ответ: 31,25. 



Задача 3.
Сторона AB треугольника ABC равна 28. Противолежащий ей угол C равен 150˚. Найдите радиус окружности, описанной около этого треугольника.

Решение: + показать Согласно т. Синусов Ответ: 28. 



Задача 4.
Угол C треугольника ABC, вписанного в окружность радиуса 47, равен 30˚. Найдите сторону AB этого треугольника.
Решение: + показать
Задача 5.
В треугольнике ABC BC , угол C равен 90°. Радиус описанной окружности этого треугольника равен 17,5. Найдите AC.
, угол C равен 90°. Радиус описанной окружности этого треугольника равен 17,5. Найдите AC.

Решение: + показать В прямоугольном треугольнике гипотенуза – диаметр описанной окружности. Значит, По теореме Пифагора Ответ: 30. 

Задача 6.
Радиус окружности, описанной около правильного треугольника, равен  Найдите сторону этого треугольника.
Найдите сторону этого треугольника.

Решение: + показать
Задача 7.
Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:6:11. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

Решение: + показать
Объемный раздел получился… Отдохнем немножко? –>+ показать


Вы может пройти тест «Окружность, описанная около треугольника. Окружность, вписанная в треугольник»
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а). Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2. Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника. Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны 1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник. Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника. Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля. Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения. Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою. Построение вписанного в окружность правильного пятиугольника. Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой. Построение правильного пятиугольника по данной его стороне. Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой. Построение вписанного в окружность правильного семиугольника. Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника.
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра. Приведённый способ годен для построения правильных многоугольников с любым числом сторон. Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
|
| Начинаем с данного круга, центр О. Примечание: Если вам не дали центр, вы можете найти его, используя метод, показанный на Нахождение центра круга с помощью циркуля и линейки. |  |
| 1. Отметьте точку в любом месте окружности. |  |
| 2. Установите циркуль в эту точку и установите ширину циркуля в центр круга. Компасы теперь установлены на радиус окружности |  |
| 3. Сделайте дугу поперек окружности. |  |
| 4. Переместите циркуль в эту новую точку и нарисуйте еще одну дугу. |  |
| 5. Продолжайте таким же образом, пока не наберете в сумме шесть очков. |  |
| 6. Обозначьте все остальные точки B, D и F |  |
| 7. Проведите линии BD, DF, FB |  |
| 8. Готово. Прямые BD, DF, FB образуют равносторонний треугольник, вписанный в данную окружность. |
Как построить круг через 3 вершины треугольника с помощью циркуля и линейки или линейки
окружность треугольника — это круг, проходящий через все три вершины треугольника. Конструкция сначала устанавливает центр описанной окружности, а затем рисует круг. Окружность треугольника — это точка, в которой перпендикулярные биссектрисы сторон пересекаются. На этой странице показано, как построить (нарисовать) описанную окружность треугольника с помощью циркуля и линейки или линейки.Эта конструкция предполагает, что вы уже знакомы с Построением серединного перпендикуляра отрезка линии.
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Проба
Изображение ниже — это последний рисунок выше с добавленными красными метками.
Примечание: это доказательство почти идентично доказательству в Построение центра описанной окружности треугольника.

| Аргумент | Причина | |
|---|---|---|
| 1 | JK — это серединный перпендикуляр AB. | По конструкции. Для доказательства см. Построение серединного перпендикуляра отрезка |
| 2 | Существуют круги, центр которых лежит на прямой JK, а AB является аккорд. (* см. примечание ниже) | Серединный перпендикуляр к аккорд всегда проходит через центр круга. |
| 3 | LM — это серединный перпендикуляр BC. | По конструкции. Для доказательства см. Построение серединного перпендикуляра отрезка |
| 4 | Существуют круги, центр которых лежит на прямой LM, а BC является хордой. (* см. примечание ниже) | Серединный перпендикуляр к аккорд всегда проходит через центр круга. |
| 5 | Точка O — это центр описанной окружности треугольника ABC, центр единственной окружности, проходящей через A, B, C. | O — единственная точка, которая лежит как на JK, так и на LM, и поэтому удовлетворяет как 2, так и 4 выше. |
| 5 | Окружность O является описанной окружностью треугольника ABC. | Окружность проходит через все три вершины A, B, C |
— Q.E.D
* Примечание
В зависимости от того, где находится центральная точка на биссектрисе, существует бесконечное количество окружностей, которые могут удовлетворить это требование.
Два из них показаны ниже.Шаги 2 и 4 работают вместе, чтобы уменьшить возможное количество до одного. 
Попробуйте сами
Щелкните здесь, чтобы распечатать рабочий лист, содержащий две задачи с описанной окружностью треугольника. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатные материалы не защищены авторским правомДругие конструкции, страницы на сайте
Строки
Уголки
Треугольники
Правые треугольники
Центры треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Как построить (начертить) окружность треугольника с помощью циркуля и линейки или линейки
Как видно на Центр треугольника, три биссектриса угла любого треугольника всегда проходят через его центр. В этой конструкции мы используем только два, так как этого достаточно, чтобы определить точку, в которой они пересекаются. Мы делим два угла пополам, используя метод, описанный в Деление угла пополам. Точка пересечения биссектрис — это инцентр. Затем мы рисуем круг, который только касается сторон треугольников.
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Проба
Изображение ниже — это последний рисунок из приведенной выше анимации.

| Аргумент | Причина | |
|---|---|---|
| 1 | I — центр треугольника ABC. | По конструкции. См. Конструкция центрирующего центра треугольника для метод и доказательство. |
| 2 | IM перпендикулярно AB | По конструкции. См. Построение перпендикуляра к линии из точки для метод и доказательство. |
| 3 | IM — радиус вписанной окружности | Из (2) M — точка касания |
| 4 | Центр окружности I — вписанная окружность треугольника | Круг, касающийся всех трех сторон. |
— Q.E.D
Попробуйте сами
Щелкните здесь, чтобы распечатать рабочий лист incircle, содержащий две проблемы, которые можно попробовать. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатные материалы не защищены авторским правомДругие конструкции, страницы на сайте
линий
Уголки
Треугольники
Правые треугольники
Центры треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Правильные многоугольники вписаны в круг Калькулятор
- Цель использования
- Оценка значения of pi
[1] 2020/06/09 16:08 Мужской / 20-летний уровень / Высшая школа / Университет / Аспирант / Полезный /
- Цель использования
- Различные расчеты
[2] 2020/05/07 18:40 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
-
Посадка круглой ореховой рощи, состоящей из концентрических круговых насаждений на расстоянии примерно 40 футов
[3] 2020/03 / 25 11:54 Мужчина / Уровень 60 и старше / Инженер / Очень /
- Назначение
- построение пятиугольника со сторонами, равными длине смежного шестиугольника
[4] 2019 / 10/10 01:01 Мужчина / Уровень 50 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Просто интересно.
[5] 2019 / 10/04 22:05 Мужской / 50-летний уровень / Self-em трудоустроенные люди / Очень /
- Цель использования
- Измерить стальную растяжку обода — покупка б / у комплекта зимних шин
[6] 2019/10/03 09:07 Мужчина / Уровень 40 лет / Инженер / Очень /
- Цель использования
- Я получил несколько точек на круге, но мне нужно было найти радиус круга на основе расстояния между точками
[7] 14.06.2019 01:30 Мужчина / Уровень 20 лет / Инженер / Полезно /
- Цель использования
- Определение размеров коробки для печати на 3D-принтере с круглой печатной платформой
[8] 2019/04/27 11:20 Мужчина / Уровень 30 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Домашнее задание
[9] 2019/03/12 10:49 Женский / До 20 лет / Высшая школа / ВУЗ / Аспирант / Полезное /
- Цель использования
- Рисование пятиконечной звезды без компаса.
- Комментарий / запрос
- Очень полезно! Спасибо!
[10] 2018/12/10 02:31 Мужской / 30-летний уровень / Другое / Очень /

 Остроугольный треугольник — все углы треугольника острые.
Остроугольный треугольник — все углы треугольника острые.
 Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
 Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
 Равнобедренный треугольник — две стороны равны.
Равнобедренный треугольник — две стороны равны.
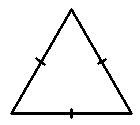 Равносторонним треугольник или правильный треугольник — все три стороны равны.
Равносторонним треугольник или правильный треугольник — все три стороны равны.
Leave A Comment