Диагональ делит угол пополам
☰
Одним из признаков ромба является то, что диагонали делят его углы пополам. В виде теоремы этот признак формулируется так:
Если диагональ параллелограмма делит его угол пополам, то такой параллелограмм является ромбом.
Если доказывать данный признак, то нам дан параллелограмм, одна диагональ которого делит один угол пополам. Требуется доказать, что у такого параллелограмма будут равны все стороны (именно этот факт является определением ромба).
Пусть дан ромб ABCD, его диагональ BD делит угол B пополам: ∠ABD = ∠CBD.
Как известно, в параллелограмме противоположные стороны параллельны. В данном случае AD || BC. Для этих прямых диагональ BD является секущей. Следовательно, ∠ABD = ∠CDB и ∠CBD = ∠ADB как накрест лежащие.
Но поскольку по условию ∠ABD = ∠CBD, то значит, что и углы при вершине D равны друг другу. Таким образом, доказано, что если диагональ параллелограмма делит один угол пополам, то она делит пополам и противоположный угол.
Оказывается, что все четыре угла, образованные диагональю в углах параллелограмма, равны друг другу. То есть в данном случае, не только накрест лежащие, но и односторонние углы при параллельных прямых тоже равны.
Рассмотрим треугольник ABD. В нем углы B и D равны. Значит, это треугольник равнобедренный с основанием BD. Так как у равнобедренных треугольников боковые стороны равны друг другу, то в данном случае AB = AD. Таким образом, доказано, что если диагональ делит угол параллелограмма пополам, то пара соседних сторон параллелограмма равна друг другу.
Но, как известно, у параллелограмма противоположные стороны не только параллельны друг другу, но и равны друг другу. Следовательно, AB = CD и AD = BC, а поскольку AB = AD, то все четыре стороны равны друг другу. Таким образом, доказано, что если диагональ делит угол параллелограмма пополам, то все стороны параллелограмма равны друг другу. А параллелограмм с равными сторонами является ромбом.
Диагональ параллелограмма делит его углы пополам
У ромба один из признаков указывает на то, что его диагонали делят углы ромба пополам.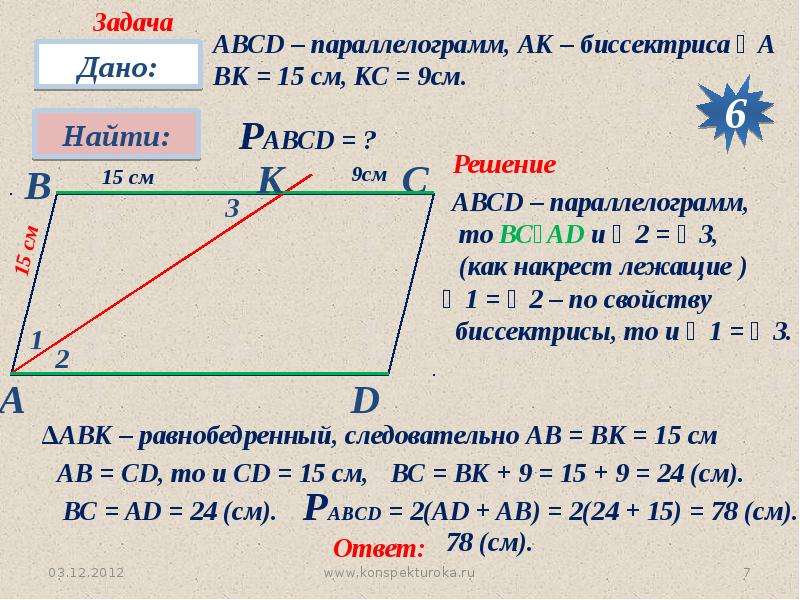
Признак сформулирован в виде теоремы:
Если диагональ параллелограмма делит его углы пополам, то этот параллелограмм – ромб.
Докажем признак.
Доказательство.
Согласно признаку есть параллелограмм, у которого одна диагональ делит один из углов пополам.
Необходимо доказать, что у этого параллелограмма все стороны будут равными, поскольку именно этот признак указывает на то, что данная фигура является ромбом.
Рассмотрим ромб ABCD. Построим диагональ BD, которая делит угол B на два равных угла ABD и CBD.
Согласно определению параллелограмма его противоположные стороны параллельны, то есть сторона AD параллельна стороне BC. В таком случае диагональ BD является для данных прямых секущей. Получаем, что угол ABD равен углу CDB, а угол CBD равен углу ADB как внутренние накрест лежащие.
Следовательно, мы доказали, что если в параллелограмме диагональ делит один из углов пополам, то она делит на два равных угла и противоположный угол.
Все четыре угла, на которые разбивает диагональ параллелограмма его противоположные углы, равны. То есть у параллелограмма равны кроме внутренних накрест лежащих и односторонние углы при параллельных прямых и секущей.
Рассмотрим треугольник ABD.
Углы AВD и BDA равны. Следовательно, данный треугольник является равнобедренным с основанием BD и равными боковыми сторонами AB и AD. Этим мы доказали, что при делении диагональю угла параллелограмма пополам его соседние стороны также равны между собой.
Утверждение доказано.
Ромб
Ромбом называется параллелограмм, все стороны которого равны. Ромб является параллелограммом и поэтому обладает всеми свойствами параллелограмма. Но у него есть и особое свойство:
- диагонали ромба взаимно перпендикулярны и делят его углы пополам

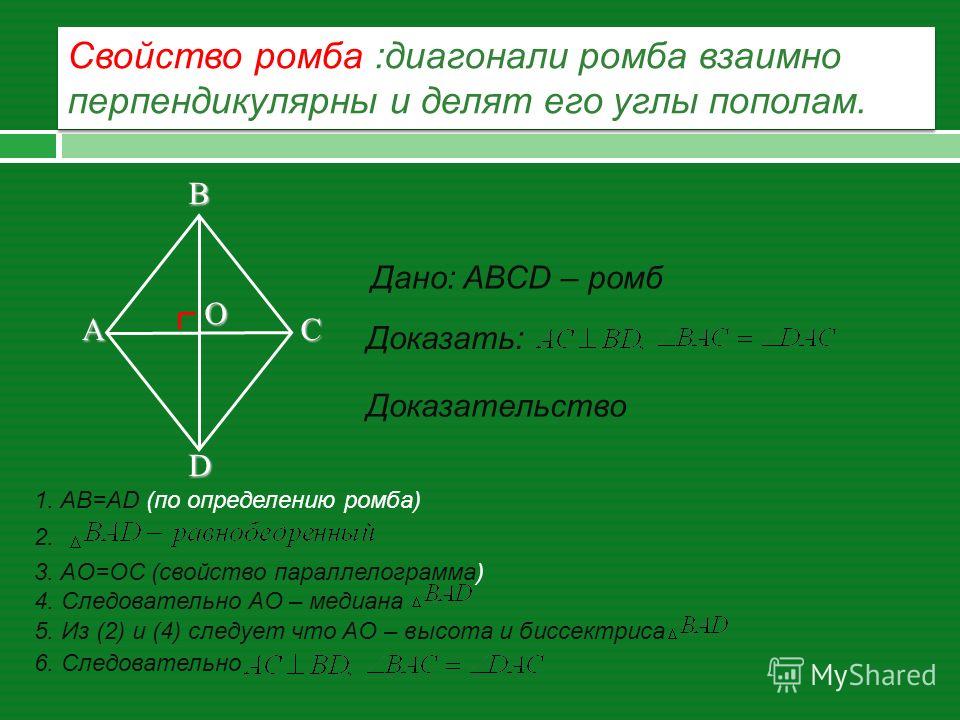
Обратимся к рисунку 63, на котором изображен ромб ABCD. Докажем, что AC ⊥ BD и каждая диагональ делит углы ромба пополам.
По условию AB = AD, поэтому треугольник BAD равнобедренный. Поскольку ромб — параллелограмм, то его диагонали пересекаются в некоторой точке O и делятся ею пополам. Отсюда следует, что медиана AO равнобедренного треугольника BAD является также его высотой и биссектрисой. Поэтому AC ⊥ BD и ∠BAC = ∠DAC. Справедливость равенства ∠BCA = ∠DCA, ∠ABD = ∠CBD и ∠ADB = ∠CDB доказывается аналогично.
Рассмотрим два признака ромба.
Теорема. Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм — ромб
Доказательство. Пусть диагонали AC и BD параллелограмма ABCD взаимно перпендикулярны (рис. 64). Докажем, что параллелограмм ABCD — ромб.
Так как диагонали параллелограмма делятся точкой пересечения пополам, то AO = OC и BO = OD. Следовательно, прямоугольные треугольники OBA, OBC, ODC и ODA равны по двум катетам, поэтому AB = BC = CD = DA, т. е. параллелограмм ABCD — ромб. Теорема доказана.
е. параллелограмм ABCD — ромб. Теорема доказана.
Теорема. Если диагональ параллелограмма делит его угол пополам, то этот параллелограмм — ромб.
Доказательство. Пусть диагональ BD параллелограмма ABCD делит угол B пополам (рис. 65): ∠ABD = ∠CBD. Докажем, что параллелограмм ABCD — ромб.
Углы ABD и CDB равны как накрест лежащие углы, образованные при пересечении параллельных прямых AB и CD секущей BD. Следовательно, ∠CDB = ∠CBD, поэтому треугольник CBD равнобедренный: BC = CD. Кроме того, AB = CD и BC = DA (как противоположные стороны параллелограмма). Таким образом, AB = BC = CD = DA, т. е. параллелограмм ABCD — ромб. Теорема доказана.
| Определение: параллелограмм | |
| Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны | |
| Определение: диагонали параллелограмма | |
| Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины | |
| Определение: высота параллелограмма | |
| Высотой параллелограмма называютперпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение | |
| Свойство: равенство противолежащих сторон | |
| Если четырёхугольник является параллелограммом, то его противолежащие стороны равны | |
| Признак: равенство противолежащих сторон | |
| Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом | |
| Признак: равенство и параллельность двух противолежащих сторон | |
| Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом | |
| Свойство: диагонали точкой пересечения делятся пополам | |
| Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам | |
| Признак: диагонали точкой пересечения делятся пополам | |
| Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом | |
| Свойство: суммы углов, прилежащих к сторонам | |
| Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° | |
| Признак: суммы углов, прилежащих к сторонам | |
| Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом | |
| Свойство: равенство противолежащих углов | |
| Если четырёхугольник является параллелограммом, то его противолежащие углы равны | |
| Признак: равенство противолежащих углов | |
| Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом | |
| Свойство: два треугольника, на которые каждая диагональ делит четырёхугольник | |
| Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника | |
| Признак: два треугольника, на которые каждая диагональ делит четырёхугольник | |
| Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом | |
| Свойство: четыре треугольника, на которые диагонали делят четырёхугольник | |
| Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) | |
| Признак: четыре треугольника, на которые диагонали делят четырёхугольник | |
| Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом | |
Быстро найти нужную формулу для расчета онлайн.
 Геометрия. Алгебра.
Геометрия. Алгебра.Высота — перпендикуляр исходящий из вершины угла на противоположенную сторону
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы длины высоты параллелограмма, через сторону и угол, ( Hb, Ha):
Острый угол пересечения высот, равен острому углу параллелограмма.
Тупой угол пересечения высот, равен тупому углу параллелограмма.
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства биссектрисы параллелограмма
— Биссектриса по определению делит угол пополам
— Биссектриса отсекает равнобедренный треугольник (в данном случае треугольники ABF и DKC)
— Биссектрисы смежных углов, пересекаются под прямым углом (90°)
— Биссектрисы противоположных углов, равны и параллельны
AF — биссектриса из острого угла
DK — биссектриса из тупого угла
α — острый угол
β — тупой угол
a — меньшая сторона
b — большая сторона
Так как треугольники ABF и DKC, равнобедренные, следовательно справедливы тождества:
Длина биссектрисы параллелограмма
L — биссектриса параллелограмма
a, b — стороны
α, β — углы
Формулы длины биссектрисы через сторону и углы, (L):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
a, b — стороны параллелограмма
D — большая диагональ
α — острый угол между диагоналями
β — тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и диагонали:
Формулы соотношения острого и тупого углов между диагоналями:
Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства углов параллелограмма:
1. Противоположные углы равны
Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и стороны:
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Формулы длины сторон через диагонали и угол между ними.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
Формулы сторон параллелограмма , (a, b):
2. Формулы длины сторон параллелограмма через высоту.
Формулы длины сторон параллелограмма через высоту.
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
3. Дополнительные, интересные формулы параллелограмма:
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
Формула суммы квадратов диагоналей:
Формула разности квадратов сторон:
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Найти больший угол параллелограмма АВСD.
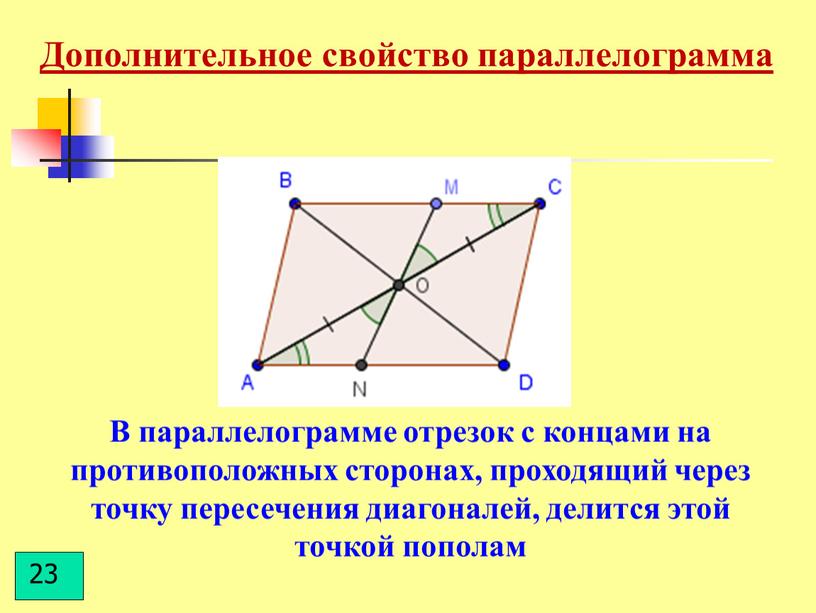
DCВ=АCD+АСВ=23°+49°=72°С+ В=180 ° В=180°- В=180°-72°=108°
Ответ: 108.
Если угол разделен на части, то его градусная мера равна сумме градусных мер его частей.
В параллелограмме сумма соседних углов равна 180°
Если в параллелограмме диагональ делит углы пополам, то этот параллелограмм является ромбом
В ромбе диагонали пересекаются под прямым углом
| АВСD параллелограмм. |
| Повторение |
75 | (3) |
° | А= АDС=75° |
| |
| АDС= DСК=75° |
DСК= DКС=75°СDК=180°-2 75°=30°
Ответ: 30.
В равнобедренной трапеции углы при основании равны
При пересечении двух параллельных прямых третьей накрест лежащие углы равны
В равнобедренном треугольнике углы при основании равны
Углы ромба относятся как 3:7 . |
Найти больший угол. |
Повторение |
(2) |
1+ 2=180° |
Пусть х° — одна часть, тогда 2=3х°,
1=7х°
3х+7х=180
10х=180
х=181=18°∙7=126°
Ответ: 126.
18
В ромбе противоположные стороны параллельны
Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°
Сумма двух углов | |
параллелограмма равна 50°. | |
Найти один из оставшихся | |
углов. | Повторение |
(2) | |
А+ С=50°С+ D=180°D=180°-50°=130°
Ответ: 130.
В параллелограмме противоположные углы равны
Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°
Определение диагонали параллелограмма.
 Параллелограмм
ПараллелограммПараллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.
Как вы уже успели догадаться, параллелограмм является выпуклым четырехугольником. Рассмотрим основные свойства параллелограмма.
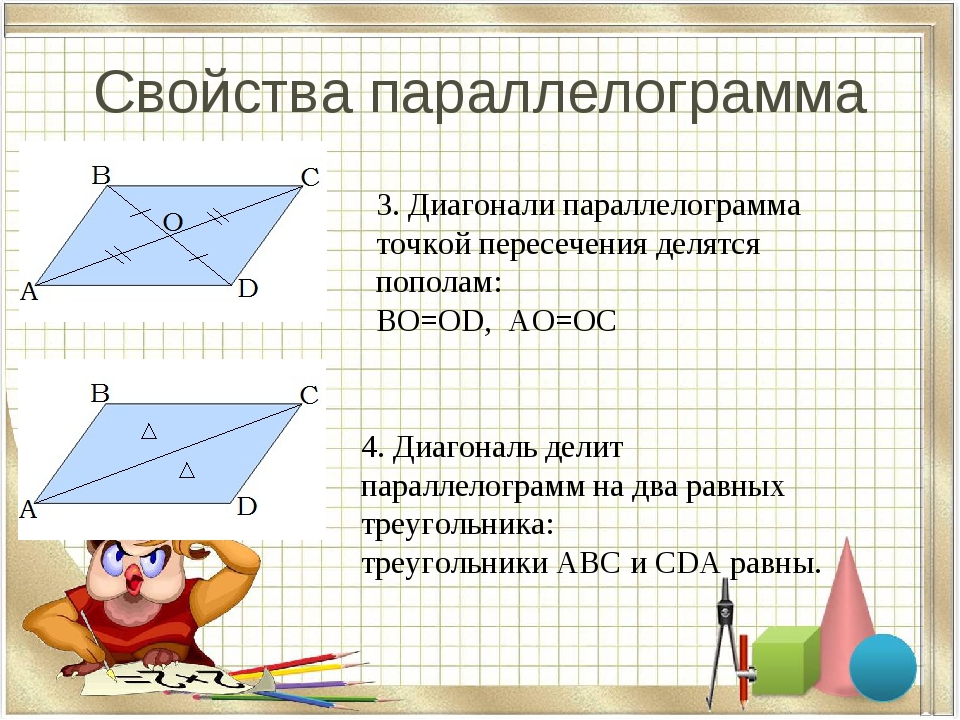
Свойства параллелограмма
1. В параллелограмме противоположные углы и противоположные стороны равны. Докажем это свойство — рассмотрим параллелограмм, представленный на следующем рисунке.
Диагональ BD разделяет его на два равных треугольника: ABD и CBD. Они равны по стороне BD и двум прилежащим к ней углам, так как углы накрест лежащие при секущей BD параллельных прямых BC и AD и AB и CD соответственно. Следовательно, AB = CD и
BC = AD. А из равенства углов 1, 2 ,3 и 4 следует, что угол A = угол1 +угол3 = угол2 + угол4 = угол С.
2. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.
Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.
Тогда треугольник AOB и треугольник COD равны между собой, по стороне и двум прилежащим к ней углам. (AB=CD так как это противоположные стороны параллелограмма. А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.
Все основные свойства проиллюстрированы на следующих трех рисунках.
1. Определение параллелограмма.
Если пару параллельных прямых пересечём другой парой параллельных прямых, то получим четырёхугольник, у которого противоположные стороны попарно параллельны.
В четырёхугольниках ABDС и ЕFNМ (рис. 224) ВD || АС и AB || СD;
ЕF || МN и ЕМ || FN.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
2. Свойства параллелограмма.
Теорема
. Диагональ параллелограмма делит его на два равных треугольника.
Диагональ параллелограмма делит его на два равных треугольника.
Пусть имеется параллелограмм ABDС (рис. 225), в котором AB || СD и АС || ВD.
Требуется доказать, что диагональ делит его на два равных треугольника.
Проведём в параллелограмме ABDС диагональ СВ. Докажем, что \(\Delta\)CAB = \(\Delta\)СDВ.
Сторона СВ общая для этих треугольников; ∠ABC = ∠BCD, как внутренние накрест лежащие углы при параллельных AB и СD и секущей СВ; ∠ACB = ∠СВD, тоже как внутренние накрест лежащие углы при параллельных АС и ВD и секущей CB.
Отсюда \(\Delta\)CAB = \(\Delta\)СDВ.
Таким же путём можно доказать, что диагональ AD разделит параллелограмм на два равных треугольника АСD и ABD.
Следствия:
1 . Противоположные углы параллелограмма равны между собой.
∠А = ∠D, это следует из равенства треугольников CAB и СDВ.
Аналогично и ∠С = ∠В.
2. Противоположные стороны параллелограмма равны между собой.
AB = СD и АС = ВD, так как это стороны равных треугольников и лежат против равных углов.
Теорема 2. Диагонали параллелограмма в точке их пересечения делятся пополам.
Пусть BC и AD — диагонали параллелограмма AВDС (рис. 226). Докажем, что АО = OD и СО = OB.
Для этого сравним какую-нибудь пару противоположно расположенных треугольников, например \(\Delta\)AOB и \(\Delta\)СОD.
В этих треугольниках AB = СD, как противоположные стороны параллелограмма;
∠1 = ∠2, как углы внутренние накрест лежащие при параллельных AB и СD и секущей AD;
∠3 = ∠4 по той же причине, так как AB || СD и СВ — их секущая.
Отсюда следует, что \(\Delta\)AOB = \(\Delta\)СОD. А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = OB.
Теорема 3. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180° .
В параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC.
Треугольники равны, так как ∠1 = ∠4, ∠2 = ∠3 (накрест лежащие углы при параллельных прямых), а сторона АС общая.
Из равенства \(\Delta\)ABC = \(\Delta\)ADC следует, что AB = CD, BC = AD, ∠B = ∠D.
Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых.
Это четырёхугольник, противоположные стороны которого попарно параллельны.
Свойство 1 . Любая диагональ параллелограмма делит его на два равных треугольника.
Доказательство . По II признаку (накрест лежащие углы и общая сторона).
Теорема доказана .
Свойство 2 . В параллелограмме противолежащие стороны равны, противолежащие углы равны.
Доказательство
.
Аналогично,
Теорема доказана .
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.
Доказательство .
Теорема доказана .
Свойство 4
. Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. — вершину — два равнобедренных?-ка).
(Ч. сл. — вершину — два равнобедренных?-ка).
Доказательство
.
Теорема доказана .
Свойство 5 . В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.
Доказательство .
Теорема доказана .
Свойство 6 . Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.
Доказательство .
Теорема доказана .
Свойство 7 . Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство .
Теорема доказана .
Построение биссектрисы угла. Свойства биссектрисы угла треугольника.
1) Построить произвольный луч DE.
2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.
3) F и G — точки пересечения окружности со сторонами данного угла, H — точка пересечения окружности с построенным лучом
Построить окружность с центром в точке H и радиусом, равным FG.
5) I — точка пересечения окружностей построенного луча.
6) Провести прямую через вершину и I.
IDH — требуемый угол.
)
Свойство 1 . Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.
Доказательство . Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.
Понятие параллелограмма
Определение 1
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).
Рисунок 1.
Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Признаки параллелограмма
Рассмотрим три признака параллелограмма и представим их в виде теорем.
Теорема 1
Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис. 2).
Рисунок 2.
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда
\[\angle CAB=\angle DCA\]
как накрест лежащие углы.
По $I$ признаку равенства треугольников,
так как $AC$ — их общая сторона, а $AB=CD$ по условию. Значит
\[\angle DAC=\angle ACB\]
Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
Теорема доказана.
Теорема 2
Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).
Рисунок 3.
Так как $AD=BC$, $AB=CD$, а $AC$ — общая сторона, то по $III$ признаку равенства треугольников,
\[\triangle DAC=\triangle ACB\]
\[\angle DAC=\angle ACB\]
Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$. Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
\[\angle DCA=\angle CAB\]
Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$. Следовательно, по определению 1, данный четырехугольник является параллелограммом.
Теорема доказана.
Теорема 3
Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).
Рисунок 4.
Так как, по условию $BO=OD,\ AO=OC$, а углы $\angle COB=\angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,
\[\triangle BOC=\triangle AOD\]
\[\angle DBC=\angle BDA\]
Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$. Также $BC=AD$. Следовательно, по теореме $1$, данный четырехугольник является параллелограммом.
Как в евклидовой геометрии точка и прямая — главные элементы теории плоскостей, так и параллелограмм является одной из ключевых фигур выпуклых четырехугольников. Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин.
Вконтакте
Определение параллелограмма
Выпуклый четырехугольник, состоящий из отрезков, каждая пара из которых параллельна, известен в геометрии как параллелограмм.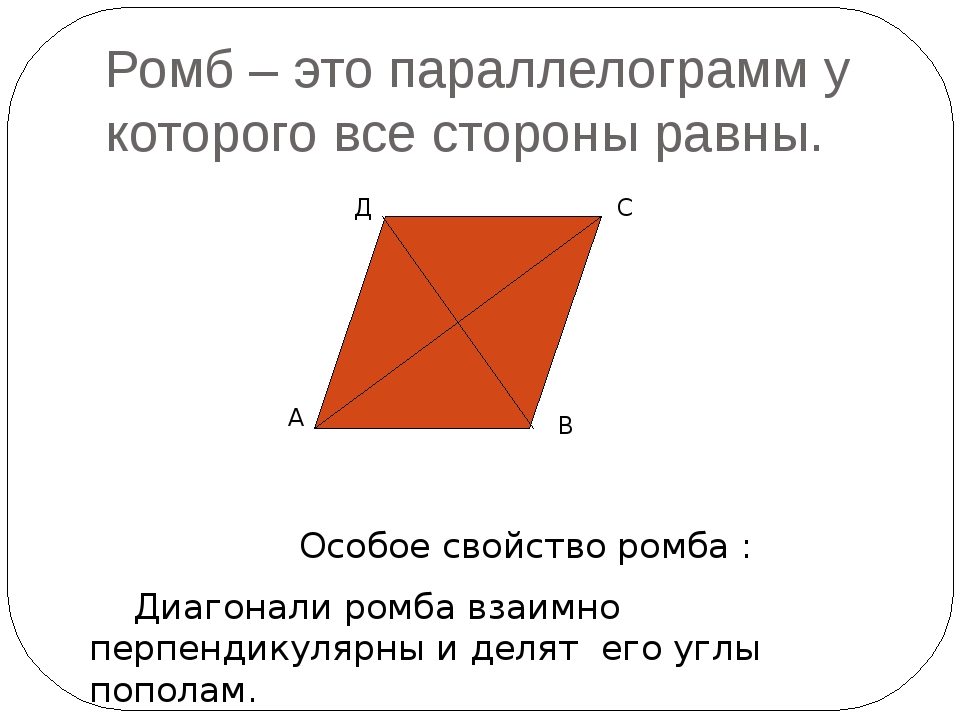
Как выглядит классический параллелограмм изображает четырехугольник ABCD. Стороны называются основаниями (AB, BC, CD и AD), перпендикуляр, проведенный из любой вершины на противоположную этой вершине сторону, — высотой (BE и BF), линии AC и BD — диагоналями.
Внимание! Квадрат, ромб и прямоугольник — это частные случаи параллелограмма.
Стороны и углы: особенности соотношения
Ключевые свойства, по большому счету, предопределены самим обозначением , их доказывает теорема. Эти характеристики следующие:
- Стороны, которые являются противоположными, — попарно одинаковые.
- Углы, расположенные противоположно друг другу — попарно равны.
Доказательство: рассмотрим ∆ABC и ∆ADC, которые получаются вследствие разделения четырехугольника ABCD прямой AC. ∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).
Отрезки AB и BC в ∆ABC попарно соответствуют линиям CD и AD в ∆ADC, что означает их тождество: AB = CD, BC = AD. Таким образом, ∠B соответствует ∠D и они равны. Так как ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, которые так же попарно одинаковые, то ∠A = ∠C. Свойство доказано.
Характеристики диагоналей фигуры
Основной признак этих линий параллелограмма: точка пересечения разделяет их пополам.
Доказательство: пусть т. Е — это точка пересечения диагоналей AC и BD фигуры ABCD. Они образуют два соизмеримых треугольника — ∆ABE и ∆CDE.
AB=CD, так как они противоположные. Согласно прямых и секущей, ∠ABE = ∠CDE и ∠BAE = ∠DCE.
По второму признаку равенства ∆ABE = ∆CDE. Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.
Особенности смежных углов
У смежных сторон сумма углов равна 180° , поскольку они лежат по одну сторону параллельных линий и секущей. Для четырехугольника ABCD:
∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º
Свойства биссектрисы:
- , опущенные на одну сторону, являются перпендикулярными;
- противолежащие вершины имеют параллельные биссектрисы;
- треугольник, полученный проведением биссектрисы, будет равнобедренным.

Определение характерных черт параллелограмма по теореме
Признаки этой фигуры вытекают из ее основной теоремы, которая гласит следующее: четырехугольник считается параллелограммом в том случае, если его диагонали пересекаются, а эта точка разделяет их на равные отрезки.
Доказательство: пусть в т. Е прямые AC и BD четырехугольника ABCD пересекаются. Так как ∠AED = ∠BEC, а AE+CE=AC BE+DE=BD, то ∆AED = ∆BEC (по первому признаку равенства треугольников). То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также. Теорема доказана.
Вычисление площади фигуры
Площадь этой фигуры находится несколькими методами, одним из самых простых: умножения высоты и основания, к которому она проведена.
Доказательство: проведем перпендикуляры BE и CF из вершин B и C. ∆ABE и ∆DCF — равные, поскольку AB = CD и BE = CF.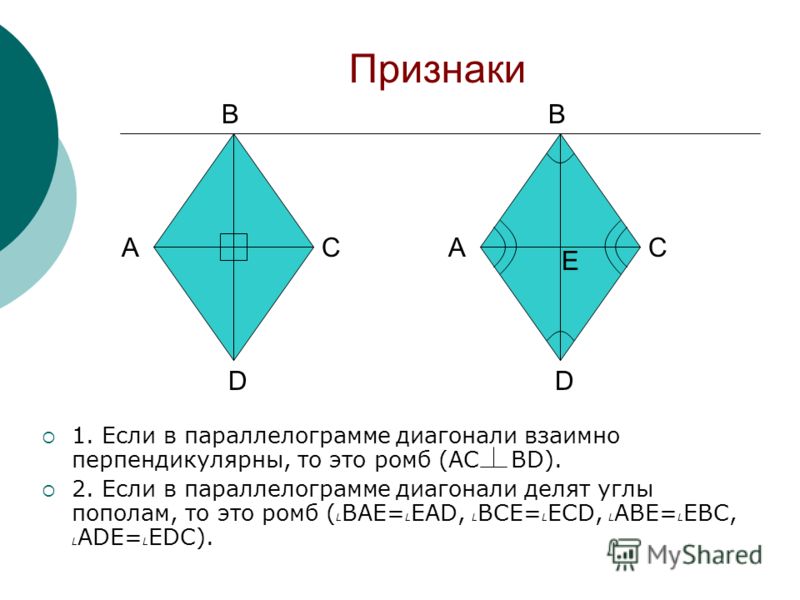 ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: S ABE и S EBCD , а также S DCF и S EBCD . Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:
ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: S ABE и S EBCD , а также S DCF и S EBCD . Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:
S ABCD = S EBCF = BE×BC=BE×AD.
Для определения общей формулы площади параллелограмма обозначим высоту как hb , а сторону — b . Соответственно:
Другие способы нахождения площади
Вычисления площади через стороны параллелограмма и угол , который они образуют, — второй известный метод.
,
Sпр-ма — площадь;
a и b — его стороны
α — угол между отрезками a и b.
Этот способ практически основывается на первом, но в случае, если неизвестна. всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть . Преобразуя соотношение, получаем . В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.
Через диагонали параллелограмма и угол, который они создают при пересечении, также можно найти площадь.
Доказательство: AC и BD пересекаясь, образуют четыре треугольника: ABE, BEC, CDE и AED. Их сумма равна площади этого четырехугольника.
Площадь каждого из этих ∆ можно найти за выражением , где a=BE, b=AE, ∠γ =∠AEB. Поскольку , то в расчетах используется единое значение синуса. То есть . Поскольку AE+CE=AC= d 1 и BE+DE=BD= d 2 , формула площади сводится до:
.
Применение в векторной алгебре
Особенности составляющих частей этого четырехугольника нашли применение в векторной алгебре, а именно: сложении двух векторов. Правило параллелограмма утверждает, что если заданные векторы и не коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.
Доказательство: из произвольно выбранного начала — т. о. — строим векторы и . Далее строим параллелограмм ОАСВ, где отрезки OA и OB — стороны. Таким образом, ОС лежит на векторе или сумме .
Формулы для вычисления параметров параллелограмма
Тождества приведены при следующих условиях:
- a и b, α — стороны и угол между ними;
- d 1 и d 2 , γ — диагонали и в точке их пересечения;
- h a и h b — высоты, опущенные на стороны a и b;
| Параметр | Формула |
| Нахождение сторон | |
| по диагоналям и косинусу угла между ними | |
| по диагоналям и стороне | |
| через высоту и противоположную вершину | |
| Нахождение длины диагоналей | |
| по сторонам и величине вершины между ними | |
Параллелограмм
(переход к области параллелограмма или периметру параллелограмма)
Параллелограмм — это плоская форма, противоположные стороны которой параллельны и равны по длине.
| и || показать равные стороны
| Противоположные стороны параллельны | |
Противоположные стороны равны по длине | |
| Противоположные углы равны (углы «а» такие же, а углы «б» такие же) | |
| Углы «a» и «b» в сумме составляют 180 °, поэтому они являются дополнительными углами. |
Играть с параллелограммом:
ПРИМЕЧАНИЕ. Квадраты, прямоугольники и ромбы — это все Параллелограммы!
Пример:
Параллелограмм , в котором все углы прямые, это прямоугольник !
Площадь параллелограмма
Площадь равна основанию , умноженному на высоту : Площадь = b × h ( h находится под прямым углом к b ) |
Пример: Параллелограмм имеет основание 6 м и высоту 3 м. Какова его площадь?
Площадь = 6 м × 3 м = 18 м 2
Периметр параллелограмма
Периметр — это расстояние по краям.
Периметр составляет в 2 раза больше (основание + длина стороны) : Периметр = 2 (ш + с) |
Пример: у параллелограмма основание 12 см и длина стороны 6 см. Каков его периметр?
Периметр = 2 × (12 см + 6 см) = 2 × 18 см = 36 см
Диагонали параллелограмма
Диагонали параллелограмма делят друг друга пополам.
Другими словами, диагонали пересекаются на полпути.
Внутри любой четырехугольник
А в любом четырехугольнике есть параллелограмм.
Как найти длину диагонали параллелограмма
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Четырехугольники Недвижимости | Параллелограммы, Трапеция, Ромб
Нажмите здесь, чтобы посмотреть это проницательное видео.Лучшие университеты мира
В этом руководстве по основным понятиям геометрии мы рассмотрим типы и свойства четырехугольников: параллелограмм, прямоугольник, квадрат, ромб, трапецию.
определение:
Четырехугольник — это простая замкнутая фигура с четырьмя сторонами.
Виды четырехугольников
Есть пять типов четырехугольников.
- Параллелограмм
- Прямоугольник
- Квадрат
- Ромб
- Трапеция
Общим свойством всех четырехугольников является то, что сумма всех их углов равна 360 °.
Давайте посмотрим на свойства различных четырехугольников.
Параллелограмм
Свойства параллелограмма
- Противоположные стороны параллельны и конгруэнтны.
- Противоположные углы совпадают.
- Смежные углы являются дополнительными.
- Диагонали делят друг друга пополам, и каждая диагональ делит параллелограмм на два равных треугольника.
- Если один из углов параллелограмма — прямой, то все остальные углы прямые, и он становится прямоугольником.
Важные формулы параллелограммов
- Площадь = Д * В
- Периметр = 2 (L + B)
Прямоугольники
Свойства прямоугольника
- Противоположные стороны параллельны и конгруэнтны.
- Все углы прямые.
- Диагонали равны и делят друг друга пополам (делят друг друга поровну).
- Противоположные углы, образованные в точке пересечения диагоналей, совпадают.
- Прямоугольник — это особый тип параллелограмма с прямыми углами.
Важные формулы для прямоугольников
- Если длина L, а ширина B, то
Длина диагонали прямоугольника = √ (L 2 + B 2 )
- Площадь = L * B
- Периметр = 2 (L + B)
Квадраты
Недвижимость квадрата
- Все стороны и углы совпадают.
- Противоположные стороны параллельны друг другу.
- Диагонали совпадают.
- Диагонали перпендикулярны и делят друг друга пополам.
- Квадрат — это особый тип параллелограмма, все углы и стороны которого равны.
- Кроме того, параллелограмм становится квадратом, если диагонали равны, а правые биссектрисы равны друг другу.
Важные формулы для квадратов
- Если «L» — длина стороны квадрата, тогда длина диагонали = L √2.
- Площадь = L 2 .
- Периметр = 4L
Ромб
Свойства ромба
- Все стороны совпадают.
- Противоположные углы совпадают.
- Диагонали перпендикулярны и делят друг друга пополам.
- Соседние углы являются дополнительными (например, ∠A + ∠B = 180 °).
- Ромб — это параллелограмм, диагонали которого перпендикулярны друг другу.
Важные формулы для ромба
Если a и b — длины диагоналей ромба,
- Площадь = (a * b) / 2
- Периметр = 4L
Трапеция
Свойства трапеции
- Основания трапеции параллельны друг другу (MN ⫽ OP).
- Нет сторон, углы и диагонали не совпадают.
Важные формулы трапеции
- Площадь = (1/2) ч (L + L 2 )
- Периметр = L + L 1 + L 2 + L 3
Обзор объектов недвижимости
Обобщая то, что мы узнали до сих пор, для удобства использования и запоминания:
| S. No. | Объект | Параллелограмм | Прямоугольник | Ромб | Площадь |
| 1 | Все стороны совпадают | ✕ | ✕ | & проверить; | & проверить; |
| 2 | Противоположные стороны параллельны и совпадают | & проверить; | & проверить; | & проверить; | & проверить; |
| 3 | Все углы совпадают | ✕ | & проверить; | ✕ | & проверить; |
| 4 | Противоположные углы совпадают | & проверить; | & проверить; | & проверить; | & проверить; |
| 5 | Диагонали совпадают | ✕ | & проверить; | ✕ | & проверить; |
| 6 | Диагонали перпендикулярны | ✕ | ✕ | & проверить; | & проверить; |
| 7 | Диагонали пересекают друг друга | & проверить; | & проверить; | & проверить; | & проверить; |
| 8 | Углы прилегающие дополнительные | & проверить; | & проверить; | & проверить; | & проверить; |
Узнать больше о:
— Свойства линий и углов
— Свойства и формулы кругов
— Типы треугольников и свойства
диагоналей делят параллелограмм на четыре равные области
На сегодняшнем уроке мы докажем, что взаимодействующие диагонали параллелограмма делят его на четыре треугольника, каждый из которых имеет равные площади.
Каждая из диагоналей параллелограмма делит его на два конгруэнтных треугольника, как мы видели, когда доказывали такие свойства, как то, что противоположные стороны равны друг другу или что две пары противоположных углов конгруэнтны. Поскольку эти два треугольника совпадают, их площади равны.
Мы также видели, что диагонали параллелограмма делят друг друга пополам, и таким образом образуются две дополнительные пары равных треугольников.
Теперь сделаем еще один шаг и, полагаясь на тот факт, что треугольники с одинаковым основанием и одинаковой высотой имеют равные площади, мы увидим, что все четыре треугольника, образованные пересекающимися диагоналями параллелограмма, имеют равные площади.
Задача
ABCD — это параллелограмм с диагоналями AC и BD, которые пересекаются в точке O. Покажите, что все четыре треугольника, образованные этими диагоналями — ΔAOD, ΔCOD, ΔAOB и ΔCOB — имеют равные площади.
Стратегия
Мы уже знаем, что противоположные пары треугольников (ΔAOD≅ ΔCOB; ΔAOB≅ ΔCOD) конгруэнтны и, следовательно, имеют равные площади. Итак, если мы сможем показать, что одна из других пар также имеет равные площади, все четыре будут равны.
Сравнивая соотношение площадей треугольников, мы часто ищем одинаковое основание или одинаковую высоту — в данном случае у нас есть и то, и другое: поскольку диагонали делят друг друга пополам, AO = OC, и ΔCOB и ΔAOB имеют одинаковые высота — БЫТЬ.
Значит, их площади равны, значит, все четыре площади равны.
Доказательство того, что диагонали делят параллелограмм на четыре равные площади
Сначала мы повторим доказательство того, что две противоположные пары треугольников совпадают:
(1) ABCD — параллелограмм // Учитывая
(2) AD || BC // Из определения параллелограмма
(3) AD = BC // Противоположные стороны параллелограмма равны по размеру
(4) ∠OBC ≅ ∠ODA // Теорема об альтернативных внутренних углах
(5) ∠OCB ≅ ∠ OAD // Теорема об альтернативных внутренних углах
(6) ΔOBC ≅ ΔODA // (3), (4), (5), Angle-Side-Angle
(7) BO = OD // Соответствующие стороны в конгруэнтных треугольниках (CPCTC)
(8) AO = OC // Соответствующие стороны в равных треугольниках (CPCTC)
(9) AB = DC // Противоположные стороны параллелограмма равны по размеру
(10) ΔAOB ≅ ΔCOD // (7), (8 ), (9), сторона-сторона-сторона
Теперь давайте посмотрим на площади этих треугольников:
(11) Площадь ΔOBC = Площадь ΔODA // (6), равные площади треугольников равны
(12 ) Площадь ΔAOB = Площадь ΔCOD // (10), конгруэнтно треугольники имеют равные площади
(13) Площадь ΔAOB = BE · AO / 2 // Площадь треугольника
(14) Площадь ΔOBC = BE · OC / 2 // Площадь треугольника
(15) Площадь ΔOBC = Площадь ΔAOB // (13), (14), (8) треугольники с одинаковым основанием и высотой.
(16) Площадь ΔOBC = Площадь ΔAOB = Площадь ΔODA = Площадь ΔCOD
Итак, мы доказали, что диагонали параллелограмма делят его на четыре треугольника, каждый из которых имеет равные площади.
Карточки с геометрией | Quizlet
Четырехсторонний правильный многоугольник со всеми сторонами равными и всеми внутренними углами 90 ° Свойства и советы
• Если диагонали ромба равны, то этот ромб должен быть квадратом. Диагонали квадрата равны (около 1.414), умноженное на длину стороны квадрата.
• Квадрат также можно определить как прямоугольник со всеми равными сторонами, или ромб со всеми равными углами, или параллелограмм с равными диагоналями, которые делят углы пополам.
• Если фигура представляет собой прямоугольник (прямые углы) и ромб (равные длины ребер), то это квадрат. (Прямоугольник (четыре равных угла) + Ромб (четыре равных стороны) = Квадрат)
• Если круг описан вокруг квадрата, площадь круга в π / 2 (примерно 1,57) раз больше площади квадрата.2/2, где dd — длина любой диагонали
• Каждая диагональ квадрата является серединным перпендикуляром другой. То есть каждая разрезает другую на две равные части, и они пересекаются под прямым углом (90 °).
• Длина каждой диагонали равна s квадратный корень из 2, где s — длина любой одной стороны.
Квадрат одновременно является ромбом (равные стороны) и прямоугольником (равные углы) и, следовательно, обладает всеми свойствами обеих этих форм, а именно:
Диагонали квадрата делят друг друга пополам.
• Диагонали квадрата делят его углы пополам.
• Диагонали квадрата перпендикулярны.
• Противоположные стороны квадрата параллельны и равны.
• Все четыре угла квадрата равны. (Каждый равен 360/4 = 90 градусов, поэтому каждый угол квадрата — прямой угол.)
• Диагонали квадрата равны.
Квадрат можно рассматривать как частный случай других четырехугольников, например
• прямоугольник, но со смежными сторонами равными
• параллелограмм, но с равными соседними сторонами и всеми углами 90 °
• ромб, но со всеми углами 90 °
Геометрия: свойства параллелограммов
Свойства параллелограммов
Параллелограмм — это четырехугольник, у которого обе пары противоположных сторон параллельны.Параллелограммы обладают множеством свойств, которые легко доказать, используя свойства параллельных прямых. Иногда вы будете использовать диагональ, чтобы разделить параллелограмм на треугольники. Если вы сделаете это осторожно, ваши треугольники будут конгруэнтными, поэтому вы можете использовать CPOCTAC.
Solid Facts
Параллелограмм — это четырехугольник, у которого обе пары противоположных сторон параллельны.
- Теорема 15.5 : Диагональ параллелограмма разделяет его на два равных треугольника.
- Пример 2 : Напишите формальное доказательство теоремы 15.5.
- Решение . Начните с просмотра списка того, что вам нужно сделать для формального доказательства. У нас уже есть формулировка теоремы. На рисунке 15.7 показан параллелограмм ABCD с диагональю AC.
Рисунок 15.7 Параллелограмм ABCD с диагональю переменного тока.
- Дано: Параллелограмм ABCD с диагональю AC.
- Докажите:? ABC ~ =? CDA.
- Доказательство: Ваш план игры состоит в том, чтобы использовать свойства параллельных прямых, пересекаемых трансверсалью, чтобы связать два из углов? ABC с двумя соответствующими углами в? CDA.Поскольку AC ~ = AC, вы можете использовать Постулат ASA, чтобы показать? ABC ~ =? CDA.
| Заявления | Причины | |
|---|---|---|
| 1. | Параллелограмм ABCD имеет диагональ переменного тока | Дано |
| 2. | BC? ? AD, разрезанный поперечно AC | Определение поперечного |
| 3. | ? BAC и? DCA — альтернативные внутренние углы | Определение альтернативных внутренних углов |
| 4. | ? BAC ~ =? DCA | Теорема 10.2 |
| 5. | BC? ? AD разрезано поперечно AC | Определение поперечного |
| 6. | ? ACB и? DAC — альтернативные внутренние углы | Определение альтернативных внутренних углов |
| 7. | ? ACB ~ =? DAC | Теорема 10.2 |
| 8. | AC ~ = AC | Отражающее свойство ~ = |
| 9. | ? ABC ~ =? CDA | Постулат ASA |
Эта теорема пригодится при установлении теорем о параллелограммах. Распространенный метод включает использование диагонали для разделения параллелограмма на два треугольника и последующее применение CPOCTAC. Следующие две теоремы используют эту технику. Я докажу первое, а вы позволите доказать второе.
- Теорема 15.6 : Противоположные стороны параллелограмма равны.
- Теорема 15.7 : Противоположные углы параллелограмма равны.
- Пример 3 : Напишите двухколоночное доказательство теоремы 15.6.
- Решение : Вы можете использовать информацию, показанную на Рисунке 15.7. Мы будем иметь дело с параллелограммом ABCD и его диагональю AC. Вам нужно будет доказать, что BC ~ = AD.
| Заявления | Причины | |
|---|---|---|
| 1. | Параллелограмм ABCD имеет диагональ переменного тока | Дано |
| 2. | ? ABC ~ =? CDA | Теорема 15.5 |
| 3. | BC ~ = AD | CPOCTAC |
Последнее свойство параллелограмма, которое я упомяну, касается пересечения диагоналей. Оказывается, диагонали параллелограмма делят друг друга пополам. Доказательство этого довольно простое, поэтому я проведу вас через план игры и предоставлю вам детали.
- Теорема 15.8 : Диагонали параллелограмма делят друг друга пополам.
Взгляните на параллелограмм ABCD на рис. 15.8. Он имеет диагонали AC и BD, которые пересекаются в M. Мы хотим показать AM ~ = MC. Самый простой способ сделать это — найти два совпадающих треугольника и использовать CPOCTAC. Два треугольника, которые мы попытаемся доказать конгруэнтностью, — это AMD и CMB. Поскольку противоположные стороны параллелограмма совпадают, BC ~ = AD. Поскольку вертикальные углы совпадают,? AMD ~ = CMB. Наконец-то у нас есть БК? ? AD, разрезанный поперечным AC, и поскольку? BCA и? CAD являются альтернативными внутренними углами, они совпадают.Используя теорему AAS, мы можем заключить, что? AMD ~ =? CMB. Завершите это с помощью CPOCTAC.
Рисунок 15.8 Параллелограмм ABCD имеет диагонали AC и BD, которые пересекаются в M.
Выдержка из The Complete Idiot’s Guide to Geometry 2004, Дениз Сечей, доктор философии. Все права защищены, включая право на воспроизведение в целом или частично в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476.Вы также можете приобрести эту книгу на Amazon.com и Barnes & Noble.
Четырехугольники
Четырехугольник — замкнутая плоская фигура, ограниченная четырьмя линиями сегменты. Например, фигура ABCD , показанная здесь, является четырехугольник.
Отрезок, проведенный от одной вершины четырехугольника к противоположной. вершиной называется диагональю четырехугольника.Например, AC — это диагональ четырехугольника ABCD , а также BD .
Типы четырехугольников и их свойства
Существует шесть основных типов четырехугольников:
1. Прямоугольник
- Противоположные стороны параллельны и равны.
- Все углы 90.
- Диагонали пересекают друг друга.
2. Квадрат
- Противоположные стороны параллельны и все стороны равны.
- Все углы 90.
- Диагонали пересекают друг друга под прямым углом.
3. Параллелограмм
- Противоположные стороны параллельны и равны.
- Противоположные углы равны.
- Диагонали пересекают друг друга.
4. Ромб
- Все стороны равны, а противоположные стороны параллельны.
- Противоположные углы равны.
- Диагонали пересекают друг друга под прямым углом.
5.Трапеция
- Трапеция имеет одну пару параллельных противоположных сторон.
- У правильной трапеции непараллельные стороны равны, а углы основания равны, как показано на следующей диаграмме.
6. Воздушный змей
- Две пары смежных сторон равны.
- Одна пара противоположных углов равна.
- Диагонали пересекаются под прямым углом.
- Самая длинная диагональ делит самую короткую диагональ пополам на две равные части. части.
Теорема 3
Докажите, что сумма углов четырехугольника равна 360.
Проба:
Следовательно, сумма углов четырехугольника равна 360.
Применение свойств углов в четырехугольниках
Доказанные теоремы можно использовать для доказательства других теорем. Они также может использоваться для поиска значений местоимений в задаче.
Пример 14
Найдите значение местоимения x на прилагаемой диаграмме. Обоснуйте свой ответ.
Решение:
Пример 15
Найдите значение каждого местоимения в показанном здесь воздушном змее.Назови причины за ваши ответы.
Решение:
Пример 16
Найдите значение каждого местоимения на прилагаемой диаграмме. Дайте причины для ваших ответов.
Решение:
Пример 17
Найдите значение местоимения на прилагаемой диаграмме.Дайте причины вашего ответа.


Leave A Comment