Физика-7-9-Задачник-Лукашик-2002 (Лукашик) » СтудИзба
№°995) найдем, чтоудельная теплоемкость нафталина равна 130фарфора — 750 Дж .кг ⋅ °C128Дж, нкеля ⎯ 460 Дж ,кг ⋅ °Cкг ⋅ °C№ 1003.Дано:∆t = 1°Cm = 2 кгРешение: c =Q;m∆t1) молокоc=2) золотоc=3) бронзаc=4) никельc=5) глицеринc=7800 ДжДж= 3900;2 кг ⋅ °Скг ⋅ °С260 ДжДж= 130;2 кг ⋅ °Скг ⋅ °С760 ДжДж= 380;2 кг ⋅ °Скг ⋅ °С920 ДжДж= 460;2 кг ⋅ °Скг ⋅ °С4800 ДжДж= 2400.2 кг ⋅ °Скг ⋅ °СНайти с.№ 1004.Дано:∆t = 1°Cm = 5 кгНайти с.Решение: ∆U = cm∆t;∆U 2100 ДжДжc=== 420..m∆t 5 кг ⋅ 1°Скг ⋅ °СДжОтвет: c = 420.кг ⋅ °С№ 1005.920 Дж; 280 Дж; 500 Дж; 420 Дж; 750 Дж.№ 1006.2100 Дж; 125 Дж; 5,25 Дж; 1950 кДж; 76 кДж.№ 1007.Дано: ∆t = 50°Cm = 20 кгДжc = 500кг ⋅ °СНайти ∆U.№ 1008.Дано: t1 = 15°C;t2 = 115°C;m=10 г = 0,01 кг;Джc = 500кг ⋅ °СНайти ∆U.Решение:∆U = cm∆t = 500Дж⋅20 кг⋅50°С = 500000 Дж.кг ⋅ °СОтвет: ∆U = 500000 Дж.Решение:∆U = cm(t2−t1) =Дж= 500⋅0,01 кг⋅(115°С−15°С) = 500 Дж.кг ⋅ °СОтвет: ∆U = 500 Дж.129№ 1009.Дано: t1 = 15°C;t2 = 750°C; m = 15 кг;Джc = 380кг ⋅ °СНайти Q.Решение: Q = cm(t2−t1) =Дж= 380⋅15 кг⋅(750°С−15°С) =кг ⋅ °С= 4189500 Дж ≈ 4200 кДж.Ответ: Q ≈ 4200 кДж.№ 1010.Дано: t1 = 100°Ct2 = 14°CV = 250 см3ρ = 1 г/см3Джc = 4200кг ⋅ °СНайти Q.Решение:m = ρV = 1 г/см3⋅250 cм3 = 250 г = 0,25 кг;Q = cm∆t = cρV(t1−t2) =Дж= 4200⋅0,25 кг⋅(100°С−14°С) =кг ⋅ °С= 90300 Дж = 90,3 кДж.Ответ: Q = 90,3 кДж.№ 1011.Дано: ∆t = 50°Cm = 0,35 т = 350 кгДжc = 880кг ⋅ °СНайти Q.№ 1012.Дано: t1 = 15°C;t2 = 1115°C; m = 32 кг;Джc = 540кг ⋅ °СНайти Q.Решение:Дж⋅350 кг⋅50°С =кг ⋅ °С= 15400000 Дж = 15400 кДж.Ответ: Q = 15400 кДж.Q = cm∆t = 880Решение: Q = cm(t2−t1) =Дж= 540⋅32 кг⋅(1115°С−15°С) =кг ⋅ °С= 19008000 Дж = 19008 кДж.Ответ: Q = 19008 кДж.№ 1013.а) Дано: t1 = 0°C; t2 = 30°C;V = 0,5 л = 0,5⋅10-3 м3;ρ = 1,29 кг/м3;Джc = 1000кг ⋅ °СНайти Q.б) Дано: t1 = 0°C;t2 = 20°C; V =60 м3 ;ρ = 1,29 кг/м3;c = 720 Джкг ⋅ °СНайти Q.130Решение:Q = cm(t2−t1) = cρV(t2−t1) =Дж= 1000⋅1,29 кг/м3⋅кг ⋅ °С⋅0,5⋅10−3 м3⋅(30°С−0°С) = 19,35 Дж.Ответ: Q = 19,35 Дж.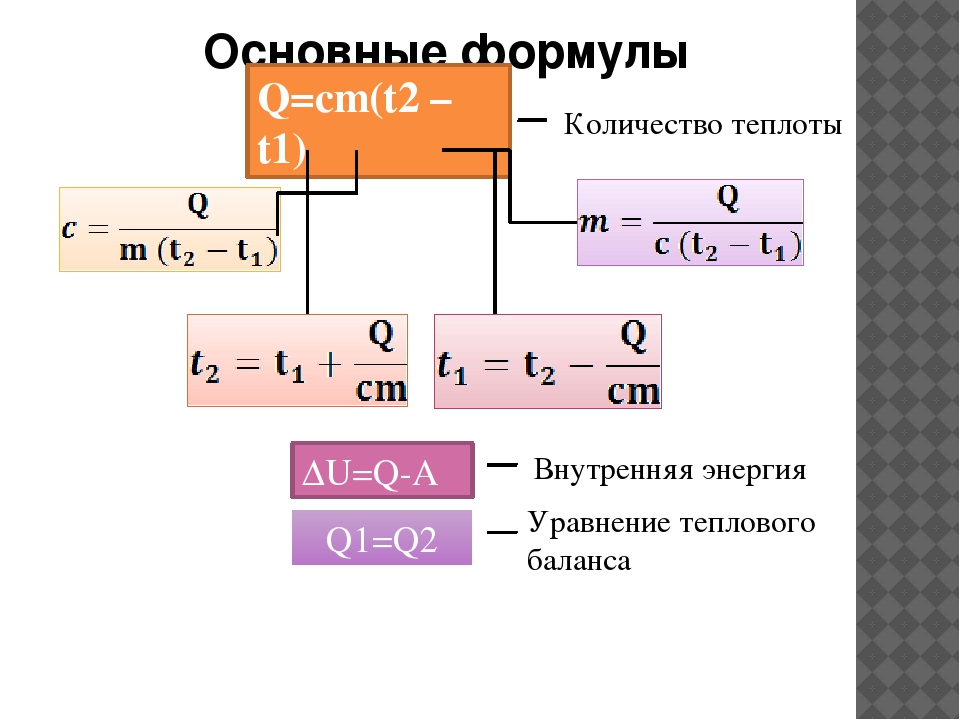 Решение:Q = cρV(t2−t1) = 720 Дж ⋅1,29 кг/м3⋅кг ⋅ °С⋅60 м3⋅(20°С−0°С)≈ 1100000 Дж =1,1 МДжОтвет: Q ≈ 1,1 МДж.№ 1014.Дано: t1 = 20°C; t2 = 30°C;m = 1,5 т = 1500 кг;Джc = 880кг ⋅ °СНайти Q.№ 1015.Дано: t1 = 20°C; t2 = 100°C;mАЛ = 200 г = 0,2 кг ;VВ = 1,5 л; ρВ = 1 кг/л;ДжcАЛ = 920;кг ⋅ °СДжcВ = 4200кг ⋅ °СНайти Q.№ 1016.Дано: t1 = 10°C; t2 = 100°C;mАЛ = 800 г = 0,8 кг;VВ = 5 л; ρВ = 1 кг/л;ДжcАЛ = 920;кг ⋅ °СДжcВ = 4200кг ⋅ °СНайти Q.Решение:Дж⋅1500 кг×кг ⋅ °С×(30°С−20°С) = 13200000 Дж = 1,32 МДж.Ответ: Q = 1,32 МДж.Q = cm(t2−t1) = 880Решение:mВ = ρВVВ = 1 кг/л⋅1,5 л = 1,5 кг;Q = QВ+QАЛ = (сАЛmАЛ+сВmВ)(t2−t1) =ДжДж⋅0,2 кг+4200⋅1,5 кг)×= (920кг ⋅ °Скг ⋅ °С×(100°С−20°С) = 518720 Дж ≈ 518,7 кДж.Ответ: Q ≈ 518,7 кДж.Решение:mВ = ρВVВ = 1 кг/л⋅5 л = 5 кг;Q = QВ+QАЛ = (сАЛmАЛ+сВmВ)(t2−t1) =ДжДж⋅0,8 кг+4200⋅5 кг)×= (920кг ⋅ °Скг ⋅ °С×(100°С−10°С) = 1956240 Дж == 1956,24 кДж.Ответ: Q = 1956,24 кДж.№ 1017.Дано: t1 = 4°C; t2 = 29°C;mЖ = 65 кг; VВ = 200 л;ρВ = 1 кг/л;cЖ=460 Дж ; cВ=4200 Джкг ⋅ °Скг ⋅ °СНайти Q.№ 1018.Дано: t1 = 20°C; t2 = 70°C;mК = 5 кг; n = 300;Джc = 880кг ⋅ °СНайти Q.Решение:mВ = ρВVВ = 1 кг/л⋅200 л = 200 кг;Q = QВ+QЖ = (сЖmЖ+сВmВ)(t2−t1) =ДжДж⋅65кг+4200⋅200кг)⋅=(460кг ⋅ °Скг ⋅ °С⋅(29°С−4°С)=21747500Дж=21747,5кДжОтвет: Q = 21747,5 кДж.Решение:Q = cm(t2−t1) = cmКn(t2−t1) =Дж⋅5 кг⋅300⋅50°С = 66000000 Дж.= 880кг ⋅ °СОтвет: Q = 66000000 Дж.131№ 1019.Дано: t1 = 15°C; t2 = 25°C;V =(100×6×2) м3;ρ = 1000 кг/м3;c = 4200 Джкг ⋅ °СНайти Q.№ 1020.Дано: Q = 10 Дж;V =200 см3ρ = 1 г/см3c = 4200 Джкг ⋅ °СНайти ∆t.Решение:Q = cm(t2−t1) = cρV(t2−t1) == 4200Дж⋅1000кг/м3⋅(100×6×2) м3⋅10°С =кг ⋅ К= 5,04⋅1010 Дж.Ответ: Q = 5,04⋅1010 Дж..Решение: Q = cm∆tm = ρV = 1 г/см3⋅200 cм3 = 200 г = 0,2 кг;Q10 Дж∆t ==≈ 0,012°С .cm 4200 Дж ⋅ 0,2 кгкг⋅°СОтвет: ∆t ≈ 0,012°C.№ 1021.Дано: ∆U = 280 Джm =100 г = 0,1 кгc = 140 Джкг ⋅ °СНайти ∆t.Решение:∆t =280 Дж∆U== 20°C.cm 140 Дж ⋅ 0,1 кгкг⋅°СОтвет: ∆t = 20°C.№ 1022.Дано: ∆U = 1000 Дж;Решение:∆U1000 Дж== 200°C.cm 250 Дж ⋅ 0,02кгДжm =20 г = 0,02 кг; c = 250кг ⋅ °С∆t =Найти ∆t.
Решение:Q = cρV(t2−t1) = 720 Дж ⋅1,29 кг/м3⋅кг ⋅ °С⋅60 м3⋅(20°С−0°С)≈ 1100000 Дж =1,1 МДжОтвет: Q ≈ 1,1 МДж.№ 1014.Дано: t1 = 20°C; t2 = 30°C;m = 1,5 т = 1500 кг;Джc = 880кг ⋅ °СНайти Q.№ 1015.Дано: t1 = 20°C; t2 = 100°C;mАЛ = 200 г = 0,2 кг ;VВ = 1,5 л; ρВ = 1 кг/л;ДжcАЛ = 920;кг ⋅ °СДжcВ = 4200кг ⋅ °СНайти Q.№ 1016.Дано: t1 = 10°C; t2 = 100°C;mАЛ = 800 г = 0,8 кг;VВ = 5 л; ρВ = 1 кг/л;ДжcАЛ = 920;кг ⋅ °СДжcВ = 4200кг ⋅ °СНайти Q.Решение:Дж⋅1500 кг×кг ⋅ °С×(30°С−20°С) = 13200000 Дж = 1,32 МДж.Ответ: Q = 1,32 МДж.Q = cm(t2−t1) = 880Решение:mВ = ρВVВ = 1 кг/л⋅1,5 л = 1,5 кг;Q = QВ+QАЛ = (сАЛmАЛ+сВmВ)(t2−t1) =ДжДж⋅0,2 кг+4200⋅1,5 кг)×= (920кг ⋅ °Скг ⋅ °С×(100°С−20°С) = 518720 Дж ≈ 518,7 кДж.Ответ: Q ≈ 518,7 кДж.Решение:mВ = ρВVВ = 1 кг/л⋅5 л = 5 кг;Q = QВ+QАЛ = (сАЛmАЛ+сВmВ)(t2−t1) =ДжДж⋅0,8 кг+4200⋅5 кг)×= (920кг ⋅ °Скг ⋅ °С×(100°С−10°С) = 1956240 Дж == 1956,24 кДж.Ответ: Q = 1956,24 кДж.№ 1017.Дано: t1 = 4°C; t2 = 29°C;mЖ = 65 кг; VВ = 200 л;ρВ = 1 кг/л;cЖ=460 Дж ; cВ=4200 Джкг ⋅ °Скг ⋅ °СНайти Q.№ 1018.Дано: t1 = 20°C; t2 = 70°C;mК = 5 кг; n = 300;Джc = 880кг ⋅ °СНайти Q.Решение:mВ = ρВVВ = 1 кг/л⋅200 л = 200 кг;Q = QВ+QЖ = (сЖmЖ+сВmВ)(t2−t1) =ДжДж⋅65кг+4200⋅200кг)⋅=(460кг ⋅ °Скг ⋅ °С⋅(29°С−4°С)=21747500Дж=21747,5кДжОтвет: Q = 21747,5 кДж.Решение:Q = cm(t2−t1) = cmКn(t2−t1) =Дж⋅5 кг⋅300⋅50°С = 66000000 Дж.= 880кг ⋅ °СОтвет: Q = 66000000 Дж.131№ 1019.Дано: t1 = 15°C; t2 = 25°C;V =(100×6×2) м3;ρ = 1000 кг/м3;c = 4200 Джкг ⋅ °СНайти Q.№ 1020.Дано: Q = 10 Дж;V =200 см3ρ = 1 г/см3c = 4200 Джкг ⋅ °СНайти ∆t.Решение:Q = cm(t2−t1) = cρV(t2−t1) == 4200Дж⋅1000кг/м3⋅(100×6×2) м3⋅10°С =кг ⋅ К= 5,04⋅1010 Дж.Ответ: Q = 5,04⋅1010 Дж..Решение: Q = cm∆tm = ρV = 1 г/см3⋅200 cм3 = 200 г = 0,2 кг;Q10 Дж∆t ==≈ 0,012°С .cm 4200 Дж ⋅ 0,2 кгкг⋅°СОтвет: ∆t ≈ 0,012°C.№ 1021.Дано: ∆U = 280 Джm =100 г = 0,1 кгc = 140 Джкг ⋅ °СНайти ∆t.Решение:∆t =280 Дж∆U== 20°C.cm 140 Дж ⋅ 0,1 кгкг⋅°СОтвет: ∆t = 20°C.№ 1022.Дано: ∆U = 1000 Дж;Решение:∆U1000 Дж== 200°C.cm 250 Дж ⋅ 0,02кгДжm =20 г = 0,02 кг; c = 250кг ⋅ °С∆t =Найти ∆t. Ответ: ∆t = 200°C.кг⋅°С№ 1023.а) Дано: ∆U = 178,5 кДж = Решение: ∆T = t2−t1 = 100°C−15°C = 85°C;= 178500 Дж∆U = cm∆T ⇒ m =t1 = 15°C; t2 = 100°C∆U178500Дж= 0,5кг.==ДжДжcT∆c = 42004200⋅ 85°Скг⋅°Скг ⋅ °СНайти m.Ответ: m = 0,5 кг.б) Дано: t1 = 15°C Решение: m1 = V1ρ = 0,003 м3⋅1000 кг/м3 = 3 кг;t2 = 100°Ccm(t3−t1) = cm1(t2−t3) ⇒t3 = 35°C⇒ m = m1 (t 2 − t3 ) = 3 кг (100°С − 35°С ) = 9,75 кг;V1 = 3 л = 0,003 м3(35°С − 15°С)(t3 − t1 )ρ = 1000 кг/м3m9,75 кг3V= == 0,00975 м = 9,75 л.3ρНайти V.1321000 кг/мОтвет: V = 9,75 л.в) Дано: t1 = 10°C;t2 = 100°C;t = 50°CV1 = 3 л = 0,003 м3ρ = 1000 кг/м3Найти V.г) Дано: t1 = 6°C;t2 = 96°C; t = 36°C;V1 = 40 л = 0,04 м3;ρ = 1000 кг/м3Найти m2.Решение: m1 = V1ρ = 0,003 м3⋅1000 кг/м3 = 3 кг;cm1(t−t1) = сm2(t2−t) ⇒⇒ m2 = 3 кг (50°С − 10 °С ) = 2,4 кг,(100 °С − 50°С )что соотвеиствует V = 2,4 л.Ответ: V = 2,4 л.Решение: m1 = V1ρ = 0,04 м3⋅1000 кг/м3 = 40 кг;cm1(t−t1) = сm2(t2−t) ⇒⇒ m2 = 40кг (36°С − 6°С ) = 20кг.(96°С − 36°С )Ответ: m2 = 20кг.№ 1024.Дано: ∆U = 152 Дж;t1 = 20°C; t2 = 24°C;m = 100 г = 0,1 кгРешение: ∆T = t2−t1 = 24°C−20°C = 4°C;c = ∆U = 152 Джm∆TНайти c.0,1 кг ⋅ 4°СОтвет: c = 380№ 1025.Дано: ∆U = 280 Дж;t1 = 20°C; t2 = 40°C;m = 100 г = 0,1 кг= 380Дж.кг ⋅ °СДж .кг ⋅ °СРешение: ∆T = t2−t1 = 24°C−20°C = 20°C;c=Найти c.∆U280 ДжДж.== 140m∆T 0,1кг ⋅ 20°Скг ⋅ °СОтвет: c = 140Дж .кг ⋅ °С№ 1026.Дано:Решение: ∆U = cm (t1−t2) = cmt1−cmt2 ⇒ t1 =∆U = 5 кДж = 5000 Дж∆U + cmt 2==t2 = 32°CcmДжm = 100 г = 0,1 кг5000Дж + 250⋅ 0,1кг ⋅ 32°С=Найти t1.№ 1027.Дано:∆U = 1680 кДж == 1680000 Джt1 = 100°CV=5лρ = 1 кг/лНайти t2.кг⋅°СДж250⋅ 0,1кгкг⋅°С= 232°С.Ответ: t1 = 232°C.Решение: m = Vρ = 5 л⋅1 кг/л = 5 кг;∆U = cmt1−cmt2 ⇒ t2 = cmt1 − ∆U =cm=4200Дж⋅ 5 м ⋅ 100°С − 1680000 Джкг⋅°СДж4200кг⋅°С= 20°C.Ответ: t2 = 20°C.133№ 1028.Дано:∆U + cmt 2Решение: t1 ==∆U = 30,4 кДж =cm= 30400 ДжДж30400 Дж + 380⋅ 0,2 кг ⋅ 20°Скг ⋅°Сt2 = 20°C== 420°С.Джm = 200 г = 0,2 кг380⋅ 0,2кгкг ⋅°СНайти t1.Ответ: t1 = 420°C.№ 1029.а) Дано: ∆tВ = 100°C Решение:m В = 800 г = 0,8 кгm c ∆tmАЛсАЛ∆tАЛ = тВcВ∆tВ ⇒ ∆tАЛ = В В В =m АЛ = 2 кгтАЛ ⋅ cАЛДжcВ = 4200Дж0 ,8кг ⋅ 4200⋅ 100°Скг ⋅ °Скг⋅°С== 182,6°С.
Ответ: ∆t = 200°C.кг⋅°С№ 1023.а) Дано: ∆U = 178,5 кДж = Решение: ∆T = t2−t1 = 100°C−15°C = 85°C;= 178500 Дж∆U = cm∆T ⇒ m =t1 = 15°C; t2 = 100°C∆U178500Дж= 0,5кг.==ДжДжcT∆c = 42004200⋅ 85°Скг⋅°Скг ⋅ °СНайти m.Ответ: m = 0,5 кг.б) Дано: t1 = 15°C Решение: m1 = V1ρ = 0,003 м3⋅1000 кг/м3 = 3 кг;t2 = 100°Ccm(t3−t1) = cm1(t2−t3) ⇒t3 = 35°C⇒ m = m1 (t 2 − t3 ) = 3 кг (100°С − 35°С ) = 9,75 кг;V1 = 3 л = 0,003 м3(35°С − 15°С)(t3 − t1 )ρ = 1000 кг/м3m9,75 кг3V= == 0,00975 м = 9,75 л.3ρНайти V.1321000 кг/мОтвет: V = 9,75 л.в) Дано: t1 = 10°C;t2 = 100°C;t = 50°CV1 = 3 л = 0,003 м3ρ = 1000 кг/м3Найти V.г) Дано: t1 = 6°C;t2 = 96°C; t = 36°C;V1 = 40 л = 0,04 м3;ρ = 1000 кг/м3Найти m2.Решение: m1 = V1ρ = 0,003 м3⋅1000 кг/м3 = 3 кг;cm1(t−t1) = сm2(t2−t) ⇒⇒ m2 = 3 кг (50°С − 10 °С ) = 2,4 кг,(100 °С − 50°С )что соотвеиствует V = 2,4 л.Ответ: V = 2,4 л.Решение: m1 = V1ρ = 0,04 м3⋅1000 кг/м3 = 40 кг;cm1(t−t1) = сm2(t2−t) ⇒⇒ m2 = 40кг (36°С − 6°С ) = 20кг.(96°С − 36°С )Ответ: m2 = 20кг.№ 1024.Дано: ∆U = 152 Дж;t1 = 20°C; t2 = 24°C;m = 100 г = 0,1 кгРешение: ∆T = t2−t1 = 24°C−20°C = 4°C;c = ∆U = 152 Джm∆TНайти c.0,1 кг ⋅ 4°СОтвет: c = 380№ 1025.Дано: ∆U = 280 Дж;t1 = 20°C; t2 = 40°C;m = 100 г = 0,1 кг= 380Дж.кг ⋅ °СДж .кг ⋅ °СРешение: ∆T = t2−t1 = 24°C−20°C = 20°C;c=Найти c.∆U280 ДжДж.== 140m∆T 0,1кг ⋅ 20°Скг ⋅ °СОтвет: c = 140Дж .кг ⋅ °С№ 1026.Дано:Решение: ∆U = cm (t1−t2) = cmt1−cmt2 ⇒ t1 =∆U = 5 кДж = 5000 Дж∆U + cmt 2==t2 = 32°CcmДжm = 100 г = 0,1 кг5000Дж + 250⋅ 0,1кг ⋅ 32°С=Найти t1.№ 1027.Дано:∆U = 1680 кДж == 1680000 Джt1 = 100°CV=5лρ = 1 кг/лНайти t2.кг⋅°СДж250⋅ 0,1кгкг⋅°С= 232°С.Ответ: t1 = 232°C.Решение: m = Vρ = 5 л⋅1 кг/л = 5 кг;∆U = cmt1−cmt2 ⇒ t2 = cmt1 − ∆U =cm=4200Дж⋅ 5 м ⋅ 100°С − 1680000 Джкг⋅°СДж4200кг⋅°С= 20°C.Ответ: t2 = 20°C.133№ 1028.Дано:∆U + cmt 2Решение: t1 ==∆U = 30,4 кДж =cm= 30400 ДжДж30400 Дж + 380⋅ 0,2 кг ⋅ 20°Скг ⋅°Сt2 = 20°C== 420°С.Джm = 200 г = 0,2 кг380⋅ 0,2кгкг ⋅°СНайти t1.Ответ: t1 = 420°C.№ 1029.а) Дано: ∆tВ = 100°C Решение:m В = 800 г = 0,8 кгm c ∆tmАЛсАЛ∆tАЛ = тВcВ∆tВ ⇒ ∆tАЛ = В В В =m АЛ = 2 кгтАЛ ⋅ cАЛДжcВ = 4200Дж0 ,8кг ⋅ 4200⋅ 100°Скг ⋅ °Скг⋅°С== 182,6°С. ДжДж2кг ⋅ 920cАЛ = 920кг⋅°Скг ⋅ °СНайти ∆tАЛ.Ответ: ∆tАЛ = 182,6°С.б) Дано: t1 = 15°Cm t + m2t2Решение: cm1(t−t1) = cm2(t2−t) ⇒ t = 1 1=t2 = 75°Cm1 + m2m 1= 50 кг50 кг ⋅ 15°С + 30 кг ⋅ 75°Сm 2= 30 кг= 37,5°C.=80 кгНайти t.Ответ: t = 37,7°С.Решение:в) Дано: t1 = 10°C;t2 = 90°C; m 1= 60 кг;m t + m2t2 60 кг ⋅ 10°С + 50 кг ⋅ 90°С ≈46,4°C.t= 1 1=m 2= 50 кг60 кг + 50 кгm +m1Найти t.№ 1030.Дано: ∆tВ = 13,2°C∆tК = 63°CДжcВ = 4200кг ⋅ °СНайти cК.2Ответ: t ≈ 46,4°С.Решение: тсК∆tК = тсВ∆tВ ⇒Дж4200⋅ 13,2°СДж .кг⋅°С⇒ cК = сВ∆tВ == 880∆tК63°Скг ⋅ °СОтвет: cК = 880 Дж .кг ⋅ °С№ 1031.Дано: t = 5 мин = 300 с; Решение: ∆U = Pt = cm∆t ⇒ ∆t =P = 75 Вт; m = 5 кг;Pt75Вт ⋅ 300с==≈ 1,07°С .ДжДжcmc = 42004200⋅ 5кгкг⋅°Скг ⋅ °СНайти ∆t.Ответ: ∆t ≈ 1,07°C.134№ 1032.Решение:Дано:t = 1,5 мин = 90 сДжQ = cm∆t = 500⋅1,2 кг⋅20° С = 12000 Дж;m = 1,2 кгкг ⋅ °СДжQ 12000Джc = 500Q = 0,4А ⇒ А === 30000Дж ;кг ⋅ °С0 ,40 ,4∆t = 20°CA 30000Дж≈ 333,3 Вт ≈ 0,3 кВт.=Р=t90сНайти P, A.Ответ: P ≈ 0,3 кВт, A = 30000 Дж.39.
ДжДж2кг ⋅ 920cАЛ = 920кг⋅°Скг ⋅ °СНайти ∆tАЛ.Ответ: ∆tАЛ = 182,6°С.б) Дано: t1 = 15°Cm t + m2t2Решение: cm1(t−t1) = cm2(t2−t) ⇒ t = 1 1=t2 = 75°Cm1 + m2m 1= 50 кг50 кг ⋅ 15°С + 30 кг ⋅ 75°Сm 2= 30 кг= 37,5°C.=80 кгНайти t.Ответ: t = 37,7°С.Решение:в) Дано: t1 = 10°C;t2 = 90°C; m 1= 60 кг;m t + m2t2 60 кг ⋅ 10°С + 50 кг ⋅ 90°С ≈46,4°C.t= 1 1=m 2= 50 кг60 кг + 50 кгm +m1Найти t.№ 1030.Дано: ∆tВ = 13,2°C∆tК = 63°CДжcВ = 4200кг ⋅ °СНайти cК.2Ответ: t ≈ 46,4°С.Решение: тсК∆tК = тсВ∆tВ ⇒Дж4200⋅ 13,2°СДж .кг⋅°С⇒ cК = сВ∆tВ == 880∆tК63°Скг ⋅ °СОтвет: cК = 880 Дж .кг ⋅ °С№ 1031.Дано: t = 5 мин = 300 с; Решение: ∆U = Pt = cm∆t ⇒ ∆t =P = 75 Вт; m = 5 кг;Pt75Вт ⋅ 300с==≈ 1,07°С .ДжДжcmc = 42004200⋅ 5кгкг⋅°Скг ⋅ °СНайти ∆t.Ответ: ∆t ≈ 1,07°C.134№ 1032.Решение:Дано:t = 1,5 мин = 90 сДжQ = cm∆t = 500⋅1,2 кг⋅20° С = 12000 Дж;m = 1,2 кгкг ⋅ °СДжQ 12000Джc = 500Q = 0,4А ⇒ А === 30000Дж ;кг ⋅ °С0 ,40 ,4∆t = 20°CA 30000Дж≈ 333,3 Вт ≈ 0,3 кВт.=Р=t90сНайти P, A.Ответ: P ≈ 0,3 кВт, A = 30000 Дж.39.
Удельная теплота сгорания топлива№ 1033.Удельная теплота всех этих дров одинакова, поэтому при их сгорании выделится одинаковое количество теплоты.№ 1034.Можно. Для этого надо знать удельную теплоту сгорания и массуполена.№ 1035.Дано: т1 = 15 кгq1 = 34⋅106 Дж/кгт2 = 200 г = 0,2 кгq2 = 46⋅106 Дж/кгНайти U1, U2.№ 1036.Дано: т1 = 5 кг;q1 = 46⋅106 Дж/кг;т2 = 10 кг;q2 = 30⋅106 Дж/кгНайти Q1, Q2.Решение:U1 = Q1 = q1т1 = 34⋅106 Дж/кг⋅15 кг = 5,1⋅108 Дж.U2 = Q2 = q2т2 = 46⋅106 Дж/кг⋅0,2 кг = 9,2⋅106 Дж.Ответ: U1 = 5,1⋅108 Дж, U2 = 9,2⋅106 Дж.Решение:Q1 = q1т1 = 46⋅106 Дж/кг⋅5 кг = 2,3⋅108 Дж.Q2 = q2т2 = 30⋅106 Дж/кг⋅10 кг = 3⋅108 Дж.Ответ: Q1 = 2,3⋅108 Дж, Q2 = 3⋅108 Дж.№ 1037.Дано: т1 = 25г = 0,025 кгq1 = 3,8⋅106 Дж/кгт2 = 0,5 т = 500 кгq2 = 14⋅106 Дж/кгт3 = 1,5 т = 1500 кгq3 = 30⋅106 Дж/кгНайти Q1, Q2, Q3.Решение:Q1 = q1т1 = 3,8⋅106 Дж/кг⋅0,025 кг == 9,5⋅104 Дж.Q2 = q2т2 = 14⋅106 Дж/кг⋅500 кг = 7⋅109 Дж.Q3 = q3т3 = 30⋅106 Дж/кг⋅1500 кг == 4,5⋅1010 Дж.Ответ: Q1=9,5⋅104Дж, Q2=7⋅109Дж,Q3=4,5⋅1010Дж135№ 1038. Дано:V = 5 м3q = 3,8⋅106 Дж/кгρ = 700 кг/м3Найти Q.№ 1039.Дано:V1 = 0,25 м3ρ1 = 800 кг/м3q1 = 46⋅106 Дж/кгV 2 = 0,00005 м3ρ2 = 800 кг/м3q2 = 27⋅106 Дж/кгV3 = 25 л = 0,025 м3ρ3 = 710 кг/м3q3 = 46⋅106 Дж/кгV4 = 250 л = 0,25 м3ρ4 = 800 кг/м3q4 = 44⋅106 Дж/кгНайти Q1, Q2, Q3, Q4.№ 1040.Дано:т = 2 кгq1 = 46⋅106 Дж/кгq2 = 13⋅106 Дж/кгНайти ∆Q.№ 1041.Дано:т = 1 кгq1 = 120⋅106 Дж/кгq2 = 13⋅106 Дж/кгНайти n.№ 1042.Дано: т1 = 2 кгq1 = 46⋅106 Дж/кгт2 = 3 кгq2 = 46⋅106 Дж/кгНайти Q.136Решение:Q = qm = qρV = 13⋅106 Дж/кг⋅700 кг/м3⋅5 м3 == 4,55⋅1010 Дж.Ответ: Q = 4,55⋅1010 Дж.Решение:Q = qm = qρV.Q1 = 800 кг/м3⋅0,25 м3⋅46⋅106 Дж/кг == 9,2⋅109Дж.Q2 = 800 кг/м3⋅0,00005 м3⋅27⋅106 Дж/кг == 1,08⋅106 Дж.Q3 = 710 кг/м3⋅0,025 м3⋅46⋅106 Дж/кг ≈≈ 8,2⋅108 Дж.Q4 = 800 кг/м3⋅0,25 м3⋅44⋅106 Дж/кг == 8,8⋅109 Дж.Ответ: Q1 = 9,2⋅109Дж, Q2 = 1,08⋅106 Дж,Q3 ≈ 8,2⋅108 Дж, Q4 = 8,8⋅109 Дж.Решение:∆Q = Q1−Q2 = m(q1−q2) == 2 кг⋅(46−13)⋅106 Дж/кг = 6,6⋅107 Дж.Ответ: ∆Q = 6,6⋅107 Дж.Решение:n=Q1 q1 120 ⋅ 106 Дж/кг==≈ 9.Q2 q2 13 ⋅ 106 Дж/кгОтвет: n ≈ 9.Решение:Q = Q1+Q2 = m1q1+m2q2 = 2 кг⋅46⋅106 Дж/кг++3 кг⋅46⋅106 Дж = 2,3⋅108 Дж.Ответ: Q = 2,3⋅108 Дж.№ 1043.Дано:V1 = 1,5 л = 0,0015 м3ρ1 = 710 кг/м3q1 = 46⋅106 Дж/кгV2 = 0,5 л = 0,0005 м3ρ2 = 800 кг/м3q2 = 27⋅106 Дж/кгНайти Q.№ 1044.Дано: т1 = 5 кгq1 = 14⋅106 Дж/кгV2 = 0,01 м3ρ2 = 400 кг/м3q2 = 13⋅106 Дж/кгНайти Q.№ 1045.Дано:V1 = 2 м3ρ1 = 400 кг/м3q1 = 13⋅106 Дж/кгm2 = 1,5 т = 1500 кгq2 = 30⋅106 Дж/кгНайти Q.Решение:Q = Q1+Q2 = ρ1V1q1+ρ2V2q2 == 710 кг/м3⋅0,0015 м3⋅46⋅106 Дж/кг++800 кг/м3⋅0,0005 м3⋅27⋅106 Дж/кг ≈ 6⋅107 Дж.Ответ: Q ≈ 6⋅107 Дж.Решение:Q = m1q1+ρ2V2q2 = 14⋅106 Дж/кг⋅5 кг++0,01 м3⋅400 кг/м3⋅13⋅106 Дж/кг = 1,22⋅108 Дж.Ответ: Q = 1,22⋅108 Дж.Решение:Q = m1q1+m2q2 = ρ1V1q1+m2q2 == 400 кг/м3⋅2 м3⋅13⋅106 Дж/кг++1500 кг⋅30⋅106 Дж/кг ≈ 5,5⋅1010 Дж.Ответ: Q ≈ 5,5⋅1010 Дж.№ 1046.Решение:а) Дано:m = 10 кгQ 2 ,9 ⋅ 10 7 Дж= 2,9⋅106 Дж/кг.Q = 2,9⋅107 Дж Q = mq ⇒ q = m =10 кгНайти q.Ответ: q = 2,9⋅106 Дж/кг.б) Дано: n = 4Решение: nmГРhg = mНq;mГР = 7,26 кгmН q0,001кг ⋅ 44 ⋅ 106 Дж/кг≈ 154,6 м.
Дано:V = 5 м3q = 3,8⋅106 Дж/кгρ = 700 кг/м3Найти Q.№ 1039.Дано:V1 = 0,25 м3ρ1 = 800 кг/м3q1 = 46⋅106 Дж/кгV 2 = 0,00005 м3ρ2 = 800 кг/м3q2 = 27⋅106 Дж/кгV3 = 25 л = 0,025 м3ρ3 = 710 кг/м3q3 = 46⋅106 Дж/кгV4 = 250 л = 0,25 м3ρ4 = 800 кг/м3q4 = 44⋅106 Дж/кгНайти Q1, Q2, Q3, Q4.№ 1040.Дано:т = 2 кгq1 = 46⋅106 Дж/кгq2 = 13⋅106 Дж/кгНайти ∆Q.№ 1041.Дано:т = 1 кгq1 = 120⋅106 Дж/кгq2 = 13⋅106 Дж/кгНайти n.№ 1042.Дано: т1 = 2 кгq1 = 46⋅106 Дж/кгт2 = 3 кгq2 = 46⋅106 Дж/кгНайти Q.136Решение:Q = qm = qρV = 13⋅106 Дж/кг⋅700 кг/м3⋅5 м3 == 4,55⋅1010 Дж.Ответ: Q = 4,55⋅1010 Дж.Решение:Q = qm = qρV.Q1 = 800 кг/м3⋅0,25 м3⋅46⋅106 Дж/кг == 9,2⋅109Дж.Q2 = 800 кг/м3⋅0,00005 м3⋅27⋅106 Дж/кг == 1,08⋅106 Дж.Q3 = 710 кг/м3⋅0,025 м3⋅46⋅106 Дж/кг ≈≈ 8,2⋅108 Дж.Q4 = 800 кг/м3⋅0,25 м3⋅44⋅106 Дж/кг == 8,8⋅109 Дж.Ответ: Q1 = 9,2⋅109Дж, Q2 = 1,08⋅106 Дж,Q3 ≈ 8,2⋅108 Дж, Q4 = 8,8⋅109 Дж.Решение:∆Q = Q1−Q2 = m(q1−q2) == 2 кг⋅(46−13)⋅106 Дж/кг = 6,6⋅107 Дж.Ответ: ∆Q = 6,6⋅107 Дж.Решение:n=Q1 q1 120 ⋅ 106 Дж/кг==≈ 9.Q2 q2 13 ⋅ 106 Дж/кгОтвет: n ≈ 9.Решение:Q = Q1+Q2 = m1q1+m2q2 = 2 кг⋅46⋅106 Дж/кг++3 кг⋅46⋅106 Дж = 2,3⋅108 Дж.Ответ: Q = 2,3⋅108 Дж.№ 1043.Дано:V1 = 1,5 л = 0,0015 м3ρ1 = 710 кг/м3q1 = 46⋅106 Дж/кгV2 = 0,5 л = 0,0005 м3ρ2 = 800 кг/м3q2 = 27⋅106 Дж/кгНайти Q.№ 1044.Дано: т1 = 5 кгq1 = 14⋅106 Дж/кгV2 = 0,01 м3ρ2 = 400 кг/м3q2 = 13⋅106 Дж/кгНайти Q.№ 1045.Дано:V1 = 2 м3ρ1 = 400 кг/м3q1 = 13⋅106 Дж/кгm2 = 1,5 т = 1500 кгq2 = 30⋅106 Дж/кгНайти Q.Решение:Q = Q1+Q2 = ρ1V1q1+ρ2V2q2 == 710 кг/м3⋅0,0015 м3⋅46⋅106 Дж/кг++800 кг/м3⋅0,0005 м3⋅27⋅106 Дж/кг ≈ 6⋅107 Дж.Ответ: Q ≈ 6⋅107 Дж.Решение:Q = m1q1+ρ2V2q2 = 14⋅106 Дж/кг⋅5 кг++0,01 м3⋅400 кг/м3⋅13⋅106 Дж/кг = 1,22⋅108 Дж.Ответ: Q = 1,22⋅108 Дж.Решение:Q = m1q1+m2q2 = ρ1V1q1+m2q2 == 400 кг/м3⋅2 м3⋅13⋅106 Дж/кг++1500 кг⋅30⋅106 Дж/кг ≈ 5,5⋅1010 Дж.Ответ: Q ≈ 5,5⋅1010 Дж.№ 1046.Решение:а) Дано:m = 10 кгQ 2 ,9 ⋅ 10 7 Дж= 2,9⋅106 Дж/кг.Q = 2,9⋅107 Дж Q = mq ⇒ q = m =10 кгНайти q.Ответ: q = 2,9⋅106 Дж/кг.б) Дано: n = 4Решение: nmГРhg = mНq;mГР = 7,26 кгmН q0,001кг ⋅ 44 ⋅ 106 Дж/кг≈ 154,6 м. =mH = 1г = 0,001 кг h =m ГРng7,26 кг ⋅ 4 ⋅ 9,8 м/с 2q = 44⋅106 Дж/кгНайти h.Ответ: h ≈ 154,6 м.№ 1047.Дано: n = 1mГР = 0,4 кгmH = 1г = 0,001 кгq = 44⋅106 Дж/кгНайти h.Решение: (см.
=mH = 1г = 0,001 кг h =m ГРng7,26 кг ⋅ 4 ⋅ 9,8 м/с 2q = 44⋅106 Дж/кгНайти h.Ответ: h ≈ 154,6 м.№ 1047.Дано: n = 1mГР = 0,4 кгmH = 1г = 0,001 кгq = 44⋅106 Дж/кгНайти h.Решение: (см.
№ 1046(б)).0 ,001кг ⋅ 44 ⋅ 106 Дж/кгh=≈ 11224,5 м.0 ,4кг ⋅ 1 ⋅ 9 ,8м/с 2Ответ: h ≈ 11224,5 м.137№ 1048.Дано:q = 30⋅106 Дж/кгQ1= 1,5⋅108 ДжQ2= 1,8⋅105 кДж= 1,8⋅108 ДжНайти m1, m2.Решение:Q = mq ⇒ m =m1 =Q.q1,5 ⋅ 108 Дж= 5 кг; m2 =30 ⋅ 106 Дж/кгОтвет: m1 = 5 кг, m2 = 6 кг.1,8 ⋅ 108 Дж30 ⋅ 106 Дж/кг= 6 кг.№ 1049.Дано:qT=mT = 20 т = 20000 кг Решение: mTqT = mУГqУГ ⇒mУГ = тТ qУГ6qT = 15⋅10 Дж/кг15 ⋅ 106 Дж/кгqУГ = 30⋅106 Дж/кг= 10000 кг = 10 т.= 20000 кг⋅30 ⋅ 106 Дж/кгНайти mУГ.Ответ: mУГ = 10 т.№ 1050.Дано:ρ = 710 кг/м3VБЕН = 6 м3qБЕН = 46⋅106 Дж/кгqК.УГ = 30⋅106 Дж/кгНайти m.№ 1051.Дано:t1 = 14°Ct2 = 50°CmВ = 2 кгqСП = 27⋅106 Дж/кгс = 4200 Дж/(кг⋅°С)Найти mСП.№ 1052.Дано:t1 = 14°Ct2 = 50°CmСП = 30 г = 0,03 кгq = 27⋅106 Дж/кгс = 4200 Дж/(кг⋅°С)Найти mB.138Решение:т = ρБЕНVБЕНqБЕН=qК.УГ= 710 кг/м3⋅60 м3⋅46 ⋅ 106 Дж/кг30 ⋅ 106 Дж/кгОтвет: m = 6532 кг.= 6532 кг.Решение: ∆T = t2−t1 = 50°C−14°C = 36°C;cmВ∆TmСПqСП = сmВ∆T ⇒тСП ==qСПДж4200⋅ 2 кг ⋅ 36°Скг⋅°С= 0,0112кг ≈ 11 г.=27 ⋅ 106 Дж/кгОтвет: mСП ≈ 11 г.Решение: ∆T = t2−t1 = 50°C−14°C = 36°C;m qmСПq = сmВ∆Т ⇒тВ = СП =c∆T=0,03 кг ⋅ 27 ⋅10 6 Дж/кгДж⋅ 36 °Cкг⋅°СОтвет: mB ≈ 5,3 кг.4200≈ 5,3 кг.№ 1053.Дано: mК.УГ = 0,5 кгρB = 1 кг/лVB = 100 лq = 30⋅106 Дж/кгс = 4200 Дж/(кг⋅°С)Найти ∆Т.кг⋅°СОтвет: ∆Т ≈ 35,7°С.№ 1054.Дано:mК = 10 г = 0,01 кгmB = 22 кгq = 46⋅106 Дж/кгс = 4200 Дж/(кг⋅°С)Найти ∆Т.Решение: mВ = ρВVВ = 1 кг/л⋅100 л = 100 кг;mК.УГq = сmВ∆Т ⇒mq 0,5 кг ⋅ 30 ⋅ 106 Дж/кг∆Т = К.УГ =≈ 35,7°С.ДжcтВ4200⋅ 100 кгРешение: mВ = ρВVВ = 1 кг/л⋅100 л = 100 кг;mКq = сmВ∆Т;∆T =mК q 0,01 кг ⋅ 46 ⋅10 6 Дж/кг=≈ 5°C.ДжcтВ4200⋅ 22 кгкг⋅°СОтвет: ∆Т ≈ 5°С.40.
Физика ОГЭ
vk.com/club152685050 | vk. |
|
Больше полезных формул и практики тут: | Бесплатный интенсив: |
Физика ОГЭ | EASY PEASY | Бесплатная теория и вебинары |
Погнали!
Ребятки, а как вы решаете 2 задание, когда там встречается график?
Давайте я расскажу свой способ быстрого решения некоторых заданий, а
вы после этого попрактикуйтесь!
1. Какой график? – координата от времени (х от t)
Что надо найти? – участки, на которых тело покоится или имеет отличную от нуля скорость. Рисунок 1.
Алгоритм:
1)пристально смотрим на график
2)если нужно найти участки, где тело покоится, то ищем на графике участки параллельные оси t
3)если нужно найти участки, где тело движется равномерно, то ищем на графике, где х линейно возрастает (убывает). Если х убывает, то
vk.com/club152685050 | vk.com/id446425943
скорость отрицательна (противоположно направлена оси х) и
наоборот.
4)если нужны участки, где тело движется равноускорено, то ищем на графике, где х возрастает (убывает) по параболе
2. Какой график? – координата от времени (х от t)
Что надо найти? – модуль перемещения тела в интервале времени (t1; t2).
Рисунок 2.
Алгоритм:
1)пристально смотрим на график
2)какой бы “заковыристый” ни был график, берем значение “x” при начальном значении времени: x при t1
3)берем значение “x” при конечном значении времени: x при t2
4)вычитаем x(t2)-x(t1). Берем модуль и готово.
vk.com/club152685050 | vk.com/id446425943
3. Какой график? – скорость от времени (v от t)
Что надо найти? – путь тела в интервале времени (t1; t2). Рисунок 3.
Алгоритм:
1)пристально смотрим на график
2)отмечаем интервал времени на графике
3)ищем площади фигур, заключенных между графиком и осью t.
4)складываем МОДУЛИ площадей
P. S. Не путаем путь и перемещение! при перемещении нужно складывать площади с учётом знака. (площади, которые лежат ниже оси t будут отрицательными)
S. Не путаем путь и перемещение! при перемещении нужно складывать площади с учётом знака. (площади, которые лежат ниже оси t будут отрицательными)
vk.com/club152685050 | vk.com/id446425943
4. Какой график? – скорость от времени (v от t)
Что надо найти? – наибольшее по модулю ускорение. Рисунок 4.
Алгоритм:
1)пристально смотрим на график
2)отметаем участки, на которых график изменения параллелен оси t (тело в этих интервалах времени движется равномерно)
3)ищем участок, на котором график наиболее отвесно подходит к оси t (участок, на котором угол между графиком и осью t ближе к 90˚)
4)ищем ускорение на этом участке, берем его по модулю
P.S. Если нужно найти положительное ускорение, рассматриваем участки,
где v возрастает; отрицательное, где убывает с течением времени.
vk.com/club152685050 | vk.com/id446425943
5. Какой график? – ускорение от времени (а от t)
Что надо найти? – участок с равноускоренным движением. Рисунок 5.
Алгоритм:
1)пристально смотрим на график
2)отметаем участки, на которых график изменения “a” параллелен оси t (тело в этих интервалах времени движется равноускорено, если график линейно возрастает (убывает), движение происходит с ускорением, но оно не равноускоренное)
3)отметаем участки, на которых график лежит на оси t.
А вообще, не забываем, что всё это следует из этих формул.
vk.com/club152685050 | vk.com/id446425943
Расчет количества теплоты, сообщенного телу при его нагревании или выделяемого при его охлаждении
Мы узнали, от каких величин зависит количество теплоты и какими единицами его измеряют.
Для подсчета количества теплоты нужно знать удельную теплоемкость вещества, из которого изготовлено тело, массу этого тела и разность между его начальной и конечной температурой.
Например, нужно подсчитать, какое количество теплоты получила железная деталь массой 5 кг при нагревании на 600 °С.
Удельная теплоемкость железа равна 460 Дж/кг*°С, это означает, что для нагревания железа массой 1 кг на 1 °С требуется 460 Дж.
Для нагревания железа массой 5 кг на 1°С потребуется в 5 раз большее количество теплоты, т. е. 460 Дж X 5 =2300 Дж; для нагревания
Итак, чтобы подсчитать количество теплоты, необходимое для нагревания тела, нужно удельную теплоемкость умножить на массу тела и на разность между конечной и начальной температурой его.
Указанное правило можно записать в виде формулы, введя следующие обозначения: Q—количество теплоты, c – кудельная теплоемкость вещества, m — масса тела, t1 —начальная и t2 – конечная температура тела. Тогда
Q = cm (t2 — t1).
Пример 1. В железный котел массой 10 кг налито 20 кг воды. Какое количество теплоты нужно передать котлу, чтобы нагреть его вместе с налитой в него водой от 10 до 100 °С?
Оба тела — и котел, и вода — будут нагреваться вместе. Между ними происходит теплообмен, и их температуры можно считать одинаковыми. Поэтому и котел, и вода нагреваются на одно и то же число градусов: 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми, ведь их массы и удельные теплоемкости различны.
Количество теплоты, полученное котлом, равно:
Q1=c1m1(t2 – t1),
Q1 =460 Дж/кг*°С • 10 кг • 90°С=414 000 Дж ≈ 400 кДж.
Количество теплоты, полученное водой, равно:
Q2 = c2m2(t2 – t1),
Q2 = 4200 Дж/кг*°С • 20 кг • 90°С = 7560000 Дж≈7600 кДж.
На нагревание и котла, и воды израсходовано количество теплоты:
Q=Q1 + Q2,
Q = 400 кДж+7 600 кДж = 8 000 кДж
Пример 2. Смешали 0,8 кг воды, имеющей температуру 25°С, и 0,2 кг кипятка. Температуру полученной смеси измерили, и она оказалась равной 40 °С.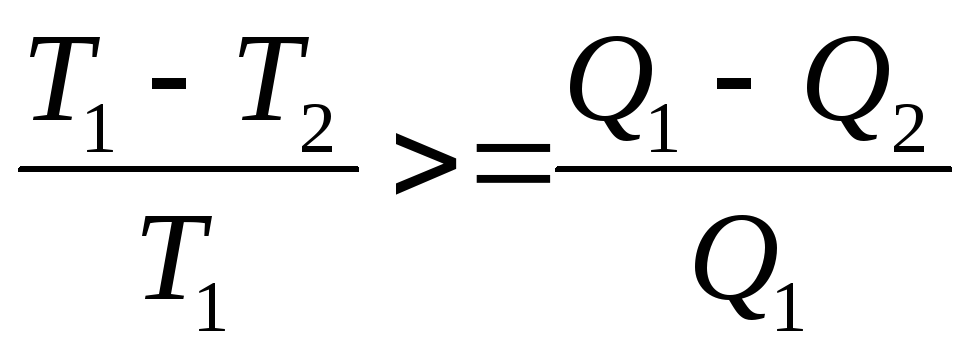 Вычислить, какое количество теплоты отдал при остывании кипяток и какое количество теплоты получила, при нагревании более холодная вода. Сравнить эти количества теплоты.
Вычислить, какое количество теплоты отдал при остывании кипяток и какое количество теплоты получила, при нагревании более холодная вода. Сравнить эти количества теплоты.
Кипяток остыл от 100 до 40 °С, при этом он отдал
Q1 = c1m1(t2 — t1),
Q1 = 4 200 Дж/кг*°С • 0,2 кг • (100° С – 40° С) = 50 400 Дж.
Вода, в которую был влит кипяток, нагрелась от 25 до 40 °С и получила количество теплоты:
Q2 = c2m2(t – t1),
Q2 = 4 200 Дж/кг*°С • 0,8 кг • (40° С – 25° С) = 50 400 Дж.
Мы видим, что количество теплоты, отданное горячей водой, и количество теплоты, полученное холодной водой, равны между собой. Это не случайный результат. Опыт показывает, что если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается настолько, насколько уменьшается внутренняя энергия остывающих тел.
Однако если провести более точные измерения в опытах по смешиванию горячей и холодной воды, то точного равенства отданной и полученной энергии не получится. Отданная энергия будет больше полученной. Объясняется это тем, что часть энергии во время опыта передается воздуху и сосуду. Разница в отданном и полученном количестве теплоты будет тем меньше, чем меньше потерь энергии допускается в опыте.
Вопросы. 1. Что нужно знать, чтобы подсчитать количество теплоты, полученное телом при нагревании? 2. Объясните на примере, как подсчитывают количество теплоты, сообщенное телу при его нагревании или выделяющееся при его охлаждении. 3. Как записывают формулу для подсчета количества теплоты? 4. Какой вывод можно сделать из опыта по смешиванию холодной и горячей воды?
Упражнения.
- Удельная теплоемкость алюминия равна 920 Дж/кг • ° С. Что это означает?
- Какая из указанных в таблице 6 жидкостей быстрее нагревается при одинаковых условиях нагревания? Почему?
- Почему в качестве охладителя (например, при охлаждении двигателя внутреннего сгорания) из всех жидкостей выгоднее всего применять воду?
- Рассчитайте количество теплоты, необходимое для нагревания: а) чугунного утюга массой 1,5 кг на 200° С, б) алюминиевой ложки массой 50 г от 20 до 90° С, в) кирпичной печи массой 2 т от 10 до 60°С,
Задачи по физике и математике с решениями и ответами
Задача по физике — 8697
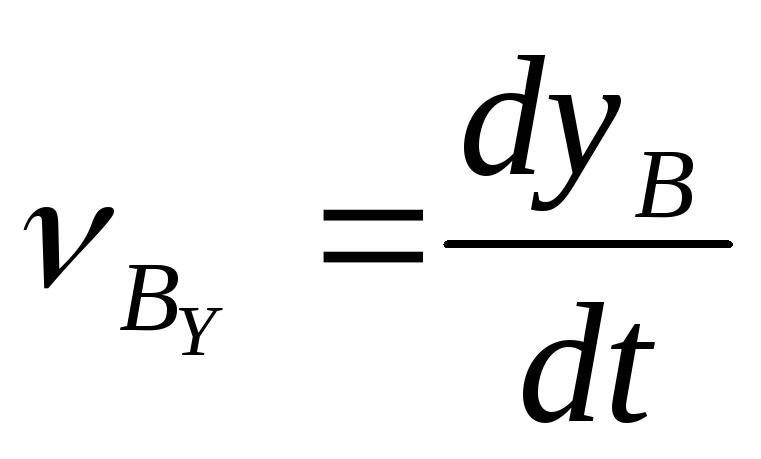 {235}$, подвергшегося делению при взрыве атомной бомбы с тротиловым эквивалентом 30 килотонн, если тепловой эквивалент тротила равен 4,1 кДж/г. Подробнее
{235}$, подвергшегося делению при взрыве атомной бомбы с тротиловым эквивалентом 30 килотонн, если тепловой эквивалент тротила равен 4,1 кДж/г. Подробнее Как узнать путь зная скорость и время. Формулы прямолинейного равноускоренного движения
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы , так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.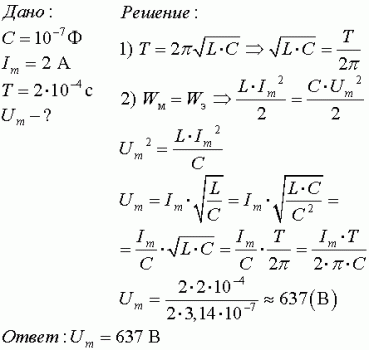
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать , если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей .
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
v — скорость,
cos α — косинус угла между векторами силы и скорости.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени , за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.
Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
- Скорость = путь / время.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Главная >  Wiki-учебник >  Физика > 7 класс >
Нужна помощь в учебе?
Главная >  Wiki-учебник >  Физика > 7 класс > Расчет пути, скорости и времени движения: равномерное и неравномерное
Обычно равномерное движение очень редко можно встретить в реальной жизни.
Как найти скорость, время и расстояние — формулы и дополнительные параметры
За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Нужна помощь в учебе?
Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:   Явление инерции: в чем заключается и примеры из жизни
Главная >  Wiki-учебник >  Физика > 7 класс > Расчет пути, скорости и времени движения: равномерное и неравномерное
Обычно равномерное движение очень редко можно встретить в реальной жизни.
Как найти скорость, формула
За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Нужна помощь в учебе?
Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:   Явление инерции: в чем заключается и примеры из жизни
Главная >  Wiki-учебник >  Физика > 7 класс > Расчет пути, скорости и времени движения: равномерное и неравномерное
Обычно равномерное движение очень редко можно встретить в реальной жизни.
Скорость время расстояние
За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Нужна помощь в учебе?
Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:   Явление инерции: в чем заключается и примеры из жизни
Главная >  Wiki-учебник >  Физика > 7 класс > Расчет пути, скорости и времени движения: равномерное и неравномерное
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением.
Формула пути
Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Нужна помощь в учебе?
Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:   Явление инерции: в чем заключается и примеры из жизни
VII = S: tII
12:3 = 4(м/с)
Составим выражение: 2 6:3 = 4 (м/с)
Ответ; 4м/с скорость второго ёжика.
Реши задачу.
1. Один кальмар плыл 4 с со скоростью 10 м/с. С какой скоростью должен плыть другой кальмар, чтобы преодолеть это расстояние за 5 с?
2. Трактор, двигаясь со скоростью 9 км/ч, прошёл путь между деревнями за 2 ч. С какой скоростью должен идти пешеход, чтобы преодолеть это расстояние за 3 ч?
3. Автобус, двигаясь со скоростью 64 км/ч, прошёл путь между городами за 2 ч. С какой скоростью должен ехать велосипедист, чтобы преодолеть это расстояние за 8 ч?
4. Чёрный стриж летел 4 мин со скоростью 3 км/мин. С какой скоростью должна лететь утка кряква, чтобы преодолеть это расстояние за 6 мин?
Составные задачи на скорость. II тип
Лыжник до горки ехал 2 ч со скоростью 15 км/ч, а потом по лесу он ехал ещё 3 ч. С какой скоростью лыжник будет ехать по лесу, если всего он проехал 66км?
Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.
Г. -15 км/ч 2 ч?км
Л. — ? км/ч З ч?км 66км
Составим план решения этой задачи. Чтобы узнать скорость движения лыжника по лесу, надо узнать какое расстояние он проехал по лесу, а для этого надо знать какое расстояние он проехал до горки.
Vл Sл Sг
Sг = Vг · tг
15 2 = 30 (км) — расстояние, которое проехал лыжник до горки.
Sл = S – Sг
66 — 30 = 36 (км) — расстояние, которое проехал лыжник по лесу.
Чтобы найти скорость, надо расстояние разделить на время.
Vл = Sл: tл
36.: 3 = 12 (км/ч)
Ответ: 12 км/ч скорость лыжника по лесу.
Реши задачу.
1. Ворона летела по полям 3 ч со скоростью 48 км/ч, а потом она летела 2 ч по городу. С какой скоростью ворона летела по городу, если всего она пролетела 244 км?
2. Черепаха ползла до камня 5 мин со скоростью 29 см/мин, а после камня черепаха ползла ещё 4 мин.
Формула скорости — математика 4 класс
С какой скоростью черепах ползла после камня, если она проползла 33 см?
3. Поезд шёл до станции 7 ч со скоростью 63 км/ч, а после станции поезд проехал ещё 4 ч. С какой скоростью поезд проедет путь от станции, если всего он прошёл 741 км?
Составные задачи на расстояние.
Образец:
Травоядный динозавр сначала бежал 3 ч со скоростью 6 км/ч, а потом он бежал ещё 4 ч со скоростью 5 км/ч. Какое расстояние пробежал травоядный динозавр?
Рассуждаем так. Это задача в одном направлении.
Составим таблицу.
Слова « скорость », «время», «расстояние» запишем зеленой ручкой.
Скорость (V) Время (t) Расстояние (S)
С. — 6 км/ч Зч? км
П. — 5 км/ч 4ч?км? км
Составим план решения этой задачи. Чтобы узнать какое расстояние пробежал динозавр, надо знать, какое расстояние он пробежал, потом и какое расстояние он пробежал сначала.
S Sп Sс
Чтобы найти расстояние, надо скорость умножить на время.
Sс =Vс t с
6· 3 = 18 (км) — расстояние, которое пробежал динозавр сначала. Чтобы найти расстояние, надо скорость умножить на время.
Sп = Vп tп
5 4 = 20 (км) — расстояние, которое пробежал динозавр потом.
18 + 20 = 38 (км)
Составим выражение:6 3 + 5 4 = 38(км)
Ответ: 38 км пробежал травоядный динозавр.
Реши задачу.
1. Ракета сначала летела 28 с со скоростью 15 км/с, а оставшийся путь летела 53 с со скоростью 16 км/с. Какое расстояние пролетела ракета?
Какое расстояние пролетела ракета?
2. Утка сначала плыла 3 ч со, скоростью 19 км/ч, а потом она плыла ещё 2 ч со скоростью 17 км/ч. Какое расстояние проплыла утка?
3. Кит полосатик сначала плыл 2 ч со скоростью 22 км/ч, а потом он плыл ещё 2 ч со скоростью 43 км/ч. Какое расстояние проплыл кит полосатик?
4. Теплоход до пристани шёл 3 ч со скоростью 28 км/ч, а после пристани плыл ещё 2 ч со скоростью 32 км/ч. Какое расстояние проплыл теплоход?
Задачи на нахождение времени совместной работы.
Образец:
Привезли 240 саженцев елей. Первый лесник может посадить эти ели за 4 дня, а второй за 12 дней. За сколько дней оба лесника могут выполнить задание, работая вместе?
240: 4 = 60 (саж,) за 1 день сажает первый лесник.
240: 12 — 20 (саж.) за 1 день сажает второй лесник.
60 + 20 = 80 (саж.) за 1 день сажают оба лесника. 240:80 = 3(дн.)
Ответ: за 3 дня лесники посадят саженцы, работая вместе.
Реши задачу.
1. В мастерской 140 мониторов. Один мастер отремонтирует их за 70 дней, а другой, за 28 дней. За сколько дней оба мастера отремонтируют эти мониторы, если будут работать вместе?
2. Было 600 кг горючего. Один трактор израсходовал его за 6 дней, а другой – за 3 дня. За сколько дней тракторы израсходуют это горючее, работая вместе?
3. Надо перевезти 150 пассажиров. Один катер перевезёт их за 15 рейсов, а другой за 10 рейсов. За сколько рейсов эти катера перевезу всех пассажиров, работая вместе?
4. Один ученик может сделать 120 снежинок 60 мин, а другой — за 30 мин. Сколько потребуется времени ученикам, если они будут работать вместе?
5. Один мастер может изготовить 90 шайбочек за 30 мин, другой—‘за 15 мин. За какое время они изготовят 90 шайбочек при совместной работе?
⇐ Предыдущая234567891011
При прямолинейном равноускоренном движении тело
- двигается вдоль условной прямой линии,
- его скорость постепенно увеличивается или уменьшается,
- за равные промежутки времени скорость меняется на равную величину.

Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с 2 .
Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.
Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:
При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:
Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:
Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с 2 . Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:
Таким образом, конечная скорость будет находиться по формуле:
Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:
Получим из этих формул формулы ускорения. В случае ускорения:
at = v – v 0
a = (v – v 0)/t
В случае торможения:
at = v 0 – v
a = (v 0 – v)/t
В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:
Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:
Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении . Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.
При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.
Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v 0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:
Таким образом получаем:
s = ½ * (v 0 + v) * t
Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v 0 + at). Поэтому в формуле пути мы можем заменить v:
s = ½ * (v 0 + v 0 + at) * t = ½ * (2v 0 + at) * t = ½ * t * 2v 0 + ½ * t * at = v 0 t + 1/2at 2
Итак, пройденный путь определяется по формуле:
s = v 0 t + at 2 /2
(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция.)
Если тело начало двигаться равноускоренно из состояния покоя (v 0 = 0), то формула пути упрощается до s = at 2 /2.
Если вектор ускорения был противоположен скорости, то произведение at 2 /2 надо вычитать. Понятно, что при этом разность v 0 t и at 2 /2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v 0 /a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле.
Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.
Скорость
Что же такое «скорость»? Можно наблюдать, как одна машина едет быстрее, другая -медленее; один человек идет быстрым шагом, другой — не торопится. Велосипедисты тоже едут с разной скоростью. Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то Допустим, что 5 км/ч. То есть за 1 час он прошел 5 километров.
Формула пути (расстояния) — произведение скорости и времени. Конечно же, самый удобный и доступный параметр — это время. Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности. Обратите внимание, какой масштаб.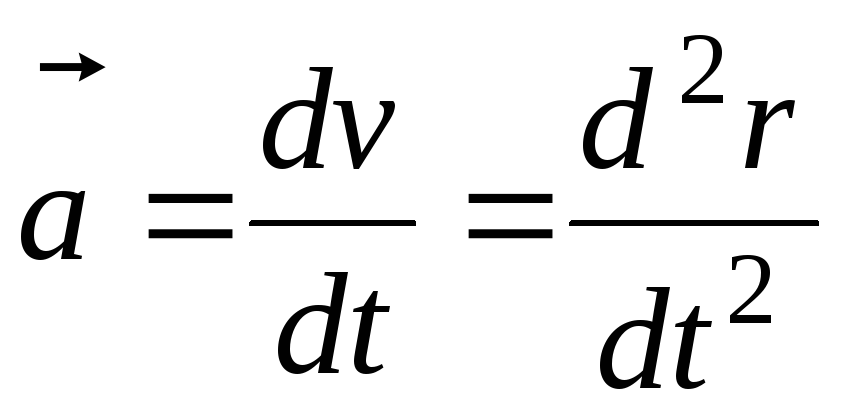 Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».
Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».
Не упустите!
Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:
Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.
Вот так легко запоминается формула «скорость, время, расстояние». Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено.
найти Т1 и Т2 из формулы кпд n= (T1- T2/ T1) •100%, физика
Kibroeva97 / 17 авг. 2014 г., 20:08:09
друга. Массы зарядов m1 = 3 мг и m2 = 1 мг. Заряды отпускают. В процессе движения заряды взаимодействуют только между собой. Все ответы в задаче необходимо дать с точностью до десятых.
Вопрос № 1
Чему равно отношение модулей сил, действующих на заряды, F2/F1 через одну секунду после начала движения?
Мой ответ
Вопрос № 2
Чему равно отношение модулей ускорений зарядов a2/a1 через две секунды после начала движения?
Мой ответ
Вопрос № 3
Чему равно отношение модулей импульсов зарядов p2/p1 через три секунды после начала движения?
Мой ответ
Вопрос № 4
Чему равно отношение кинетических энергий зарядов E2/E1 через четыре секунды после начала движений?
Мой ответ
Вопрос № 5
Чему равно отношение путей, пройденных зарядами за первые пять секунд движения, S2/S1?
Мой ответ
Задание № 2
Электрическая цепь состоит из двух резисторов сопротивлениями 100 Ом и 150 Ом, подключенных к идеальному (напряжение на выходе источника всегда равно ЭДС и не зависит от подключенной нагрузки) источнику с ЭДС 5 В.
Вопрос № 1
Чему равен ток, текущий в цепи? Ответ укажите в миллиамперах с точностью до десятых.
Мой ответ
Вопрос № 2
Для измерения силы тока в цепь включают амперметр (последовательно), внутреннее сопротивление которого равно 10 Ом. Какую силу тока покажет амперметр? Ответ укажите в миллиамперах с точностью до десятых.
Мой ответ
Вопрос № 3
Каким максимальным внутренним сопротивлением может обладать амперметр, подключаемый в такую цепь, чтобы его показания отличались от силы тока, текущего по цепи до подключения амперметра, не более, чем на 1%. Ответ укажите в омах с точностью до десятых.
Мой ответ
Вопрос № 4
Предположим, что мы захотели с помощью амперметра измерить ток в такой цепи, но не знаем ни значений сопротивлений резисторов, ни напряжение источника. Нам известны только показания амперметра, включенного в цепь, и его внутреннее сопротивление. Достаточно ли этих данных для того, чтобы рассчитать ток, который тек в цепи до подключения амперметра? Если нет, то какие ещё данные необходимы?
Достаточно.
Не достаточно. Нужно знать сопротивления резисторов.
Не достаточно. Нужно знать напряжение на источнике.
Не достаточно. Нужно знать напряжение на источнике или сопротивления резисторов
Задание № 3
Теплоизолированный цилиндрический сосуд разделен на две части подвижным невесомым поршнем. Первоначально поршень делит объём сосуда пополам. По одну сторону поршня находится ν1молей гелия при температуре Т1 и давлении р0, по другую — ν2 молей атомарного азота (при достаточно высоких температурах молекула азота распадается на атомы: N2 → 2N) при температуре Т2и таком же давлении р0. Причем ν1 = 2ν2.
Вопрос № 1
Каково соотношение температур газов?
Т2 = Т1
Т2 = 2Т1
Т2 = Т1/2
Т2 = 4Т1
Т2 = Т1/4
Вопрос № 2
Если поршень проводит тепло, то как из-за этого будут изменяться объёмы, занимаемые газами?
Объёмы изменяться не будут
Определенно на этот вопрос ответить нельзя
Объём азота будет уменьшаться, гелия — увеличиваться
Объём гелия будет уменьшаться, азота — увеличиваться
Вопрос № 3
Пусть поршень проводит тепло, а начальные температуры газов таковы, что азот все время находится в атомарном состоянии.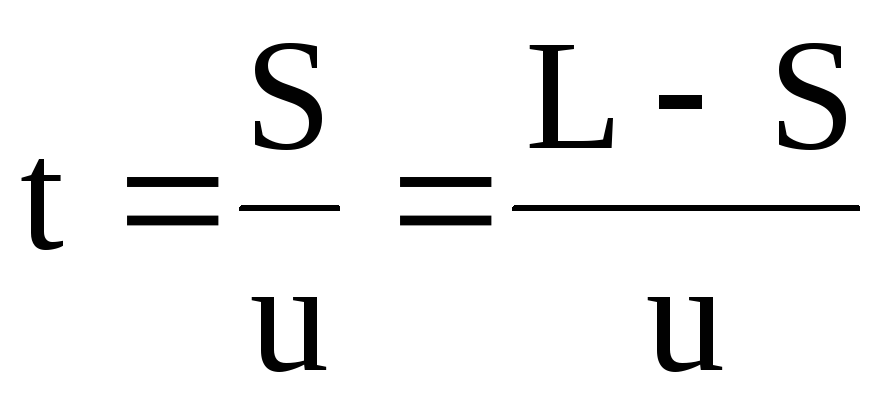 Какая температура (Т) установится в системе?
Какая температура (Т) установится в системе?
Т = 4Т1/3
Т = (Т1+Т2)/2
Т = Т2/3
Т = 3Т1/2
Т = 5Т1/3
Вопрос № 4
Пусть начальные температуры таковы, что после выравнивания температур половина атомов азота рекомбинировали (2N → N2). Какая температура (Т) установится в системе в этом случае, если при образовании одного моля молекул N2 выделяется ε джоулей энергии?
Указание. Внутренняя энергия одноатомного и двухатомного газов рассчитываются по формулам U=3νRT/2 и U=5νRT/2 соответственно.
Т = (48Т1+2ε/R)/33
Т = (24Т1+ε/R)/18
Т = (41Т1+2ε/R)/25
Т = (48Т1+2ε/R)/35
Т = (24Т1+ε/R)/9
Обучение Онлайн: домашняя школа физики
Расчет количества теплоты, необходимого для нагревания тела или выделяемого им при охлаждении.
На практике часто пользуются тепловыми расчетами. Например, при строительстве зданий необходимо учитывать, какое количество теплоты должна отдавать зданию вся система отопления. Следует также знать, какое количество теплоты будет уходить в окружающее пространство через окна, стены, двери.
Покажем на примерах, как нужно вести простейшие расчеты.
Итак, необходимо узнать, какое количество теплоты получила при нагревании медная деталь. Ее масса 2 кг, а температура увеличивалась от 20 до 280 °С. Вначале по таблице 1 определим удельную теплоемкость меди (с = 400 Дж/кг*°С) Это означает, что на нагревание детали из меди массой 1 кг на 1 °С потребуется 400 Дж. Для нагрева¬ния медной детали массой 2 кг на 1 °С необходимо в 2 раза большее количество теплоты — 800 Дж. Температуру медной детали необходимо увеличить не на 1 °С, а на 260 °С, значит, потребуется в 260 раз большее количество теплоты, т. е. 800 Дж * 260 °С = 208 000 Дж.
Чтобы рассчитать количество теплоты, необходимое для нагревания тела или выделяемое им при охлаждении, следует удельную теплоемкость умножить на массу тела и на разность между конечной и начальной температурами.
Если обозначить массу m, разность между конечной (t2) и начальной (t1) температурами — t2 — t1 получим формулу для расчета количества теплоты:
Q = cm(t2 — t1).
Пример 1. В железный котел массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котел, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоемкости различны.
Запишем условие задачи и решим ее.
Дано:
с1 = 460 Дж/кг*°С
m1 = 5 кг
с2 = 4200 Дж/кг*°С
m2 = 10 кг
t1 = 10 °C
t2 = 100 °C
Найти:
Q = ?
Решение:
Количество теплоты, полученное котлом,
равно:
Q1 = c1*m1*(t2 — t1),
Q1i = 460 Дж/(кг*С) * 5 кг * 90 °C = 207 000 Дж = 207 кДж.
Количество теплоты, полученное водой, равно:
Q2 = c2m2(t2 — t1),
Q2 = 4200 Дж/(кг*С) * 10 кг * 90 °С — 3 780 ООО Дж = 3780 кДж.
На нагревание и котла, и воды израсходовано количество теплоты: Q = Q1 + Q2,
Q = 207 кДж + 3780 кДж = 3987 кДж.
Ответ:
Q = 3987 кДж.
Пример 2. Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.
Запишем условие задачи и решим ее.
Дано:
m1 = 0,2 кг
c1 = с2 = 4200 Дж/кг*°С
m2 = 0,8 кг
t1 = 25 °C
t2 = 100 °C
t = 40 °C
Найти:
Q1 = ?
Q2 = ?
Решение:
Горячая вода остыла от 100 до 40 °С, при этом она отдала количество теплоты:
Q1 = c1*m1*(t2 — t).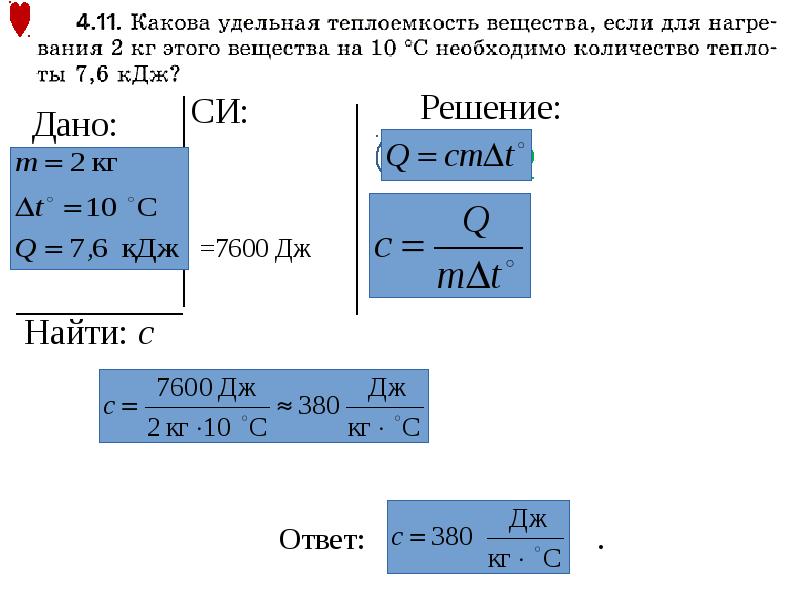
Q1 — 4200 Дж/(кг*°С) * 0,2 кг * (100 °С — 40 °С) = 50 400 Дж.
Холодная вода нагрелась с 25 до 40 °С и получила количество теплоты:
Q2 = 4200 Дж/(кг*°С) * 0,8 кг * (40 °С — 25 °С) = 50 400 Дж.
Ответ:
Q1 = 50 400 Дж, Q2 = 50 400 Дж
Мы видим, что количество теплоты, отданное горячей водой, и количество теплоты, полученное холодной водой, равны между собой. Это не случайный результат. Опыт показывает, что если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
При проведении опытов обычно получается, что отданная горячей водой энергия больше энергии, полученной холодной водой. Это объясняется тем, что часть энергии передается окружающему воздуху, а часть энергии — сосуду, в котором смешивали воду. Равенство отданной и полученной энергий будет тем точнее, чем меньше потерь энергии допускается в опыте. Если подсчитать и учесть эти потери, то равенство будет точным.
Напряжение — AP Physics 1
Пояснение:Чтобы найти массу блока 2, нам нужно будет вычислить еще несколько вещей, например, натяжение веревки.
Для начала нам нужно определить различные силы на нашей диаграмме свободного тела. Для этого мы начнем с блока 1 и будем использовать повернутую систему координат для упрощения. В такой системе ось X будет проходить параллельно поверхности пандуса, а ось Y будет перпендикулярна поверхности пандуса, как показано ниже:
Теперь мы можем определить силы, действующие на блок 1.Вдоль повернутой оси y сила тяжести, действующая на блок, равна, а сила наклонной поверхности на блоке равна нормальной силе,. Поскольку блок 1 не движется в направлении y, мы можем установить эти две силы равными друг другу.
Теперь, учитывая силы, действующие вдоль повернутой оси x, мы имеем силу, направленную вниз, равную.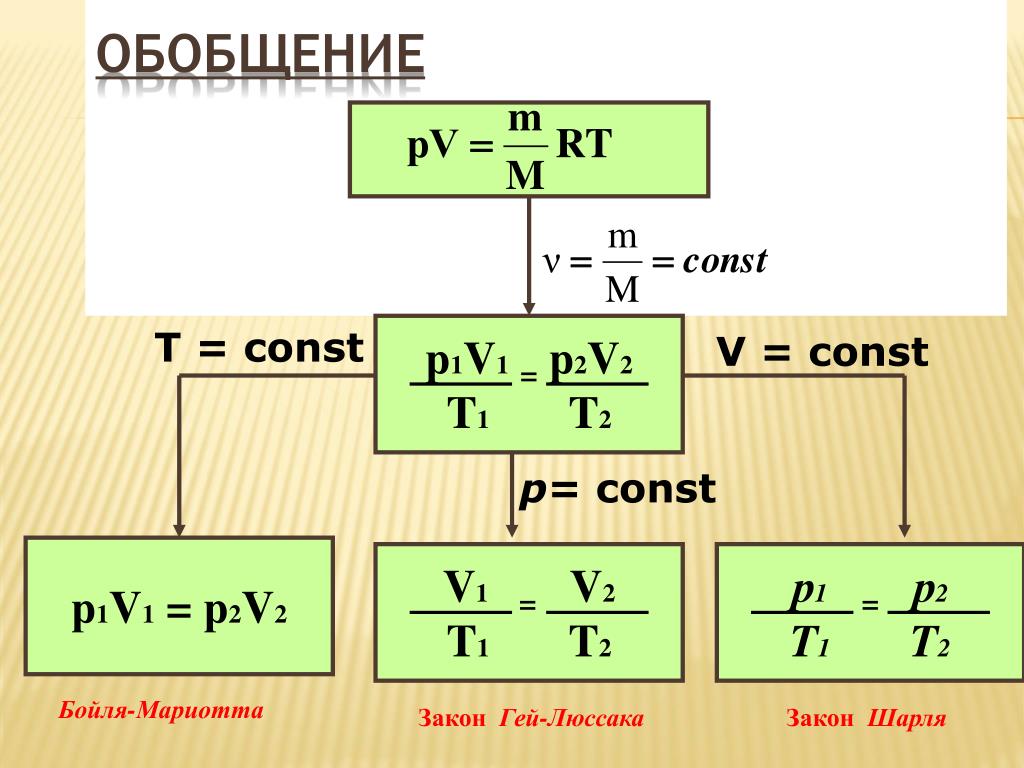 Если направить вверх, у нас есть сила натяжения и сила трения.
Если направить вверх, у нас есть сила натяжения и сила трения.
Формула для расчета силы кинетического трения:
Поскольку мы уже определили, что такое нормальная сила, мы можем подставить это выражение в приведенное выше уравнение, чтобы получить:
Теперь мы можем написать выражение для чистой силы, действующей на блок 1 в направлении x:
Измените приведенное выше выражение, чтобы найти напряжение.
До сих пор мы рассматривали только блок 1. Теперь давайте обратим наше внимание на блок 2 и посмотрим, какие силы действуют на него. В направлении вниз у нас есть вес блока из-за силы тяжести, который равен. В восходящем направлении, как мы видим на диаграмме, натяжение веревки. Нам нужно написать выражение, которое сообщает нам чистую силу, действующую на блок 2.
Поскольку мы вычислили выражение для натяжения на основе информации о блоке 1, мы можем вставить это выражение в приведенное выше уравнение, чтобы получить:
Теперь переставьте, чтобы вычислить массу блока 2.
Затем, подставив значения, мы можем, наконец, вычислить массу блока 2:
Формула натяжения веревки, прикрепленной к грузу под углом
Сила натяжения возникает в канате, когда к нему прикреплен груз. Создаваемое в канате натяжение должно быть равным силе тяжести груза. Но это справедливо только для случая, когда веревка подвешена вертикально. Формула натяжения также зависит от угла подвеса.В этой статье мы рассмотрим примеры, формулу и численную задачу для натяжения веревки, подвешенной под углом к потолку.
Формула натяжения тетивы, прикрепленной под углом к потолку Груз массой m подвешен на двух веревках с натяжением T1 и T2. Натяжение обеих веревок будет разным, поэтому нам нужно вывести два отдельных набора формулы для натяжения обеих струн. Поскольку груз статичен, чистые силы, действующие на груз в направлениях x и y, должны быть равны нулю.
Начнем с рисования диаграммы свободного тела и определим силы в направлениях x и y.
Разрешение сил в направлении y: Силы, действующие в направлении y, представляют собой направленное вниз гравитационное притяжение и составляющую сил растяжения T1 и T2 в направлении вверх. Приравнивая силу, получаем:
T1 sin (a) + T2 sin (b) = m * g ———- (1)
Разрешение сил в направлении x: Силы, действующие в направлении x, являются компонентами сил растяжения T1 и T2 в противоположных направлениях.Приравнивая силы получаем:
T1cos (a) = T2cos (b) ——————— (2)
Решая уравнения (1) и (2), получаем формулу для натяжения.
T1 = [T2cos (b)] / cos (a)]
T2 = [T1cos (a)] / cos (b)]
Из приведенных выше уравнений мы также можем сделать вывод, что чем больше угол подвески, тем выше будет натяжение с максимальным натяжением при подвеске 90 градусов.
Реальные примеры объекта, прикрепленного к веревке под углом Струна, используемая в парусе, крепится под углом, обеспечиваемым силой натяжения.Изображение skeeze с сайта Pixabay
- Веревки, используемые во время скалолазания
- Веревки подвесного моста
- Веревки, прикрепленные к парусу корабля
- Веревки, используемые для удержания палатки
- Веревки, используемые в водных видах спорта
Гирю массой 10 кг подвешивают на двух тросах под углом, найдите натяжение тросов.
Задачи о натяжении струны под угломМы будем следовать тому же подходу, который мы использовали выше для вывода формулы для натяжения.Сначала мы решим силы в направлениях x и y и сформируем два уравнения.
Диаграмма свободного телаРазрешив силы в направлении x, мы имеем:
T1 sin30 + T2 sin60 = 98 Н ———- (1)
Разрешив силы в направлении y, мы имеем:
T1cos30 = T2cos60 ——————— (2)
Решая приведенные выше уравнения, получаем значения для натяжения T1 и T2:
T1 = 65,1 Н T2 = 112,3 Н
Мы можем видеть, что T2 выше, чем T1, что также показывает, что угол b больше, чем a.
Груз весом 10 кг подвешен горизонтально на двух тросах с натяжением Т1 и Т2. Длина веревок одинакова.
Формула натяжения для горизонтально подвешенной струныТеперь, в этом случае, углы, образованные веревками с потолком, равны 0. Попробуем разрешить силы и найти значение натяжения веревок. Но такие проблемы легче решить логически, чем с помощью уравнений. Такие проблемы могут быть решены только при многих предположениях, таких как одинаковая длина канатов, безмассовые канаты, 100% горизонтальная подвеска и т. Д.
В направлении x:
T1 и T2 противоположны, и нет результирующей силы, действующей в x-направлении, следовательно, они должны быть равны. Применим формулу для натяжения и проверим это.
T1cos0 = T2cos0 => T1 = T2
Теперь по оси Y:
Ящик удерживал веревки, поэтому сумма натяжений должна равняться весу. Чтобы выяснить это, применим формулу напряжения.
T1cos0 + T2cos0 = 98 N => T1 + T2 = 98
T1 = T2 = 49 Н
См. ТакжеНапряжение
НапряжениеРаспространенной формой напряжения является умственное или эмоциональное напряжение.Но этот сайт не об этом, поэтому, если вы ищете способ справиться со своим напряжением, уходите.
Напряжение, о котором я говорю, связано с физикой. Конкретная проблема, о которой я говорю, — это когда у вас есть объект, подвешенный на 2 строки. Вот пример:
Допустим, у вас есть проблема, показанная выше. Подвешиваемый объект 50N. К нему подключена линия T3. Это, в свою очередь, идет вверх как для T1, так и для T2. Поскольку сила, тянущая объект вниз, составляет 50 Н, чтобы удерживать его, сила Т3 также должна быть 50 Н.2 = 3900
б = 62,44997998
Поскольку T1 совпадает с b, T1 составляет около 62,45N.

Другой тип проблемы с натяжением очень похож на первый, но с такой разницей, что ее нужно решать практически полностью по-другому. Он также имеет T3, присоединенный к двум другим линиям. Однако в первой задаче одна линия (T1) была горизонтальной, а другая — под углом. В этой задаче оба T1 и T2 расположены под углом. Вот пример:
В этой задаче объект — 200N.Чтобы удержать это, T3 снова должен иметь направленную вверх силу, равную силе, тянущей объект вниз. T3 присоединен к T1 и T2, но на этот раз оба находятся под углом, и вам дано только значение T3. Эта проблема требует больше работы, чем другая, но у вас есть вся необходимая информация. Первая формула, которая вам понадобится:
(T1 * cos a) + (T2 * cos b) = 0
Подставьте числа в проблему, и вы получите:
(T1 * cos 15) + (T2 * cos 20) = 0
Определите косинус каждого угла, и вы получите:
(Т1 * 0.97) — (Т2 * 0,94) = 0
Теперь добавьте (T2 * 0,0.94) к обеим сторонам, и у вас должно получиться:
(Т1 * 0,97) = (Т2 * 0,94)
Затем разделите обе стороны на 0,94, чтобы получить:
Т1 * 1.03 = Т2
Следующая формула, необходимая для решения этой задачи:
(T1 * sin a) + (T2 * sin b) — Fw = 0
Подставьте числа в проблему, и вы получите:
(T1 * sin 15) + (T2 * sin 20) — 200 = 0
Определите синус каждого угла, и вы получите:
(Т1 * 0.26) + (Т2 * 0,34) — 200 = 0
У вас также есть ответ из другой последней формулы, которая приводит нас к:
(T1 * 0,26) + ((T1 * 1,03) * 0,34) — 200 = 0
Решите все в скобках, чтобы получить:
(T1 * 0,26) + (T1 * 0,35) — 200 = 0
Добавьте оба T1, чтобы получить:
T1 * 0,61 — 200 = 0
Добавляем по 200 соток в обе стороны, получаем:
Т1 * 0.
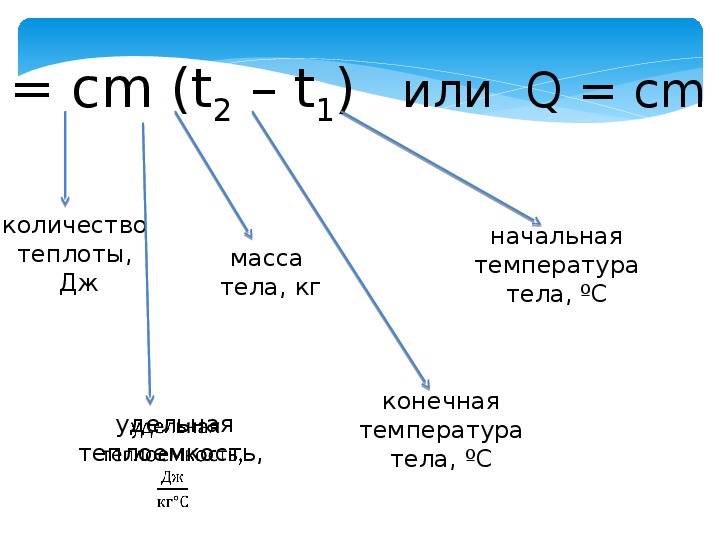 61 = 200
61 = 200 Наконец, разделите обе стороны на 0,61, чтобы получить T1
T1 = 328N
На данный момент решить T2 легко. Помните, что ответ от использования первой формулы был:
Т1 * 1.03 = Т2
Теперь вы знаете, что такое T1, поэтому остается:
328 * 1.03 = T2
Эта информация сводится к:
338N = T2
После решения вся проблема должна выглядеть так:
Хорошего дня.
Калькулятор натяжения
Как рассчитать натяжение канатов, на которых подвешен объект
На рисунке ниже видно, что сила F, необходимая для поднятия объекта, равна весу объекта W. Эта идея является фундаментальной концепцией, лежащей в основе нашей формулы силы натяжения. Также ниже показана диаграмма свободного тела объекта, на которой показаны силы натяжения T, действующие в струне. Как видите, силы натяжения идут попарно и в противоположных направлениях:
Следуя второму закону движения Ньютона, мы можем выразить сумму сил, используя диаграмму свободного тела объекта, как показано в правой части иллюстрации выше.Мы используем диаграмму свободного тела , чтобы показать различные направления и величины сил, действующих на тело. В состоянии равновесия все эти силы должны равняться нулю. Рассматривая все восходящие силы как положительные, а нисходящие как отрицательные, наше уравнение:
ΣF ↑ = 0 = T + (-W)
T = W
где вес W становится отрицательным, поскольку он направлен вниз. Перенеся W на другую сторону уравнения, теперь мы можем видеть, что сила натяжения веревки равна весу объекта, который она несет, как также показано выше.
Если мы используем больше веревок для подъема объекта, общая сила натяжения делится на веревки. Сила натяжения в каждой веревке зависит от их углов по отношению к направлению силы, которой она противодействует.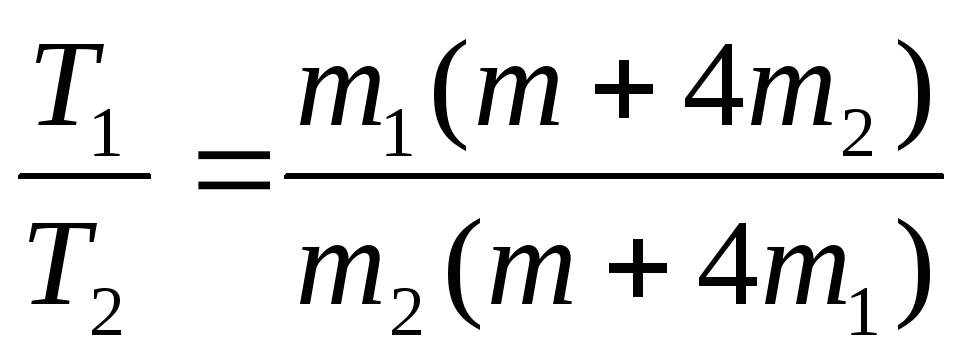 Чтобы лучше понять это, давайте рассмотрим другую диаграмму свободного тела объекта, подвешенного на двух веревках, как показано ниже:
Чтобы лучше понять это, давайте рассмотрим другую диаграмму свободного тела объекта, подвешенного на двух веревках, как показано ниже:
На диаграмме свободного тела, показанной выше, мы можем видеть горизонтальную и вертикальную составляющие сил натяжения, T₁ и T₂. Силы являются векторами, что означает, что они всегда имеют величину и направление .Как и все векторы, силы могут быть выражены в этих компонентах, что дает влияние силы вдоль горизонтальной и вертикальной осей. T₁ₓ и T₂ₓ — вертикальные компоненты T₁ и T₂ соответственно. С другой стороны, T₁ᵧ и T₂ᵧ являются вертикальными составляющими одних и тех же сил соответственно. Поскольку гравитация действует на объект по вертикальной оси, нам необходимо учитывать вертикальные компоненты сил натяжения для нашего суммирования сил следующим образом:
ΣF ↑ = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ
Поскольку мы также знаем углы сил натяжения, мы можем выразить T₁ᵧ и T₂ᵧ через T₁ и T₂, соответственно, с помощью тригонометрических функций:
T₁ᵧ = T₁ * sin (α)
T₂ᵧ = T₂ * sin (β)
W = T₁ * sin (α) + T₂ * sin (β)
Мы также можем сказать, что для того, чтобы система находилась в равновесии, объект не должен двигаться горизонтально или вдоль оси x.Следовательно, горизонтальные компоненты T₁ и T₂ должны тогда равняться нулю. Кроме того, с помощью тригонометрии мы можем выразить T₁ₓ и T₂ₓ через T₁ и T₂ соответственно:
T₁ₓ = T₂ₓ
T₁ * cos (α) = T₂ * cos (β)
Если мы разделим обе части на cos (α) , мы получим уравнение, в котором T₁ выражается через T₂ и углы:
T₁ = T₂ * cos (β) / cos (α)
Затем мы можем использовать это уравнение для определения T₂, подставив T₂ * cos (β) / cos (α) в качестве T₁ в нашем уравнении суммирования сил, как показано ниже:
W = T₁ * sin (α) + T₂ * sin (β)
W = T₂ * [cos (β) / cos (α)] * sin (α) + T₂ * sin (β)
W = T₂ * [cos (β) * sin (α) / cos (α) + sin (β)]
T₂ = W / [cos (β) * sin (α) / cos (α) + sin (β)]
Наконец, если мы умножим все это уравнение на cos (β) / cos (α) , как мы вывели значение T₁ через T₂, а затем все упростив, мы получим следующее уравнение:
T₁ = W / [cos (β) * sin (α) / cos (α) + sin (β)] * [cos (β) / cos (α)]
T₁ = W / [cos (β ) * sin (α) / cos (α) + sin (β)] * [cos (β) / cos (α)]
T₁ = W / [cos (α) * sin (β) / cos ( β) + sin (α)]
Теперь все, что вам нужно знать, это углы натяжных тросов по отношению к горизонтали. Если задан угол от вертикали, просто вычтите этот угол из 90 °. Так вы получите угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90 ° или даже 180 °, вы можете воспользоваться нашим калькулятором опорных углов, чтобы помочь вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы можем теперь решить для сил натяжения.
Если задан угол от вертикали, просто вычтите этот угол из 90 °. Так вы получите угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90 ° или даже 180 °, вы можете воспользоваться нашим калькулятором опорных углов, чтобы помочь вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы можем теперь решить для сил натяжения.
Практика — гипертекст по физике
Для всех решений пусть T 1 будет кабелем слева, а T 2 — кабелем справа.Знак всегда имеет вес ( W ), который указывает вниз. Знак никуда не денется (не ускоряется), поэтому три силы находятся в равновесии. Опишите это состояние на языке физики — уравнения; в частности, уравнения компонентного анализа. Как всегда, сделайте красивый рисунок, чтобы показать, что происходит. Если хотите, воспользуйтесь линейкой и транспортиром.
Два восходящих компонента должны равняться друг другу. Вместе они должны равняться по весу, что означает, что каждый несет половину груза.
T 1 = T 2 = ½ W
T 1 = T 2 = ½ (100 Н)
T 1 T 2 = 50 НВес указывает вниз (270 °) и T 1 точек влево (180 °). Это оба хороших вектора — хороших в том смысле, что с ними легко иметь дело. T 1 — нарушитель спокойствия. Разбейте его на составляющие и сформулируйте условия равновесия в вертикальном и горизонтальном направлениях. Мне нравится помещать отрицательные векторы слева от знака равенства и положительные векторы справа. Я также предлагаю сначала поработать с вертикальным уравнением.
горизонтальный ∑ F — x = ∑ Факс + x T 1 = T 2 cos θ 2 T 1 = 141 N cos 45 ° T 1 = 100 Н вертикальный ∑ F — y = ∑ Факс + y Вт = T 2 sin θ 2 T 2 = Вт = 100 N sin θ 2 грех 45 ° T 2 = 141 N Вес — единственная сила с удобным направлением.
 Разложите противоречия на их составляющие. Задайте условие равновесия по обеим осям. Я предлагаю сначала поработать с горизонтальным уравнением.
Разложите противоречия на их составляющие. Задайте условие равновесия по обеим осям. Я предлагаю сначала поработать с горизонтальным уравнением.горизонтальный ∑ F — x = ∑ Факс + x T 1 cos θ 1 = T 2 cos θ 2 вертикальный ∑ F — y = ∑ Факс + y Вт = T 1 sin θ 1 + T 2 sin θ 2 Это конец физики.Остальная работа — математика. Решите горизонтальное уравнение для T 1 .
T 1 = T 2 cos θ 2 cos θ 1 Подставьте результат в вертикальное уравнение.
W = T 2 cos θ 2 sin θ 1 + T 2 sin θ 2 cos θ 1 Решите это для T 2 , замените значения и вычислите T 2 .
T 2 = Вт (sin θ 1 cos θ 2 ) / (cos θ 1 + sin θ 2 ) T 2 = 100 N (sin 60 ° cos 30 °) / (cos 60 ° + sin 30 °) T 2 = 50.  0 N
0 N Подставим обратно в горизонтальное уравнение и вычислим T 1 .
T 1 = Т 2 cos θ 2 cos θ 1 T 1 = 50.0 N cos 30 ° cos 60 ° T 1 = 86,6 Н
Ой, последнее было не очень весело. Посмотрим, нет ли более простого решения. Мы использовали компонентный анализ, поскольку это подход по умолчанию. Всякий раз, когда вам предоставляется куча векторов и вам нужно их объединить, можно использовать компоненты, особенно если вы не ожидаете каких-либо особых отношений между векторами.Мы постоянно используем этот безмозглый грубый подход к проблемам. Разберитесь в правилах, опишите их с помощью команд, понятных компьютеру, введите числа, получите ответы.
Иногда, однако, доступны умные решения. Они не работают постоянно, но когда они работают, мы должны их использовать. В этой практической задаче векторы настроены так, чтобы альтернативное решение было проще, чем решение по умолчанию. Графический метод сложения векторов требует их размещения головой к хвосту.Сумма будет результирующим вектором, соединяющим хвост первого вектора с головой последнего. Когда силы находятся в равновесии, их сумма равна нулю, и их результат не будет. Это означает, что должно быть возможно объединить три вектора в этой практической задаче в замкнутую фигуру — треугольник. Давай попробуем.
Это то, что мы называем вырожденным треугольником. Конечно, у него есть три стороны, но он не покрывает никакой площади.
 Две короткие стороны лежат поверх длинной стороны. Симметрия говорит нам, что две короткие стороны должны иметь одинаковую длину.Таким образом, каждое натяжение равно половине веса. Об этом мы уже говорили, поэтому преимуществ этого метода перед предыдущим нет.
Две короткие стороны лежат поверх длинной стороны. Симметрия говорит нам, что две короткие стороны должны иметь одинаковую длину.Таким образом, каждое натяжение равно половине веса. Об этом мы уже говорили, поэтому преимуществ этого метода перед предыдущим нет.T 1 = T 2 = ½ W
T 1 = T 2 = ½ (100 Н)
T 1 T 2 = 50 НГоризонтальное натяжение и вертикальный вес — это катеты треугольника 45–45–90, гипотенуза которого является диагональным натяжением.Эти силы должны составлять соотношение 1: 1: √2.
Т 1 = Вт = Т 2 1 1 √2 Т 1 = 100 N = Т 2 1 1 √2 T 1 = 1 (100 Н) T 1 = 100 Н T 2 = √2 (100 Н) T 2 = 141 N Два натяжения — это катеты треугольника 30–60–90, а вес — гипотенуза.Это означает, что стороны должны составлять соотношение 1: √3: 2. Просто убедитесь, что натяжения соответствуют правильным частям этого соотношения.
Т 2 = Т 1 = Вт 1 √3 2 Т 2 = Т 1 = 100 N 1 √3 2 T 1 = √3 100 N 2 T 1 = 86.  6 N
6 N T 2 = 1 100 N 2 T 2 = 50.0 N
И, наверное, есть другие способы решения этой проблемы.
Напишите что-нибудь совсем другое.
Скорость — Кинематика — (научный лагерь)
Скорость — Кинематика — (научный лагерь) Скорость определяется как скорость изменения смещения во времени .
Как и в случае со скоростью, мы можем вычислить как среднюю скорость за определенный период времени, так и мгновенную скорость.
Скорость — это векторная величина, т.е. она имеет величину и направление.
v = Δs / Δt
- v = скорость — в метрах (мс -1 )
- s = смещение — в метрах (м)
- t = время, затраченное на смещение — в секундах (с)
Рассмотрим то же путешествие из Манчестера в Лондон, которое использовалось в предыдущем примере. Однако на этот раз нас интересует средняя скорость по Бирмингем, поэтому мы будем учитывать расстояния по прямой, а не общее пройденное расстояние.
Используя смещение и время, измеренные в Манчестере
v ср = Δs / Δt
Изменение рабочего объема = s 2 -s 1
Изменение во времени = t 2 -t 1
v ср = (s 2 -s 1 ) / (t 2 -t 1 )
Как и в случае со скоростью, если мы возьмем точку отсчета с момента, когда транспортное средство впервые прибывает в Бирмингем, уравнение упрощается и
символы Δ часто опускаются
в пр.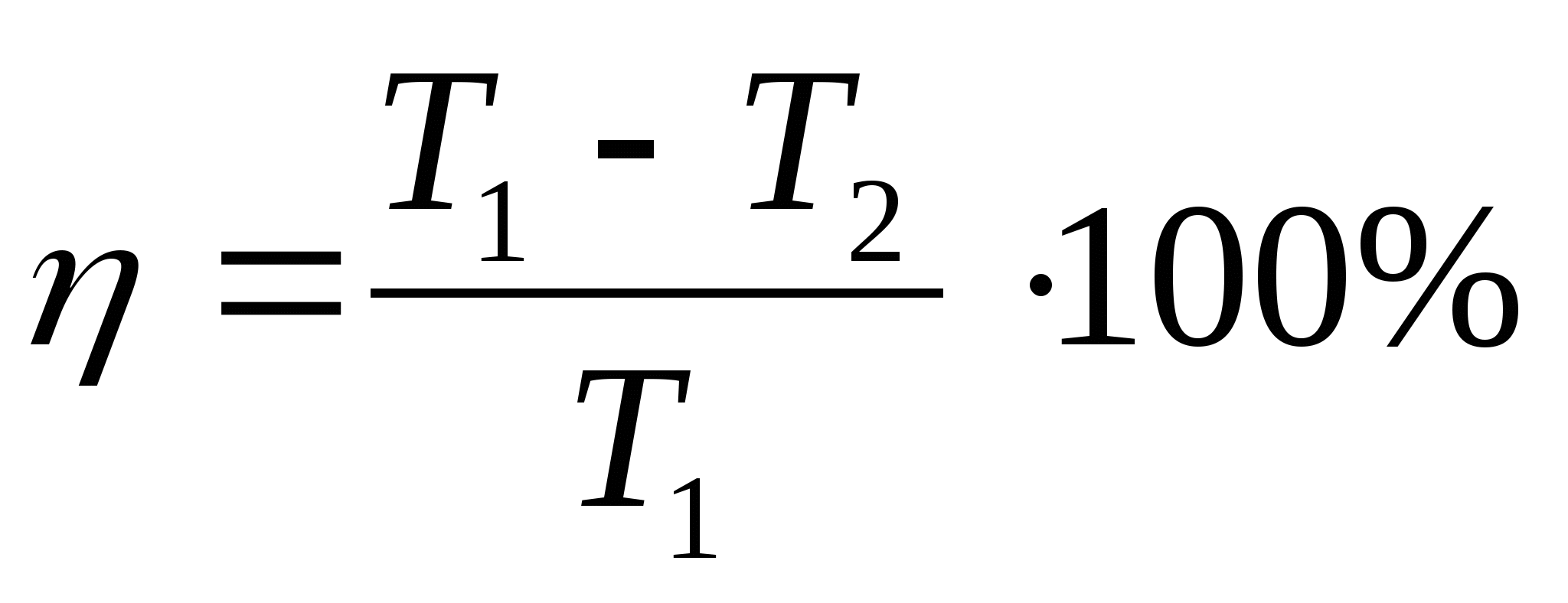 = с / т
= с / т
Пример 1
Объект движется с постоянной скоростью.
Если его смещение от исходного положения составляет 20 м, когда время составляет 2 секунды, и увеличивается до 34 м, когда время составляет 9 секунд.
Что это за скорость?
s1 = 20 м
s2 = 34 мс
t1 = 2 с
t2 = 9 с
v = Δs / Δt
v = (s2 — s1) / (t2 — t1) = 14/7 = 2 мс -1
Пример 2
Смещение объекта от опорной точки увеличивается на 3 м в 6 секунд.Какая у него скорость?
s = 3 мс
t = 6 с
в пр. = с / т
v ave = 3/6 = 0,5 мс -1
Примечание: поскольку мы не знаем из вопроса 2, постоянна ли скорость, мы можем только заявить, что знаем среднюю скорость!
| Автор Администрация ,
Понедельник, 19 октября 2020 г. | Доктор.Андреас Зигфридссон отвечает на ваши вопросы из сентябрьского вебинара по физике. Чтобы просмотреть запись, посетите: http://scmr.peachnewmedia.com/store/seminar/seminar.php?seminar=162995.
|

 com/id446425943
com/id446425943
 Разложите противоречия на их составляющие. Задайте условие равновесия по обеим осям. Я предлагаю сначала поработать с горизонтальным уравнением.
Разложите противоречия на их составляющие. Задайте условие равновесия по обеим осям. Я предлагаю сначала поработать с горизонтальным уравнением.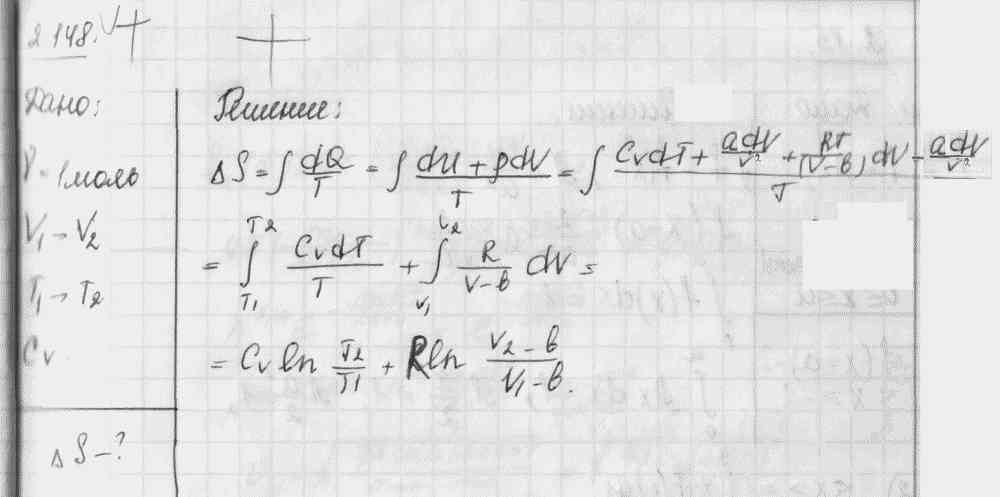 0 N
0 N  Две короткие стороны лежат поверх длинной стороны. Симметрия говорит нам, что две короткие стороны должны иметь одинаковую длину.Таким образом, каждое натяжение равно половине веса. Об этом мы уже говорили, поэтому преимуществ этого метода перед предыдущим нет.
Две короткие стороны лежат поверх длинной стороны. Симметрия говорит нам, что две короткие стороны должны иметь одинаковую длину.Таким образом, каждое натяжение равно половине веса. Об этом мы уже говорили, поэтому преимуществ этого метода перед предыдущим нет.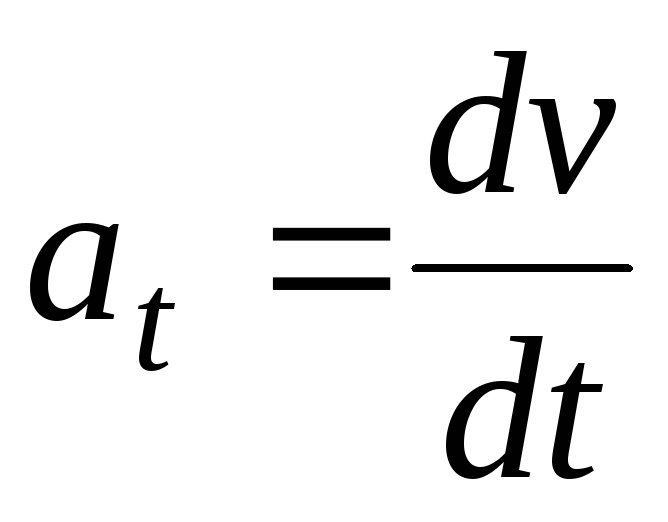 6 N
6 N 
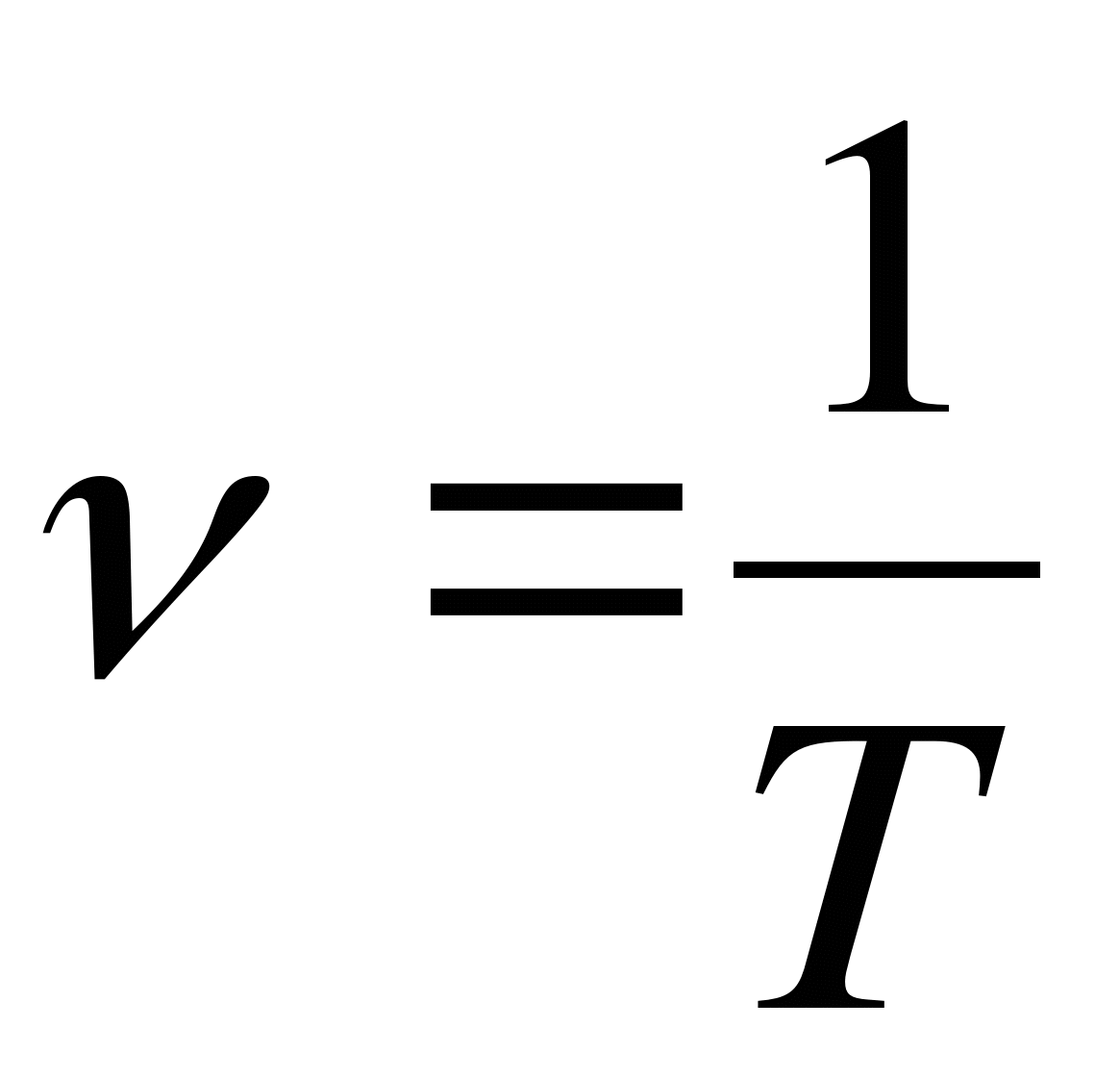 Я бы не стал доверять ценностям MOLLI. Может быть какой-нибудь специально настроенный вариант с меньшей внерезонансной чувствительностью.
Я бы не стал доверять ценностям MOLLI. Может быть какой-нибудь специально настроенный вариант с меньшей внерезонансной чувствительностью.

Leave A Comment