Помогите установить соответствие! Вариант 13. Часть 1. Задание 5. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. – Рамблер/класс
Помогите установить соответствие! Вариант 13. Часть 1. Задание 5. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Установите соответствие между графиками функций и формулами, которые их задают.
у = х2-7х + 9 2) у = -х2-7х-9 3) у = -х2+7х-9
В таблице под каждой буквой укажите соответствующий номер.
ответы
Ответ:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Олимпиады
Экзамены
Оценки
3 класс
похожие вопросы 5
Вариант 1. Часть 2. Задание 26. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Помогите найти АН.
На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту АD в точке М, АD (Подробнее…)
ГДЗМатематикаОГЭ9 классЯщенко И.В.
ГДЗ. Математика.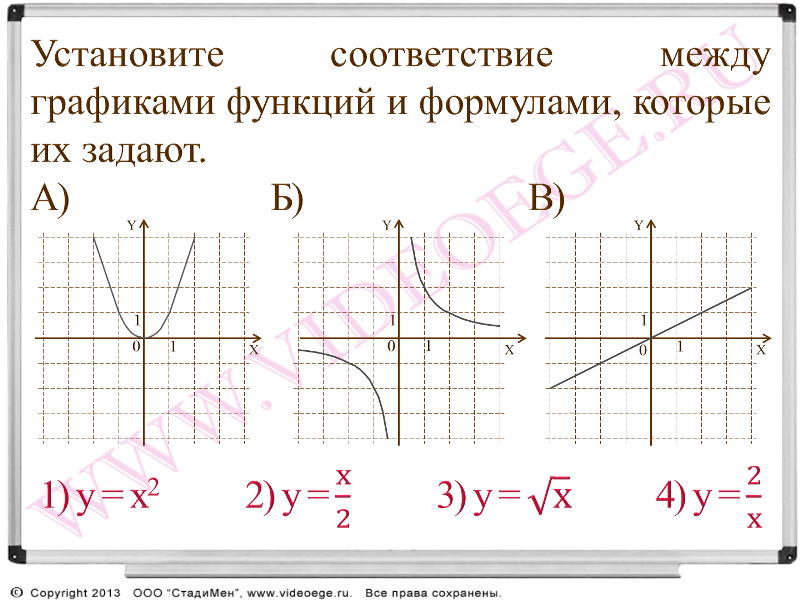 Базовый уровень ЕГЭ — 2017. Вар.№26. Зад.№9.Под руководством Ященко. Помогите установить соответствие.
Базовый уровень ЕГЭ — 2017. Вар.№26. Зад.№9.Под руководством Ященко. Помогите установить соответствие.
Здравствуйте! Помогите установить соответствие между величинами и их возможными значениями: к каждому элементу первого столбца (Подробнее…)
Задание 38 Однородные члены предложения. Что такое однородные члены предложения? Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ
Всем привет, поделитесь ответом на задание
Прочитайте.
Рассмотрите условные обозначения однородных членов.
(Подробнее…)
ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс
А что интересного будет происходить в эти выходные? Куда сходить с учителем?
А что интересного будет происходить в эти выходные? Куда сходить с учителем?
9 класс
4. Теорему синусов можно записать в виде… Ященко И. В. Математика ЕГЭ-2017 ГДЗ.
(Подробнее…)
ГДЗЕГЭМатематикаЯщенко И.В.
Установление соответствия между графиком функции и ее формулой. Подготовка к ОГЭ | План-конспект занятия по алгебре (8 класс) по теме:
Название работы | Установление соответствия между графиком функции и его формулой. Учебно-тренировочное занятие для подготовки к ОГЭ |
Класс | 8-9класс |
Предметная область | Математика |
Цель | К концу занятия учащиеся смогут: 1. Различать графики параболы. гиперболы и прямой; различать формулы обратной пропорциональности, линейной функции и квадратичной функции; 2. Устанавливать соответствие между формулой функции и ее графиком; 3. |
Аннотация | Краткое описание работы. К экзамену в 9 классе нужно начинать подготовку с младших классов. В 8 классе уже изучены практически все функции, которые выносятся на экзамен. Поэтому данный материал целесообразно использовать с восьмиклассниками. В демоверсии — это задание №5.На уроке используется система для голосования в режиме обучения, для этого используется функция мгновенного вопроса. Учащиеся учатся работать со справочными материалами. Все решенные задания оцениваются определенным количеством баллов и суммируются. В конце занятия подводится итог. |
Тема: Установление соответствия между графиком функции и его формулой.
Учебно-тренировочное занятие для подготовки к ОГЭ.
Цель: К концу занятия учащиеся смогут:
1. Различать графики параболы. гиперболы и прямой; различать формулы обратной пропорциональности, линейной функции и квадратичной функции;
2. Устанавливать соответствие между формулой функции и ее графиком;
Устанавливать соответствие между формулой функции и ее графиком;
3. Устанавливать взаимосвязь между знаками коэффициентов функции и ее графиком
Метапредметные результаты: работают со справочным материалом; устанавливают соответствие, осуществляют контроль и оценку своих знаний и умений, сверяют свое решение с предложенным эталоном.
Оборудование: ПК, презентация, интерактивная доска, система для голосования, справочные материалы, тренировочные задания,[1] файл для работы с системой голосования
Этап урока | Деятельность учителя | Деятельность ученика | |
1. Орг момент | Приветствует учащихся, проверяет готовность учащихся к уроку | Включаются в ритм урока | |
2. Актуализация знаний | Слайд 1 . | Учащиеся выполняют задание на соответствие в тетрадях. | |
| А) Прямая; Б) Ветвь параболы; В) Гипербола; Г) Парабола; Д) Прямая, проходящая через начало координат | ||
Показывает эталон выполнения задания, предлагает оценить выполнение задания и выставить себе баллы. | Учащиеся осуществляют самопроверку выполнения задания и выставляют по 1 баллу за каждое правильно установленное соответствие | ||
2) Предлагает учащимся записать название каждой из предложенных шести функций. После выполнения показывает правильные ответы на задание(слайд 2) | Учащиеся осуществляют самопроверку выполнения задания и выставляют по 1 баллу за каждое правильное название функции | ||
3. | Учащимся предлагается заполнить таблицу. (слайд 3)Если учащийся согласен с утверждением, то ставит «+», если не согласен, то ставит «-« | Проводят первичную рефлексию собственных знаний и умений , заполняют таблицу, расставляя «+» и «-« Формулируют тему и цель урока | |
Исходя из заполненной таблицы, учащимся предлагается сформулировать тему и цель урока | |||
4. Отработка умений | 1) На уроке используется система для голосования с функцией мгновенного ответа. Файл Учитель предлагает задания №1-№6 (если нет системы для голосования, то можно использовать слайдовую презентацию слайды№5-10. )
После выполнения каждого задания организуется обсуждение. Учащимся предлагается обосновать выбор своего ответа. 2) прежде чем решать задание №7, предлагает учащимся в справочных материалах. Лист 3. Разобрать пример из табл№3., а затем выполнить задание №7. Слайд №11. | Учащиеся читают задание, решают его . При решении используют справочный материал, имеющийся на партах. Вводят свои ответы, используя пульты системы голосования. На экране выводится таблица ответов., где видны результаты ответов каждого учащегося. Обосновывают свой ответ и сверяют свой ответ с названным эталоном, оценивают и корректируют свое решение, ставят баллы за правильные ответы | |
За аргументированное объяснение материала учитель может добавить учащимся баллы на свое усмотрение | Учащиеся работают с текстом справочных материалов в паре. Обсуждают предложенное решение, определяют какой способ лучше. Решают задание №7. Сверяют свое решение с решениями товарищей | ||
5. | Учитель предлагает учащимся в паре решить 4 задачи (Тренировочные задания)самостоятельно и сверить свои ответы с ответами, лежащими на столе учителя. | Решают задания, обсуждая решение в паре. Выставляют баллы за верные ответы | |
6. Итог урока и рефлексия | Предлагает посчитать баллы, которые были набраны в ходе урока и выставить себе оценки по следующим критериям. После этого возвращаемся к таблице заполненной в начале урока и заполнить ее на конец урока, расставив «+» и «-« Организует обсуждение достигнутых целей | Считают баллы, выставляют оценки, заполняют таблицу рефлексии. Высказывают свое мнение о достижении поставленной на урок цели | |
Интернет- ресурсы
Тренировочные задания и задания к уроку взяты с сайта
1. http://opengia. ru/subjects/mathematics-9/topics/1
ru/subjects/mathematics-9/topics/1
Как построить график функции в Excel? 2 Easy Ways
Home > Microsoft Excel > Как построить график функции в Excel? 2 Easy Ways
(Примечание. Это руководство о том, как построить график функции в Excel, подходит для всех версий Excel, включая Office 365)
Время от времени Excel доказывал, что является полезным инструментом для выполнения различных расчетов. Excel предлагает вычисления и упрощения для огромного количества математических функций, начиная от простых функций сложения и заканчивая сложными квадратичными, экспоненциальными и тригонометрическими функциями.
В дополнение к вычислению значений в Excel также есть возможность установить взаимосвязь между входными и выходными значениями. Это представление в виде графиков обеспечивает простой способ сравнения и интерпретации данных.
В этой статье я покажу вам, как использовать функцию в Excel и как построить график функции в Excel двумя простыми способами.
Вы узнаете:
- Что такое функции?
- Как использовать функции в Excel?
- С помощью функций из библиотеки Excel
- Вводом функции вручную
- Как построить график функции в Excel?
- Как настроить график?
Посмотрите наше видео о том, как построить график функции в Excel.
Логические функции в Excel (ЕСЛИ, ЕСЛИ, И, ИЛИ, СЧЁТЕСЛИ, СУММЕСЛИ)
Что такое функции?
Прежде чем мы приступим к использованию функции, дайте нам знать, что такое функции.
Обычно функции представляют собой набор вычислений, имеющих конечный набор операций вместе с переменной для получения результата. Другими словами, они обеспечивают взаимосвязь между входом и выходом.
Давайте посмотрим на пример, чтобы узнать больше о функциях.
Возможно, вы все слышали о тригонометрических функциях, таких как теорема Пифагора (c 2 =a 2 +b 2 ) или квадратные уравнения типа ax 2 +bx+c=0.
Возможно, вы все слышали о формуле для расчета радиуса круга. Мы используем формулу πr 2 , где r — радиус окружности и является переменной. Для разных радиусов круга площадь тоже будет разной.
В этом случае радиус (r) считается входом, а площадь — выходом. Когда дело доходит до построения точек на графике, входные данные берутся по оси x, а выходные данные — по оси y.
Как использовать функции в Excel?
В Excel вы можете использовать функции, чтобы легко установить взаимосвязь между вводом и выводом. Есть два способа использования функций в Excel.
1. Использование функций из библиотеки Excel
Если вы собираетесь работать с какой-либо основной функцией, в Excel есть огромная библиотека встроенных функций, из которых вы можете выбирать. Вы можете просто выбрать функции, ввести значения, и Excel выдаст вам результат.
- Выберите ячейку и введите любое значение. Пусть входным значением будет угол, а выходным значением будет значение синуса, поскольку мы будем работать с синусоидальной функцией.
 В этом случае я ввел значение 0 в ячейку A4. Вы также можете ввести несколько значений в качестве входных данных.
В этом случае я ввел значение 0 в ячейку A4. Вы также можете ввести несколько значений в качестве входных данных.
- Теперь, чтобы добавить функцию, щелкните любую ячейку назначения.
- Перейдите к Формулы в строке меню. В библиотеке функций вы найдете множество категорий, состоящих из различных функций, таких как финансовые, логические, математические и триггерные и т. д. В зависимости от вашей операции выберите функцию из библиотеки функций.
Если вам трудно найти местоположение функции, нажмите Вставить функцию из библиотеки функций или из любого раскрывающегося списка категорий.
Использовать функцию Вставки- Откроется новое диалоговое окно Вставить функцию . Вы можете выбрать категорию и выбрать нужную функцию. В случае, если вы все еще не можете найти подходящую функцию, вы можете ввести описание, и Excel покажет вам список связанных функций.

- Теперь, когда вы нашли функцию, нажмите Хорошо .
- Откроется другое диалоговое окно, в котором вам будет предложено ввести аргументы для функции. Вы можете ввести любое постоянное значение или если вы хотите выбрать или добавить имя ячейки в текстовое поле и нажать OK . В этом случае я передам аргумент как A4, так как эта ячейка содержит значение для ввода.
- Это дает значение синуса для данного входа. Теперь вы можете использовать манипулятор перетаскивания для выполнения этой функции и в других ячейках.
2. Вводом функции вручную
Некоторые функции могут быть недоступны в библиотеке функций Excel. В таких случаях вы можете вручную создать функцию и получить результат.
Ввести функцию вручную в Excel очень просто. Просто добавьте «=» перед функцией в ячейке назначения и введите их. В случае переменных выберите или введите номер ячейки, чтобы получить вывод.
В случае переменных выберите или введите номер ячейки, чтобы получить вывод.
Рассмотрим пример квадратного уравнения y=4x 2 +2x+5. В этом случае x — это вход, а y — результат, который необходимо вычислить. Чтобы получить несколько значений квадратичной функции, добавьте разные входные данные в разные ячейки.
Введите входные данные в один столбец. Пусть он будет называться х. Входные данные могут быть положительными, десятичными, отрицательными или даже нулевыми.
Введите входные данныеЗдесь целевой ячейкой является B4. Итак, вместо x теперь введите функцию =4(A4) 2 +2(A4)+5 в ячейке назначения. Всегда не забывайте добавлять «*» вместо умножения при ручном вводе функций. Нажмите Введите .
Введите функцию в ячейку назначения Это даст вам результат, соответствующий функции и вводу. Вы можете использовать маркер перетаскивания, чтобы добавить функцию в другие ячейки и получить серию выходных данных.
Читайте также:
Как использовать СРЗНАЧЕСЛИ в Excel? С 5 различными критериями
IFERROR Excel-полное руководство по обнаружению ошибок в Excel
Как фильтровать в Excel? Пошаговое руководство
Как построить график функции в Excel?
Когда у вас есть ввод и вывод для требуемой функции, построить график довольно просто.
- Чтобы построить график, выберите ось X (вход) и ось Y (выход) графика.
- Перейдите в меню Вставить . В разделе Charts выберите Scatter . Хотя есть способы представить ваши данные с помощью других графических представлений, таких как гистограммы или круговые диаграммы, разброс представляет график, указав каждую точку в функции.
- Щелкните тип точечной диаграммы для представления данных.
 Это строит график функции с входными и выходными данными по оси x и оси y соответственно.
Это строит график функции с входными и выходными данными по оси x и оси y соответственно.
Как настроить график
Когда вы нажимаете на точечную диаграмму, график обычно заполняется в центре листа Excel. Вы можете переместить график в нужное место, нажав на график и перетащив его. Переместите указатель к краям графика, чтобы изменить размер области диаграммы.
Вы также можете настроить диаграмму с помощью параметров быстрого доступа, которые появляются при нажатии на диаграмму.
Настройка графика в ExcelИспользуйте параметр Chart Element для добавления, отображения или скрытия любых элементов, таких как заголовки, легенды и другие проекции.
Использование элементов диаграммы Используйте параметр Стили диаграммы для изменения стиля и цвета диаграммы. Изменение стиля и цвета придает диаграмме более подходящий вид для представления данных.
Если ваша диаграмма содержит более одного представления данных, вы можете использовать фильтр , чтобы добавить или удалить любые данные в зависимости от ваших предпочтений.
Использование фильтраДля более глубокой и расширенной настройки диаграммы можно использовать параметры Chart Design и Format в главном меню.
Используя опцию Chart Design , вы можете изменять компоновку диаграммы, цвет диаграммы, переключать оси и перемещать диаграмму между листами.
Использование Chart DesignИспользуя параметр Format , вы можете добавить любые фигуры или текст, чтобы добавить подсказки о диаграмме, выровнять и изменить размер диаграммы.
Использование форматаРекомендуемое чтение:
Как добавить ведущие нули в Excel? 4 простых метода
Сравнение строк в Excel – 5 простых методов
Как скрыть и показать столбцы в Excel? (3 простых шага)
Заключительные мысли
Построение функции в виде графика дает представление об использовании функции, легко интерпретирует данные.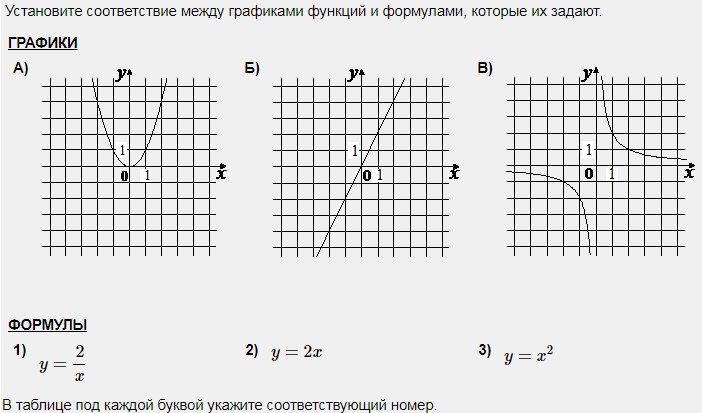
В этой статье мы увидели, как использовать функцию и построить график функции в Excel. Мы также узнали, как настроить график в Excel.
Если вам нужно больше высококачественных руководств по Excel, посетите наш бесплатный центр ресурсов Excel. Саймон Сез ИТ преподает Excel более десяти лет. За небольшую ежемесячную плату вы можете получить доступ к 130+ обучающим курсам по ИТ. Нажмите здесь, чтобы перейти к продвинутым курсам Excel с углубленными учебными модулями.
Саймон Колдер
Крис «Саймон» Колдер работал руководителем проекта в области ИТ в одном из самых престижных культурных учреждений Лос-Анджелеса, LACMA. Он научился использовать Microsoft Project с помощью гигантского учебника и ненавидел каждый его момент. Онлайн-обучение тогда было в зачаточном состоянии, но он увидел возможность и сделал онлайн-курс MS Project — остальное, как говорится, уже история!
Похожие сообщения
1.3 Функции
Функция $y=f(x)$ есть правило для определения
$y$, когда нам дано значение $x$. Например, правило
$y=f(x)=2x+1$ — функция. Любая линия $y=mx+b$ называется линейной функцией . График функции
выглядит как кривая выше (или ниже) оси $x$, где для любого значения
$x$ правило $y=f(x)$ говорит нам, как далеко можно подняться выше (или ниже)
Ось $x$, чтобы достичь кривой.
Например, правило
$y=f(x)=2x+1$ — функция. Любая линия $y=mx+b$ называется линейной функцией . График функции
выглядит как кривая выше (или ниже) оси $x$, где для любого значения
$x$ правило $y=f(x)$ говорит нам, как далеко можно подняться выше (или ниже)
Ось $x$, чтобы достичь кривой.
Функции могут быть определены различными способами: алгебраической формулой или несколькими алгебраические формулы, графиком или экспериментально установленной таблицей значений. (В последнем случае таблица дает набор точек на плоскости, которые мы могли бы затем интерполируйте плавной кривой, если это имеет смысл.) 92$
Рисунок 1.3.1. Некоторые графики.
Например, функция квадратного корня $y=f(x)=\sqrt{x}$ является правилом
в котором говорится, что для заданного значения $x$ нужно взять неотрицательное число,
квадрат равен $x$. Это правило имеет смысл только в том случае, если $x$ положительно или равно нулю.
Другой пример функции, областью определения которой является не вся ось $x$. есть: $y=f(x)=1/x$, обратная функция. Мы не можем заменить $x=0$ в этой формуле. Однако функция имеет смысл для любого ненулевого $x$, поэтому мы берем домен следующим образом: $\{x\in\R\mid x\ne 0\}$. График этой функции нет точек $(x,y)$ с $x=0$. Как $х$ приближается к 0 с любой стороны, график уходит в бесконечность. Мы называем вертикальную линию $x=0$ асимптотой
 2$ — это все
$\R$. Но в контексте задачи-рассказа о нахождении площадей квадратов
мы ограничиваем область определения положительными значениями $x$, потому что квадрат
с отрицательной или нулевой стороной не имеет смысла.
93$.
Кроме того, могут использоваться буквы, отличные от $f$. Например, если $y$ равно
скорость чего-либо в момент времени $t$, мы можем написать $y=v(t)$ с
буква $v$ (вместо $f$), обозначающая функцию скорости (и
$t$ играет роль $x$).
2$ — это все
$\R$. Но в контексте задачи-рассказа о нахождении площадей квадратов
мы ограничиваем область определения положительными значениями $x$, потому что квадрат
с отрицательной или нулевой стороной не имеет смысла.
93$.
Кроме того, могут использоваться буквы, отличные от $f$. Например, если $y$ равно
скорость чего-либо в момент времени $t$, мы можем написать $y=v(t)$ с
буква $v$ (вместо $f$), обозначающая функцию скорости (и
$t$ играет роль $x$).Буква, играющая роль $x$, называется независимыми. переменная , а буква, играющая роль $y$, называется зависимая переменная (поскольку ее значение «зависит от» значения независимого переменная). В задачах истории, когда один должен перевести с английского языка на математический, решающим шагом является определить, какие буквы обозначают переменные. Если только слова и нет буквы даны, то мы должны решить, какие буквы использовать. Некоторый буквы традиционные. Например, почти всегда $t$ означает время.
Пример 1. 3.1. Ящик с открытым верхом сделан из $a\times b$ прямоугольного куска
картона, вырезав квадрат со стороной $x$ из каждого из четырех
углы, а затем загибаем стороны вверх и герметизируем их воздуховодом
лента. Найдите формулу зависимости объема $V$ ящика от
$x$ и найти область определения этой функции.
3.1. Ящик с открытым верхом сделан из $a\times b$ прямоугольного куска
картона, вырезав квадрат со стороной $x$ из каждого из четырех
углы, а затем загибаем стороны вверх и герметизируем их воздуховодом
лента. Найдите формулу зависимости объема $V$ ящика от
$x$ и найти область определения этой функции.
Получившийся ящик будет иметь высоту $x$ и прямоугольное основание размеры $a-2x$ на $b-2x$. Таким образом, $$ V=f(x)=x(a-2x)(b-2x). $$ Здесь $a$ и $b$ — константы, а $V$ — переменная, зависящая от на $x$, т. е. $V$ играет роль $y$. 92
Функция не всегда должна быть задана одной формулой, поскольку мы
уже видели (в проблеме подоходного налога, например).
Предположим, что $y=v(t)$ — функция скорости автомобиля
который выходит из состояния покоя (нулевой скорости) в момент времени $t=0$; затем
неуклонно увеличивает скорость до 20 м/с, на это требуется 10 секунд.
этот; затем движется с постоянной скоростью 20 м/сек в течение 15 секунд; и
наконец, применяет тормоза, чтобы неуклонно снижать скорость до 0, что занимает 5
секунды, чтобы сделать это.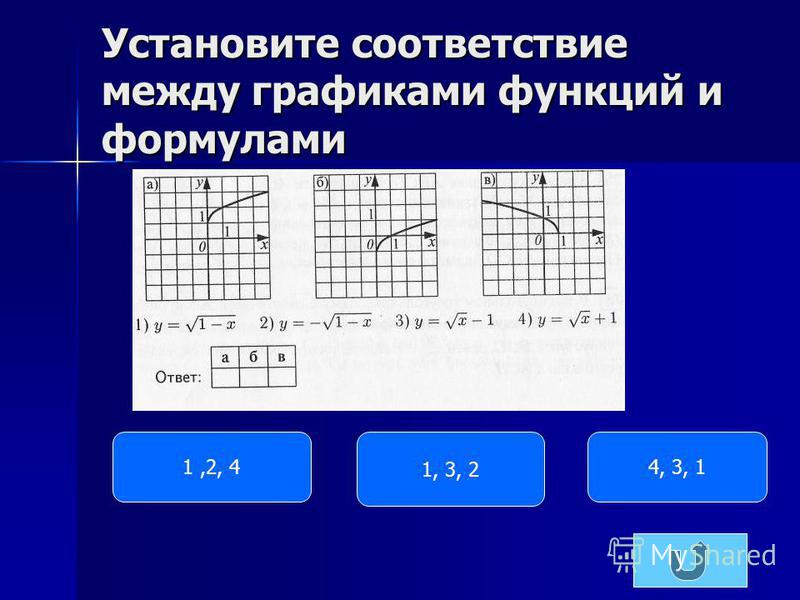 Формула для $y=v(t)$ различна в каждом из
три временных интервала: сначала $y=2x$, затем $y=20$, затем $y=-4x+120$.
График этой функции показан на рисунке 1.3.3.
Формула для $y=v(t)$ различна в каждом из
три временных интервала: сначала $y=2x$, затем $y=20$, затем $y=-4x+120$.
График этой функции показан на рисунке 1.3.3.
Рисунок 1.3.3. Функция скорости.
Вообще не все функции задаются формулами. Функция может быть определяется экспериментально установленной таблицей значений или описание, отличное от формулы. Например, население $y$ США является функцией времени $t$: мы можем написать $y=f(t)$. Этот — совершенно хорошая функция — мы могли бы изобразить ее (с точностью до присутствует), если бы у нас были данные для различных $t$ — но мы не можем найти алгебраическая формула для него.
Найдите область определения каждой из следующих функций: 92-9)/(x-3)& $x\neq 3$\cr 6& если $x=3$.\cr}$ (отвечать)
Пример 1.3.13
Пример 1.

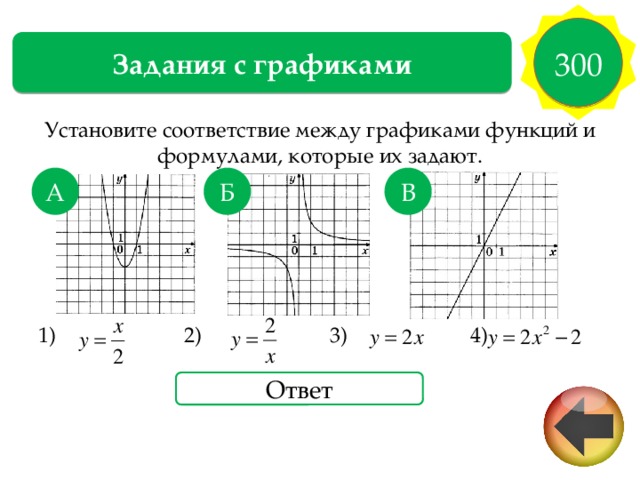 Устанавливать взаимосвязь между знаками коэффициентов функции и ее графиком
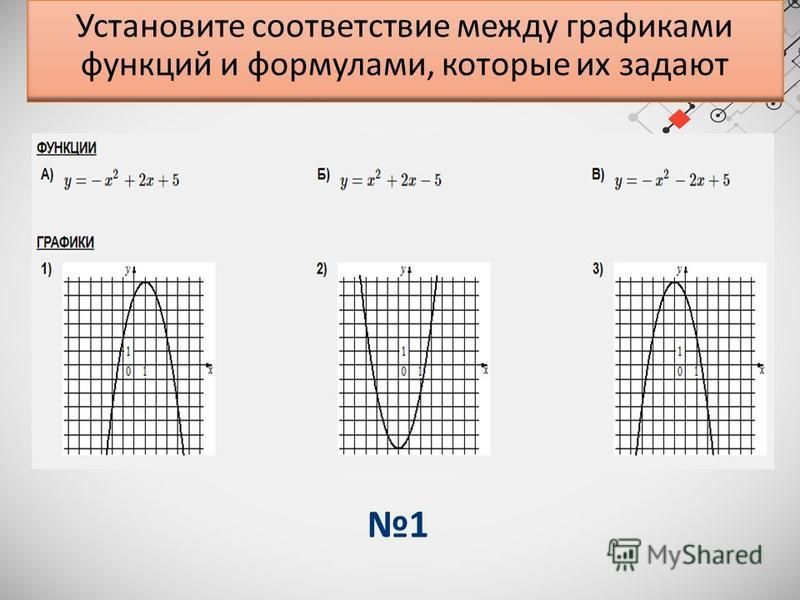
Устанавливать взаимосвязь между знаками коэффициентов функции и ее графиком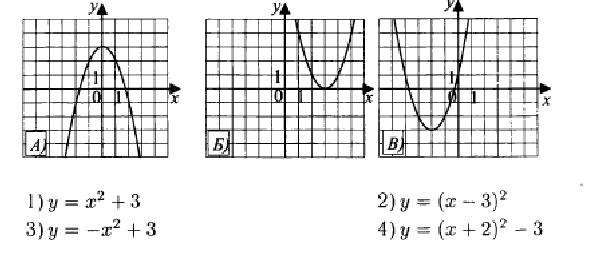 Предлагает учащимся выполнить задание.: Установите соответствие между формулой и названием графика
Предлагает учащимся выполнить задание.: Установите соответствие между формулой и названием графика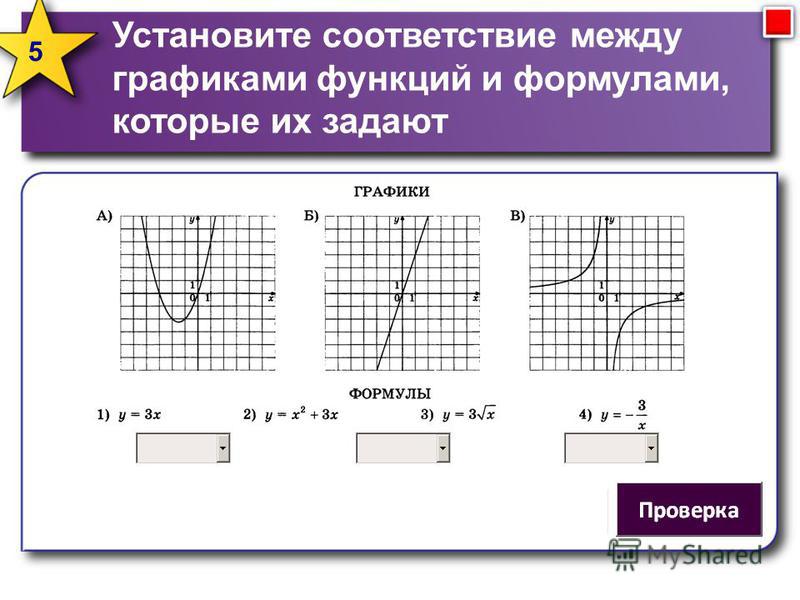 Первичная рефлексия и постановка целей на урок
Первичная рефлексия и постановка целей на урок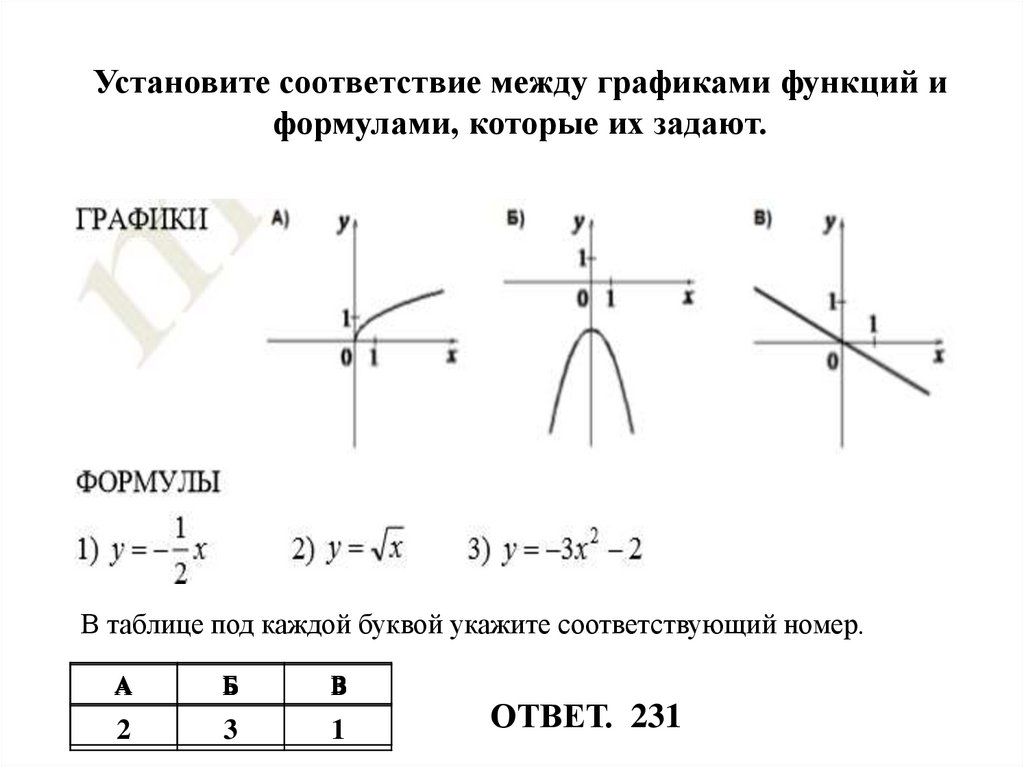
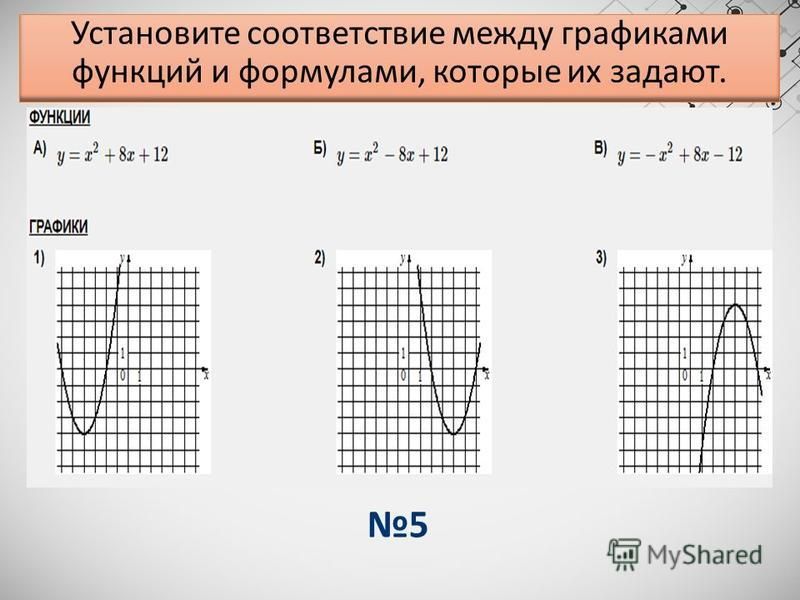 Самостоятельная работа в парах
Самостоятельная работа в парах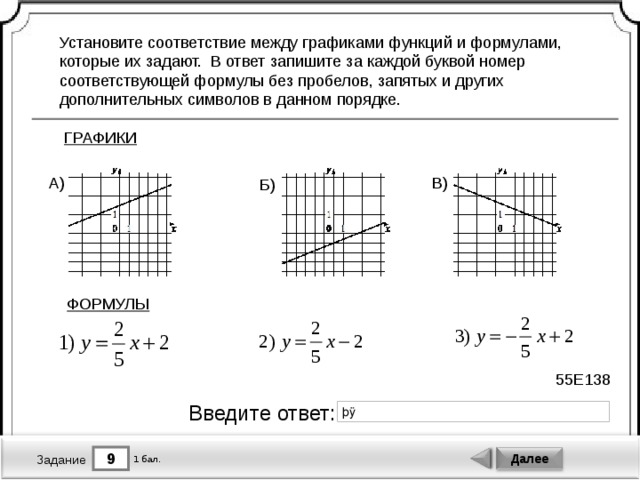 В этом случае я ввел значение 0 в ячейку A4. Вы также можете ввести несколько значений в качестве входных данных.
В этом случае я ввел значение 0 в ячейку A4. Вы также можете ввести несколько значений в качестве входных данных.
 Это строит график функции с входными и выходными данными по оси x и оси y соответственно.
Это строит график функции с входными и выходными данными по оси x и оси y соответственно.
Leave A Comment