Задачи на параллелограмм 8 класс онлайн-подготовка на Ростелеком Лицей
Повторение определения, свойств и признака параллелограмма
Сегодня мы основное внимание уделим задачам на параллелограмм. Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их.
Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).
Рис. 1. Параллелограмм
Основные свойства параллелограмма:
Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 2. Первый признак параллелограмма
Рис. 3. Второй признак параллелограмма
Теорема. Второй признак параллелограмма.
Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник – параллелограмм. параллелограмм.
Теорема. Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 4. Третий признак параллелограмма
Задачи на параллелограммы
Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма.
Пример 1. В параллелограмме проведены биссектрисы и , которые пересекаются в точке . Найти .
Решение. Изобразим Рис. 5.
Рис. 5
Обозначим для удобства: . Следовательно, поскольку и биссектрисы.
По теореме о сумме внутренних углов треугольника .
Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: . Тогда:
.
Ответ.
.
Пример 2. Прямая , проведенная через середину стороны параллельно стороне треугольника пересекает третью его сторону в середине. Доказать, что – это середина .
Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем .
Рис. 6
Рассмотрим четырехугольник :
параллелограмм по определению. Тогда по свойству равенства противоположных сторон , но по условию еще известно, что , следовательно, .
Рассмотрим треугольники и :
по второму признаку равенства треугольников (по стороне и прилежащим углам).
Из равенства указанных треугольников следует равенство их соответствующих сторон, т.е., например, что . Это означает, что точка является серединой стороны . Что и требовалось доказать.
Доказано.
3. Теорема Фалеса
Теорема Фалеса. Если параллельные прямые, которые пересекают стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство. Изобразим Рис. 7.
Рис. 7. Теорема Фалеса
Рассмотрим . В нем точка – середина стороны , а прямая . Из предыдущего примера следует, что точка делит сторону на две равные части, т.е. . Равенство двух отрезков, ближайших к вершине угла доказано. Аналогично доказывается попарное равенство всех остальных отрезков на второй стороне угла, если проводить прямые параллельные первой стороне угла через начало первого отрезка в любой рассматриваемой паре.
Доказано.
4. Пример задачи на применение теоремы Фалеса
Рассмотрим пример на доказанную теорему.
Пример 3. Дан отрезок , разделить его на три равные части.
Решение. Изобразим указанный отрезок на Рис. 8 и сделаем дополнительные построения: отложим три равных отрезка любой длины вдоль одной прямой, не совпадающей с указанным в условии отрезком.
Рис. 8. Применение теоремы Фалеса
Соединим прямой точки и , а затем проведем прямые, параллельные прямой , через точки и : .
Полученные при пересечении отрезка точки и будут делить отрезок на три равных части по теореме Фалеса. Необходимое построение выполнено и задача решена.
Ответ: построено.
Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях. А на следующем уроке мы познакомимся с таким видом четырехугольников, как трапеция, и обсудим ее свойства.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Narod.ru (Источник).
- Фестиваль педагогических наук «Открытый урок» (Источник).
Домашнее задание
- № 50 (г, д, е, ж, з, и), 51 (б, в, г, ж), 52 (б, в, е, ж). Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- В параллелограмме см, см, биссектрисы углов и пересекают сторону в точках и . Найдите длину отрезка .
- Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен . Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.
- ∗ Через середину диагонали параллелограмма проведена прямая, которая пересекает стороны и в точках и соответственно. Докажите, что четырехугольник параллелограмм.
Задачи по геометрии параллелограмм. | Геометрия
Добрый день, дорогие друзья!
Сегодня мы продолжим решение задач из сборника под редакцией М.И. Сканави.
И на этот раз мы будем решать задачи по геометрии параллелограмма.
Понятно, что прежде, чем приступать к решению таких задач, надо понимать, что такое параллелограмм и какие у него есть свойства.
Параллелограмм — выпуклый четырёхугольник, у которого противоположные стороны попарно параллельны.
У параллелограмма противоположные стороны и противоположные углы равны;
диагонали его делят параллелограмм на 2 равных треугольника,
а сами диагонали точкой пересечения делятся пополам.
И сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
Вот в основном те свойства, которые в первую очередь необходимы для понимания и решения задач по геометрии параллелограмма. А теперь задачи.
Задача 1. Периметр параллелограмма равен 90 см, а его острый угол равен 60°.
Диагональ параллелограмма делит его тупой угол на части в отношении 1:3. Найти стороны параллелограмма.
Решение: Если угол А равен 60°, то угол В, лежащий рядом с ним , будет равен 180-60=120°.
Но диагональ BD делит его в соотношении 1:3, или на 4 равные части.
Получается, что одной части принадлежит 120:4 = 30°.
Следовательно, диагональ BD делит угол В на 2 угла 30° и 90°.
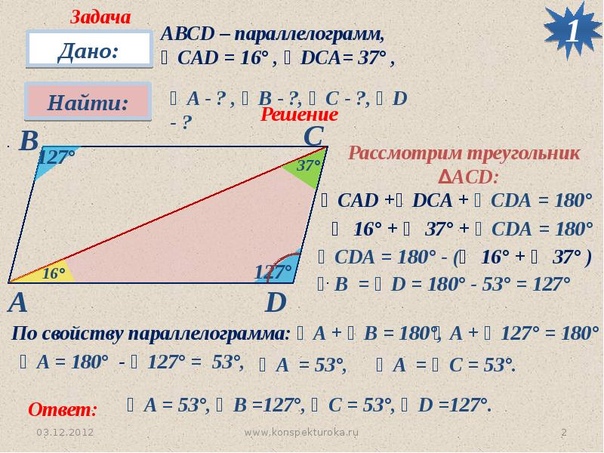
По рисунку угол 1 — прямой. Треугольник ABD — прямоугольный.
И угол 2 в треугольнике равен 30º, как накрест лежащий при параллельных прямых AB и CD и секущей BD.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы. Получается, что АВ=1/2 AD.
Теперь составляем уравнение для периметра.
AB+BC+CD+AD=90
1/2AD+AD+1/2AD+AD= 90
3AD=90 AD=30 AB=1/2*30 = 15.
Ответ: стороны параллелограмма равны 30 см и 15 см.
Задача 2. Биссектриса острого угла параллелограмма делит его диагональ на отрезки длиной 3,2 см и 8,8 см.
Найти стороны параллелограмма, если его периметр равен 30 см.
Решение: Мы знаем, что биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные сторонам угла.
А именно, AB:AD = BO:OD, но BO и OD равны соответственно 3,2 см и 8,8 см.
Поэтому, можно принять, что АВ = 3,2х, а AD равно 8,8х.
Противоположные стороны параллелограмма равны.
Периметр это есть сумма всех сторон параллелограмма.
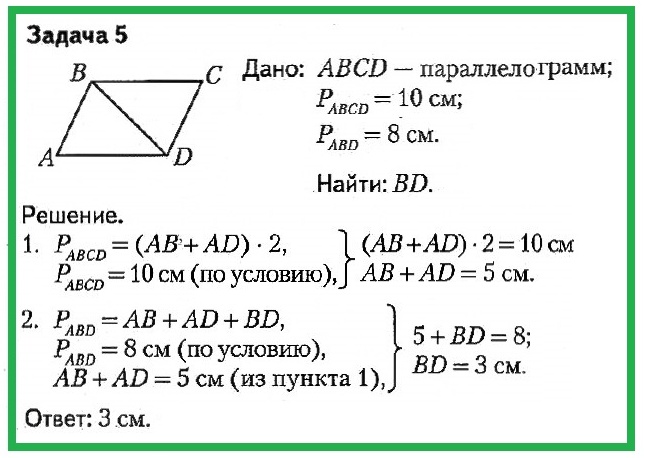
Составляем уравнение: 3,2х+8,8х+3,2х+8,8х = 30 24х = 30 х = 30/24 = 5/4.
Мы нашли коэффициент пропорциональности Х=5/4.
Отсюда, сторона АВ = 3,2х = 3,2 * 5/4 = 4 см.
Сторона AD равна 8,8х = 8,8 * 5/4 = 11 см.
Ответ: стороны параллелограмма равны 4 см, 4 см, 11 см, 11 см.
Задача 3. Параллелограмм с периметром 44 см разделён диагоналями на 4 треугольника.
Разность между периметрами двух смежных треугольников равна 6 см.
Найти стороны параллелограмма.
Решение: Рассмотрим два треугольника, лежащих выше диагонали d.
Периметр первого равен b+c+d.
Периметр второго равен a+c+d.
Разность периметров двух треугольников равна 6 см.
Составляем уравнение:
a+c+d — (b+c+d) = a+c+d-b-c-d = a-b = 6.
Получилось, что разность двух сторон параллелограмма равна 6 см.
Второе уравнение составляем из свойства периметра параллелограмма:
a+b+a+b = 44
2a+2b=44
a+b=22.
Получили систему двух уравнений с двумя неизвестными:
a — b = 6
a + b = 22 Решим её методом сложения.
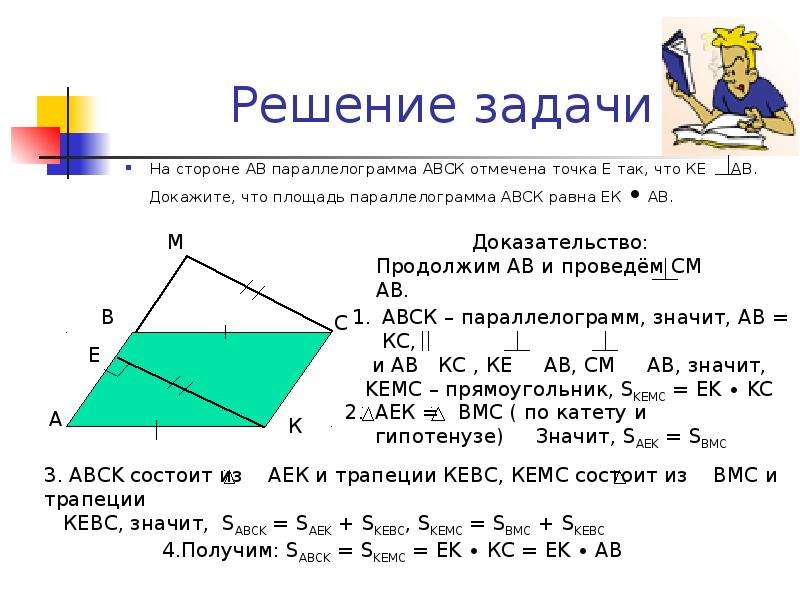Сложим левые и правые части уравнений. Получим:a — b + a + b = 6 + 22 2a = 28 a = 14.
a — b = 6 b = a — 6 = 14 — 6 = 8.
Ответ: Стороны параллелограмма равны 14 см, 14 см, 8 см, 8 см.
Задача 4. Перпендикуляр, опущенный из вершины параллелограмма на его диагональ, делит эту диагональ на отрезки АМ и МС длиной 6 см и 15 см соответственно.
Разность сторон параллелограмма равна 7 см.
Найти длины сторон и диагонали параллелограмма.
Решение: Примем сторону AB за a, сторону BC за b.
Из двух прямоугольных треугольников АВМ и ВМС выразим равный для них катет ВМ по теореме Пифагора.
АВ² — АМ² = ВС² — МС².
Подставляем вместо сторон известные выражения:
а² — 6² = b² — 15² или 15² — 6² = b² — а² (b — а) (b + а) = (15 — 6) (15 + 6),
но b — а = 7
7 (b + а) = 9 * 21 b + a = 9 * 3 = 27.
Имеем систему двух уравнений с двумя неизвестными, как в задаче 3.
b + a = 27
b — а = 7 Отсюда получаем 2b = 34 b = 17, a = 27 — 17 = 10.
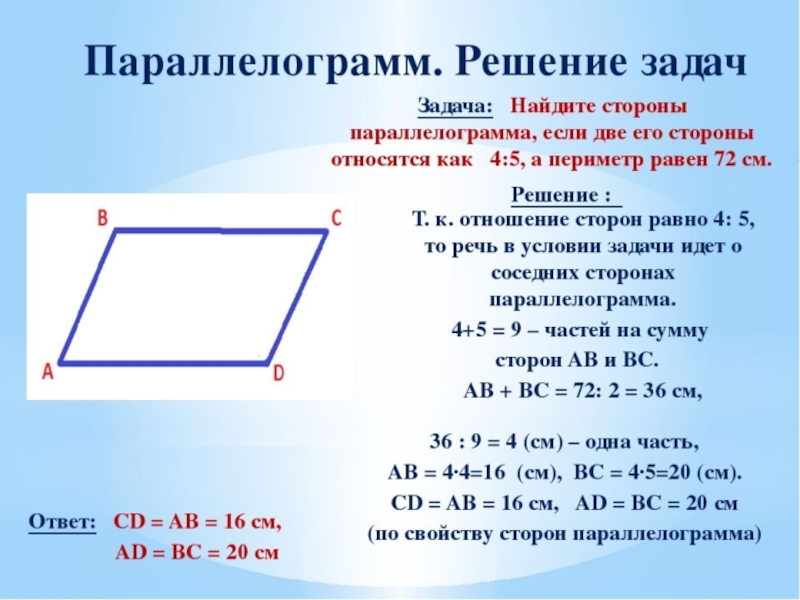
Теперь, зная стороны параллелограмма, мы можем найти высоту ВМ.
ВМ² = 10² — 6² = 64. Отсюда ВМ = 8 см.
А теперь, из прямоугольного треугольника ВМО находим ВО.
ВМ = 8 см,
МО = АО — АМ = АС/2 — АМ = (6+15)/2 — 6 = 21/2 — 6 = 10,5 — 6 = 4,5 см.
По теореме Пифагора находим ВО.
ВО² = 8² + 4,5² = 64 + (9/2)² = 64 + 81/4 = 337/4. Или ВО = √337/2.
Поскольку BD в 2 раза больше, чем ВО, то её длина будет равна √337.
Ответ: Длины сторон параллелограмма 17 см, 17 см, 10 см, 10 см. Длина диагонали √337.
На сегодня всё. В следующий раз мы продолжим решение задач по геометрии из «Сборника для поступающих во ВТУЗы». Успехов!
Параллелограммы — Математика для старших классов
Все ресурсы по математике для старших классов
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы
Ниже показан параллелограмм с размерами в см.
Чему равен периметр параллелограмма в см?
Возможные ответы:
Правильный ответ:
Объяснение:
Треугольник в левой части рисунка имеет угол a и . Поскольку сумма всех углов треугольника должна быть равна , мы можем найти угловую меру третьего угла:
Наш третий угол равен , и у нас есть треугольник.
Треугольник имеет стороны, которые находятся в соответствующем отношении . В этом случае сторона, противоположная нашему углу, равна , поэтому
Теперь мы также знаем, что
Теперь мы знаем длины всех недостающих сторон. Правая и левая стороны параллелограмма будут равны . Нижний и верхний будут каждый . Объединим их, чтобы найти периметр:
Сообщить об ошибке
Найдите периметр следующего параллелограмма:
9000 4Возможные ответы:
Правильный ответ:
Объяснение:
Формула периметра трапеции:
,
, где – длина основания, а – длина ребра.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите периметр следующего параллелограмма:
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для периметра параллелограмма:
где это длина большей стороны и это длина более короткой стороны.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите периметр следующего параллелограмма:
Возможные ответы:
Правильный ответ:
Объяснение:
Формула периметра параллелограмма:
.
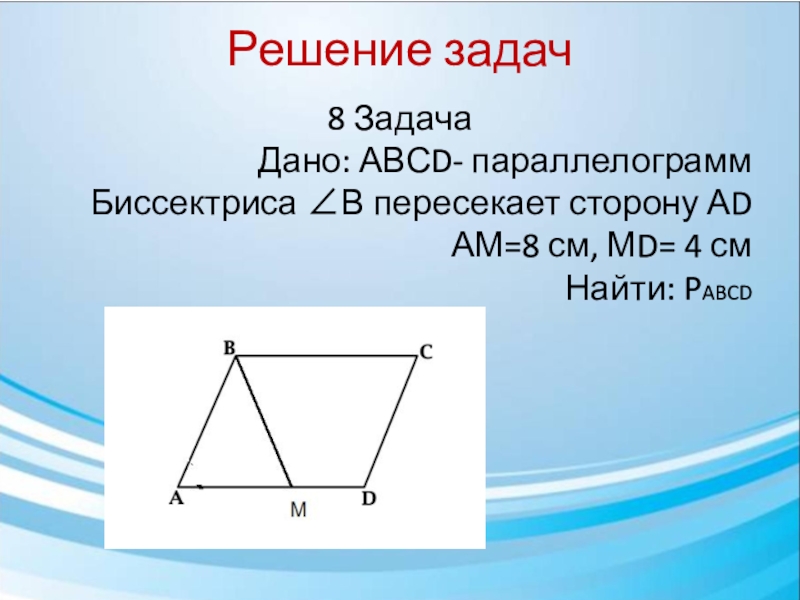
Подставив наши значения, мы получим:
Сообщить об ошибке
ABCD — параллелограмм. BD = 5. Все углы треугольника ABD равны. Чему равен периметр параллелограмма?
Возможные ответы:
Правильный ответ:
Пояснение:
Если в треугольнике ABD все углы равны, а прямая BD делит параллелограмм, то и в треугольнике BDC должны быть равны все углы.
Теперь у нас есть два равносторонних треугольника, поэтому все стороны треугольников будут равны.
Следовательно, все стороны равны 5.
5+5+5+5 = 20
Сообщить об ошибке
Каково значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Противоположные углы равны, а соседние углы должны суммироваться до 180.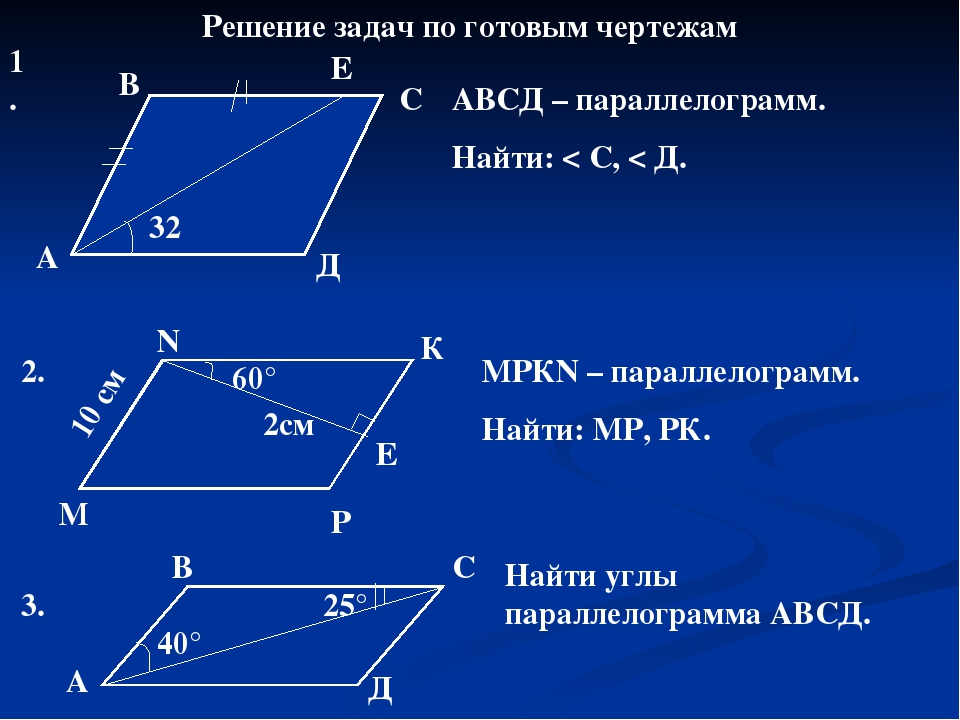
Следовательно, мы можем настроить уравнение для решения для z:
(z — 15) + 2Z = 180
3Z — 15 = 180
3z = 195
z = 65
Теперь найдите x:
2 z = x = 130°
Сообщить об ошибке
Какова площадь параллелограмма с основанием и высотой ?
Правильный ответ:
Пояснение:
Чтобы решить этот вопрос, вы должны знать формулу площади параллелограмма.
В этом уравнении длина основания и длина высоты. Мы можем указать длину стороны как для основания, так и для высоты, как указано в вопросе.
Сообщить об ошибке
Какова площадь параллелограмма с основанием и высотой ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить этот вопрос, вы должны знать формулу площади параллелограмма.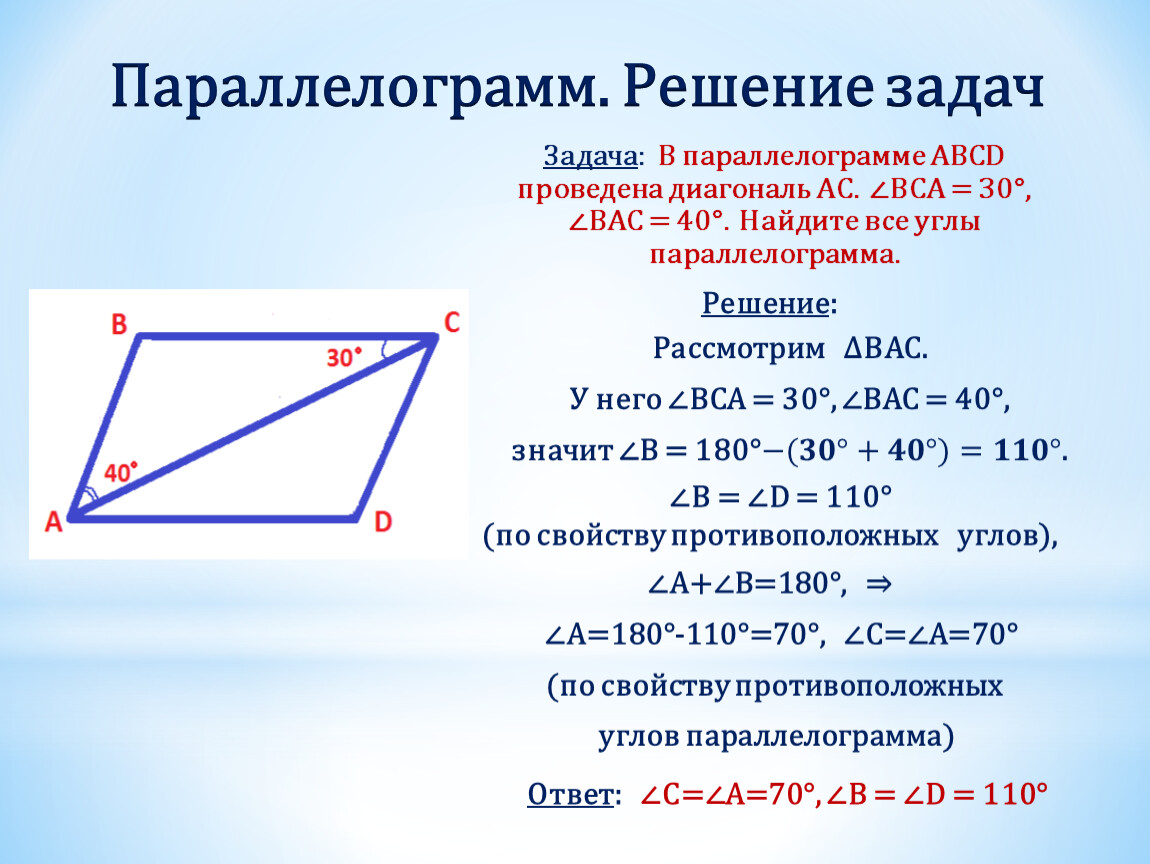
Формула
Таким образом, мы можем подставить длину стороны как для основания, так и для высоты, чтобы получить
Выполните умножение, чтобы получить ответ .
Сообщить об ошибке
Найдите площадь следующего параллелограмма:
Возможные ответы:
Невозможно определить по данной информации.
Правильный ответ:
Объяснение:
Формула площади параллелограмма:
,
где — длина основания, а — длина высоты.
Чтобы найти высоту параллелограмма, воспользуйтесь формулой для треугольника:
, где – сторона, противоположная .
Левая сторона параллелограмма образует следующий треугольник:
, где длина высоты.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите площадь следующего параллелограмма:
Правильный ответ:
Пояснение:
Используйте теорему Пифагора для определения длины диагонали:
Площадь параллелограмма в два раза больше площади прямоугольного треугольника:
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
Урок КАК решать задачи на углы параллелограммов
Этот урок (КАК решать задачи на углы параллелограммов — Примеры) был создан пользователем ikleyn(48172) : Посмотреть исходный код, Показать
Про иклейн :
В этом уроке вы найдете решения некоторых типичных задач на углы параллелограмма.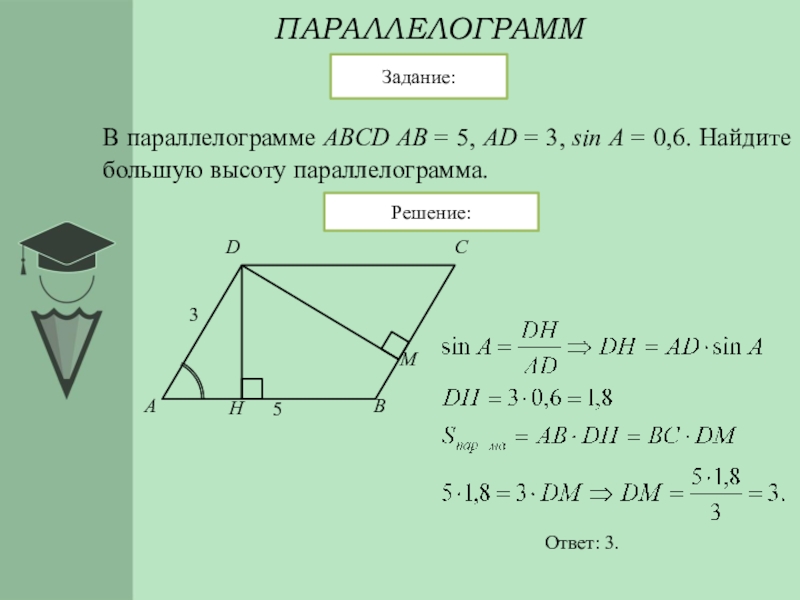
Для решения такого рода задач используйте основные свойства параллелограмма:
— противоположные углы параллелограмма равны
(см. урок Противоположные углы параллелограмма по теме Параллелограммы раздела Геометрия на этом сайте) , и
— сумма последовательных углов параллелограмма равна 180
(см. урок Последовательные углы параллелограмма в этой же теме того же раздела на этом сайте).
Проблема 1
В параллелограмме один угол имеет градусную меру 73. Найдите остальные углы параллелограмма.
Решение
Так как сумма последовательных углов параллелограмма равна 180, два других последовательных угла параллелограмма имеют угловую меру
180-73 = 107.
Поскольку противоположные углы параллелограмма равны, угол, противоположный данному углу 73, также имеет угловую меру 73.
Ответить . Остальные углы параллелограмма имеют угловую меру 107 (последний угол), 73 (противоположный угол) и 107 (второй последовательный угол).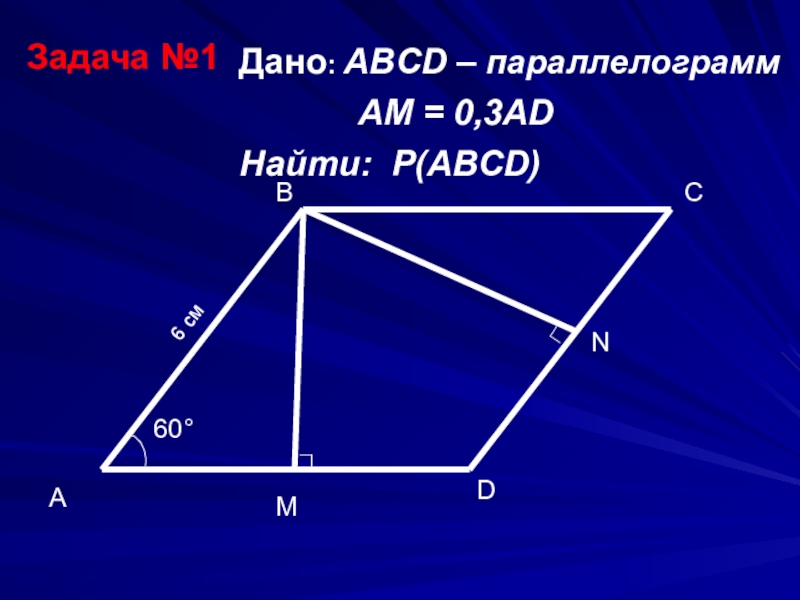
Проблема 2
В параллелограмме один угол в 28 раз больше другого.
Найдите углы параллелограмма.
Решение
Пусть x будет угловой мерой (в градусах) первого из двух заданных углов.
Тогда угловая мера второго угла равна x — 28 в соответствии с условием задачи.
Поскольку данные два угла параллелограмма не равны, они не противоположны. Следовательно, они последовательные.
Следовательно, вы можете написать уравнение
x + (x-28) = 180
, говоря, что сумма последовательных углов параллелограмма равна 180.
Упростите и решите это уравнение:
2x — 28 = 180,
2x = 180 + 28,
2x = 208,
x = 104.
Таким образом, первый угол имеет угловую меру 104.
Тогда два последовательных угла равны 180 — 104 = 76.
Можно проверить, что первый угол на 28 больше, чем последующие, так как это утверждается условием :
104 — 76 = 28.
Ответ . Углы параллелограмма равны 108, 76, 108 и 76.
Проблема 3
В параллелограмме один угол в четыре раза больше другого.
Найдите углы параллелограмма.
Решение
Пусть x будет угловой мерой (в градусах) меньшего из двух заданных углов.
Тогда мера большего угла равна 4x в соответствии с условием задачи.
Поскольку данные два угла параллелограмма не равны, они не противоположны. Следовательно, они последовательные.
Следовательно, вы можете написать уравнение
x + 4x = 180
, говорящее, что сумма последовательных углов параллелограмма равна 180.
Упростите и решите это уравнение:
5x = 180,
x = 36.
Таким образом, меньший угол имеет угловую меру 36.
Тогда больший угол имеет угловую меру 4*36 = 144 в соответствии с условием задачи.
Вы можете проверить, что сумма этих двух последовательных углов равна 180:
36 + 144 = 180.
Ответить . Углы параллелограмма равны 36, 144, 36 и 144.
Мои другие уроки по параллелограммам на этом сайте
— В параллелограмме каждая диагональ делит его на два равных треугольника.
Leave A Comment