Трапеция. Формулы, признаки и свойства трапеции
Навигация по странице: Определение трапеции Элементы трапеции Виды трапеций Основные свойства трапеции Стороны трапеции Средняя линия трапеции Высота трапеции Диагонали трапеции Площадь трапеции Периметр трапеции Окружность описанная вокруг трапеции Окружность вписанная в трапецию Другие отрезки трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны

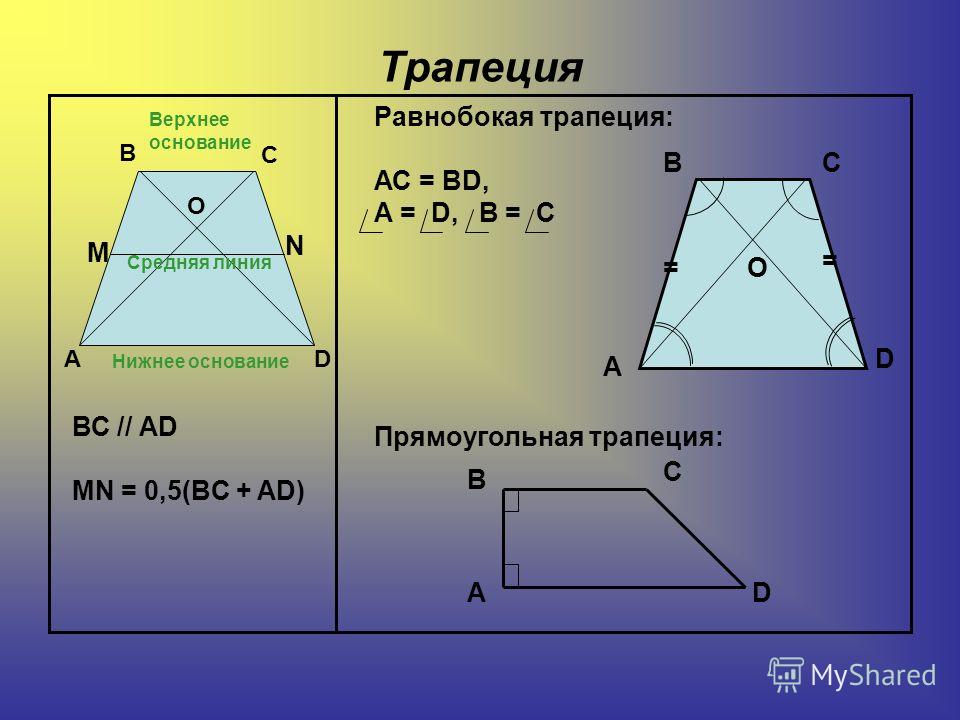
Виды трапеций:
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
| Рис.1 | Рис.2 |
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m — b
b = 2m — a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a — h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a — c·cos α — d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Средняя линия трапеции
Определение.
Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b | |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Высота трапеции
Формулы определения длины высоты трапеции:
1.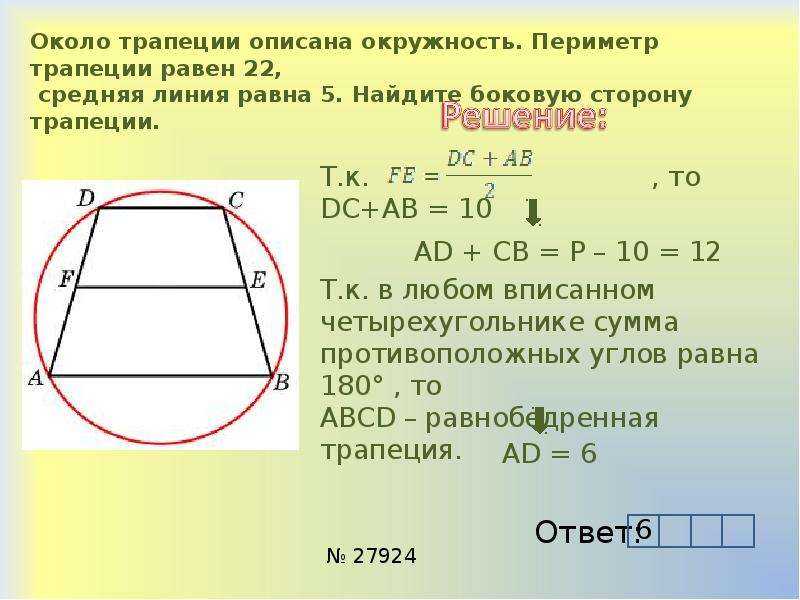 Формула высоты через сторону и прилегающий угол при основании:
Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 — 2ad·cos β
d2 = √a2 + c2 — 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab — | a(d 2 — c2) |
| a — b |
| d2 = | c2 + ab — | a(c2 — d 2) | a — b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a — h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a — h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab — d22
d2 = √c2 + d 2 + 2ab — d
Площадь трапеции
Формулы определения площади трапеции:
1.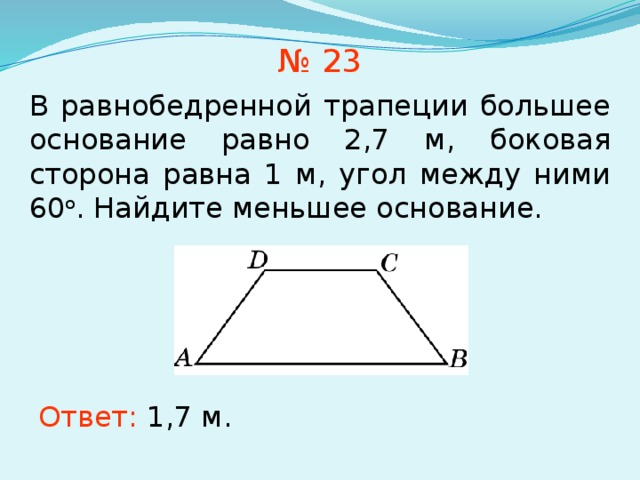 Формула площади через основания и высоту:
Формула площади через основания и высоту:
| S = | (a + b) | · h |
| 2 |
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции
| S = | a + b | √(p — a)(p — b)(p — a — c)(p — a — d) |
| |a — b| |
| p = | a + b + c + d | — полупериметр трапеции.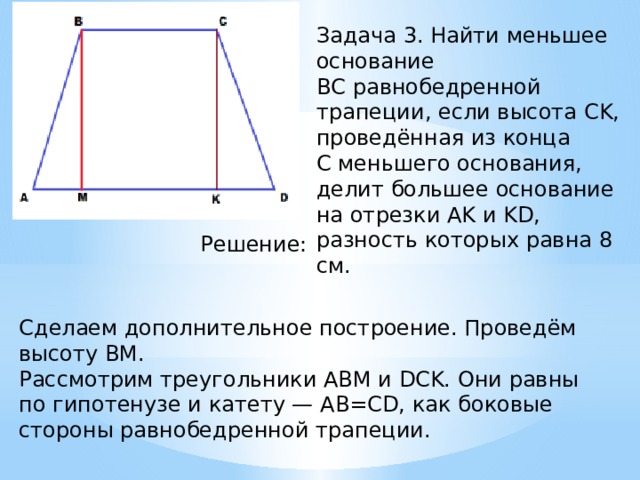 |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
| p = | a + c + d1 |
| 2 |
a — большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1.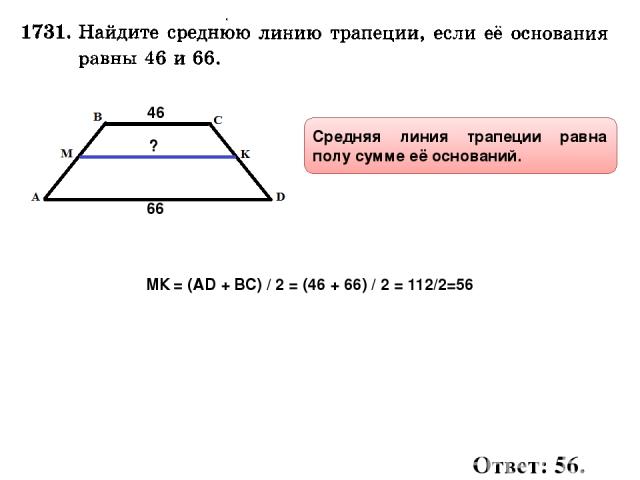 Формула радиуса вписанной окружности через высоту:
Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Все таблицы и формулы
Стороны трапеций найти онлайн, правила, формулы, примеры
Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными боковыми сторонами.
Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.
Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других значимых параметров.
- Длина основания через среднию линию и другое известное основание
- Нижнее основание через верхнее основание, высоту и углы при нижнем основании
- Верхнее основание через нижнее основание, высоту и углы при нижнем основании
- Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
- Верхнее основание через боковые стороны, нижнее основание и углы при нижнем основании
- Боковую сторону через высоту и угол при нижнем основании
Длина основания через среднюю линию и известное основание
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
a = 2m – b
Средняя линия (m):
ммсмдмм
Изв. основание (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в формулу, показывают, что b = 2*6 – 9 = 3.
Нижнее основание через верхнее основание, высоту и углы при нижнем основании
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:
a = b + h*(ctga + ctgb)
Верх. основание (b):
основание (b):
ммсмдмм
Высота (h):
ммсмдмм
Угол (α):
градусырадианыctg
Угол (β):
градусырадианыctg
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63. Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5. Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1
Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF = 10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24
Верхнее основание через нижнее основание, высоту и углы при нижнем основании
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при ней:
b = a – h*(ctg α + ctg β)
Ниж. основание (a):
основание (a):
ммсмдмм
Высота (h):
ммсмдмм
Угол (α):
градусырадианыctg
Угол (β):
градусырадианыctg
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) = 15 + 16 = 31
Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.
- Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
- Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35
Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов углов при них
a = b + c * cos α + d * cos β
Верх.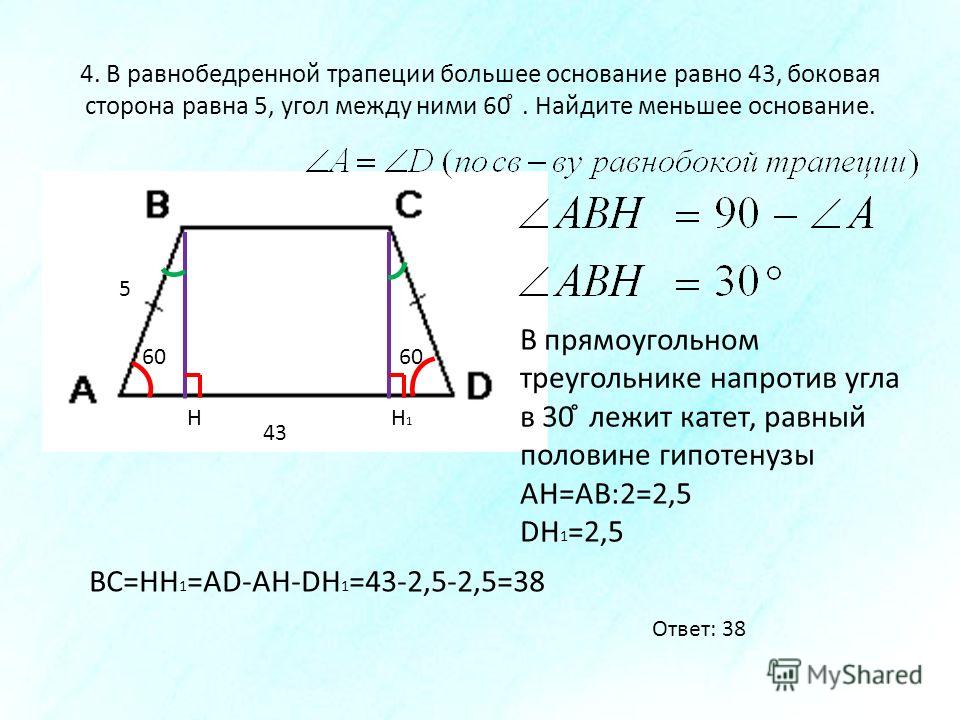 2)/b и a = b +
2c*cosa.
2)/b и a = b +
2c*cosa.
- трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4 = (144 – 64)/4 = 20
- В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 + 4*2*3/2 = 7 + 43
Верхнее основание через боковые стороны, нижнее основание и углы при нем
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов при них
b = a – c * cos α – d * cos β
Ниж. основание (a):
ммсмдмм
Сторона (c):
ммсмдмм
Сторона (d):
ммсмдмм
Угол (α):
градусырадианыcos
Угол (β):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов.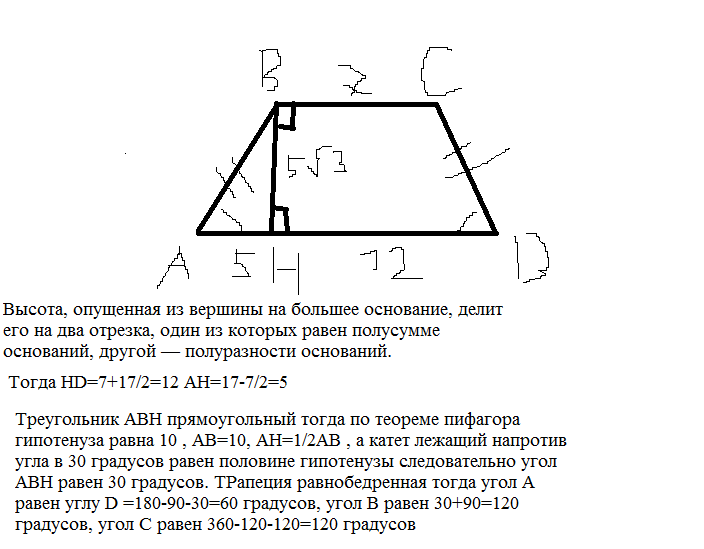 2)/a и b = a — 2c*cosa.
2)/a и b = a — 2c*cosa.
- В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 – 11*11)/12= (169 – 121)/12 = 4
- Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD: CD = 25 – 10*2*1/2 = 15
Боковая сторона через высоту и угол при нижнем основании
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней
d = h / sin α
Высота (h):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 = 24, d = 12/3/2 = 243
Для прямоугольного типа формулы несколько отличаются.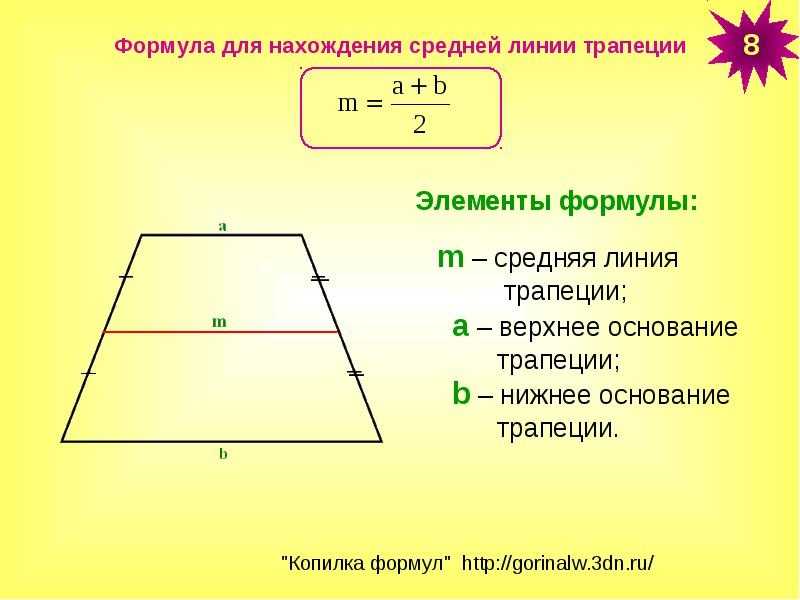 2 – 16*6 =
100 – 96 = 4
2 – 16*6 =
100 – 96 = 4
Виды трапеций
Существуют следующие виды трапеций:
- Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
равнобедренными.
 Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. - Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный треугольник.
- Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
являются прямыми.
 2.
2. - Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую площадь.
- В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
- Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
- Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней линии.
- Трапеция — это четырехугольник, у которого ровно одна пара параллельных сторон.
- Площадь трапеции определяется пространством, заключенным в ее границах, как занятое в двумерной плоскости.
- Площадь трапеции находится по формуле: \(\text{Площадь} = \frac{1}{2} h (a + b)\).
- Если вам дана трапеция с длинами всех ее оснований и катетов, но не указана высота, вам нужно сначала вычислить ее высоту, используя теорему Пифагора, чтобы иметь возможность найти площадь трапеции.

- Когда вам нужно вычислить площадь трапеции, когда даны только длины ее диагоналей и угол между ними, вы можете использовать формулу: \(\text{Площадь} = \frac{1}{2} d_1 \cdot d_2 \cdot \sin(\alpha)\).
- Свойство №1) Углы на одной стороне катета называются смежными и являются дополнительными ( еще )
- Свойство № 2) Площадь трапеции = $$ Площадь = высота \cdot \left( \frac{ \text{сумма оснований} }{ 2 } \right) $$ ( еще )
- Свойство № 3) Трапеции имеют среднюю часть, которая соединяет точки миоконцов ( еще )
- параллельна обоим основаниям
- мера его длины равна средней длине оснований
Площадь трапеций: формула, типы и уравнение
Вы можете встретить трапеции, когда видите тачку в саду или когда проходите по мосту и смотрите на его фермы. Эти геометрические формы важны в приложениях архитектуры и строительства. Возможно, вы уже знакомы с тем, как вычислять площадь треугольников, что будет полезно для этой статьи, когда мы рассмотрим формулу площади трапеции и несколько примеров ее использования.
Начнем с того, что вспомним, что такое трапеция.
Трапеция Определение
Трапеция — это четырехугольник (четырехсторонняя плоская фигура), который имеет ровно одну пару параллельных сторон.
Следующая фигура представляет собой трапецию.
Рис. 1. Иллюстрация трапеции.
На приведенном выше рисунке параллельных сторон (в данном случае \(\overline{AD}\) и \(\overline{BC}\)) называются основаниями трапеции . непараллельных сторон (\(\overline{AB}\) и \(\overline{DC}\)) называются 92\) и т. д.
Формула площади трапеции
Рассмотрим следующую трапецию:
Рис. 2. Трапеция с основаниями \(a\) и \(b\) и высотой \(h\ ).
Площадь трапеции определяется по формуле:
\[\text{Площадь} = \frac{1}{2} h (a + b)\]
где: \Стрелка вправо\) высота трапеции (перпендикулярное расстояние между основаниями),
\(a, b \стрелка вправо\) длины оснований.
Как мы получили эту формулу, спросите вы? Давайте покажем вам.
Напомним, что площадь треугольника определяется по формуле:
\[\text{Площадь} = \frac{1}{2} \text{основание} \cdot \text{высота}\]
Мы можем разделить эту трапецию на два треугольника по любой из диагоналей. Возьмем диагональ \(\overline{BD}\) и разделим трапецию на треугольники \(\triangle{BAD}\) и \(\triangle{BCD}\).
Рис. 3. Трапеция, разделенная диагональю \(\overline{BD}\) на \(\треугольник{BAD}\) и \(\треугольник{BCD}\).
Тогда мы можем сказать, что
\[\begin{align}\text{Площадь трапеции ABCD} & = \text{Площадь } \triangle{BAD} + \text{Площадь } \triangle{BCD} \\ \\& = \frac{1}{2} b \cdot h + \frac{1}{2} a \cdot h \\ \\& = \frac{1}{2} h (a + b )\end{align}\]
Представьте себе параллелограмм, у которого обе пары противоположных сторон параллельны. Вы можете применить приведенную выше формулу, чтобы вывести формулу площади параллелограмма.
\[\begin{align}\text{Area} & = \frac{1}{2} h (a + b) \\ \\& = \frac{1}{2} h (b + b) \qquad \text{Противоположные стороны параллелограмма имеют одинаковую длину} \\ \\& = \frac{1}{2} h (2b) \\ \\& = b \cdot h\end{align}\]
Это формула площади параллелограмма.
Примеры площади трапеции
Теперь давайте рассмотрим некоторые примеры, связанные с площадью трапеции.
Трапеция имеет длины оснований \(10\,\text{см}\) и \(15\,\text{см}\). Перпендикулярное расстояние между основаниями равно \(8\,\text{см}\). Найдите площадь трапеции.
Решение
Чтобы решить эту задачу, нам просто нужно подставить значения длин оснований и высоты в площадь формулы трапеции. 92\).
Теперь давайте рассмотрим пример с использованием координатной плоскости.
Найдите площадь следующей трапеции.
Рис. 4. Трапеция на координатной плоскости.
Решение
В этом случае, чтобы найти площадь вышеуказанной трапеции, нам нужно найти длину оснований и высоту трапеции.
Эти значения не даны, но мы можем использовать координатную плоскость для их расчета.
Нам нужно рассчитать расстояние между каждой из точек, как мы можем это сделать?
Расстояние между точками \(B(6, 2)\) и \(C(9, 2)\) можно рассчитать, найдя абсолютное значение разницы между их координатами x, используя \(|x_2 — х_1|\). То же самое относится и к расстоянию между точками \(A(2, 7)\) и \(D(10, 7)\).
Расстояние между точками \(B(6, 2)\) и \(E(6, 7)\) можно рассчитать, найдя абсолютное значение разницы между их координатами y, используя \(|y_2 — у_1|\).
\[\begin{align}a &= \overline{BC} = |x_2 — x_1| = |92\) имеет базы длин, \(3\,\text{m}\) и \(4\,\text{m}\). Найдите расстояние между параллельными сторонами.
Решение
Расстояние между параллельными сторонами равно высоте трапеции. Итак, давайте подставим значения, которые у нас есть, в формулу площади трапеции, а затем найдем \(h\).
\[\begin{align}\text{Area} & = \frac{1}{2} h (a + b) \\ \\35 & = \frac{1}{2} \cdot h (3 + 4) \\ \\35 & = \frac{7 \cdot h}{2} \\ \\h & = \frac{35 \cdot 2}{7} \\ \\& = \frac{70} {7} \\ \\& = 10\,\text{m}\end{align}\]
Высота трапеции равна \(10\, \text{м}\).
Площадь трапеции без известной высоты
Если вам дана трапеция с длинами всех ее оснований и катетов, но не указана высота, то вам нужно сначала вычислить ее высоту, чтобы иметь возможность найти площадь трапеция. Давайте посмотрим на пример, чтобы показать вам, что делать в этом случае.
Найдите площадь следующей трапеции.
Рис. 5. Пример трапеции без высоты.
Обратите внимание, что стороны трапеции имеют одинаковую длину \(6\, \text{м}\), следовательно, это равнобедренная трапеция , и мы можем вычислить ее высоту следующим образом.
Рис. 6. Высота трапеции по Пифагору.
Обратите внимание, что у нас есть прямоугольный треугольник с каждой стороны. Основания каждого треугольника рассчитывались путем нахождения разницы между \(18\) и \(10\), а затем деления результата на \(2\).
\[18 — 10 = \frac{8}{2} = 4\, \text{m}\]
Теперь мы можем вычислить высоту, используя теорему Пифагора , которая утверждает, что в прямоугольном треугольнике 92\).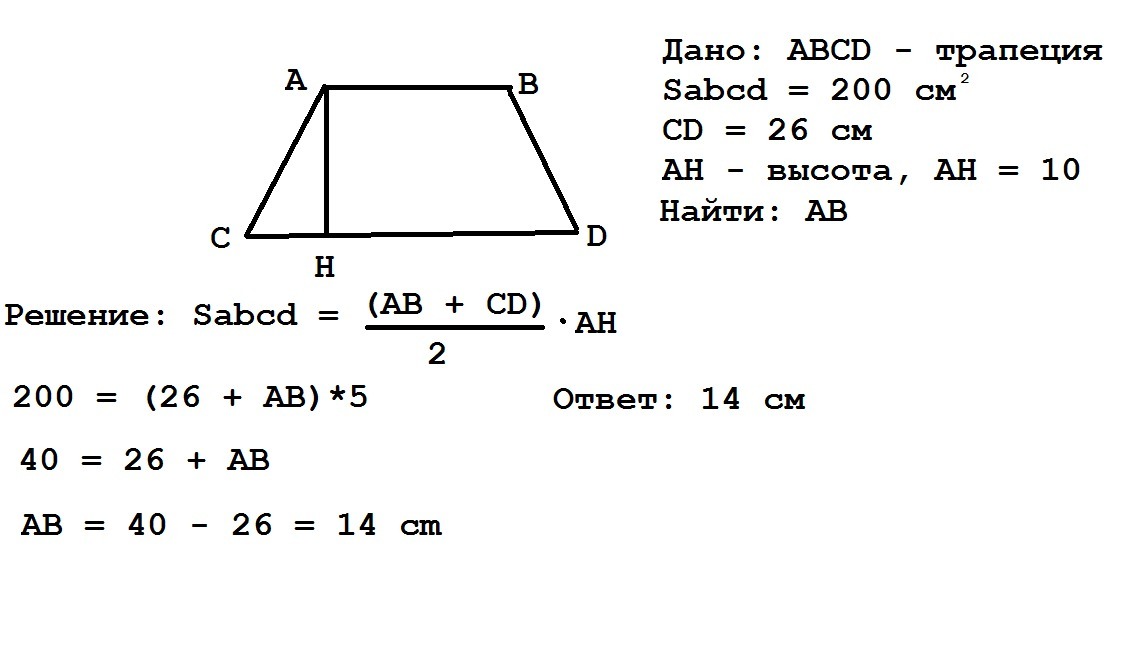
Площадь трапеции при заданных диагоналях
Еще один интересный сценарий, когда вам нужно вычислить площадь трапеции, когда заданы только длины ее диагоналей и угол между ними.
Рассмотрим трапецию с длинами диагоналей \(d_1\) и \(d_2\) и углом \(\alpha\) между ними.
Рис. 7. Трапеция с диагоналями \(d_1\) и \(d_2\).
В этом случае площадь трапеции определяется как
\[\text{Площадь} = \frac{1}{2} d_1 \cdot d_2 \cdot \sin(\alpha)\] 92\).
Площадь трапеций — основные выводы
Основания трапеций, катеты, углы и площади, правила и формулы
К сожалению, в прошлом году рекламный блок начал отключать загрузку почти всех изображений на нашем сайте, что привело к тому, что mathwarehouse стало непригодным для использования пользователями adlbock.
Трапеция – это четырехугольник с одной парой параллельных прямых
Основания. Две параллельные прямые называются основаниями.
Ноги — две непараллельные линии — это ноги.
Диаграмма 1
Диаграмма 2
НедвижимостьСмежные углы трапеции
Углы с одной и той же стороны катета называются смежными, например, $$\угол A $$ и $$\угол D $$ являются дополнительными. По той же причине $$ \angle B $$ и $$ \angle C $$ являются дополнительными.
По той же причине $$ \angle B $$ и $$ \angle C $$ являются дополнительными.
Проблема 1
Используйте теорему о смежных углах, чтобы определить m $$ \angle ZWX $$.
$$ \угол ZWX = 180 − 44 = 136° $$
Проблема 2
Используйте теорему о смежных углах для вычисления m $$ \angle MLO $$.
$$ \угол MLO = 180-124 = 56° $$
Проблема 3
Найдите значение x в трапеции ниже, затем определите меру углов $$ \angle WXY $$ и $$ \angle XYZ $$.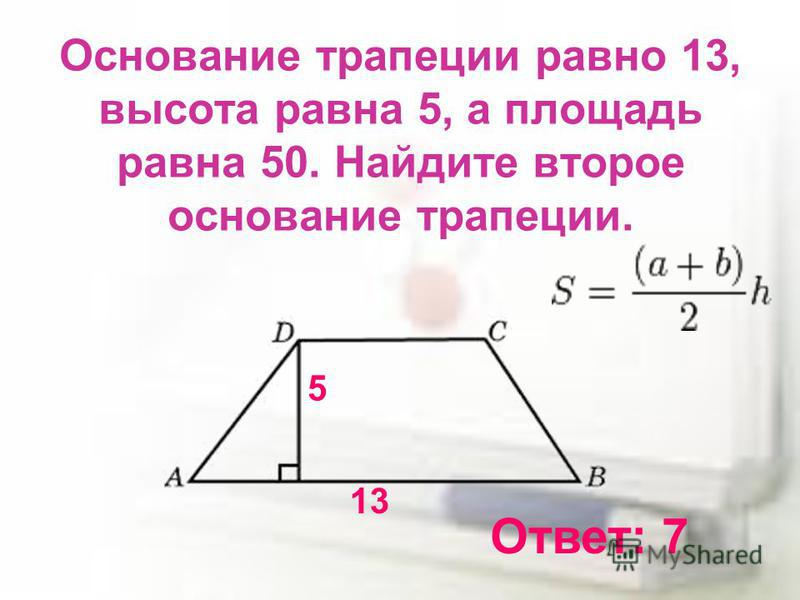
Проблема 4
Что не так с трапецией LMNO, изображенной ниже? (Объясните, почему LMNO не может быть трапецией на основе предоставленной информации) .
Если LMNO трапеция и ее основания LO и MN параллельны, то $$ \угол MNO $$ и $$ \угол NOL $$, которые должны быть дополнительными, однако сумма этих углов не равна 180 111 + 68 ≠ 180.
Площадь трапеции
Проблема 5
$ Площадь = высота \cdot \left( \frac{ \text{сумма оснований} }{ 2 } \right) \\ = 7 \cdot \left( \frac{ 4 + 8 }{ 2 } \right) \\ =7 \cdot \left( \frac{ 12 }{ 2 } \right) \\ = 7 \cdot 6 \\ = \fbox {42 } футов^2 $
Средняя часть трапеции
Средняя часть трапеции:
Проблема 6
Используйте теорему о среднем отрезке, чтобы определить длину среднего отрезка ON.
Чтобы вычислить длину среднего отрезка, найдите среднее значение длины основания среднего отрезка = (6 + 4) / 2 = 5.
Средняя часть трапеции
Краткий обзор Midpoint
Самое важное, что нужно помнить, это то, что середина делит линию пополам (делит линию на две равные половины).
Середина красного сегмента, изображенного ниже, — это точка $$(A, 2b)$$ (нажмите кнопку ниже, чтобы увидеть).
Средняя линия трапеции — это отрезок, соединяющий середины непараллельных сторон трапеции.
В приведенной ниже трапеции середины непараллельных сторон — это точки S и V. Середина — это отрезок красной линии от S до V.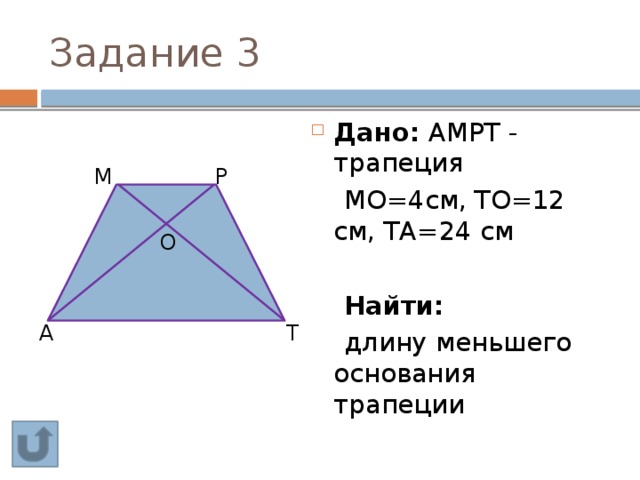
Пример среднего сегмента
Трапеция #10
Шаг 1
Вычисление длины оснований. Верхняя база:
35$ — 16 = 9$$
Шаг 2
Расчет низкой базы:
45$ — 0 = 45 $$
Шаг 3
Вычисление суммы оснований
$$ 9 + 45 = 54 $$
Шаг 4
Разделите сумму на 2
$$ \frac {54}{2} = \boxed{27}$$
Проблема 8
Какова длина среднего отрезка SV в трапеции внизу?
Шаг 1
Вычисление длины оснований. Верхняя база:
$$ 17 — 8 = 9 $$
Шаг 2
Расчет низкой базы:
20$ — 0 = 20 $$
Шаг 3
Вычисление суммы оснований
$$ 9 + 20 = 29 $$
Шаг 4
Разделите сумму на 2
$$ \frac {29}{2} = \boxed{14.

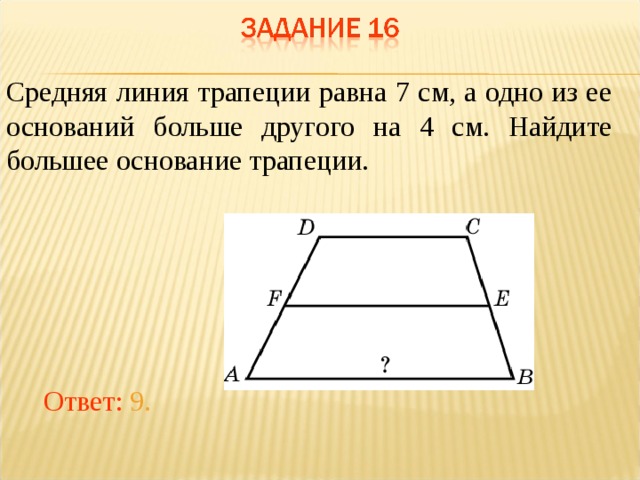 Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. 2.
2.
Leave A Comment