Вписанный и центральный угол окружности
С появлением окружности, а затем колеса человечество сильно упростило себе жизнь.
И через много веков на ЕГЭ появились задачи по этой теме, конечно же 🙂
Зная свойства вписанного и центрального угла окружности, ты сможешь решить множество таких задач. И в этой статье мы тебе с этим поможем.
- Как измерить дуги и окружности
- Свойства вписанного угла и следствия из них
- Как выразить углы между хордами и секущими через центральный угол
- и многое другое…
Поехали!
Вписанный и центральный угол окружности – коротко о главном
Центр окружности – такая точка, расстояния от которой до всех точек окружности одинаковые.
Радиус – отрезок, соединяющий центр и точку на окружности.
Радиусов очень много (столько же, сколько и точек на окружности), но длина у всех радиусов – одинаковая.
Иногда для краткости радиусом называют именно длину отрезка «центр – точка на окружности», а не сам отрезок.
А вот что получится, если соединить две точки на окружности? Тоже отрезок? Так вот, этот отрезок называется «хорда».
Тут есть ещё одно принятое выражение: «хорда стягивает дугу». Вот, здесь на рисунке, например, хорда \( \displaystyle AB\) стягивает дугу \( \displaystyle AB\).
А если хорда вдруг проходит через центр, то у неё есть специальное название: «диаметр».
Так же, как и в случае с радиусом, диаметром часто называют длину отрезка, соединяющего две точки на окружности и проходящего через центр. Кстати, а как связаны диаметр и радиус? Посмотри внимательно. Конечно же,
Радиус равен половине диаметра.
Кроме хорд бывают еще и секущие.

Вспомнили самое простое?
А теперь – названия для углов.
Центральный угол – угол между двумя радиусами.
Естественно, не правда ли? Стороны угла выходят из центра – значит, угол – центральный.
А теперь – вписанный угол.
Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.
При этом говорят, что вписанный угол \( \displaystyle ABC\) опирается на дугу (или на хорду) \( \displaystyle AC\).
Вот здесь иногда возникают сложности. Обрати внимание – НЕ ЛЮБОЙ угол внутри окружности – вписанный, а только такой, у которого вершина «сидит» на самой окружности.
Смотри на картинку:
Измерение дуг и углов окружности
Длина окружности. Дуги и углы измеряются в градусах и радианах.
Сперва о градусах
Для углов проблем нет – нужно научиться измерять дугу в градусах.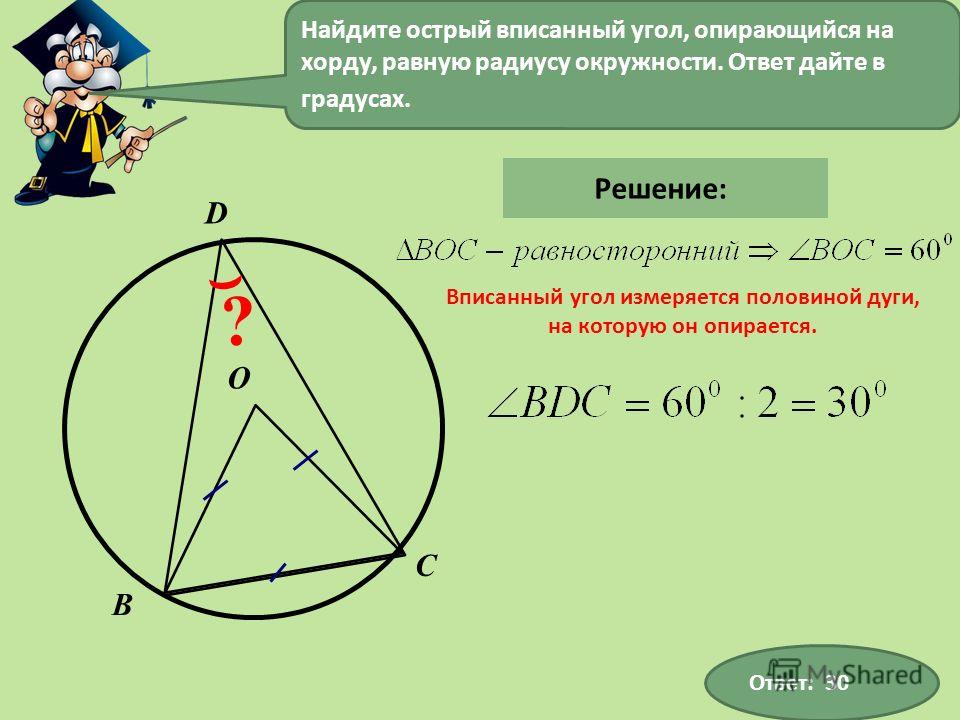 \circ \)), а меньшей дуге соответствует меньший угол.
\circ \)), а меньшей дуге соответствует меньший угол.
Итак, договорились: в дуге содержится столько же градусов, сколько в соответствующем центральном угле.
А теперь о радианах
Что же это за зверь такой «радиан»?
Представь себе: радианы – это способ измерения угла … в радиусах!
Угол величиной \( \displaystyle 1\) радиан – такой центральный угол, длина дуги которого равна радиусу окружности.
Тогда возникает вопрос – а сколько же радиан в развёрнутом угле?
Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?
Этим вопросом задавались учёные ещё в Древней Греции.
И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде \( \displaystyle 1,\text{ }2,\text{ }3,\frac{7}{5},\frac{2}{239}\) и т.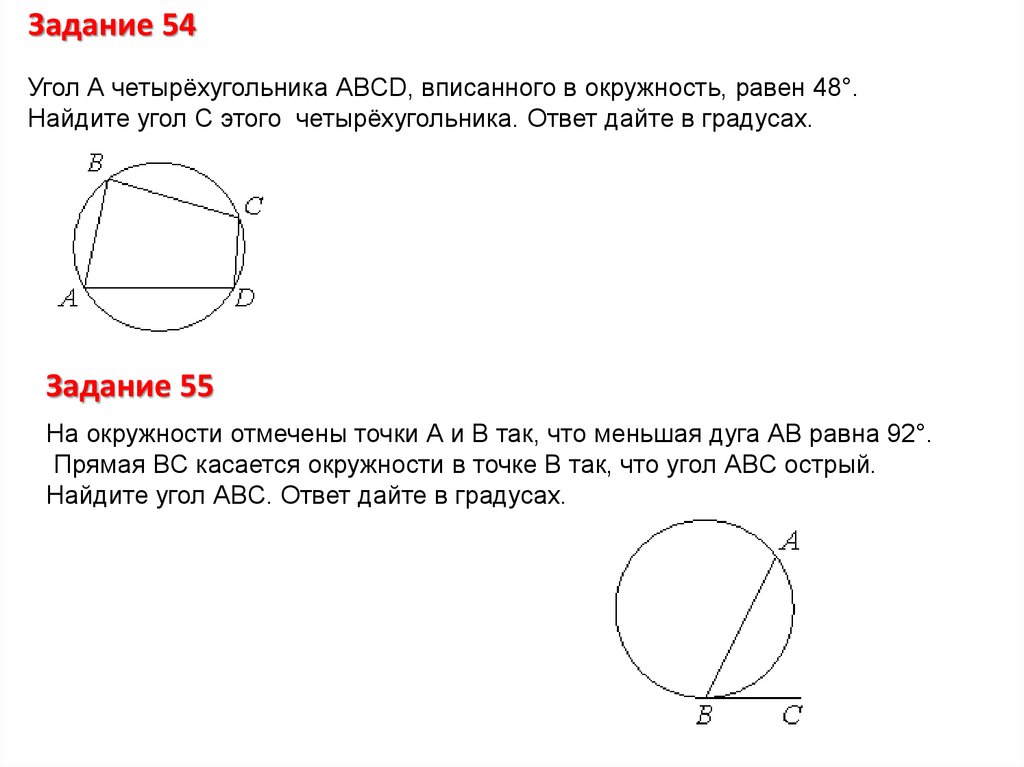 п.
п.
И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в \( \displaystyle 2,5\) раза или в \( \displaystyle \sqrt{17}\) раз больше радиуса!
Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву \( \displaystyle \pi \).
Итак, \( \displaystyle \pi \) – это число, выражающее отношение длины полуокружности к радиусу.
Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём \( \displaystyle \pi \) радиан. Именно оттого, что половина окружности в \( \displaystyle \pi \) раз больше радиуса.
Древние (и не очень) люди на протяжении веков (!) попытались поточнее подсчитать это загадочное число \( \displaystyle \pi \), получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы – нам достаточно двух знаков после занятой, мы привыкли, что
\( \displaystyle \pi \approx 3,14\)
Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна \( \displaystyle 6,28\), а точно эту длину просто невозможно записать «человеческим» числом – нужна буква \( \displaystyle \pi \). \circ \), то есть \( \displaystyle 2\pi \)
\circ \), то есть \( \displaystyle 2\pi \)
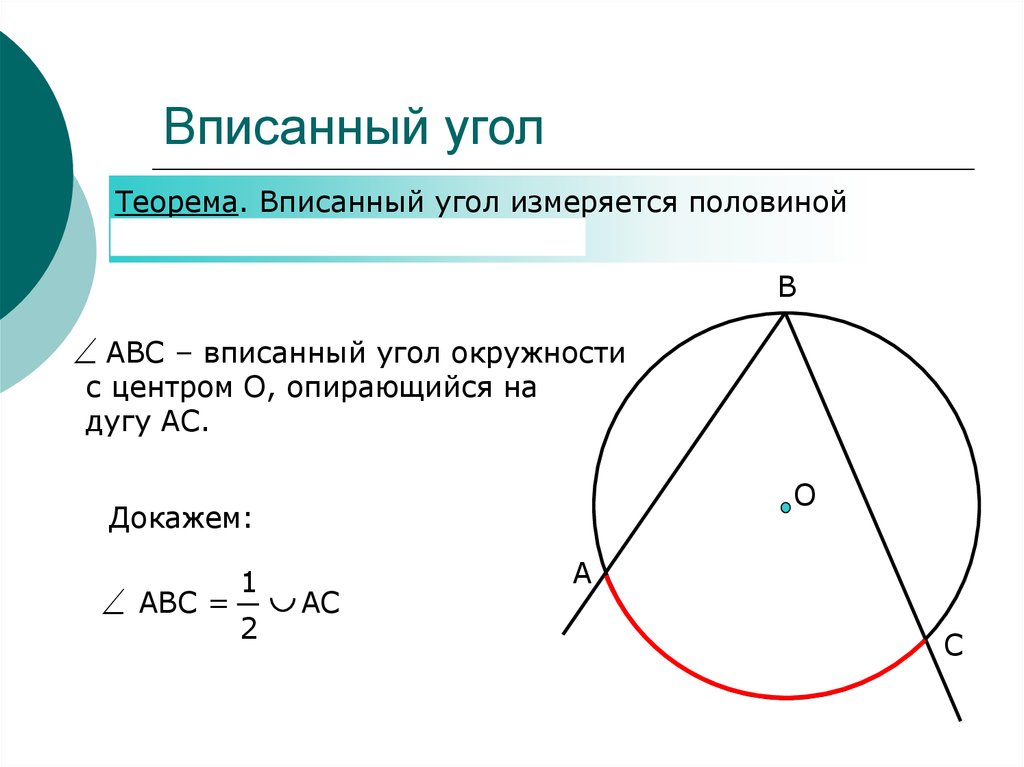
Вписанный угол вдвое меньше центрального – доказательство
Имеет место удивительный факт:
Величина вписанного угла вдвое меньше, чем величина соответствующего центрального угла.
Посмотри, как это утверждение выглядит на картинке. «Соответствующий» центральный угол такой, у которого концы совпадают с концами вписанного угла, а вершина в центре.
И при этом «соответствующий» центральный угол должен «смотреть» на ту же хорду (\( \displaystyle AC\)), что и вписанный угол.
Почему же так? Почему вписанный угол вдвое меньше центрального?
Давай разберёмся сначала на простом случае.
Вписанный угол вдвое меньше центрального – следствия
Давай теперь сформируем два главных и очень важных следствия из утверждения о том, что вписанный угол вдвое меньше центрального:
- Все вписанные углы, опирающиеся на одну дугу, равны между собой
- Следствие 2.
 Угол, опирающийся на диаметр – прямой
Угол, опирающийся на диаметр – прямой
Угол между хордами и секущими, выраженный через центральный угол
А что, если интересующий нас угол НЕ вписанный и НЕ центральный, а, например, такой:
Или такой:
Можно ли его как-то выразить всё-таки через какие-то центральные углы?
Оказывается, можно.
Угол между хордами равен полусумме угловых величин дуг, заключённых в этот уголНас интересует \( \displaystyle \angle ABC\).
\( \displaystyle \angle \text{ }\!\!~\!\!\text{ ABC}=\text{ }\!\!~\!\!\text{ }\angle \text{ }\!\!\alpha\!\!\text{ }+\angle \text{ }\!\!\beta\!\!\text{ }\) ( как внешний угол для \( \displaystyle \Delta ADB\)).
Но \( \displaystyle \angle \text{ }\!\!\alpha\!\!\text{ }\) – вписанный, опирается на дугу \( \displaystyle DE\) – \( \displaystyle \angle \text{ }\!\!\alpha\!\!\text{ }=\frac{1}{2}\text{ }\!\!~\!\!\text{ }\angle \text{DOE}\).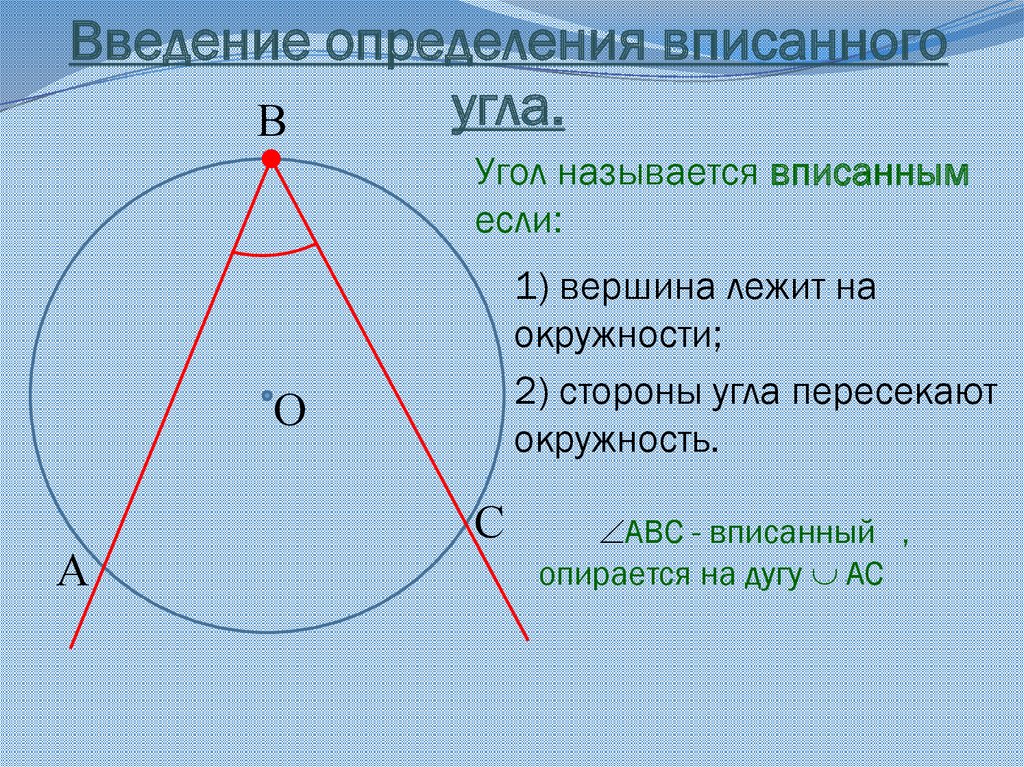
\( \displaystyle \angle \text{ }\!\!\beta\!\!\text{ }\) – вписанный, опирается на дугу \( \displaystyle AC\) – \( \displaystyle \angle \text{ }\!\!\beta\!\!\text{ }=\frac{1}{2}\text{ }\!\!~\!\!\text{ }\angle \text{AOC}\).
Значит, \( \displaystyle \angle ~ABC=\frac{1}{2}\angle \text{DOE}+\frac{1}{2}\angle \text{AOC}\).
Для красоты говорят:
Угол между хордами равен полусумме угловых величин дуг, заключённых в этот угол.
\( \displaystyle \angle \text{ }\!\!~\!\!\text{ ABC}=\frac{\text{AC}}{2}+\frac{\text{DE}}{2}\) – так пишут для краткости, но конечно, при использовании этой формулы нужно иметь в виду центральные углы.
Вписанный угол, теория и задачи
Вписанный угол, теория задачи. Друзья! В этой статье речь пойдёт о заданиях, для решения которых необходимо знать свойства вписанного угла. Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.
Есть задачи посложнее, но и они большой трудности для вас не представят, необходимо знать свойства вписанного угла.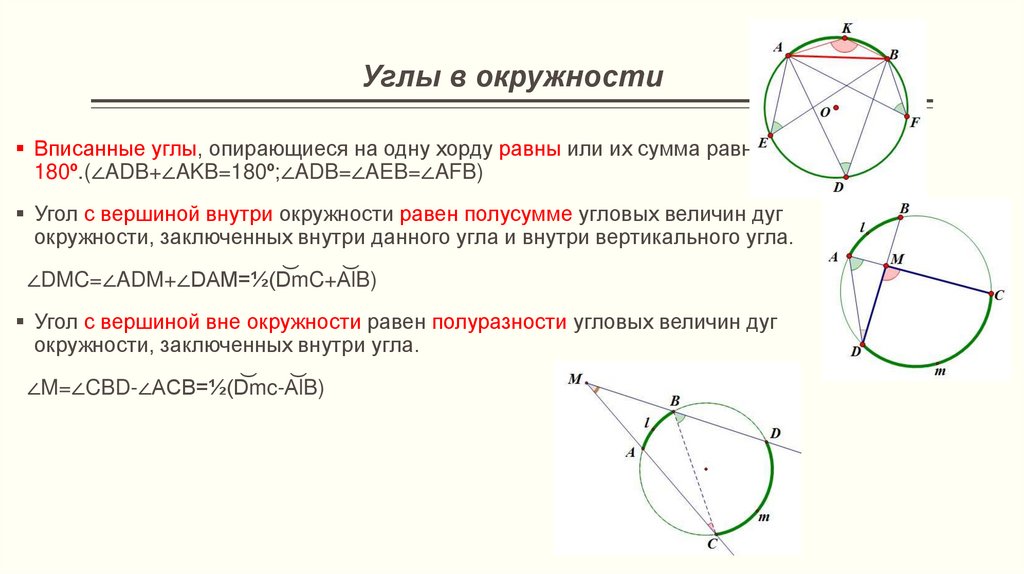 Постепенно мы разберём все прототипы задач, приглашаю вас на блог!
Постепенно мы разберём все прототипы задач, приглашаю вас на блог!
Теперь необходимая теория. Вспомним, что такое центральный и вписанный угол, хорда, дуга, на которые опираются эти углы:
Центральным углом в окружности называется плоский угол с вершиной в ее центре.
Часть окружности, расположенная внутри плоского угла, называется дугой окружности.
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Угол, называется вписанным в окружность, если вершина угла лежит на окружности, а стороны угла пересекают эту окружность.
Отрезок соединяющий две точки окружности называется хордой. Самая большая хорда проходит через центр окружности и называется диаметр.
Для решения задач на вписанные в окружность углы, вам необходимо знать следующие свойства:
1. Вписанный угол равен половине центрального, опирающегося на ту же дугу.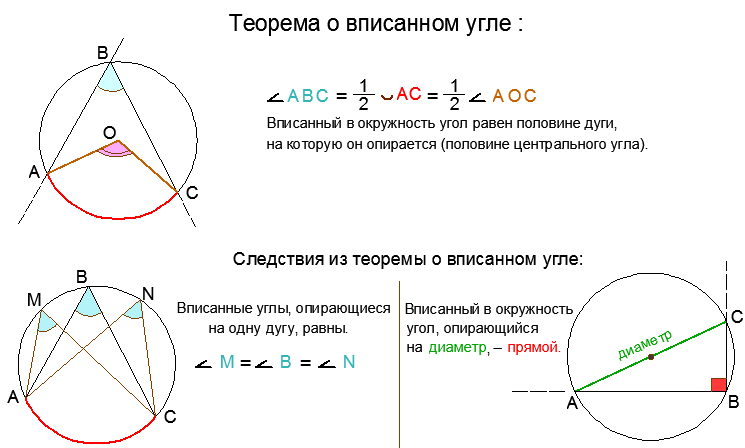
2. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.
3. Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.
4. Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.
Следствие: противолежащие углы четырёхугольника вписанного в окружность в сумме составляют 180 градусов.
5. Все вписанные углы, опирающиеся на диаметр, прямые.
Вообще, это свойство является следствием из свойства (1), это его частный случай. Посмотрите – центральный угол равен 180 градусам (и этот развёрнутый угол есть не что иное, как диаметр), значит по первому свойству вписанный угол С равен его половине, то есть 90 градусам.
Знание данного свойства помогает в решении многих задач и часто позволяет избежать лишних расчётов. Хорошо усвоив его — вы более половины задач такого типа сможете решать устно. Два следствие, которые можно сделать:
Два следствие, которые можно сделать:
Следствие 1: если в окружность вписан треугольник и одна его сторона совпадает с диаметром этой окружности, то треугольник является прямоугольным (вершина прямого угла лежит на окружности).
Следствие 2: центр описанной около прямоугольного треугольника окружности совпадает с серединой его гипотенузы.
Многие прототипы стереометрических задач также решаются благодаря использованию этого свойства и данных следствий. Запомните сам факт: если диаметр окружности является стороной вписанного треугольника, то этот треугольник прямоугольный (угол лежащий против диаметра равен 90 градусов). Все остальные выводы и следствия вы сможете сделать сами, учить их не надо.
Как правило, половина задач на вписанный угол даётся с эскизом, но без обозначений. Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать. Рассмотрим задачи:
Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.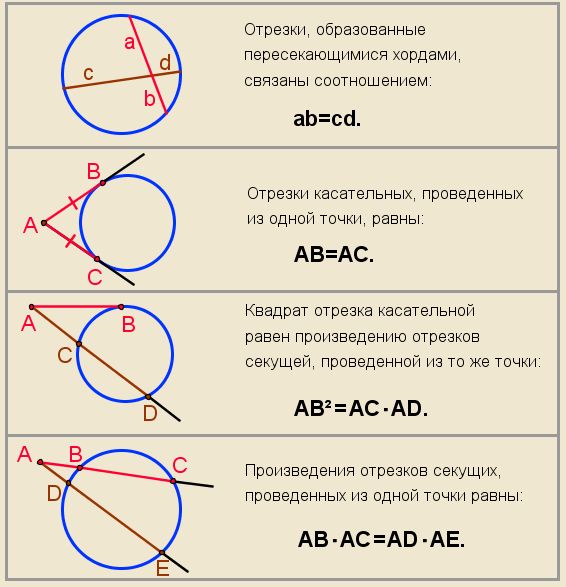
Построим центральный угол для заданного вписанного угла, обозначим вершины:
По свойству вписанного в окружность угла:
Угол АОВ равен 600, так как треугольник АОВ равносторонний, а в равностороннем треугольнике все углы равны по 600. Стороны треугольника равны, так как в условии сказано, что хорда равна радиусу.
Таким образом, вписанный угол АСВ равен 300.
Ответ: 30
Найдите хорду, на которую опирается угол 300, вписанный в окружность радиуса 3.
Это по сути обратная задача (предыдущей). Построим центральный угол.
Он в два раза больше вписанного, то есть угол АОВ равен 600. От сюда можно сделать вывод, что треугольник АОВ равносторонний. Таким образом, хорда равна радиусу, то есть трём.
Ответ: 3
Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.
Построим центральный угол:
Зная радиус и хорду мы можем найти центральный угол АСВ. Это можно сделать по теореме косинусов. Зная центральный угол мы без труда найдём вписанный угол АСВ.
Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Следовательно, второй центральный угол равен 3600 – 900 = 2700.
Угол АСВ по свойству вписанного угла равен его половине, то есть 135 градусам.
Ответ: 135
Найдите хорду, на которую опирается угол 120 градусов, вписанный в окружность радиуса корень из трёх.
Соединим точки А и В с центром окружности. Обозначим её как О:
Нам известен радиус и вписанный угол АСВ. Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ.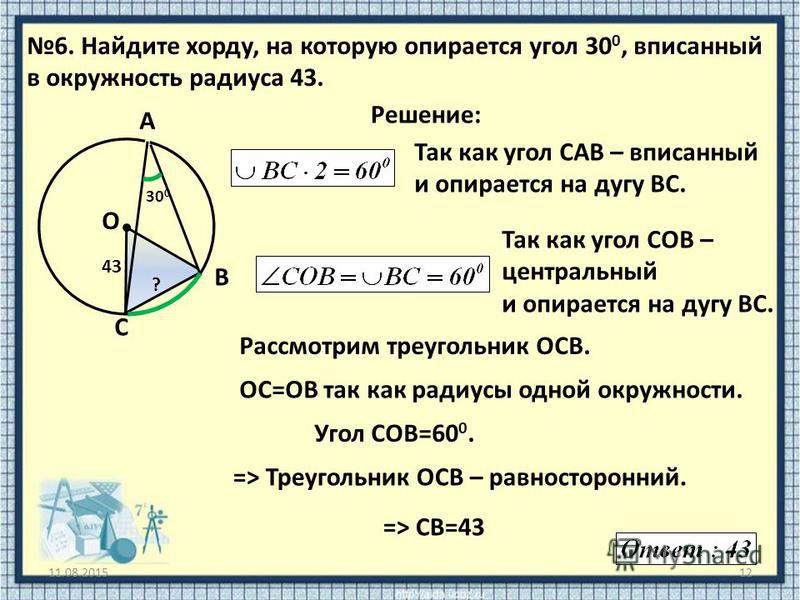 А далее по теореме косинусов вычислить АВ.
А далее по теореме косинусов вычислить АВ.
По свойству вписанного угла центральный угол АОВ (который больше 180 градусов) будет равен вдвое больше вписанного, то есть 240 градусам. Значит, угол АОВ в треугольнике АОВ равен 3600 – 2400 = 1200.
По теореме косинусов:
Ответ:3
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.
По свойству вписанного угла он вдвое меньше центрального угла, опирающегося на ту же дугу, в данном случае речь идёт о дуге АВ.
Сказано, дуга АВ составляет 20 процентов от окружности. Это означает, что центральный угол АОВ составляет так же 20 процентов от 3600. *Окружность это угол в 360 градусов. Значит,
Таким образом, вписанный угол АСВ равен 36 градусам.
Ответ: 36
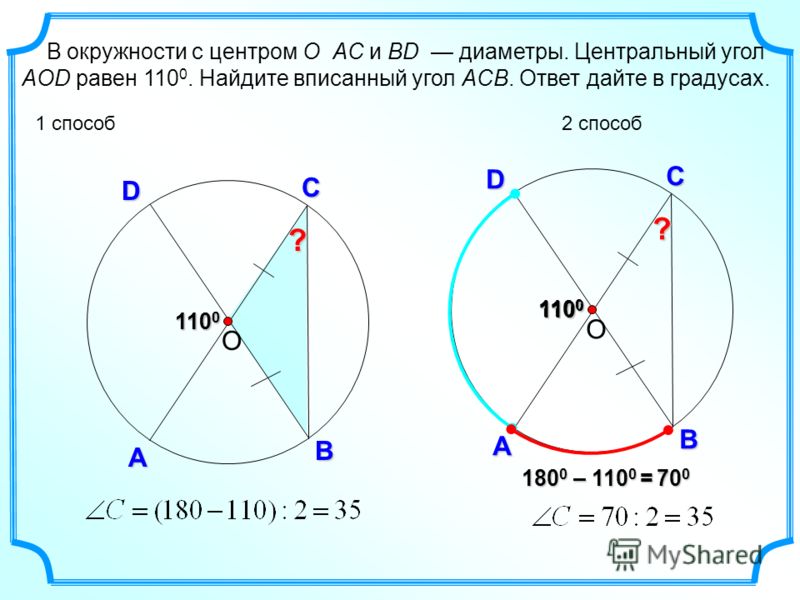
Дуга окружности AC, не содержащая точки B, составляет 200 градусов. А дуга окружности BC, не содержащая точки A, составляет 80 градусов.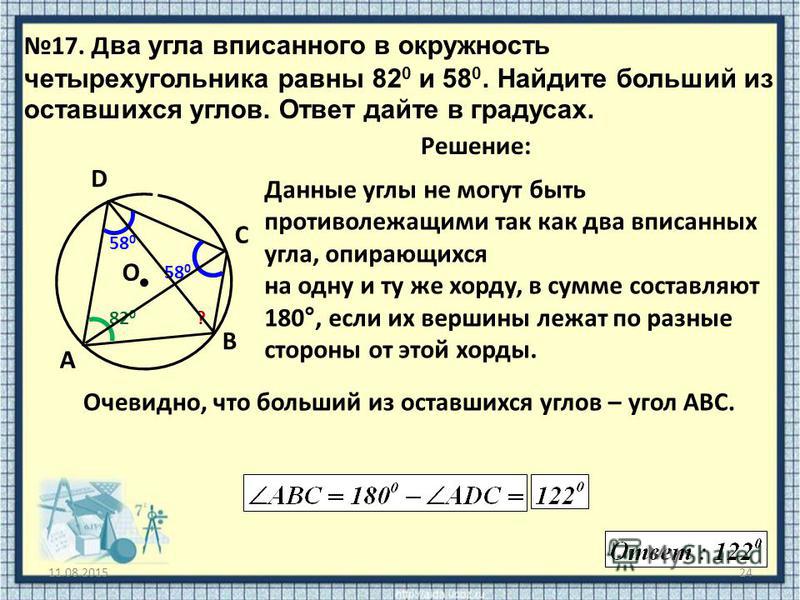 Найдите вписанный угол ACB. Ответ дайте в градусах.
Найдите вписанный угол ACB. Ответ дайте в градусах.
Обозначим для наглядности дуги, угловые меры которых даны. Дуга соответствующая 200 градусам – синий цвет, дуга соответствующая 80 градусам – красный цвет, оставшаяся часть окружности – жёлтый цвет.
Таким образом, градусная мера дуги АВ (жёлтый цвет), а значит и центральный угол АОВ составляет: 3600 – 2000 – 800 = 800.
Вписанный угол АСВ вдвое меньше центрального угла АОВ,то есть равен 40 градусам.
Ответ: 40
Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Посмотреть решение
Найдите хорду, на которую опирается угол 900, вписанный в окружность радиуса 1.
Посмотреть решение
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Посмотреть решение
Радиус окружности равен 1.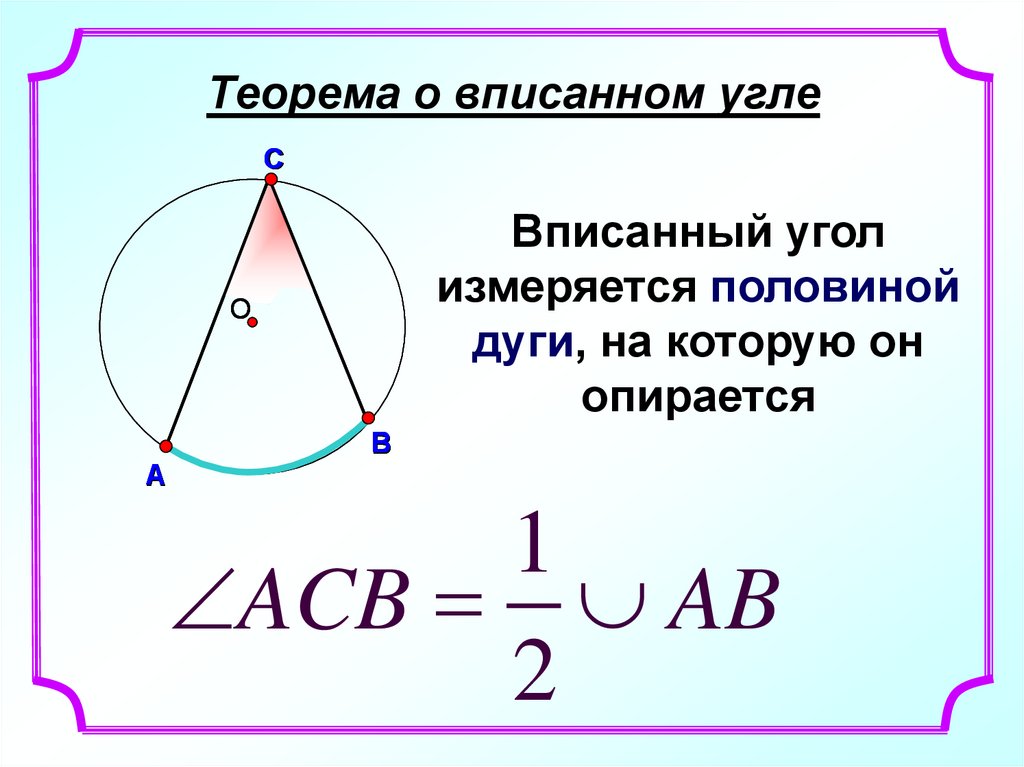 Найдите величину острого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.
Найдите величину острого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.
Посмотреть решение
Центральный угол на 360 больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Посмотреть решение
Найдите вписанный угол, опирающийся на дугу АВ, которая составляет 0,2 окружности. Ответ дайте в градусах.
Посмотреть решение
Хорда делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Посмотреть решение
Точки А, В, С, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5. Найдите больший угол треугольника АВС. Ответ дайте в градусах.
Посмотреть решение
На что обратить внимание при решении подобных задач?
Необходимо знать свойство вписанного угла; понимать, когда и как необходимо использовать теорему косинусов, подробнее о ней посмотрите здесь.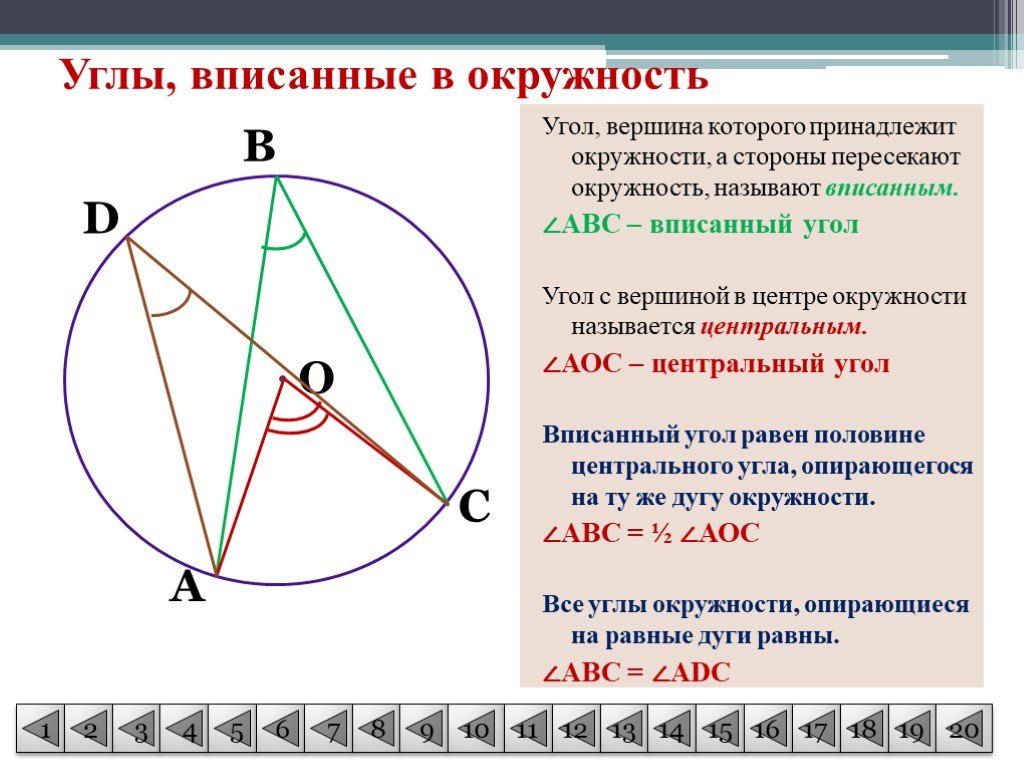
На этом всё! Успехов Вам!
С уважением, Александр Крутицких
Учительница математики в школе в третьем классе:
— Дети, а скажите мне, сколько будет 6*6?
Дети дружно хором отвечают:
— Семьдесят шесть!
— Ну, что вы, такое говорите детки! Шесть на шесть будет тридцать шесть… ну может быть еще 37, 38, 39… ну максимум 40… но никак не семьдесят шесть!
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Вписанные углы окружностей — Криста Кинг Математика
Как построить вписанные углы и дуги, пересекаемые ими?
В этом уроке мы рассмотрим вписанные углы окружностей и то, как они связаны с дугами, называемыми перехваченными дугами.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Хорда окружности
Хорда — это отрезок прямой линии, концы которого лежат на окружности окружности.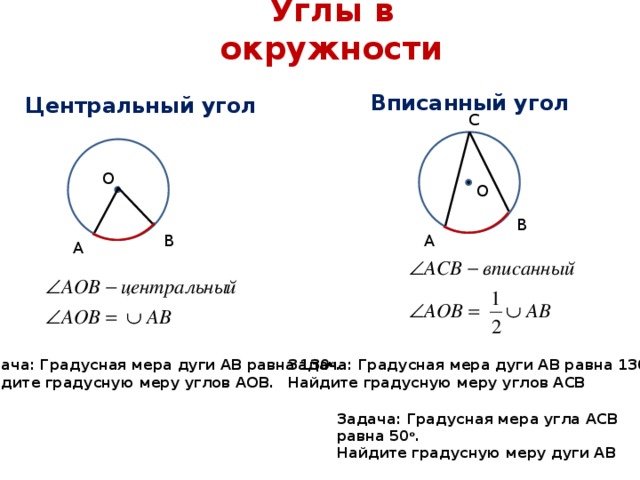 Диаметр окружности — это хорда особого типа, проходящая через центр окружности. Желтая линия является примером хорды.
Диаметр окружности — это хорда особого типа, проходящая через центр окружности. Желтая линия является примером хорды.
Вписанный угол
Вписанный угол образован двумя хордами. Эти хорды имеют общую вершину угла. Дуга, касающаяся концов хорд, называется перехваченной дугой.
Меры вписанных углов, центральных углов и дуг, образуемых при пересечении
Мера образуемой дуги равна мере ее центрального угла.
Мера вписанного угла равна половине меры центрального угла, охватываемого дугой.
Вписанный угол равен половине длины дуги, на которую он опирается.
???м\текст{ дуга }{WX}=м\угол WCX???
???\frac{1}{2}м\угол WCX=м\угол WVX???
???\frac{1}{2}m\text{ arc }{WX}=m\angle WVX???
Мы можем произвести некоторые алгебраические вычисления, чтобы показать, что следующее утверждение также верно.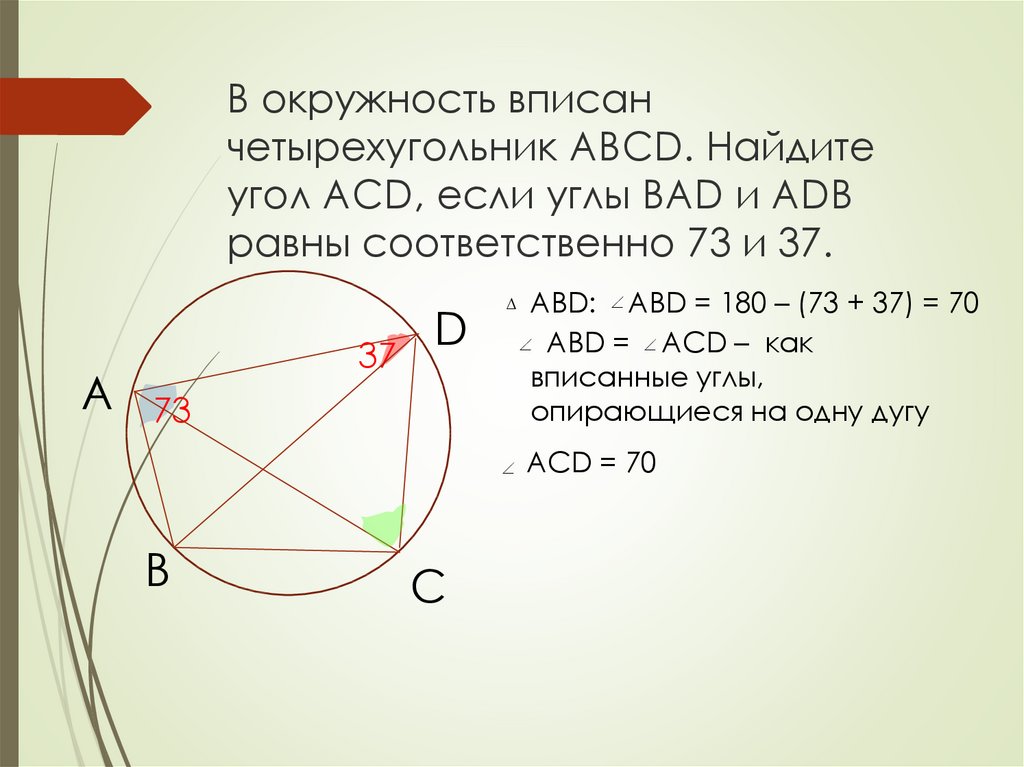
???м\угол WCX=\frac{1}{2}m\text{ arc }{WX}=\угол WCX=2м\угол WVX???
Вычисление измерений вписанных углов в окружности
9\циркуляр???Получить доступ к полному курсу геометрии
Начать
Learn mathKrista King математика, выучить онлайн, онлайн курс, онлайн математика, геометрия, окружности, вписанные углы окружностей, вписанные углы, хорды, вписанные углы в окружности, геометрия окружностей, центральные углы, пересеченные дуги
Вписанный угол (теорема, определение и формула)
Написано
Malcolm McKinsey
Проверка по фактам
Paul Mazzola
Части круга
A Circle -сет из всех очков на равенстве.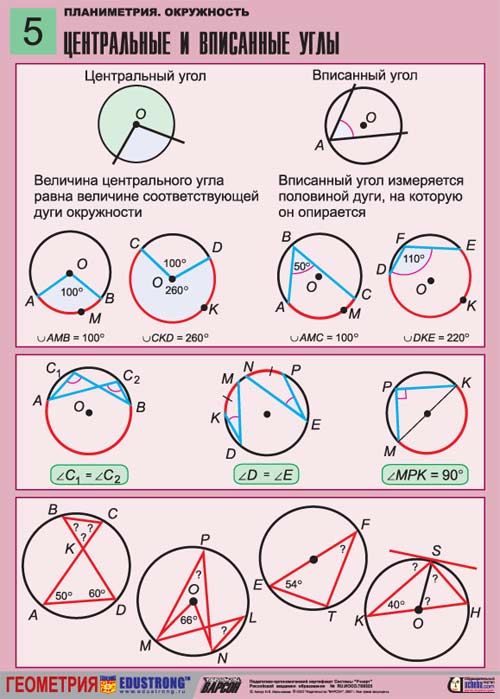 заданная точка, являющаяся центром окружности. Единственный способ собрать все точки, находящиеся на одинаковом расстоянии от точки, — это создать кривую линию.
заданная точка, являющаяся центром окружности. Единственный способ собрать все точки, находящиеся на одинаковом расстоянии от точки, — это создать кривую линию.
Круг состоит из частей:
ARC — Часть окружности круга
Центр — Центральная точка направления внутри круга
Chord — Линия, соединяющая два очка на кругу
- 9 . расстояние по окружности
Диаметр — хорда, проходящая через центр окружности
Радиус — половина диаметра
У круга есть и другие части, не важные для данного обсуждения: секущая и точка касания — две такие части. Круги почти всегда обозначаются математическим символом, за которым следует буквенное обозначение круга, его центральная точка. Это, например, A с аккордом до н.э. и ARC DE :
части круга, если вы построили линейный сегмент . до Точка D на окружности, этот отрезок будет радиусом. Проведя хорду от точки B до точки E , вы получите диаметр, который должен проходить через центр окружности.
до Точка D на окружности, этот отрезок будет радиусом. Проведя хорду от точки B до точки E , вы получите диаметр, который должен проходить через центр окружности.
С кругами геометрия становится одновременно интереснее и сложнее. Сочетая кривые и прямые линии, круги создают совершенно новые возможности. Обычная фигура, включающая окружность, представляет собой вписанный угол.
Определение вписанного угла
Вписанный угол это угол, вершина которого лежит на окружности, а две его стороны являются хордами одной и той же окружности. In the circle below, we have constructed an inscribed angle:
Inscribed angle theoremWe selected three points on the circle, Points G , H , and I
Соединили G и H хордой, GH
We connected H to I with a chord, HI
∠H\angle H∠H is the inscribed angle
Теорема о вписанном угле
Теорема о вписанном угле говорит нам, что вписанный угол всегда равен половине меры либо центрального угла, либо дуги, на которую опирается дуга, имеющая конечные точки сторон вписанного угла.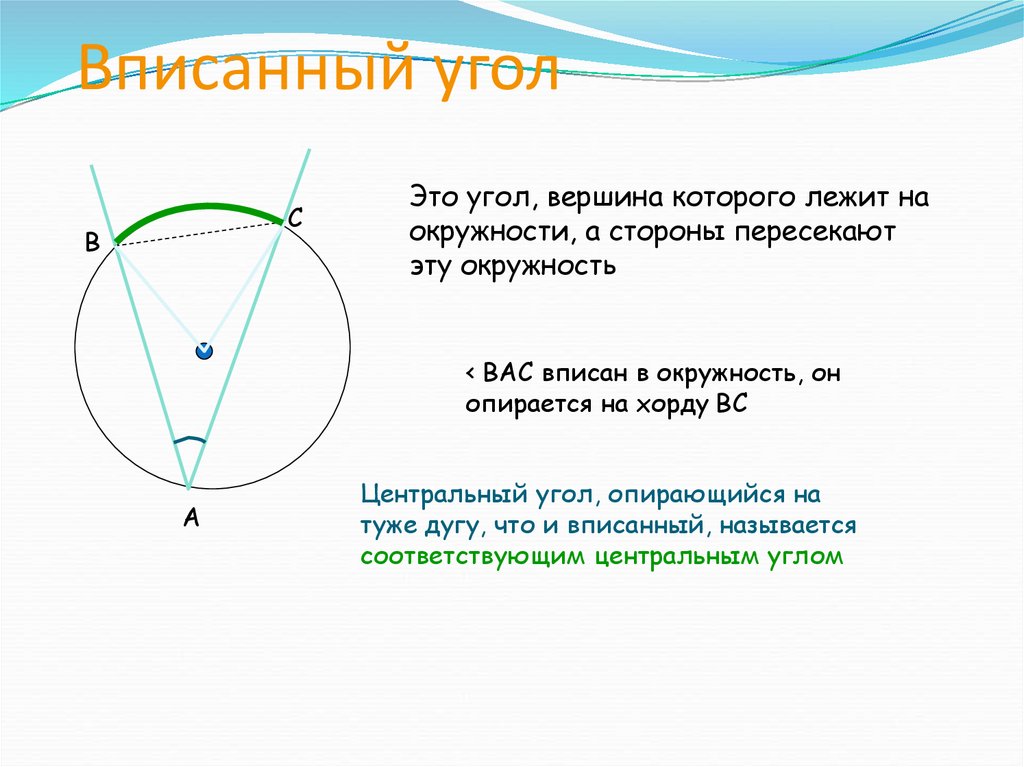
Давайте посмотрим на нашу формулу:
Например, давайте возьмем нашу точку пересечения дуги 80° . Если вписанный угол составляет половину дуги, на которую опирается, половина 80 равна 40 . Значит, вписанный угол равен 40° .
Другой способ сказать то же самое состоит в том, что любой центральный угол или дуга, проведенная с ним, в два раза больше соответствующего вписанного угла.
Оба направления равны 40° !
Что такое центральный угол?
Центральный угол окружности — это угол, вершина которого находится в центре окружности, а две его стороны — радиусы. Центральный угол создает дугу между двумя конечными точками сторон угла на окружности.
Что такое перехваченная дуга?
дуга, пересекаемая , – это часть окружности, ограниченная сторонами вписанного угла. На нашем рисунке выше часть круга от точки G до точки I — дуга пересечения. Это удобно обозначается символом небольшой дуги над буквами: GI⌢\overset\frown{GI}GI⌢
Это удобно обозначается символом небольшой дуги над буквами: GI⌢\overset\frown{GI}GI⌢
Соотношение вписанных углов
Окружности имеют некоторые удивительные отношения между своими частями. Для любого вписанного угла мера вписанного угла равна половине меры дуги, на которую опирается. Это, конечно же, теорема о вписанном угле.
Вписанный угол имеет очень мало правил. Его вершина и концы сторон должны лежать на окружности, и все. Это означает, что на перехваченной дуге могут быть десятки и даже сотни даже тысячи! — вписанных углов. Вы можете перемещать вершину вписанного угла по окружности, удерживая концы сторон прижатыми к перехваченной дуге.
Вот, смотри. Все эти вписанные углы относятся к той же дуге, на которую опираются:
на дугу, на которую опираютсяИ тем не менее каждый из этих вписанных углов измеряет 30° , в соответствии с теоремой о вписанном угле!
Итоги урока
Теперь, когда вы изучили этот урок, вы можете определить вписанный угол и центральный угол окружности, определить и назвать дугу окружности, образуемую вписанным углом, а также вспомнить, сформулировать и применить Теорема о вписанном угле, в которой говорится, что мера данной дуги пересечения в два раза больше меры вписанного угла к этой дуге пересечения.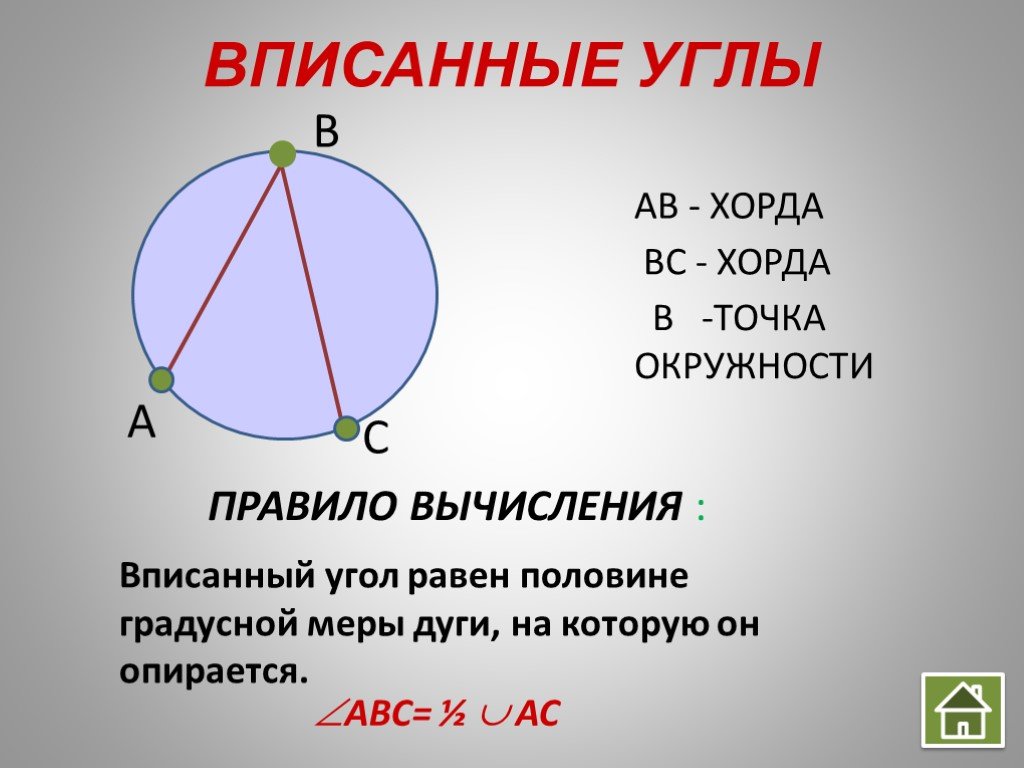

 Угол, опирающийся на диаметр – прямой
Угол, опирающийся на диаметр – прямой
Leave A Comment