Найдите площадь поверхности прямой призмы
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-02-26
Заключительная статья про параллелепипеды. По крайней мере, на данный момент рассмотрены все задания, которые имеются в открытом банке заданий ЕГЭ. Здесь представлены две задачи, связанные с площадью поверхности прямого параллелепипеда.
Это взаимообратные задачи: в одной даны диагонали ромба лежащего в основании и боковое ребро, требуется найти площадь поверхности параллелепипеда; в другой задаче дана площадь поверхности, диагонали ромба лежащего в основании и требуется найти боковое ребро. Напомню формулы. Площадь поверхности прямой призмы:
Так же для нахождения площади ромба будет использована формула площади четырёхугольника:
Понятно, что диагонали ромба пересекаются под углом 900. Известно, что синус этого угла равен единице, поэтому формула примет вид:
Рассмотрим задачи:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 40, и боковым ребром, равным 55.
Площадь поверхности данной призмы равна сумме площадей оснований и четырёх боковых граней:
Основание призмы – ромб, его площадь мы найдём по формуле:
Значит:
Так как призма прямая, то её высота равна боковому ребру:
Используя теорему Пифагора можем выразить сторону ромба через его диагонали d1 и d2 как:
Значит:
Тогда площадь поверхности призмы равна:
Ответ: 4870
В основании прямой призмы лежит ромб с диагоналями, равными 15 и 36. Площадь ее поверхности равна 2100. Найдите боковое ребро этой призмы.
Данная задача является обратной предыдущей. Здесь известна площадь поверхности и требуется найти боковое ребро. У прямой призмы боковое ребро равно её высоте.
Запишем формулу площади поверхности призмы:
Площадь поверхности известна, значит нам необходимо найти площадь ромба лежащего в основании и его сторону.
Площадь ромба:
Используя теорему Пифагора можем выразить сторону ромба через его диагонали d1 и d2 как:
Значит:
Таким образом:
Ответ: 20
27062.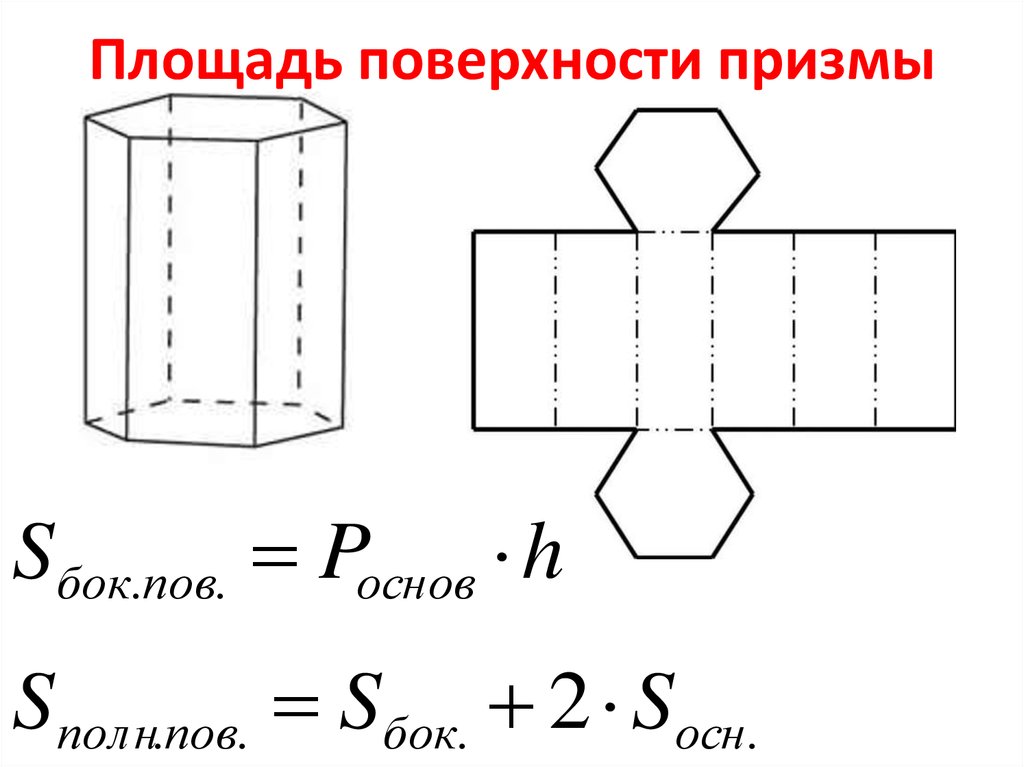 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Посмотреть решение
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Посмотреть решение
В будущем вас ожидают задачи с пирамидами, не пропустите! На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Как найти площадь поверхности правильной призмы: боковой, полной, основания
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.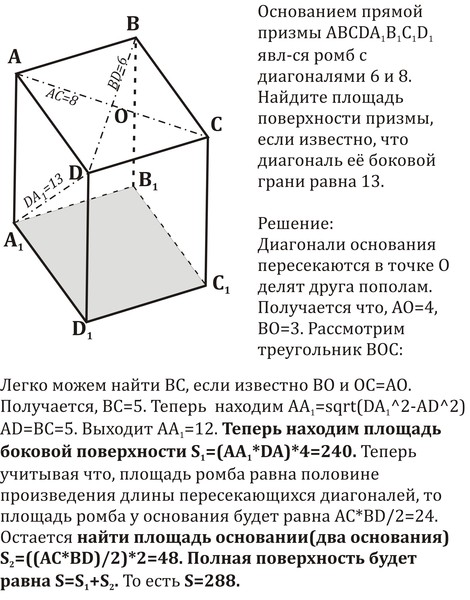 ru Математика Геометрия Нахождение площади правильной призмы: формула и задачи
ru Математика Геометрия Нахождение площади правильной призмы: формула и задачи
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
- Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1.
 Общая формула
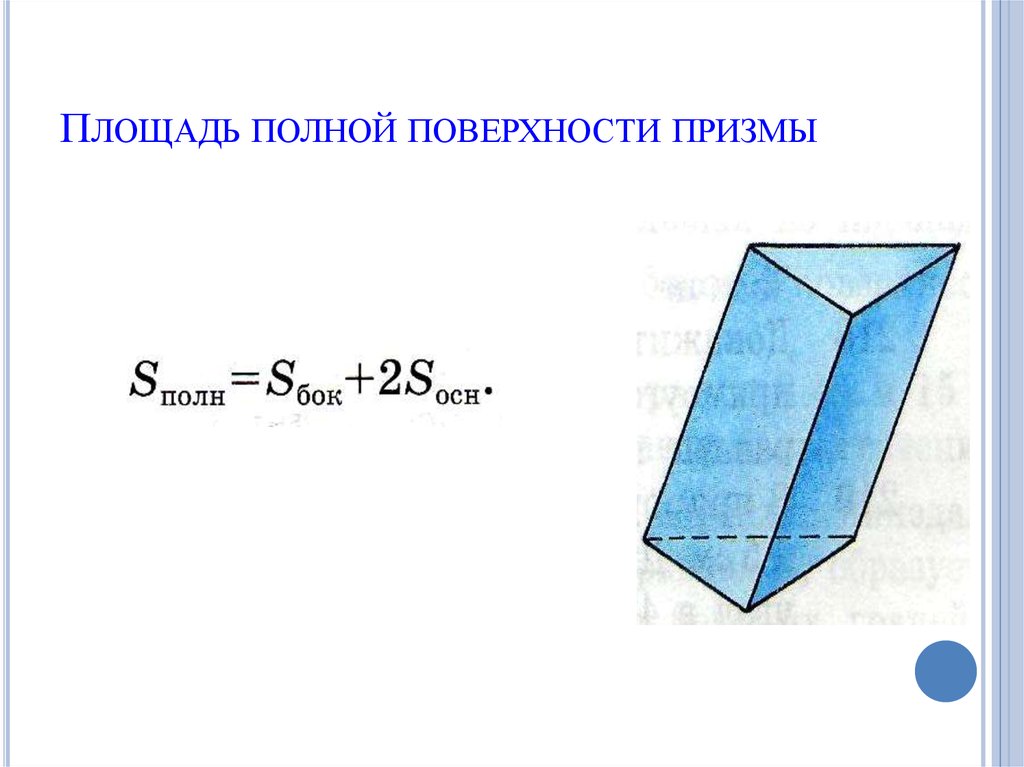
Общая формулаПлощадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание | ru/wp-content/uploads/2020/04/ploshad-pravilnoy-prizmy-6.png" class="stbSkipLazy aligncenter size-full" width="100" height="224" data-full="https://microexcel.ru/wp-content/uploads/2020/04/ploshad-pravilnoy-prizmy-6.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/04/ploshad-pravilnoy-prizmy-6.png" class="stbSkipLazy aligncenter size-full" width="100" height="224" data-full="https://microexcel.ru/wp-content/uploads/2020/04/ploshad-pravilnoy-prizmy-6.png" />»> |
| боковая поверхность | </sub> = 3ah</span></em></nobr>»>Sбок. = 3ah |
| полная |
microexcel.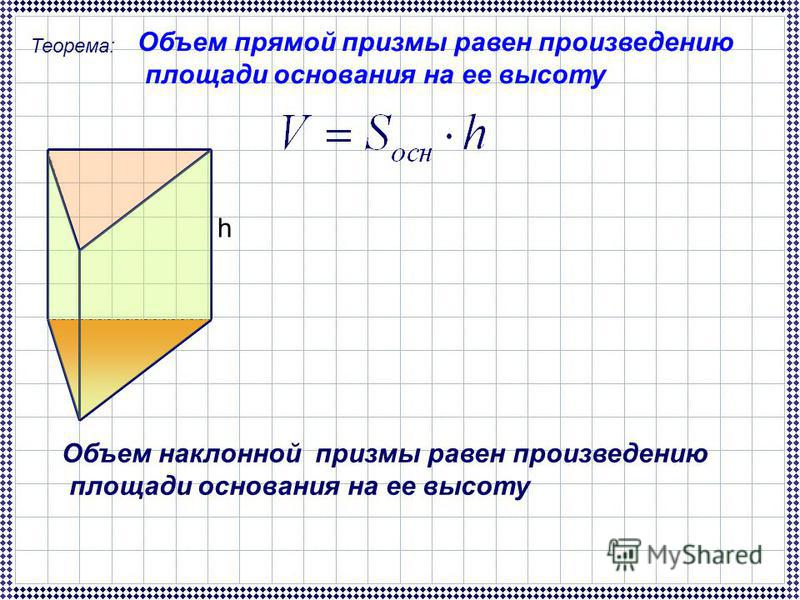 ru
ru
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | </sub> = a<sup>2</sup></span></em></nobr>» data-order=»<nobr><em><span class="math">S<sub>осн.</sub> = a<sup>2</sup></span></em></nobr>»>Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | </sub> = 2a<sup>2</sup> + 4ah</span></em></nobr>» data-order=»<nobr><em><span class="math">S<sub>полн.</sub> = 2a<sup>2</sup> + 4ah</span></em></nobr>»>Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
YYYY» data-time-format=»HH:mm» data-features=»["after_table_loaded_script"]» data-search-value=»» data-lightbox-img=»» data-head-rows-count=»1″ data-pagination-length=»50,100,All» data-auto-index=»off» data-searching-settings=»{"columnSearchPosition":"bottom","minChars":"0"}» data-lang=»default» data-override=»{"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default"}» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>| Площадь | Формула |
| основание | ru/wp-content/uploads/2020/04/ploshad-pravilnoy-prizmy-7.png" class="stbSkipLazy aligncenter size-full" width="105height="244" data-full="https://microexcel.ru/wp-content/uploads/2020/04/ploshad-pravilnoy-prizmy-7.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/04/ploshad-pravilnoy-prizmy-7.png" class="stbSkipLazy aligncenter size-full" width="105height="244" data-full="https://microexcel.ru/wp-content/uploads/2020/04/ploshad-pravilnoy-prizmy-7.png" />»> |
| боковая поверхность | </sub> = 6ah</span></em></nobr>»>Sбок. = 6ah |
| полная |
microexcel.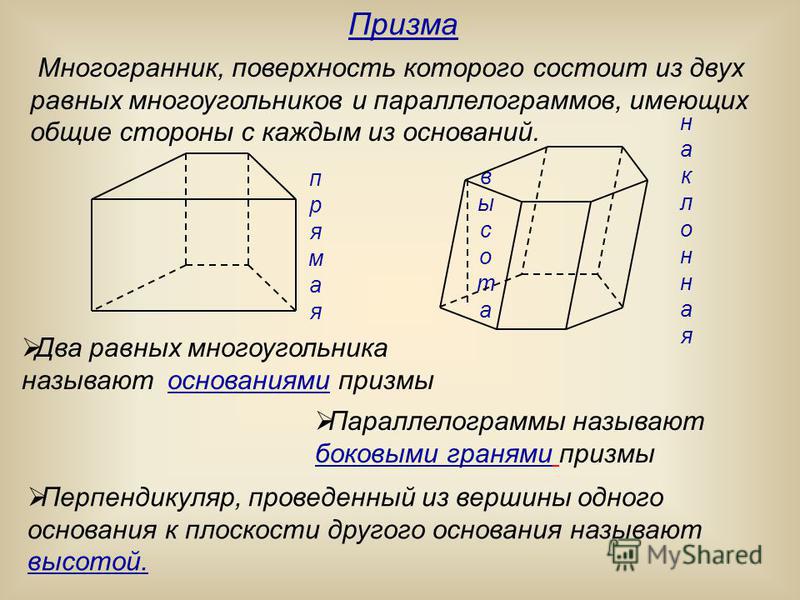 ru
ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Объем и площадь поверхности призмы (Видео)
TranscriptPractice
Привет, и добро пожаловать в это видео о нахождении объема и площади поверхности призмы !
Прежде чем мы перейдем к тому, как найти объем и площадь поверхности призмы, давайте рассмотрим несколько ключевых терминов, которые мы увидим в наших формулах. Первое слово, которое нам нужно определить, это base. Основания призмы — это две уникальные стороны, в честь которых названа призма. Например, если у вас шестиугольная призма , основаниями являются два шестиугольника на концах призмы.
Первое слово, которое нам нужно определить, это base. Основания призмы — это две уникальные стороны, в честь которых названа призма. Например, если у вас шестиугольная призма , основаниями являются два шестиугольника на концах призмы.
Другое слово, которое будет регулярно встречаться в наших формулах, — это рост. Важно различать высоту, потому что она отличается от высоты, используемой в некоторых наших формулах площади. Высота призмы – это длина ребра между двумя основаниями.
И, наконец, я хочу рассмотреть слово обычный . Помните, что правильность многоугольников означает, что каждая сторона многоугольника имеет одинаковую длину.
Теперь, когда мы рассмотрели некоторые из наших ключевых терминов, давайте посмотрим на наши две формулы.
Чтобы найти объем призмы, умножьте площадь основания призмы на ее высоту. Это записывается как \(V=Bh\). Обратите внимание, что большая буква B обозначает площадь основания. Важно, чтобы вы писали эту букву B с большой буквы, потому что в противном случае она просто означает основание. Мы видим это в формуле площади треугольника ½ bh.
Мы видим это в формуле площади треугольника ½ bh.
Формула площади поверхности призмы \(SA=2B+ph\), где B, опять же, обозначает площадь основания, p представляет периметр основания, а h обозначает высоту призмы. призма.
Теперь, когда мы знаем, что такое формулы, давайте рассмотрим несколько примеров задач с их использованием.
Найдите объем и площадь поверхности этой прямоугольной призмы.
Начнем с громкости.
\(V=Bh\)
Так как большая B обозначает площадь основания, мы подставим в формулу площади прямоугольника длину, умноженную на ширину.
Формула объема прямоугольной призмы
Итак \(V=lwh\)
Теперь подставим наши значения. 93\). Помните, поскольку мы умножаем на три измерения, наши единицы измерения кубичны.
Теперь давайте посмотрим на нашу поверхность.
\(SA=2B+ph\)
Опять же, мы подставим в нашу формулу площадь прямоугольника, а также подставим в нашу формулу периметр прямоугольника.
\(SA=2lw+2l+wh\)
Теперь мы можем подставить наши известные значения.
\(SA=24\times 7+2(4+7)(13)\)
И упростим, чтобы получить ответ.
Площадь поверхности 342 квадратных метра.
Помните, что с площадью поверхности мы складываем площади каждой грани вместе, поэтому мы умножаем только на два измерения, поэтому мы возводим наши единицы в квадрат.
Давайте попробуем другой пример.
Найдите объем и площадь поверхности этой правильной пятиугольной призмы.
Начнем с нашего тома.
\(V=Bh\)
Мы хотим подставить в нашу формулу площадь правильного пятиугольника. Эта формула не является общепринятой, так что ничего страшного, если вам нужно ее найти.
Площадь правильного пятиугольника определяется как \(V=(\frac{1}{2}pa)h\)
Теперь мы можем подставить наши значения. Помните, правильный означает, что все стороны пятиугольника конгруэнтны, поэтому мы можем найти наш периметр, умножив значение стороны на 5.
\(V=(\frac{1}{2}\times 5\times 5\ умножить на 3)(14)\)
Что, если мы умножим это, даст нам 525 кубических футов.
Теперь перейдем к площади поверхности.
\(SA=2B+ph\)
Во-первых, мы хотим произвести замену в наших формулах. 92\)
Площадь поверхности нашей призмы составляет 425 квадратных футов.
Давайте рассмотрим еще один пример, но на этот раз я хочу, чтобы вы попробовали его самостоятельно.
Найдите объем и площадь поверхности этой правильной треугольной призмы.
Поставьте видео на паузу и посмотрите, сможете ли вы найти ответы самостоятельно. Тогда сравните их с моими.
Готовы проверить?
Давайте сначала посмотрим на громкость.
\(V=Bh\)
Подставим в нашу формулу площадь треугольника. 93\)
Объем нашей треугольной призмы равен 750 кубических дюймов.
Теперь на поверхность.
\(SA=2B+ph\)
Сначала подставьте в свои формулы.
\(SA=2(\frac{1}{2}bh)+(3s)h\)
Мы можем использовать 3s для периметра, потому что это правильный треугольник или равносторонний треугольник, поэтому все стороны имеют одинаковую длину.
Теперь подставим наши значения и решим.
\(SA=2(\frac{1}{2}\times 5\times 12)+(3\times 12)(25)=60+900=93\)
Ответ:

 3\) 93\). Следовательно, ответ Б правильный.
3\) 93\). Следовательно, ответ Б правильный.
 Поскольку \((3\times13)=393\)
Поскольку \((3\times13)=393\) 5)=1.5\), перепишите уравнение, используя это произведение.
5)=1.5\), перепишите уравнение, используя это произведение.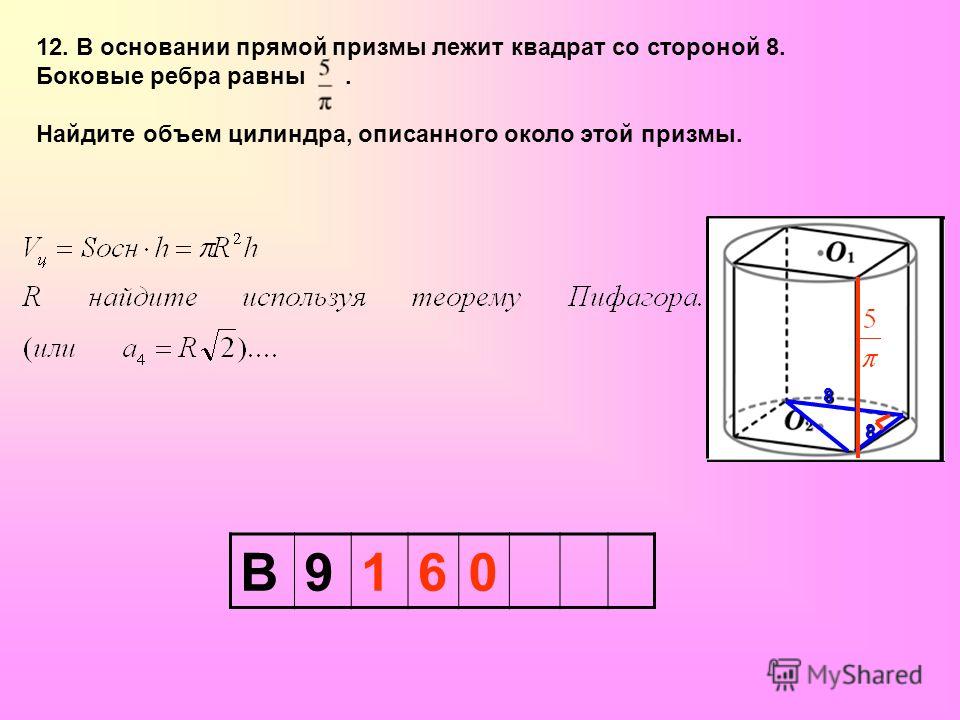 «=»
п
час
где
п
представляет собой периметр основания и
час
представляет собой высоту призмы.
«=»
п
час
где
п
представляет собой периметр основания и
час
представляет собой высоту призмы.  С
.
А
.
«=»
п
час
+
2
Б
где
п
представляет собой периметр основания,
час
высота призмы и
Б
площадь базы.
С
.
А
.
«=»
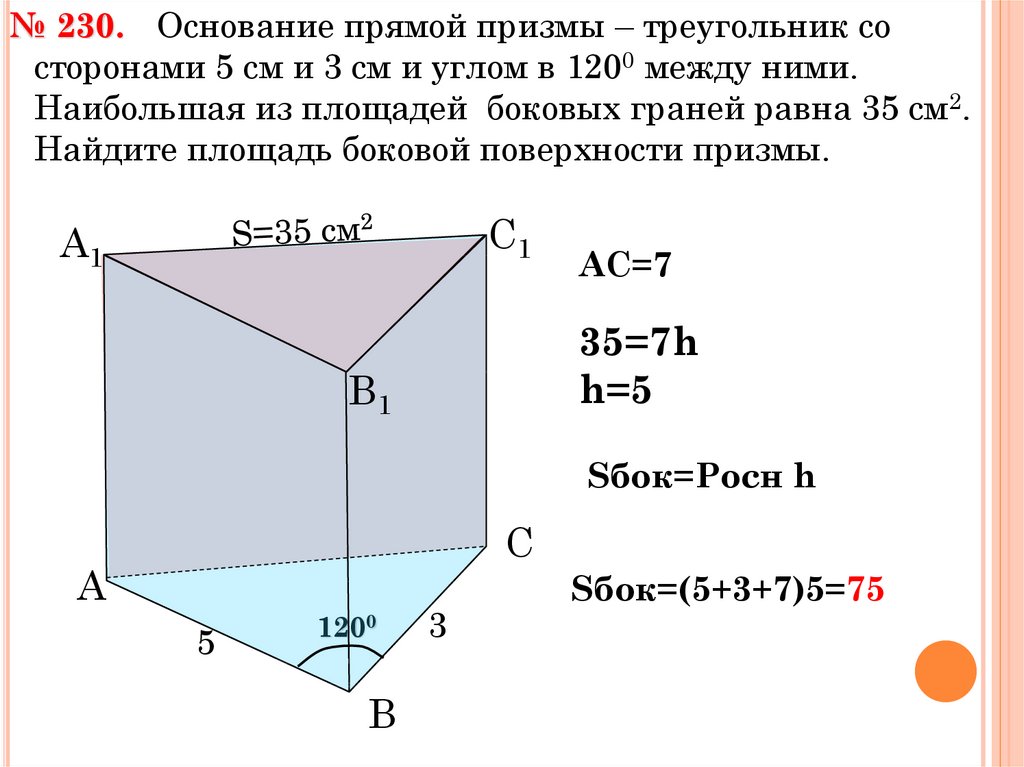
п
час
+
2
Б
где
п
представляет собой периметр основания,
час
высота призмы и
Б
площадь базы.
Leave A Comment