Как найти основания равнобедренной трапеции если известны боковые стороны: Все формулы сторон равнобедренной трапеции

как найти, формула, через среднюю линию

Содержание:

Основные свойства трапеции
Способы нахождений периметра
- По всем сторонам
- По сторонам равнобедренной трапеции
- Через среднюю линию
Примеры решения задач

Содержание

Основные свойства трапеции
Способы нахождений периметра
- По всем сторонам
- По сторонам равнобедренной трапеции
- Через среднюю линию
Примеры решения задач

Определения

Трапеция

— это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.

Периметр трапеции — это сумма длин всех его сторон.

Основные свойства трапеции

средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;

биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;

треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;

треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;

если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;

точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;

середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;

Свойства равнобедренной трапеции

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).

Если нет возможности написать самому, закажите тут.

в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
диагонали равны;
равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.

Способы нахождений периметра

Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.

По всем сторонам

Формула для нахождения периметра выглядит так:

P=a+b+c+d

где a, b, c, d — стороны трапеции.

По сторонам равнобедренной трапеции

Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:

\(P=2\times a+b+c\)

или

\(P=2\times c+a+b\)

Через среднюю линию

Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:

\(P=2\times l+AB+CD\)

где l — средняя линия фигуры.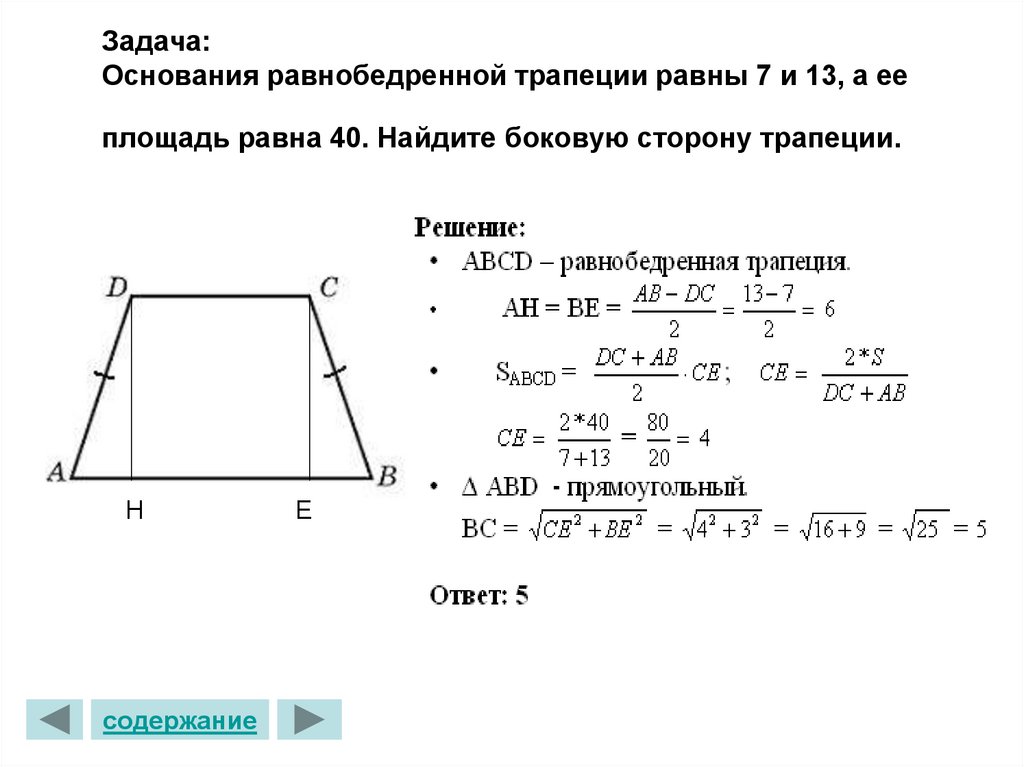

Примеры решения задач

Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.

Задача 1

Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.

Решение:

Нам пригодится самая первая формула для расчета:

P=a+b+c+d.

Подставляем значения и получаем:

P=4+7+5+10=26\;см.

Ответ: 26 см.

Задача 2

Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.

Решение:

Так как трапеция равнобедренная, удобнее всего будет использовать формулу:

\(P=2\times a+b+c\)

Таким образом, получается:

\(P=2\times 7+5+8=27\) см.

Ответ: 27 см.

Задача 3

Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.

Решение:

Считать будем по формуле

\(P=2\times l+a+c\)

\(P=2\times 6+5+9=26\) см.

Ответ: 26 см.

Насколько полезной была для вас статья?

Рейтинг: 3.82 (Голосов: 11)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

определение, формула вычисления, примеры решения задач

Что такое трапеция

Трапеция — это плоская фигура, ее изучают в курсе геометрии 8 класса.

Определение 1

Трапеция — четырехугольник, две стороны которого параллельны, и две другие стороны не параллельны.

Определение 2

Основаниями называются параллельные стороны трапеции. Непараллельные — боковые стороны.

Частный случай трапеции — равнобедренная трапеция, боковые стороны которой равны. Трапеция с углами по 90 градусов, прилежащими к одной боковой стороне, называется прямоугольной.

Определение 3

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон и параллельный основаниям.

ABCD — трапеция, EF — ее средняя линия, BC||EF||AD, BE=CF, AE=DF.

Формулы площади трапеции

Чтобы найти площадь трапеции можно использовать несколько формул. Выбор зависит от данных условия.

Площадь трапеции равна произведению половины суммы ее оснований на высоту.

Формула 1

Рассмотрим трапецию ABCD, AD||BC, BF — высота. формула для нахождения площади трапеции будет выглядеть как .

Площадь трапеции равна произведению ее средней линии на высоту.

Формула 2

Для данной трапеции , а формула выглядит так: S=h·m, где h — высота, m — средняя линия.

Площадь трапеции равна половине произведения ее диагоналей на синус угла между ними.

Формула 3

Формула 4

У трапеции, диагонали которой перпендикулярны, , так как sin 90º=1.

Площадь трапеции равна произведению половины ее периметра на радиус вписанной окружности. Если суммы противолежащих сторон трапеции равны, то в трапецию можно вписать окружность. Полупериметр трапеции равен половине суммы ее четырех сторон или сумме ее оснований. Зная основания трапеции и радиус вписанной окружности, можно посчитать ее площадь: , где a и b — основания, r — радиус вписанной окружности. Радиус вписанной в трапецию окружности равен половине высоты трапеции h, поэтому из формулы можно получить .

Формула площади равнобедренной трапеции

Площадь равнобедренной трапеции можно рассчитать по тем же формулам. Некоторые из них имеют упрощенный вид.

Если известны основания a и b и высота трапеции h, то площадь рассчитывают как и в общем случае: .
S=h·m, где h — высота, m — средняя линия.
Площадь равнобедренной трапеции равна половине произведения её диагоналей на синус угла между ними. У равнобедренной трапеции (половине произведения квадрата ее диагонали на синус угла между диагоналями).

Площадь равнобедренной трапеции с перпендикулярными диагоналями

Так как sin 90º=1, то .
Площадь равнобедренной трапеции, диагонали которой перпендикулярны, равна квадрату ее высоты:
Если в трапецию можно вписать окружность, то применяется общая формула

Формула площади криволинейной трапеции

Определение 2

Криволинейная трапеция — это плоская фигура, ограниченная графиком непрерывной и неотрицательной на отрезке [а;b] функции y=f(х), прямыми х=а, x=b и осью абсцисс.

Отрезок [a;b] называют основанием криволинейной трапеции. Отрезки, ограничивающие криволинейную трапецию слева и справа, могут вырождаться в точку. Верхняя граница криволинейной трапеции может быть задана разными формулами на разных частях отрезка.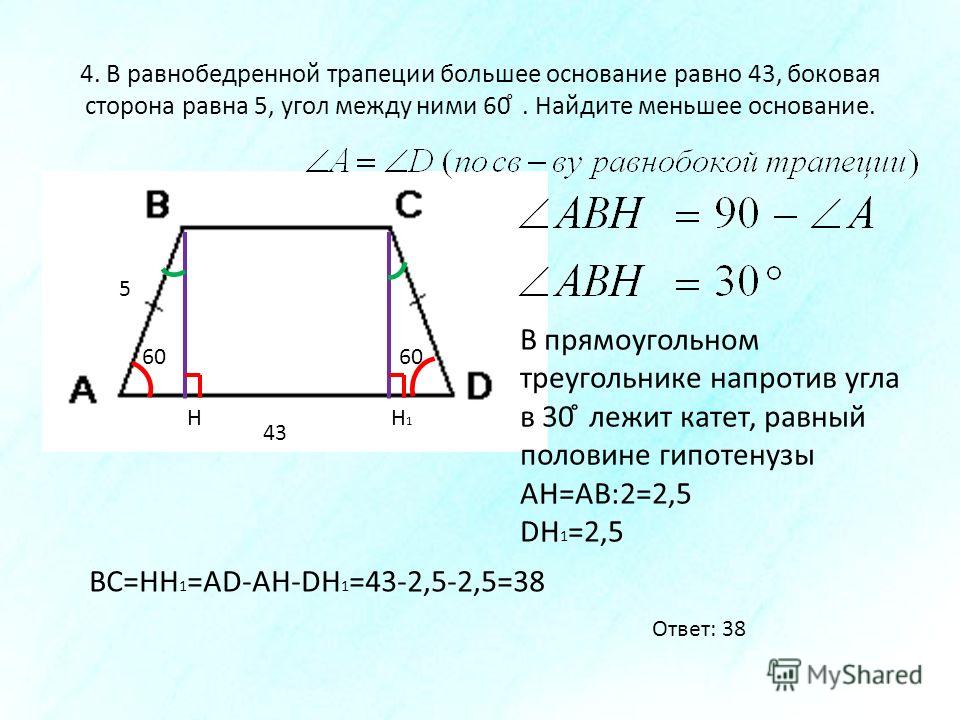

Формула Ньютона-Лейбница

Нахождение площади криволинейной трапеции рассматривают в 11 классе как пример применения интеграла.

Площадь криволинейной трапеции, образованной графиком функции y=f(x) на интервале [a;b] записывают в виде определенного интеграла:

По формуле Ньютона-Лейбница определенный интеграл равен:.

Пояснение на примерах

Задача 1

Найдите площадь трапеции, если ее основания равны 4 и 7 см, а высота — 4 см.

Решение:

Чтобы узнать площадь трапеции, используем формулу .

Ответ:

Задача 2

Найдите площадь фигуры под кривой на заданном интервале: f(x)=x3+3, x∈[−1;1].

Решение:

S=∫−11(x3+3)dx=(x44+3x)|−11=14+3−(14−3)=6

Ответ: 6.

Свойства трапеций и равнобедренных трапеций

Автор: Марк Райан и

Обновлено: 09.07.2021 mmies

Геометрия для чайников

Книга для изучения Купить на Amazon

Трапеция — это четырехугольник (форма с четырьмя сторонами) с ровно одной парой параллельных сторон (параллельные стороны называются основаниями ).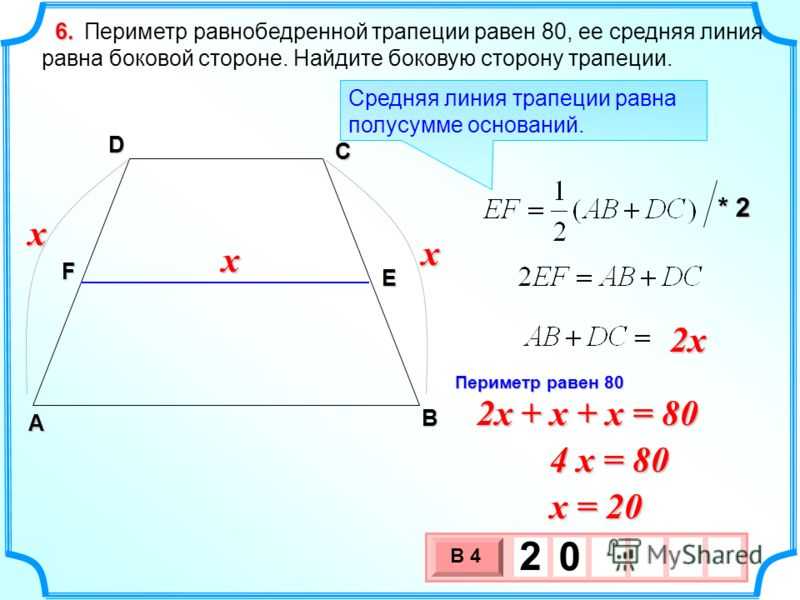

На следующем рисунке показана трапеция слева и равнобедренная трапеция справа.

Свойства трапеции следующие:
Свойства равнобедренной трапеции следующие:
- Свойства трапеции применяются по определению (параллельные основания).
- Ноги конгруэнтны по определению.
- Нижние углы при основании равны.
- Верхние углы при основании равны.
- Любой нижний угол основания является дополнительным к любому верхнему углу основания.
- Диагонали равны.

Дополнительные углы, пожалуй, труднее всего заметить на приведенных выше диаграммах. Из-за того, что стороны параллельны, последовательные углы являются односторонними внутренними углами и, таким образом, являются дополнительными. (Кстати, все специальные четырехугольники, кроме воздушного змея, содержат последовательные дополнительные углы.)

Вот вам доказательство равнобедренной трапеции:

Утверждение 1 :

Причина выписки 1 : Дано.

Утверждение 2 :

Причина утверждения 2 : Катеты равнобедренной трапеции конгруэнтны.

Утверждение 3 :

Причина утверждения 3 : Верхние углы при основании равнобедренной трапеции равны.

Выписка 4 :

Причина выписки 4 : Рефлексивное свойство.

Заявление 5 :

Причина заявления 5 : Сторона-Угол-Сторона или SAS (2, 3, 4)

Выписка 6 :

Причина выписки 6 : CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны).

Выписка 7 :

Основание выписки 7 : Если углы равны, то равны и стороны.

Эта статья взята из книги:

Геометрия для чайников,

Об авторе книги:

Марк Райан — основатель и владелец Математического центра в районе Чикаго, где он занимается репетиторством по всем математическим предметам а также подготовка к тесту.

Марк является автором книг «Исчисление для чайников», рабочей тетради по математическому анализу для чайников и рабочей тетради по геометрии для чайников .

Этот артикул находится в категории:

Геометрия ,

Что такое равнобедренная трапеция?

В геометрии есть много разных форм и фигур, с которыми вы столкнетесь. Некоторые из этих форм более сложны, чем другие, но все они имеют определенные свойства, которые делают их такими, какие они есть. Сегодня мы поговорим об одной конкретной форме: равнобедренной трапеции. Читайте дальше, чтобы узнать больше об этой фигуре и о том, как ее идентифицировать!

Равнобедренная трапеция — это тип четырехугольника — четырехсторонней фигуры, у которой две параллельные стороны (основания) и две непараллельные стороны (катеты). Однако то, что отличает равнобедренную трапецию от других четырехугольников, заключается в том, что у нее есть одна пара сторон одинаковой длины (катеты). Это означает, что трапеция имеет два угла, которые также равны по величине.

Чтобы визуализировать эту фигуру, представьте себе прямоугольник с двумя срезанными углами. В результате получится четырехсторонняя фигура с двумя параллельными сторонами и двумя непараллельными сторонами, что делает ее трапецией. Теперь, если мы возьмем этот же прямоугольник и отрежем углы так, чтобы две непараллельные стороны тоже были одинаковой длины, у нас получилась бы равнобедренная трапеция.

Заключение

В заключение, равнобедренная трапеция является типом четырехугольника, который имеет две параллельные стороны, две непараллельные стороны и одну пару сторон одинаковой длины. Эту фигуру можно визуализировать, представив прямоугольник с двумя срезанными углами, так что получившаяся фигура имеет две пары сторон одинаковой длины. Теперь вы знаете немного больше об этой увлекательной геометрической фигуре!