Алгебра свободных и скользящих векторов
Алгебра свободных и скользящих векторов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам.  4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест.  5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II. 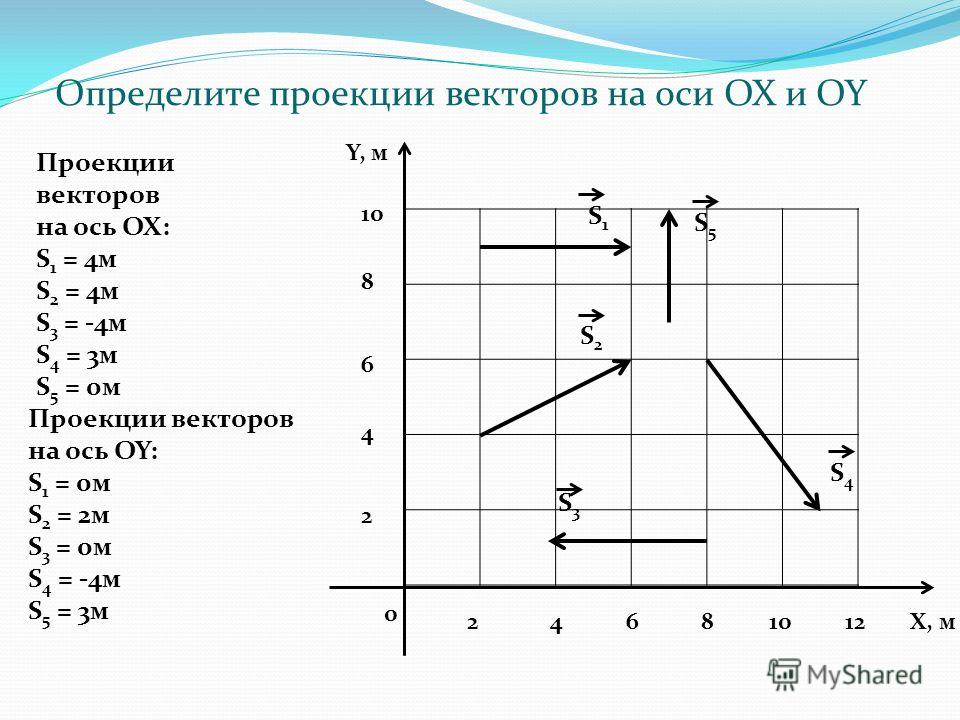 АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ§ 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 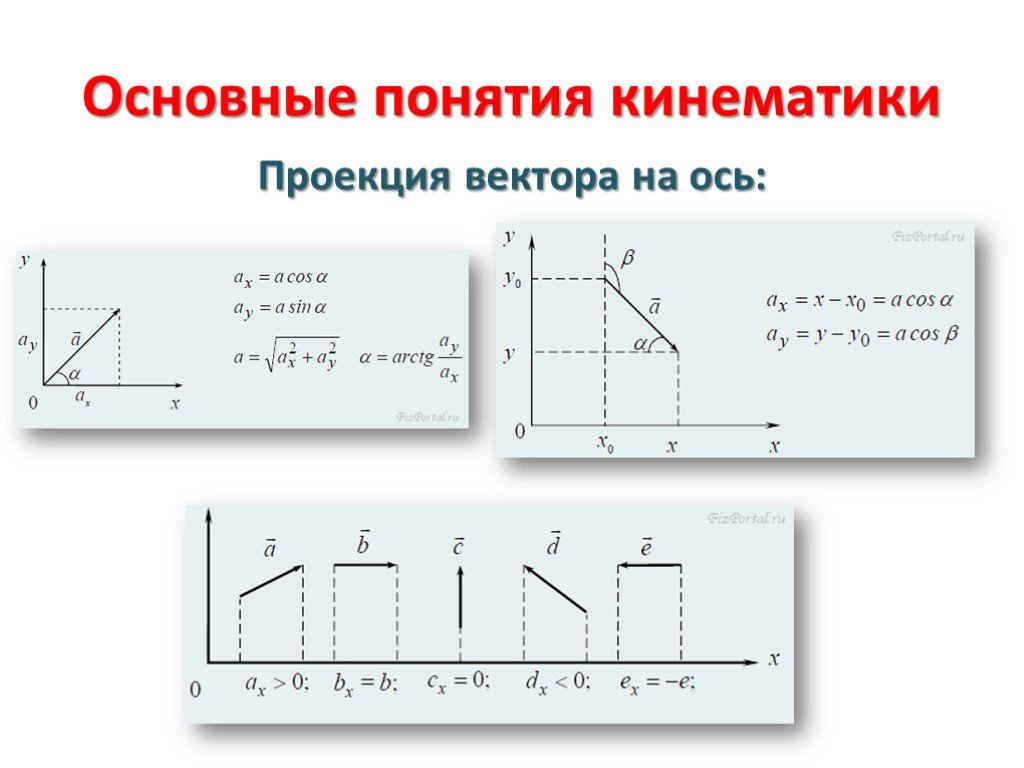 § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов. |
Вычислить сумму проекций вектора на координатные оси. Проекция вектора
а. Проекцией точки А на ось PQ (рис. 4) называется основание а перпендикуляра, опущенного из данной точки на данную ось. Та ось, на которую мы проектируем, называется осью проекций.
4) называется основание а перпендикуляра, опущенного из данной точки на данную ось. Та ось, на которую мы проектируем, называется осью проекций.
Ь. Пусть даны две оси и вектор А В, указанные на рис. 5.
Вектор началом которого служит проекция начала и концом — проекция конца данного вектора, называется проекцией вектора А В на ось PQ, Записывается это так;
Иногда указатель PQ внизу не пишется, это делается в тех случаях, когда кроме PQ нет другой осиг на которую можно было бы проектировать.
с. Теорема I. Величины векторов, лежащих на одной оси, относятся как величины их проекций на любую ось.
Пусть даны оси и векторы, указанные на рис, 6. Из подобия треугольников видно, что длины векторов относятся, как длины их проекций, т. е.
Так как векторы на чертеже направлены в разные стороны, то величины их имеют различный внак, следовательно,
Очевидно, величины проекций также имеют различный знак:
подставляя (2) в (3) в (1), получим
Меняя знаки на обратные, получим
Если векторы будут одинаково направлены, то будут одного направления и их проекции; в формулах (2) и (3) знаков минус не будет.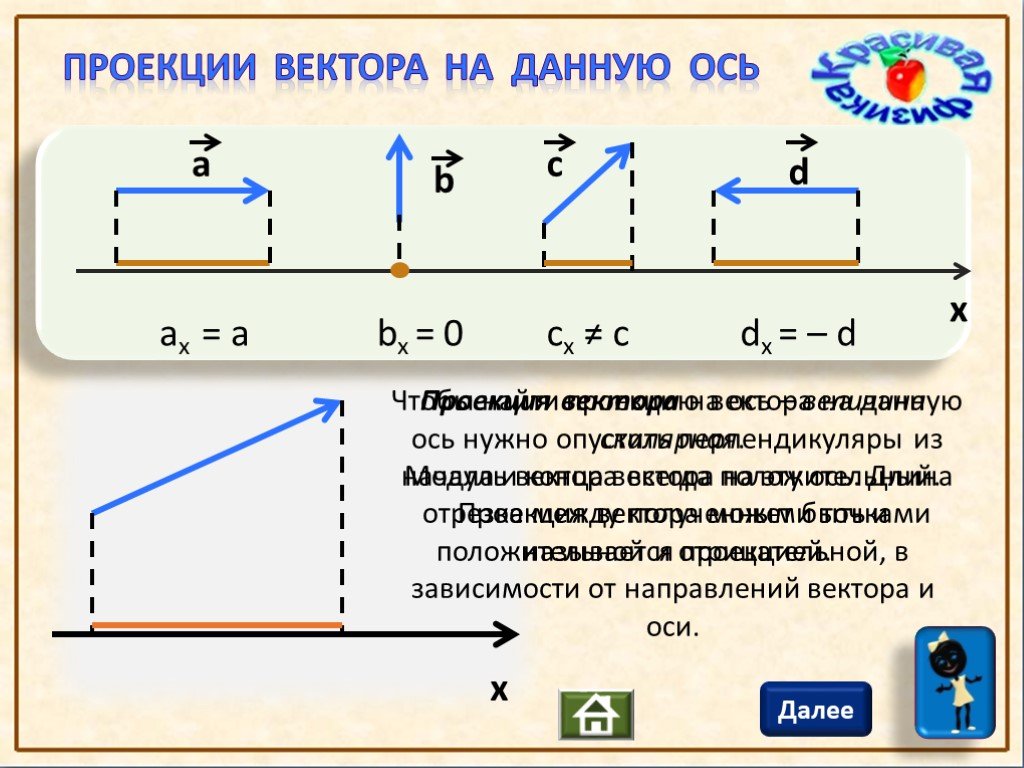 Подставляя (2) и (3) в равенство (1), мы сразу получим равенство (4). Итак, теорема доказана для всея случаев.
Подставляя (2) и (3) в равенство (1), мы сразу получим равенство (4). Итак, теорема доказана для всея случаев.
d. Теорема II. Величина проекции вектора на любую ось равна величине вектора, умножен» ной на косинус угла между осью проекций и осью вектора, Пусть даны оси вектор как указано на рис. 7. Построим вектор одинаково направленный со своей осью и отложенный, например, от точки пересечения осей. Пусть длина его равна единице. Тогда и величина его
Пусть в пространстве задана ось l, т. е. направленная прямая.
Проекцией точки М на ось l называется основание М 1 перпендикуляра ММ 1 , опущенного из точки на ось.
Точка М 1 есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).
Если точка М лежит на оси l, то проекция точки М на ось совпадает с М1.
Пусть АВ — произвольный вектор (АВ¹ 0). Обозначим через А 1 и b 1 проекции на ось l соответственно начала А и конца В вектора АВ и рассмотрим векторА 1 В 1
Проекцией вектора АВ на ось l называет ся положительное число |A 1 B 1 | , есливектор А 1 В 1 и ось l одинаково направлены и отрица тельное число — |A 1 B 1 | , если вектор А 1 В 1 и ось l противоположно направлены (см. l , то пр l АВ=0.
l , то пр l АВ=0.
Угол j между вектором а и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно,0£j£p
Рассмотрим некоторые основные свойства проекций.
Свойство 1. Проекция вектора a на ось l равна произведению модуля вектора aна косинус угла j между вектором и осью, т. е. пр l a =|a | cos j .
Следствие 5.1. Проекция вектора на ось положительна (отрицательна), есливектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось
Свойство 3. При умножении вектора а на число А его проекция на ось также умножается на это число, т. е.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
5.4. Разложение вектора по ортам координатных осей.
Модуль вектора.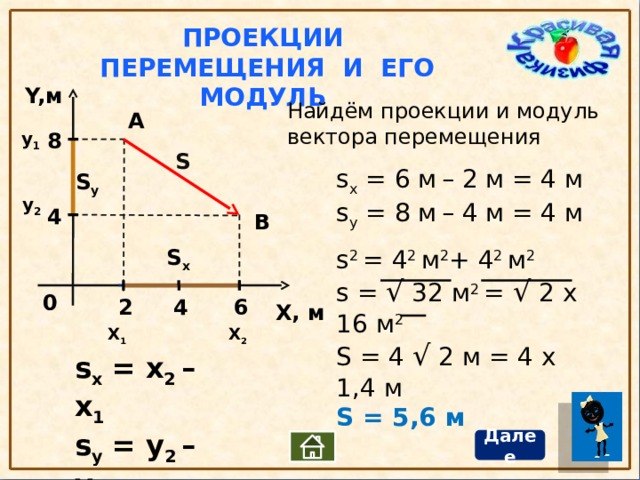 Направляющие косинусы.
Направляющие косинусы.
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые i, j , k соответственно (см. рис. 12).
Выберем произвольный вектор а пространства и совместим его начало с началом координат: а=ОМ.
Найдем проекции вектора а на координатные оси. Проведем через конецвектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М 1 , М 2 и Мз.Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда пр х а=|OM 1 |, np y a = |ОМ 2 |, пр z а=|ОМз|. По определению суммы нескольких векторов находим а = ОМ 1 + M 1 N + NM.
А так как M 1 N=OM 2 , NM =ОМз, то
а=ОМ 1 + ОМ 2 + ОМ 3 (5.1)
Обозначим проекции вектора а=ОМ на оси Ох, Оу и Oz соответственно через а х, а у и a z , т.е. |OM 1 | = а х,|ОМ 2 | = а у, |ОМ 3 | = а z . Тогда из равенств (5.1) и (5.2) получаем
a=a x i+a y j+a z k (5. 3)
3)
Эта формула является основной в векторном исчислении и называетсяразложением вектора по ортам координатных осей. Числа а х, а у, a z называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде: a = (a x ;a y ;a z).
Равенство b = (b x ;b y ; b z) означает, что b = b х i +b у j + b z k . Зная проекциивектора а, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора а с осями Ох, Оу и Oz соответственно равны a,b,g. По свойству проекции вектора на ось, имеем
Или, что то же самое,
Числа называются направляющими косинусами вектора а.
Подставим выражения (5.5) в равенство (5.4), получаем
Сократив на получим соотношение
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора e являются числа
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.
Решение задач на равновесие сходящихся сил с помощью построения замкнутых силовых многоугольников сопряжено с громоздкими построениями. Универсальным методом решения таких задач является переход к определению проекций заданных сил на координатные оси и оперирование с этими проекциями. Осью называют прямую линию, которой приписано определенное направление.
Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.
Проекция вектора считается положительной, если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной, если направление от начала проекции к ее концу противоположно положительному направлению оси.
Таким образом, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.
Рассмотрим ряд случаев проецирования сил на ось:
Вектор силы F (рис. 15) составляет с положительным направлением оси х острый угол .
Чтобы найти проекцию, из начала и конца вектора силы опускаем перпендикуляры на ось oх ; получаем
1. F x = F cos α
Проекция вектора в данном случае положительна
Сила F (рис. 16) составляет с положительным направлением оси х тупой угол α.
Тогда F x = F cos α, но так как α = 180 0 — φ,
F x = F cos α = F cos180 0 — φ =- F cos φ.
Проекция силы F на ось oх в данном случае отрицательна.
Сила F (рис. 17) перпендикулярна оси oх .
Проекция силы F на ось х равна нулю
F x = F cos 90° = 0.
Силу, расположенную на плоскости хоу (рис. 18), можно спроектировать на две координатные оси ох и оу .
Силу F можно разложить на составляющие: F x и F y . Модуль вектора F x равен проекции вектора F на ось ox , а модуль вектора F y равен проекции вектора F на ось oy .
Из ΔОАВ : F x =F cos α, F x =F sin α.
Из ΔОАС : F x =F cos φ, F x =F sin φ.
Модуль силы можно найти по теореме Пифагора:
Проекция векторной суммы или равнодействующей на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Рассмотрим сходящиеся силы F 1 , F 2 , F 3 , и F 4 , (рис. 19, а). Геометрическая сумма, или равнодействующая, этих сил F определяется замыкающей стороной силового многоугольника
Опустим из вершин силового многоугольника на ось x перпендикуляры.
Рассматривая полученные проекции сил непосредственно из выполненного построения, имеем
F = F 1x +F 2x +F 3x + F 4x
где n — число слагаемых векторов. Их проекции входят вышеуказанное уравнение с соответствующим знаком.
В плоскости геометрическую сумму сил можно спроецировать на две координатные оси, а в пространстве – соответственно на три.
Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
Если имеем ось L и ненулевой вектор A B → , то можем построить вектор A 1 B 1 ⇀ , обозначив проекции его точек A 1 и B 1 .
A 1 B → 1 будет являться проекцией вектора A B → на L .
Определение 1
Проекцией вектора на ось называют вектор, начало и конец которого являются проекции начала и конца заданного вектора. n p L A B → → принято обозначать проекцию A B → на L . Для построения проекции на L опускают перпендикуляры на L .
n p L A B → → принято обозначать проекцию A B → на L . Для построения проекции на L опускают перпендикуляры на L .
Пример 1
Пример проекции вектора на ось.
На координатной плоскости О х у задается точка M 1 (x 1 , y 1) . Необходимо построить проекции на О х и О у для изображения радиус-вектора точки M 1 . Получим координаты векторов (x 1 , 0) и (0 , y 1) .
Если идет речь о проекции a → на ненулевой b → или проекции a → на направление b → , то имеется в виду проекция a → на ось, с которой совпадает направление b → . Проекция a → на прямую, определяемая b → , имеет обозначение n p b → a → → . Известно, что когда угол между a → и b → , можно считать n p b → a → → и b → сонаправленными. В случае, когда угол тупой, n p b → a → → и b → противоположно направлены. В ситуации перпендикулярности a → и b → , причем a → — нулевой, проекция a → по направлению b → является нулевым вектором.
Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось. , мы можем найти числовую проекцию a → направленную по вектору b → и получим n p b → a → = a → , b → b → . Формула эквивалента определению, указанному в начале пункта.
, мы можем найти числовую проекцию a → направленную по вектору b → и получим n p b → a → = a → , b → b → . Формула эквивалента определению, указанному в начале пункта.
Определение 3
Числовой проекцией вектора a → на ось, совпадающей по направлению с b → , называют отношение скалярного произведения векторов a → и b → к длине b → . Формула n p b → a → = a → , b → b → применима для нахождения числовой проекции a → на прямую, совпадающую по направлению с b → , при известных a → и b → координатах.
Пример 3
Задан b → = (- 3 , 4) . Найти числовую проекцию a → = (1 , 7) на L .
Решение
На координатной плоскости n p b → a → = a → , b → b → имеет вид n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 , при a → = (a x , a y) и b → = b x , b y . Чтобы найти числовую проекцию вектора a → на ось L , нужно: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5 .
Ответ: 5.
Пример 4
Найти проекцию a → на L , совпадающей с направлением b → , где имеются a → = — 2 , 3 , 1 и b → = (3 , — 2 , 6) . Задано трехмерное пространство.
Решение
По заданным a → = a x , a y , a z и b → = b x , b y , b z вычислим скалярное произведение: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Длину b → найдем по формуле b → = b x 2 + b y 2 + b z 2 . Отсюда следует, что формула определения числовой проекции a → будет: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .
Подставляем числовые значения: n p L a → = n p b → a → = (- 2) · 3 + 3 · (- 2) + 1 · 6 3 2 + (- 2) 2 + 6 2 = — 6 49 = — 6 7 .
Ответ: — 6 7 .
Просмотрим связь между a → на L и длиной проекции a → на L . Начертим ось L , добавив a → и b → из точки на L , после чего проведем перпендикулярную прямую с конца a → на L и проведем проекцию на L . Существуют 5 вариаций изображения:
Первый случай при a → = n p b → a → → означает a → = n p b → a → → , отсюда следует n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → . = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
= 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
По условию угол острый, тогда числовая проекция a → = длине проекции вектора a → : n p L a → = n p L a → → = 9 . Данный случай показывает, что векторы n p L a → → и b → сонаправлены, значит имеется число t , при котором верно равенство: n p L a → → = t · b → . Отсюда видим, что n p L a → → = t · b → , значит можем найти значение параметра t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .
Тогда n p L a → → = 3 · b → с координатами проекции вектора a → на ось L равны b → = (- 2 , 1 , 2) , где необходимо умножить значения на 3. Имеем n p L a → → = (- 6 , 3 , 6) . Ответ: (- 6 , 3 , 6) .
Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b) или
Где a b — скалярное произведение векторов , |a| — модуль вектора a .
Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A»B» , начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A»B» , взятая со знаком + или — , в зависимости от того, имеет ли вектор A»B» то же направление, что и ось (вектор).
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).

- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.
AC» =AB» +B»C»
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|·cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Видео-вопрос: нахождение проекции вектора в направлении другого, представленного в квадрате
Стенограмма видео
Учитывая, что 𝐴𝐵𝐶𝐷 является квадратом имея длину стороны 53 сантиметра, вычислить алгебраическую проекцию 𝐂𝐀 в сторону 𝐁𝐂.
Ладно, скажем, для начала что это наш квадрат с отмеченными углами 𝐴, 𝐵, 𝐶 и 𝐷. Нам говорят, что длина каждого сторона квадрата 53 см. И мы хотим рассчитать алгебраическая проекция этого вектора 𝐂𝐀 в направлении другого вектора 𝐁𝐂.
Начнем с набросков в этих
два вектора. 𝐂𝐀 — это вектор, идущий от
точка 𝐶 к точке 𝐴. И тогда вектор 𝐁𝐂 начинается с
точка 𝐵 и заканчивается в точке 𝐶. Затем мы хотим выяснить,
проекция этого вектора на этот. Чтобы помочь нам в этом, давайте вспомним
что в общем случае, если мы проецируем вектор 𝐀 на другой вектор 𝐁, это называется
скалярная или алгебраическая проекция 𝐀 на 𝐁, то это равно скалярному произведению
этих векторов, разделенных на величину вектора, на который проецируется.
Нашим следующим шагом будет найдите компоненты этих двух векторов, определенных на нашем квадрате. Для этого укажем 𝐴, этот угол нашего квадрата представляет начало 𝑥𝑦-плоскости. Затем положительная ось 𝑥 перемещается горизонтально вправо от этой точки, а положительные точки оси 𝑦 вертикально вверх от него. С помощью этой структуры мы можем теперь определить координаты наших трех точек интереса 𝐴, 𝐵 и 𝐶. Точка 𝐴 находится в начале координат, поэтому ее координаты ноль, ноль. Точка 𝐵 находится на расстоянии одного длина стороны нашего квадрата вдоль оси 𝑥. Мы знаем, что это 53 сантиметра. И его 𝑦-координата равна нулю. И, наконец, точка 𝐶 имеет 𝑥- и 𝑦-координаты 53.
Теперь вектор 𝐂𝐀 равен
векторная форма координат точки 𝐴 за вычетом координат точки 𝐶. Ноль, ноль минус 53, 53 дает нам
окончательный результат отрицательного 53, отрицательного 53. Это 𝑥- и 𝑦-компоненты
вектора 𝐂𝐀. Аналогично для вектора 𝐁𝐂 это
равен векторной форме разности координат точки 𝐶
и точка 𝐵. Точка 𝐶 имеет координаты 53,
53. А точка 𝐵 имеет координаты 53,
нуль. Таким образом, мы получаем вектор с компонентами
ноль, 53. Это 𝑥- и 𝑦-компоненты
из 𝐁𝐂.
Это 𝑥- и 𝑦-компоненты
вектора 𝐂𝐀. Аналогично для вектора 𝐁𝐂 это
равен векторной форме разности координат точки 𝐶
и точка 𝐵. Точка 𝐶 имеет координаты 53,
53. А точка 𝐵 имеет координаты 53,
нуль. Таким образом, мы получаем вектор с компонентами
ноль, 53. Это 𝑥- и 𝑦-компоненты
из 𝐁𝐂.
Теперь мы готовы начать
вычисление этой проекции вектора 𝐂𝐀 в направлении 𝐁𝐂. Наше уравнение показывает нам, что это равно
скалярное произведение 𝐂𝐀 и 𝐁𝐂, деленное на величину 𝐁𝐂. Освобождение места для этого
вычисления, в нашем числителе мы вычислим этот скалярный продукт. И в нашем знаменателе мы помним
что величина вектора равна квадратному корню из суммы квадратов
из его компонентов. Наверху, умножая наши векторы
компонент за компонентом, мы получаем отрицательное число 53 в квадрате. А внизу у нас площадь
корень из 53 кв.
А внизу у нас площадь
корень из 53 кв.
Но тогда в нашем знаменателе это квадрат и корень квадратный компенсируют друг друга. И тогда оставшийся множитель 53 в знаменателе сокращается с одним множителем в числителе, так что после всех отмена все, что остается, это отрицательное 53. И это наш ответ. Это алгебраическая проекция 𝐂𝐀 в направлении 𝐁𝐂.
Векторы в двух- и трехмерных декартовых координатах
Во введении к векторам мы обсуждали векторы без привязки к какой-либо системе координат. Работая только с геометрическим определением величины и направления векторов, мы смогли определить такие операции, как сложение, вычитание, и умножение на скаляры. Мы также обсудили свойства этих операций.
Часто система координат оказывается полезной, потому что проще управлять координатами вектора, чем напрямую управлять его величиной и направлением.
Когда мы выражаем вектор в системе координат, мы идентифицируем вектор с помощью списка чисел, называемых координатами или компонентами, которые определяют геометрию вектора в терминах системы координат.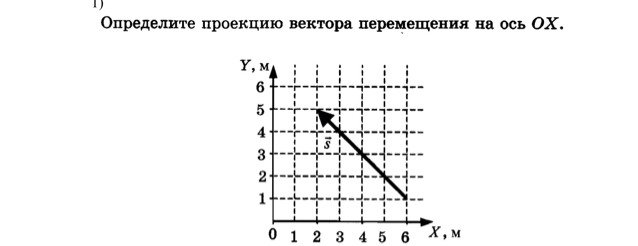 2$, чтобы обозначить, что его можно описать двумя действительными координатами. 92} = 5$.
2$, чтобы обозначить, что его можно описать двумя действительными координатами. 92} = 5$.
Приведенный ниже апплет, повторяющийся из введения вектора, позволяет вам исследовать взаимосвязь между компонентами вектора и его величиной.
Величина и направление вектора. Синяя стрелка обозначает вектор $\vc{a}$. Два определяющих свойства вектора, величина и направление, показаны красной полосой и зеленой стрелкой соответственно. Длина красной полосы — это величина $\|\vc{a}\|$ вектора $\vc{a}$. Зеленая стрелка всегда имеет длину единицу, но ее направление совпадает с направлением вектора $\vc{a}$. Единственным исключением является случай, когда $\vc{a}$ является нулевым вектором (единственным вектором с нулевой величиной), для которого направление не определено. Вы можете изменить любой конец $\vc{a}$, перетащив его мышью. Вы также можете переместить $\vc{a}$, перетащив середину вектора; однако изменение положения $\vc{a}$ таким образом не меняет вектор, так как его величина и направление остаются неизменными.
Дополнительная информация об апплете.
Векторные операции, которые мы определили во введении к векторам, легко выразить в терминах этих координат. Если $\vc{a}=(a_1,a_2)$ и $\vc{b}=(b_1,b_2)$, их сумма просто $\vc{a}+\vc{b}=(a_1+b_1,a_2+b_2)$, как показано на рисунке ниже. Также легко видеть, что $\vc{b}-\vc{a} = (b_1-a_1,b_2-a_2)$ и $\lambda \vc{a} = (\lambda a_1, \lambda a_2)$ для любого скаляра $\lambda$.
Приведенный ниже апплет, также повторяющийся из введения вектора, позволяет вам исследовать взаимосвязь между геометрическим определением сложения векторов и суммированием компонентов вектора.
Сумма двух векторов. Сумма $\vc{a}+\vc{b}$ вектора $\vc{a}$ (синяя стрелка) и вектора $\vc{b}$ (красная стрелка) показана зеленой стрелкой . Поскольку векторы не зависят от их начального положения, обе синие стрелки представляют один и тот же вектор $\vc{a}$, а обе красные стрелки представляют один и тот же вектор $\vc{b}$. Сумму $\vc{a}+\vc{b}$ можно составить, поместив хвост вектора $\vc{b}$ в начало вектора $\vc{a}$. То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.
То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.
Дополнительная информация об апплете.
Вы могли заметить, что мы используем одни и те же обозначения для обозначения точки и вектора. Мы не склонны подчеркивать какое-либо различие между точкой и вектором. Вы можете думать о точке как о представлении вектора, хвост которого зафиксирован в начале координат. Вам придется выяснить по контексту, думаем ли мы о векторе или нет. как с фиксированным хвостом в начале координат.
Другой способ обозначения векторов — стандартные единичные векторы
обозначаются $\vc{i}$ и $\vc{j}$. Единичный вектор — это вектор, длина которого равна единице.
Вектор $\vc{i}$ является единичным вектором в направлении положительной оси $x$. В координатах мы можем написать $\vc{i}=(1,0)$. Точно так же вектор $\vc{j}$ является единичным вектором в направлении положительной оси $y$: $\vc{j}=(0,1)$.
Мы можем записать любой двумерный вектор в терминах этих единичных векторов как
$\vc{a}=(a_1,a_2) = a_1\vc{i}+a_2\vc{j}$.
В координатах мы можем написать $\vc{i}=(1,0)$. Точно так же вектор $\vc{j}$ является единичным вектором в направлении положительной оси $y$: $\vc{j}=(0,1)$.
Мы можем записать любой двумерный вектор в терминах этих единичных векторов как
$\vc{a}=(a_1,a_2) = a_1\vc{i}+a_2\vc{j}$.
Векторы в трехмерном пространстве
В трехмерном пространстве существует стандартная декартова система координат $(x,y,z)$.
Начиная с точки, которую мы называем началом координат, построим три взаимно
перпендикулярные оси, которые мы называем осью $x$, осью $y$ и осью $z$.
Вот один из способов изобразить эти оси.
Встаньте в углу комнаты и посмотрите вниз, в точку, где стены соприкасаются с полом.
Затем пол и стена слева от вас пересекаются по линии, являющейся положительной осью $x$. Пол и стена справа от вас пересекаются по линии, являющейся положительной осью $y$. Стены пересекаются по вертикальной линии, являющейся положительной осью $z$.
Эти положительные оси изображены в приведенном ниже апплете и помечены как $x$, $y$ и $z$. Отрицательная часть каждой оси находится на противоположной стороне начала координат, где оси пересекаются.
Отрицательная часть каждой оси находится на противоположной стороне начала координат, где оси пересекаются.
Загрузка апплета
Трехмерные декартовы оси координат. Представление трех осей трехмерной декартовой системы координат. Положительная ось $x$, положительная ось $y$ и положительная ось $z$ — это стороны, помеченные $x$, $y$ и $z$. Начало — это пересечение всех осей. Ветвь каждой оси на противоположной стороне от начала координат (немаркированная сторона) является отрицательной частью. Вы можете перетащить фигуру с помощью мыши, чтобы повернуть ее.
Дополнительная информация об апплете.
Мы установили относительное расположение положительных осей $x$, $y$ и $z$ чтобы сделать систему координат правой системой координат . Обратите внимание, что если согнуть пальцы правой руки от положительной оси $x$ к положительной оси $y$, большой палец правой руки будет указывать в направлении положительной оси $z$.
Если вы поменяли местами положительную ось $x$ и положительную ось $y$,
тогда у вас будет левосторонняя система координат.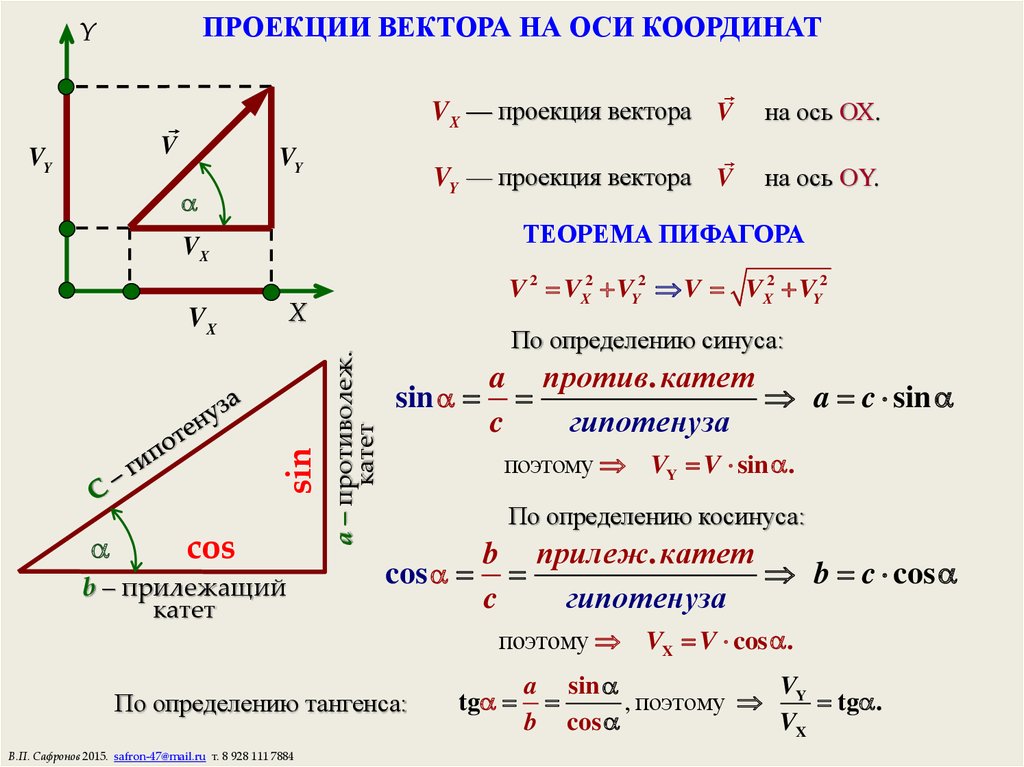 Если вы сделаете это, вы будете жить в математической вселенной, в которой некоторые формулы будут отличаться на знак минус от формулы во вселенной, которую мы здесь используем. Ваша вселенная будет такой же достоверной, как и наша, но будет много путаницы.
Мы предлагаем вам жить в нашей вселенной, изучая эти страницы.
Если вы сделаете это, вы будете жить в математической вселенной, в которой некоторые формулы будут отличаться на знак минус от формулы во вселенной, которую мы здесь используем. Ваша вселенная будет такой же достоверной, как и наша, но будет много путаницы.
Мы предлагаем вам жить в нашей вселенной, изучая эти страницы.
С помощью этих осей любой точке $\vc{p}$ в пространстве можно присвоить три координаты
$\vc{p}=(p_1,p_2,p_3)$. Например, учитывая приведенную выше аналогию с углом комнаты,
предположим, вы начинаете с угла комнаты и проходите четыре метра по оси $x$, затем поворачиваете налево и проходите три метра вглубь комнаты. Если ваш рост два метра, то ваша макушка находится в точке $(4,3,2)$. 93$ для обозначения того, что его можно описать тремя действительными координатами. Суммы, разности и скалярные умножения трехмерных векторов выполняются для каждого компонента. Если $\vc{a}=(a_1,a_2,a_3)$ и $\vc{b}=(b_1,b_2,b_3)$, то $\vc{a}+\vc{b}=(a_1+ b_1,a_2+b_2,a_3+b_3)$, $\vc{b}-\vc{a}=(b_1-a_1,b_2-a_2,b_3-a_3)$ и $\lambda\vc{a}= (\лямбда а_1, \лямбда а_2, \лямбда а_3)$.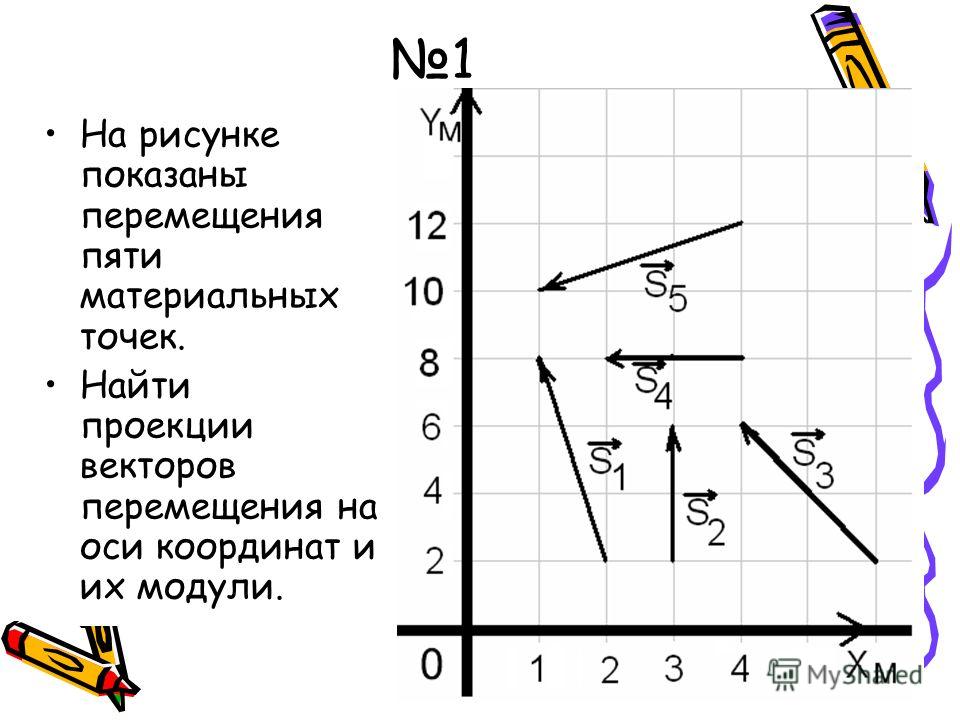
Загрузка апплета
Вектор в трехмерном пространстве. Представление вектора $\vc{a}=(a_1,a_2,a_3)$ в трехмерной декартовой системе координат. Вектор $\vc{a}$ изображается в виде зеленой стрелки с хвостом, закрепленным в начале координат. Вы можете перетащить мышкой кончик зеленой стрелки, чтобы изменить вектор. Чтобы показать трехмерную перспективу, розовый треугольник соединяет вектор с его проекцией $(a_1,a_2,0)$ на $xy$-плоскость (серая стрелка). Фиолетовые векторы показывают проекции $\vc{a}$ на каждую ось и представляют координаты $a_1$, $a_2$ и $a_3$. Вы также можете перетаскивать головки фиолетовых векторов, чтобы изменить только одну из координат вектора. Или перетащите вершину серого вектора в плоскости $xy$, чтобы изменить только координаты $x$ и $y$.
Дополнительная информация об апплете.
Так же, как и в двух измерениях, мы также можем обозначать трехмерные векторы is в терминах стандартных единичных векторов $\vc{i}$, $\vc{j}$ и $\vc{k}$.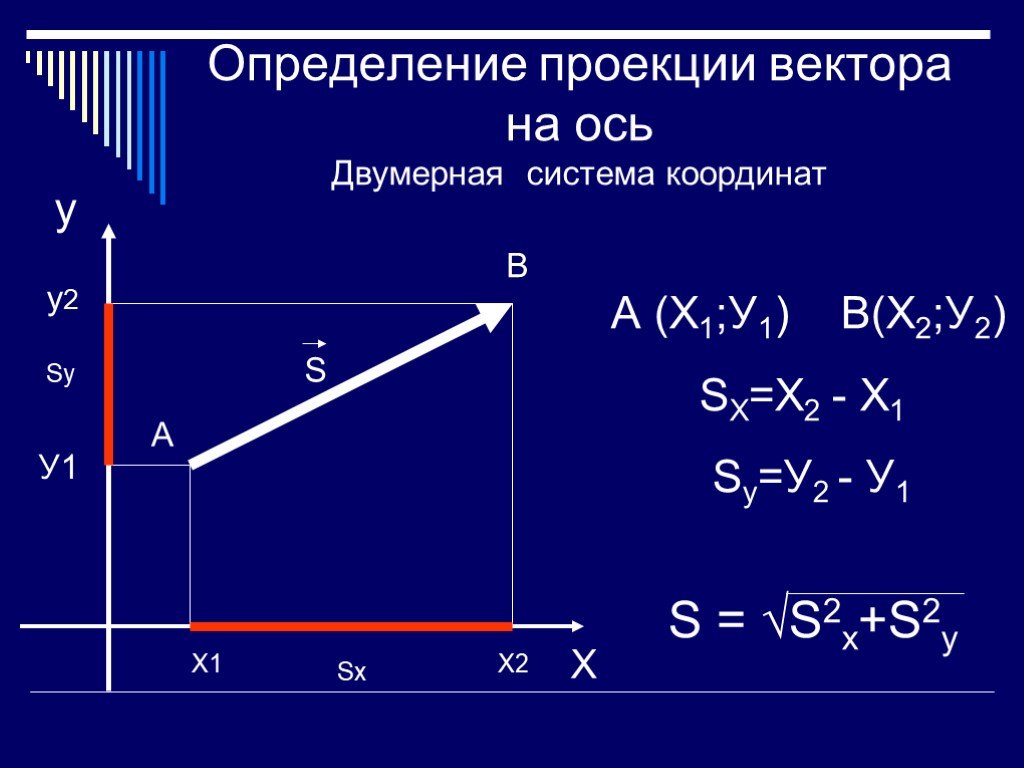 Эти векторы являются единичными векторами в положительных направлениях $x$, $y$ и $z$ соответственно. В терминах координат мы можем записать их как $\vc{i}=(1,0,0)$, $\vc{j}=(0,1,0)$ и $\vc{k}= (0,0,1)$.
Мы можем выразить любой трехмерный вектор как сумму скалярных кратных этих единичных векторов в форме
$\vc{a}=(a_1,a_2,a_3) = a_1\vc{i}+a_2\vc{j}+a_3\vc{k}$.
Эти векторы являются единичными векторами в положительных направлениях $x$, $y$ и $z$ соответственно. В терминах координат мы можем записать их как $\vc{i}=(1,0,0)$, $\vc{j}=(0,1,0)$ и $\vc{k}= (0,0,1)$.
Мы можем выразить любой трехмерный вектор как сумму скалярных кратных этих единичных векторов в форме
$\vc{a}=(a_1,a_2,a_3) = a_1\vc{i}+a_2\vc{j}+a_3\vc{k}$.
Загрузка апплета
Стандартные единичные векторы в трех измерениях. Стандартные единичные векторы в трех измерениях, $\vc{i}$ (зеленый), $\vc{j}$ (синий) и $\vc{k}$ (красный), являются векторами длины один, которые указывают параллельно ось $x$, ось $y$ и ось $z$ соответственно. Перемещение их с помощью мыши не меняет вектора, поскольку они всегда указывают в положительном направлении соответствующей оси.
Дополнительная информация об апплете.
Какова длина вектора $\vc{a}=(a_1,a_2,a_3)$? Мы можем разложить вектор на $(a_1,a_2,a_3) = (a_1,a_2,0)+(0,0,a_3)$, где два вектора
справа соответствуют двум зеленым сегментам линии
в вышеуказанном апплете.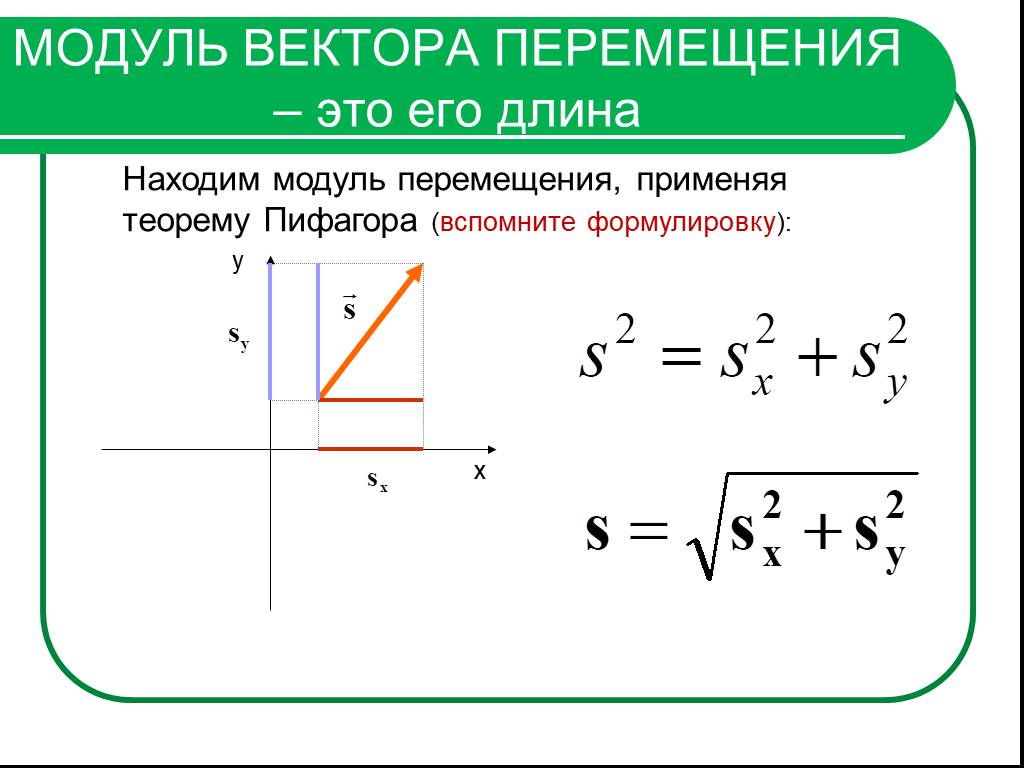



Leave A Comment