Как найти модуль скорости по графику: Как определить по графику модуль скорости тела

Как определить по графику модуль скорости тела

14.04.2020

Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.

Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.

Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости. Все точки камня движутся по окружностям. Во время опыта хорошо видно, что отрывающиеся раскаленные частички-опилки уходят по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек вращающегося точильного камня.

Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.

Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.

Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.

Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис.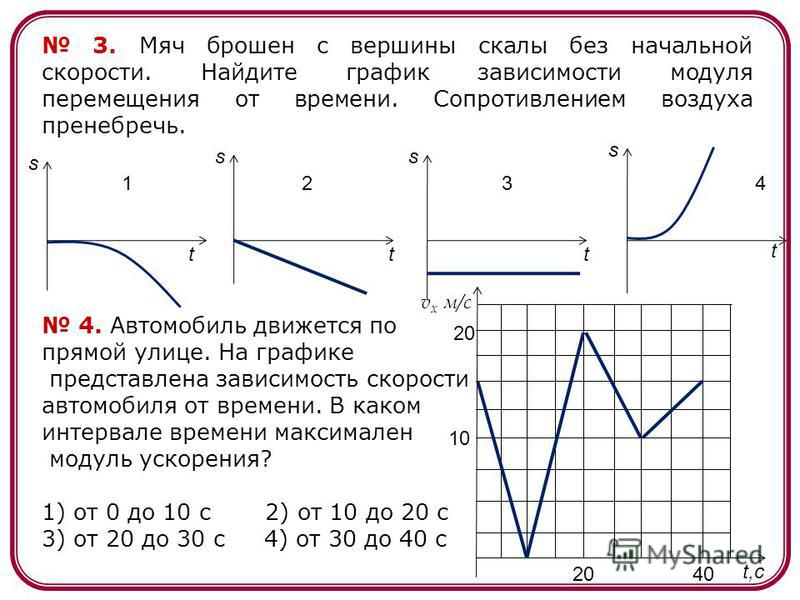 1.54. Возьмем приращение длины пути соответствующее малому вектору по которому определяется вектор скорости. Вспомним, что Знак указывает

направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.

Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения

Здесь является алгебраической величиной, знак которой указывает, в какую сторону по касательной к траектории направлен вектор скорости.

Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение определяет угол наклона а касательной на этом графике. Наклон касательной на графике закона движения будет тем больше, чем больше т. е. чем больше в выбранный момент скорость движения.

Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения.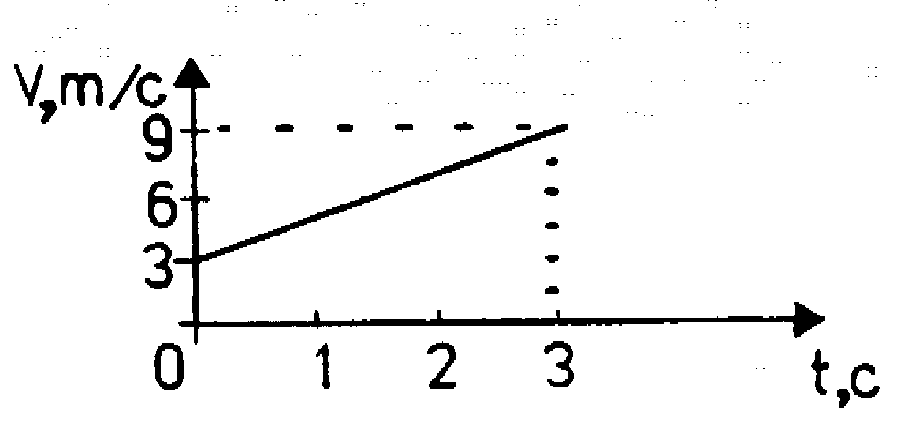

Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.

Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.

По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный телом за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). 2) / 2 т.е. S1= 0 + 0 + 2*1/2=1 ; S2= 0 + 2*1 + 0*1/2= 2 ;

S3 = S1 + S2=2+1=3; так же правильно ?

Правильно. Так тоже можно.

В общем, соглашусь, что здесь правильнее говорить, что этот способ не более длинный, а скорее менее вариативный. Подсчет по формула соответствует подсчету площади как суммы фигур,соответствующих определенному типу движения (здесь у вас получился один участок с ускорением и один участок равномерного движения). Площадь же можно считать и иначе, например, сразу рассмотреть эту фигуру как трапецию.

В любом случае, как делать, это личное дело каждого, я не навязываю свое мнение 🙂

А почему бы не сделать всё проще: в первую секунду авто проехало 1 метр (т.е. оно двигалось со скоростью 1 метр в секунду), а во вторую секунду 2 метра, т.к. двигалось со скоростью 2 метра в секунду. Итого — 3 метра

Утверждение «в первую секунду авто проехало 1 метр (т.е. оно двигалось со скоростью 1 метр в секунду)» не совсем верно, правильно тогда уж говорить так: «за первую секунду авто переместилось на такое расстояние, как если бы оно двигалось с постоянной скоростью в 1 м/с».

Однако такое утверждение в свою очередь требует разъяснений.

так путь же нужно найти почему нельзя воспользоваться формулой S=Vt

Эта формула подходит только для равномерного движения, а здесь это скорость тела изменяется

В задании не сказано, но тело двигалось прямолинейно

Решение и ответ задачи не зависят от того, двигалось ли тело прямолинейно или нет.

На рисунке представлен график зависимости модуля скорости автомобиля от времени. Определите по графику путь, пройденный автомобилем в интервале от момента времени 0 с до момента времени 5 с после начала отсчета времени. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале от момента времени 0 с до момента времени 5 с после начала движения автомобиль прошел путь

Другой способ решения заключается в анализе каждого участка графика в отдельности, определения из графика начальных скоростей и ускорений на каждом этапе и использования стандартных кинематических формул для пути.

Познакомимся подробнее с самым наглядным способом описания движения — графическим — на примере равномерного прямолинейного движения.

График модуля скорости

При равномерном прямолинейном движении скорость v_x = const. Следовательно, и ее модуль v = const, т. е. не изменяется с течением времени. Графиком зависимости модуля скорости от времени 1 является прямая АВ, параллельная оси времени и расположенная выше этой оси, так как v > О (рис. 1.9).

Площадь прямоугольника ОАВС, заштрихованного на рисунке, численно равна пути, пройденному телом за время t. Ведь сторона ОА в определенном масштабе есть модуль скорости v, а сторона ОС — время движения t, поэтому s = vt.

График скорости

В отличие от модуля скорости скорость, определяемая выражением (1.4.1), может быть положительной или отрицательной. Поэтому графиком зависимости скорости v_x от времени t может быть либо прямая ВС, либо прямая KF (рис. 1.10).

Обе прямые параллельны оси времени.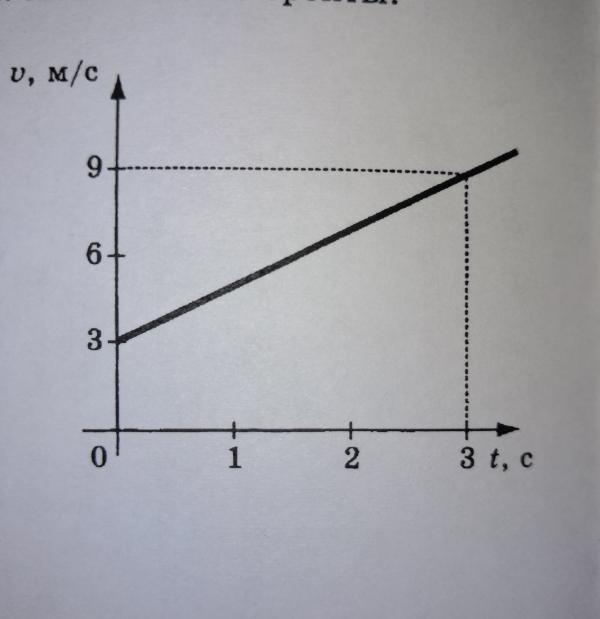

Прямая ВС соответствует положительному значению скорости (v_1x > 0), а прямая KF — отрицательному значению (v_2x О, то изменение координаты первого тела Аx₁ = v_1xt₁ положительно. Поэтому и площади прямоугольника OBCD приписывается положительный знак. Скорость движения второго тела отрицательна: v_2x 0; прямая 2 — случаю, когда х₀₂ 0; а прямая 3 — случаю, когда х₀₃ > 0, v_3x

Скорость тела равна v_x = = -0,5 м/с, а модуль скорости v = 0,5 м/с.

Обратите внимание на то, что по графику зависимости x(t) можно судить о «прошлом» в движении тела, т. е. можно находить положения тела до начала отсчета времени при условии, что и до этого момента тело двигалось равномерно и прямолинейно с той же скоростью. Моменты времени до начала отсчета считаются отрицательными. Согласно рисунку 1.13 за 3 с до начала отсчета времени тело имело координату 4,5 м.

Все графики равномерного прямолинейного движения представляют собой прямые линии.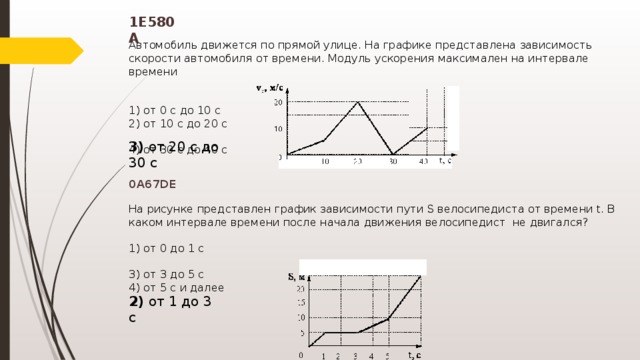 Для их построения достаточно указать значения x(t) или s(t) для двух моментов времени.

1 В дальнейшем для краткости мы будем часто говорить: «график модуля скорости», «график проекции скорости» и т. д.

Поделиться с друзьями:

Твитнуть

Поделиться

Поделиться

Отправить

Класснуть

Adblock
detector

Физические основы механики

Скорость — векторная величина, характеризующая не только быстроту передвижения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.

Средняя скорость за время от t₁ до t₂ равна отношению перемещения за это время к промежутку времени , за которое это перемещение имело место:

Тот факт, что это именно средняя скорость мы будем отмечать, заключая среднюю величину в угловые скобки: <…> , как это сделано выше.

Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения <f(x)> произвольной функции f(x) на промежутке [a,b]:

Действительно

Средняя скорость может оказаться слишком грубой характеристикой движения. Например, средняя скорость за период колебаний всегда равна нулю, в независимости от характера этих колебаний, по той простой причине, что за период — по определению периода — колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю. По этой и ряду других причин, вводится мгновенная скорость — скорость в данный момент времени. В дальнейшем, подразумевая мгновенную скорость, будем писать просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумениям.Для получения скорости в момент времени t надо сделать очевидную вещь: вычислить предел отношения при стремлении промежутка времени t₂ – t₁ к нулю. Сделаем переобозначения: t₁ = t и t₂ = t + и перепишем верхнее соотношение в виде:

Скорость в момент времени t равна пределу отношения перемещения за время к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю

Рис.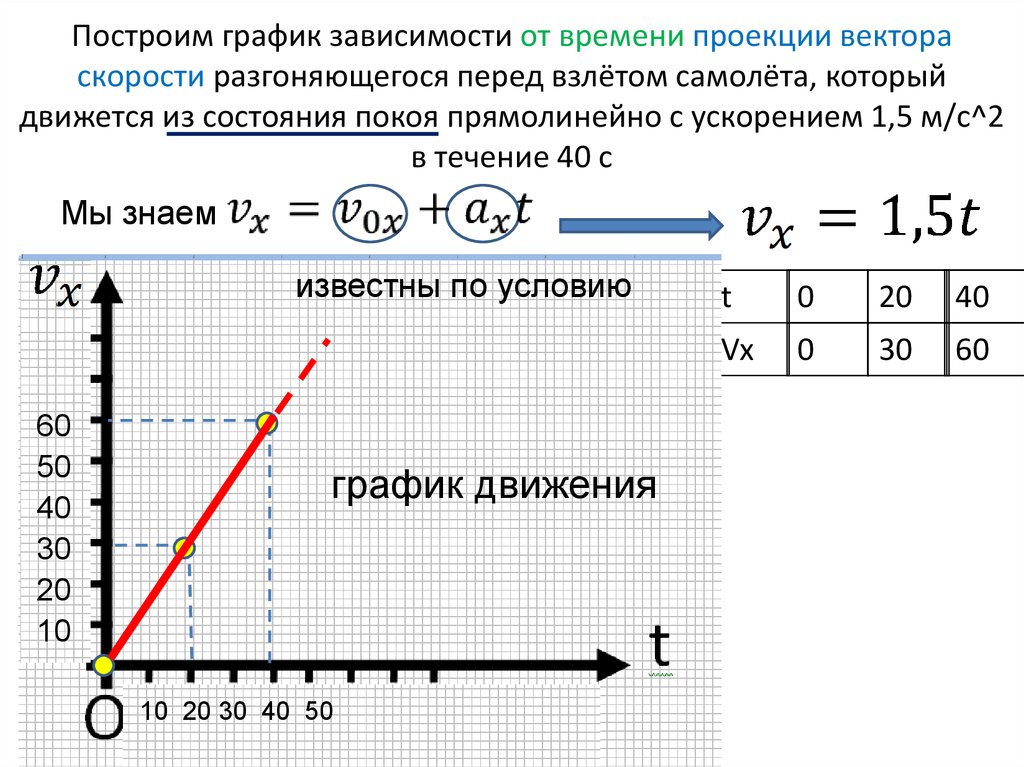 2.5. К определению мгновенной скорости.

В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметим, что если и есть конечное перемещение и конечный промежуток времени, то и — их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости

есть ничто иное как дробь — частное от деления на , поэтому последнее соотношение может быть переписано и весьма часто используется в виде

Здесь и далее мы часто для удобства будем использовать восходящее к Ньютону обозначение производной по времени в виде точки над соответствующей величиной:

По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке в её сторону движения.

Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.

Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей OX,OY,OZ используем обозначения , , или , соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки

Учитывая постоянство декартовых единичных векторов , , , продифференцируем это выражение по времени

С другой стороны, разложение по базису вектора скорости имеет вид

опоставление двух последних выражений, с учетом единственности разложения любого вектора по базису, дает следующий результат: проекции вектора скорости на декартовы оси равны производным по времени от соответствующих координат, то есть

Модуль вектора скорости равен

Получим ещё одно, важное, выражение для модуля вектора скорости.

Уже отмечалось, что при величина || все меньше и меньше отличается от соответствующего пути (см. рис. 2). Поэтому

и в пределе (>0)

Иными словами, модуль скорости — это производная пройденного пути по времени.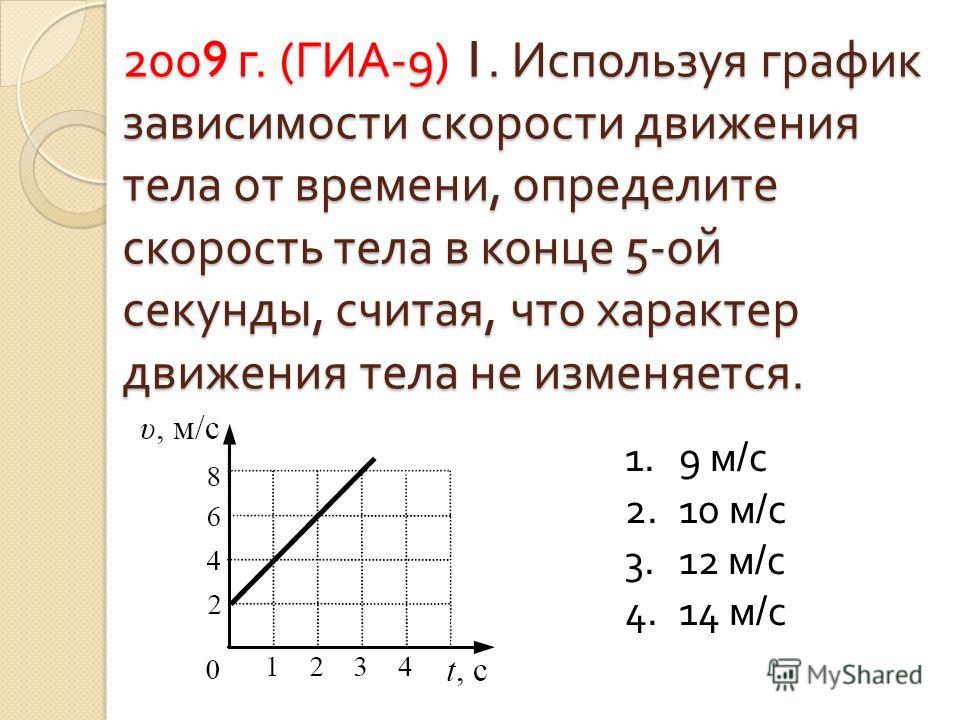

Окончательно имеем:

Средний модуль вектора скорости, определяется следующим образом:

Среднее значение модуля вектора скорости равно отношению пройденного пути ко времени, в течение которого этот путь был пройден:

Здесь s(t₁, t₂) — путь за время от t₁ до t₂ и, соответственно, s(t₀, t₂) — путь за время от t₀ до t₂ и s(t₀, t₂) — путь за время от t₀ до t₁.

Средний вектор скорости или просто средняя скорость, как указано выше, равен

Отметим, что прежде всего, это вектор, его модуль — модуль среднего вектора скорости не следует путать со средним значением модуля вектора скорости. В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.

Рассмотрим пример. Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени (за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени , в который мгновенная скорость равна средней путевой скорости за первые секунд движения точки.

Рис. 2.6. Определение мгновенной и средней скорости тела

Модуль скорости в данный момент времени

будучи производной пути по времени, равен угловому коэффициенту качательной к графику зависисмости точке соответствующей моменту времени t*. Средний модуль скорости за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории.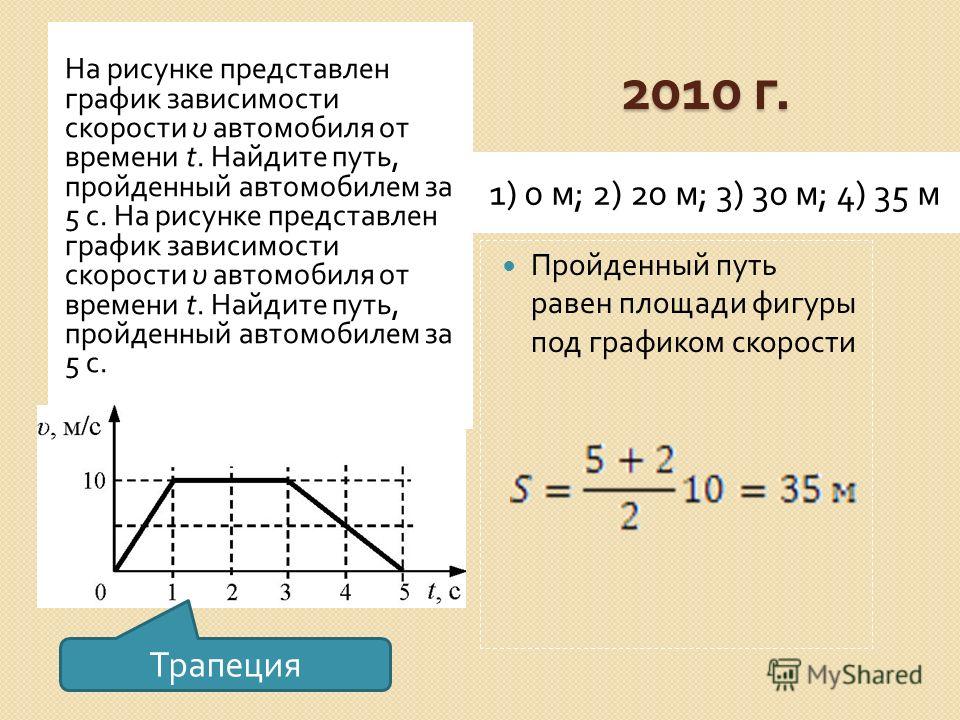 Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается

Определение площади (и смещения)

Как уже говорилось в предыдущей части этого урока, график зависимости скорости от времени можно использовать для определения ускорения объекта (наклона). В этой части урока мы узнаем, как можно использовать график зависимости скорости от времени для определения смещения объекта. Для графиков зависимости скорости от времени площадь, ограниченная линией и осями, представляет смещение. На приведенной ниже диаграмме показаны три различных графика зависимости скорости от времени. заштрихованные области между линией и осью времени представляют смещение в течение указанного интервала времени.

 

Заштрихованная область соответствует смещению за период от 0 до 6 секунд. Эта область принимает форму прямоугольника , и ее можно рассчитать с помощью соответствующего уравнения.
Заштрихованная область представляет смещение в течение от 0 секунд до 4 секунд. Эта площадь принимает форму треугольника , и ее можно рассчитать с помощью соответствующего уравнения.
Заштрихованная область соответствует смещению в течение от 2 до 5 секунд. Эта площадь принимает форму трапеции и может быть рассчитана с помощью соответствующего уравнения.

 

Метод, используемый для нахождения площади под линией на графике зависимости скорости от времени, зависит от того, является ли сечение, ограниченное линией и осями, прямоугольником, треугольником или трапецией. Формулы площади для каждой фигуры приведены ниже.

Прямоугольник	Треугольник	Трапеция
Площадь = b • h	Площадь = ½ • b • h	Площадь = ½ • b • (h 1 + h 2 )

 

 

Вычисление площади прямоугольника

Теперь мы рассмотрим несколько примеров вычисления площади для каждой из приведенных выше геометрических фигур.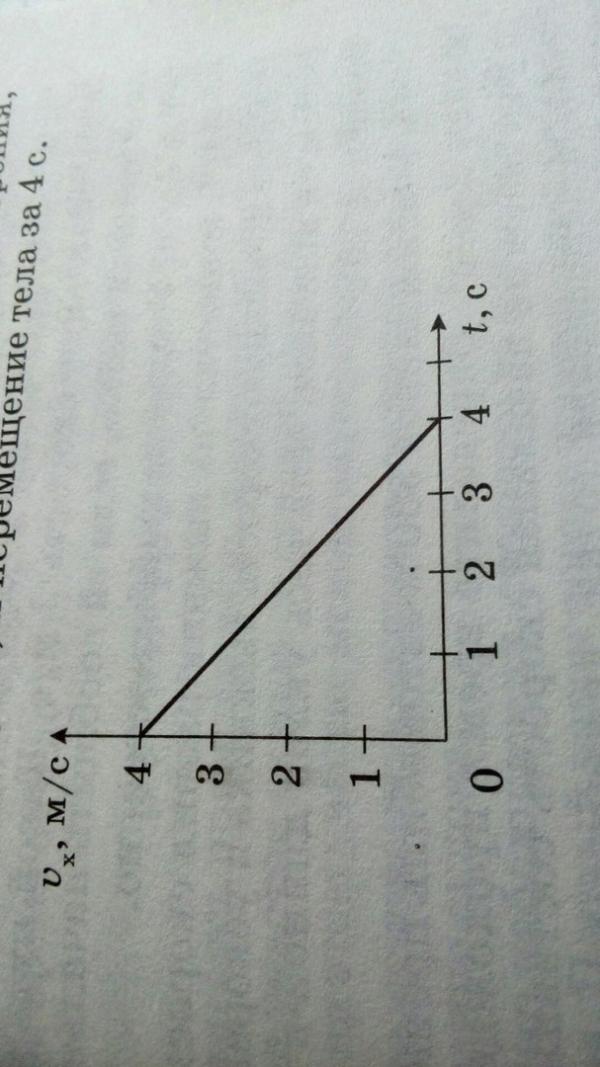 Сначала рассмотрим расчет площади для нескольких прямоугольников. Решение для нахождения площади показано для первого примера ниже. Заштрихованный прямоугольник на графике скорость-время имеет основание 6 с и высоту 30 м/с. Поскольку площадь прямоугольника находится по формуле A = b x h, площадь равна 180 м (6 с x 30 м/с). То есть за первые 6 секунд движения объект сместился на 180 метров.

Площадь = b * h Площадь = (6 с) * (30 м/с) Площадь = 180 м

Теперь попробуйте выполнить следующие две практические задачи для проверки своего понимания. Определите смещение (т. е. площадь) объекта в течение первых 4 секунд (практика А) и от 3 до 6 секунд (практика Б).

 

Вычисление площади треугольника

Теперь мы рассмотрим несколько примеров вычисления площади для нескольких треугольников. Решение для нахождения площади показано для первого примера ниже. Заштрихованный треугольник на графике скорость-время имеет основание 4 секунды и высоту 40 м/с. Поскольку площадь треугольника находится по формуле A = ½ * b * h, площадь равна ½ * (4 с) * (40 м/с) = 80 м. То есть за четыре секунды движения объект сместился на 80 метров.

Площадь = ½ * b * h Площадь = ½ * (4 с) * (40 м/с) Площадь = 80 м

Теперь попробуйте выполнить следующие две практические задачи для проверки своего понимания. Определите перемещение объекта в течение первой секунды (упражнение А) и в течение первых 3 секунд (упражнение Б).

 

Вычисление площади трапеции

Наконец, мы рассмотрим несколько примеров вычисления площади для нескольких трапеций. Решение для нахождения площади показано для первого примера ниже. Заштрихованная трапеция на графике скорость-время имеет основание в 2 секунды и высоты 10 м/с (слева) и 30 м/с (справа).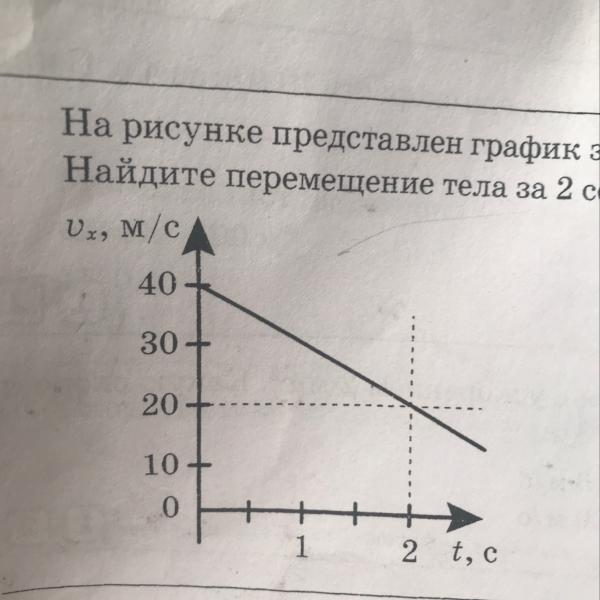 Так как площадь трапеции находится по формуле A = ½ * (b) * (h ₁ + h ₂ ), площадь 40 м [½ * (2 с) * (10 м/с + 30 м/с)]. То есть объект сместился на 40 метров за промежуток времени от 1 секунды до 3 секунд.

Площадь = ½ * b * (h 1 + h 2 ) Площадь = ½ * (2 с) * (10 м/с + 30 м/с) Площадь = 40 м

Теперь попробуйте решить следующие две практические задачи, чтобы проверить свое понимание. Определить перемещение объекта в течение интервала времени от 2 до 3 секунд (Занятие А) и в течение первых 2 секунд (Занятие Б).

 

Альтернативный метод для трапеций

Альтернативный способ определения площади трапеции включает разбиение трапеции на треугольник и прямоугольник. Площади треугольника и прямоугольника можно вычислить по отдельности; тогда площадь трапеции равна сумме площадей треугольника и прямоугольника. Этот метод проиллюстрирован на рисунке ниже.

Треугольник: Площадь = ½ * (2 с) * (20 м/с) = 20 м

Прямоугольник: Площадь = (2 с) * (10 м/с) = 20 м

Общая площадь = 20м + 20м = 40м период. Площадь может быть идентифицирована как прямоугольник, треугольник или трапеция. Площадь можно впоследствии определить по соответствующей формуле. После расчета эта площадь представляет собой смещение объекта.

Расследуй!

Виджет ниже вычисляет площадь между линией на графике скорость-время и осями графика. Эта площадь является смещением объекта. Используйте виджет, чтобы изучить или просто попрактиковаться в решении нескольких самодельных задач.

Мы хотели бы предложить …

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom.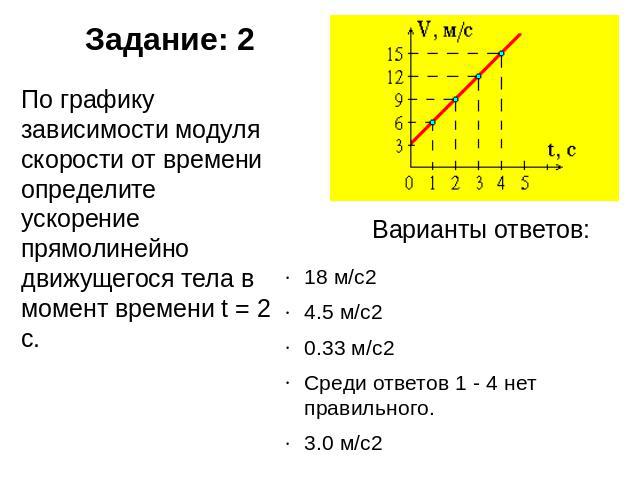 Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактива Two Stage Rocket Interactive. Этот интерактив находится в разделе «Физические интерактивы» на нашем веб-сайте и позволяет учащимся применить навыки расчета площадей и связывания их со значениями смещения для двухступенчатой ​​ракеты.

Посетите: Two Stage Rocket Interactive

 

Перейти к следующему уроку:

2.5: Скорость и ускорение — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

594

В исчислении с одной переменной скорость определяется как производная функции положения. Для векторного исчисления мы делаем такое же определение.

Определение: Скорость

Пусть \(r(t)\) — дифференцируемая векторнозначная функция, представляющая вектор положения частицы в момент времени \(t\). Тогда вектор скорости является производной вектора положения.

\[\textbf{v}(t) = \textbf{r}'(t) = x'(t) \hat{\textbf{i}}+ y'(t) \hat{\textbf{j }} + z'(t) \hat{\textbf{k}} . \] 92 \ шляпа {\ textbf {j}} + \ sin (t) \ шляпа {\ textbf {k}} . \]

Решение

Возьмем производную

\[\textbf{v} (t) = 3 \hat{\textbf{i}} + 4t \hat{\textbf{j}} + \ cos (t) \шляпа{\textbf{k}} . \]

Когда мы думаем о скорости, мы думаем о том, как быстро мы движемся. Скорость не должна быть отрицательной. В одном исчислении переменных скорость была абсолютным значением скорости. Для векторного исчисления это величина скорости.

Определение: Скорость

Пусть \(\textbf{r}(t)\) — дифференцируемая векторнозначная функция, представляющая положение частицы. Тогда скорость частицы есть величина вектора скорости.

\[\text{Скорость}= ||\textbf{v}(t) || = || \textbf{r}'(t) ||. \]

Пример \(\PageIndex{2}\)

Пусть

\[ \textbf{r} (t) = 3 \hat{\textbf{i}}+ 2 \hat{\textbf{j}} + \ cos t \hat{\textbf{k}} .\]

Найдите скорость через \(\frac{p}{4}\) секунд.

92}= \sqrt{4.5}. \]

Ускорение

В одном исчислении переменных мы определили ускорение частицы как вторую производную функции положения. Для векторного исчисления ничего не меняется.

Определение: вектор ускорения

Пусть \(\textbf{r}(t)\) — дважды дифференцируемая векторная функция, представляющая вектор положения частицы в момент времени \(t\). Тогда вектор ускорения является второй производной вектора положения.

92+t+1) \hat{\textbf{j}} \]

, когда \(t = -1\). Затем нарисуйте векторы.

Решение

Вектор скорости равен

\[\textbf{v}(t)= \textbf{r}'(t) = 2 \hat{\textbf{i}} + (2t+1) \шляпа{\textbf{j}} . \]

Подстановка -1 вместо \(t\) дает

\[\textbf{b}(-1)= 2 \hat{\textbf{i}} — \hat{\textbf{j}} . \]

Возьмите другую производную, чтобы найти ускорение.

\[\textbf{a}(t) = \textbf{v}'(t) = 2 \hat{\textbf{j}} . \]

Ниже приведено изображение векторов.

Движение снаряда

Поскольку векторы скорости и ускорения определяются как первая и вторая производные вектора положения, мы можем вернуться к вектору положения путем интегрирования.

Пример \(\PageIndex{4}\)

Вы оператор противоракетной обороны и заметили летящую к вам ракету в точке

\[\textbf{r}_e = 1000 \hat{\textbf{ i}} + 500 \шляпа{\textbf{j}} \]

со скоростью

\[ \textbf{v}_e = -30 \hat{\textbf{i}} + 3 \hat{\textbf{j}} . \]

Вы можете стрелять противоракетами со скоростью 100 метров в секунду. Под каким углом нужно стрелять, чтобы перехватить ракету. Предположим, что гравитация является единственной силой, действующей на снаряды.

Решение

Вектор ускорения ракеты противника равен

\[ \textbf{a}_e (t)= -9,8 \hat{\textbf{j}}. \]

Интегрируя, получаем вектор скорости 92+3t+500) \шляпа{\textbf{j}}. \]

Ускорение вашей противоракеты тоже

\[\textbf{a}_y(t) = -9,8 t \hat{\textbf{j}} . \]

Интегрируя, получаем вектор скорости

\[\textbf{v}_y(t) = v_1 \hat{\textbf{i}} + (v_2-9.8t) \hat{\textbf{j} }. \]

Поскольку величина нашей скорости равна 100, мы можем сказать

\[\textbf{v}_y(0) = 100 \cos q \hat{\textbf{i}} + 100 \sin q \hat {\textbf{j}} . \]

Таким образом,

\[\textbf{v}_y(t) = 100 \cos q \hat{\textbf{i}} + (100 \sin q -92 + 3t + 500 .\]

Первое уравнение дает

\[ t= \dfrac{1000}{100\cos q + 30}. \]

Упрощение второго уравнения и подстановка дает

\[ \dfrac{100000 \sin q }{100\cos q + 30} = \dfrac{3000}{ 100\cos q + 30 } + 500.