Что такое частное чисел? Ответ на webmath.ru
Определение
Частное чисел — это результат деления одного числа на другое. Таким образом, частное чисел $a$ и $b$ будет число $c$, которое равно $c = a : b$ . При этом число $a$ будет делимым, а число $b$ — делителем.
Пример
Задание. Найти частное чисел:
1) $39 : 3$ ; 4) $124 : 4$
Ответ. $39 : 3 = 13$
$124 : 4 = 31$
Для нахождения частного больших чисел или десятичных дробей используют способ деления в столбик.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти частное чисел:
1) $564 : 12$ ; 2) $0,567 : 0,21$
Решение. Для нахождения частного в первом примере выполним деление в столбик.
Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком. Возьмем по $4 : 4 \cdot 12 = 48$ . Записываем 48 под 56 и находим остаток: $56 — 48 = 8$ . Восьмерку записываем под чертой и сносим к ней следующее число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.
Таким образом, $564 : 12 = 47$
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число. Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее запишем полученные числа в столбик, как и в первом примере:
Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем $56 : 21$ , можно взять по 2. Двойку записываем в частное.
И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем $2 \cdot 21 = 42$ , записываем 42 под 56 и вычитаем:
$56 — 42 = 14$ . Остаток 14 списываем к нему следующую
незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное,
и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.
Умножаем $2 \cdot 21 = 42$ , записываем 42 под 56 и вычитаем:
$56 — 42 = 14$ . Остаток 14 списываем к нему следующую
незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное,
и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.
Таким образом $0,567 : 0,21 = 2,7$
Ответ. $564 : 12 = 47$
$0,567 : 0,21 = 2,7$
Десятичные дроби Деления чисел столбиком онлайн
Частное рациональных дробей находится по правилу
$$\frac{m}{n}: \frac{p}{q}=\frac{m \cdot q}{n \cdot p}$$
Пример
Задание. Найти частное рациональных дробей:
1) $\frac{2}{3}: \frac{1}{3}$ ; 2) $1 \frac{1}{14}: 1 \frac{3}{7}$
Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:
$$\frac{2}{3}: \frac{1}{3}=\frac{2 \cdot 3}{3 \cdot 1}=2$$
Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей.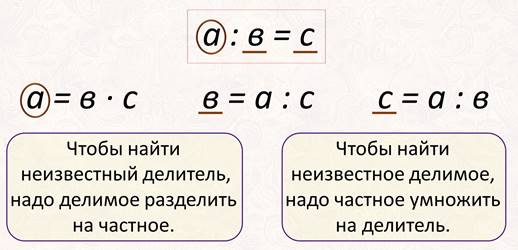 Для этого целую часть
умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:
Для этого целую часть
умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:
$$1 \frac{1}{14}: 1 \frac{3}{7}=\frac{1 \cdot 14+1}{14}: \frac{1 \cdot 7+3}{7}=\frac{15}{14}: \frac{10}{7}=$$ $$=\frac{15 \cdot 7}{14 \cdot 10}=\frac{15}{2 \cdot 10}=\frac{15}{20}=\frac{3}{4}$$
Ответ.
$1 \frac{1}{14}: 1 \frac{3}{7}=\frac{3}{4}$
Больше примеров решений Операции с дробями онлайн
Читать дальше: что такое иррациональное число.
ЧАСТНОЕ (функция ЧАСТНОЕ) — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЧАСТНОЕ в Microsoft Excel.
Совет:
Описание
Возвращает целую часть результата деления с остатком. Эта функция используется, когда нужно отбросить остаток от деления.
Синтаксис
ЧАСТНОЕ(числитель;знаменатель)
Аргументы функции ЧАСТНОЕ указаны ниже.
Замечание
Пример
Скопируйте пример данных из следующей таблицы и вставьте его в ячейку A1 нового листа Excel. Для переключения между формулами и их результатами нажмите клавишу F2. При необходимости измените ширину столбцов, чтобы видеть все данные.
Для переключения между формулами и их результатами нажмите клавишу F2. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|---|---|---|
|
=ЧАСТНОЕ(5; 2) |
Целая часть результата деления 5/2 |
2 |
|
|
Целая часть результата деления 4,5/3,1 |
1 |
|
=ЧАСТНОЕ(-10;3) |
Целая часть результата деления -10/3 |
-3 |
См.
 также
также
ПРОИЗВЕД
Расчет процентов
Краткое руководство: форматирование чисел на листе
Калькулятор коэффициентов
Задачи на деление спрашивают, сколько копий чего-то может быть, если мы распределим числа поровну . Например, предположим, что вы купили большую пиццу из 8 кусочков для семьи из 4 . Чтобы вычислить, сколько ломтиков получает каждый человек, мы используем деление:
8 / 4 = 2 .
Но что, если бы вместо них было 3 человек? Очевидно, что у каждого по-прежнему может быть два ломтика, но  И вот где частное и остаток пригодятся.
И вот где частное и остаток пригодятся.
Как сказано в предыдущем разделе, результат деления называется частным . Однако не все числа делятся друг на друга (например, 4 разделить на 3 или 25 разделить на 2 ). В таких случаях мы можем распределить столько, сколько возможно, пока не оставим последние неделимые части: это остаток.
В приведенном выше примере с пиццей 3 людям, дает 2 ломтиков каждому по с остатком 2 . Другими примерами могут быть, скажем, 4 , разделенные на 3 , что дает 1 с остатком 1 , или 25 , разделенное на 2 , что дает 6 5 0 0 90 090 с остатком 0,0. Символически мы записываем результат такого деления в математике как s , отделяя частное и остаток заглавной 9. 0004
0004 R (см. ниже).
8 / 3 = 2 R 24 / 3 = 1 Р 125 / 2 = 12 Р 1
Мы также можем использовать это обозначение, когда делимое в математических задачах меньше делителя:
2 / 3 = 0 R 217 / 20 = 0 Р 17
Или когда числа делятся друг на друга, например 12 разделить на 4 :
-
12 / 4 = 3 R 0
Однако нам нужно быть осторожными с остатками при работе с отрицательными числами. Как правило, мы определяем остаток в математике как положительное число на меньше абсолютного значения делителя. Тем не менее, некоторые приложения (особенно информатика) допускают отрицательные остатки. Чтобы удовлетворить обе стороны, калькулятор целочисленного деления Omni предлагает обе возможности , поэтому, если вы используете калькулятор, чтобы найти частное, скажем, -4 разделить на 3 или 25 разделить на -2 , вы получите два результата:
(-4 ) / 3 = -1 R (-1) = -2 R 2
25 / (-2) = -13 R (-1)= -12 R 1
Наконец, отметим, что иногда нам нужно для решения задач деления без упоминания остальных . Если вспомнить пример с пиццей
Если вспомнить пример с пиццей 8 -ломтиков на 3 человек, это будет означать разрезание 2 оставшихся ломтиков на более мелкие части , чтобы закончить. С математической точки зрения это означает, что представляет собой дробное частное .
8 / 3 = 2⅔ ≈ 2,666 .
По сути, каждый получает два полных куска пиццы и еще две трети куска. Здесь нет остатков. При необходимости обязательно проверьте конвертер дроби в десятичную.
Как видите, вы можете использовать наш калькулятор, чтобы найти частное, в зависимости от того, какая форма вам нужна . Неплохой инструмент, не так ли? Итак, давайте закончим несколькими четкими инструкциями о том, как с ним работать.
Коэффициент — Значение, что такое коэффициент?
Частное — это ответ, который получается при делении одного числа на другое. Например, если мы разделим число 6 на 3, мы получим результат как 2, то есть частное. Частное может быть целым или десятичным числом. Для точных делений, таких как 10 ÷ 5 = 2, у нас есть целое число в качестве частного, а для таких делений, как 12 ÷ 5 = 2,4, частное представляет собой десятичную дробь. Частное может быть больше делителя, но всегда меньше делимого. Давайте изучим и узнаем больше о частном и методах его нахождения.
Частное может быть целым или десятичным числом. Для точных делений, таких как 10 ÷ 5 = 2, у нас есть целое число в качестве частного, а для таких делений, как 12 ÷ 5 = 2,4, частное представляет собой десятичную дробь. Частное может быть больше делителя, но всегда меньше делимого. Давайте изучим и узнаем больше о частном и методах его нахождения.
| 1. | Что такое частное в делении? |
| 2. | Определение коэффициента |
| 3. | Как найти частное? |
| 4. | Делитель дивидендов |
| 5. | Частное и остаток |
| 6. | Часто задаваемые вопросы о коэффициенте |
Что такое частное в делении?
Частное — это окончательный ответ, который мы получаем при делении числа. Деление — это метод равномерного распределения предметов по группам, обозначаемый математическим символом (÷). Например, есть 15 шариков, которые нужно разделить поровну на 3 группы. Итак, когда мы делим эти шары на 3 равные группы, утверждение о делении может быть выражено как 15 ÷ 3 = 5. Здесь 5 — это частное. Это значит, что в каждой группе будет по 5 мячей.
Например, есть 15 шариков, которые нужно разделить поровну на 3 группы. Итак, когда мы делим эти шары на 3 равные группы, утверждение о делении может быть выражено как 15 ÷ 3 = 5. Здесь 5 — это частное. Это значит, что в каждой группе будет по 5 мячей.
Определение коэффициента
Частное в математике может быть определено как результат деления числа на любой делитель. Это количество раз, когда делитель содержится в делимом. На следующем рисунке показано выражение деления, которое отмечает делитель, делимое и частное. Делитель 2 содержится 6 раз в делимом 12. Частное может быть больше или меньше делителя, но всегда меньше делимого.
Как найти частное?
Частное получается после завершения процесса деления. Это означает, что когда делитель делит делимое, ответ, который мы получаем, является частным. Деление — одна из четырех основных математических операций, остальные три — сложение, вычитание и умножение. Частное является результатом процесса деления.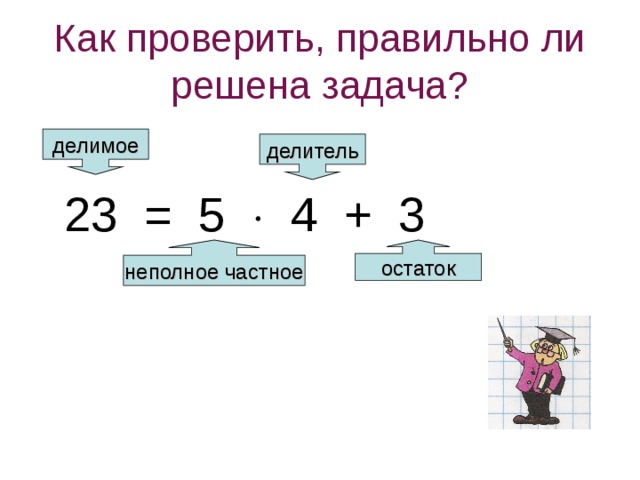 После того, как мы полностью разделим число, мы получим частное. В некоторых случаях, когда мы делим число, оно не делится полностью, и мы получаем остаток. Однако даже в этом случае в качестве ответа остается частное, а остаток мы упоминаем отдельно.
После того, как мы полностью разделим число, мы получим частное. В некоторых случаях, когда мы делим число, оно не делится полностью, и мы получаем остаток. Однако даже в этом случае в качестве ответа остается частное, а остаток мы упоминаем отдельно.
Когда мы делим число, помимо частного в процессе деления используются и другие термины. Давайте разберемся в этом с помощью примера. Например, есть плитка шоколада на 12 штук. Можно ли разделить бар поровну между двумя друзьями? Ответ: да, если плитку шоколада разделить поровну между двумя друзьями, каждый из них получит по 6 кусочков шоколада. Вы замечали, что ни один кусочек шоколада не остается нераспределенным. Следовательно, остатка нет. Мы можем записать оператор деления для этого примера как 12 ÷ 2 = 6. Здесь каждое из чисел в делении может быть обозначено специальными терминами. Проверим следующие члены, тесно связанные с частным.
| Условия | Описания | Значения |
|---|---|---|
| Дивиденд | Общее количество частей, которые должны быть разделены. | 12 |
| Делитель | Количество равных групп, которые необходимо создать. | 2 |
| Частное | Количество штук в каждой группе. | 6 |
| Остаток | Оставшаяся часть, не входящая ни в одну группу. | 0 |
Этот пример также может быть математически представлен следующим образом:
Частное и остаток
Когда мы делим число и если оно не делится полностью, у нас остается остаток. Давайте разберемся в этом с помощью примера. Частное можно вычислить, разделив делимое на делитель. Частное = Дивиденд ÷ Делитель. Решим 435 ÷ 4. Здесь 435 — делимое, а 4 — делитель.
Следующие шаги помогут понять процесс деления и найти частное и остаток.
- Шаг 1: Возьмите первую цифру делимого. Если эта цифра больше или равна делителю, то разделите ее на делитель и сверху запишите ответ как часть частного.
 Умножьте это число на делитель и запишите произведение под первой цифрой делимого. Вычтите результат из цифры и запишите его под этим числом. Здесь первая цифра 4 и она равна делителю. Итак, 4 ÷ 4 = 1 написано сверху на черте. Произведение 4 × 1 = 4 вычитается из цифры и ниже записывается 0. Теперь сократите следующее число делимого, равное 3, и поместите его рядом с 0,9.0074
Умножьте это число на делитель и запишите произведение под первой цифрой делимого. Вычтите результат из цифры и запишите его под этим числом. Здесь первая цифра 4 и она равна делителю. Итак, 4 ÷ 4 = 1 написано сверху на черте. Произведение 4 × 1 = 4 вычитается из цифры и ниже записывается 0. Теперь сократите следующее число делимого, равное 3, и поместите его рядом с 0,9.0074 - Шаг 2: Мы видим, что у нас есть 3 в результате шага 1. Повторите тот же шаг, чтобы проверить, больше или меньше это число, чем делитель. Поскольку 3 меньше 4, мы не можем разделить это число. Следовательно, мы записываем 0 сверху и записываем произведение 4 × 0 = 0 под цифрой 3, затем вычитаем 3 — 0 = 3. Следующим шагом является уменьшение следующего числа из делимого и размещение его рядом с 3. Получается 35. Поскольку 35 > 4, мы можем разделить это число на 4. После записи 8 сверху мы записываем произведение 4 × 8 = 32 под 35, как показано на рисунке. Вычтите 35 — 32 = 3. Теперь эта 3 меньше, чем делитель 4, и из делимого не осталось числа, которое можно было бы уменьшить.
 Это означает, что мы оставим 3 в качестве остатка и завершим деление. Таким образом, 3 известен как 9Остаток 0003 и 108 называется частным .
Это означает, что мы оставим 3 в качестве остатка и завершим деление. Таким образом, 3 известен как 9Остаток 0003 и 108 называется частным .
Проверка результата деления
Мы легко можем проверить, верен ли ответ, который мы получили при делении в большую сторону. Поскольку процесс деления является обратным умножению, давайте выясним, как мы можем проверить наш ответ, используя эту информацию. Мы используем формулу: Дивиденд = (Делитель × Частное) + Остаток. Это означает, что если мы умножим делитель на частное и добавим остаток, мы должны получить число как делимое. Если числа удовлетворяют этому уравнению, то ответ считается правильным, в противном случае нужно проверить наше деление. Давайте еще раз рассмотрим рассмотренный выше пример. Здесь делимое равно 435, делитель равен 4, частное равно 108, а остаток равен 3. Подставляя значение в формулу, получаем 435 = (4 × 108) + 3. Это доказывает, что ответ правильный. Возьмем другой пример. Если мы разделим 6 ÷ 2 = 3, мы получим остаток как 0. Теперь давайте подставим эти значения в формулу, 6 = (2 × 3) + 0. Это означает, что ответ правильный.
Возьмем другой пример. Если мы разделим 6 ÷ 2 = 3, мы получим остаток как 0. Теперь давайте подставим эти значения в формулу, 6 = (2 × 3) + 0. Это означает, что ответ правильный.
Оценка частного
Оценка частного означает нахождение частного после округления делителя и делимого. Идея состоит в том, чтобы преобразовать заданные числа в такие числа, которые легко вычислить. Давайте разберемся в этом на примере, используя следующие шаги. Разделим 64 ÷ 22
- Шаг 1: Нам нужно разделить 64 ÷ 22. Здесь 64 — это делимое, а делитель равен 22, и нам нужно вычислить частное.
- Шаг 2: Сначала нам нужно округлить делимое 64 до ближайших десятков, потому что последнее разрядное значение здесь равно десяткам. После проверки цифры, стоящей на единицах, она будет округлена до 60, поскольку цифра на единицах (то есть 4) меньше 5. Точно так же делитель также будет округлен до ближайших десятков, потому что в 22 последняя разрядное значение — десятки.
 Поэтому нам нужно проверить цифру в единицах (то есть 2), которая меньше 5. Следовательно, 22 будет округлено до 20.
Поэтому нам нужно проверить цифру в единицах (то есть 2), которая меньше 5. Следовательно, 22 будет округлено до 20. - Шаг 3: Теперь мы округли данные числа, и получилось 60 ÷ 20. Мы можем просто разделить это число, и мы получим 3 как расчетное частное.
- Шаг 4: Другой метод оценки частного заключается в удалении наименьшего количества нулей в расчетном (округленном) делителе и предполагаемом (округленном) делимом. Итак, в этом случае, после исключения наименьшего количества нулей, 60 ÷ 20 становится 6 ÷ 2, и мы получаем частное как 3. Таким образом, мы получили одинаковое оценочное частное обоими методами.
Пример: Определить частное 825 от деления на 24.
Решение: В заданном вопросе нужно разделить 825 ÷ 24.
- Шаг 1: дивиденд. Поскольку в 825 последнее разрядное значение равно сотням, нам нужно округлить его до ближайших сотен. Для этого нам нужно проверить цифру на разряде десятков.
 Здесь это 2, что меньше 5. Таким образом, 825 будет округлено до 800. Точно так же, поскольку в 24 последнее разрядное значение равно десяткам, нам нужно округлить его до ближайших десятков. Для этого нам нужно проверить цифру на единицу. Здесь это 4, что меньше 5. Таким образом, 24 будет округлено до 20.
Здесь это 2, что меньше 5. Таким образом, 825 будет округлено до 800. Точно так же, поскольку в 24 последнее разрядное значение равно десяткам, нам нужно округлить его до ближайших десятков. Для этого нам нужно проверить цифру на единицу. Здесь это 4, что меньше 5. Таким образом, 24 будет округлено до 20. - Шаг 2: Теперь нам нужно разделить 800 ÷ 20, что можно просто разделить, и мы получим расчетное частное как 40.
☛ Статьи по теме
- Формула остатка делителя дивиденда
- Калькулятор коэффициентов
- Длинная дивизия
- Остаток
- Делитель
- Подразделение
Примеры на частное
Пример 1: 4000 долларов распределяются между 25 рабочими за работу, выполненную ими на строительной площадке. Подсчитайте сумму, которую дали каждому работнику.
Решение:
Общая сумма для распределения = 4000 долларов.
 Количество рабочих = 25. Нам нужно рассчитать сумму, отдаваемую каждому рабочему. Для этого мы разделим 4000 на 25, используя метод деления в длинную сторону, и найдем частное.
Количество рабочих = 25. Нам нужно рассчитать сумму, отдаваемую каждому рабочему. Для этого мы разделим 4000 на 25, используя метод деления в длинную сторону, и найдем частное.Полученное частное равно 160. Следовательно, сумма, выдаваемая каждому рабочему, составляет 160 долларов.
Пример 2: Разделите 66 ÷ 7 и найдите частное и остаток.
Решение:
Мы будем использовать метод деления в длину, чтобы найти частное.
После деления 66 на 7 мы получим 9 в частном и 3 в остатке.
Пример 3: Укажите истинное или ложное значение
а.) Частное — это окончательный ответ, который мы получаем при делении числа.
б.) Когда мы делим число и если оно не делится полностью, у нас остается остаток.
Решение:
а.) Верно, частное — это окончательный ответ, который мы получаем при делении числа.
б.) Правда, когда мы делим число и если оно не делится полностью, у нас остается остаток.

перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по Quotient
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о коэффициенте
Что такое частное в математике?
Частное — это окончательный ответ, который мы получаем при делении числа. Например, если мы разделим 63 ÷ 9, мы получим ответ как 7. Здесь 7 называется частным. Следует отметить, что частное может быть больше или меньше делителя, но всегда меньше делимого.
Как найти частное при делении?
Частное получается после завершения процесса деления. Это означает, что когда делитель делит делимое, ответ, который мы получаем, является частным.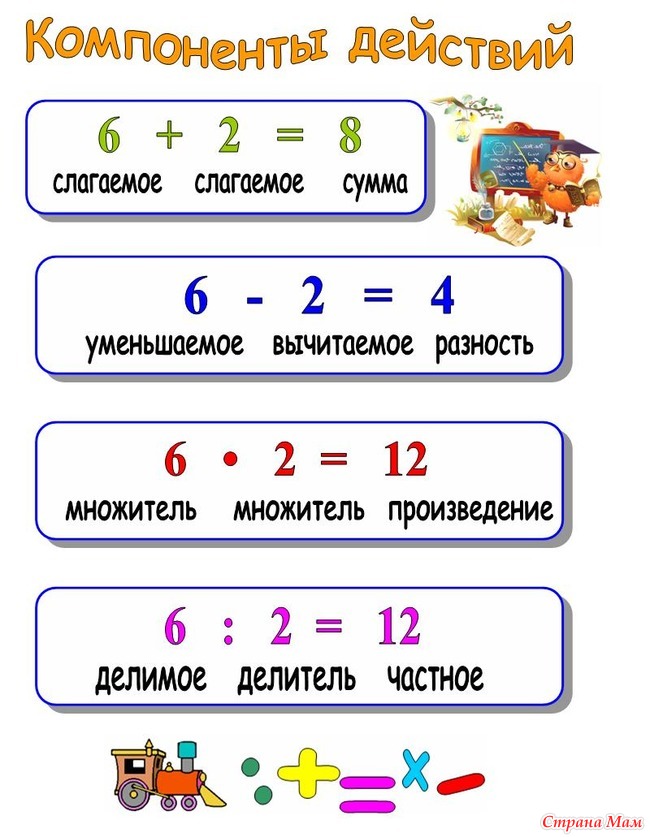 Другими словами, частное можно найти по формуле Дивиденд ÷ Делитель = Частное. Поясним это на простом примере 12 : 4 = 3. Здесь 12 — делимое, 4 — делитель, а 3 — частное.
Другими словами, частное можно найти по формуле Дивиденд ÷ Делитель = Частное. Поясним это на простом примере 12 : 4 = 3. Здесь 12 — делимое, 4 — делитель, а 3 — частное.
Всегда ли частное является целым числом?
Нет, частное не всегда может быть целым числом. Частное может быть целым или десятичным числом. Для совершенного деления, такого как 16 ÷ 2 = 8, частное представляет собой целое число, а для чисел, в которых у нас остался остаток, мы делим число дальше, помещая десятичную дробь в частное. Следовательно, в этих случаях частное становится десятичным числом. Например, если мы разделим 16 ÷ 5, мы получим 3,2 как частное, которое является десятичным числом.
В чем разница между частным и остатком?
Частное — это ответ, который мы получаем при делении числа. Число, оставшееся после окончания деления, называется остатком. Это относится к оставшейся части после завершения процесса деления. Например, если нам нужно распределить 7 мячей между 2 детьми поровну, мы даем каждому ребенку по 3 мяча и у нас остается 1 мяч. Этот 1 шар является остатком. Математически число 7 нельзя полностью разделить на число 2. После деления в остатке остается число 1. Для совершенных делений частное равно целому числу, а остаток равен нулю.
Этот 1 шар является остатком. Математически число 7 нельзя полностью разделить на число 2. После деления в остатке остается число 1. Для совершенных делений частное равно целому числу, а остаток равен нулю.
Как проверить частное при делении?
Деление также известно как обратное умножение. Мы можем проверить частное, используя следующую формулу:
Делимое = (Делитель × Частное) + Остаток
Это означает, что если мы умножим делитель на частное и добавим остаток, мы должны получить число как делимое. Если числа удовлетворяют этому уравнению, то ответ считается правильным, в противном случае нужно проверить наше деление.
Как найти частное, если известны остаток и делитель?
Если известны остаток, делитель и делимое, мы можем легко найти частное, подставив значения в формулу Делимое = (Делитель × Частное) + Остаток. После подстановки известных значений мы можем получить значение частного.
Чему равно частное 21 при делении на 7?
При делении 21 на 7 в частном получается 3.

 Умножьте это число на делитель и запишите произведение под первой цифрой делимого. Вычтите результат из цифры и запишите его под этим числом. Здесь первая цифра 4 и она равна делителю. Итак, 4 ÷ 4 = 1 написано сверху на черте. Произведение 4 × 1 = 4 вычитается из цифры и ниже записывается 0. Теперь сократите следующее число делимого, равное 3, и поместите его рядом с 0,9.0074
Умножьте это число на делитель и запишите произведение под первой цифрой делимого. Вычтите результат из цифры и запишите его под этим числом. Здесь первая цифра 4 и она равна делителю. Итак, 4 ÷ 4 = 1 написано сверху на черте. Произведение 4 × 1 = 4 вычитается из цифры и ниже записывается 0. Теперь сократите следующее число делимого, равное 3, и поместите его рядом с 0,9.0074 Это означает, что мы оставим 3 в качестве остатка и завершим деление. Таким образом, 3 известен как 9Остаток 0003 и 108 называется частным .
Это означает, что мы оставим 3 в качестве остатка и завершим деление. Таким образом, 3 известен как 9Остаток 0003 и 108 называется частным . Поэтому нам нужно проверить цифру в единицах (то есть 2), которая меньше 5. Следовательно, 22 будет округлено до 20.
Поэтому нам нужно проверить цифру в единицах (то есть 2), которая меньше 5. Следовательно, 22 будет округлено до 20. Здесь это 2, что меньше 5. Таким образом, 825 будет округлено до 800. Точно так же, поскольку в 24 последнее разрядное значение равно десяткам, нам нужно округлить его до ближайших десятков. Для этого нам нужно проверить цифру на единицу. Здесь это 4, что меньше 5. Таким образом, 24 будет округлено до 20.
Здесь это 2, что меньше 5. Таким образом, 825 будет округлено до 800. Точно так же, поскольку в 24 последнее разрядное значение равно десяткам, нам нужно округлить его до ближайших десятков. Для этого нам нужно проверить цифру на единицу. Здесь это 4, что меньше 5. Таким образом, 24 будет округлено до 20.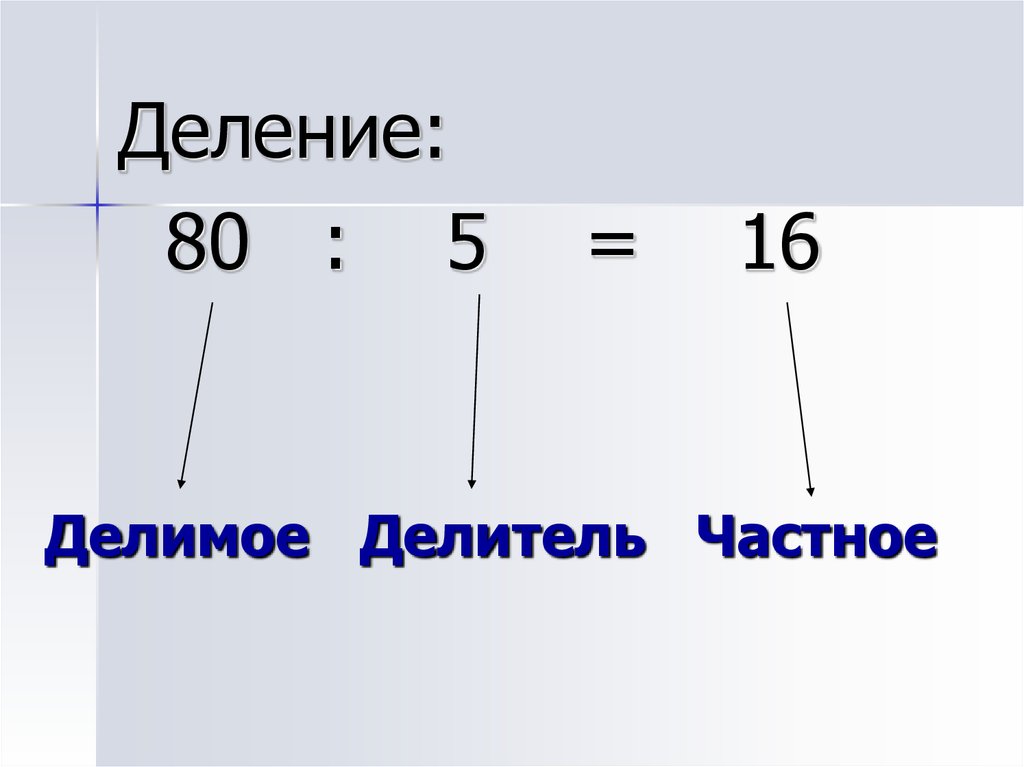 Количество рабочих = 25. Нам нужно рассчитать сумму, отдаваемую каждому рабочему. Для этого мы разделим 4000 на 25, используя метод деления в длинную сторону, и найдем частное.
Количество рабочих = 25. Нам нужно рассчитать сумму, отдаваемую каждому рабочему. Для этого мы разделим 4000 на 25, используя метод деления в длинную сторону, и найдем частное.
Leave A Comment