Как изменятся время и дальность полета тела брошенного горизонтально: № 222. ГДЗ Физика 10 класс Рымкевич. Как изменятся время и дальность полета тела? – Рамблер/класс

№ 222. ГДЗ Физика 10 класс Рымкевич. Как изменятся время и дальность полета тела? – Рамблер/класс

№ 222. ГДЗ Физика 10 класс Рымкевич. Как изменятся время и дальность полета тела? – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Как изменятся время и дальность полета тела, брошенного горизонтально с некоторой высоты, если скорость бросания увеличить вдвое?

 

ответы

Выберем систему, связанную с землей. Ось OY направлена вертикально вверх, ось ОХ’   —   горизонтально. Тогда уравнения, определяющие закон движения тела, имеют вид:
 
На основании (1), а также с учетом условия у(t₁) = 0 определим время полета:
 
Из формулы (2) видно, что время полета не зависит от
начальной скорости.
Дальность полета определяется из условия
 
Из (3) видно, что дальность полета увеличится вдвое, если скорость бросания удвоить.
Ответ: время полета не изменится; дальность полета увеличится вдвое.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

№ 77. ГДЗ Физика 10 класс Рымкевич. Какую скорость приобрел троллейбус?

Троллейбус за время t прошел путь s. Какую скорость v приобрел он в конце пути и с каким ускорением а двигался, если начальная скорость (Подробнее…)

ГДЗФизика10 классРымкевич А.П.

№ 113. ГДЗ Физика 10 класс Рымкевич. Действия каких сил компенсируются?

Парашютист спускается, двигаясь равномерно и прямолинейно. Объяснить, действия каких сил компенсируются.
 

ГДЗФизика10 классРымкевич А.П.

ГДЗ.Физика 11. класс.Рымкевич.Глава 11.Электромагнитная индукция.Задание 912.Найти скорость изменения магнитного потока..

Нужно ответить :
Найти скорость изменения магнитного потока1 в соле-
ноиде из 2000 витков при возбуждении в нем ЭДС индукции (Подробнее…)

ГДЗФизика11 классРымкевич А.П.

ГДЗ по математике, 2 класс, Моро М.И. Разбей все разности на две группы.

Разбей все разности на две группы.
90-50      80-60      30-10      70-30
60-20      50-30      90-70      40-20 (Подробнее. ..)

ГДЗМатематика2 классМоро М.И.

Значение выражения. ГДЗ Математика 6 класс Чесноков. Дидактические материалы по математике для 6 класса. Вар.1 Вопр.259

Кто выполнит?   Найдите значение выражения:
  (Подробнее…)

ГДЗМатематика6 классЧесноков А.С.

Движение тела, брошенного горизонтально | СПАДИЛО

Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.

Кинематические характеристики движения

Важные факты!

Графически движение горизонтально брошенного тела описывается следующим образом:

1. Вектор скорости горизонтально брошенного тела направлен по касательной к траектории его движения.
2. Проекция начальной скорости на ось ОХ равна v₀: v_ox = v₀. Ее проекция на ось ОУ равна нулю: v_oy = 0.
3. Проекция мгновенной скорости на ось ОХ равна v₀: v_x = v₀. Ее проекция на ось ОУ равна нулю: v_y = –gt.
4. Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:

Минимальная скорость в течение всего времени движения равна начальной скорости: v_min = v₀.

Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: v_max = v.

Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:

h₀ — высота, с которой тело бросили в горизонтальном направлении.

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой

l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

l = s_x = v₀t_пад

Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:

x = v₀t

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?

Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:

Выразим начальную скорость и вычислим ее:

Горизонтальный бросок тела с горы

Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.

График горизонтального броска тела с горы

α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения

Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения.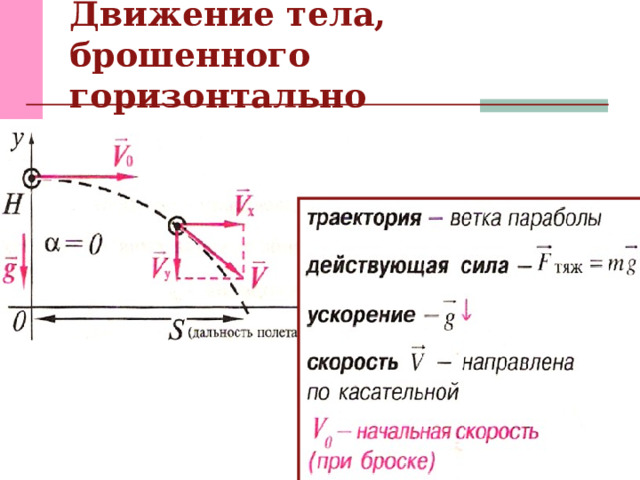

Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:

l = s • cosα

Начальная высота — высота, с которой было брошено тело. Обозначается h₀. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:

h₀ = s sinα

Пример №2. На горе с углом наклона 30^о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?

Выразим это расстояние через дальность полета:

Дальность полета выражается по формуле:

Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:

Выразим с учетом формулы начальной высоты:

Преобразуем:

Поделим обе части выражения на общий множитель s:

Подставим известные значения:

Задание EF18083

Шарик, брошенный горизонтально с высоты H с начальной скоростью υ₀, за время t пролетел в горизонтальном направлении расстояние L (см.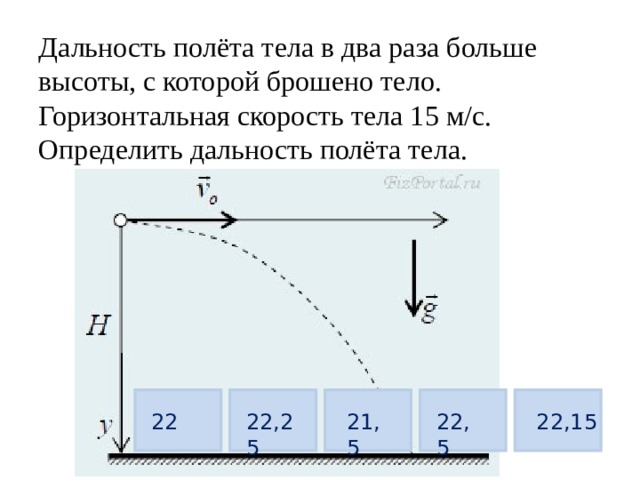 рисунок).

В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2

υ₀.

Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:

1. увеличится
2. уменьшится
3. не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

---

Алгоритм решения

1. Записать формулы для каждой из величин.
2. Определить, как зависит эта физическая величина от начальной скорости и массы.
3. Определить характер изменения физической величины при увеличении начальной скорости и массы шарика.

Решение

Время полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.

Дальность полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.

Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.

Значит, верный ответ — 313.

Ответ: 313

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18048

Шарик, брошенный горизонтально с высоты H с начальной скоростью υ₀, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).

Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь.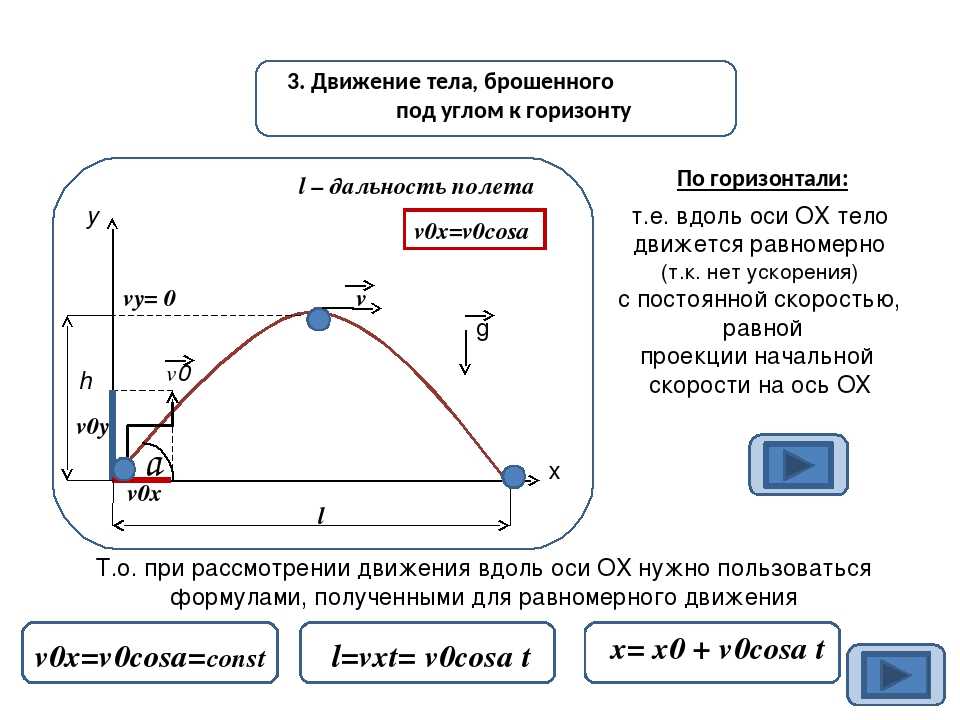 Для каждой величины определите соответствующий характер её изменения:

1. увеличится
2. уменьшится
3. не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

---

Алгоритм решения

1. Записать формулы для каждой из величин.
2. Определить, как зависит эта физическая величина от начальной скорости.
3. Определить характер изменения физической величины при уменьшении начальной скорости.

Решение

Время полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.

Дальность полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально.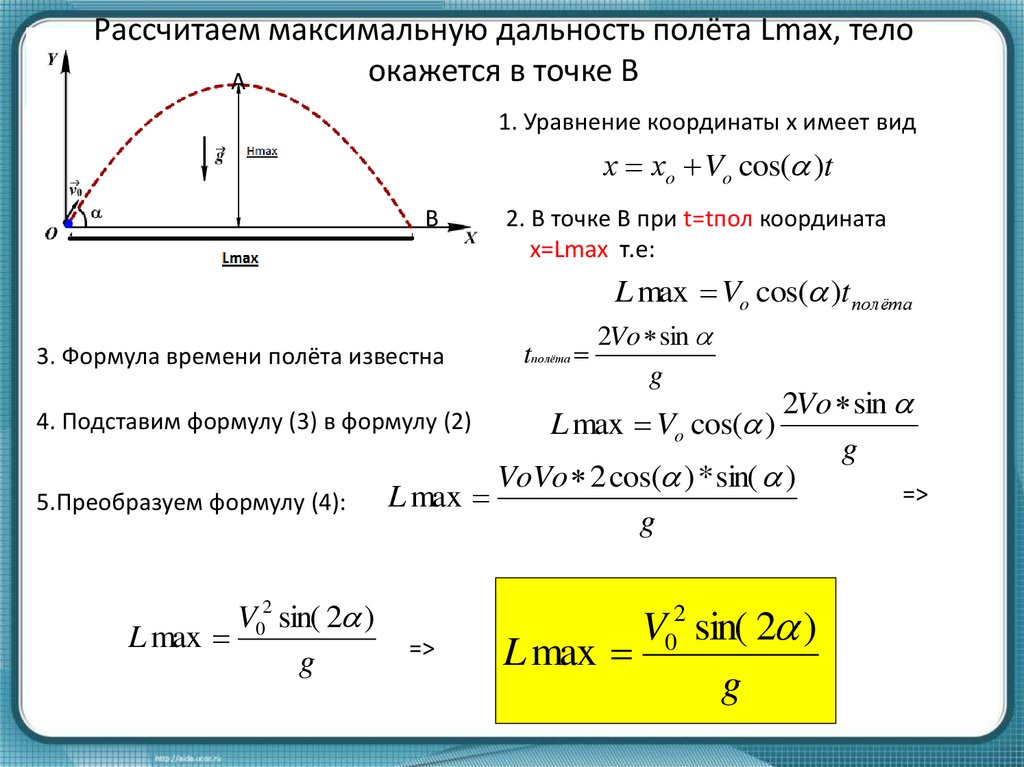 Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).

Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.

Значит, верный ответ — 323.

Ответ: 323

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 16.8k

Движение снаряда, брошенного горизонтально

Рассмотрим объект, брошенный горизонтально со скоростью u из точки А, находящейся на высоте h от горизонтальной плоскости ОХ (рис.). Объект одновременно приобретает следующие движения: (i) Равномерная скорость, с которой он проецируется в горизонтальном направлении OX (ii) Вертикальная скорость, которая неравномерна из-за ускорения под действием силы тяжести.

Движение снаряда, брошенного горизонтально

Рассмотрим объект, брошенный горизонтально со скоростью u из точки А, находящейся на высоте h от горизонтальной плоскости ОХ (рис. ). Объект приобретает следующие движения одновременно:

(i) Равномерная скорость, с которой он проецируется в горизонтальном направлении OX

(ii) Вертикальная скорость, которая неравномерна из-за ускорения под действием силы тяжести.

Две скорости не зависят друг от друга. Горизонтальная скорость объекта должна оставаться постоянной, поскольку ускорение в горизонтальном направлении не действует.

Скорость в вертикальном направлении будет продолжать изменяться из-за ускорения силы тяжести.

Путь снаряда

Пусть время, затрачиваемое объектом для достижения C с A = T Вертикальное расстояние, пройденное по объекту T = S = Y

Из уравнения движения s = u1t + 1/2 at 2

Подставляя известные значения в уравнение (1),

y = (0) T + 1/2 GT 2 = 1/2 GT 2

При A, Первоначальная скорость в горизонтальной направлении — . ты  Горизонтальное расстояние, пройденное объектом за время  t  равно x. ???.(1)

x = горизонтальная скорость ? время = u t (или) t = x/u  ………(3)

Подставляя t  в уравнение (2),   y  =1/2 g(x/u)2 = 1/2 g(x2/u2)        ….(4)

(или) y = kx2  , где k = 2/gu2 – константа.

Приведенное выше уравнение является уравнением параболы. Таким образом, путь, пройденный снарядом, представляет собой параболу.

 

Результирующая скорость в точке C

В момент времени t тело находится в точке C.

В точке A начальная вертикальная скорость (u1) = 0 ux) = u

При C вертикальная скорость = u2

Из уравнения движения u2 = u1 + g t

Подставляя все известные значения, u2 = 0 + g t

Результирующая скорость в точке C равна v = root[ux2+u22] = root[u2+g2t2 ]    ..(6)

      Направление v определяется выражением tanθ = v2/ux =gt/u   . .(7)

, где θ — угол, образуемый v с осью X.

Время полета и дальность полета

Расстояние OB = R, называется дальностью полета снаряда.

Диапазон = горизонтальная скорость ? время, необходимое для достижения земли

R = u tf …(8)

, где tf – время полета

В точке A начальная вертикальная скорость (u1) = 0

Вертикальное расстояние, пройденное объектом в время tf = sy = h

Из уравнений движения Sy = ut t f + 1/2 g f f2…(9)

Подставляя известные значения в уравнение (9),

h = (0) tf = 1/2 г tf2

tf= root[2h/g]  …(10)

Подставляя tf в уравнение (8), диапазон R = u . корень[2ч/г]  ..(11)

Учебный материал, Лекционные заметки, Задание, Справочник, Вики-описание, пояснение, краткое описание

11-й 12-й стандартный класс Физика Высшая средняя школа Колледж Примечания: Движение снаряда, брошенного горизонтально |

Объяснение урока: Движение снаряда | Nagwa

В этом объяснителе мы научимся анализировать движение движущихся объектов. горизонтально, испытывая при этом постоянное вертикальное ускорение.

Вспомните, что снаряды — это объекты, ненулевое равномерное вертикальное ускорение при горизонтальном движении с постоянной скоростью. Движение снаряда относится к движению любого снаряда, например камень, брошенный с высоты, или брошенный мяч.

Если снаряд летит с большой скоростью, то нам, возможно, придется учитывать эффекты сопротивления воздуха, но большинство снарядов, с которыми мы будем иметь дело, путешествуют достаточно медленно, чтобы мы могли игнорировать эти эффекты. Это означает, что единственная сила на объект действует сила тяжести, действующая вниз. Горизонтальный объект следовательно, скорость постоянна, пока он находится в движении.

На приведенной ниже диаграмме показан снаряд массой 𝑚, запущенный с скорость пуска 𝑣 под углом 𝜃 от горизонтальный.

Горизонтальная скорость снаряда 𝑣 равна 𝑣𝜃кос. Точно так же вертикальная скорость снаряд, 𝑣, равен 𝑣𝜃грех.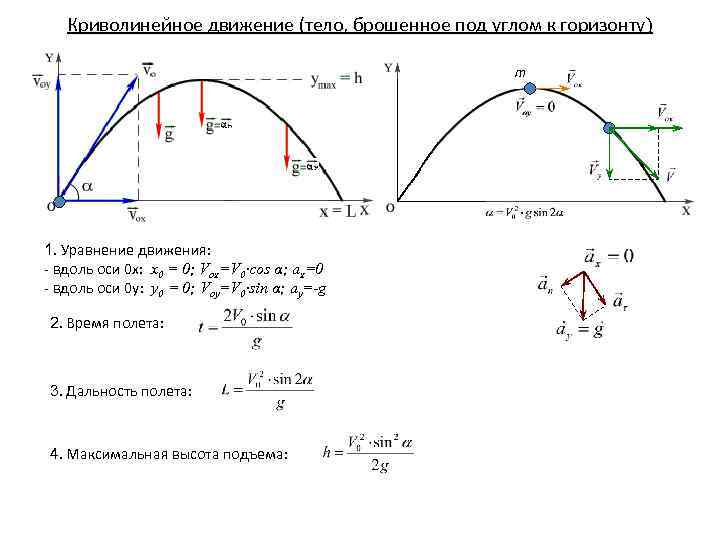

Три важные величины, которые мы хотели бы рассчитать:

• время полета ,
• дальность (горизонтальное расстояние, пройденное снарядом),
• максимальная высота (максимальное расстояние по вертикали, снаряд).

Эти три величины показаны для снаряда, запускаемого из такое же вертикальное смещение, при котором он заканчивает движение на диаграмме ниже.

Время полета снаряда можно найти, исходя из уравнения для смещения, 𝑠, с постоянным ускорением, 𝑎 и начальная скорость 𝑢 с течением времени, 𝑡: 𝑠=𝑢𝑡+12𝑎𝑡.

Мы будем рассматривать только вертикальное движение, поэтому мы можем заменить наш начальный скорость с начальной вертикальной скоростью, 𝑢=𝑣, и постоянное ускорение силы тяжести, 𝑎=−𝑔. Обратите внимание, что гравитация действует вниз, что отрицательно в вертикальном направлении, поэтому отрицательное слагаемое в наших расчетах.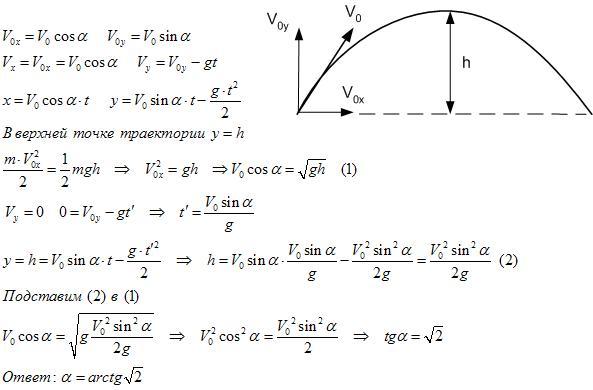 Это дает нам уравнение для вертикального водоизмещение, 𝑠: 𝑠=𝑣𝑡−12𝑔𝑡.

В качестве общего множителя можно взять 𝑡: 𝑠=𝑡𝑣−12𝑔𝑡.

Мы хотели бы знать, когда вертикальное перемещение снаряда равно нулю, 𝑠=0: 0=𝑡𝑣−12𝑔𝑡.

Это говорит нам о том, что есть два случая, когда вертикальное смещение равно нулю: один в начале движения снаряда и один в конце движение снаряда.

В конце движения время 𝑡=𝑇. Второе решение может быть найденным, когда 𝑣−12𝑔𝑇=0,

Затем мы переставляем 𝑇 субъектом уравнения: 𝑇=2𝑣𝑔.

Наконец, подставив начальную вертикальную скорость, 𝑣=𝑣𝜃sin, получим уравнение для времени полета: 𝑇=2𝑣(𝜃)𝑔.sin

Определение: время полета

Когда конечное вертикальное перемещение снаряда равно начальное вертикальное смещение, время полета, 𝑇, можно рассчитать как 𝑇=2𝑣(𝜃)𝑔, грех где 𝑣 — начальная скорость снаряда, 𝜃 — угол запуска, измеренный над горизонтом, 𝑔 — гравитационная постоянная.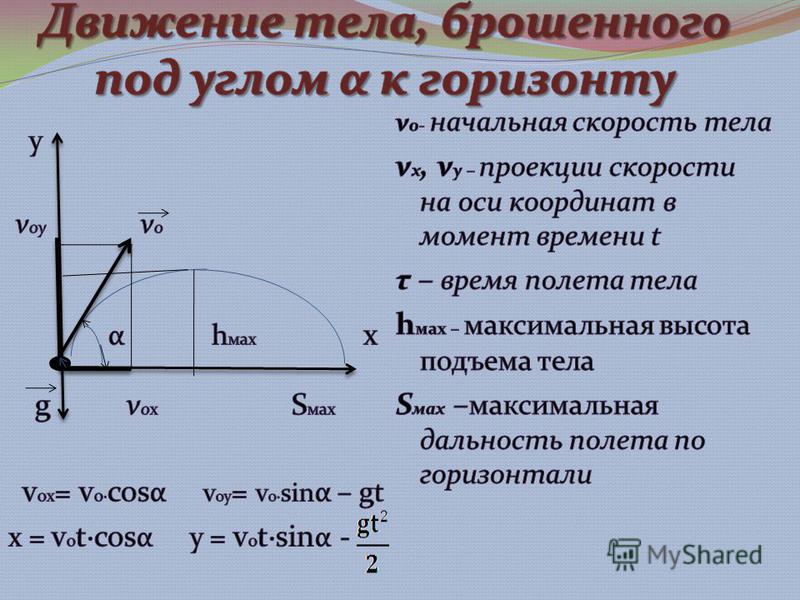

Давайте рассмотрим пример вопроса, в котором нам необходимо вычислить время полета снаряда.

Пример 1: Расчет времени полета снаряда

Снаряд имеет начальную скорость 25 м/с и стреляет под углом 48∘ выше горизонтали. Какое время между снарядом отрываясь от земли и возвращаясь на землю на той же высоте, что и запущен с?

Ответ

Давайте начнем с рисования схемы этого сценария.

Вопрос задается по времени полета снаряда.

Для расчета времени полета используем следующую формулу: 𝑇=2𝑣𝑔=2𝑣(𝜃)𝑔.sin

Как указано в вопросе, снаряд выпущен под углом 𝜃=48∘ над горизонтом с начальной скоростью 𝑣=/мс, поэтому вертикальная скорость снаряда рассчитывается как 𝑣=𝑣(𝜃)=25(48)грех в результате чего вертикальная скорость (с точностью до двух знаков после запятой) равна 𝑣=18,58/. мс

Подставив это в наше уравнение времени полета с гравитационным постоянный 𝑔=9,8/мс, дает нам 𝑇 (до двух знаков после запятой): 𝑇=2×18,589,8=3,79/.мс

Мы можем использовать уравнение для времени полета снаряда для расчета пройденное горизонтальное расстояние, также известное как диапазон. Потому что нет силы действуя на объект в горизонтальном направлении, уравнение для горизонтального перемещение 𝑠=𝑅 снаряда в конце движение — это просто горизонтальная скорость снаряда, 𝑣, умноженное на время полета, 𝑇: 𝑅=𝑣𝑇.

Ввод горизонтальной скорости, 𝑣=𝑣𝜃cos, и уравнение для времени пролета, 𝑇=2𝑣𝜃𝑔sin, мы получаем 𝑅=(𝑣𝜃)2𝑣𝜃𝑔.cossin

Это дает нам окончательное уравнение для дальности полета снаряда: 𝑅=2𝑣(𝜃)(𝜃)𝑔.sincos

Используя формулу sinsincos(2𝜃)=2(𝜃)(𝜃), диапазон снаряд также может быть записан как 𝑅=𝑣(2𝜃)𝑔.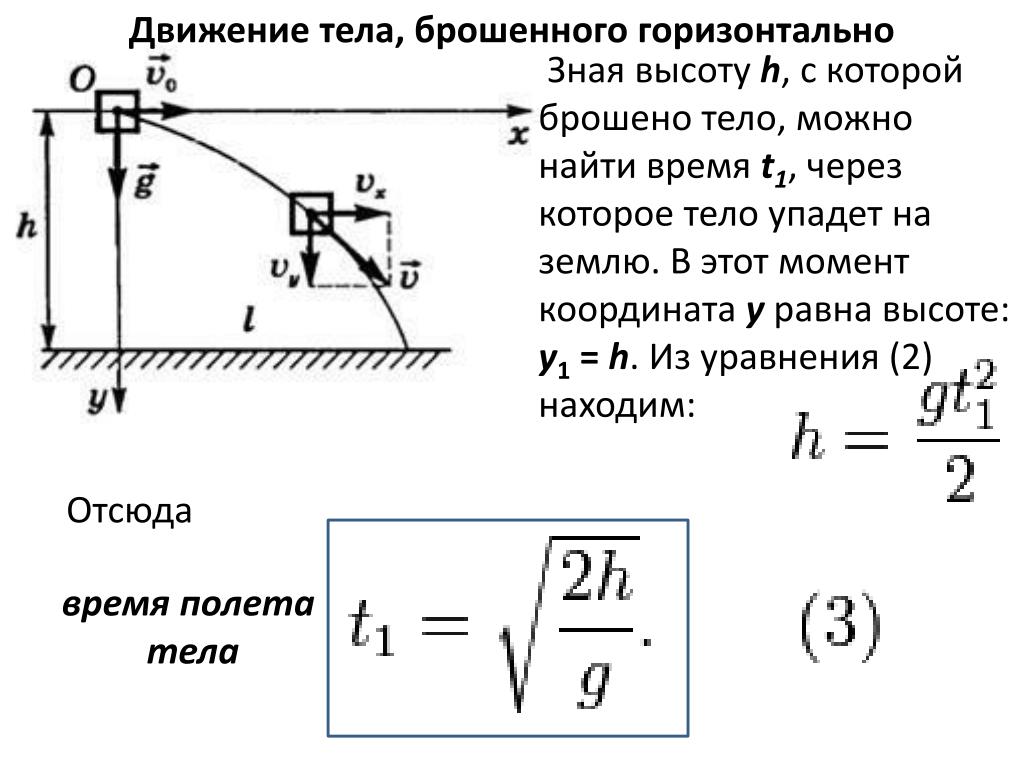 sin

Определение: Горизонтальная дальность

Горизонтальная дальность, 𝑅, снаряда, выпущенного из одинаковое начальное и конечное вертикальное смещение можно рассчитать как 𝑅=2𝑣(𝜃)(𝜃)𝑔,sincos где 𝑣 — начальная скорость снаряда, 𝜃 — угол запуска, измеренный над горизонтом, 𝑔 — гравитационная постоянная.

Давайте рассмотрим пример вопроса, где нам необходимо рассчитать дальность полета снаряда.

Пример 2: Расчет дальности полета снаряда

Снаряд имеет начальную скорость 15 м/с при угле пуска 28∘ выше горизонтали. Чему равно горизонтальное смещение снаряд из положения пуска туда, куда он приземлится, если его вертикальное смещение от стартовой позиции равно нулю?

Ответ

Этот вопрос требует, чтобы мы рассчитали диапазон снаряд — горизонтальное смещение снаряда при он возвращается к вертикальному смещению нуля от своего стартовая позиция.

Мы можем начать с нашего уравнения для диапазона: 𝑅=2𝑣(𝜃)(𝜃)𝑔.sincos

Мы можем сразу подставить данные нам значения для 𝑣=15/мс, 𝜃=28∘, и 𝑔=9.8/мс: 𝑅=2×15×(28)×(28)9,8.sincos

Это дает нам наше горизонтальное смещение 𝑅=19.03.м

Мы можем рассчитать максимальную высоту снаряда, учитывая пик траектория. Это происходит, когда вертикальная скорость снаряда равна нулю.

Здесь мы можем начать с другого уравнения постоянного ускорения, которое связывает скорость во время движения, 𝑣, к начальная скорость, 𝑢; постоянное ускорение, 𝑎; и смещение объекта от начала движение, 𝑠: 𝑣=𝑢+2𝑎𝑠.

При вычислении максимальной высоты мы хотели бы найти вертикальное смещение, 𝑠=𝑠 снаряда с начальной вертикальной скоростью 𝑢=𝑣 в точке, когда вертикальная скорость снаряд равен нулю, 𝑣=0. В этот момент вертикаль водоизмещение снаряда находится на его максимальной высоте, которую мы запишем как 𝑠=ℎ. Как и в предыдущих расчетах, гравитационное ускорение действует в отрицательном вертикальном направлении, поэтому 𝑎=−𝑔: 0=𝑣−2𝑔ℎ.

Мы можем изменить это уравнение, чтобы сделать 𝑠 его предметом сначала добавив 2𝑔ℎ к обеим сторонам: 2𝑔ℎ=𝑣.

Тогда, разделив обе части на 2𝑔, получим ℎ=𝑣𝑔.

Затем мы можем подставить наше выражение для начальной вертикальной скорости снаряд, запущенный со скоростью 𝑣 под углом 𝜃 над горизонталью, 𝑣=𝑣𝜃грех. Это дает нам наше окончательное уравнение для максимальная высота: ℎ=𝑣(𝜃)𝑔.sin

Определение: Максимальная высота

Максимальная высота снаряда, ℎ, может быть рассчитывается как ℎ=𝑣(𝜃)𝑔,грех где 𝑣 — начальная скорость снаряда, 𝜃 — угол запуска, измеренный над горизонтом, 𝑔 — гравитационная постоянная.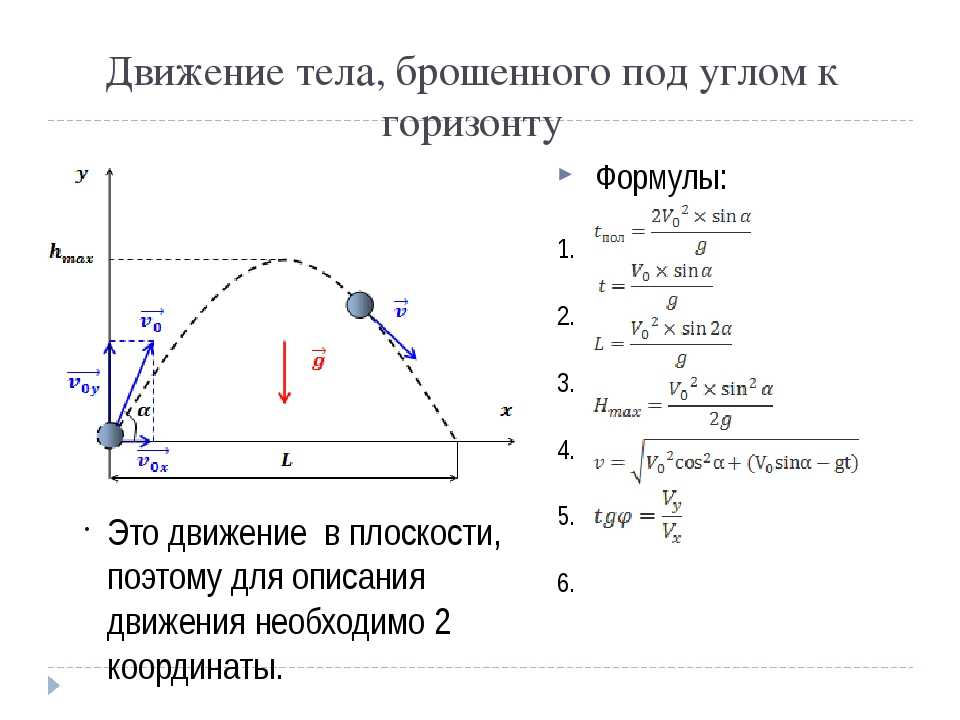

Теперь давайте посмотрим на пример, где мы должны работать в обратном порядке. с максимальной высоты, чтобы определить угол над горизонтом, снаряд был запущен в.

Пример 3. Расчет угла запуска снаряда из Максимальная высота

Снаряд выпущен с начальной скоростью 28 м/с и имеет максимальное вертикальное смещение вверх от стартового положения 4,4 м. Под каким углом над горизонтом запущен снаряд?

Ответ

Этот вопрос требует, чтобы мы работали в обратном направлении с максимальной высоты. найти угол над горизонтом снаряда запускается в.

Мы можем начать с нашего уравнения для максимальной высоты: ℎ=𝑣(𝜃)𝑔.грех

Мы должны изменить это, чтобы получить уравнение для угла над горизонтальный, 𝜃. Давайте начнем с умножив обе части уравнения на 2𝑔: 2𝑔ℎ=𝑣(𝜃). sin

Тогда мы можем извлечь квадратный корень из обеих частей: √2𝑔ℎ=𝑣𝜃.sin

Затем мы можем разделить обе части на 𝑣: грех𝜃=√2𝑔ℎ𝑣.

Наконец, возьмем арксинус обеих сторон 𝜃=√2𝑔𝑠𝑣.sin

Теперь мы можем заменить наши значения на максимальную высоту, 𝑠=4,4м, а начальная скорость, 𝑣=28/мс, а гравитационная постоянная, 𝑔=9.8/мс: 𝜃=√2×9,8×4,428.sin

Это дает нам угол запуска над горизонталью: 𝜃=19.3.∘

Нас также должны устраивать изменения механической энергии во время движение снаряда.

При отсутствии сопротивления воздуха механическая энергия сохраняется на протяжении всего движения. Что означает, что сумма кинетической энергии и гравитационного потенциала энергия в любой момент движения постоянна: ()+()=()+().КЕПЕКЕПЕ

Однако при значительном сопротивлении воздуха — когда снаряд при движении с высокой скоростью — при этом теряется некоторая механическая энергия.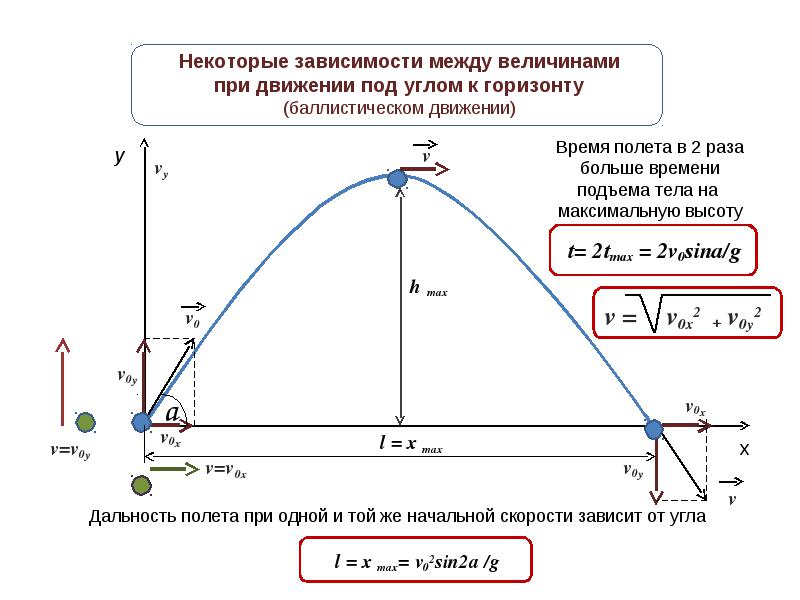 движение.

Сила сопротивления воздуха изменяется в зависимости от скорости, с которой летит снаряд перемещение, которое является нелинейным, поэтому потери механической энергии во всем движение тоже нелинейное .

Давайте теперь рассмотрим вопрос о механической энергии снаряд.

Пример 4: Механическая энергия снаряда при движении

Изменение вертикального смещения снаряда от его стартовое положение и его горизонтальное смещение от положение запуска показано на графике. Какой из следующих графиков наиболее правильно представляет, как механическая энергия снаряда меняется с момента его запуска до момента, когда он приземляется?

Ответ

Когда мы смотрим на график вертикального и горизонтального смещения, сразу видно, что снаряд замедлился во время движение. Это означает, что он потерял некоторую механическую энергию. к сопротивлению воздуха. Это исключает граф V.

Далее мы можем видеть, что снаряд все еще находится в движении, когда он завершает полет. его траектория; это означает, что у него все еще есть некоторая механическая энергия при конец движения. Это означает, что графики II и IV не могут корректно представляют механическую энергию снаряда.

Остаются графики I и III: оба показывают механическую энергию уменьшается со временем, все еще больше нуля, когда снаряд приземляется. Однако граф I нелинейный, а граф III линейный.

Напомним, что сопротивление воздуха сильно нелинейно, поэтому потери механической энергии. Это означает, что граф III не может корректно представляют механическую энергию снаряда.

Это означает, что график I правильно представляет механическую энергию снаряда с момента его пуска до момента, когда он приземляется.

Когда точка запуска снаряда находится выше или ниже точки его приземления, мы должны рассмотреть общее уравнение для вертикального смещения снаряд: 𝑠=𝑣𝑡−12𝑔𝑡.

Как и прежде, 𝑠 — вертикальное смещение снаряда, 𝑣 — начальная вертикальная скорость снаряд, 𝑡 время, 𝑔 — гравитационная постоянная.

Вертикальное смещение точки приземления отличается от точка запуска. Мы запишем эту разницу как 𝑠=𝑑. Мы можем подставить это в уравнение для вертикального перемещения в момент времени 𝑡=𝑇 время полета снаряда: 𝑑=𝑣𝑇−12𝑔𝑇.

Обратите внимание, что 𝑑 будет положительным, если точка приземления снаряд выше точки старта и отрицателен, если точка приземления находится ниже точки запуска.

Чтобы найти время полета, мы можем сначала преобразовать уравнение в стандартное квадратичная форма относительно 𝑇: 12𝑔𝑇−𝑣𝑇+𝑑=0,

Мы можем решить это квадратное уравнение, чтобы найти время полета, 𝑇.

Горизонтальная дальность снаряда, 𝑅, тогда рассчитывается как раньше: 𝑅=𝑣𝑇, где 𝑣 — начальная горизонтальная скорость снаряда 𝑇 — время полета.

Наконец, давайте рассмотрим несколько более сложный вопрос, где точка запуска снаряда находится выше точки приземления.

Пример 5: Расчет дальности полета снаряда из Elevated Point

Камень брошен горизонтально с высоты 9,6 м от земли со скоростью 5,2 м/с. Вычислите горизонтальный диапазон скалы. Используйте 𝑔=10/мс.

1. 9,6 м
2. 2,4 м
3. 7,2 м
4. 16,8 м

Ответ

В этом вопросе мы должны вычислить горизонтальный диапазон снаряд, запущенный с возвышенности.

Сначала надо рассчитать время полета снаряда. Мы начнем с нашего исходного уравнения для вертикального смещения: 𝑠=𝑣𝑡−12𝑔𝑡.

Зная, что окончательное вертикальное смещение равно 9,6 м ниже точки старта и начальной вертикальной скорости равен нулю, мы можем подставить значения для 𝑠=−9. 6, 𝑣=0 и 𝑔=10. Это достигается в конце движения, поэтому время 𝑡=𝑇: −9,6=−12×10×𝑇.

Сначала переставим 𝑇: 𝑇=9,6×210=1,92.

Затем извлекаем квадратный корень, чтобы получить время полета снаряд (до двух знаков после запятой): 𝑇=√1.92=1.38.s

Теперь мы можем рассчитать дальность полета снаряда, зная, что его горизонтальная скорость остается постоянной на протяжении всего движения.

Дальность полета снаряда равна 𝑅=𝑣𝑇.

В данном случае снаряд был запущен горизонтально, поэтому 𝑣=5,2/мс. Подставляя наши значения для 𝑣 и 𝑇, 𝑅=5,2×1,38=7,21.м

Итак, правильный ответ C 7,2 м (до одного десятичного знака).

Ключевые моменты

• Как правило, единственной силой, действующей на снаряд, является гравитация:
  • Это означает, что вертикальная скорость испытывает постоянное ускорение 𝑔 вертикально вниз.