Как изменится период свободных колебаний в электрическом контуре: 1.Как изменится период свободных колебаний в электрическом колебательном контуре при увеличении электроемкости конденсатора в 4…

Глава 24. Электромагнитные колебания и волны

Электрическая цепь, состоящая из катушки индуктивности и конденсатора (см. рисунок), называется колебательным контуром. В этой цепи могут происходить своеобразные электрические колебания. Пусть, например, в начальный момент времени мы заряжаем пластины конденсатора положительным и отрицательным зарядами, а затем разрешим зарядам двигаться. Если бы катушка отсутствовала, конденсатор начал бы разряжаться, в цепи на короткое время возник электрический ток, и заряды пропали бы. Здесь же происходит следующее. Сначала благодаря самоиндукции катушка препятствует увеличению тока, а затем, когда ток начинает убывать, препятствует его уменьшению, т.е. поддерживает ток. В результате ЭДС самоиндукции заряжает конденсатор с обратной полярностью: та пластина, которая изначально была заряжена положительно, приобретает отрицательный заряд, вторая — положительный. Если при этом не происходит потерь электрической энергии (в случае малого сопротивления элементов контура), то величина этих зарядов будет такая же, как величина первоначальных зарядов пластин конденсатора.

В дальнейшем движение процесс перемещения зарядов будет повторяться. Таким образом, движение зарядов в контуре представляет собой колебательный процесс.

Для решения задач ЕГЭ, посвященных электромагнитным колебаниям, нужно запомнить ряд фактов и формул, касающихся колебательного контура. Во-первых, нужно знать формулу для периода колебаний в контуре. Во-вторых, уметь применять к колебательному контуру закон сохранения энергии. И, наконец (хотя такие задачи встречаются редко), уметь использовать зависимости силы тока через катушку и напряжения на конденсаторе от времени

Период электромагнитных колебаний в колебательном контуре определяется соотношением:

(24.1)

где — емкость конденсатора, — индуктивность катушки.

При электромагнитных колебаниях энергия колебательного контура складывается из энергии конденсатора и энергии тока в катушке:

(24. 2)

где и — заряд на конденсаторе и сила тока в катушке в этот момент времени, и — емкость конденсатора и индуктивность катушки. Если электрическое сопротивление элементов контура мало, то электрическая энергия контура (24.2) остается практически неизменной, несмотря на то, что заряд конденсатора и ток в катушке изменяются с течением времени. Из формулы (24.4) следует, что при электрических колебаниях в контуре происходят превращения энергии: в те моменты времени, когда ток в катушке равен нулю, вся энергия контура сводится к энергии конденсатора. В те моменты времени, когда равен нулю заряд конденсатора, энергия контура сводится к энергии магнитного поля в катушке. Очевидно, в эти моменты времени заряд конденсатора или ток в катушке достигают своих максимальных (амплитудных) значений.

При электромагнитных колебаниях в контуре заряд конденсатора изменяется с течением времени по гармоническому закону:

(24. 3)

где — амплитуда колебаний заряда на конденсаторе, — циклическая (или круговая) частота колебаний, — начальная фаза. Циклическая частота колебаний связана с периодом по формуле

(24.4)

стандартной для любых гармонических колебаний. Поскольку сила тока в катушке представляет собой производную заряда конденсатора по времени, из формулы (24.4) можно найти зависимость силы тока в катушке от времени

(24.5)

В ЕГЭ по физике часто предлагаются задачи на электромагнитные волны. Необходимый для решения этих задач минимум знаний включает в себя понимание основных свойств электромагнитной волны и знание шкалы электромагнитных волн. Сформулируем кратко эти факты и принципы.

Согласно законам электромагнитного поля переменное магнитное поле порождает поле электрическое, переменное электрическое поле порождает поле магнитное. Поэтому если одно из полей (например, электрическое) начнет меняться, возникнет второе поле (магнитное), которое затем снова порождает первое (электрическое), затем снова второе (магнитное) и т.д. Процесс взаимного превращения друг в друга электрического и магнитного полей, который может распространяться в пространстве, называется электромагнитной волной. Опыт показывает, что направления, в которых колеблются векторы напряженности электрического и индукции магнитного поля в электромагнитной волне перпендикулярны направлению ее распространения. Это означает, что электромагнитные волны являются поперечными. В теории электромагнитного поля Максвелла доказывается, что электромагнитная волна создается (излучается) электрическими зарядами при их движении с ускорением. В частности, источником электромагнитной волны является колебательный контур.

Длина электромагнитной волны , ее частота (или период ) и скорость распространения связаны соотношением, которое справедливо для любой волны (см.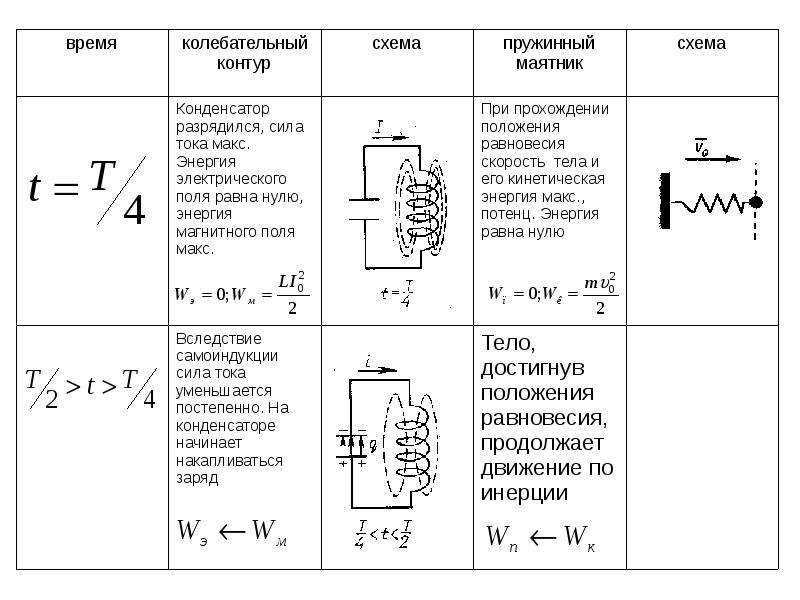 также формулу (11.6)):

(24.6)

Электромагнитные волны в вакууме распространяются со скоростью = 3 • 10⁸ м/с, в среде скорость электромагнитных волн меньше, чем в вакууме, причем эта скорость зависит от частоты волны. Такое явление называется дисперсией волн. Электромагнитной волне присущи все свойства волн, распространяющихся в упругих средах: интерференция, дифракция, для нее справедлив принцип Гюйгенса. Единственное, что отличает электромагнитную волну, это то, что для ее распространения не нужна среда — электромагнитная волна может распространяться и в вакууме.

В природе наблюдаются электромагнитные волны с сильно отличающимися друг от друга частотами, и обладающие благодаря этому существенно различными свойствами (несмотря на одинаковую физическую природу). Классификация свойств электромагнитных волн в зависимости от их частоты (или длины волны) называется шкалой электромагнитных волн.

Дадим краткий обзор этой шкалы.

Электромагнитные волны с частотой меньшей 10⁵ Гц (т.е. с длиной волны, большей нескольких километров) называются низкочастотными электромагнитными волнами. Излучают волны такого диапазона большинство бытовых электрических приборов.

Волны с частотой от 10⁵ до 10¹² Гц называются радиоволнами. Этим волнам отвечают длины волн в вакууме от нескольких километров до нескольких миллиметров. Эти волны применяются для радиосвязи, телевидения, радиолокации, сотовых телефонов. Источниками излучения таких волн являются заряженные частицы, движущиеся в электромагнитных полях. Радиоволны излучаются также свободными электронами металла, которые совершают колебания в колебательном контуре.

Область шкалы электромагнитных волн с частотами, лежащими в интервале 10¹² — 4,3 • 10¹⁴ Гц (и длинами волн от нескольких миллиметров до 760 нм) называется инфракрасным излучением (или инфракрасными лучами). Источником такого излучения служат молекулы нагретого вещества. Человек излучает инфракрасные волны с длиной волны 5 — 10 мкм.

Электромагнитное излучение в интервале частот 4,3 • 10¹⁴ — 7,7 • 10¹⁴ Гц (или длин волн 760 — 390 нм) воспринимается человеческим глазом как свет и называется видимым светом. Волны различных частот внутри этого диапазона воспринимаются глазом, как имеющие различный цвет. Волна с самой маленькой частотой из видимого диапазона 4,3 • 10

14 воспринимается как красная, с самой большой частотой внутри видимого диапазона 7,7 • 10¹⁴ Гц — как фиолетовая. Видимый свет излучается при переходе электронов в атомах, молекулами твердых тел, нагретых до 1000 °С и более.

Волны с частотой 7,7 • 10¹⁴ — 10¹⁷ Гц (длина волны от 390 до 1 нм) принято называть ультрафиолетовым излучением. Ультрафиолетовое излучение имеет выраженное биологическое действие: оно способно убивать ряд микроорганизмов, способно вызвать усиление пигментации человеческой кожи (загар), при избыточном облучении в отдельных случаях может способствовать развитию онкологических заболеваний (рак кожи).

Ультрафиолетовые лучи содержатся в излучении Солнца, в лабораториях создаются специальными газоразрядными (кварцевыми) лампами.

За областью ультрафиолетового излучения лежит область рентгеновских лучей (частота 10¹⁷ — 10¹⁹ Гц, длина волны от 1 до 0,01 нм). Эти волны излучаются при торможении в веществе заряженных частиц, разогнанных напряжением 1000 В и более. Обладают способностью проходить сквозь толстые слои вещества, непрозрачного для видимого света или ультрафиолетового излучения. Благодаря этому свойству рентгеновские лучи широко используются в медицине для диагностики переломов костей и ряда заболеваний. Рентгеновские лучи оказывают губительное действие на биологические ткани. Благодаря этому свойству их можно использовать для лечения онкологических заболеваний, хотя при избыточном облучении они смертельно опасны для человека, вызывая целый ряд нарушений в организме. Из-за очень малой длины волны волновые свойства рентгеновского излучения (интерференцию и дифракцию) можно обнаружить только на структурах, сравнимых с размерами атомов.

Гамма-излучением (-излучением) называют электромагнитные волны с частотой, большей, чем 10²⁰ Гц (или длиной волны, меньшей 0,01 нм). Возникают такие волны в ядерных процессах. Особенностью -излучения является его ярко выраженные корпускулярные свойства (т.е. это излучение ведет себя как поток частиц). Поэтому о -излучении часто говорят как о потоке -частиц.

В задаче 24.1.1 для установления соответствия между единицами измерений используем формулу (24.1), из которой следует, что период колебаний в контуре с конденсатором емкостью 1 Ф и индуктивностью 1 Гн равен секунд (ответ 1).

Из графика, данного в задаче 24.1.2, заключаем, что период электромагнитных колебаний в контуре составляет 4 мс (ответ 3).

По формуле (24.1) находим период колебаний в контуре, данном в задаче 24.1.3: (ответ 4). Отметим, что согласно шкале электромагнитных волн такой контур излучает волны длинноволнового радиодиапазона.

Периодом колебания называется время одного полного колебания. Это значит, что если в начальный момент времени конденсатор заряжен максимальным зарядом (задача 24.1.4), то через половину периода конденсатор будет также заряжен максимальным зарядом, но с обратной полярностью (та пластина, которая изначально была заряжена положительно, будет заряжена отрицательно). А максимальный в контуре ток будет достигаться между этими двумя моментами, т.е. через четверть периода (ответ 2).

Если увеличить индуктивность катушки в четыре раза (задача 24.1.5), то согласно формуле (24.1) период колебаний в контуре возрастет в два раза, а частота уменьшится в два раза (ответ 2).

Согласно формуле (24.1) при увеличении емкости конденсатора в четыре раза (задача 24.1.6) период колебаний в контуре увеличивается в два раза (ответ 1).

При замыкании ключа (задача 24.1.7) в контуре вместо одного конденсатора будут работать два таких же конденсатора, соединенных параллельно (см. рисунок). А поскольку при параллельном соединении конденсаторов их емкости складываются, то замыкание ключа приводит к двукратному увеличению емкости контура. Поэтому из формулы (24.1) заключаем, что период колебаний увеличивается в раз (ответ 3).

Пусть заряд на конденсаторе совершает колебания с циклической частотой (задача 24.1.8). Тогда согласно формулам (24.3)-(24.5) с той же частотой будет совершать колебаний ток в катушке. Это значит, что зависимость тока от времени может быть представлена в виде . Отсюда находим зависимость энергии магнитного поля катушки от времени

Из этой формулы следует, что энергия магнитного поля в катушке совершает колебания с удвоенной частотой, и, значит, с периодом, вдвое меньшим периода колебания заряда и тока (ответ 1).

В задаче 24.1.9 используем закон сохранения энергии для колебательного контура. Из формулы (24.2) следует, что для амплитудных значений напряжения на конденсаторе и тока в катушке справедливо соотношение

(здесь в отличие от (24.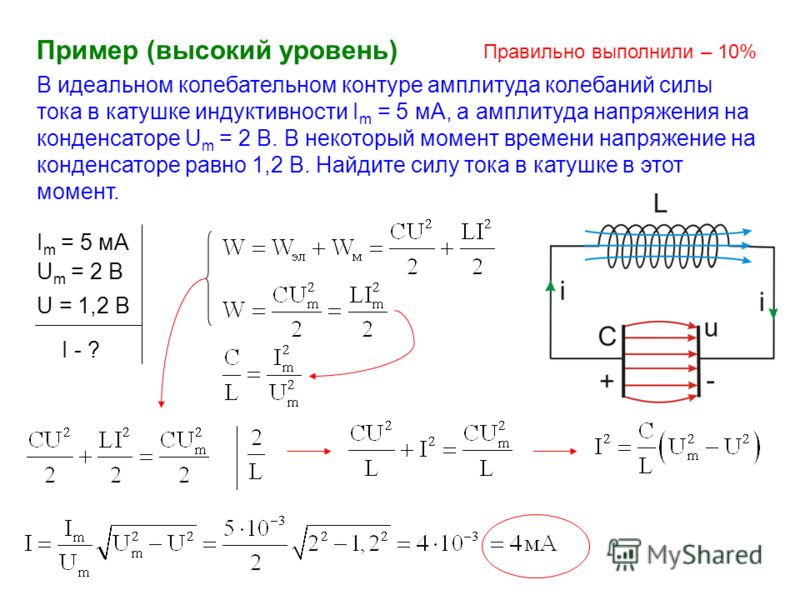 2) использовано другое выражение для энергии конденсатора). Или А (ответ 2).

В задаче 24.1.10 удобно использовать закон сохранения энергии в виде (24.2). Имеем

где и — амплитудные значения заряда конденсатора и тока в катушке. Из этой формулы с использованием соотношения (24.1) для периода колебаний в контуре находим амплитудное значение тока

ответ 3.

Радиоволны — электромагнитные волны с определенными частотами. Поэтому скорость их распространения в вакууме равна скорости распространения любых электромагнитных волн, и в частности, рентгеновских. Эта скорость — скорость света (задача 24.2.1 — ответ 1).

Как указывалось ранее, заряженные частицы излучают электромагнитные волны при движении с ускорением. Поэтому волна не излучается только при равномерном и прямолинейном движении (задача 24. 2.2 — ответ 1).

Электромагнитная волна — это особым образом изменяющиеся в пространстве и времени и поддерживающие друг друга электрическое и магнитное поля. Поэтому правильный ответ в задаче 24.2.3 — 2.

Из данного в условии задачи 24.2.4 графика следует, что период данной волны — = 4 мкс. Поэтому из формулы (24.6) получаем м (ответ 1).

В задаче 24.2.5 по формуле (24.6) находим

(ответ 4).

С антенной приемника электромагнитных волн связан колебательный контур. Электрическое поле волны действует на свободные электроны в контуре и заставляет их совершать колебания. Если частота волны совпадает с собственной частотой электромагнитных колебаний, амплитуда колебаний в контуре возрастает (резонанс) и может быть зарегистрирована. Поэтому для приема электромагнитной волны частота собственных колебаний в контуре должна быть близка к частоте этой волны (контур должен быть настроен на частоту волны). Поэтому если контур нужно перенастроить с волны длиной 100 м на волну длиной 25 м (задача 24.2.6), собственная частота электромагнитных колебаний в контуре должна быть увеличена в 4 раза. Для этого согласно формулам (24.1), (24.4) емкость конденсатора следует уменьшить в 16 раз (ответ 4).

Согласно шкале электромагнитных волн (см. введение к настоящей главе), максимальной длиной из перечисленных в условии задачи 24.2.7 электромагнитных волн обладает излучение антенны радиопередатчика (ответ 4).

Среди перечисленных в задаче 24.2.8 электромагнитных волн максимальной частотой обладает рентгеновское излучение (ответ 2).

Электромагнитная волна является поперечной. Это значит, что векторы напряженности электрического поля и индукции магнитного поля в волне в любой момент времени направлены перпендикулярно направлению распространения волны. Поэтому при распространении волны в направлении оси (задача 24.2.9), вектор напряженности электрического поля направлен перпендикулярно этой оси. Следовательно, обязательно равна нулю его проекция на ось = 0 (ответ 3).

Скорость распространения электромагнитной волны — есть индивидуальная характеристика каждой среды. Поэтому при переходе электромагнитной волны из одной среду в другую (или из вакуума в среду) скорость электромагнитной волны изменяется. А что можно сказать о двух других параметрах волны, входящих в формулу (24.6), — длине волны и частоте . Будут ли они изменяться при переходе волны из одной среды в другую (задача 24.2.10)? Очевидно, что частота волны не изменяется при переходе из одной среды в другую. Действительно, волна это колебательный процесс, в котором переменное электромагнитное поле в одной среде создает и поддерживает поле в другой среде благодаря именно этим изменениям. Поэтому периоды этих периодических процессов (а значит и частоты) в одной и другой среде должны совпадать (ответ 3). А поскольку скорость волны в разных средах разная, то из проведенных рассуждений и формулы (24. 6) следует, что длина волны при ее переходе из одной среды в другую — изменяется.

Физика Колебательный контур. Превращение энергии при электромагнитных колебаниях

Материалы к уроку

Конспект урока

Электромагнитные колебания — это периодические изменения со временем электрических и магнитных величин (заряда, силы тока, напряжения, напряженности, магнитной индукции и др.) в электрической цепи. Для возбуждения и поддержания электромагнитных колебаний требуются определенные системы, простейшей из которых является колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R (это может быть сопротивление провода катушки и проводов, соединяющих катушку с конденсатором). Идеальный контур Томсона — колебательный контур без активного сопротивления (R = 0). После того как изобрели лейденскую банку, которая является первым конденсатором, и научились сообщать ей большой заряд с помощью электростатической машины, начали изучать электрический разряд банки. Замыкая обкладки лейденской банки с помощью проволочной катушки, можно обнаружить, что стальные спицы внутри катушки намагничиваются. Здесь все было понятно: электрический ток должен намагничивать стальной сердечник катушки. Удивительным было то, что невозможно было предсказать какой конец сердечника катушки окажется северным полюсом, а какой – южным. В 1870–1880 гг. Гельмгольц Герман Людвиг Фердинанд, немецкий ученый, много занимался проблемами электродинамики, пытаясь найти критерии для выбора в пользу одной из существовавших тогда электродинамических теорий. Под его влиянием Г. Герц провел исследования, приведшие к обнаружению электромагнитных волн. Большую роль в развитии электромагнетизма сыграли и собственные опыты Гельмгольца, поставленные им еще в 1869 г. Обратив внимание на колебательный характер разряда лейденской банки, он показал, что аналогичные колебания возникают в индукционной катушке, соединенной с конденсатором (т. е. по существу создал колебательный контур, состоящий из индуктивности и ёмкости). Повторяя опыт примерно в одинаковых условиях, в одних случаях получался один результат, а в других — другой. Позже ученые пришли к выводу, что при разрядке конденсатора через катушку возникают колебания. За время разрядки конденсатор успевает много раз перезарядиться, и ток много раз меняет направление, в результате чего сердечник может намагничиваться различным образом. Периодические или почти периодические изменения заряда силы тока и напряжения называются электромагнитными колебаниями, которые происходят с очень большой частотой, значительно превышающей частоту механических колебаний. Поэтому для их наблюдения и исследования самым подходящим прибором является электронный осциллограф. В электронно-лучевой трубке осциллографа узкий пучок электронов попадает на экран. Экран светится при бомбардировке его электронами. На горизонтально отклоняющие пластины трубки подается переменное напряжение развертки пилообразной формы. Сравнительно медленно напряжение нарастает, а потом очень резко уменьшается. Электрическое поле между пластинами заставляет электронный луч пробегать экран в горизонтальном направлении с постоянной скоростью, потом мгновенно возвращаться назад.  Этот процесс повторяется. Если теперь присоединить вертикально отклоняющие пластины трубки к конденсатору, то колебания напряжения при его зарядке вызовут колебания луча в вертикальном направлении. В результате на экране образуется временная развертка колебаний, подобная той, которую вычерчивают маятник с песочницей над движущимся листом бумаги. Обычно колебания в цепи затухают за доли секунды. Поэтому используют осциллограф с экраном, способным светиться долго. Колебания в системе, которые возникают после выведения ее из положения равновесия, называются свободными колебаниями. В описываемом случае система выводится из равновесия при сообщении конденсатору заряда. Зарядка конденсатора эквивалентна отклонению маятника от положения равновесия. Рисунок иллюстрирует характерные стадии колебаний в контуре за один период. Легко получить в электрической цепи и вынужденные электромагнитные колебания, которые возникают в цепи под действием внешней периодической электродвижущей силы.  При замыкании цепи переменная ЭДС  создает переменный ток, и стрелка гальванометра начинает колебаться около положения равновесия. Силовые линии этого магнитного поля направлены по правилу буравчика. Свободные электромагнитные колебания возникают при разрядке конденсатора через катушку индуктивности. Вынужденные колебания же вызываются периодической ЭДС. Простейшая система, в которой могут происходить свободные электромагнитные колебания, состоит из конденсатора и катушки, присоединенной к его обкладкам. Такая система называется колебательным контуром.
Рассмотрим, каким образом в контуре возникают электромагнитные колебания. Зарядим конденсатор, присоединив его на некоторое время к батарее с помощью переключателя. При этом конденсатор получит энергию. Между обкладками конденсатора возникнет разность потенциалов. Переведем переключатель в положение 2. Конденсатор начнет разряжаться, и в цепи появится электрический ток. Сила тока будет увеличиваться постепенно, пока достигнет максимального значения. Это обусловлено явлением самоиндукции. Появление тока порождает переменное магнитное поле. Это переменное магнитное поле порождает вихревое электрическое поле в проводнике, которое при возрастании магнитного поля действует против тока и препятствует его мгновенному увеличению. По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля тока. Полная энергия электромагнитного поля контура будет равна сумме энергий магнитного и электрического полей. В момент, когда конденсатор полностью разрядится, энергия электрического поля станет равной нулю. Энергия же магнитного поля тока согласно закону сохранения энергии будет максимальной. В этот момент сила тока также достигнет максимального значения.
Электрический ток не может прекратиться сразу. Здесь проявляется самоиндукция. Как только сила тока и созданное им магнитное поле начнут уменьшаться, возникает вихревое электрическое поле, которое поддерживает ток. В результате конденсатор будет перезаряжаться до тех пор, пока сила тока не станет равной нулю. Энергия магнитного поля в этот момент будет равна нулю, энергия электрического поля конденсатора опять станет максимальной. После этого конденсатор вновь начнет перезаряжаться, и система возвратится в исходное состояние. Если бы не было потерь энергии, то этот процесс продолжался бы сколь угодно долго. В действительности происходят потери энергии. Катушка и соединительные провода обладают сопротивлением, что приводит к постепенному превращению энергии электромагнитного поля во внутреннюю энергию проводника. В колебательном контуре энергия электрического поля заряженного конденсатора периодически превращается в энергию магнитного поля тока. Если бы сопротивления не было, то полная энергия электромагнитного поля осталась бы неизменной.
Электромагнитные колебания в контуре имеют характерные сходства со свободными механическими колебаниями тела, закрепленного на пружине. При механических колебаниях периодически изменяются координата тела и проекция его скорости, а при электромагнитных колебаниях изменяются заряд конденсатора и сила тока в цепи. Одинаковый характер изменения величин при механических и электрических колебаниях объясняется тем, что имеется аналогия в условиях, при которых порождаются механические и электромагнитные колебания. Возвращение к положению равновесия тела на пружине вызывается силой упругости пропорциональной смешению тела от положения равновесия. Коэффициентом пропорциональности является жесткость пружины. Разрядка конденсатора, то есть появление тока, обусловлена напряжением между пластинами конденсатора, которое пропорционально заряду. Коэффициентом пропорциональности является величина обратная емкости конденсатора. Аналогично тому, как вследствие инертности тело постепенно увеличивает скорость под действием силы, и эта скорость после прекращения действия силы не становится сразу равной нулю, электрический ток в катушке за счет явления самоиндукции увеличивается под действием напряжения постепенно и не исчезает сразу, как только напряжение становится равным нулю. Индуктивность контура играет ту же роль, что и масса тела в механике. Соответственно кинетической энергии тела отвечает энергия магнитного поля тока. Зарядке конденсатора от батареи соответствует сообщение телу, прикрепленному к пружине потенциальной энергии при смещении тела на расстояние икс-эм от положения равновесия (рисунок а). Сравнивая это выражение с энергией конденсатора, замечаем, что жесткость k (ка) пружины играет при механическом  колебательном процессе такую же роль как величина  обратная емкости при электромагнитных колебаниях, а начальная координата  икс-эм соответствует заряду ку-эм. Возникновение в электрической цепи тока и за счет разности потенциалов соответствует появлению в механической колебательной системе скорости вэ-икс под действием силы упругости пружины (рисунок б). Моменту, когда конденсатор разрядится, а сила тока достигнет максимума, соответствует прохождения тела через положение равновесия с максимальной скоростью (рисунок в). Далее конденсатор начнет перезаряжаться, а тело – смещаться влево от положения равновесия (рисунок г).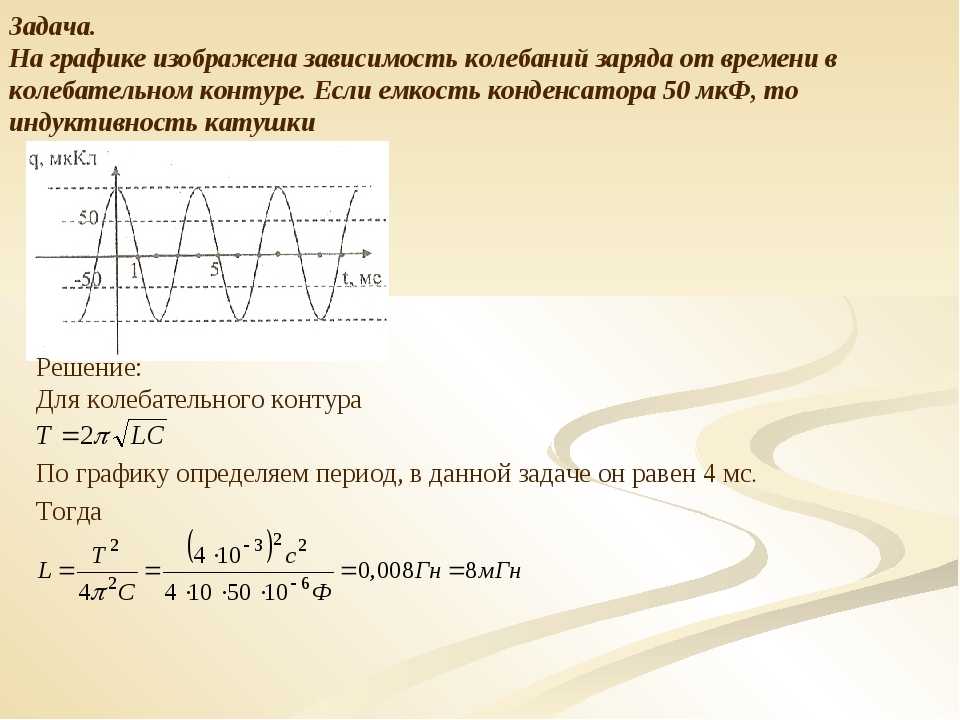 По прошествии половины периода тэ конденсатор полностью перезарядится, и сила тока станет равной нулю. Этому состоянию соответствует отклонение тела в крайнее левое положение, когда его скорость равна нулю (рисунок д). Соответствие между механическими и электрическими величинами при колебательных процессах можно свести в таблицу. Перейдем теперь к количественной теории процессов в колебательном контуре.  Получим уравнение, описывающее процессы в колебательном контуре. Рассмотрим колебательный контур, сопротивлением которого можно пренебречь.
Уравнение, описывающее свободные электрические колебания в контуре, можно получить с помощью закона сохранения энергии. Значение полной электромагнитной энергии контура в любой момент времени равно сумме значений энергий магнитного и электрического полей.  Эта энергия не меняется с течением времени, если сопротивление контура равно нулю.
Производная полной энергии по времени равна нулю, так как энергия постоянна. Следовательно, равна нулю сумма производных от энергии магнитного и электрического полей. Вычисляем производные по времени. То есть нужно найти производную сложной функции. Поэтому производная квадрата силы тока равна удвоенному произведению силы тока на производную силы тока по времени. То же самое относится к производной квадрата заряда. Но производная заряда по времени представляет собой силу тока в данный момент времени. Производная силы тока по времени есть не что иное, как вторая производная заряда по времени, подобно тому как производная скорости (ускорение) есть вторая производная координаты по времени. Получили уравнение, описывающее свободные электрические колебания в контуре. Физический смысл уравнений полученного уравнения состоит в том, что скорость изменения энергии магнитного поля по модулю равна скорости изменения энергии электрического поля; знак минус указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля убывает и наоборот. Именно благодаря этому полная энергия не меняется. Уравнение, описывающее свободные электромагнитные колебания в контуре, ничем, кроме обозначений, не отличается от уравнения, описывающее свободные механические колебания пружинного маятника. Коэффициент ка-на-эм представляет собой квадрат собственной частоты колебаний. Поэтому и коэффициент единица на-эл-цэ так же представляет собой квадрат циклической частоты свободных электрических колебаний. Аналогию можно заметить и в формулах, определяющих период свободных колебаний в контуре.
Эта формула называется формулой Томсона в честь английского физика У. Томсона (Кельвина), который ее впервые вывел. Подобно тому, как координата при механических колебаниях изменяется со временем по гармоническому закону, так и заряд конденсатора меняется с течением времени по такому же закону. Где дэ-макс — амплитуда колебаний заряда. Сила тока совершает гармонические колебания, где и-макс — амплитуда колебаний силы тока. Колебания силы тока опережают по фазе на пи-пополам колебания заряда. Точно так же колебания скорости при движении шарика, прикрепленного к пружине, или математического маятника опережают на пи-пополам колебания координаты (смещения).
Задача Колебательный контур состоит из катушки индуктивности и конденсатора. Индуктивность катушки уменьшили от 32 миллигенри до 4 миллигенри. Как и во сколько раз изменится в результате этого период электромагнитных колебаний в контуре? При решении задач воспользуемся формулой Томпсона. Составим отношение периодов колебаний для обоих случаев и после сокращений приходим к результату 4. Период колебаний увеличится в 4 раза, частота колебаний уменьшиться в 4 раза.
Задача
В колебательном контуре зависимость заряда q на конденсаторе от времени t имеет вид….  Какую информацию о колебаниях заряда в контуре можно получить из этого уравнения?
Ответ: 10 амплитуда колебаний заряда в электромагнитном контуре составляет 1 десятая милликулон, а квадрат циклической частоты равен 10-пи.
 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

14.

5 Колебания в LC-контуре – University Physics Volume 2

Глава 14. Индуктивность

Цели обучения

К концу этого раздела вы сможете:

• Объяснять, почему заряд или ток колеблются между конденсатором и индуктивностью, соответственно, при последовательном соединении
• Опишите взаимосвязь между зарядом и током, колеблющимся между конденсатором и катушкой индуктивности, соединенными последовательно

Стоит отметить, что и конденсаторы, и катушки индуктивности хранят энергию в своих электрических и магнитных полях соответственно. Цепь, содержащая катушку индуктивности ( L ) и конденсатор ( C ), может колебаться без источника ЭДС, перемещая энергию, хранящуюся в цепи, между электрическим и магнитным полями. Таким образом, концепции, которые мы развиваем в этом разделе, непосредственно применимы к обмену энергией между электрическим и магнитным полями в электромагнитных волнах или свете. Мы начнем с идеализированной цепи с нулевым сопротивлением, которая содержит катушку индуктивности и конденсатор, 9{2}}{С}.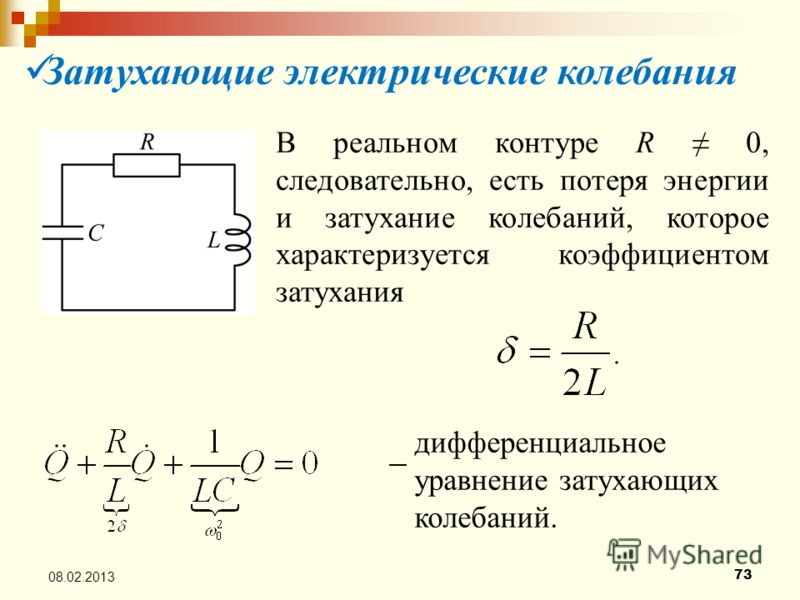 [/латекс]

Когда переключатель замкнут, конденсатор начинает разряжаться, создавая ток в цепи. Ток, в свою очередь, создает магнитное поле в индукторе. Конечным результатом этого процесса является передача энергии от конденсатора с его уменьшающимся электрическим полем к индуктору с его увеличивающимся магнитным полем.

Рисунок 14.16  (a–d) Колебания накопления заряда при изменении направления тока в LC-цепи. д) На графиках показано распределение заряда и тока между конденсатором и катушкой индуктивности. 9{2}.[/латекс]

После достижения своего максимума [латекс]{I}_{0},[/латекс] ток i(t) продолжает переносить заряд между обкладками конденсатора, тем самым перезаряжая конденсатор. Поскольку индуктор сопротивляется изменению тока, ток продолжает течь, даже если конденсатор разряжен. Этот непрерывный ток заставляет конденсатор заряжаться с противоположной полярностью. Электрическое поле конденсатора увеличивается, а магнитное поле индуктора уменьшается, и общий эффект заключается в передаче энергии от индуктора 9. 0017 обратно на конденсатор. Согласно закону сохранения энергии, максимальный заряд, который вновь приобретает конденсатор, равен [латекс]{q}_{0}.[/латекс] Однако, как показано на рис. 14.16(в), пластины конденсатора заряжены против . к тому, чем они были изначально.

При полной зарядке конденсатор снова передает свою энергию катушке индуктивности, пока снова не разрядится полностью, как показано на рис. 14.16(d). Затем в последней части этого циклического процесса энергия возвращается к конденсатору, и восстанавливается исходное состояние цепи. 9{2}\text{/}2[/латекс]. При отсутствии трения в системе масса-пружина колебания продолжались бы бесконечно. Точно так же колебания цепи LC без сопротивления будут продолжаться вечно, если их не беспокоить; однако эта идеальная схема LC с нулевым сопротивлением непрактична, и любая схема LC будет иметь по крайней мере небольшое сопротивление, которое со временем будет излучать и терять энергию.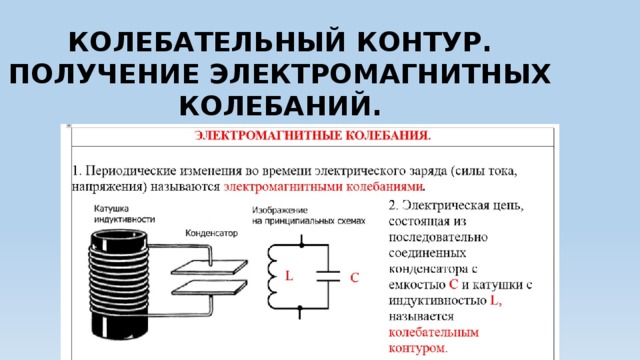

Частота колебаний без сопротивления 9{2}.[/латекс]

Эквивалентность двух систем очевидна. Чтобы перейти от механической системы к электромагнитной, мы просто заменим m на L , v на i , k на 1/ C и x на q. Теперь x(t) равно

.

[латекс] х \ влево (т \ вправо) = А \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ влево (\ омега т + \ varphi \ вправо) [/латекс]

, где [латекс]\омега =\sqrt{k\текст{/}м}.[/латекс] Следовательно, заряд конденсатора в Цепь LC задается

[латекс] q \ влево (т \ вправо) = {q} _ {0} \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ влево (\ омега т + \ varphi \ вправо) [ /латекс]

где угловая частота колебаний в контуре

[латекс]\омега =\sqrt{\frac{1}{LC}}.[/латекс]

Наконец, ток в цепи LC находится путем взятия производной по времени от q(t) :

[латекс] я \ влево (т \ вправо) = \ гидроразрыва {dq \ влево (т \ вправо)} {дт} = \ текст {-} \ омега {q} _ {0} \ фантом {\ правило {0,2 em}{0ex}}\text{sin}\left(\omega t+\varphi \right). [/latex] 9{-5}[/latex] C. (a) Какова угловая частота колебаний в цепи? б) Каков максимальный ток, протекающий по цепи? в) Через какое время конденсатор полностью разрядится? (d) Найдите уравнение, которое представляет q(t) .

Стратегия

Угловая частота цепи LC определяется уравнением 14.41. Чтобы найти максимальный ток, максимальная энергия в конденсаторе устанавливается равной максимальной энергии в катушке индуктивности. Время, в течение которого конденсатор разрядится, если он изначально заряжен, составляет четверть периода цикла, поэтому, если мы вычислим период колебаний, мы сможем узнать, какую четверть от этого времени нужно найти. Наконец, зная начальный заряд и угловую частоту, мы можем составить косинусное уравнение, чтобы найти 9{-2}\phantom{\rule{0.2em}{0ex}}\text{A}.[/latex]

Этот результат также можно найти по аналогии с простым гармоническим движением, где ток и заряд являются скоростью и положением осциллятора.

Конденсатор полностью разряжается за одну четвертую цикла или за время T /4, где T — период колебаний. {3}t\right).[/latex]

Значение

Соотношение энергий, установленное в части (b), — не единственный способ, которым мы можем приравнять энергии. В большинстве случаев некоторая энергия сохраняется в конденсаторе, а некоторая энергия хранится в катушке индуктивности. Мы можем поместить оба термина в каждую часть уравнения. Исследуя цепь только при отсутствии заряда на конденсаторе или отсутствии тока в катушке индуктивности, мы упрощаем уравнение энергии.

Проверьте свои знания

Угловая частота колебаний в 9{3}[/latex] рад/с. (a) Если [латекс]L=0,10\фантом{\правило{0,2em}{0ex}}\текст{H}[/латекс], что такое C ? (b) Предположим, что при [latex]t=0,[/latex] вся энергия запасается в индукторе. Каково значение [latex]\varphi ?[/latex] (c) Второй идентичный конденсатор подключен параллельно исходному конденсатору. Какова угловая частота этого контура?

Показать раствор

а. [латекс] 2,5 мк\текст {F}[/латекс]; б. [латекс]\pi \text{/}2\phantom{\rule{0. {3} \ фантом {\ правило {0.2em} {0ex} }\text{рад/с}[/латекс]

Резюме

• Энергия, передаваемая колебательным образом между конденсатором и катушкой индуктивности в цепи LC , происходит с угловой частотой [латекс]\омега =\sqrt{\frac{1}{LC}}[/latex] .
• Заряд и ток в цепи задаются как

  [латекс]\begin{array}{ccc}\hfill q\left(t\right)& =\hfill & {q}_{0}\phantom{\rule {0.2em}{0ex}}\text{cos}\left(\omega t+\varphi \right),\hfill \\ \hfill i\left(t\right)& =\hfill & \text{-}\ omega {q}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\omega t+\varphi \right).\hfill \end{array}[/latex]

Концептуальные вопросы

Применяются ли правила Кирхгофа к цепям, содержащим катушки индуктивности и конденсаторы?

Показать решение

да

Может ли элемент схемы иметь как емкость, так и индуктивность?

Что в схеме LC определяет частоту и амплитуду колебаний энергии в дросселе или конденсаторе?

Показать решение

Амплитуда колебаний энергии зависит от начальной энергии системы. Частота в 9Схема 0017 LC зависит от значений индуктивности и емкости.

Проблемы

Конденсатор емкостью 5000 пФ заряжается до 100 В, а затем быстро подключается к катушке индуктивности 80 мГн. Определите (а) максимальную энергию, запасенную в магнитном поле индуктора, (б) пиковое значение тока и (в) частоту колебаний цепи.

Собственная индуктивность и емкость схемы LC составляют 0,20 мГн и 5,0 пФ. С какой угловой частотой колеблется контур? 9{-7}\phantom{\rule{0.2em}{0ex}}\text{s}[/latex]

Собственная индуктивность и емкость колебательного контура LC составляют [латекс] L = 20\phantom{\rule{0.2em}{0ex}}\text{мГн и}\phantom{\rule{0.2em}{ 0ex}}C=1.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},[/latex] соответственно. а) Какова частота колебаний? б) Если максимальная разность потенциалов между пластинами конденсатора равна 50 В, какова максимальная сила тока в цепи?

В качающемся LC , максимальный заряд конденсатора [латекс]{q}_{м}[/латекс]. Определить заряд конденсатора и ток через катушку индуктивности, когда энергия распределяется поровну между электрическим и магнитным полями. Выразите ответ в терминах [латекс]{q}_{m}[/латекс], L и C .

Показать раствор

[латекс]q=\frac{{q}_{m}}{\sqrt{2}},I=\frac{{q}_{m}}{\sqrt{2LC}} [/латекс]

В схеме, показанной ниже, [латекс]{\текст{S}}_{1}[/латекс] одновременно размыкается и [латекс]{\текст{S}}_{2}[/латекс] закрывается. Определить: а) частоту результирующих колебаний, б) максимальный заряд конденсатора, в) максимальный ток через катушку индуктивности, г) электромагнитную энергию колебательного контура. 9{-12}\phantom{\rule{0.2em}{0ex}}\text{F}\hfill \end{массив}[/latex]

Глоссарий

LC схема

Схема

, состоящая из источника переменного тока, катушки индуктивности и конденсатора

.

Лицензии и атрибуты

Колебания в цепи LC. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/14-5-oscillations-in-an-lc-circuit. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction

6. Свободные колебания — Заметки по линейной алгебре и ОДУ

Наиболее распространенное использование уравнений второго порядка — моделирование колебательного или другого периодического поведения. Такое поведение встречается во множестве контекстов. Когда колебательная система не подвергается никаким внешним силам, мы называем ее невынужденным осциллятором или свободным осциллятором.

6.1. Механический осциллятор

Объект, прикрепленный к идеальной пружине, удовлетворяет ОДУ

(6.2)\[mx» + b x’ + kx = 0,\]

где \(x(t)\) — смещение от естественного покоя положение, \(m\) — масса объекта, \(b\) — коэффициент затухания из-за трения или механического демпфирования, а \(k\) — свойство пружины, называемое жесткостью пружины. Эта константа представляет собой отношение восстанавливающей силы пружины к величине, на которую она растягивается или сжимается.

Внимание

Все именованные параметры, такие как \(m\), \(k\) и \(b\), считаются неотрицательными, если не указано иное.

Примечание

Уравнение (6.2) одинаково хорошо применимо к горизонтальным и вертикальным колебаниям. Гравитация не появляется в вертикальном случае, потому что она учитывается путем измерения \(x\) из положения статического равновесия.

Если даны, начальные значения для (6.2) задают начальное положение и начальную скорость, которые однозначно определяют решение.

Маятник — это другой тип механического осциллятора. Правильное ОДУ:

\[\theta» + \gamma \theta + \frac{g}{L}\sin (\theta) = 0,\]

, где \(\theta(t)\) угол, образованный вертикально-вниз, \(L\) — длина руки, а \(g\) — ускорение свободного падения. Это уравнение является нелинейным, и его трудно анализировать без разработки новых инструментов. Но если угол остается малым, то разумное приближение равно

\[\theta» + \gamma \theta + \frac{g}{L}\theta = 0,\]

, который представляет собой линейный осциллятор с постоянными коэффициентами.

6.2. Электрические генераторы

Цепь переменного тока обычно имеет элементы сопротивления, емкости и индуктивности. Они прекрасно аналогичны трению/демпфированию, жесткости пружины и массе. Если эти элементы соединены последовательно, определяющим ОДУ будет

\[LI» + RI’ + \frac{1}{C}I = 0,\]

, где \(I(t)\) ток, протекающий через цепь, \(L\) — индуктивность, \(R\) — сопротивление, а \(C\) — емкость.

6.3. Унификация обозначений

Когда у вас есть много версий одной и той же корневой задачи, каждая из которых использует разные символы и единицы измерения, у вас есть три варианта.

1. Решайте каждую новую проблему с нуля.

2. Получение пользовательских формул для каждого приложения.

3. Найдите минимальный набор параметров и выразите через них задачу и решение.

Вариант 1 крайне неэффективен. Вариант 2 подойдет для инженерного курса. Здесь мы выбираем вариант 3 и разрабатываем обобщенные знания, которые можно переинтерпретировать для каждого нового приложения.

ОДУ пружинно-массового генератора, записанное в нашей стандартной форме, равно

\[x» + \frac{b}{m} x’ + \frac{k}{m} x = 0. \]

Это сразу говорит о том, что нам нужны только два параметра, а не три, чтобы выразить весь диапазон поведения. (Дополнительное удобство состоит в том, что и \(b/m\), и \(\sqrt{k/m}\) имеют единицы обратного времени.) Соответственно, мы вводим

\[\omega_0 = \sqrt{\frac{ k}{m}}, \qquad Z = \frac{b/m}{2\omega_0} = \frac{b}{\sqrt{4km}}.\]

Параметр \(\omega_0\) известен как собственная частота с единицами, обратно пропорциональными времени, а \(Z\) представляет собой безразмерный коэффициент демпфирования, описывающий относительную интенсивность демпфирования.

Важно

В математике мы обычно используем частоту для обозначения множителя \(t\) в функции sin или cos. Это наше использование. В некоторых областях это называется угловой частотой, а частота используется для обозначения количества циклов в единицу времени, например, в Гц.

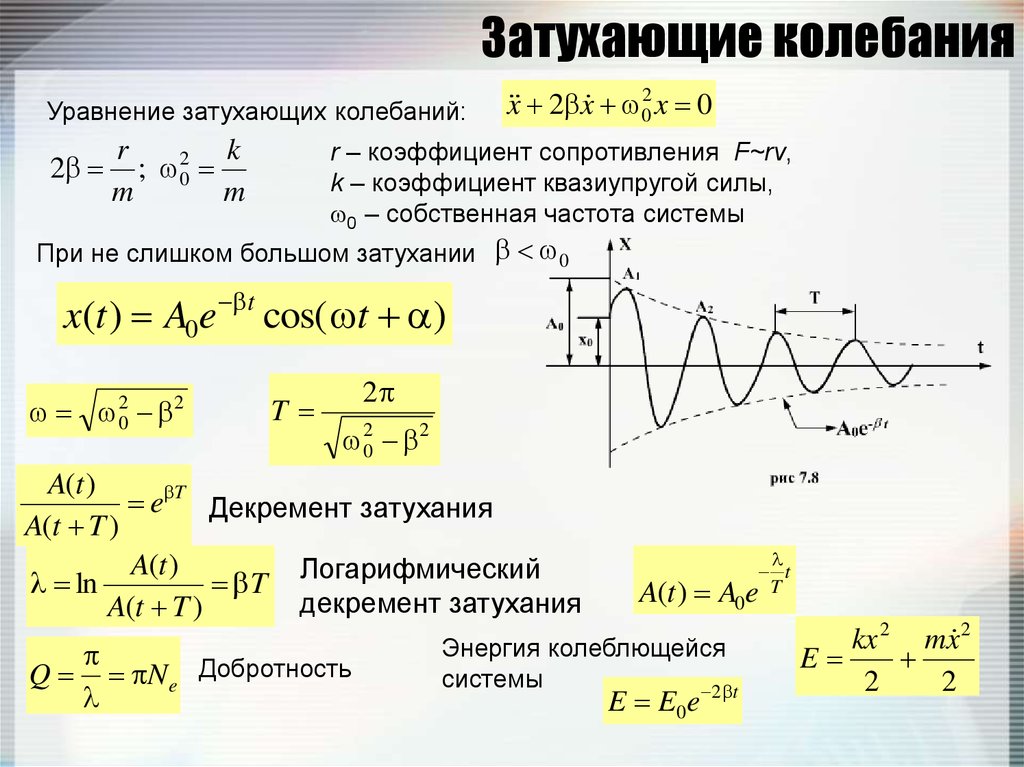
Теперь ОДУ свободного осциллятора становится равным 92x = 0\) обсуждалось в разделе 5. Это приводит к чистому колебанию на частоте \(\omega_0\). Это известно как простое гармоническое движение.

Пример

Когда на пружину подвешивают груз массой 2 кг, пружина растягивается на 0,25 м. Какова собственная частота системы масса-пружина? Предположим, что груз опустили на 0,2 м ниже положения равновесия, а затем подбросили вверх со скоростью 1 м/с. Какова амплитуда движения?

Закон Гука для пружины утверждает, что \(F=k x\), поэтому мы находим постоянную пружины из \(k=F/x=2g/0,25=8g\), где \(g=9{-Z\omega_0 t} \cos( \omega_d t + \theta),\]

где \(R\) и \(\theta\) определяются начальными условиями. Это решение является псевдопериодическим, комбинируя колебания с частотой \(\omega_d <\omega_0\) внутри экспоненциального затухания.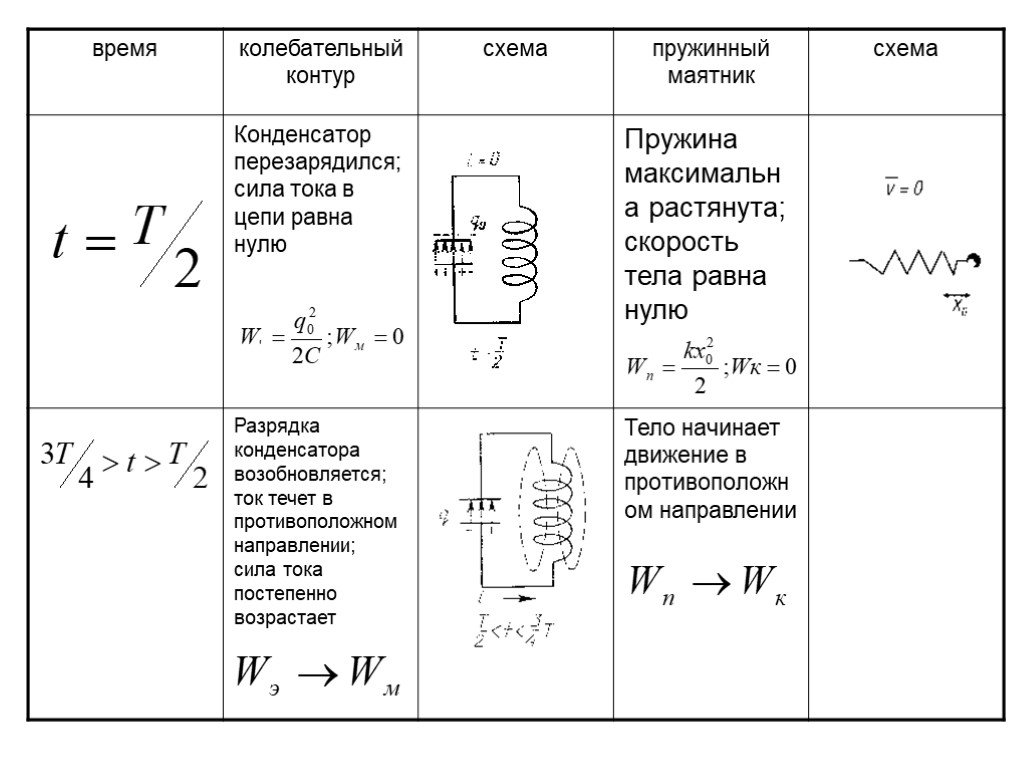 Мы называем это недодемпфированным генератором.

6.6. Критически затухающий осциллятор, \(Z=1\)

При \(Z=1\) комплексные корни сливаются в двойной действительный корень,

\[\lambda_1 = \lambda_2 = -\omega_0,\]

с общий гомогенный раствор 92-1},\]

, которые отрицательны и действительны. Это дает экспоненциально убывающее однородное решение. В этом случае мы имеем передемпфированный осциллятор.

Таблица 6.1 Коэффициент демпфирования и характеристические значения

Коэффициент демпфирования	Корневое свойство	Описание
\(Z=0\)	мнимый	недемпфированный
\(0	комплекс	с недостаточным демпфированием
\(Z=1\)	реальный, отрицательный, повторный	критически демпфированные
\(Z > 1\)	действительное, отрицательное, отличное	сверхдемпфированный

Пример

Груз массой 5 ​​кг подвешен на пружине с постоянным \(11\) Н на м и соединен с амортизатором, обеспечивающим сопротивление 8 Н-с на метр.