Касательная к окружности и свойства отрезков касательных
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Расскажем подробнее, что такое касательная и секущая.
Напомним, что расстояние от точки до прямой — это длина перпендикуляра, опущенного из точки на прямую.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности. В этом случае она имеет с окружностью ровно одну общую точку. Такую прямую называют касательной к окружности.
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность в двух точках. Такую прямую называют секущей.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая не имеет с окружностью общих точек.
Запишем основные теоремы о касательных. Они помогут нам при решении задач ЕГЭ и ОГЭ.
Теорема 1.
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
На рисунке радиус OA перпендикулярен прямой m.
Теорема 2. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Доказательство:
Дана окружность с центром O.
Прямые AB и AC — касательные, точки B и C — точки касания. Докажем, что
AB = AC и
Проведем радиусы OB и OC в точки касания.
По свойству касательной, и .
В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC и
Теорема 3. Отрезки касательных, проведенных к окружности из одной точки, равны.
Доказательство:
Пусть из точки A к окружности проведены касательные AB и AC. Соединим точку A с центром окружности точкой O. Треугольники AOB и AOC равны по гипотенузе и катету, следовательно, AB = AC.
Теорема 4. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Угол ACМ на рисунке равен половине угловой величины дуги AC.
Доказательство теоремы здесь.
Теорема 5, о секущей и касательной.
Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
Доказательство теоремы смотрите здесь.
Разберем задачи ЕГЭ и ОГЭ по теме: Касательная к окружности.
Задача 1.
Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Решение:
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол CAO — прямой. Из треугольника ACO получим, что угол AOC равен 62 градуса. Bеличина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги AB— тоже 62 градуса.
Ответ: 62.
Задача 2.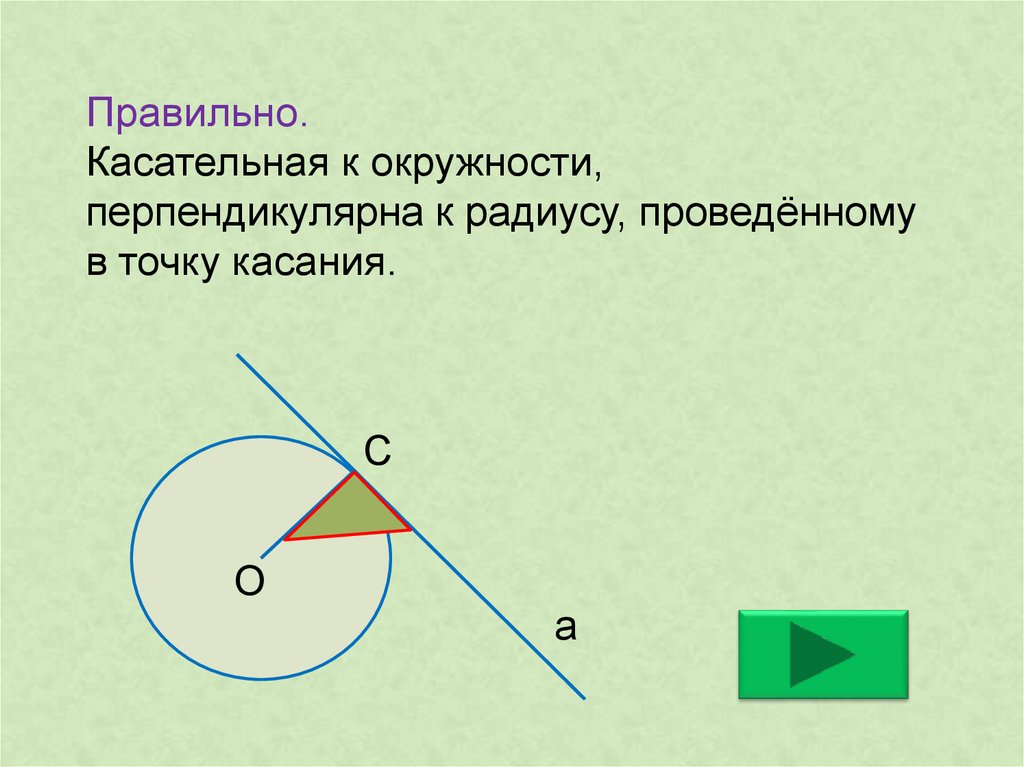
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.
Решение:
Это чуть более сложная задача. Центральный угол AOD опирается на дугу AD, следовательно, он равен 116 градусов. Тогда угол AOC равен Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол OAC — прямой. Тогда угол ACO равен
Ответ: 26.
Задача 3.
Хорда AB стягивает дугу окружности в Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Решение:
Проведем радиус OB в точку касания, а также радиус OA. Угол OBC равен Треугольник BOA — равнобедренный. Нетрудно найти, что угол OBA равен 44 градуса, и тогда угол CBA равен 46 градусов, то есть половине угловой величины дуги AB.
Мы могли также воспользоваться теоремой: Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.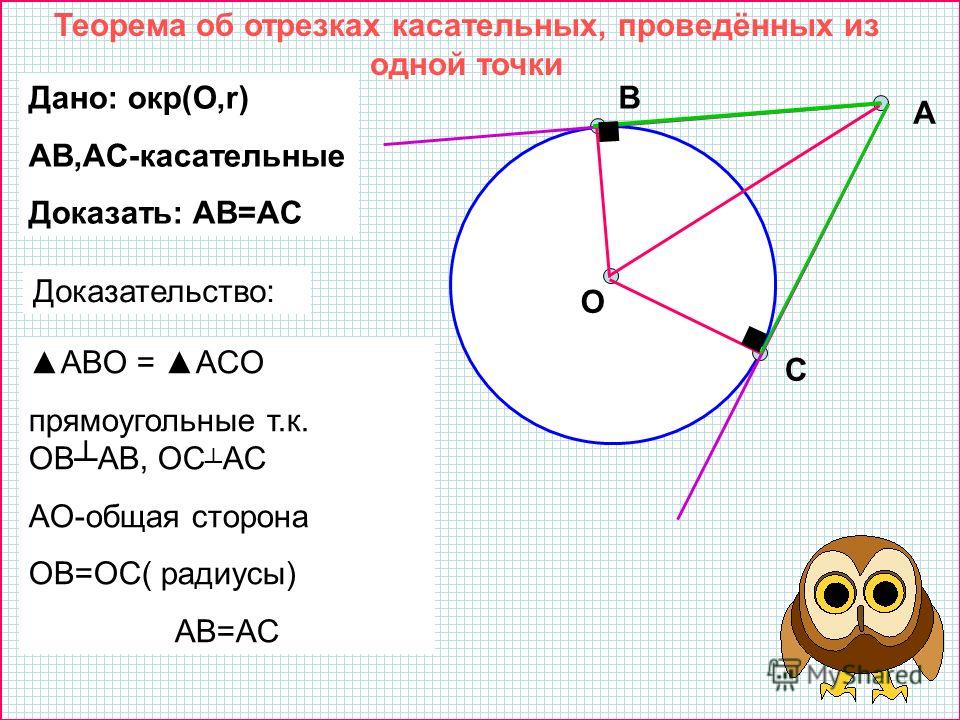
Задача 4.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
Решение:
Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника ABC складывается из периметров отсеченных треугольников.
Ответ: 24.
Вот более сложная задача из вариантов ЕГЭ:
Задача 5.
Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Решение:
Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника.
Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку O — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините точку O с вершинами A, B, C, D, E. Получились треугольники AOB, BOC, COD, DOE и EOA.
Очевидно, что площадь многоугольника
Треугольники АОВ, ВОС, COD, DOE и ЕОА имеют равные высоты, причем все эти высоты равны радиусу окружности.
где p — полупериметр многоугольника.
По условию, P = 10, S = 5, тогда
Ответ: 1
Задачи ЕГЭ
1. Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B . Найдите величину меньшей дуги AB окружности. Ответ дайте в градусах.
Решение:
По условию, CA — касательная, A — точка касания.
. Треугольник ACO — прямоугольный, .
Угол — центральный, и он равен угловой величине дуги AB, на которую опирается.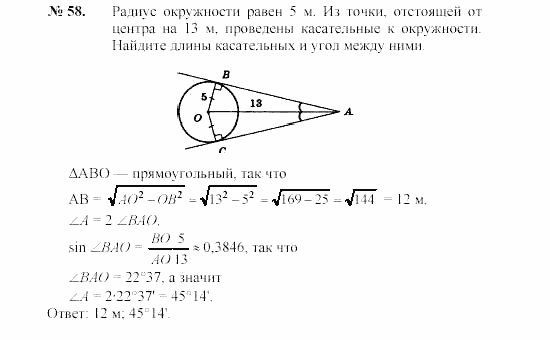
Ответ: 63.
2. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна . Найдите угол ACB. Ответ дайте в градусах.
Решение:
Центральный угол AOB равен угловой величине дуги, на которую он опирается, то есть
AC и BC — касательные, поэтому , поскольку касательная перпендикулярна радиусу, проведенному в точку касания.
Сумма углов четырехугольника ACBO равна
Ответ: 122.
3. Хорда AB стягивает дугу окружности в . Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Решение:
Применим теорему об угле между касательной и хордой.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Значит, угол ABC равен .
Ответ: 46.
4. Через концы A и B дуги окружности с центром О проведены касательные AC и BC. Угол CAB равен . Найдите угол AOB. Ответ дайте в градусах.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Поэтому меньшая дуга AB окружности равна . Центральный угол равен угловой величине дуги, на которую он опирается, значит, угол AOB равен .
Мы могли бы решить задачу и по-другому, рассматривая четырехугольник ACBO, как в задаче 2.
Ответ: 64.
5. Через концы A, B дуги окружности в проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
Решение:
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними. В треугольнике ABC:
Ответ: 118.
6. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, сторона CO пересекает окружность в точках B и D, а дуга AD окружности, заключенная внутри этого угла, равна .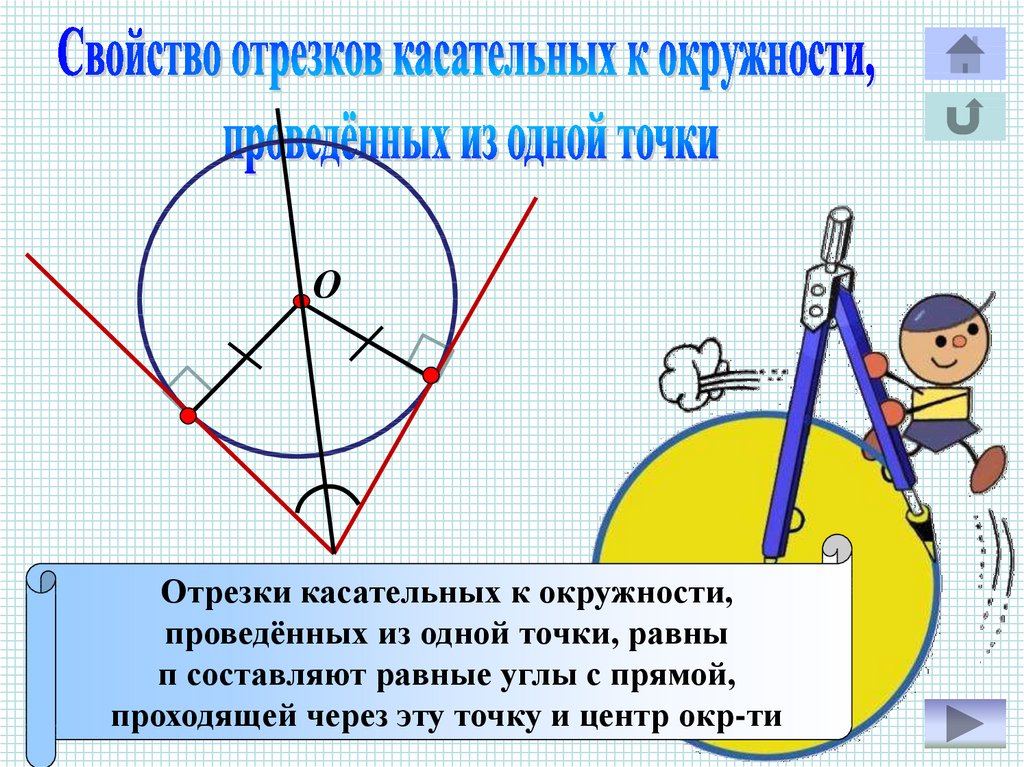
Решение:
По условию, DB — диаметр окружности, поэтому дуга AВ, не содержащая точки D, равна . На эту дугу опирается центральный угол AOB, он равен . Треугольник AOC прямоугольный, так как касательная CA перпендикулярна радиусу ОA, проведенному в точку касания.
Ответ: 26.
Задачи ОГЭ по теме: Касательная к окружности
1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Решение:
Отрезок OB — радиус, проведённый в точку касания, поэтому AB и OB перпендикулярны, треугольник AOB — прямоугольный. По теореме Пифагора:
Ответ: 5.
2. Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный . Найдите величину угла OMK. Ответ дайте в градусах.
Решение:
Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому угол OКD — прямой.
Тогда Треугольник OMK — равнобедренный, его стороны OК и OМ являются радиусами окружности, поэтому
Ответ: 7.
3. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение:
Касательная перпендикулярна радиусу, проведенному в точку касания, значит, треугольник AOB — прямоугольный. Из прямоугольного треугольника AOB по теореме Пифагора найдём AO:
Ответ: 10.
4. На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Решение:
Проведём радиус AH в точку касания. Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому треугольник ABН — прямоугольный. Из прямоугольного треугольника ABH по теореме Пифагора найдём BH:
Ответ: 40.
5. Касательные в точках A и B к окружности с центром O пересекаются под углом .
Найдите угол ABO. Ответ дайте в градусах.
Решение:
Касательные, проведённые к окружности из одной точки, равны, поэтому AC=BC и треугольник ABC — равнобедренный.
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними, значит, дуга AB равна . Угол AOB — центральный, он равен дуге, на которую опирается, то есть . Треугольник AOB равнобедренный,
Ответ: 36.
6. Из точки A проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен , а расстояние от точки A до точки O равно 8.
Решение:
Проведём радиусы OB и OC в точки касания. Треугольники AOB и AOC — прямоугольные. Эти треугольники равны по катету и гипотенузе.
OB — OC как радиусы окружности, гипотенуза общая. Значит,
Из треугольника AOB найдём OB, то есть радиус окружности.
Ответ: 4.
7. Через точку A, лежащую вне окружности, проведены две прямые.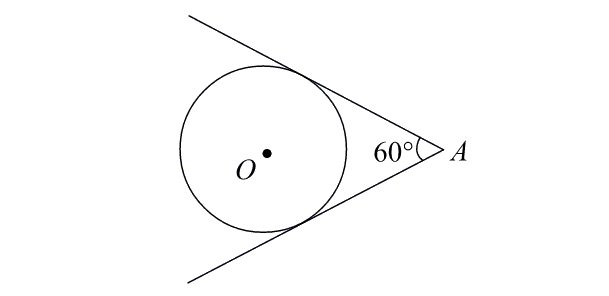
Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK.
Решение:
По теореме о секущей и касательной,
Ответ: 4.
8. На окружности отмечены точки A и B так, что меньшая дуга AB равна . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.
Ответ: 36.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Касательная к окружности» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 09.03.2023
Геометрия 7-9 класс. Касательная к окружности — math200.ru
Skip to contentГеометрия 7-9 класс. Касательная к окружностиadmin2022-12-24T18:10:38+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Касательная к окружности
Окружностью называется множество всех точек плоскости, находящихся на равном положительном расстоянии от некоторой точки этой же плоскости. Эта точка называется центром окружности, а данное расстояние радиусом окружности.
Отрезок, соединяющий две точки окружности, называется хордой. Диаметр, делящий хорду пополам, перпендикулярен ей. Равные хорды окружности равноудалены от ее центра; равноудаленные от центра окружности хорды равны.
Касательная к окружности: если из точки к окружности проведены две касательные, то длины отрезков от этой точки до точек касания равны \(\left( {AM = AN} \right)\) и прямая, проходящая через центр окружности и эту точку, обладает свойством: \(\angle \,MAO = \angle \,NAO\). | |
Касательная перпендикулярна радиусу, проведённому к точке касания (\(OA \bot AB\)). Мера угла между касательной и хордой, имеющими общую точку на окружности, равна половине градусной меры дуги стягиваемой этой хордой, т.е. \(\angle \,AOC = 2\angle \,BAC\). | |
Говорят, что две окружности касаются, если они имеют единственную общую точку (точку касания). 1) Точка касания двух окружностей лежит на линии центров этих окружностей. 2) Окружности радиусов r и R с центрами О1 и О2 касаются внешним образом тогда и только тогда, когда \(R + r = {O_1}{O_2}.\) 3) Окружности радиусов r и R \(\left( {r < R} \right)\) с центрами О1 и О2 касаются внутренним образом тогда и только тогда, когда \(R — r = {O_1}{O_2}.\) 4) Окружности с центрами О1 и О2 касаются внешним образом в точке K. 5) Отрезок общей внешней касательной AB к двум касающимся окружностям радиусов r и R равен отрезку общей внутренней касательной CD, заключённому между общими внешними касательными и эти отрезки \(AB = CD = MN = 2\sqrt {Rr} .\) |
\circ }\) и CA = CB = CK.| Задача 1. Радиус окружности равен 4. Расстояние от центра окружности до прямой равно \(\sqrt {19} .\) Сколько общих точек имеет окружность и прямая. Ответ ОТВЕТ: 0. | ||
| Задача 2. Радиус окружности равен 14. Расстояние от центра окружности до прямой равно 14. Сколько общих точек имеет окружность и прямая. Ответ ОТВЕТ: 1. | ||
| Задача 3. Радиус окружности равен 4. Расстояние от центра окружности до прямой равно 3,4. Сколько общих точек имеет окружность и прямая. Ответ ОТВЕТ: 2. Ответ ОТВЕТ: 64. | ||
| Задача 7. По данным на рисунке найдите KL, если ОК = 6, OL = 10, а прямая KL является касательной к окружности. Ответ ОТВЕТ: 8. | ||
| Задача 8. По данным на рисунке найдите ОL, если ОК = 5, КL = 12, а прямая KL является касательной к окружности. Ответ ОТВЕТ: 13. | ||
| Задача 9. По данным на рисунке найдите \(\angle \,NMK,\) если ON = 3, OM = 6, а прямые MN и MK являются касательными к окружности. Ответ дайте в градусах. Ответ ОТВЕТ: 60. | ||
Задача 10. По данным на рисунке найдите KO, если OM = 7, \(\angle \,NOM = {120^ \circ },\) а прямые KM и KN являются касательными к окружности. \circ }\) и точка О – центр окружности.Ответ ОТВЕТ: 1,25. | ||
| Задача 16. По данным на рисунке найдите AD, если ABCD равнобедренная трапеция и OE = 7,5. Ответ ОТВЕТ: 30. | ||
\circ }\), а прямая KL является касательной к окружности. Ответ дайте в градусах.| Задача 17. По данным на рисунке найдите ОК, если OМ = ON = 29, MN = 40, а прямая MN является касательной к окружности. Ответ ОТВЕТ: 21. | |
| Задача 18. По данным на рисунке найдите АС, если АВ = 4, ОС = 3 и прямая АВ является касательной к окружности. Ответ ОТВЕТ: 8. | |
Задача 19. По данным на рисунке найдите ВС, если КВ = 4, ОС = 3, а прямая АВ является касательной к окружности. Ответ ОТВЕТ: 2. | |
| Задача 20. По данным на рисунке найдите АВ, если радиусы окружностей равны 25 и 16, а прямая АВ является касательной к окружностям. Ответ ОТВЕТ: 40. | |
| Задача 21. По данным на рисунке найдите радиус меньшей окружности, если радиус большей окружности равен 9 и АВ = 12, а прямая АВ является касательной к окружностям. Ответ ОТВЕТ: 4. | |
| Задача 22. По данным на рисунке найдите МК, если радиусы окружностей равны 15 и 8, расстояние между центрами окружностей равно 25, а прямая МК является касательной к окружностям. Ответ ОТВЕТ: 24. | |
Задача 23. По данным на рисунке найдите АВ, если АМ = 1, ВN = 4, а прямые АМ, ВN и MN являются касательными к окружности. \circ },\) а прямые АМ и ВМ являются касательными к окружности.Ответ ОТВЕТ: \(10 + 5\sqrt 3 .\) | |
| Задача 25. По данным на рисунке найдите периметр треугольника MEF, если ОA = 12, а прямые АМ, ВМ и EF являются касательными к окружности. Ответ ОТВЕТ: 24. | |
| Задача 26. По данным на рисунке найдите MN, если периметр треугольника МАВ равен 25, а прямые МN, МK и AB являются касательными к окружности. Ответ ОТВЕТ: 12,5. | |
| Задача 27. По данным на рисунке найдите DC, если OB = OA = 10, радиус окружности равен 6, а прямая AB является касательной к окружности. Ответ ОТВЕТ: 9,6. | |
Задача 28. \circ }.\) Ответ дайте в градусах.Ответ ОТВЕТ: 57. | |
| Задача 31. По данным на рисунке найдите МК, если радиусы окружностей равны 5 и 3, расстояние между центрами окружностей равно 10, а прямая МК является касательной к окружностям. Ответ ОТВЕТ: 6. | |
| Задача 32. Две окружности вписаны в угол ВАС. Одна из окружностей имеет в двое больший радиус и проходит через центр другой. Найдите \(\angle BAC.\) Ответ дайте в градусах. Ответ ОТВЕТ: 60. | |
| Задача 33. По данным на рисунке найдите радиус окружности. Ответ ОТВЕТ: 6. | |
Реклама
Поддержать нас
Если угол между двумя касательными, проведенными из точки P к окружности радиуса a с центром O, равен 90, то O.
..Перейти к
- Круги — упражнение 9.1
- Круги — упражнение 9.2
- Круги — упражнение 9.3
- Круги — упражнение 9.4
- Вещественные числа
- Полиномы
- Пара линейных уравнений с двумя переменными
- Квадратные уравнения
- Арифметические прогрессии
- Треугольники
- Согласованная геометрия
- Введение в тригонометрию и ее уравнения
- Круги
- Конструкции
- Области, связанные с кругами
- Площади поверхности и объемы
- Статистика и вероятность
Главная >
Образцовые решения NCERT
Класс 10
Математика
>
Глава 9 — Круги
>
Круги — упражнение 9.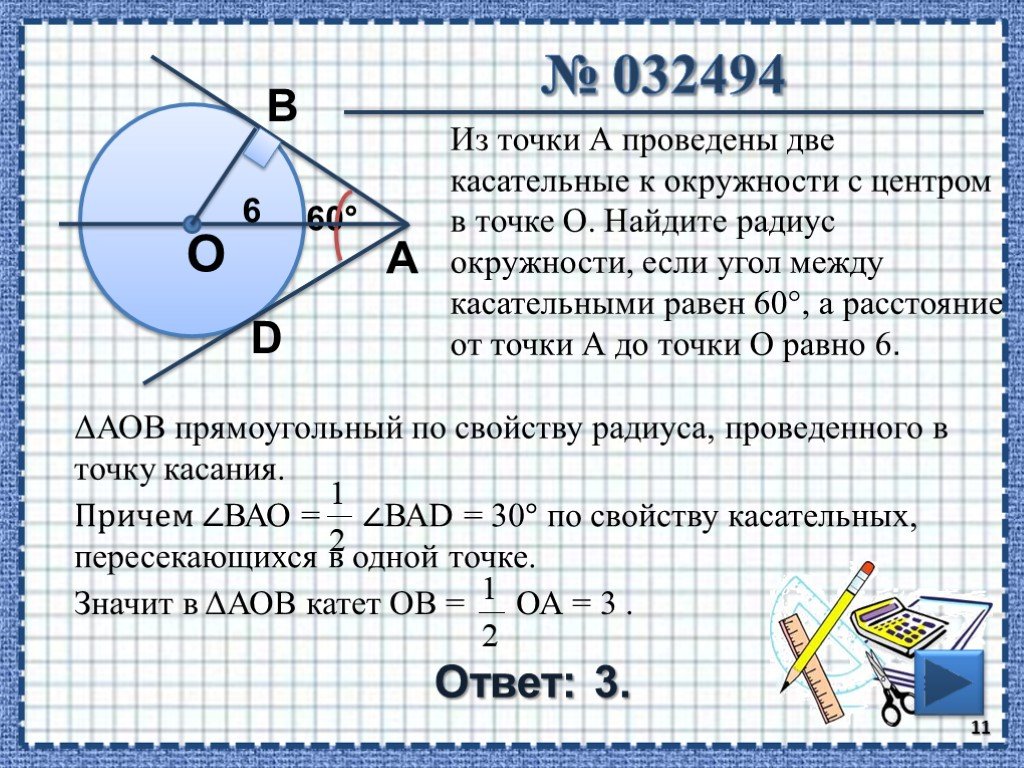
2
>
Вопрос 5
Вопрос 5. Окружности. Упражнение 9.2
Если угол между двумя касательными, проведенными из точки P к окружности радиуса a с центром O, равен 90°, то OP = a √ 2.
Ответ:
Тангенс всегда перпендикулярен радиусу в точке контакта.
Следовательно, ∠RPT = 90
Если 2 касательные проведены из внешней точки, то они одинаково наклонены к отрезку, соединяющему центр с этой точкой.
Рассмотрим следующий рисунок,
Из точки P проводятся две касательные.
Следовательно, ∠PTO = ∠PRO = 90°
Поскольку три угла четырехугольника PROT равны 90°, четвертый угол также равен 90°.
Следовательно, PROT — прямоугольник, но смежные стороны прямоугольника также равны. (OT = OR = a и PT = PR)
Следовательно, PROT — квадрат со стороной a.
OP диагональ квадрата PROT, значит, OP a√2.
Связанные вопросы
**Если угол между двумя касательными, проведенными из точки P к окружности радиуса a с центром O, равен 60°, то.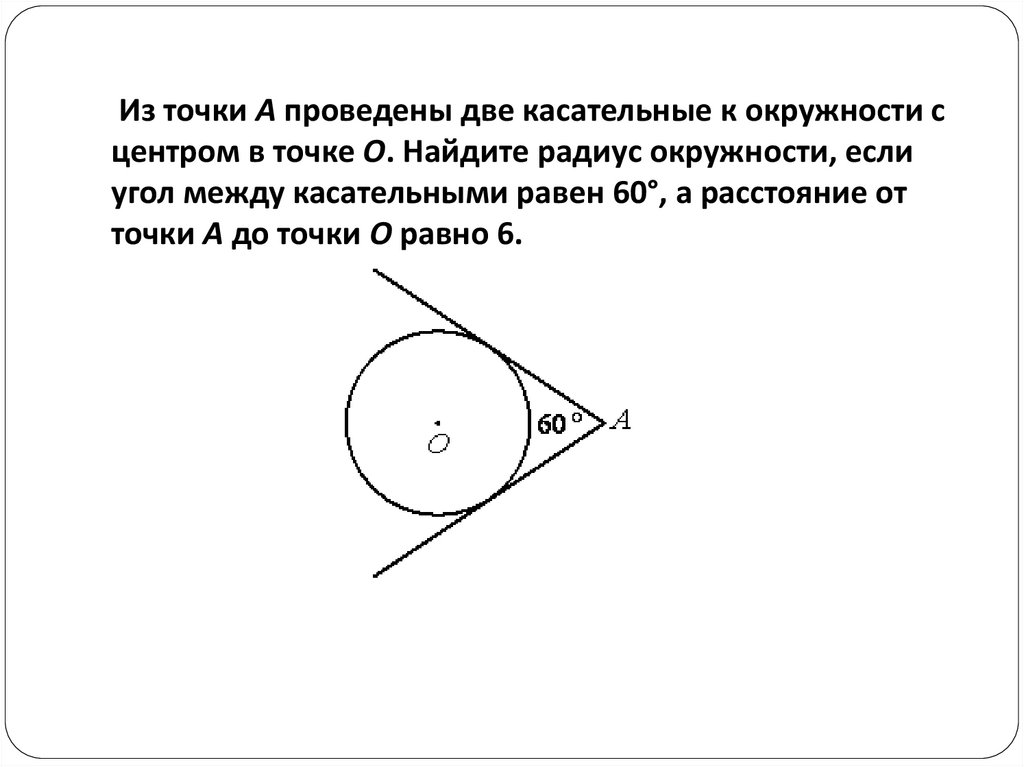
..
**Если хорда AB образует угол 60° в центре окружности, то угол между касательными …
**Длина касательной от внешней точки P к окружности с центром O всегда меньше OP.**…
Касательная к описанной вокруг равнобедренной окружности ΔABC в точке A, в которой AB = AC, параллельна BC.
AB — диаметр окружности, а AC — ее хорда, так что ∠BAC = 30°. Если касательная в точке С пересекает…
**Угол между двумя касательными к окружности может быть равен 0°.**
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Exercises
Circles — Exercise 9.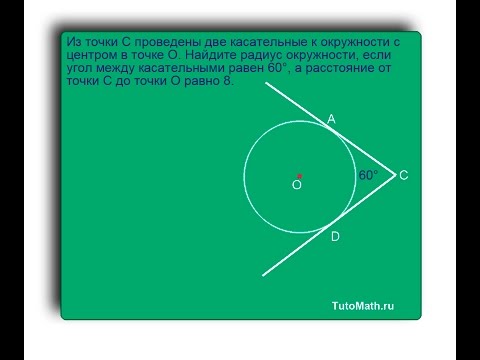
1
Circles — Exercise 9.2
Circles — Exercise 9.3
Circles — Exercise 9.4
Chapters
Real Numbers
Polynomials
Pair of Linear Equations in Two Variables
Quadratic Equations
Арифметические прогрессии
Треугольники
Координатная геометрия
Введение в тригонометрию и ее уравнения
Окружности
Построения
Площади, связанные с окружностями
Площади и объемы поверхностей
Статистика и вероятность
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
[Решено] В круге с центром O и радиусом 13 см хорда AB равна dr
Этот вопрос был ранее задан в
SSC CGL 2020 Office I Tier-I Официальная статья 13 (состоится: 20 августа 2021 Shift 1)
Посмотреть все документы SSC CGL>
- 12
- 11
- 24
- 22 22
Вариант 3: 24
Бесплатно
PYST 1: SSC CGL — Общая информация (продлен: 20 апреля 2022 г.
, смена 2)
2.2 миллион пользователей
25 вопросов
50 баллов
10 минут
Дано:
Радиус = 13 см
∠APB = 60°
Расстояние AB от центра O равно 5 см
Используемая концепция:
окружности, то они имеют равные касательные сегменты.
Расчет:
На данном рисунке,
утра = (AO 2 — OM 2 ) 1/2
AM = (169 — 25) 1/2
AM = (169 — 25) 1/2
AM = (169 — 25) 1/2
АМ = 12 см
Sin 30° = AM/AP
⇒ 1/2 = 12/AP
AP = 24 см принимая Δ APM и Δ APO.
Мы знаем, что радиус от центра окружности до точки касания
перпендикулярен касательной. Следовательно, Δ APO также является прямоугольным треугольником
.
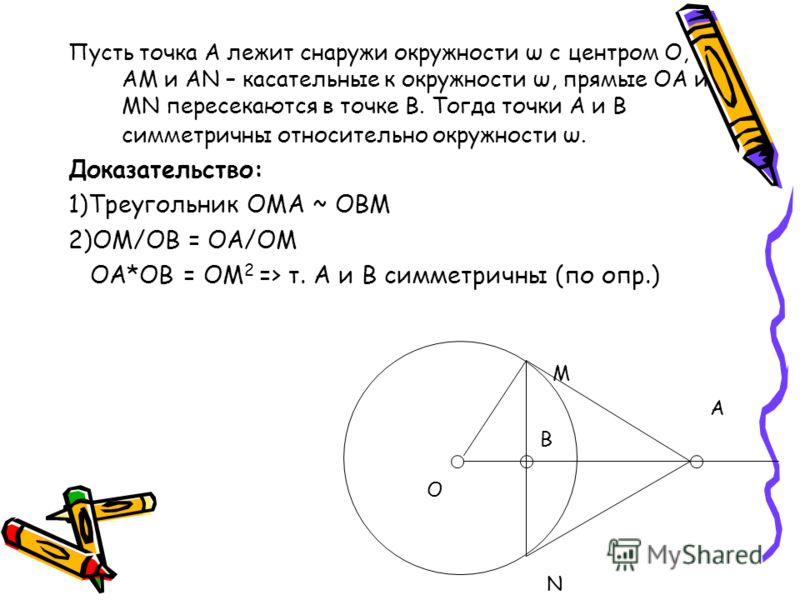в Δ APO,
tan 30° = OA/AP
⇒ 1/√3 = 13/PA
⇒ AP = 13√3, что не указано в опциях.
Дополнительная информация Критерии подобия треугольников:
Угол-Угол-Угол: пропорция
) и, следовательно, два треугольника подобны.
SSS (Сторона-Сторона-Сторона): Если в двух треугольниках стороны одного треугольника равны
пропорциональны сторонам другого треугольника, то их соответствующие
углы равны и, следовательно, эти два треугольника подобны.
SAS (Side-Angle-Side): Если один угол треугольника равен
одному углу другого треугольника, а стороны, включающие эти углы,
пропорциональны, то два треугольника подобны.
Скачать решение PDFПоделиться в WhatsApp
Последние обновления SSC CGL
Последнее обновление: 2 марта 2023 г.
Знаки SSC CGL 2022 Tier I будут доступны с 28 февраля по 13 марта 2023 г. Окончательный ключ для ответов на экзамен Tier I будет доступен на веб-сайте комиссии с 27 февраля 2023 г. по 13 марта 2023 г. SSC CGL Tier II Расписание экзаменов и пропускная карта также загружены. Экзамен запланирован со 2 по 7 марта 2023 года. Для экзамена уровня II ссылка на статус заявки SSC CGL активна для различных регионов. Ранее результаты SSC CGL Tier I 2022 для уровня I были опубликованы 9 сентября.февраль 2023 г. Общее количество вакансий – 37 409 для SSC CGL Recruitment. Экзамен SSC CGL Tier-II запланирован на период со 2 по 7 марта 2023 г. Экзамен SSC CGL 2022 Tier I был проведен с 1 по 13 декабря. 2022. Право на участие в программе SSC CGL – это степень бакалавра в соответствующей дисциплине. В этом году SSC полностью изменила схему экзаменов. Подготовиться на основе той же практики с нашими пробными тестами SSC CGL. Кандидаты также должны использовать документы SSC CGL за предыдущий год для хорошей проверки.
Leave A Comment