Из пункта а в пункт б расстояние между которыми 30 км навстречу друг другу: Из пунктов А и В, расстояние между которыми 30км, навстречу друг другу одновременно вышли два…

ГДЗ алгебра 7 класс, дидактический материал, Звавич. 2 вариант, С-31, упр. 2-1. Найдите скорость автомобиля и скорость мотоцикла – Рамблер/класс

ГДЗ алгебра 7 класс, дидактический материал, Звавич. 2 вариант, С-31, упр. 2-1. Найдите скорость автомобиля и скорость мотоцикла – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Скорость автомобиля на 30 км/ч больше скорости мотоцикла.

Они едут навстречу друг другу из пунктов А и В,
расстояние между которыми 240 км, и встречаются в
пункте С. Найдите скорость автомобиля и скорость мотоцикла, если известно, что автомобиль был в пути 3 ч,
а мотоцикл — 2 ч.

ответы

x- скорость мотоцикла; х + 30 — скорость
автомобиля; 3(х + 30) + 2х = 240; Зх + 90 + 2х =
= 240; 5х = 150; х = 30 км/ч — скорость мото-
цикла; 30 + 30 — 60(км/ч) — скорость автомоби-
ля;

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

10 класс

9 класс

11 класс

похожие вопросы 5

Вариант 1. С-51. № 1. ГДЗ Алгебра 7 класс Звавич. помогите найти значения алгебраических дробей

 Найдите значения алгебраических дробей   при соответствующих значениях х и заполните таблицу: (Подробнее. 2

ГДЗ

Как решать задачи на движение – 3 простых шага

Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение. Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.

Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.

1. Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
2. Как решать задачи на движение: 3 простых шага
3. Задачи на движение вдогонку: примеры с решением
4. Задачи на движение навстречу: примеры с решением
5. Задачи на движение по течению и против течения: примеры с решением

Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить

Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:И уметь правильно выражать из этой формулы скорость и время:Многие ученики путаются при записи этих формул, допуская ошибки. Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается  – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем  – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:

3 простых шага решения задачи на движение

Чтобы правильно решить задачу на движение нужно:

1. Определить неизвестное и составить таблицу на основании условия задачи.
2. Составить уравнение на основании таблицы.
3. Вернуться к условиям задачи и записать правильный ответ.

Давайте подробнее разберем каждый шаг:

1. Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
2. На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
3. После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.

Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.

Задачи на движение вдогонку: примеры с решением

При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:

1. Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
2. Если условия задачи содержат общее время, то дроби, выражающее время, складываются.

Давайте разберем, как работают эти правила при решении задач.

Задача 1

Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.

Решение:

1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.

В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.

Составляем таблицу, данные для которой берем из условий задачи.

Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40). 2. На основании таблицы и условий задачи необходимо составить уравнение.

Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,

50 / (х + 40) + 4 = 50 / х

Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:

50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0

(50х + 4х² + 160х – 50х – 2000) / х (х+40) = 0

(4х² + 160х – 2000) / (х² + 40х) = 0

Умножим обе части уравнение на х² + 40х:

4х² + 160х – 2000 = 0

Разделим обе части уравнения на 4:

х² + 40х – 500 = 0

Находим дискриминант:

D = 40² – 4 * 1 * (-500) = 3600

Далее находим корни уравнения:

х₁ = 10

х₂= — 50

3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.

Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.

Скорость велосипедиста должна быть положительна, поэтому х₂ не подходит по смыслу задачи. Следовательно, нас интересует только х₁ и скорость велосипедиста равна 10 км/ч.

Ответ: 10 км/ч.

Задача 2

Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.

Решение:

1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.

Составим таблицу.

Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т. е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.

Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило).  Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:

80 / (х + 2) + 2 =  (80 / х)

Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:

(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0

Умножаем обе части уравнения на х (х + 2):

160 – 2х² + 4х = 0

— 2х² — 4х + 160 = 0

Делим обе части уравнения на -2:

х² + 2х – 80 = 0

Находим дискриминант:

D = 2² – 4 * 1 * (-80) = 4 + 320 = 324

Тогда корни уравнения равны:

х₁ = 8

х₂ = — 10

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.

Скорость должна быть положительна, поэтому х₂ = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.

Ответ: 8 км/ч.

Задачи на движение навстречу: примеры с решением

Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.

В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.

Примеры решения задач на движение навстречу:

Задача 1

Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.

Решение:

1. Обозначим скорость автомобилиста как Х.

Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.

Составим таблицу:2. Составим уравнении на основании таблицы и условий задачи.

Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:

350/х = 120/60 + 3

350/х = 5

Решаем полученное уравнение:

5х = 350

х = 70

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.

Ответ: 70 км/ч.

Задача 2

Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б.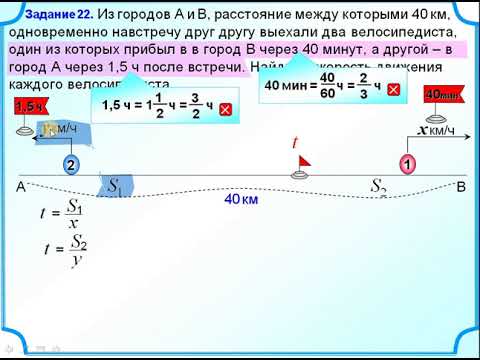 Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?

Решение:

1. Время автомобилиста обозначим как Х.

Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.

Составим таблицу:2. Составим уравнение на основании таблицы и условий задачи.

Известно, что велосипедист и автомобилист встретились через  4 часа после начала движения  и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.

Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:

((1 / х) +  (1 / (х — 6))) * 4 = 1

Решаем полученное уравнение:

(4 / х) +  (4 / (х — 6)) = 1

Приводим дроби к одному знаменателю:

(4х — 24 + 4х — х² + 6х) / (х (х — 6))  = 0

Делим обе части уравнения на х (х — 6), при условии, что х > 6:

-х² + 14х — 24 = 0

Умножим обе части уравнение на -1:

х² — 14х + 24 = 0

Находим дискриминант нашего квадратного уравнения:

D = 14² – 4 * 1 * 24 = 100

Находим корни уравнения:

х₁ = 12

х₂ = 2

х₂ < 6, следовательно, корнем уравнения не является.

3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько времени затратил автомобилист на путь из города Б в город А. Это время мы обозначали за Х. Следовательно, автомобилист затратил на путь из города Б в город А 12 часов.

Ответ: 12 часов.

Задачи на движение по течению и против течения: примеры с решением

В условиях задач на движение по реке всегда дано две скорости: собственная скорость судна (скорость, с которой он может двигаться в неподвижной воде) и скорость течения.

При этом возможны две ситуации: когда судно движется по течению и когда судно движется против течения.

Когда судно движется по течению, то течение помогает судну двигаться, оно начинает двигаться быстрее, следовательно, собственная скорость судна и скорость течения складываются.

Когда же судно двигается против течения, то оно ощущает сопротивление, плыть ему становится тяжелее. В этом случае скорость течения будет вычитаться из собственной скорости судна.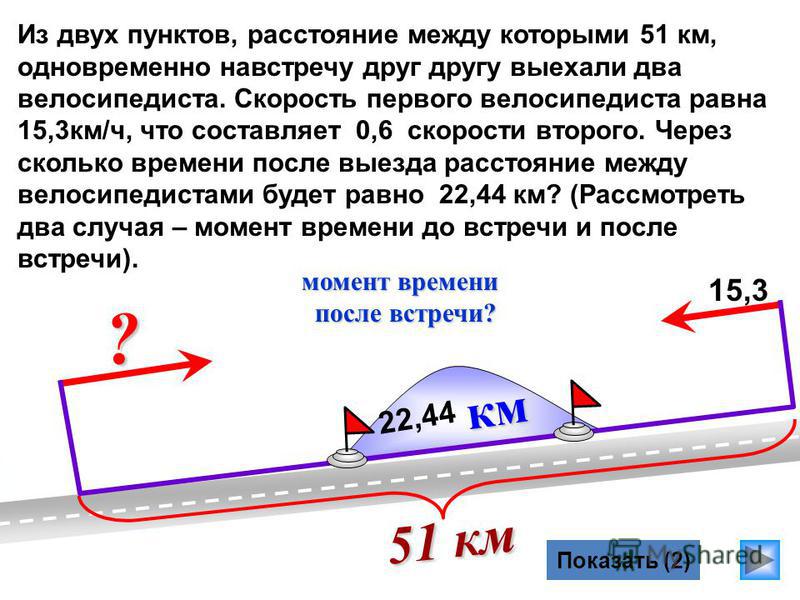

Давайте рассмотрим примеры решения задач на движение по реке.

Задача 1

Катер прошел против течения реки 160 км/ч и вернулся в пункт отправления, затратив времени на обратный путь на 8 часов меньше. Найдите скорость катера в неподвижной воде, если известно, что скорость течения реки равна 5 км/ч.

Решение:

1. Обозначим собственную скорость катера – х.

Составим таблицу:2. На основании таблицы и условий задачи составим уравнение.

По условиям задачи известно, что время, затраченное на путь по течению реки, на 8 часов меньше, чем время, затраченное на путь против течения реки (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Соответственно:

160 / (х + 5) + 8 = 160 / (х — 5)

Решаем данное уравнение. Для этого приводим дроби к общему знаменателю:

(160 (х – 5) + 8 (х – 5) (х + 5) – 160 (х + 5)) / (х – 5) (х + 5) = 0

(160х – 800 + (8х – 40) (х + 5) – 160х — 800) / (х – 5) (х + 5)  = 0

Умножаем обе части уравнения на (х – 5) (х + 5):

-1600 + 8х² + 40х – 40х – 200 = 0

8х² – 1800 = 0

8х² = 1800

х² = 225

х_1,2 = ±15

3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х₁ = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.

Ответ: 15 км/ч.

Задача 2

Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.

Решение:

1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.

Составим таблицу:2. Составим уравнение.

Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:

30 / (8+х) + 30 / (8-х) = 8

Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:

(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0

Умножаем обе части уравнения на (8-х) (8+х):

240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0

480 – 512 – 64х + 64х – 8х² = 0

8х² = 32

х² = 4

х_1,2 = ±2

3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х₁ = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.

Ответ: 2 км/ч.

Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2023 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте, а также .

 

Q6 Рита проходит 20 км на восток из точки A в точку B.

Из B она движется на 30 км на запад все время…

Перейти к

• Упражнение 1.1
• Упражнение 1.2
• Упражнение 1.3
• Упражнение 1.4

• Целые числа
• Дроби и десятичные дроби
• Обработка данных
• Простые уравнения
• Линии и углы
• Треугольник и его свойства.
• Конгруэнтность треугольников
• Сравнение количеств
• Рациональное число
• Практическая геометрия
• Периметр и площадь
• Алгебраические выражения
• Показатели и силы
• Симметрия
• Визуализация твердых фигур

Главная > Решения НЦЭРТ Класс 7 Математика > Глава 1 — Целые числа > Упражнение 1. 1 > Вопрос 43

Вопрос 43 Упражнение 1.1

Рита проходит 20 км на восток из точки А в точку В. Из В она движется на 30 км на запад по той же дороге. Если расстояние на восток представлено положительным целым числом, то как вы представите расстояние, пройденное на запад?

Каким целым числом вы представите ее конечную позицию из A?

Ответ:

ОТВЕТ:

Из вопроса следует, что:

Положительное целое число представляет расстояние на восток.

Тогда расстояние, пройденное на запад, будет представлено отрицательным целым числом.

Рита проходит расстояние в восточном направлении = 20 км

Рита проходит расстояние в западном направлении = — 30 км

∴ Расстояние, пройденное от А = 20 + (- 30)

= 20 – 30

= -10 км

Следовательно, расстояние, пройденное Ритой из точки А, представим в виде Отрицательного Целого числа, т.е. – 10 км Внутри резервуара для воды есть ступеньки. Обезьяна сидит на самой верхней ступеньке (т. е. на первой ступеньке). Т…

В следующей числовой строке показана температура в градусах Цельсия в разных местах на конкретном…

В следующей числовой строке показана температура в градусах Цельсия в разных местах на конкретном…

Следующая числовая строка показывает температуру в градусах Цельсия (co) в разных местах на конкретном…

В следующей числовой строке показана температура в градусах Цельсия в разных местах на конкретном…

В следующей числовой строке показана температура в градусах Цельсия в разных местах на конкретном…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 1. 1

Упражнение 1.2

Упражнение 1,3

Упражнение 1.4

Главы

Целые числа

Фракции и десятичные десятичные

Конгруэнтность треугольников

Сравнение величин

Рациональные числа

Практическая геометрия

Периметр и площадь

Алгебраические выражения

Экспоненты и степени

Симметрия

Визуализация объемных фигур

Курсы

Быстрые ссылки

Условия и правила

Условия и правила

2022 © Quality Tutorials Pvt Ltd Все права защищены на расстоянии между двумя поездами?

спросил 4 года 8 месяцев назад

Изменено 4 года, 8 месяцев назад

Просмотрено 2к раз

$\begingroup$

Два поезда приближаются друг к другу со скоростью 25 км/ч и 30 км/ч соответственно из двух точек А и В. Второй поезд проходит на 20 км больше, чем первый. Каково расстояние между А и В?

Мой подход:

Поскольку $расстояние = скорость \cdot время$ [Я просто добавил время, которое потребовалось для преодоления пути вторым поездом ($30$ км/ч), чтобы преодолеть $20$ км, к Первому поезду ($25$ км/ч), чтобы получить расстояние постоянным]

(Первый Поезд)

Для $20$ км при $25$ км/ч время будет равно

time $= \frac{20}{25} = \frac45$

Итак, первому поезду потребуется на $4/5$ больше времени, чтобы преодолеть расстояние $d$

$d = 25 \cdot (t + 4/5 )$ —> (1)

$d = 30 \cdot t$ —> (2)

Теперь, поскольку расстояние постоянно, а скорость обратно пропорциональна времени,

Отношение скоростей $= \frac{25}{30} = \frac56 $

Отношение времен $ = \frac{t+4/5}{t} = \frac{\frac{5t+4}{5}}{t} = \frac{5t+4}{5t}$

Итак,

$\frac56= \frac{5t+4}{5t}$

Поскольку обратно пропорционально

$5(5t+4)=6(5t)$

$25t+20=30t$

25-30т=-20$

-5т=-20$

$t= 4$

Таким образом, применяя $t=4$ в (2) $d=30 \cdot 4 = 120$ км, но это неправильно

Правильный ответ $220$ км

Я не понимаю! помощь

• алгебра-предварительное исчисление

$\endgroup$

3

$\begingroup$

Пусть встретятся через $x$ часов. Мы знаем, что $25x+20=30x$, следовательно, $x=4$. Итак, один поезд проехал $25\cdot4$ км, другой $30\cdot4$ км, всего $220$ км.

$\endgroup$

2

$\begingroup$

Я думаю, что лучше всего описать все данные в таблице, подобной этой

$\begin{array}{cccc} & \text{V} & \text{T} & \text{D}\\ \text{Поезд 1} и 25\,\left[\frac{km}{h}\right]\\ \text{Поезд 2} и 30\,\left[\frac{km}{h}\right] \end{array}$

Обозначим расстояние, пройденное первым поездом до встречи на $х$. Следовательно, второй поезд проехал $x+20$. Давайте добавим это к столу:

$\begin{массив}{cccc} & \text{V} & \text{T} & \text{D}\\ \text{Поезд 1} & 25\,\left[\frac{km}{h}\right] & & x\,[km]\\ \text{Поезд 2} & 30\,\left[\frac{km}{h}\right] & & x+20\,[km] \end{array}$

Теперь мы можем заполнить нашу таблицу, используя эту $T=\frac{D}{V}$

$\begin{array}{cccc} & \text{V} & \text{T} & \text{D}\\ \text{Поезд 1} и 25\,\left[\frac{km}{h}\right] & \frac{25}{x}\,\left[h\right] & x\,[km]\ \ \text{Поезд 2} & 30\,\left[\frac{km}{h}\right] & \frac{30}{x+20}\,\left[h\right] & x+20\, [км] \end{массив}$

Предполагая, что оба поезда вышли из обоих пунктов в одно и то же время, мы получаем, что $T_{1}=T_{2}$, где $T_{1},T_{2}$ — время в пути для каждого поезда. до встречи. Так $$ \frac{25}{x}=\frac{30}{x+20}\qquad\Rightarrow\qquad x=100\,\left[km\right] $$ Следовательно, расстояние между $A$ и $B$ равно $D_{1}+D_{2}$, где $D_{1},D_{2}$ расстояние, пройденное каждым поездом до встречи. Итак, расстояние является $$ \влево(100\вправо)+\влево(100+20\вправо)=220\,\влево[км\вправо] $$

$\endgroup$

12

$\begingroup$

Пусть единица расстояния километров , а единица времени часов . В приведенных ниже расчетах все единицы измерения опущены. Поскольку постановка задачи не ясна, я предполагаю, что поезда одновременно вышли из конечных точек ($A$ и $B$) и двинулись навстречу друг другу.

Напишите $L$ для общего расстояния $AB$. Если $u$ и $v$ — скорости первого и второго поездов соответственно, то имеем $$\frac{\,\,\frac{Ld}{2}\,\,}{u}=\frac{\,\,\frac{L+d}{2}\,\,}{v }\,$$ где $d$ — разница между пройденными расстояниями двух поездов из-за их разных скоростей (при условии, что $u Из приведенного выше уравнения $$L=\left(\frac{v+u}{v-u}\right)d\,.$$ Для $u=25$, $v=30$ и $d=20$ получаем $$L=\left(\frac{55}{5}\right)(20)=220\,.$$

$\endgroup$

8

$\begingroup$

$Расстояние = скорость\умножить на время$.

Для поезда 1; $v_1 = 25$. Для поезда 2; $v_2 =30$. Оба они путешествуют одинаковое количество времени; $t_1=t_2 = t$. А поезд 2 проходит на $20$ км больше, поэтому $d_2 = d_1+20$.

Итак, $d_1 = 25*t$ и $d_2 = 30*t$.

Как далеко они друг от друга? $D = d_1 +d_2$.

Итак:

1) $d_1 = 25t$

2) $d_2 = 30t$

3) $d_2 = d_1 + 5$ или $30t = 25t + 20$

4) $D = d_1 + d_2$ или $D = 25t +30t$ или $D= 25t + 25t + 20$

Четыре линейных уравнения с четырьмя неизвестными Просто выполните их.

=====

Альтернативно. Разница в скорости $5 км/ч$.