Стороны равностороннего треугольника равна 12 корней из 3: «Сторона равностороннего треугольника равна 12√3. Как найти высоту этого треугольника?» — Яндекс Кью

Вычислить сторону треугольника онлайн

Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными, тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны треугольника.

• Сторона треугольника равностороннего через радиус описанной окружности
• Сторона треугольника равностороннего через радиус вписанной окружности
• Сторона треугольника равностороннего через высоту
• Сторона треугольника равностороннего через площадь треугольника
• Основание равнобедренного треугольника через боковые стороны и угол между ними
• Основание равнобедренного треугольника через боковые стороны и угол при основании
• Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами
• Боковая сторона равнобедренного треугольника через основание и угол при основании
• Катет прямоугольного треугольника через гипотенузу и острый угол
• Катет прямоугольного треугольника через гипотенузу и другой известный катет
• Гипотенуза прямоугольного треугольника через катет и острый угол
• Гипотенуза прямоугольного треугольника через катеты
• Сторона треугольника через две известные стороны и угол между ними
• Сторона треугольника через известную сторону и два угла

Сторона равностороннего треугольника через радиус описанной окружности

Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности необходимо ее радиус умножить на корень квадратный из трех.

Таким образом, формула будет выглядеть следующим образом:

a = R * √3

где а — сторона треугольника, R — радиус описанной окружности.

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.

Сторона равностороннего треугольника через радиус вписанной окружности

Для нахождения стороны правильного треугольника через радиус вписанной окружности следует использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6 / √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на квадратный корень из трех):

a = 2r * √3

где а — сторона треугольника, R — радиус вписанной окружности.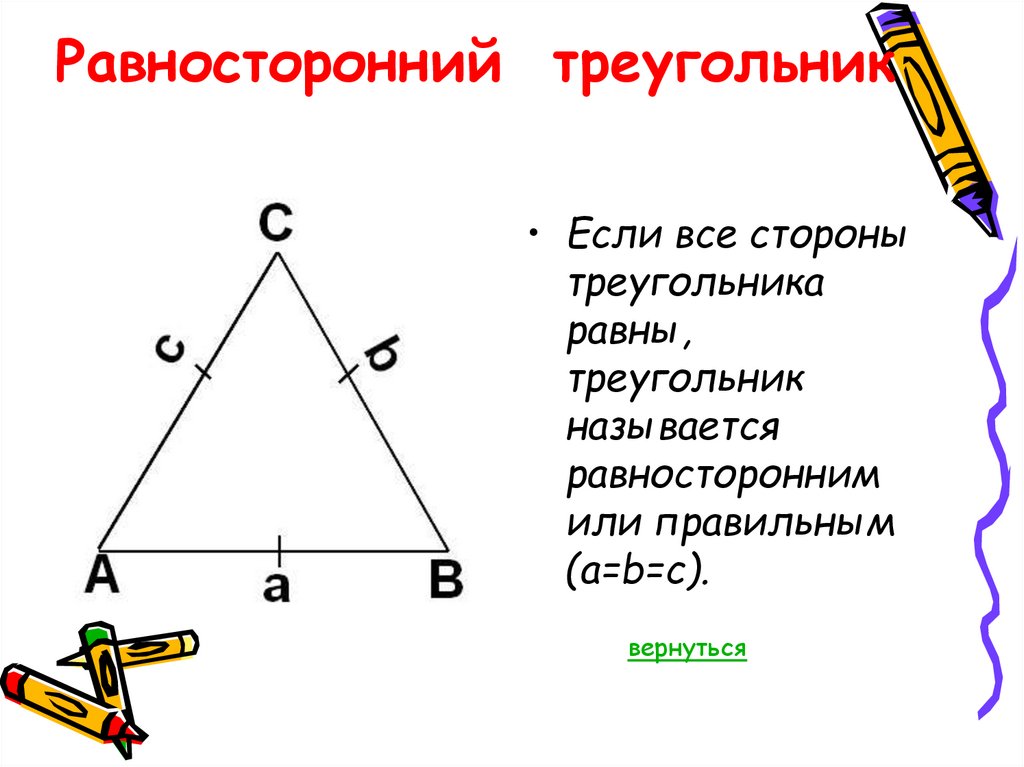

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.

Сторона равностороннего треугольника через высоту

Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4 =h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести формулу для нахождения стороны через высоту:

a = 2h / √3

где а — сторона, h —  высота равностороннего треугольника.

Высота (h):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 * 45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.

Сторона равностороннего треугольника через площадь

Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую формулу

a = √(4S / √3)

где а — сторона, S —  площадь равностороннего треугольника.

Площадь (S):

мм²см²дм²м²

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a = √(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.

Основание равнобедренного треугольника через боковые стороны и угол между ними

Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:

a = 2b * sin (α/2)

где a — длина основания треугольника, b — длина стороны треугольника; α — это угол, который противоположен основанию.

Сторона (b):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.

Основание равнобедренного треугольника через боковые стороны и угол при основании

Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и чем больше угол при вершине равнобедренного треугольника, тем он меньше.

Может быть только острым, то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то можно найти основание равнобедренного треугольника по следующей формуле:

a = 2b + cos β

где b — боковая сторона, β — угол при основании.

Сторона (b):

ммсмдмм

Угол (β):

градусырадианыcos

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.

Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами

В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны, из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит он является равнобедренным.   Это значит, что α = β.

Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми сторонами:

b = a / (2 * sin(α/2))

где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.

Основание (a):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11 см.

Боковая сторона равнобедренного треугольника через основание и угол при основании

Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет выглядеть следующим образом:

b = a / 2 * cos β

где a — это основание, β — угол при основании равнобедренного треугольника.

Основание (a):

ммсмдмм

Угол (β):

градусырадианыcos

Цифр после запятой:

012345678910Результат в: ммсмдмм

Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.

Пример

. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b = 35 / 2 * 0,5=35 мм.

Катет прямоугольного треугольника через гипотенузу и острый угол

Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет, противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть следующим образом:

a = c * sin α

где c — гипотенуза, α — острый угол прямоугольного треугольника.

Гипотенуза (c):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим следующее:  a = 77 * 0,98 = 75,8см.

Катет прямоугольного треугольника через гипотенузу и другой известный катет

Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо воспользоваться формулой:

a = √(c² — b²)

где c — гипотенуза, b — катет который известен прямоугольного треугольника.

Гипотенуза (c):

ммсмдмм

Катет (b):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см

Гипотенуза прямоугольного треугольника через катет и острый угол

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол можно узнать по формуле:

c = a / sin(β)

где a — катет, β — острый угол прямоугольного треугольника.

Катет (a):

ммсмдмм

Угол (β):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.

Гипотенуза прямоугольного треугольника через катеты

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов: c² = a² + b² следовательно:

c = √(a² + b²)

где c — гипотенуза, a и b — катеты.

Катет (a):

ммсмдмм

Катет (b):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см

Сторона треугольника через две известные стороны и угол между ними

По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны треугольника:

a = b² + c² — 2bc * cos α

где a, b, c — стороны произвольного треугольника, α — угол между сторонами который известен.

Сторона (b):

ммсмдмм

Сторона (c):

ммсмдмм

Угол (α):

градусырадианыcos

Цифр после запятой:

012345678910Результат в: ммсмдмм

Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение.

Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.

Сторона треугольника через известную сторону и два угла

Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться теоремой синусов и формула будут следующая:

a = (b * sin α) / sin β

где b — сторона треугольника; β, α — углы треугольника.

Сторона (b):

ммсмдмм

Угол (α):

градусырадианыsin

Угол (β):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Пусть сторона треугольника b равна 10, угол β  = 30º, угол α = 35º. Тогда получим подставив в формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30   = 8.71723 мм.

Сторона равностороннего треугольника равна 12 корней из 3. Найдите радиус окружности, описанной около этого треугольника — Знания.site

Последние вопросы

• Литература

  2 минуты назад

  Литература. 6 класс

• Физика

  8 минут назад

  Вопрос на состав ядра

• Математика

  17 минут назад

  Задача по математике, помогите, пожалуйста

• География

  18 минут назад

  Что находится на 18 градусах южной широты и 49 градусов северной долготы

• Физика

  18 минут назад

  Газ при расширении совершил работу, равную 500 Дж; при этом его внутренняя энергия изменилась на 750 Дж.

• Биология

  22 минут назад

  Биология 6 класс, пожалуйста помогите срочно

• Математика

  27 минут назад

  Математика 10 класс. В бассейн вода поступает из двух труб с различным напором. Отдельно малая труба набирает 21 м3…

• Русский язык

  28 минут назад

  «Харя» это грубое слово в отношении лица?

• Химия

  32 минут назад

  Умоляю помогите с тестом это срочно остался 1 час

• Экономика

  32 минут назад

  Решите пожалуйста 2 номер.

• Алгебра

  33 минут назад

  Докажите неравенство 12a(a−2) < (3a−5)(4a−1)+a.

• Геометрия

  33 минут назад

  Пожалуйста помогите с геометрией

• Русский язык

  37 минут назад

  Литература ответ срочно

• Обществознание

  37 минут назад

  СРОЧНО ПОМОГИТЕ!! Нужно 2 аргумента на высказывание- родина там, где чувствуешь себя свободно. Пожалуйста помогите ??

• Экономика

  37 минут назад

  Назвать многонациональные кампании Гвинеи (МНК) + транснациональные кампании Гвинеи

Все предметы

Выберите язык и регион

English

United States

Polski

Polska

Português

Brasil

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

Формула площади равностороннего треугольника

Равносторонний треугольник — это тип треугольника, в котором все три стороны имеют одинаковую длину.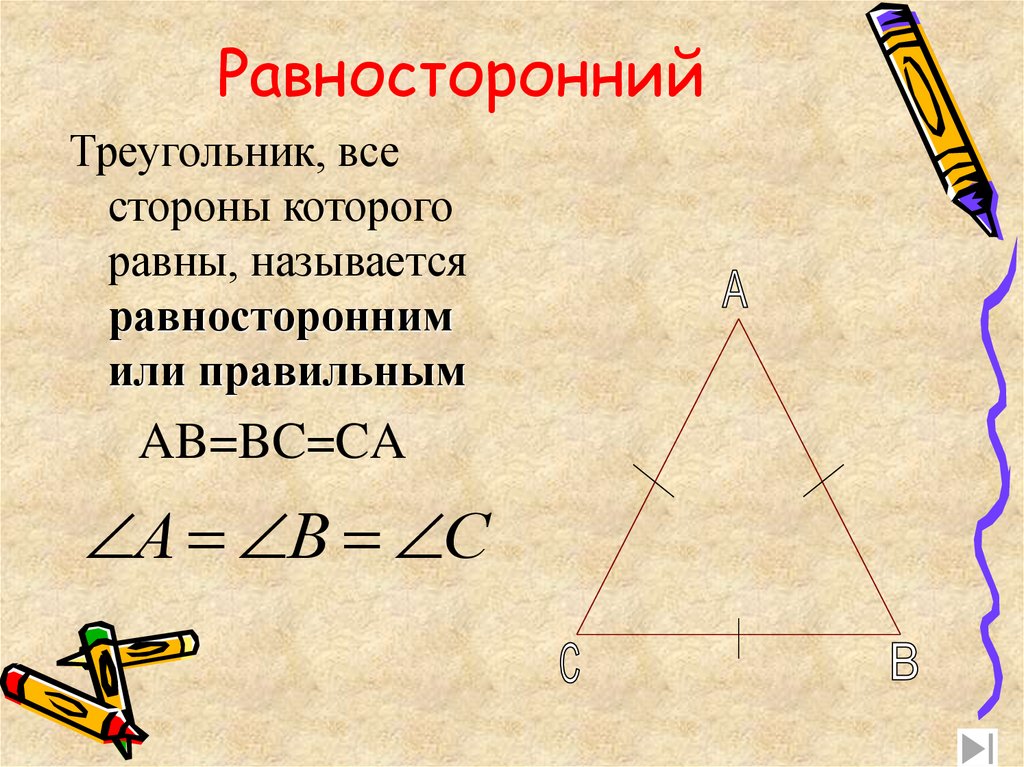 Другими словами, три стороны конгруэнтны. В результате три внутренних угла, противолежащие сторонам, также имеют одинаковую меру. Вот почему равносторонний треугольник также является равноугольным (все углы равны).

Формула для нахождения площади равностороннего треугольника очень проста, потому что нам не нужно знать основание или высоту треугольника. Единственное, что нам нужно, это мера одной стороны. Вот и все! 92[/латекс] на константу [латекс]\большой{{\sqrt 3} \over 4}[/латекс]. Обратите внимание, что единственным требуемым входным значением является мера одной стороны равностороннего треугольника, выраженная как [латекс]\большой{s}[/латекс] для стороны.

Прежде чем мы начнем использовать формулу, было бы неплохо узнать, как ее вывести.

Вывод формулы равностороннего треугольника

Вывод очень прост. Он основан на идее, что площадь треугольника равна половине произведения основания на высоту. Мы знаем основание, которое является просто одной из сторон [латекса]s[/латекса].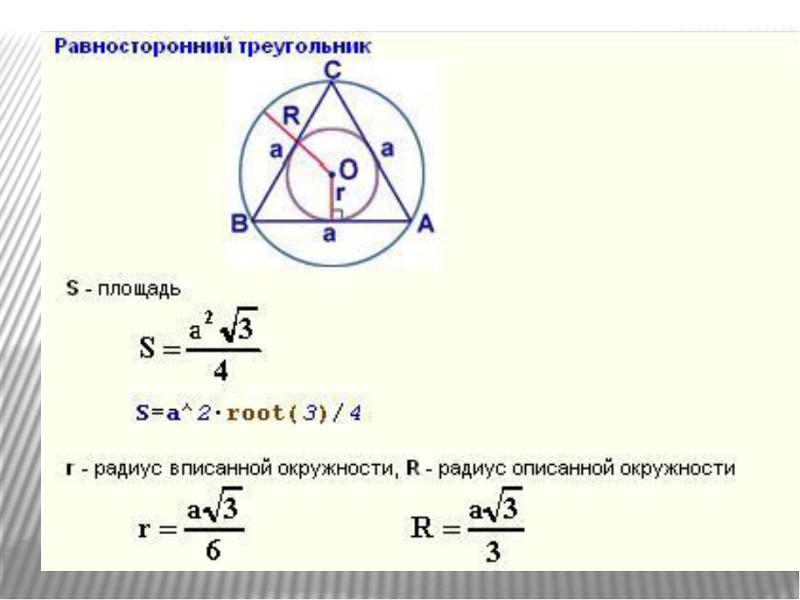 Но высота нам не дана. Это то, что мы собираемся выяснить здесь.

Первый шаг — нарисовать равносторонний треугольник. Затем нарисуйте высоту от верхней вершины до противоположной стороны, которая также известна как основание. Эта высота является как биссектрисой угла, так и биссектрисой перпендикулярного сегмента. Высота равностороннего треугольника также служит высотой треугольника. Построение этой высоты делит этот равносторонний треугольник на два конгруэнтных прямоугольных треугольников.

Давайте сосредоточимся на одном из прямоугольных треугольников. Обратите внимание, что этот прямоугольный треугольник имеет высоту [латекс]h[/латекс], основание [латекс]\большой{{s \более 2}}[/латекс] и гипотенузу [латекс]\большой{s }[/латекс]. Это означает, что мы можем использовать теорему Пифагора для вычисления высоты [латекс]h[/латекс].

Помните, что теорема Пифагора в двух словах утверждает, что если мы знаем две стороны прямоугольного треугольника, мы можем найти третью сторону. Чтобы это работало, треугольник должен быть прямоугольным, что означает, что один из его углов имеет размер [латекс]90[/латекс] градусов.

В формуле теоремы Пифагора стороны [латекс]а[/латекс] и [латекс]b[/латекс] являются катетами прямоугольного треугольника. Обратите внимание, что стороны образуют угол в 90 градусов, что говорит нам о том, что мы имеем дело с прямоугольным треугольником. Кроме того, самая длинная сторона — это сторона [латекс]с[/латекс], которая является стороной, противоположной 9.Угол 0 градусов. Самая длинная сторона прямоугольного треугольника имеет особое название. Гипотенуза называется.

Итак, в нашем исходном прямоугольном треугольнике катеты имеют длины [латекс]h[/латекс] и [латекс]\большие{s \более 2}[/латекс], а гипотенуза равна [латекс]S[/латекс]. Мы можем подставить эти значения в формулу теоремы Пифагора и найти высоту [латекс]h[/латекс].

Высота равностороннего треугольника равна [латекс]\большой{h = {{\sqrt 3} \over 2}s}[/латекс].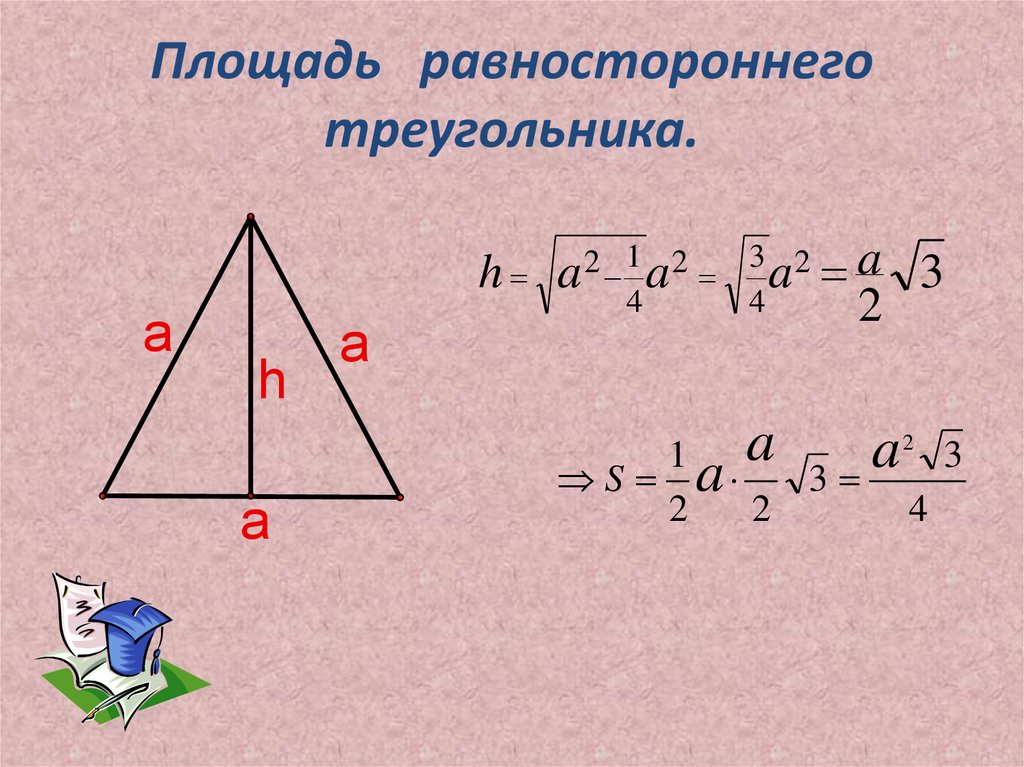

Вернемся к нашему исходному равностороннему треугольнику. Теперь мы можем найти площадь, потому что у нас есть вся необходимая информация.

Здесь основание равно [латекс]s[/латекс], а высота [латекс]{{{\sqrt 3 } \over 2}s}[/латекс]. Подставим эти значения в формулу, чтобы получить формулу площади равностороннего треугольника.

Теперь, когда мы можем вывести формулу равностороннего треугольника, пришло время рассмотреть несколько примеров!

---

Примеры формул площади равностороннего треугольника

Пример 1: Какова площадь равностороннего треугольника с длиной [латекс]2[/латекс]?

Равносторонний треугольник — это треугольник с тремя равными сторонами. Нам нужно знать меру только одной стороны, так как все они одинаковы. Дано, что мера стороны равна [латекс]2[/латекс], что означает [латекс]s=2[/латекс]. Давайте подставим это значение в формулу, а затем упростим, чтобы получить площадь равностороннего треугольника.

Следовательно, площадь равностороннего треугольника составляет [латекс]\sqrt 3[/латекс] квадратных единиц, что приблизительно равно [латекс]1,73[/латекс] квадратных единиц.

---

Пример 2: Сторона равностороннего треугольника равна [латекс]4\sqrt 3[/латекс] фута. Найдите площадь равностороннего треугольника.

Длина равностороннего треугольника содержит радикал. Поскольку мы возводим его в квадрат в формуле, это в конечном итоге исчезнет.

Следовательно, площадь равностороннего треугольника равна [латекс]12\sqrt 3[/латекс] квадратных футов. Это также приблизительно равно [латексу]20,78[/латекса] квадратных футов.

---

Пример 3: Периметр равностороннего треугольника составляет [латекс]18[/латекс] дюймов. Вычислите площадь равностороннего треугольника.

Периметр треугольника равен сумме его сторон, а у треугольника три стороны. Мы знаем, что стороны равностороннего треугольника имеют одинаковую меру. Это означает, что мы можем легко найти длину стороны, разделив периметр на [латекс]3[/латекс].

[латекс]s = {P \более 3}[/латекс]

[латекс] s = {{18} \более 3}[/латекс]

[латекс] s = 6[/латекс]

Мы нашли, что сторона равностороннего треугольника равна [латекс]6[/латекс] дюймов. Зная меру одной из его сторон, теперь мы сможем найти его площадь, используя формулу.

Следовательно, площадь равностороннего треугольника равна [латекс]9\sqrt 3[/латекс] квадратных дюймов. Это примерно равно [латексным]15,59[/латексным] квадратным дюймам.

---

Пример 4: Площадь равностороннего треугольника равна [латекс]10[/латекс] квадратных сантиметров. Какова длина стороны равностороннего треугольника?

Эта формула имеет только две переменные ([latex]A[/latex] и [latex]s[/latex]). Если мы знаем значение одного из них, мы можем решить для другого. Поскольку нам дана площадь равностороннего треугольника [латекс]А[/латекс], это означает, что мы можем найти другую переменную, которая является стороной [латекс]s[/латекс].

Давайте подставим значение площади, а затем найдем сторону:

Следовательно, сторона составляет около [латекс]4,81[/латекс] сантиметра.

---

Вас также может заинтересовать:

Теорема Пифагора

Площадь равностороннего треугольника – формула, расчет, примеры

Площадь равностороннего треугольника – это площадь, которую занимает равносторонний треугольник в двумерной плоскости. Равносторонний треугольник – это треугольник, у которого все стороны равны, а все углы равны 60º. Площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Здесь «единица» относится к единице (1), а единичный квадрат — это квадрат со стороной, равной 1 единице. В качестве альтернативы площадь равностороннего треугольника — это общее количество пространства, которое он заключает в двумерной плоскости.

1.	Какова площадь равностороннего треугольника?
2.	Формула площади равностороннего треугольника
3.	Доказательство площади равностороннего треугольника
4.	Как найти площадь равностороннего треугольника?
5.	Часто задаваемые вопросы о площади равностороннего треугольника

Какова площадь равностороннего треугольника?

Площадь равностороннего треугольника определяется как площадь, охватываемая тремя сторонами треугольника. Выражается в квадратных единицах. Некоторые важные единицы, используемые для выражения площади равностороннего треугольника: ² , м ​​ ² , см ² , ярды ² и т. д. Давайте поймем формулу для расчета площади равностороннего треугольника и ее вывод в разделах ниже.

Площадь равностороннего треугольника Формула

Формула площади равностороннего треугольника используется для расчета пространства, занимаемого между сторонами равностороннего треугольника в 2D-плоскости. Вычисление площадей любой геометрической формы — очень важный навык, которым пользуются многие люди в своей работе. Для равностороннего треугольника у нас есть формула его площади. В общем треугольнике нахождение площади треугольника может быть немного сложным по определенным причинам. Но найти площадь равностороннего треугольника довольно просто.

Общая формула площади треугольника, основание и высота которого известны, имеет следующий вид:

Площадь = 1/2 × основание × высота

В то время как формула для расчета площади равностороннего треугольника имеет вид

Площадь = √3/4 × (сторона) ² квадратных единиц

В данном треугольнике ABC площадь ΔABC = (√3/4) × (сторона) ² квадратных единиц, где, AB = BC = CA = a единиц (длина равных сторон треугольника).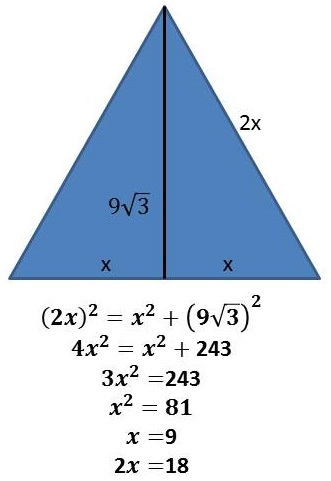

Таким образом, формула площади указанного выше равностороннего треугольника может быть записана как:

Площадь равностороннего треугольника ΔABC = (√3/4) × a ² квадратных единиц

Пример: Как найти площадь равностороннего треугольника, одна сторона которого равна 4 единицам?

Решение:

Используя формулу площади равностороннего треугольника: (√3/4) × a ² квадратных единиц,

подставим значения длины стороны.

Следовательно, площадь равностороннего треугольника (√3/4) × 4 ² = 4√3 квадратных единиц.

Доказательство площади равностороннего треугольника

В равностороннем треугольнике все стороны равны, а все внутренние углы равны 60°. Итак, площадь равностороннего треугольника можно вычислить, если известна длина одной стороны. Формула для вычисления площади равностороннего треугольника дается как,
Площадь равностороннего треугольника = (√3/4) × a ² квадратных единиц
где,
a = длина каждой стороны равностороннего треугольника

Приведенная выше формула для нахождения площади равностороннего треугольника может быть получена следующими способами:

• Используя общую формулу площади треугольника
• Использование формулы Герона
• Использование тригонометрии

Вычисление площади равностороннего треугольника с использованием формулы площади треугольника

Формулу, используемую для вычисления площади равностороннего треугольника, можно вывести с помощью общей формулы площади треугольника. Для этого нам потребуется длина каждой стороны и высота равностороннего треугольника. Таким образом, мы будем вычислять высоту равностороннего треугольника через длину стороны.

Формула площади равностороннего треугольника получается из общей формулы площади треугольника, которая равна ½ × основание × высота. Вывод формулы равностороннего треугольника приведен ниже.

Площадь треугольника = ½ × основание × высота

Для нахождения высоты равностороннего треугольника воспользуемся теоремой Пифагора (гипотенуза ² = основание ² + высота ² ).

Здесь основание = a/2, высота = h и гипотенуза = a (см. рисунок выше).

Теперь применим теорему Пифагора к треугольнику.

а ² = ч ² + (а/2) ²

⇒ ч ² = а ² – (а 8 2 4)1390 ⇒ ч ² = ( 3a ² )/4

Или h = ½(√3a)

Теперь поместите значение «h» в область уравнения треугольника.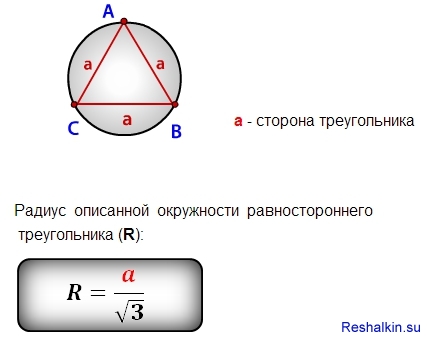

Площадь треугольника = ½ × основание × высота

⇒ A = ½ × a × ½(√3a) [Основание треугольника равно a единиц]

Или, площадь равностороннего треугольника = ¼(√3a ² )

Итак, формула высоты получается как ½ × (√3 × сторона), и далее площадь равностороннего треугольника становится √3/4 × сторона ² кв. шт.

Определение площади равностороннего треугольника с помощью формулы Герона

Формула Герона используется для нахождения площади треугольника, когда известны длины трех сторон треугольника. В математике формула Герона названа в честь Героя Александрийского, который дает площадь любого треугольника, когда известны длины всех трех сторон. Мы не используем углы или другие расстояния для нахождения площади треугольника по формуле Герона.

Ниже приведены шаги для нахождения площади треугольника:

Рассмотрим треугольник ABC со сторонами a, b и c. Формула Герона для нахождения площади треугольника:

Площадь = √s(s — a)(s — b)(s — c)

, где

с — полупериметр, который определяется как:

s = (a + b + c)/2

Для равностороннего треугольника: a = b = c.

s = (a + a + a)/2

s = 3a/2

Теперь площадь равностороннего треугольника = \(\sqrt {s(s — a)(s — a)(s — a) }\) 94}}{16}})}\)

Площадь равностороннего треугольника = √3/4 × (сторона) ² квадратных единиц.

Определение площади равностороннего треугольника с двумя сторонами и прилежащим к ней углом (SAS)

Чтобы найти площадь треугольника с двумя сторонами и прилежащим к ней углом, используйте синусоидальную тригонометрическую функцию для вычисления высоты треугольника и используйте это значение для найти площадь треугольника. Есть три варианта одной и той же формулы, в зависимости от того, какие стороны и прилежащий угол даны.

Предположим, что a, b и c — разные стороны треугольника.

• Когда стороны ‘b’ и ‘c’ и угол A между ними известны, площадь треугольника составляет: 1/2 × bc × sin(A)
• Когда известны стороны b и a и угол C между ними, площадь треугольника равна: 1/2 × ab × sin(C)
• Когда известны стороны ‘a’ и ‘c’ и угол между ними B, площадь треугольника равна: 1/2 × ac × sin(B)

В равностороннем треугольнике ∠A = ∠B = ∠C = 60°. Следовательно, sin A = sin B = sin C. Теперь площадь △ABC = 1/2 × b × c × sin(A) = 1/2 × a × b × sin(C) = 1/2 × a × с × грех (В).

Для равностороннего треугольника a = b = c (см. рисунок выше).

Площадь = 1/2 × a × a × sin(C) = 1/2 × a ² × sin(60°) = 1/2 × a ² × √3/2

Итак, площадь равностороннего треугольника = (√3/4)a ² квадратных единиц.

Как найти площадь равностороннего треугольника?

Чтобы найти площадь равностороннего треугольника, используя длину стороны, можно выполнить следующие шаги:

• Шаг 1: Запишите меру длины стороны равностороннего треугольника.
• Шаг 2: Примените формулу для расчета площади равностороннего треугольника, заданную как A = (√3/4)a ² , где a — мера длины стороны равностороннего треугольника.
• Шаг 3: Выразите ответ соответствующей единицей измерения.

Теперь, когда мы изучили формулу и метод вычисления площади равностороннего треугольника, давайте рассмотрим несколько решенных примеров для лучшего понимания.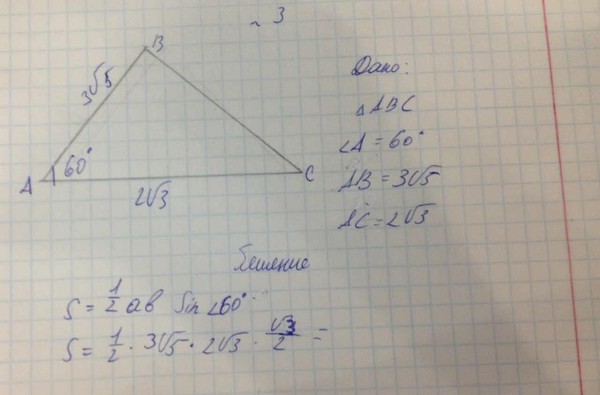

 

Примеры площади равностороннего треугольника

1. Пример 1: Найдите площадь равностороннего треугольника со стороной 9 см.

   Решение:

   Формула площади равностороннего треугольника задается как формулы, получаем,

   = √(3)/4 × 9 ²

   = 35,07 дюйма ²

   Ответ: Площадь = 35,07 дюйма ²

2. Пример 2: Используя формулу площади равностороннего треугольника, вычислите площадь равностороннего треугольника, каждая сторона которого равна 12 дюймам.

   Решение:

   Дано: Сторона = 12 дюймов

   Площадь = √(3)/4 × (Сторона) ²

   = √(3)/4 × (12) ²

   = 36√3

   Следовательно, площадь равностороннего треугольника равна 36√3 в ² = 62,35 в ²

   Ответ: Площадь данного равностороннего треугольника = 62,005 в 2

3. Пример 3: Чему равна площадь равностороннего треугольника со стороной 2 см?

   Решение:

   Дано: Сторона = 2 см

   Используя формулу площади равностороннего треугольника,

   Площадь = √(3)/4 × (Сторона) ²

   = √(3)/4 × (2) ²

   = 1,732 см ²

   Следовательно, площадь равностороннего треугольника равна 1,732 8 2

   03 Ответ: Площадь данный равносторонний треугольник = 1,732 см ²

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила.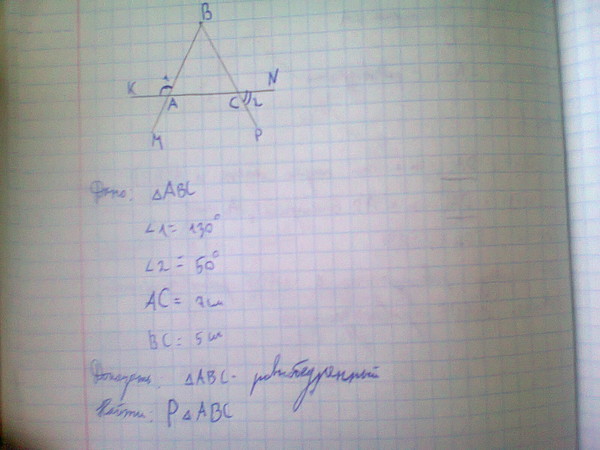 Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по площади равностороннего треугольника

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о площади равностороннего треугольника

Какова площадь равностороннего треугольника в математике?

Площадь равностороннего треугольника в математике — это область, охватываемая или заключенная внутри трех сторон равностороннего треугольника. Выражается в квадратных единицах или (единица измерения) ² .

Какая формула площади равностороннего треугольника?

Мы можем вычислить площадь равностороннего треугольника, зная длину каждой стороны. Формула площади равностороннего треугольника равна произведению √3/4 квадрата длины стороны равностороннего треугольника.

☛ Также проверьте:

• Формула треугольника
• Формулы равностороннего треугольника
• Формулы площади

Как найти площадь и периметр равностороннего треугольника?

Площадь равностороннего треугольника составляет √3/4 × (сторона) ² квадратных единиц, а периметр равностороннего треугольника в 3 раза больше стороны равностороннего треугольника.

Какова формула высоты равностороннего треугольника?

Зная площадь равностороннего треугольника, мы можем найти меру каждой стороны по формуле Площадь = √3/4 × (сторона) ² . Для нахождения высоты равностороннего треугольника по длине стороны воспользуемся теоремой Пифагора (гипотенуза ² = основание ² + высота ² ). Итак, формула высоты выглядит как ½ × (√3 × сторона).

Как найти стороны равностороннего треугольника, если известна площадь равностороннего треугольника?

Если известна площадь равностороннего треугольника, мы подставляем данное значение в следующую формулу и находим длину стороны:

Площадь равностороннего треугольника = (√3/4)a ² где a равно длина стороны равностороннего треугольника.

Для чего нужен калькулятор площади равностороннего треугольника?

Калькулятор площади равностороннего треугольника — это онлайн-инструмент, используемый для определения площади. Это самый быстрый режим для вычисления площади равностороннего треугольника путем предоставления входного значения, такого как длина стороны. Попробуйте вычислить площадь равностороннего треугольника по Куэмату прямо сейчас и рассчитайте площадь за несколько секунд.

Какова площадь равностороннего треугольника со стороной 2 см?

Площадь равностороннего треугольника со стороной 2 см определяется как Площадь = √3/4 × (сторона) ² . Подставив значение стороны на 2, мы получим Площадь = √3/4 × (2) ² = √3 см ² . Следовательно, площадь равностороннего треугольника со стороной 2 см равна √3 квадратных сантиметра.

Как найти площадь равностороннего треугольника без высоты?

Если высота треугольника не указана, то площадь равностороннего треугольника можно рассчитать, используя длину его стороны по формуле Площадь = √3/4 × (сторона) ² квадратных единиц.

Как найти площадь равностороннего треугольника с периметром?

Когда известен периметр равностороннего треугольника, мы можем сначала найти сторону треугольника, разделив периметр на 3.