Равноускоренное движение: формулы, примеры
Равноускоренное движение
Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению (в случае равнозамедленного движения модуль скорости равномерно меняется). Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение, в отличие от неравномерного, — частный случай ускоренного в равной степени движения с ускорением, равным нулю.
Рассмотрим случай свободного падения (тело брошено под углом к горизонту) более подробно с вычислением. Такое движение можно рассчитать и представить в виде суммы движений относительно вертикальной и горизонтальной осей.
Как найти ускорение в физике? Нахождение ускорения в физике происходит с учетом того, что в любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону.
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — движение равноускоренное и прямолинейное. Будем рассматривать определенные проекции векторов скорости и ускорения на оси.
Будем рассматривать определенные проекции векторов скорости и ускорения на оси.
Формулы для равноускоренного движения
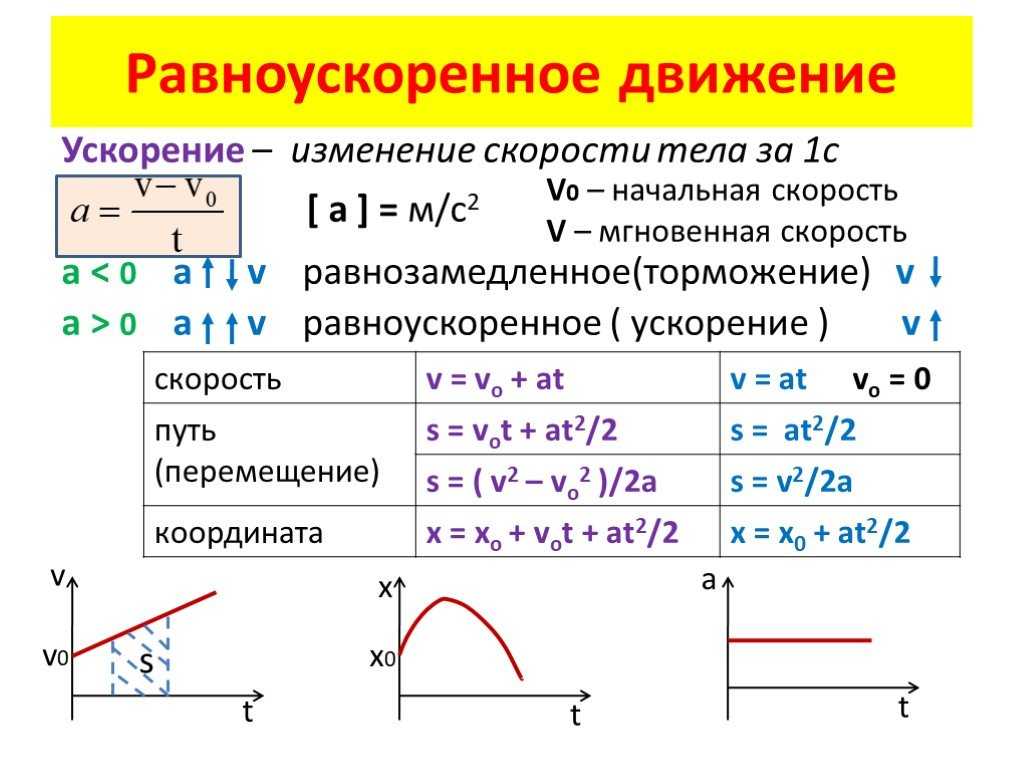
Формула для скорости (формула ускорения) при равноускоренном движении:
v=v0+at.
Здесь v0 — начальная скорость тела, a=const — ускорение.
Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии. Вот небольшой тест.
Как найти ускорение? Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC. Вот как выглядит формула ускорения в физике.
a=v-v0t=BCAC
Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.
Для первого графика: v0=-2 мс; a=0,5 мс2.
Для второго графика: v0=3 мс; a=-13 мс2.
По данному графику физик может также вычислить (произвести определение) перемещение тела за время t. Как это сделать?
Выделим на графике малый отрезок времени ∆t.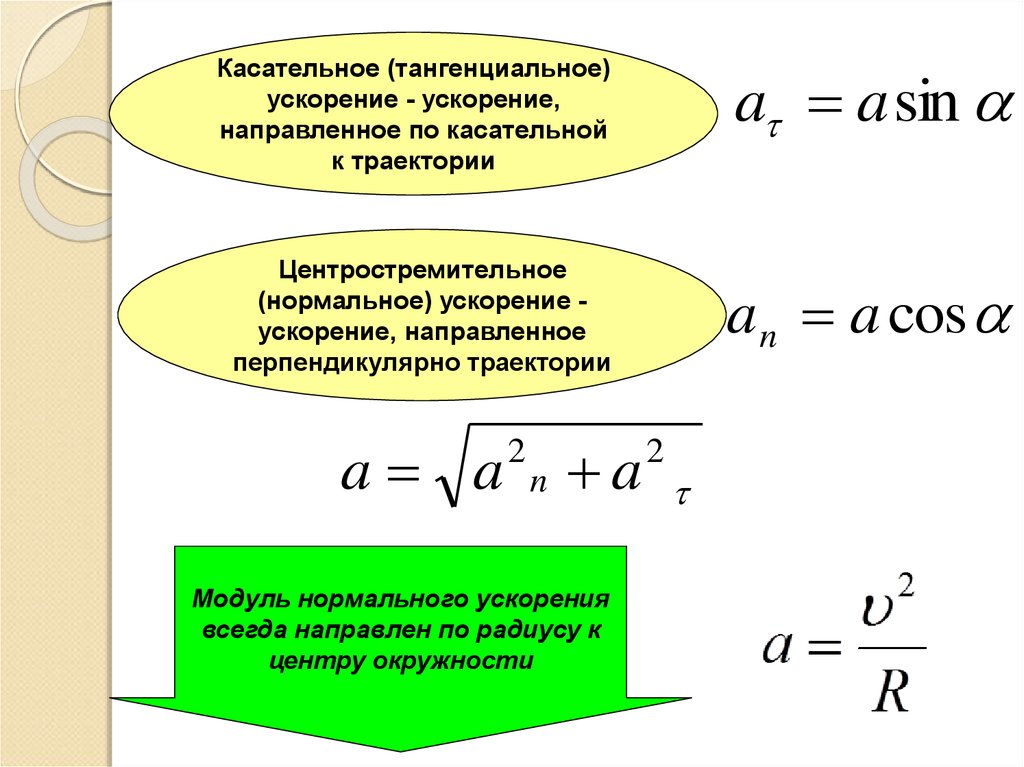 Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.
Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.
Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.
s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.
Мы знаем, что v-v0=at, поэтому окончательная формула или расчет для перемещения тела примет вид:
s=v0t+at22
Для того чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение (расстояние). Изменение координаты в зависимости от времени выражает закон равноускоренного движения.
Какова будет формула пути при равноускоренном движении? В этом случае путь изменяется согласно квадратной зависимости: 8=v0t + at²/2.
Закон равноускоренного движения
Закон равноускоренного движенияy=y0+v0t+at22.
Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — находить координаты при заданных значениях начальной и конечной скоростей и ускорения.
Исключая из записанных выше уравнений t и решая их, получаем:
s=v2-v022a.
По известным начальной скорости, ускорению и перемещению может находиться конечная скорость тела:
v=v02+2as.
При v0=0 s=v22a и v=2as
Важно!Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. Они могут принимать как положительные, так и отрицательные значения — это будет зависеть от характера движения и направления координатных осей в условиях конкретной задачи.
Ускорение при равноускоренном прямолинейном движении
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени,
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
Проекция ускорения на ось ОХvx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.

- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину.
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.

- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался.
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.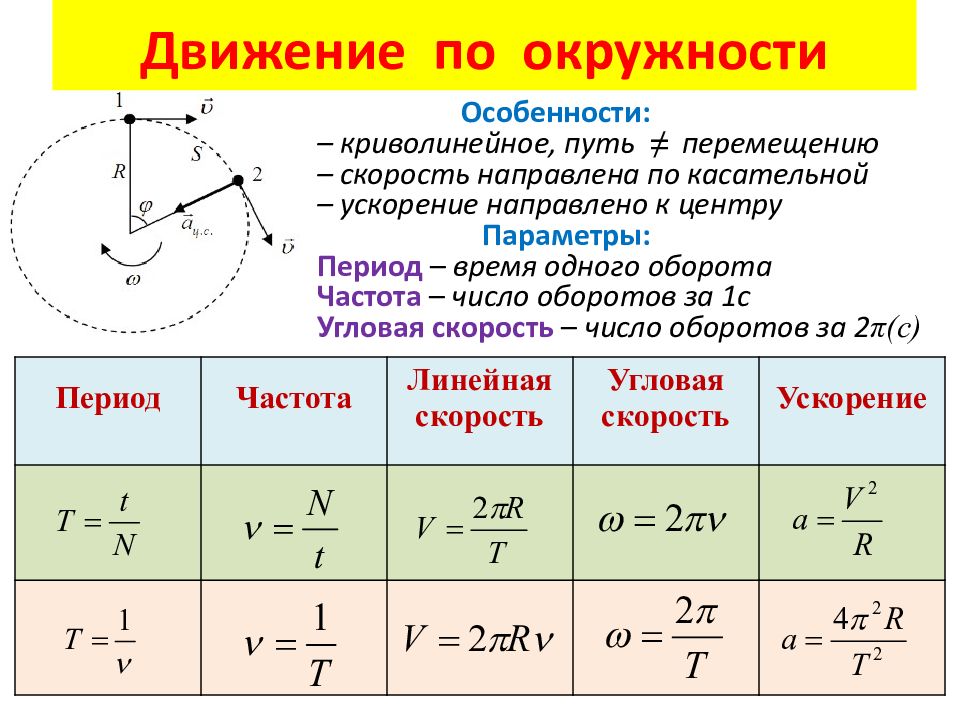
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции).
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17992 Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».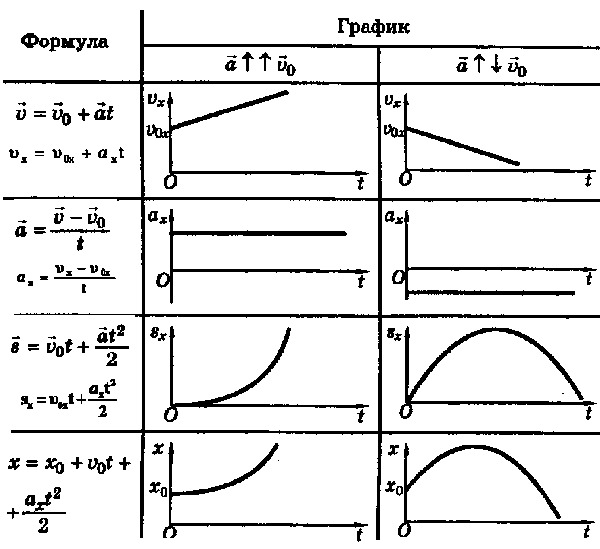
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18202Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: гpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18027 На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.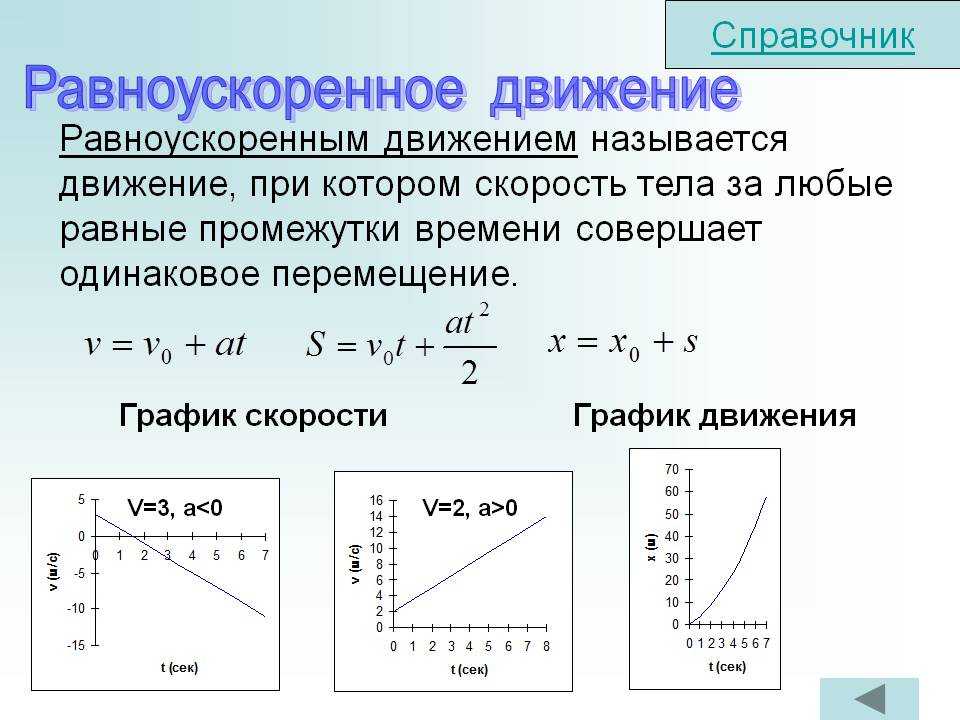
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 13k
6.
 2: Равноускоренное движение — Физика LibreTexts
2: Равноускоренное движение — Физика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 6961
- Джереми Татум
- Университет Виктории
Прежде чем изучать движение в сопротивляющейся среде, может быть уместно сделать краткий обзор равноускоренного движения. То есть движение, при котором сопротивление равно нулю. Любые формулы, которые мы разрабатываем для движения в сопротивляющейся среде, должны сводиться к формулам равноускоренного движения при стремлении сопротивления к нулю.
Можно представить себе ситуацию, когда тело стартует со скоростью \( v_{0}\), а затем ускоряется со скоростью \( a\). Можно задать три вопроса:
Можно задать три вопроса:
С какой скоростью он движется через время \( t\) ? 92 +2ос. \tag{6.2.3}\label{eq:6.2.3} \]
Поскольку ускорение равномерное, нет необходимости использовать вычисления для их получения. Первое следует непосредственно из смысла ускорения. Пройденное расстояние – это площадь под графиком скорость: время. На рисунке VI.1 показан график скорость : время для постоянного ускорения, и уравнение \( \ref{eq:6.2.2}\) становится очевидным с первого взгляда на график. Уравнение \( \ref{eq:6.2.3}\) можно получить, исключив \( t\) между уравнениями \( \ref{eq:6.2.1}\) и \( \ref{eq:6.2. 2}\). (Это также можно вывести из энергетических соображений, хотя это, скорее, ставит телегу впереди лошади.)
Тем не менее, хотя исчисление не обязательно, поучительно посмотреть, как исчисление можно использовать для анализа равномерно ускоренного движения, поскольку исчисление будет необходимо в менее простых ситуациях. Мы будем использовать исчисление, чтобы ответить на три вопроса, поставленных ранее в этом разделе.
Для равноускоренного движения Уравнение движения равно
\[ \\ddot{x}=а. \tag{6.2.4}\label{eq:6.2.4} \]
Чтобы ответить на первый вопрос, мы пишем \( \ddot{x}\) как 92. \tag{6.2.6}\label{eq:6.2.6} \]
Это второй интеграл времени .
Чтобы получить ответ на третий вопрос, который будет называться пространственным интегралом , мы должны не забыть записать \( \ddot{x} \) как \( v \frac{dv}{dt}\ ). Таким образом, уравнение движения (уравнение \(\ref{eq:6.2.4}\)) равно
\[ \ v\frac{dv}{dx}= а. \tag{6.2.7}\label{eq:6.2.7} \]
Когда это интегрируется по \(x\) (с начальным условием \(v=v_{0}\), когда \(x=0\)) мы получаем 92_{0} +2акс. \tag{6.2.8}\label{eq:6.2.8} \]
Это пространственный интеграл.
Примеры.
Вот несколько быстрых примеров задач равномерно ускоренного движения. Вероятно, это хорошая идея — поработать в алгебре и получить алгебраических решений каждой задачи. {2}=4ac\).
{2}=4ac\).
Пример \(\PageIndex{1}\)
Тело удалено из состояния покоя. Последняя треть пути перед падением на землю проходится за время T. Покажите, что время полного падения на землю равно 5,45T.
Пример \(\PageIndex{2}\)
Дама находится в 8 метрах от автобусной остановки, когда Автобус, стартовав из состояния покоя на остановке, начинает трогаться с ускорением 0,4 м с -2 . С какой наименьшей скоростью должна бежать Дама, чтобы догнать Автобус?
Ответ: 2,53 мс -1 .
Пример \(\PageIndex{3}\)
Парашютист спускается с постоянной скоростью 10 футов в секунду. Когда она находится на высоте 900 футов, ее друг, прямо под ней, бросает ей яблоко. С какой наименьшей скоростью он должен бросить яблоко, чтобы оно долетело до нее? Сколько времени потребуется, чтобы добраться до нее, на какой высоте она будет в это время и какова относительная скорость парашютиста и яблока? Предположим, что \(g\) = 32 фута с -2 . Сопротивлением воздуха для яблока (но не для парашютиста!) пренебречь!
Сопротивлением воздуха для яблока (но не для парашютиста!) пренебречь!
Пример \(\PageIndex{4}\)
Исследователь Луны проводит следующий эксперимент на Луне, чтобы определить гравитационное ускорение \(g\) на Луне. Он подбрасывает лунный камень вверх с начальной скоростью 15 м с -1 . Через восемь секунд он подбрасывает вверх другой камень с начальной скоростью 10 м с -1 . Он наблюдает, как камни сталкиваются через 16,32 секунды после запуска первого камня. Рассчитайте g, а также высоту столкновения.
Ответ: 1,64 мс -2 , 26,4 м
Пример \(\PageIndex{5}\)
Г-н А и г-н В обсуждают достоинства своих автомобилей. Мистер А может разогнаться с 0 до 50 миль в час за десять секунд, а мистер Б может разогнаться с 0 до 60 миль в час за 20 секунд. Мистер Б дает мистеру А старт в одну секунду. Если предположить, что каждый водитель сначала равномерно разгоняется до своей максимальной скорости, а затем движется с одинаковой скоростью, то сколько времени потребуется г-ну В, чтобы догнать г-на А, и какое расстояние к тому времени проедут автомобили?
Ответ: 41 с, полмили.
Я делаю ответы следующим образом. Дайте мне знать ([email protected]), если вы думаете, что я что-то неправильно понял.
Эта страница под названием 6.2: Равномерно ускоренное движение распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джереми Татум
- Лицензия
- CC BY-NC
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- источник@http://orca.
 phys.uvic.ca/~tatum/classmechs.html
phys.uvic.ca/~tatum/classmechs.html
- источник@http://orca.
2.6: Перемещение при равномерном ускорении
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2808
Бегуны на длинные дистанции стараются поддерживать постоянную скорость с очень небольшим ускорением или замедлением для сохранения энергии.
Перемещение при постоянном ускорении
Когда ускорение постоянное, существуют три уравнения, связывающие перемещение с двумя из трех других величин, которые мы используем для описания движения – временем, скоростью и ускорением. Эти уравнения работают только тогда, когда ускорение постоянно, но, к счастью, есть довольно много случаев движения, когда ускорение постоянно. Одними из самых распространенных, если не учитывать сопротивление воздуха, являются предметы, падающие под действием силы тяжести.
Одними из самых распространенных, если не учитывать сопротивление воздуха, являются предметы, падающие под действием силы тяжести.
Когда объект движется с постоянной скоростью, смещение можно найти, умножив скорость на интервал времени, как показано в уравнении ниже
d=vt
Если объект движется с постоянным ускорением, но не постоянная скорость, мы можем использовать вывод этого уравнения. Вместо того, чтобы использовать v в качестве скорости, мы должны вычислить и использовать среднюю скорость, используя это уравнение:0257 f +v i )
Расстояние для равноускоренного движения можно найти, умножив среднюю скорость на время. (уравнение 1) результат к начальной скорости, v f = v i +at.
Второе уравнение, связывающее перемещение, время, начальную скорость и конечную скорость, получается путем подстановки этого уравнения в уравнение 1.
Начните с распределения 1/2 в уравнении 1 через:
d=1/2(v f +v i )(t)=(1/2)v f t+(1/2 )v i t
Мы знаем, что v f = v i +at .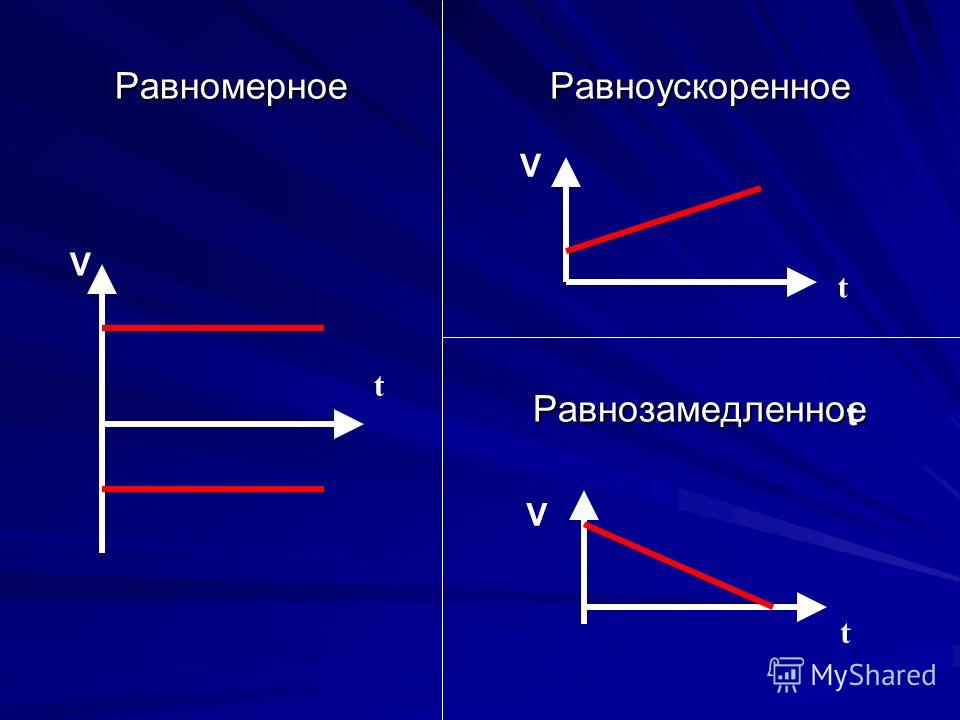 Следовательно:
Следовательно:
(1/2)v i t+(1/2)(v i +at)
=(1/2)v i t+(1/2)v i t+ (1/2)at 2
=v i t+(1/2)at 2 (уравнение 2)
Третье уравнение формируется путем объединения v f =v i +at и d=1/2(v f +v i )(t). Если мы решим первое уравнение относительно t, а затем подставим его во второе уравнение, мы получим
d=1/2(v f +v i )(v f −v i a)=( 1/2) ((V F 2 -V I 2 )/A)
и решение для V F 2 Yields
9182 V 8 287878788 2887878788 287878 2887878 2878788 287878 2887878 2887878 287878 287878 287878 2887 2878 2878 287878 2878 2878 287878 2878 287878 2. i 2 +2ad (уравнение 3)
Имейте в виду, что эти три уравнения действительны только при постоянном ускорении.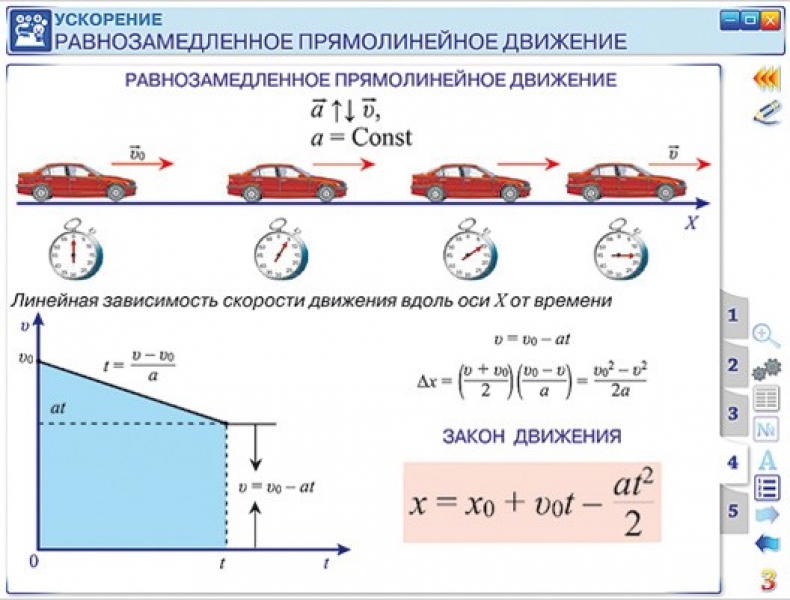 Во многих случаях начальную скорость можно установить равной нулю, что значительно упрощает три уравнения. Когда ускорение постоянно, а начальная скорость равна нулю, уравнения можно упростить до: 2 =2ad
Во многих случаях начальную скорость можно установить равной нулю, что значительно упрощает три уравнения. Когда ускорение постоянно, а начальная скорость равна нулю, уравнения можно упростить до: 2 =2ad
Пример 2.6.1
Предположим, планировщик проектирует аэропорт для небольших самолетов. Такие самолеты перед взлетом должны развивать скорость 56 м/с и могут разгоняться до 12,0 м/с9.0102 2 . Какова минимальная длина взлетно-посадочной полосы этого аэропорта?
Решение
Ускорение в этой задаче постоянно, а начальная скорость самолета равна нулю. Следовательно, мы можем использовать уравнение vf2=2ad и решить для d.
d=(v f 2 )/2a=(56 м/с) 2 /((2)(12,0 м/с 2 ))=130 м
Пример 2.63.2 9003.2
За какое время автомобиль проедет 30,0 м, если из состояния покоя он разгоняется со скоростью 2,00 м/с 9(1/2)=5,48 с
Пример 2.6.3
Бейсбольный питчер бросает фастбол со скоростью 30,0 м/с. Предположим, что ускорение равномерное, а расстояние, на которое движется мяч, равно 3,50 м. Каково ускорение?
Предположим, что ускорение равномерное, а расстояние, на которое движется мяч, равно 3,50 м. Каково ускорение?
Решение
Поскольку ускорение равномерное, а начальная скорость равна нулю, мы можем использовать v f 2 =2ad решить для a.
a=v f 2 /2d=(30,0 м/с) 2 /(2)(3,50 м)=900 (м 2 /с 2 )/7,00 м=129 м/с 2
Предположим, мы построили график зависимости скорости от времени для объекта, подвергающегося равномерному ускорению. В этом первом случае мы будем считать, что объект запущен из состояния покоя.
Если объект имеет равномерное ускорение 6,0 м/с 2 и начал движение из состояния покоя, то каждую последующую секунду скорость будет увеличиваться на 6,0 м/с. Вот таблица значений и график.
Рисунок 2.6.2 На графиках зависимости смещения от времени наклон линии представляет собой скорость объекта. В этом случае графика зависимости скорости от времени наклон линии представляет собой ускорение.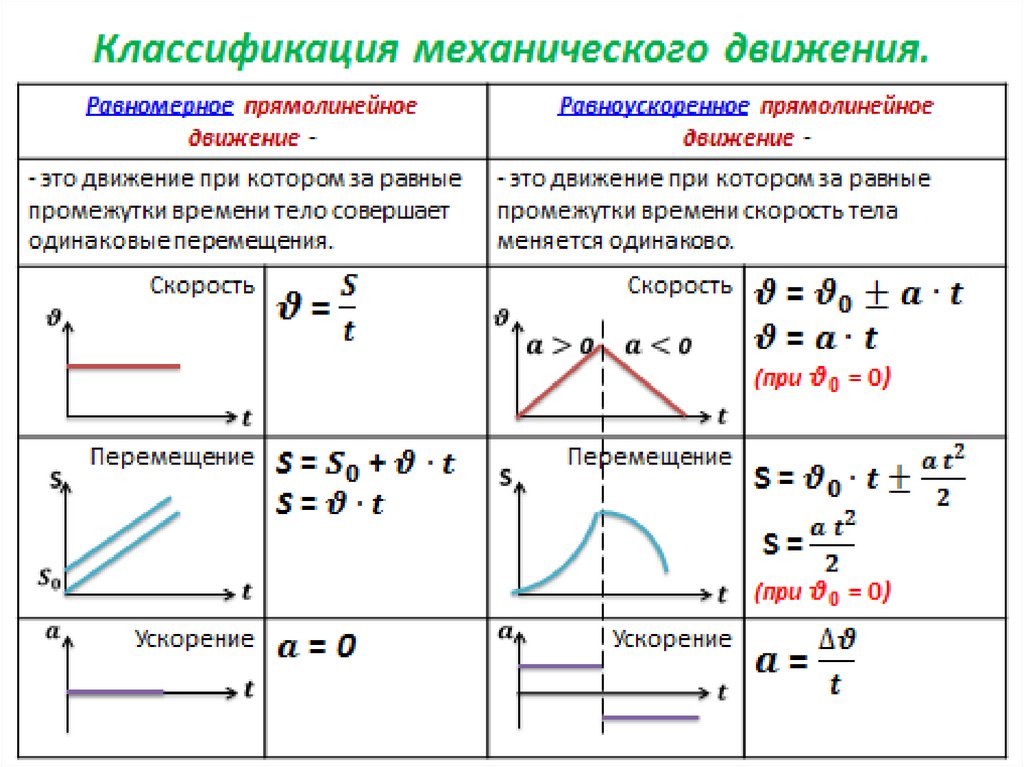 Если вы возьмете любой отрезок этой линии и определите отношение Δy к Δx, вы получите 6,0 м/с 2 , которое, как мы знаем, является постоянным ускорением этого объекта.
Если вы возьмете любой отрезок этой линии и определите отношение Δy к Δx, вы получите 6,0 м/с 2 , которое, как мы знаем, является постоянным ускорением этого объекта.
Из геометрии мы знаем, что площадь треугольника вычисляется путем умножения половины основания на высоту. Площадь под кривой на изображении выше — это площадь треугольника, показанного ниже. Площадь этого треугольника будет рассчитана как площадь = (1/2) (6,0 с) (36 м / с) = 108 м.
Рисунок 2.6.3Возвращаясь к уравнению 2, мы знаем, что смещение = (1/2) при 2 .
Используя это уравнение, мы можем определить, что перемещение этого объекта за первые 6 секунд пути =(1/2)(6,0 м/с2)(6,0 с) 2 =108 м.
Не случайно это число совпадает с площадью треугольника. На самом деле площадь под кривой на графике зависимости скорости от времени всегда равна смещению, которое происходит в течение этого временного интервала.
Используйте PLIX Interactive ниже, чтобы проанализировать движение собаки Джейн, Спарки, и визуализировать, как ускорение и перемещение могут быть получены из графика зависимости скорости от времени:
Интерактивный элемент
Резюме
- Есть три уравнения, которые мы можем использовать, когда ускорение постоянно, чтобы связать перемещение с двумя из трех других величин, которые мы используем для описания движения – временем, скоростью и ускорением:
- d=(1/2)(v f +v i )(t) (Уравнение 1)
- d=v i t+(1/2)at 2 (Уравнение 2)
- v f 2 =v i 2 +2ad (уравнение 3)
- Когда начальная скорость объекта равна нулю, эти три уравнения принимают вид:
- d=(1/2)(v f )(t) (Уравнение 1’)
- d=1/2at 2 (Уравнение 2’)
- v f 2 =2ad (уравнение 3’)
- Наклон графика зависимости скорости от времени представляет собой ускорение объекта.

- Площадь под кривой графика зависимости скорости от времени представляет собой смещение, которое происходит в течение заданного интервала времени.
Обзор
- Самолет разгоняется с постоянной скоростью 3,0 м/с 2 начиная со скорости 21 м/с. Чему равна конечная скорость, если расстояние, пройденное при этом ускорении, равно 535 м?
- Автомобиль останавливается на расстоянии 484 м с постоянным ускорением -8,0 м/с 2 . Какова была скорость автомобиля в момент начала разгона?
- Самолет стартует из состояния покоя и разгоняется с постоянной скоростью 3,00 м/с 2 в течение 20,0 с. Каково его перемещение за это время?
- Водитель полностью останавливает автомобиль за 2,0 с.
- Если автомобиль изначально двигался со скоростью 22 м/с, каково было ускорение?
- Какое расстояние проехал автомобиль при торможении?
Узнать больше
Используйте этот ресурс, чтобы ответить на следующий вопрос.


 phys.uvic.ca/~tatum/classmechs.html
phys.uvic.ca/~tatum/classmechs.html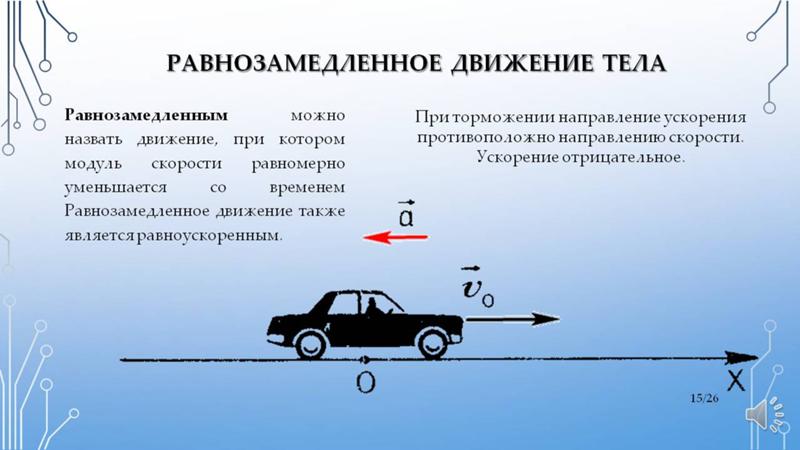
Leave A Comment