Графики по физике: Графики равномерного, равноускоренного движения, сравнение. Линейная, квадратная зависимость. Правила определения параметров

Графические задачи по физике и графическое решение задач

Часто графическое представление физического процесса делает его более наглядным и тем самым облегчает понимание рассматриваемого явления. Позволяя порой значительно упростить расчеты, графики широко используются на практике для решения различных задач. Умение строить и читать их сегодня является обязательным для многих специалистов.

К графическим задачам мы относим задачи:

на построение, где очень помогают, рисунки, чертежи;
схемы, решаемые с помощью векторов, графиков, диаграмм, эпюр и номограмм.

1) Мячик бросают с земли вертикально вверх с начальной скоростью v_о. Постройте график зависимости скорости мячика от времени, считая удары о землю абсолютно упругими. Сопротивлением воздуха пренебречь. [решение]

2) Пассажир, опоздавший к поезду, заметил, что предпоследний вагон прошел мимо него за t₁ = 10 c, а последний — за t₂ = 8 с. Считая движение поезда равноускоренным, определите время опоздания. [решение]

3) В комнате высотой H к потолку одним концом прикреплена легкая пружина жесткостью k, имеющая в недеформированном состоянии длину l_о (l_о < H). На полу под пружиной размещают брусок высотой x с площадью основания S, изготовленный из материала плотностью ρ. Построить график зависимости давления бруска на пол от высоты бруска. [решение]

4) Букашка ползет вдоль оси Ox. Определите среднюю скорость ее движения на участке между точками с координатами x₁ = 1,0 м и x₂ = 5,0 м, если известно, что произведение скорости букашки на ее координату все время остается постоянной величиной, равной

c = 500 см²/с. [решение]

5) К бруску массой 10 кг, находящемуся на горизонтальной поверхности, приложена сила. Учитывая, что коэффициент трения равен 0,7, определите:

cилу трения для случая, если F = 50 Н и направлена горизонтально.
cилу трения для случая, если F = 80 Н и направлена горизонтально.
построить график зависимости ускорения бруска от горизонтально приложенной силы.
с какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать брусок? [решение]

6) Имеются две трубы, подсоединенных к смесителю. На каждой из труб имеется кран, которым можно регулировать поток воды по трубе, изменяя его от нуля до максимального значения J_o = 1 л/с. В трубах течет вода с температурами t₁ = 10° C и t₂ = 50° C. Постройте график зависимости максимального потока воды, вытекающей из смесителя, от температуры этой воды. Тепловыми потерями пренебречь. [решение]

7) Поздним вечером молодой человек ростом h идет по краю горизонтального прямого тротуара с постоянной скоростью v. На расстоянии l от края тротуара стоит фонарный столб. Горящий фонарь закреплен на высоте

H от поверхности земли.

Постройте график зависимости скорости движения тени головы человека от координаты x. [решение]

Вы читате материалы из пособия для подготовки к олимпиадам по физике. Далее: многоступенчатые задачи по физике.

Графики. Часть вторая | Кинематика | Физика

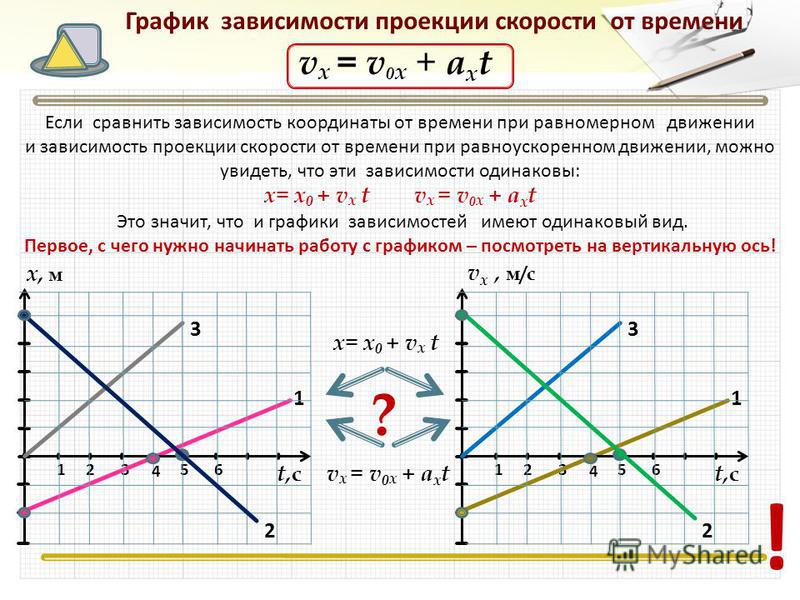
Пришло время познакомиться с еще одним известным графиком движения – графиком зависимости скорости тела от времени.

Давайте предположим, что неизвестный объект – это человек на велосипеде. Так интереснее.

Итак, что же мы можем сказать о его движении?

Если предположить, что ось x, вдоль которой происходило движение, направлена вправо, тогда в течение первой секунды велосипедист двигался в этом же направлении с постоянной скоростью пять метров в секунду. За следующие две секунды его скорость упала до нуля. Он медленно затормозил. Затем знак скорости поменялся: человек начал двигаться в отрицательном направлении (влево). Он ускорялся, его скорость постепенно увеличивалась. Это продолжалось две секунды, после чего велосипедист начал двигаться равномерно.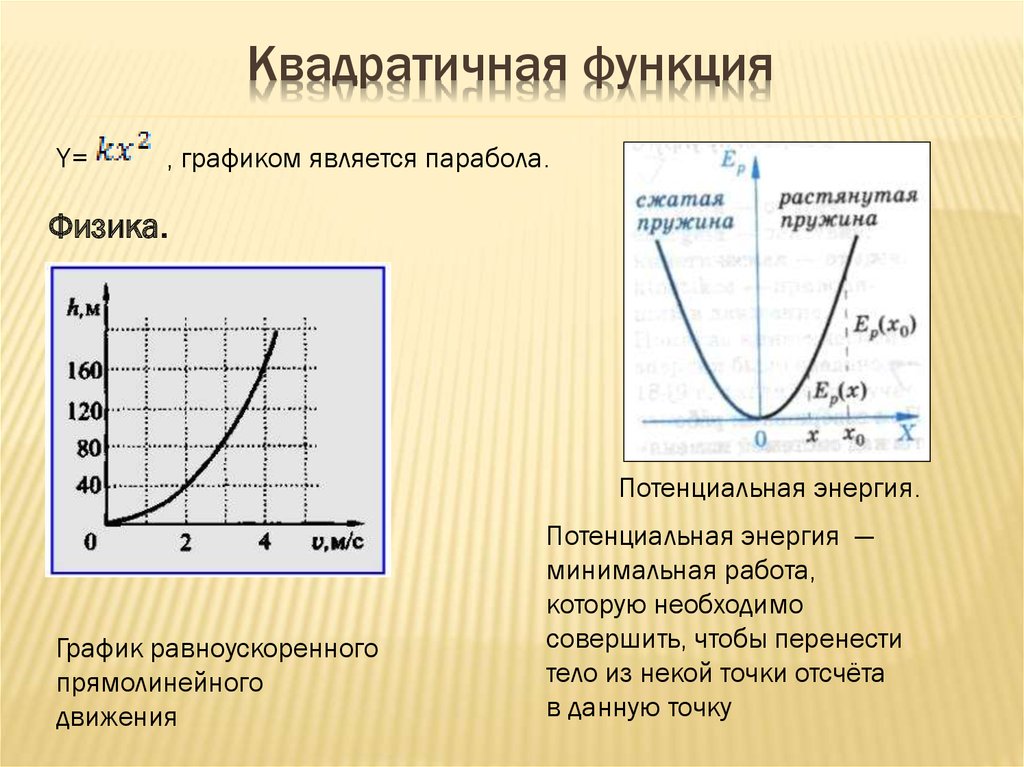 2

При равномерном движении площадь под графиком равна модулю перемещения. А что делать, если движение неравномерное?

Давайте попробуем найти перемещение тела в промежутке от первой до третьей секунды. Теперь под интересующей нас частью графика находится уже не прямоугольник, а треугольник. Но мы можем кое-что сделать:

Сумма этих прямоугольников немного отличается от нужного нам треугольника. Но можно нарисовать прямоугольники поуже, а потом еще уже. В конце концов сумма этих маленьких четырехугольников будет неотличима от треугольника, внутри которого они находятся. При этом каждый прямоугольник обозначает крошечный участок равномерного движения: его площадь будет равна перемещению тела за совсем небольшой промежуток времени. Таким образом, сумма площадей всех кусочков будет численно совпадать с итоговым перемещением тела. Но эта сумма также будет совпадать с площадью фигуры, внутри которой находятся прямоугольники. Получается, что площадь треугольника, находящегося под графиком, будет численно равна перемещению тела:

S_\triangle=\dfrac{1}{2}\textcolor{#2D9CDB}{ab}=\dfrac{1}{2}×5\thickspaceед×2\thickspaceед=5\thickspaceед^2

Человек двигался вправо, в положительном направлении. Значит, его перемещение:

\vec{s}=+\,5\thickspaceм

Используя предложенный график, мы также можем найти ускорение тела. Оно будет равно угловому коэффициенту касательной, проведенной к этому графику:

\vec{a}=k=\dfrac{\vec{v}_2-\vec{v}_1}{t_2-t_1}

Давайте найдем ускорение велосипедиста через четыре секунды и через шесть секунд после включения секундомера.

Сначала поймем, чтобы было через шесть секунд.

Касательная не пересекается с временной осью, ее угловой коэффициент равен нулю. У тела не было ускорения в этот момент, что логично, ведь скорость человека не менялась в промежутке от пяти до восьми секунд.

Теперь найдем ускорение велосипедиста через четыре секунды после включения секундомера.

Из рисунка видно, что касательная полностью совпала с графиком на отрезке от первой до пятой секунды. Выберем две подходящие точки и найдем ускорение:

\vec{a}=k=\dfrac{\textcolor{#219653}{\vec{v}_2-\vec{v}_1}}{\textcolor{#F2994A}{t_2-t_1}}=\dfrac{-\thickspace5\thickspaceм/с-5\thickspaceм/с}{5\thickspaceс-1\thickspaceс}=\dfrac{-\thickspace10\thickspaceм/с}{4\thickspaceс}=-\thickspace2,5\thickspaceм/с^2

Кратко повторим самое главное.

График зависимости скорости тела от времени позволяет судить о том, в каком направлении перемещалось тело и насколько быстро оно это делало. Площадь под этим графиком всегда численно совпадает с перемещением тела, а ускорение, с которым двигался объект, можно найти, построив касательную к предлагаемому графику и отыскав ее угловой коэффициент.

Что такое граф в физике? — Определение и шаги для построения базового x

1 Комментарий / К физикакатализатор / 16 февраля 2020 г.

В этой статье вы узнаете о том, что такое график в физике и как строить графики в физике. Здесь вы узнаете о

Зачем нужны графики
Что такое графики и
Как строить графики

Прочитав эту статью, студенты смогут определять графики и строить графики, используя данные о зависимых и независимых переменных.

Теперь начнем с зачем нам графики . Нам нужны графы в физике, потому что граф — очень мощный метод представления информации.

Мы можем использовать как таблицы, так и графики для представления одной и той же информации, но графики намного легче читать и интерпретировать информацию, чем таблицы. Установив необходимость графов, давайте теперь определим, что такое граф.

Что такое граф в физике?

График – это прямая или изогнутая линия, показывающая отношение между двумя величинами, из которых одна изменяется в результате изменения другой.

Чтобы было понятнее, давайте представим, что у нас есть две переменные x и y, где
\(y=2x\)
Переменная, которая предназначена для изменения или изменения, называется независимой переменной . Здесь в нашем случае x — независимая переменная. Другая переменная, которая изменяется в результате изменения независимой переменной, называется зависимой переменной .
Здесь \(y\) — зависимая переменная, значение которой изменяется при изменении значения \(x\).
Это отношение между независимой переменной и зависимой переменной можно показать с помощью графика.

Построение простого графика в физике

Мы уже знаем, что график строится для отображения отношения между двумя величинами. Чтобы понять, как можно построить график, рассмотрим автомобиль, который движется по прямой. Расстояние, проходимое автомобилем каждые 6 минут, указано в этой таблице.

90 096

давайте теперь используйте пример приведенной выше таблицы и начните рассматривать шаги, связанные с построением графика. Прежде чем начать, важно отметить, что здесь время t является независимой величиной и от нее зависит пройденное расстояние.

Шаг 1:

Выбор осей

Шаг 1 построения графика: Выбор осей. На этом шаге сначала отметьте ось, нарисовав две перпендикулярные линии, пересекающие друг друга в точке. Теперь отметьте ось X и ось Y.

Мы отложим время по оси абсцисс, потому что обычно независимые переменные берутся по оси абсцисс. Мы возьмем расстояние, которое является зависимой переменной по оси Y. Таким образом, линия OX представляет время, а линия OY представляет расстояние. Эти линии OX и OY названы в честь величин, которые они представляют.

Время — независимая переменная, берется по оси x, а расстояние — по оси y.

Шаг 2:

Выберите масштаб

На втором шаге мы бы выбрали масштаб . Мы должны выбрать масштаб, потому что размер бумаги, на которой рисуется график, ограничен. Значения отмечены на равных расстояниях по доступной длине оси. Вы должны сделать это таким образом, чтобы все значения количества, представленного на оси, могли быть размещены в доступной длине.

Шаг 3:

Нанесение точек

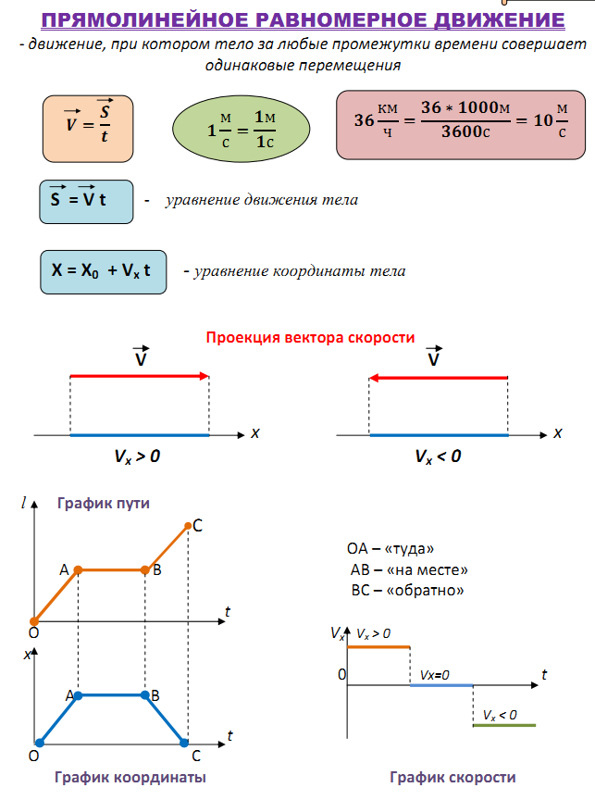На третьем этапе мы будем наносить точки . Теперь каждый набор значений двух величин представлен точкой на графике. Например, набор 6 минут и 10 километров представлен точкой A на графике. Чтобы получить эту точку, мы отмечаем 6 минут на оси абсцисс и проводим перпендикуляр в точке на оси абсцисс. Точно так же отметьте 10 километров по оси Y и проведите перпендикуляр по оси Y в этой точке.

Точкой пересечения этих перпендикуляров является точка А. Таким образом, мы отметим на графике всю информацию, приведенную в таблице.

Шаг 4:

Соединение точек

Четвертым шагом будет соединение точек . Как только все эти точки, соответствующие доступной информации в таблице, нанесены на график, они соединяются плавной кривой, чтобы получить график.

Здесь, в данном случае, мы получаем прямую линию, представляющую равномерное движение. Я думаю, теперь у вас есть представление об основах графика и о том, как его построить.

Таким образом, если вы знаете, как расстояние зависит от времени для любого объекта, вы сможете построить график зависимости расстояния от времени или положение-время. Точно так же вы можете построить график зависимости скорости от времени, используя эту процедуру. Итак, мы можем легко построить график движения объекта с помощью этих шагов.

Статьи по теме

Дополнительные сведения о графах движения см. на http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/motgraph.html
Подробнее о графах в физике: https://www. slideshare.net/simonandisa/graphs-in-physics

Клемсон У. Учебное пособие по физике: Графики

Время (в минутах	Расстояние (в секундах)
0	0
6	10
12	20
18	30
24	40
30	50
36	60

Учебник по физике: построение графиков

Лаборатория физики

Преподаватели лаборатории

Лабораторные добавки

Учитель физики

Дом

Лабораторные занятия по физике

Все графики должны быть выполнены от руки карандашом на миллиметровой бумаге. (По ходу семестра вам может быть разрешено использовать компьютер для создания графиков после владения рисованием показаны графики.)

Если не указано иное, рисуйте только один график на странице.

График должен использовать как можно больше миллиметровой бумаги. Для этого необходим тщательный выбор наилучшего масштаба. Оси должны выходить за пределы первой и последней точек данных в оба направления.

Все графики должны иметь краткое описательное название в начале вверху каждого графика с подробным описанием того, что измеряется.

Каждая ось должна быть четко обозначена названиями и единицами измерения.

Четко обозначьте масштаб каждой оси. Например, «1 квадрат = 0,1 метра».

Никогда не соединяйте точки на графике, а давайте наиболее подходящая линия или кривая.

Наиболее подходящая линия должна быть проведена с помощью линейки или аналогичного предмета прямолинейный край, и должен точно соответствовать тренду всех данные, а не какую-то одну точку или группу точек.

Линия наилучшего соответствия должна выходить за пределы точек данных.

Наклон следует рассчитывать по двум точкам на наиболее подходящая строка . Две точки должны быть расположены достаточно далеко друг от друга. отдельно. Точки данных должны , а не , можно использовать для расчета уклона.

На линейном графике изобразите рост, у, и запустить, x, чтобы сформировать треугольник с наиболее подходящая линия. Обязательно пометьте эти значения и включите единицы измерения.

Расчет уклона, следует должны быть четко показаны на самом графике. Единицы должны быть включены, и значение наклона должно быть хорошо видно.

См. приведенный ниже образец графика, который включает указанные выше требования.

Лабораторные занятия по физике

Если у вас есть вопрос или комментарий, отправьте электронное письмо координатору лаборатории: Джерри Хестер

Графические задачи по физике и графическое решение задач

Графики. Часть вторая | Кинематика | Физика