Наименьшее значение функции по графику производной
Рассмотрим примеры, в которых дан график производной и требуется определить, в какой точке данного отрезка функция принимает наименьшее значение.
№1
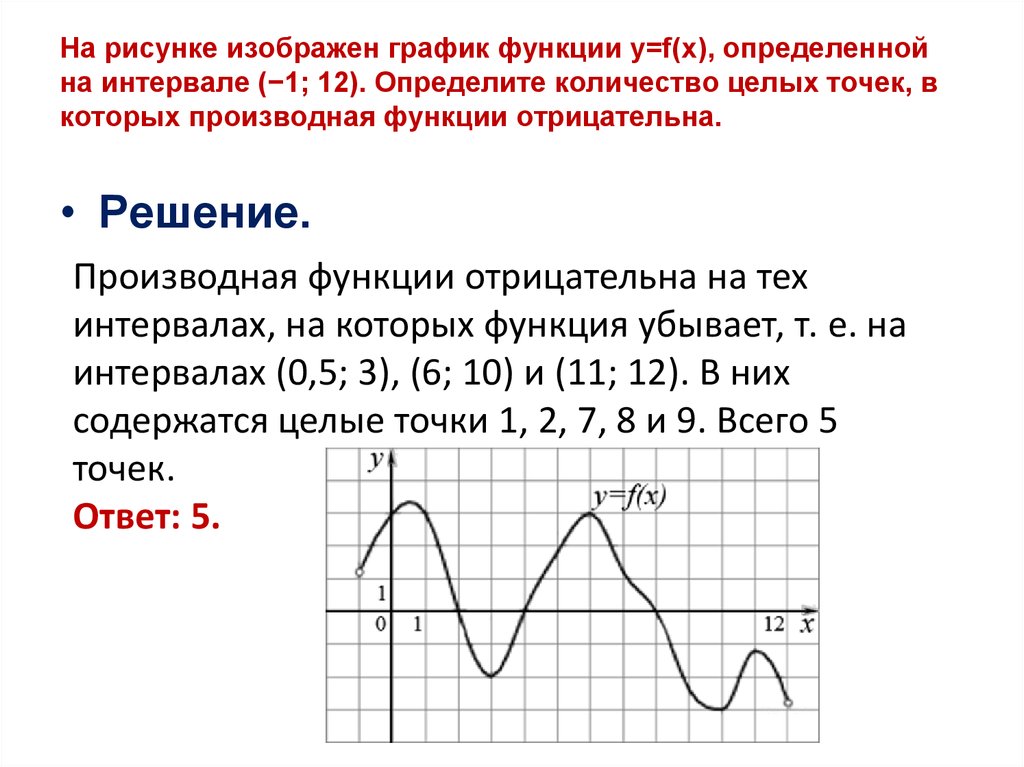
На рисунке изображён график производной функции f(x), определённой на интервале (-10;8). В какой точке отрезка [-8;-1] функция f(x) принимает наименьшее значение?
Решение:
Выделяем отрезок [-8;-1].
На этом отрезке производная f'(x) принимает положительные значения.
Значит, на [-8;-1] функция f(x) возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:
x1,x2 ∈[-8;-1], x2>x1, ⇒ f(x2)>f(x1).
Следовательно, наименьшее значение f(x) принимает при наименьшем значении аргумента, то есть на левом конце отрезка, при x=-8.
Ответ: -8.
№2
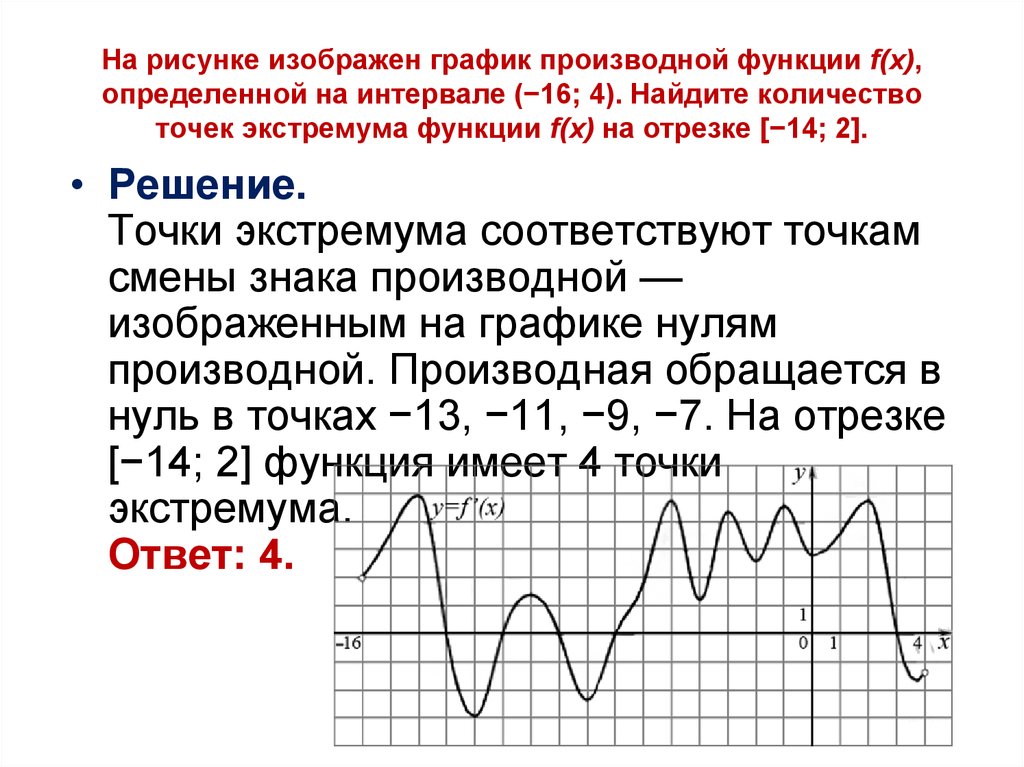
На рисунке изображён график производной функции f(x), определённой на интервале (-6;8).
Решение:
Выделяем отрезок [-3;6].
На этом отрезке f'(x)<0, поэтому f(x) убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:
x1,x2 ∈[-3;6], x2>x1, ⇒ f(x2)<f(x1).
Поэтому наименьшее значение функция f(x) в этом случае принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=6.
Ответ: 6.
№3
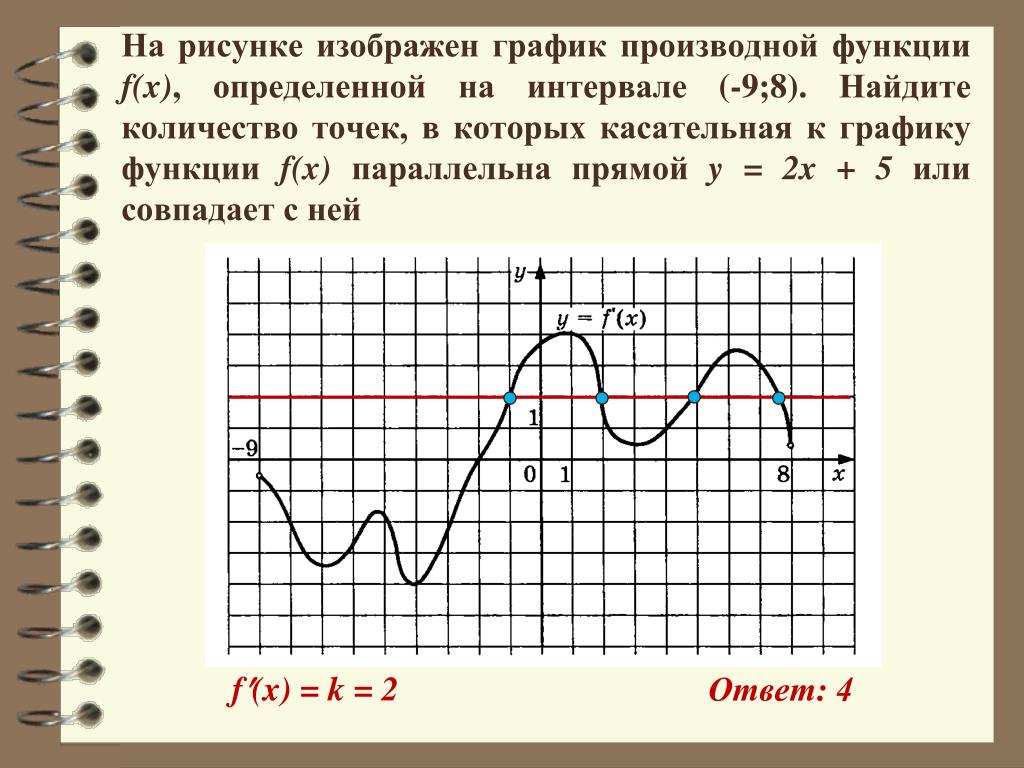
Функция y=f(x) определена на промежутке (-9;6). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наименьшее значение.
Решение:
В точке с абсциссой x=2 производная меняет знак с минуса на плюс.
Значит, x=2 — точка минимума.
Производная f'(x) существует на всём интервале (-9;6), следовательно, функция f(x) на (-9;6) непрерывна.
Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума xo и это точка минимума, то на (a;b) функция принимает своё наименьшее значение в точке xo.
Таким образом, наименьшее значение функция f(x) принимает в точке с абсциссой x=2.
№4
Функция y=f(x) определена и непрерывна на отрезке [-4;9]. На рисунке изображён график её производной. Найти точку xo, в которой функция принимает наименьшее значение, если f(9)≤f(-4).
Решение:
На промежутках (-4;-3) и (2;9) производная f'(x) принимает положительные значения, поэтому функция f(x) на этих промежутках возрастает.
На промежутке (-3;2) производная f'(x)<0, поэтому функция f(x) убывает.
Так как функция определена и непрерывна на отрезке [-4;9], то точки -4, -3, 2 и 9 можно включить в промежутки монотонности.
Следовательно, функция f(x) возрастает на промежутках [-4;-3] и [2;9] и убывает на [-3;2].
На промежутках возрастания своё наименьшее значение функция принимает на левом конце отрезка. На отрезке [2;9] наименьшее значение f(x) принимает в точке x=2 (точке минимума), на [-4;-3] — в точке x=-4.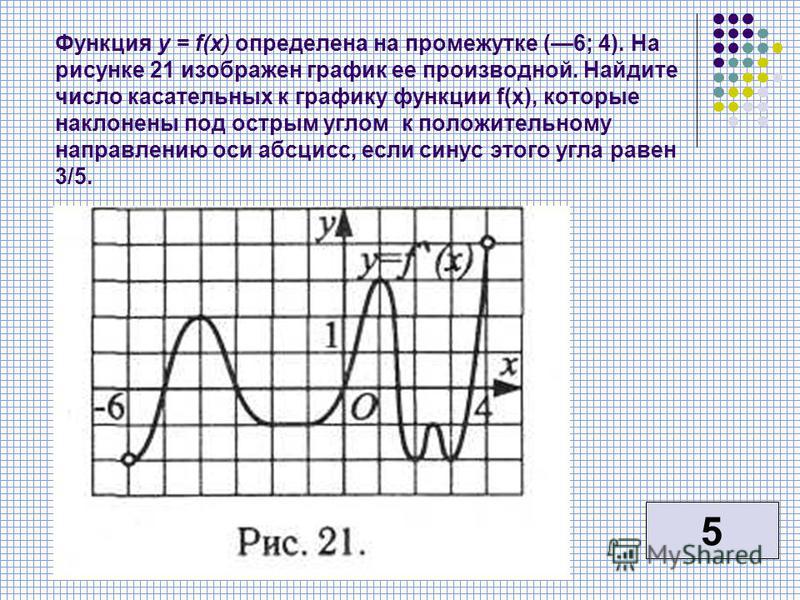
Так как на [2;9] функция f(x) возрастает, то f(2)<f(9).
По условию, f(9)≤f(-4). Значит, f(2)<f(-4).
Таким образом, наименьшее значение функция f(x) принимает в точке x=2.
Ответ: 2.
Возрастание и убывание функций | Алгебра
Определения
1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
То есть для любых двух значений x1,x2 из этого промежутка выполняется условие
2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.
То есть для любых двух значений x1,x2 из этого промежутка выполняется условие
Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.
Обычно промежуток — это отрезок, интервал или полуинтервал.
График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).
На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).
Пример 1.
Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x1;x5]:
Функция y=f(x) возрастает на промежутках [x2;x3] и [x4;x5]
Функция y=f(x) убывает на промежутках [x1;x2] и [x3;x4].
Кратко это записывают так:
3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).
4) Если функция возрастает на всей своей области определения, то её называют возрастающей.
Если функция убывает на всей своей области определения, то её называют убывающей.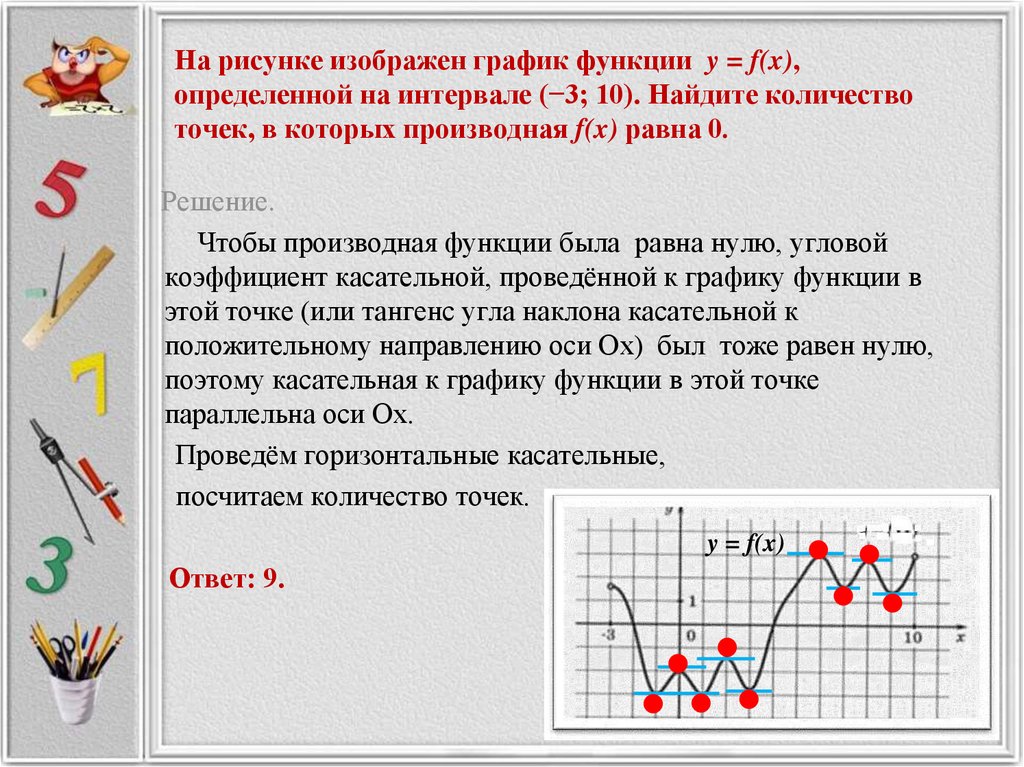
Например, y=√x, y=x³ — возрастающие функции.
Линейная функция y=kx+b возрастающая при k>0 и убывающая при k<0.
5) Если для любых двух значений x1,x2 из некоторого промежутка выполняется условие
то функция y=f(x) называется неубывающей на этом промежутке.
6) Если для любых двух значений x1,x2 из некоторого промежутка выполняется условие
то функция y=f(x) называется невозрастающей на этом промежутке.
7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.
Пример 2.
Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x
Функция y=g(x) является неубывающей на промежутке [x1;x2].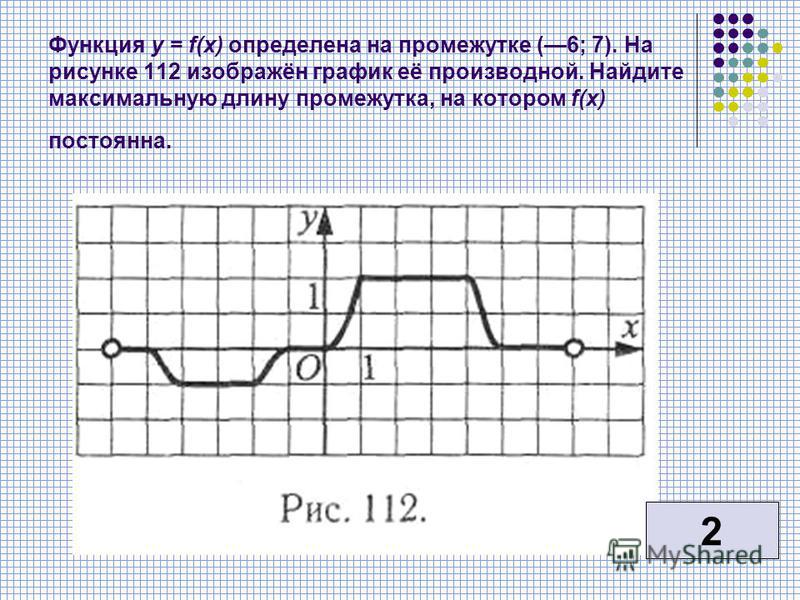
Функция y=g(x) является невозрастающей на промежутке [x2;x3].
Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.
Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?
Для этого при условии x2>x1 на промежутке надо доказать выполнение одного из неравенств: f(x
Примеры.
1) Доказать, что функция f(x)=x²+4x убывает на промежутке (-∞;-2).
Доказательство:
Функция определена на всей числовой прямой.
Пусть x2>x1.
f(x1)=x1²+4x1, f(x2)=x2²+4x2,
f(x2)-f(x1)=(x2²+4x2)-(x1²+4x1)=x2²+4x2-x1²-4x1=
группирует первое слагаемое с третьим, второе — с четвертым.
=(x2²-x1²)+(4x2-4x1)=(x2-x1)(x2+x1)+4(x2-x1)=
Теперь выносим общий множитель (x2-x1) за скобки:
=(x2-x1)(x2+x1+4).
Так как x2>x1, то x2-x1>0. Следовательно, знак произведения зависит от знака второго множителя.
Для x1, x2 ∈(-∞;-2) x2+x1+4<0. Значит, (x2-x1
Что и требовалось доказать.
2) Доказать, что функция
возрастает на промежутке (2;+∞).
Доказательство:
Функция определена при x∈(-∞;2) и (2;+∞).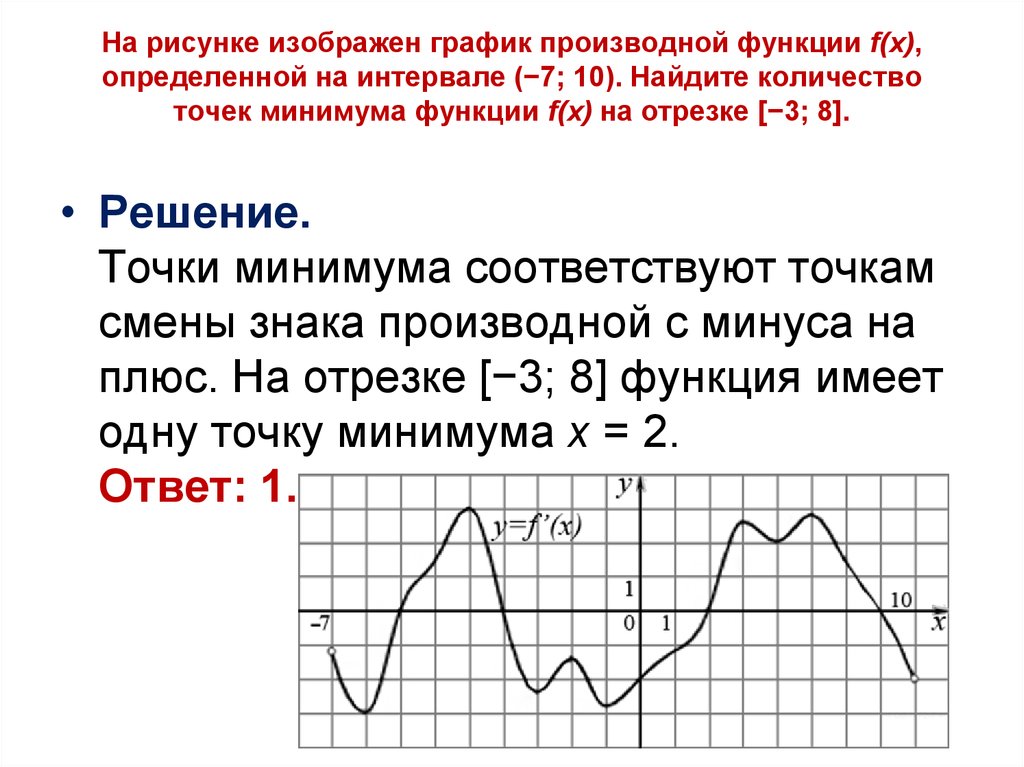
Пусть x2>x1.
Так как x2>x1, то x2-x1>0.
Для x1, x2 ∈ (2;+∞) (2-x1)(2-x
Отсюда y(x2)-y(x1)>0. Поэтому данная функция возрастает на промежутке (2;+∞).
Что и требовалось доказать.
Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).
Рубрика: Функции | Комментарии4.4 Теорема о среднем значении. Расчет, том 1
Цели обучения
- 4.4.1 Объясните смысл теоремы Ролля.
- 4.4.2 Опишите значение теоремы о среднем значении.
- 4.4.3
Укажите три важных следствия теоремы о среднем значении.

Теорема о среднем значении — одна из самых важных теорем математического анализа. Мы рассмотрим некоторые из его следствий в конце этого раздела. Во-первых, давайте начнем с частного случая теоремы о среднем значении, называемого теоремой Ролля.
Теорема Ролля
Неформально теорема Ролля утверждает, что если выходы дифференцируемой функции ff равны на концах интервала, то должна существовать внутренняя точка cc, где f′(c)=0,f′(c)=0. 4.21 иллюстрирует эту теорему.
Рисунок 4.21 Если дифференцируемая функция f удовлетворяет условию f(a)=f(b),f(a)=f(b), то ее производная должна быть равна нулю в некоторой точке(ах) между aa и b.b.
Теорема 4.4
Теорема Ролля
Пусть ff — непрерывная функция на отрезке [a,b][a,b] и дифференцируемая на открытом отрезке (a,b)(a,b) такая, что f(a)=f(b). f (а) = f (б). Тогда существует по крайней мере одно c∈(a,b)c∈(a,b) такое, что f′(c)=0. f′(c)=0.
f′(c)=0.
Доказательство
Пусть k=f(a)=f(b).k=f(a)=f(b). Рассмотрим три случая:
- f(x)=kf(x)=k для всех x∈(a,b).x∈(a,b).
- Существует x∈(a,b)x∈(a,b) такой, что f(x)>k.f(x)>k.
- Существует x∈(a,b)x∈(a,b) такой, что f(x)
Случай 1: Если f(x)=kf(x)=k для всех x∈(a,b),x∈(a,b), то f′(x)=0f′(x)=0 для все x∈(a,b).x∈(a,b).
Случай 2: Поскольку ff является непрерывной функцией на замкнутом ограниченном интервале [a,b],[a,b], по теореме об экстремальных значениях она имеет абсолютный максимум. Кроме того, поскольку существует точка x∈(a,b)x∈(a,b) такая, что f(x)>k,f(x)>k, абсолютный максимум больше kk. Следовательно, абсолютный максимум не возникает ни в одной конечной точке. В результате абсолютный максимум должен приходиться на внутреннюю точку c∈(a,b).c∈(a,b). Поскольку ff имеет максимум во внутренней точке c, c, а ff дифференцируема в c, c, по теореме Ферма f′(c)=0.f′(c)=0.
Случай 3: Случай, когда существует точка x∈(a,b)x∈(a,b) такая, что f(x)
□
Важным моментом в теореме Ролля является то, что дифференцируемость функции ff является критической. Если ff не дифференцируем даже в одной точке, результат может быть неверным. Например, функция f(x)=|x|−1f(x)=|x|−1 непрерывна на [−1,1][−1,1] и f(−1)=0=f( 1),f(−1)=0=f(1), но f′(c)≠0f′(c)≠0 для любого c∈(−1,1)c∈(−1,1), как показано на следующем рисунке.
Рисунок 4.22 Поскольку f(x)=|x|−1f(x)=|x|−1 не дифференцируема при x=0,x=0, условия теоремы Ролля не выполняются. На самом деле этот вывод здесь неверен; не существует c∈(−1,1)c∈(−1,1) такого, что f′(c)=0.f′(c)=0.
Теперь рассмотрим функции, удовлетворяющие условиям теоремы Ролля, и вычислим в явном виде точки cc, где f′(c)=0.f′(c)=0.
Пример 4.14
Использование теоремы Ролля
Для каждой из следующих функций проверьте, что функция удовлетворяет критериям, указанным в теореме Ролля, и найдите все значения cc в заданном интервале, где f′(c)=0.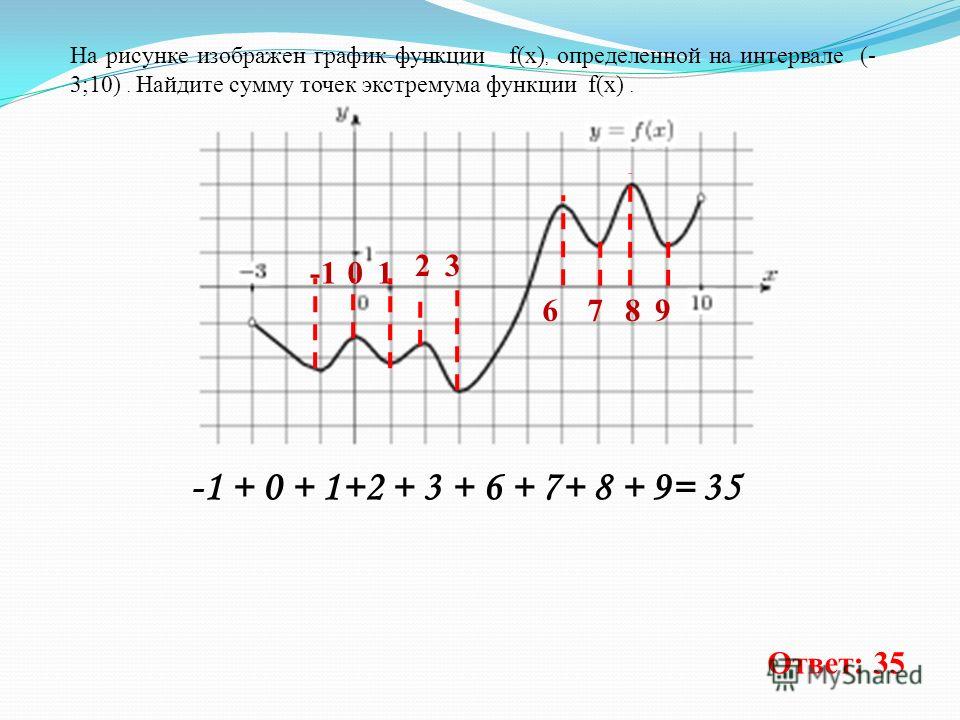 f′(c)=0 .
f′(c)=0 .
- f(x)=x2+2xf(x)=x2+2x свыше [−2,0][−2,0]
- f(x)=x3−4xf(x)=x3−4x на [−2,2][−2,2]
Решение
- Поскольку ff — полином, он непрерывен и дифференцируем всюду. Кроме того, f(-2)=0=f(0).f(-2)=0=f(0). Следовательно, ff удовлетворяет критериям теоремы Ролля. Мы заключаем, что существует по крайней мере одно значение c∈(−2,0)c∈(−2,0) такое, что f′(c)=0.f′(c)=0. Поскольку f′(x)=2x+2=2(x+1),f′(x)=2x+2=2(x+1), мы видим, что f′(c)=2(c+1) =0f′(c)=2(c+1)=0 подразумевает c=−1c=−1, как показано на следующем графике.
Рисунок 4.23 Эта функция непрерывна и дифференцируема на [−2,0],[−2,0],f′(c)=0f′(c)=0, когда c=−1.c=−1.
- Как и в части а. ff — полином, а значит, непрерывен и всюду дифференцируем. Кроме того, f(−2)=0=f(2).f(−2)=0=f(2). При этом ff удовлетворяет критериям теоремы Ролля. Дифференцируя, находим, что f′(x)=3×2−4.f′(x)=3×2−4. Следовательно, f′(c)=0f′(c)=0, когда x=±23.
 x=±23. Обе точки находятся в интервале [−2,2],[−2,2], и, следовательно, обе точки удовлетворяют заключению теоремы Ролля, как показано на следующем графике.
x=±23. Обе точки находятся в интервале [−2,2],[−2,2], и, следовательно, обе точки удовлетворяют заключению теоремы Ролля, как показано на следующем графике. Рисунок 4.24 Для этого многочлена над [−2,2],[−2,2],f′(c)=0f′(c)=0 при x=±2/3.x=±2/3.
Контрольно-пропускной пункт 4.14
Убедитесь, что функция f(x)=2×2−8x+6f(x)=2×2−8x+6, заданная на интервале [1,3][1,3], удовлетворяет условиям теоремы Ролля. Найдите все точки cc, гарантированные теоремой Ролля.
Теорема о среднем значении и ее значение
Теорема Ролля является частным случаем теоремы о среднем значении. В теореме Ролля мы рассматриваем дифференцируемые функции ff, определенные на отрезке [a,b][a,b] с f(a)=f(b)f(a)=f(b). Теорема о среднем значении обобщает теорему Ролля, рассматривая функции, которые не обязательно имеют одинаковое значение в конечных точках. Следовательно, мы можем рассматривать теорему о среднем значении как искаженную версию теоремы Ролля (рис.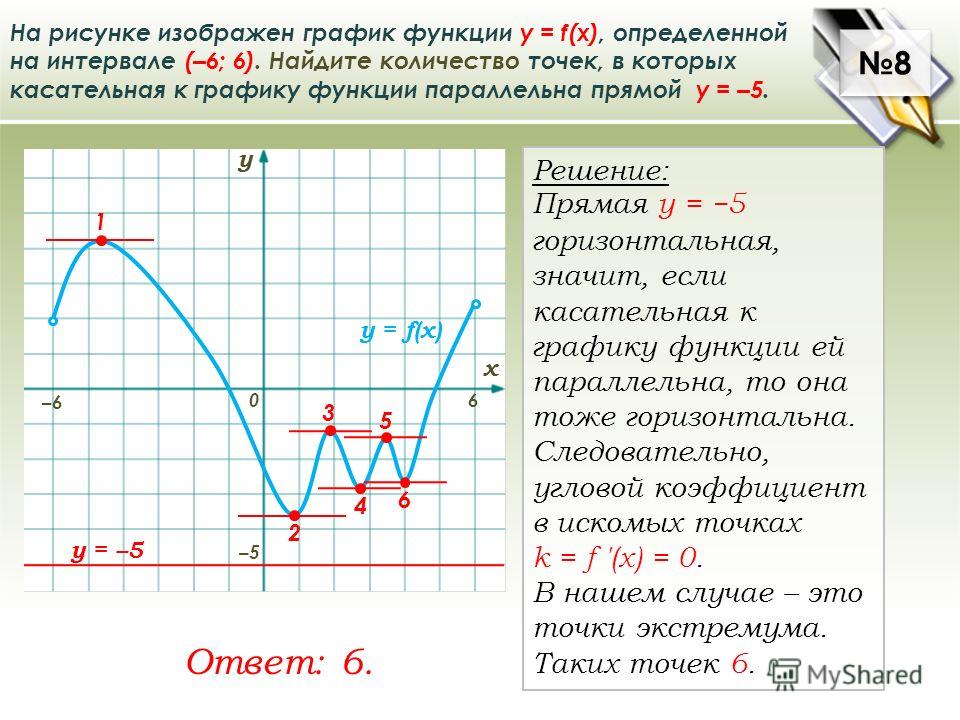 4.25). Теорема о среднем значении утверждает, что если ff непрерывна на замкнутом интервале [a,b][a,b] и дифференцируема на открытом интервале (a,b),(a,b), то существует точка c∈( a,b)c∈(a,b), касательная к графику ff в точке cc параллельна секущей, соединяющей (a,f(a))(a,f(a)) и (b, f(b)).(b,f(b)).
4.25). Теорема о среднем значении утверждает, что если ff непрерывна на замкнутом интервале [a,b][a,b] и дифференцируема на открытом интервале (a,b),(a,b), то существует точка c∈( a,b)c∈(a,b), касательная к графику ff в точке cc параллельна секущей, соединяющей (a,f(a))(a,f(a)) и (b, f(b)).(b,f(b)).
Рисунок 4,25 Теорема о среднем значении говорит, что для функции, которая удовлетворяет своим условиям, в некоторой точке касательная имеет тот же наклон, что и секущая между концами. Для этой функции есть два значения c1c1 и c2c2, так что касательная к ff в точках c1c1 и c2c2 имеет тот же наклон, что и секущая.
Теорема 4,5
Теорема о среднем значении
Пусть ff непрерывна на отрезке [a,b][a,b] и дифференцируема на открытом отрезке (a,b).(a,b). Тогда существует по крайней мере одна точка c∈(a,b)c∈(a,b) такая, что
f′(c)=f(b)−f(a)b−a.f′(c)=f(b)−f(a)b−a.
Доказательство
Доказательство следует из теоремы Ролля введением соответствующей функции, удовлетворяющей критериям теоремы Ролля. Рассмотрим линию, соединяющую (a,f(a))(a,f(a)) и (b,f(b)).(b,f(b)). Поскольку наклон этой линии равен
Рассмотрим линию, соединяющую (a,f(a))(a,f(a)) и (b,f(b)).(b,f(b)). Поскольку наклон этой линии равен
ж(б)-ф(а)б-аф(б)-ф(а)б-а
и прямая проходит через точку (a,f(a)),(a,f(a)), уравнение этой прямой можно записать как
y=f(b)−f(a)b−a(x−a)+f(a).y=f(b)−f(a)b−a(x−a)+f(a) .
Пусть g(x)g(x) обозначает разницу по вертикали между точкой (x,f(x))(x,f(x)) и точкой (x,y)(x,y) на этой прямой. Следовательно,
g(x)=f(x)−[f(b)−f(a)b−a(x−a)+f(a)].g(x)=f(x)−[f(b )−f(a)b−a(x−a)+f(a)].
Рисунок 4,26 Значение g(x)g(x) представляет собой разницу по вертикали между точкой (x,f(x))(x,f(x)) и точкой (x,y)(x,y) на секущей. соединяющие (a,f(a))(a,f(a)) и (b,f(b)).(b,f(b)).
Поскольку график ff пересекает секущую при x=ax=a и x=b,x=b, мы видим, что g(a)=0=g(b).g(a)=0=g(b ). Поскольку ff — дифференцируемая функция над (a, b), (a, b), gg — также дифференцируемая функция над (a, b) (a, b). Кроме того, поскольку ff непрерывен над [a,b],[a,b], gg также непрерывен над [a,b]. [a,b]. Следовательно, gg удовлетворяет критериям теоремы Ролля. Следовательно, существует точка c∈(a,b)c∈(a,b) такая, что g′(c)=0.g′(c)=0. С
[a,b]. Следовательно, gg удовлетворяет критериям теоремы Ролля. Следовательно, существует точка c∈(a,b)c∈(a,b) такая, что g′(c)=0.g′(c)=0. С
g′(x)=f′(x)−f(b)−f(a)b−a,g′(x)=f′(x)−f(b)−f(a)b−a ,
мы видим, что
g′(c)=f′(c)−f(b)−f(a)b−a.g′(c)=f′(c)−f(b)−f(a)b−a.
Поскольку g′(c)=0,g′(c)=0, мы заключаем, что
f′(c)=f(b)−f(a)b−a.f′(c)=f(b)−f(a)b−a.
□
В следующем примере мы покажем, как теорему о среднем значении можно применить к функции f(x)=xf(x)=x на интервале [0,9].[0,9]. Метод такой же для других функций, хотя иногда с более интересными последствиями.
Пример 4.15
Проверка применимости теоремы о среднем значении и поэтому существует по крайней мере одно значение c∈(0,9)c∈(0,9) такое, что f′(c)f′(c) равно наклону линии, соединяющей (0,f(0) )(0,f(0)) и (9,f(9)).(9,f(9)). Найдите эти значения cc, гарантированные теоремой о среднем значении.
Решение
Мы знаем, что f(x)=xf(x)=x непрерывна на [0,9][0,9] и дифференцируема над (0,9). (0,9). Следовательно, ff удовлетворяет условиям теоремы о среднем значении, и должно существовать хотя бы одно значение c∈(0,9)c∈(0,9), такое что f′(c)f′(c) равно наклон линии, соединяющей (0,f(0))(0,f(0)) и (9,f(9))(9,f(9)) (рис. 4.27). Чтобы определить, какие значения cc гарантированы, сначала вычислите производную f.f. Производная f′(x)=1(2x).f′(x)=1(2x). Наклон линии, соединяющей (0,f(0))(0,f(0)) и (9,f(9))(9,f(9)) равен
(0,9). Следовательно, ff удовлетворяет условиям теоремы о среднем значении, и должно существовать хотя бы одно значение c∈(0,9)c∈(0,9), такое что f′(c)f′(c) равно наклон линии, соединяющей (0,f(0))(0,f(0)) и (9,f(9))(9,f(9)) (рис. 4.27). Чтобы определить, какие значения cc гарантированы, сначала вычислите производную f.f. Производная f′(x)=1(2x).f′(x)=1(2x). Наклон линии, соединяющей (0,f(0))(0,f(0)) и (9,f(9))(9,f(9)) равен
f(9)−f(0)9−0=9−09−0=39=13.f(9)−f(0)9−0=9−09−0=39=13.
Мы хотим найти cc такое, что f′(c)=13.f′(c)=13. То есть мы хотим найти cc такое, что
12c=13.12c=13.
Решая это уравнение относительно c,c, получаем c=94.c=94. В этой точке наклон касательной равен наклону линии, соединяющей конечные точки.
Рисунок 4,27 Наклон касательной при c=9/4c=9/4 такой же, как наклон отрезка, соединяющего (0,0)(0,0) и (9,3).(9,3).
Одно приложение, помогающее проиллюстрировать теорему о среднем значении, касается скорости. Например, предположим, что мы едем на автомобиле в течение 1 часа по прямой дороге со средней скоростью 45 миль в час.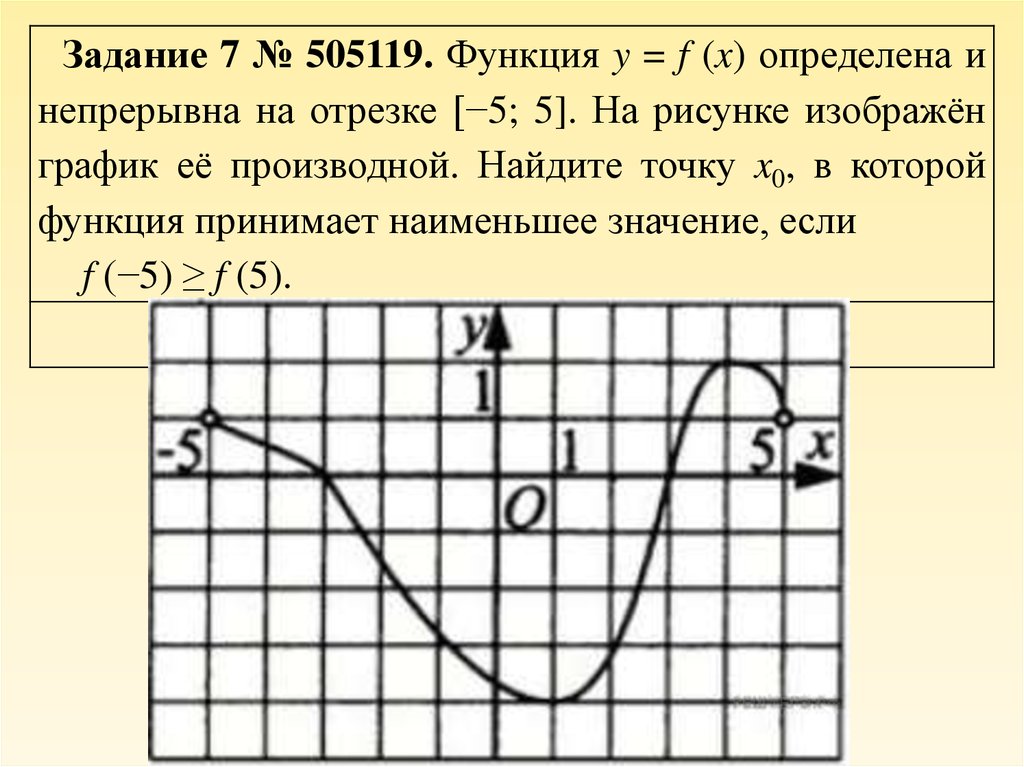 Пусть s(t)s(t) и v(t)v(t) обозначают положение и скорость автомобиля соответственно для 0≤t≤10≤t≤1 ч. Предполагая, что функция положения s(t)s(t) дифференцируема, мы можем применить теорему о среднем значении, чтобы заключить, что в некоторый момент времени c∈(0,1),c∈(0,1) скорость машина была именно
Пусть s(t)s(t) и v(t)v(t) обозначают положение и скорость автомобиля соответственно для 0≤t≤10≤t≤1 ч. Предполагая, что функция положения s(t)s(t) дифференцируема, мы можем применить теорему о среднем значении, чтобы заключить, что в некоторый момент времени c∈(0,1),c∈(0,1) скорость машина была именно
v(c)=s′(c)=s(1)−s(0)1−0=45mph.v(c)=s′(c)=s(1)−s(0)1−0 = 45 миль в час.
Пример 4.16
Теорема о среднем значении и скорость
Если камень брошен с высоты 100 футов, его положение через tt секунд после того, как камень будет брошен до удара о землю, определяется функцией s(t)=−16t2+100.s (t)=−16t2+100.
- Определите, сколько времени пройдет, прежде чем камень упадет на землю.
- Найдите среднюю скорость vavgvavg камня в тот момент, когда камень падает на землю.
- Найдите время tt, гарантированное теоремой о среднем значении, когда мгновенная скорость камня равна vavg.vavg.
Решение
- Когда камень падает на землю, его положение s(t)=0.
 s(t)=0. Решая уравнение −16t2+100=0−16t2+100=0 относительно t,t, находим, что t=±52сек.t=±52сек. Поскольку мы рассматриваем только t≥0,t≥0, мяч упадет на землю через 5252 с после того, как будет брошен.
s(t)=0. Решая уравнение −16t2+100=0−16t2+100=0 относительно t,t, находим, что t=±52сек.t=±52сек. Поскольку мы рассматриваем только t≥0,t≥0, мяч упадет на землю через 5252 с после того, как будет брошен. - Средняя скорость определяется как
ср=с(5/2)-с(0)5/2-0=0-1005/2=-40 футов/с. )5/2−0=0−1005/2=−40 футов/сек.
- Мгновенная скорость определяется производной функции положения. Следовательно, нам нужно найти время tt такое, что v(t)=s'(t)=vavg=-40ft/sec.v(t)=s'(t)=vavg=-40ft/sec. Поскольку s(t)s(t) непрерывна на интервале [0,5/2][0,5/2] и дифференцируема на интервале (0,5/2),(0,5/2), по формуле по теореме о среднем значении гарантированно существует точка c∈(0,5/2)c∈(0,5/2) такая, что
s′(c)=s(5/2)−s(0)5/2−0=−40.s′(c)=s(5/2)−s(0)5/2−0= −40.
Взяв производную функции положения s(t),s(t), находим, что s′(t)=−32t.s′(t)=−32t. Следовательно, уравнение сводится к s′(c)=−32c=−40.s′(c)=−32c=−40. Решив это уравнение относительно c,c, мы получим c=54.c=54. Следовательно, через 5454 с после падения камня мгновенная скорость равна средней скорости камня при его свободном падении: -40-40 фут/с.
Рисунок 4,28 В момент времени t=5/4t=5/4 с скорость камня равна его средней скорости с момента падения до момента удара о землю.
Контрольно-пропускной пункт 4.15
Предположим, что мяч брошен с высоты 200 футов. Его положение в момент времени tt равно s(t)=−16t2+200.s(t)=−16t2+200. Найдите момент времени tt, когда мгновенная скорость мяча сравняется с его средней скоростью.
Следствия теоремы о среднем значении
Давайте теперь рассмотрим три следствия теоремы о среднем значении. Эти результаты имеют важные следствия, которые мы используем в следующих разделах.
На данный момент мы знаем, что производная любой постоянной функции равна нулю. Теорема о среднем значении позволяет сделать вывод, что верно и обратное. В частности, если f′(x)=0f′(x)=0 для всех xx в некотором интервале I,I, то f(x)f(x) постоянна на этом интервале. Этот результат может показаться интуитивно очевидным, но он имеет важные неочевидные последствия, которые мы вскоре обсудим.
Теорема 4.6
Следствие 1. Функции с производной нуля
Пусть ff дифференцируема на интервале I.I. Если f′(x)=0f′(x)=0 для всех x∈I,x∈I, то f(x)=f(x)= константа для всех x∈I.x∈I.
Доказательство
Поскольку ff дифференцируема над I, I, ff должна быть непрерывной над I.I. Предположим, что f(x)f(x) не является константой для всех xx в I.I. Тогда существуют a,b∈I,a,b∈I, где a≠ba≠b и f(a)≠f(b).f(a)≠f(b). Выберите обозначение так, чтобы a f(b)−f(a)b−a≠0.f(b)−f(a)b−a≠0. Поскольку ff — дифференцируемая функция, по теореме о среднем значении существует c∈(a,b)c∈(a,b) такое, что f′(c)=f(b)−f(a)b−a.f′(c)=f(b)−f(a)b−a. Следовательно, существует c∈Ic∈I такое, что f′(c)≠0,f′(c)≠0, что противоречит предположению, что f′(x)=0f′(x)=0 для всех x∈ I.x∈I. □ Из следствия 1: функции с производной от нуля следует, что если две функции имеют одну и ту же производную, то они отличаются не более чем на константу. Если ff и gg дифференцируемы на интервале II и f′(x)=g′(x)f′(x)=g′(x) для всех x∈I,x∈I, то f(x) =g(x)+Cf(x)=g(x)+C для некоторой константы C.C. Пусть h(x)=f(x)−g(x).h(x)=f(x)−g(x). Тогда h′(x)=f′(x)−g′(x)=0h′(x)=f′(x)−g′(x)=0 для всех x∈I.x∈I. По следствию 1 существует константа CC такая, что h(x)=Ch(x)=C для всех x∈I.x∈I. Следовательно, f(x)=g(x)+Cf(x)=g(x)+C для всех x∈I.x∈I. □ Третье следствие теоремы о среднем значении обсуждает, когда функция возрастает и когда она убывает. Напомним, что функция ff возрастает по II, если f(x1) Этот факт важен, потому что он означает, что для данной функции f,f, если существует функция FF такая, что F′(x)=f(x);F′(x)=f(x); тогда единственными другими функциями, имеющими производную, равную ff, являются F(x)+CF(x)+C для некоторой константы C.C. Мы обсудим этот результат более подробно позже в этой главе. Рисунок
4.29
Если функция имеет положительную производную на некотором интервале I,I, то функция возрастает на этом интервале I;I; если на некотором интервале I,I производная отрицательна, то функция убывает на этом интервале I.I. Пусть ff непрерывна на отрезке [a,b][a,b] и дифференцируема на открытом отрезке (a,b). Докажем i.; доказательство II. похож. Предположим, что ff не является возрастающей функцией на I.I. Тогда существуют aa и bb в II такие, что a f′(c)=f(b)−f(a)b−a.f′(c)=f(b)−f(a)b−a. Поскольку f(a)>f(b),f(a)>f(b), мы знаем, что f(b)−f(a)<0.f(b)−f(a)<0. Кроме того, a f′(c)=f(b)−f(a)b−a<0.f′(c)=f(b)−f(a)b−a<0. Однако f′(x)>0f′(x)>0 для всех x∈I.x∈I. Противоречие, поэтому ff должна быть возрастающей функцией над I.I. □ 148. Почему вам нужна непрерывность, чтобы применить теорему о среднем значении? Постройте контрпример. 149. Зачем нужна дифференцируемость, чтобы применить теорему о среднем значении? Найдите контрпример. 150. Когда теорема Ролля и теорема о среднем значении эквивалентны? 151. Если у вас есть функция с разрывом, возможно ли, чтобы f′(c)(b−a)=f(b)−f(a)?f′(c)(b−a)=f (б)−f(а)? Приведите такой пример или докажите, почему нет. Для следующих упражнений определите, для каких интервалов (если есть) применяется теорема о среднем значении. Обосновать ответ. 152. y=sin(πx)y=sin(πx) 153. у=1х3у=1х3 154. у=4-х2у=4-х2 155. у=х2-4у=х2-4 156. y=ln(3x−5)y=ln(3x−5) Для следующих упражнений постройте графики функций на калькуляторе и нарисуйте секущую, соединяющую конечные точки. Оцените количество точек cc таких, что f′(c)(b−a)=f(b)−f(a).f′(c)(b−a)=f(b)−f(a). 157. [T] y=3×3+2x+1y=3×3+2x+1 свыше [−1,1][−1,1] 158. [T] y=tan(π4x)y=tan(π4x) более [−32,32][−32,32] 159. [T] y=x2cos(πx)y=x2cos(πx) на [−2,2][−2,2] 160. [T] y=x6−34×5−98×4+1516×3+332×2+316x+132y=x6−34×5−98×4+1516×3+332×2+316x+132 свыше [−1,1][−1,1] В следующих упражнениях используйте теорему о среднем значении и найдите все точки 0 161. f(x)=x3f(x)=x3 162. f(x)=sin(πx)f(x)=sin(πx) 163. f(x)=cos(2πx)f(x)=cos(2πx) 164. f(x)=1+x+x2f(x)=1+x+x2 165. f(x)=(x−1)10f(x)=(x−1)10 166. f(x)=(x−1)9f(x)=(x−1)9 В следующих упражнениях покажите, что не существует cc такого, что f(1)−f(−1)=f′(c)(2).f(1)−f(−1)=f′(c)( 2). Объясните, почему теорема о среднем значении неприменима на интервале [−1,1].[−1,1]. 167. f(x)=|x−12|f(x)=|x−12| 168. f(x)=1x2f(x)=1×2 169. е (х) = | х | е (х) = | х | 170. f(x)=⌊x⌋f(x)=⌊x⌋ ( Подсказка : Это называется функцией пола и определяется так, что f(x)f(x) является наибольшим целым числом меньше больше или равно x. В следующих упражнениях определите, применима ли теорема о среднем значении для функций на заданном интервале [a,b].[a,b]. Обосновать ответ. 171. y=exy=ex свыше [0,1][0,1] 172. y=ln(2x+3)y=ln(2x+3) свыше [−32,0][−32,0] 173. f(x)=tan(2πx)f(x)=tan(2πx) на [0,2][0,2] 174. y=9−x2y=9−x2 свыше [−3,3][−3,3] 175. у=1|х+1|у=1|х+1| более [0,3][0,3] 176. y=x3+2x+1y=x3+2x+1 свыше [0,6][0,6] 177. y=x2+3x+2xy=x2+3x+2x свыше [−1,1][−1,1] 178. y=xsin(πx)+1y=xsin(πx)+1 свыше [0,1][0,1] 179. y=ln(x+1)y=ln(x+1) на [0,e−1][0,e−1] 180. y=xsin(πx)y=xsin(πx) свыше [0,2][0,2] 181. у=5+|х|у=5+|х| более [−1,1][−1,1] В следующих упражнениях рассмотрим корни уравнения. 182. Покажите, что уравнение y=x3+4x+16y=x3+4x+16 имеет ровно один действительный корень. Что это такое? 183. Найдите условия ровно одного корня (двойного корня) для уравнения y=x2+bx+cy=x2+bx+c 184. Найдите условия, при которых y=ex-by=ex-b имеет один корень. Возможно ли иметь более одного корня? В следующих упражнениях используйте калькулятор, чтобы построить график функции на интервале [a,b][a,b] и построить секущую от aa до b.b. Используйте калькулятор для оценки всех значений cc, гарантированных теоремой о среднем значении. Затем найдите точное значение c, c, если возможно, или напишите окончательное уравнение и используйте калькулятор, чтобы оценить его до четырех цифр. 185. [T] y=tan(πx)y=tan(πx) свыше [−14,14][−14,14] 186. [T] y=1x+1y=1x+1 свыше [0,3][0,3] 187. [T] y=|x2+2x−4|y=|x2+2x−4| более [−4,0][−4,0] 188. [T] y=x+1xy=x+1x свыше [12,4][12,4] 189. [T] y=x+1+1x2y=x+1+1×2 свыше [3,8][3,8] 190. В 10:17 вы проезжаете мимо полицейской машины на скорости 55 миль в час, которая остановилась на шоссе. Вы проезжаете мимо второй полицейской машины со скоростью 55 миль в час в 10:53, которая находится на 39-й улице.миль от первой полицейской машины. Если ограничение скорости составляет 60 миль в час, может ли полиция привлечь вас к ответственности за превышение скорости? 191. Две машины едут от одного светофора к другому, выезжают и прибывают в одно и то же время. Бывают ли моменты, когда они движутся с одинаковой скоростью? Докажи или опровергни. 192. Покажите, что y=sec2xy=sec2x и y=tan2xy=tan2x имеют одну и ту же производную. Что вы можете сказать о y=sec2x−tan2x?y=sec2x−tan2x? 193. Покажите, что y=csc2xy=csc2x и y=cot2xy=cot2x имеют одну и ту же производную. Что вы можете сказать о y=csc2x-cot2x?y=csc2x-cot2x? Вопрос Обновлено: 15.05.2021 РЕЗОНАНС АНГЛИЙСКИЙ-ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ-Упражнение -1F 90 РЕКЛАМА 90 90 РЕКЛАМА 9013 Ответьте Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах. Ab Padhai каро бина объявления ке Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке! Похожие видео A
функция y= f(x)
является
определяется на [0,4] как
f(x)={2x если 0≤x≤1(x−2)2 если 1 305335 Наименьший и наибольший
значения f(x)=x3−6×2+9x
в [0, 6]
, являются
3, 4
(б) 0, 6
(в) 0, 3
(г) 3, 6 1461083 यदि (0,6) पर f अवलंकनिये है तथा f'(4)=5 हथा हथो त।थो त 2−x का मान होगा- 121324213 Пусть f(x) непрерывна на [0,6] и дифференцируема на (0,6). Пусть f(0)=12 и f(6)=-4. Если g(x) =f(x)x+1, то для некоторой константы Лагранжа c∈ (0,6),g'( c)= 127791189 Text Solution Пусть f(x) непрерывна на [ 0, 6] и дифференцируемой на (0, 6). Пусть f(0) = 12 и f(6)=−4. 9(2))+f'(x)f»(x)=0 Если начало координат равно n//2 Значение 642735063 Если y=f(x) Интервал [0,6] непрерывен на интервале постоянна на интервале (0,6), f (0) = — 2 и f (6) = 16, поэтому в какой-то точке между x = 0 и x = 6 должно быть f (x) 642740595 यदि f(x) अंतराल (−∞,∞) में त्रिअवकालनीतय अनय अनर फलन को परिभाषित किया जाता है इस प्रकार f(x)=f(6−x) तथा=0 f'(0) (2)=f'(5) यदि अंतराल [0,6] में n न्यूनतम संख्या या (f»(x))2+f'(x)॥ »'(x)=h ल हो , तो n/2 का मान है 642740933 Проверить теорему Ролля для функции f, которая определяется формулой f(x)=x2+2x−8,x∈[−4,2].
Теорема
4.7
Следствие 2. Теорема о постоянной разности
Доказательство
Теорема
4,8
Следствие 3. Возрастающие и убывающие функции
 (a,b).
(a,b). Доказательство
Раздел 4.
 4 Упражнения
4 Упражнения
 )x.)
)x.)


Функция y=f(x) определена на [0,6] как f(x)=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩−8x , 0≤x≤1(x−3)3 , 1

 x=±23. Обе точки находятся в интервале [−2,2],[−2,2], и, следовательно, обе точки удовлетворяют заключению теоремы Ролля, как показано на следующем графике.
x=±23. Обе точки находятся в интервале [−2,2],[−2,2], и, следовательно, обе точки удовлетворяют заключению теоремы Ролля, как показано на следующем графике. 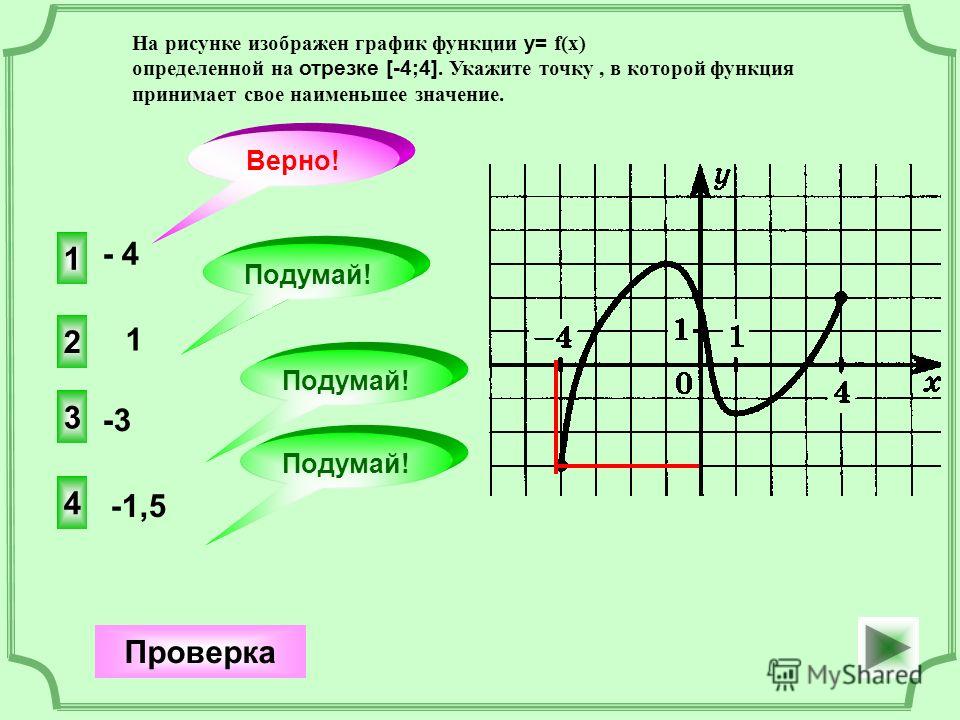 s(t)=0. Решая уравнение −16t2+100=0−16t2+100=0 относительно t,t, находим, что t=±52сек.t=±52сек. Поскольку мы рассматриваем только t≥0,t≥0, мяч упадет на землю через 5252 с после того, как будет брошен.
s(t)=0. Решая уравнение −16t2+100=0−16t2+100=0 относительно t,t, находим, что t=±52сек.t=±52сек. Поскольку мы рассматриваем только t≥0,t≥0, мяч упадет на землю через 5252 с после того, как будет брошен.
Leave A Comment