Радиус описанной окружности около треугольника онлайн
С помощю этого онлайн калькулятора можно найти радиус описанной около треугольника окружности. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Радиус окружности описанной около треугольника, если известны три стороны треугольника
- Радиус окружности описанной около треугольника, если известны сторона a и противолежащий угол A
- Радиус окружности описанной около треугольника, если известны стороны b и c треугольника и угол между ними A
- Радиус окружности описанной около треугольника, если известны сторона треугольника a и прилежащие углы B и C
1.
 Радиус окружности описанной около треугольника, если известны три стороны треугольника
Радиус окружности описанной около треугольника, если известны три стороны треугольникаПлощадь треугольника по трем сторонам a, b, c и радиусу R описанной окружности имеет вид:
| \( \small S=\frac{\large abc}{\large 4R}, \) |
откуда
| \( \small R=\frac{\large abc}{\large 4S}. \) | (1) |
Площадь треугольника по трем сторонам имеет вид:
| \( \small S= \sqrt{p(p-a)(p-b)(p-c),}\) | (2) |
где
| \( \small p= \frac{\large a+b+c}{\large 2}. \) |
Подставляя (2) в (1), получим формулу радиуса описанной окружности около треугольника:
\( \small R=\frac{\large abc}{\large 4\ \cdot \ \sqrt{p(p-a)(p-b)(p-c)}}.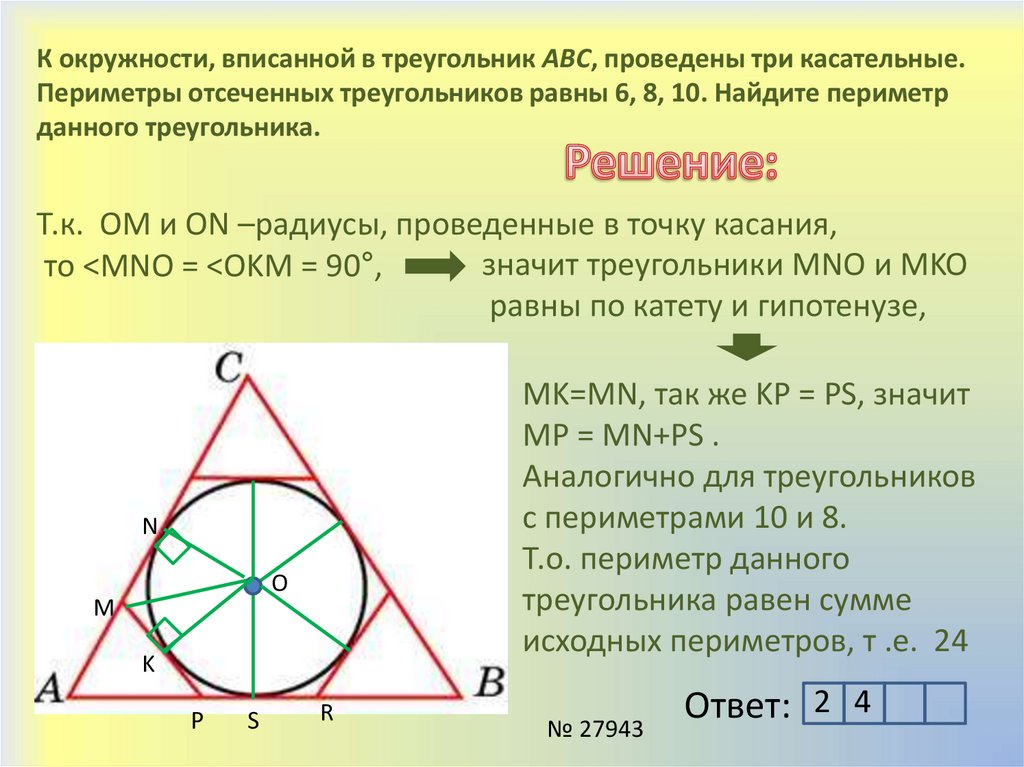 \) \) | (4) |
где p вычисляется из формулы (3).
Пример 1. Известны три стороны треугольника: \( \small a=6, \ b=5, \ c=4.5 \). Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (4), где \( \small р \) вычисляется из формулы (3).
Найдем p из (2):
Подставим значения a, b, c, p в (1):
Ответ:
2. Радиус окружности описанной около треугольника, если известны сторона
a и противолежащий угол AПусть известны сторона a и противолежащий угол A. Найдем радиус описанной окружности около треугольника. Из расширенной теоремы синусов имеем:
Откуда:
Пример 2. Сторона треугольника равна: а противолежащий угол \( \small \angle A=35°.\) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (5).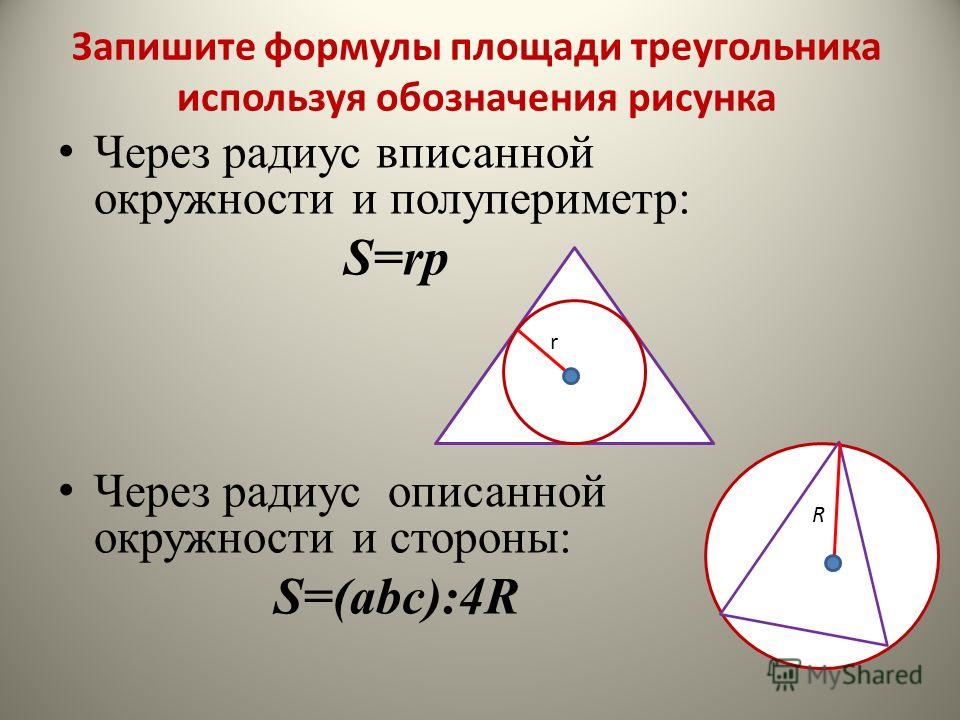 Подставим значения и \( \small \angle A=35° \) в (5):
Подставим значения и \( \small \angle A=35° \) в (5):
Ответ:
3. Радиус окружности описанной около треугольника, если известны стороны
b и c треугольника и угол между ними AПусть известны стороны b и c треугольника и угол между ними A. Найдем радиус описанной окружности около треугольника.
Из теоремы косинусов, имеем:
или
Подставляя (6) в (5), получим требуемую формулу:
Пример 3. Известны две стороны треугольника: и угол между ними: \( \small \angle A=30°. \) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения и \( \small \angle A=30° \) в (7):
Ответ:
4. Радиус окружности описанной около треугольника, если известны сторона треугольника
a и прилежащие углы B и CПусть известны сторона a треугольника и прилежащие к ней углы B и C.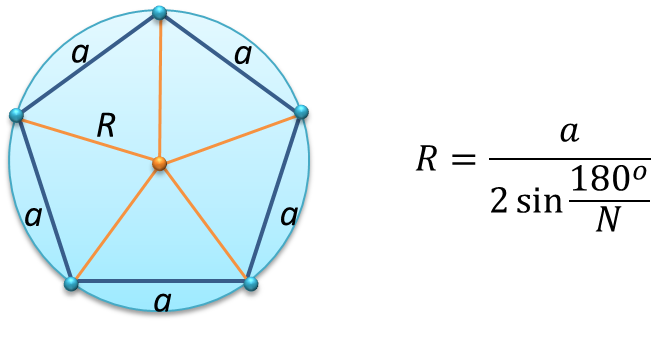 Найдем радиус описанной окружности около треугольника. Как известно, сумма углов треугольника равна 180°. Поэтому легко найти треий угол треугольника: \( \small \angle A=180°- (\angle B+ n\angle C). \) Тогда для нахождения радиуса описанной около треугольника окружности можно воспользоваться формулой (5):
Найдем радиус описанной окружности около треугольника. Как известно, сумма углов треугольника равна 180°. Поэтому легко найти треий угол треугольника: \( \small \angle A=180°- (\angle B+ n\angle C). \) Тогда для нахождения радиуса описанной около треугольника окружности можно воспользоваться формулой (5):
Получили следующую формулу:
Пример 4. Известны сторона треугольника: и прилежащие к ней углы: \( \small \angle B=21°, \;\angle C=34°. \) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (8). Подставим значения и \( \small \angle B=21°, \;\angle C=34° \) в (8):
Ответ:
Смотрите также:
- Радиус описанной окружности около равнобедренного треугольника онлайн
- Радиус описанной окружности около равностороннего треугольника онлайн
- Радиус описанной окружности около прямоугольного треугольника онлайн
Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника (формулы и примеры).
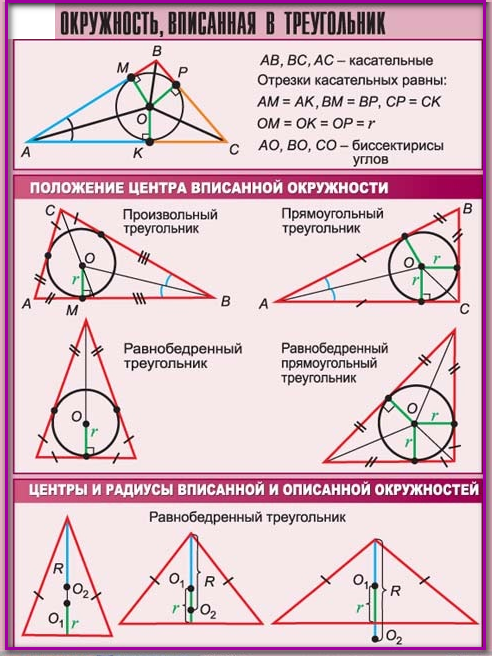
Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника (формулы и примеры). / Ответы на экзамен по геометрии / Готовые сочинения на экзаменПоступим.ру — сообщество школьников, выпускников и абитуриентов, егэ 2021, ответы на экзамены, мобильные шпаргалки, готовые сочинения, егэ, экзаменационные сочинения, темы сочинений, форум, коллективный блог
|
Последние публикации в коллективном блоге:Интернет-порталы, которые помогут вам успешно сдать ЕГЭ. 1 / Автор: Miriada 1 / Автор: MiriadaЕсли бы вы инвестировали 00 в Amazon 10 лет назад, вот сколько у вас было бы сейчас 2 / Автор: admin В Минпросвещения допустили повторный перенос даты сдачи ЕГЭ 1 / Автор: admin ЕГЭ не отменят из-за коронавируса, но проведут позже 1 / Автор: admin Рособрнадзор будет выявлять нарушения во время ЕГЭ 2020 с помощью нейросетей 1 / Автор: admin ФИПИ опубликовал проекты контрольных измерительных материалов ЕГЭ-2020, существенных изменений нет 4 / Автор: admin Рособрнадзор проанализировал поступившие предложения по совершенствованию ЕГЭ 2 / Автор: admin Посещаемые разделы форума: Последние обсуждаемые темы на форуме:Детские игровые комплексы 0 / Раздел: Помогаем друг другуМягкая кровать без изголовья 2 / Раздел: Помогаем друг другу Очень нужно купить права на трактор 0 / Раздел: Помогаем друг другу кто знает бактерицидные лампы где можно приобрести? 2 / Раздел: Помогаем друг другу мне нужен магазин со стройматериалами 3 / Раздел: Помогаем друг другу Можно ли накрутить голосование в конкурсе? 4 / Раздел: Помогаем друг другу Управление медиафайлами 0 / Раздел: Помогаем друг другу Скажите, пожалуйста, вот в маршрутках в которых мы ездим 3 / Раздел: ВУЗЫ РОССИИ Изучение итальянского языка 5 / Раздел: Помогаем друг другу |
|
|
Как найти площадь равностороннего треугольника
Все математические ресурсы верхнего уровня SSAT
6 Диагностические тесты 311 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике верхнего уровня SSAT » Геометрия » Свойства треугольников » Равнобедренные треугольники » Как найти площадь равностороннего треугольника
 Назовите площадь треугольника.
Назовите площадь треугольника.Возможные ответы:
Правильного ответа нет среди других вариантов.
Правильный ответ:
Объяснение:
Окружность и треугольник, указанные ниже, вместе с радиусом до одной стороны и сегментом до одной вершины: сторона треугольника, поэтому длина стороны равна . Площадь треугольника
Сообщить об ошибке
На приведенном выше рисунке равностороннее. Укажите его площадь.
Возможные ответы:
Правильный ответ отсутствует среди других ответов.
Правильный ответ:
Правильного ответа нет среди других ответов.
Пояснение:
Все внутренние углы равностороннего треугольника равны 60 градусам, то есть по соотношению 30-60-90 Теорема,
Кроме того, это середина , поэтому ; это база.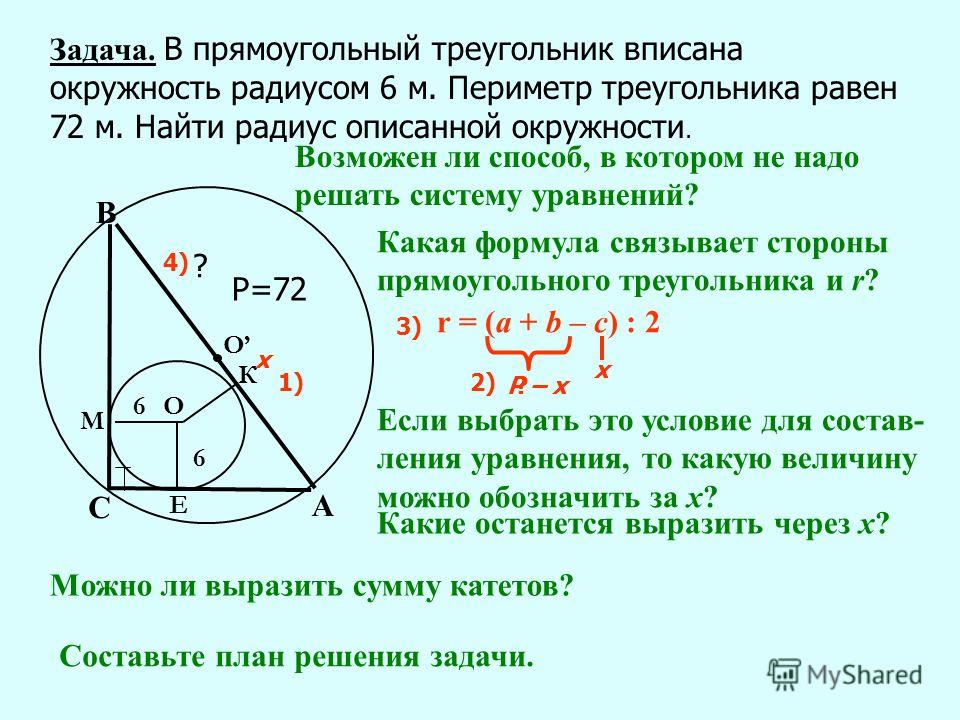
Площадь этого треугольника равна половине произведения основания на высоту :
Этот ответ не входит в число предложенных вариантов.
Сообщить об ошибке
Периметр равностороннего треугольника . Укажите его площадь.
Возможные ответы:
Правильный ответ:
Объяснение:
Равносторонний треугольник с периметром имеет три равные стороны длины
Площадь этого треугольника
Сообщить об ошибке
Шестиугольник правильный и имеет периметр 72. построен. Какова его площадь?
Возможные ответы:
Правильный ответ:
Пояснение:
Так как периметр (шестиконгруэнтного) правильного шестиугольника равен 72, каждая сторона имеет длину в одну шестую, или 12.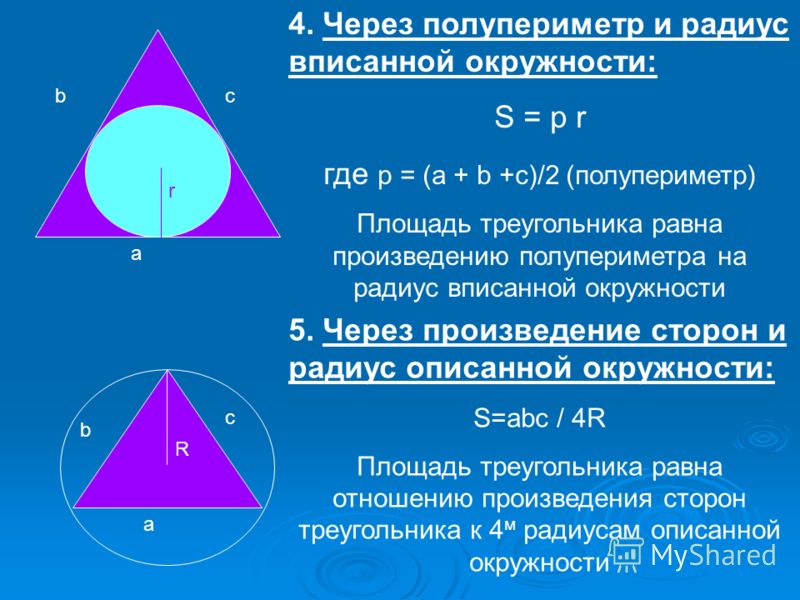
Фигура, описанная ниже, с перпендикулярным отрезком, проведенным от в сторону :
Каждый угол правильного шестиугольника измеряет . Следовательно, , и является треугольником 30-60-90.
По теореме 30-60-90
и
.
является равносторонним и является длиной его стороны, что составляет его площадь
Сообщить об ошибке
Периметр равностороннего треугольника равен . Укажите его площадь.
Возможные ответы:
Правильный ответ:
Пояснение:
Равносторонний треугольник с периметром 54 имеет три конгруэнтные стороны длины
Площадь этого треугольника
Сообщить об ошибке
Равносторонний треугольник вписан в круг радиусом . Укажите площадь треугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
Хитрость заключается в том, чтобы знать, что описанная окружность или описанная окружность имеет своим центром пересечение трех высот треугольника, и что этот центр или центр описанной окружности делит каждую высоту на два сегмента. , один в два раза длиннее другого, причем больший из них является радиусом. Из-за этого мы можем построить следующее:
, один в два раза длиннее другого, причем больший из них является радиусом. Из-за этого мы можем построить следующее:
Каждый из шести меньших треугольников равен 30-60-9.0 треугольник, и все шесть конгруэнтны.
Мы найдем площадь и умножим ее на 6.
По теореме 30-60-90, площадь равна
.
Шесть раз это — — площадь .
Сообщить об ошибке
Длины сторон равностороннего треугольника . Чему равна площадь этого треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Площадь равностороннего треугольника можно найти по следующей формуле:
Используя , мы можем найти площадь равностороннего треугольника.
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы верхнего уровня SSAT
6 диагностических тестов 311 практических тестов Вопрос дня Карточки Learn by Concept
Калькулятор формул для уравнений равностороннего треугольника
Изменить уравнение
Выберите, чтобы найти другое неизвестное
Разносторонний треугольник:
Нет сторон с одинаковой длиной
Нет равных углов
Уравнения разностороннего треугольника
Эти уравнения применимы к любому типу треугольника.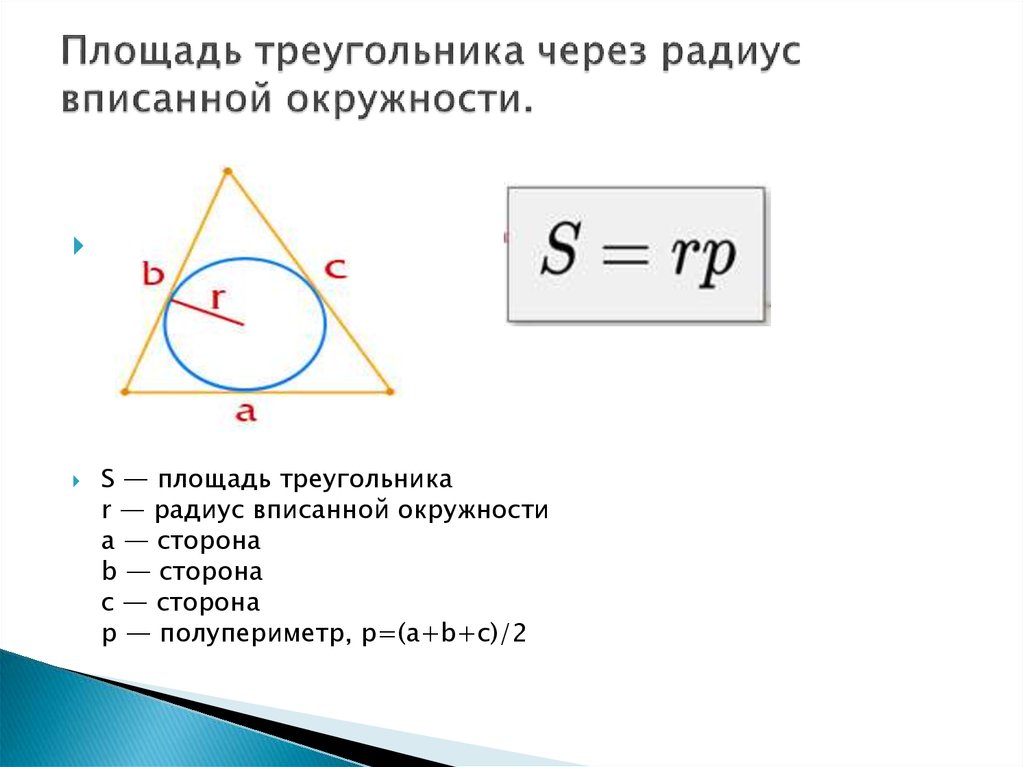


Leave A Comment