Главная → Видеоуроки → ЕГЭ по математике. Профильный уровень. Задание 14. Описание видеоурока: В пирамиде SABC в основании лежит правильный треугольник ABC со стороной 2*sqrt3, SA=SC=sqrt33, SB=7. Точка O — основание высоты пирамиды, проведённой из вершины S. а) Докажите, что точка O лежит вне треугольника ABC. Валерий Волков 2 09.08.2017 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
Сборник заданий №16 (базовый уровень)
Тренажер заданий: задачи стереометрии
Чтобы решить задание 16 по математике базового уровня:
- нужно знать определения основных понятий и базовые формулы
- после чего
задача сводится к элементарным вычислениям.

1. Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды
2. Объём параллелепипеда ABCDA1B1C1D1 равен 15. Найдите объём пирамиды D1ABC (см. рисунок).
3.Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 9 и 6. Объем параллелепипеда равен 756. Найдите площадь его поверхности.
4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 5. Объем параллелепипеда равен 280. Найдите площадь его поверхности.
5.Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 4. Объем параллелепипеда равен 240. Найдите площадь его поверхности.
6.
В прямоугольном параллелепипеде рёбра CD, CB и диагональ равны соответственно и Найдите объём параллелепипеда
7.
В прямоугольном параллелепипеде рёбра DA, DC и диагональ равны соответственно и Найдите объём параллелепипеда
8.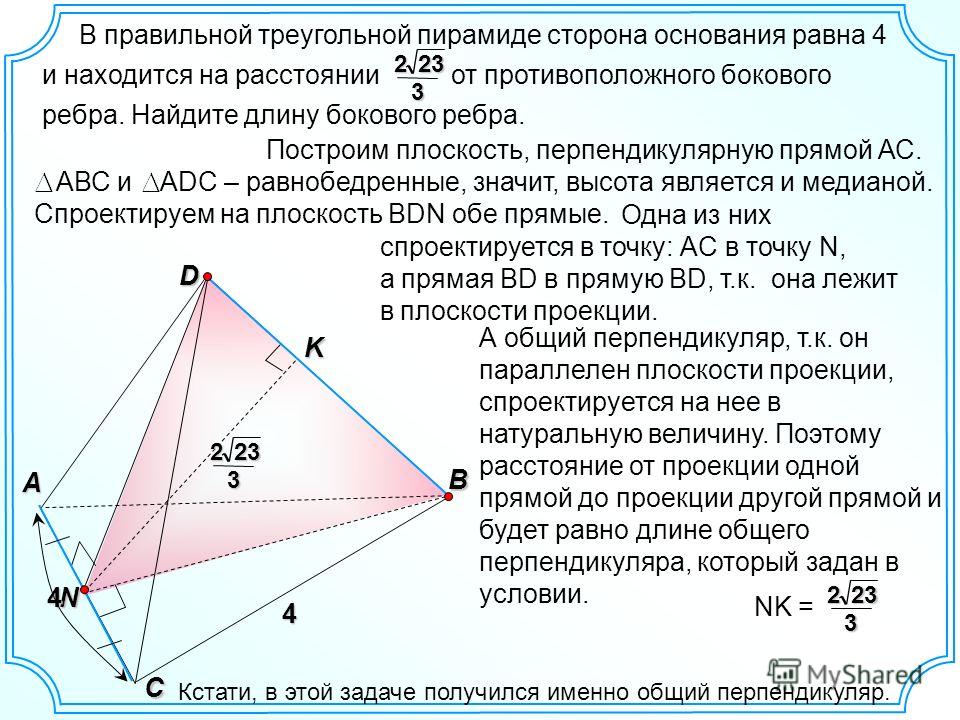
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и диагональ CD1 боковой грани равны соответственно 4, 7 и Найдите объем параллелепипеда ABCDA1B1C1D1.
9.
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра BC, BA и диагональ BC1 боковой грани равны соответственно 3, 7 и Найдите площадь поверхности параллелепипеда
10. В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и
диагональ CD1 боковой грани равны соответственно 2,
4 и Найдите площадь поверхности
параллелепипеда ABCDA1B1C1D1.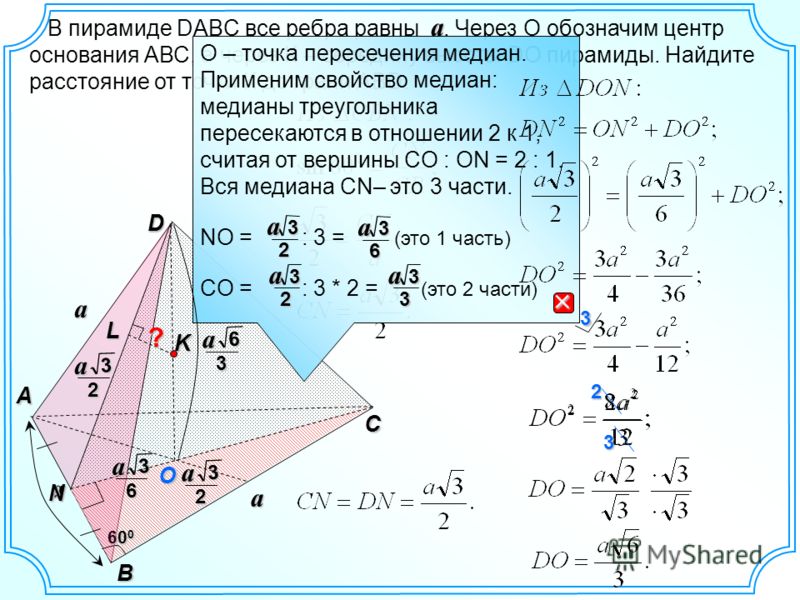
11.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 6, боковое ребро равно 6. Найдите объем призмы.
12.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 7, боковое ребро равно 4. Найдите объем призмы.
13.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 6, боковое ребро равно 6. Найдите объем призмы.
14.
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен а гипотенуза равна Найдите объём призмы, если её высота равна
15. В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 4, а гипотенуза равна Найдите объём призмы, если её высота равна 3.
16. В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 4, а гипотенуза равна Найдите объём призмы, если её высота равна 6.
17.
Стороны
основания правильной шестиугольной пирамиды равны 48, боковые ребра равны 51. Найдите площадь боковой поверхности этой пирамиды.
Найдите площадь боковой поверхности этой пирамиды.
18.Стороны основания правильной шестиугольной пирамиды равны 14, боковые рёбра равны 25. Найдите площадь боковой поверхности этой пирамиды.
19.Стороны основания правильной шестиугольной пирамиды равны 16, боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
20.Основанием пирамиды является прямоугольник со сторонами 4 и 5. Ее объем равен 80. Найдите высоту этой пирамиды.
21.Основанием пирамиды является прямоугольник со сторонами 4 и 6. Ее объем равен 48. Найдите высоту этой пирамиды.
22.Основанием пирамиды является прямоугольник со сторонами 5 и 6. Ее объем равен 40. Найдите высоту этой пирамиды.
23. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 11, а высота равна
24.Найдите объем правильной треугольной пирамиды, стороны основания которой равны 3, а высота равна
25.Найдите объем правильной треугольной пирамиды, стороны основания которой равны 2, а высота равна
26.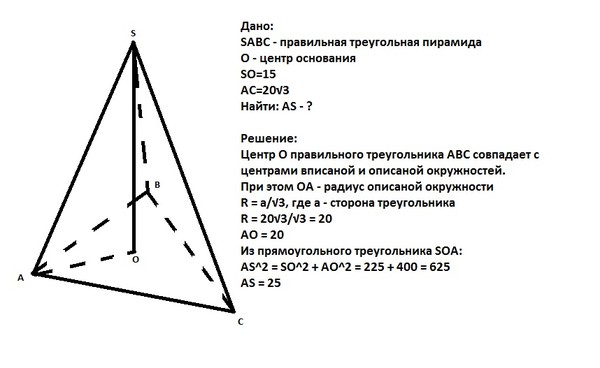
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно
27.Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно
28.Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна а боковое ребро равно
29
В основании пирамиды SABC лежит правильный треугольник ABC со стороной 2, а боковое ребро SA перпендикулярно основанию и равно Найдите объём пирамиды SABC.
30.В основании пирамиды SABC лежит правильный треугольник ABC со стороной 6, а боковое ребро SA перпендикулярно основанию и равно Найдите объём пирамиды SABC.
31.В основании пирамиды SABC лежит правильный треугольник ABC со стороной 4, а боковое ребро SA перпендикулярно основанию и равно Найдите объём пирамиды SABC.
32.
В
треугольной пирамиде ABCD рёбра AB, AC и AD взаимно
перпендикулярны.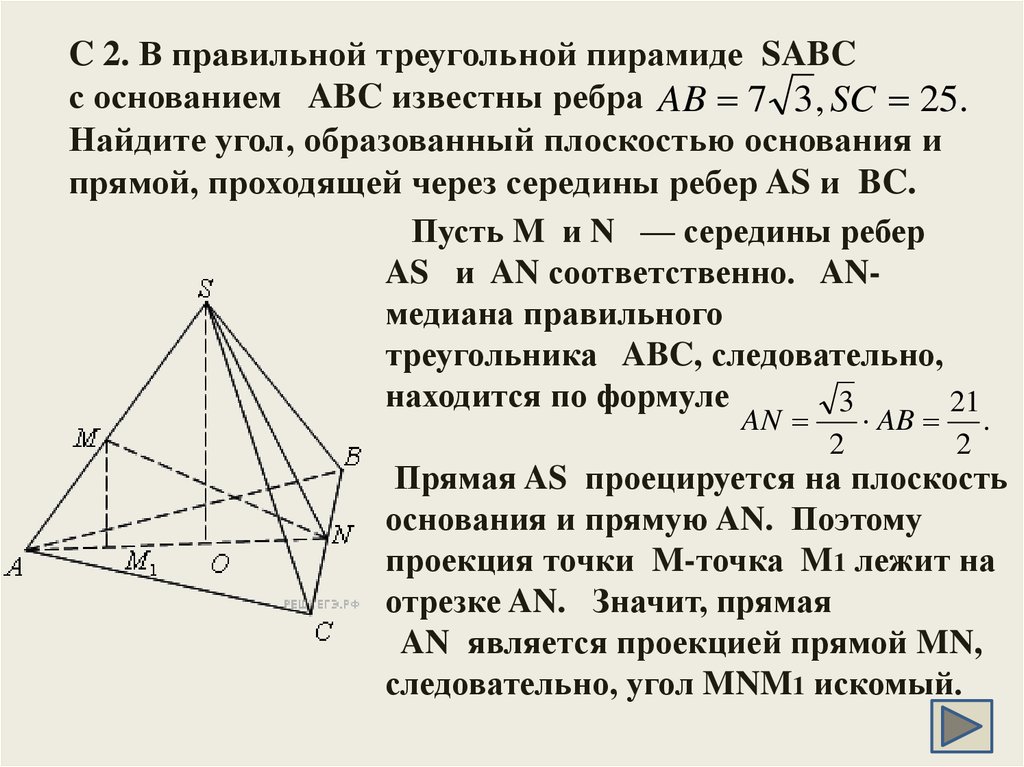 Найдите объём этой пирамиды, если AB =
5, AC = 24 и AD = 3.
Найдите объём этой пирамиды, если AB =
5, AC = 24 и AD = 3.
33.В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB = 2, AC = 15 и AD = 7.
34.В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB = 10, AC = 18 и AD = 3.
35.
Стороны основания правильной треугольной пирамиды равны 42, а боковые рёбра равны 29. Найдите площадь боковой поверхности этой пирамиды.
36.Стороны основания правильной треугольной пирамиды равны 14, а боковые рёбра равны 25. Найдите площадь боковой поверхности этой пирамиды.
37. Стороны основания правильной треугольной пирамиды равны 6, а боковые рёбра равны 5. Найдите площадь боковой поверхности этой пирамиды.
38. Даны два цилиндра. Радиус основания и высота первого равны
соответственно 3 и 2, а второго — 8 и 9. Во сколько раз объём второго цилиндра
больше объёма первого?
Во сколько раз объём второго цилиндра
больше объёма первого?
39.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 8, а второго — 4 и 9. Во сколько раз объём первого цилиндра больше объёма второго?
40.Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 1, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
41.Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 3, а второго — 3 и 9. Во сколько раз объём первого цилиндра больше объёма второго?
42. Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
43.Радиус основания цилиндра равен 15, а его образующая равна 19. Сечение, параллельное оси цилиндра, удалено от неё на расстояния, равное 9. Найдите площадь этого сечения.
44.Радиус основания цилиндра равен 20, а его образующая равна 8. Сечение, параллельное оси цилиндра, удалено от неё на расстояния, равное 12.
Найдите площадь этого сечения.
Сечение, параллельное оси цилиндра, удалено от неё на расстояния, равное 12.
Найдите площадь этого сечения.
45.Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от неё на расстояния, равное 12. Найдите площадь этого сечения.
46.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 3, а второго — 12 и 5. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?
47.Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго — 7 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
48.Даны два цилиндра. Радиус основания и высота первого равны соответственно 15 и 6, а второго — 2 и 5. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
49. Объём конуса равен а его высота равна Найдите радиус
основания конуса.
50. Объём конуса равен а его высота равна Найдите радиус основания конуса.
51.Объём конуса равен а его высота равна Найдите радиус основания конуса.
52. Объём конуса равен 135. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
53. Объём конуса равен 27. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
54. Объём конуса равен 32. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
55. Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 3 и 9, а второго — 6 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
56.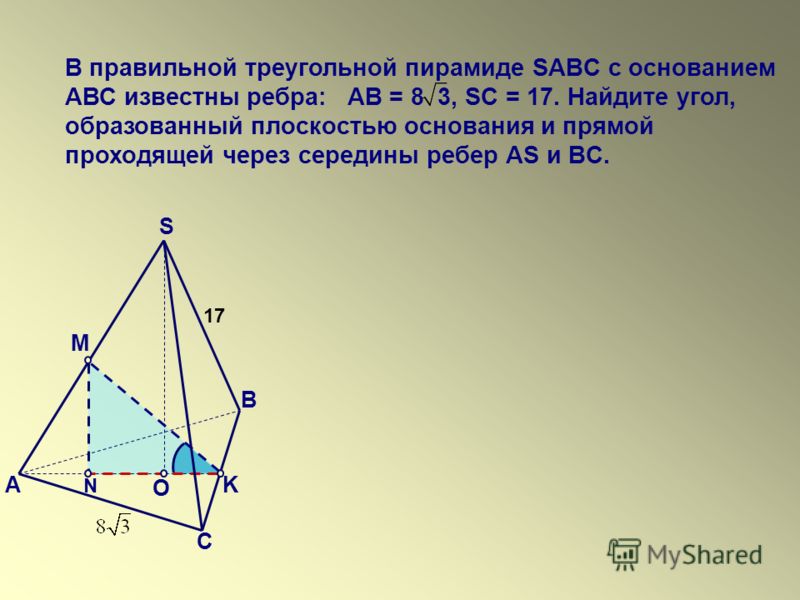
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 5, а второго — 5 и 6. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
57.Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 4 и 6, а второго — 2 и 8. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?
58.Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 7 и 9, а второго — 2 и 9. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?
59.
Даны два конуса. Радиус основания и высота первого конуса равны соответственно 9 и 6, а второго — 6 и 3. Во сколько раз объём первого конуса больше объёма второго?
60.Даны два конуса. Радиус основания и высота первого конуса равны соответственно 9 и 4, а второго — 6 и 6. Во сколько раз объём первого конуса больше объёма второго?
61. Даны два конуса. Радиус основания и высота первого конуса равны
соответственно 2 и 2, а второго — 4 и 9. Во сколько раз объём второго конуса
больше объёма первого?
Даны два конуса. Радиус основания и высота первого конуса равны
соответственно 2 и 2, а второго — 4 и 9. Во сколько раз объём второго конуса
больше объёма первого?
62.
Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?
63. Даны два шара с радиусами 8 и 4. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
64. Даны два шара с радиусами 14 и 2. Во сколько раз площадь поверхности большего шара больше площади поверхности другого?
65. Даны два шара с радиусами 2 и 1. Во сколько раз объём первого шара больше объёма второго?
66.
Даны два шара с радиусами 6 и 1. Во сколько раз объём большего шара больше объёма меньшего?
В разработке использованы материалы:
Математика в таблицах;
сайт http://reshuege.ru
методическая разработка может быть задействована в урочное и внеурочное время в
условиях работы в различных структурах; как этап подготовки к ЕГЭ;
как творческие домашние задания.
Объяснение урока: Объемы треугольных и четырехугольных пирамид
В этом объяснителе мы научимся находить объемы треугольных или четырехугольных пирамид и решать задачи, в том числе в реальных жизненных ситуациях.
Определение: Пирамиды
Пирамиды представляют собой трехмерные геометрические фигуры или твердые объекты, где основание многоугольник (треугольник, квадрат, прямоугольник, пятиугольник и т. д.) и все остальные стороны являются треугольниками которые встречаются в вершина или вершина .
Правая пирамида — это пирамида, вершина которой лежит выше центра тяжести основания.
Правильная пирамида — это правильная пирамида, основание которой представляет собой правильный многоугольник: все стороны основания имеют одинаковую длину, а все боковые ребра пирамиды равны длина.
высота пирамиды — это расстояние от вершины до основания.
Наклонная высота пирамиды – это расстояние, измеренное вдоль боковой грани от вершины к краю основания. Другими словами, это высота треугольника, состоящего из боковая грань.
Теперь, когда мы узнали, что такое пирамида, давайте посмотрим на ее объем.
Представьте, что мы можем полностью заполнить пирамиду, скажем, водой. Если мы нальем эту воду в призме того же основания и высоты, что и у пирамиды, мы заметим, что уровень воды находится точно на одной трети высоты призмы.
Это общее правило для любой пирамиды.
Объем пирамиды
Объем пирамиды составляет одну треть объема призмы с тем же основанием и height:
Давайте рассмотрим некоторые вопросы.
Пример 1. Нахождение объема пирамиды
Определите объем данной пирамиды.
Ответ
Чтобы найти объем данной пирамиды, нужно найти площадь ее основания (здесь
прямоугольник) и его высота, которая задается как
9 см.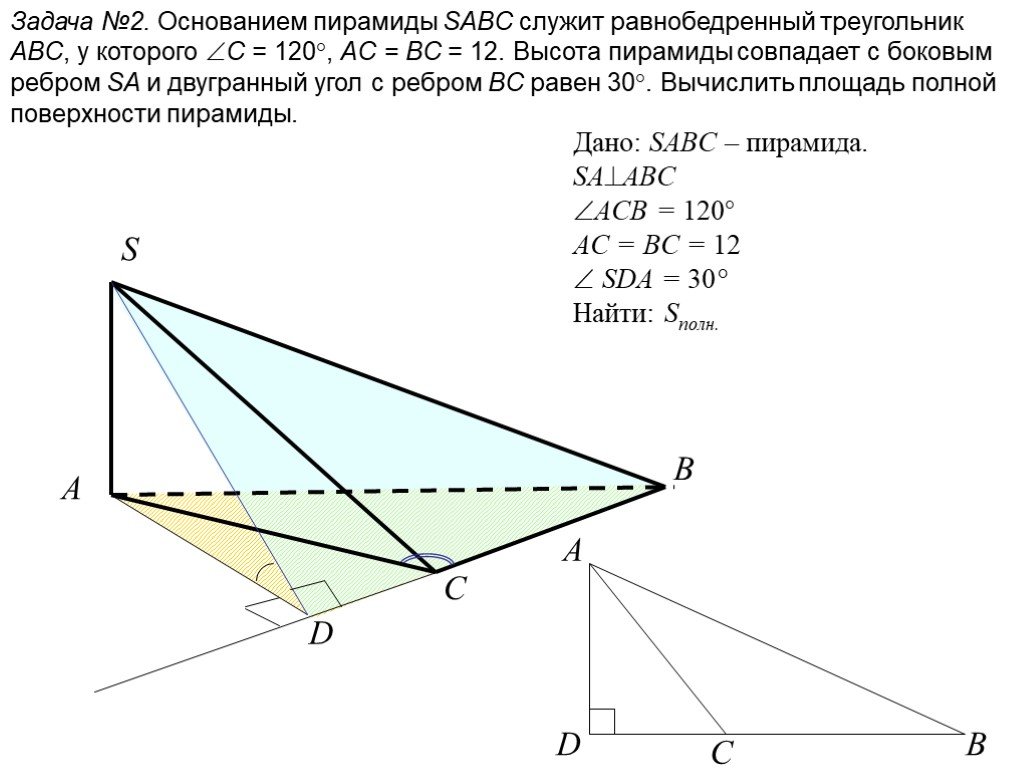
Площадь прямоугольного основания равна 𝐴=6×4=24 basecm.
Путем подстановки площади основания и высоты в уравнение 𝑉=13(𝐴×ℎ)основание пирамиды, находим 𝑉=13(24×9)=72пирамидсм.
Объем данной пирамиды 72 см 3 .
Пример 2. Нахождение объема треугольной пирамиды
Определите объем данного твердого тела.
Ответ
Данное тело является пирамидой (треугольное основание и все остальные грани являются треугольниками как хорошо). Чтобы найти объем данной пирамиды, нам нужно найти площадь ее основания (мы можно выбрать любое лицо) и его высоту.
Если мы выберем нижний треугольник в качестве основания, его площадь будет следующей (обратите внимание, что все грани — прямоугольные треугольники):
𝐴=12𝑎×𝑏основание, где 𝑎 и 𝑏 — стороны прямоугольного треугольника. Мы нашли 𝐴=18×222=198базсм.
Высота 14 см.
Путем подстановки площади основания и высоты в уравнение
𝑉=13(𝐴×ℎ)основание пирамиды,
находим, что с точностью до десяти объем данного твердого тела равен
𝑉=13(198×14)=924пирамидсм.
Объем данного твердого тела 924 см 3 .
Пример 3. Нахождение объема правильной пирамиды, зная ее боковое ребро и высоту наклона
Найдите объем следующей правильной пирамиды, приблизив результат к ближайшая сотая.
Ответ
Данная пирамида правильная , а это значит, что ее основание – правильный многоугольник: все стороны основания имеют одинаковую длину. Следовательно, основание здесь — квадрат.
Кроме того, правильная пирамида – это правильная пирамида с боковыми ребрами, равными по длина, здесь 17 см.
Чтобы найти объем данной пирамиды, нужно найти площадь ее основания и высота.
Нам дана наклонная высота
(15 см) и боковой край. В
правильная пирамида, наклонная высота которой соответствует стороне основания в ее середине. Половина
сторона квадрата 𝑠 и наклонная высота образуют на каждой грани прямоугольные треугольники
гипотенуза которого является боковым ребром.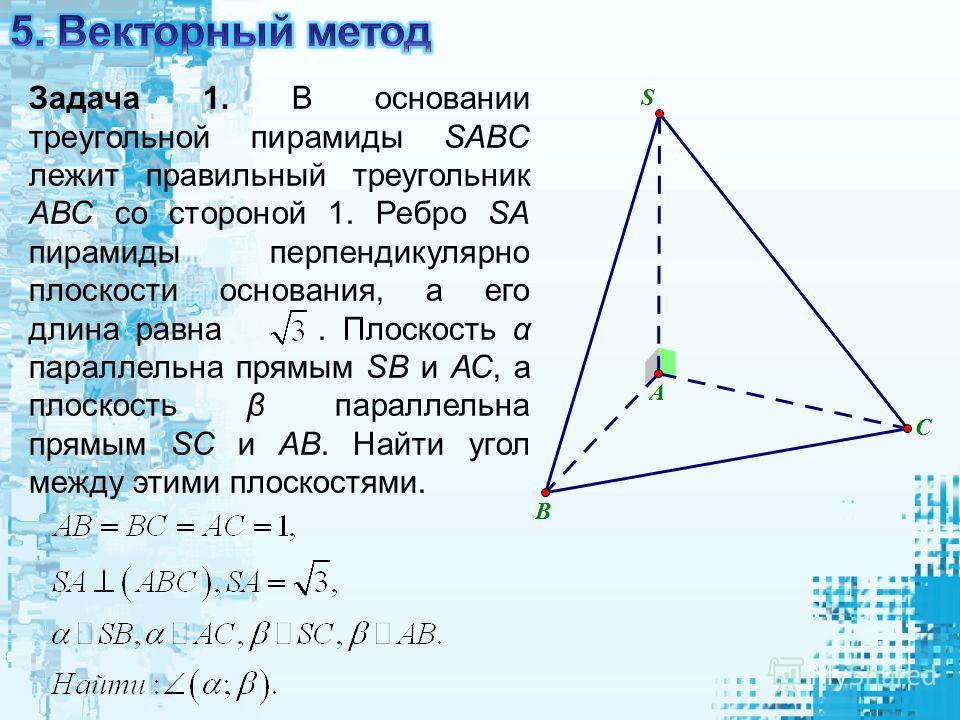
Таким образом, мы можем применить теорему Пифагора к одному из этих прямоугольных треугольников, чтобы найти сторона, 𝑠, квадрата в сантиметрах: 12𝑠+15=1714𝑠+225=28914𝑠+225−225=289−22514𝑠=644×14𝑠=4×64𝑠=256√𝑠=√256𝑠
Теперь, когда мы знаем, что сторона квадрата 16 см, мы можем найти его площадь, возведя сторону в квадрат:
Нам нужно найти высоту пирамиды. Для этого рассмотрим прямоугольный треугольник внутри пирамиды, образованной высотой пирамиды и ее наклонной высотой как гипотенуза. Третья сторона — это отрезок, длина которого равна половине стороны квадрата.
Применение теоремы Пифагора к этому прямоугольному треугольнику дает
Путем подстановки площади основания и высоты в уравнение 𝑉=13(𝐴×ℎ)основания пирамиды, находим, что с точностью до сотых объем данного твердого тела равен 𝑉=13256×√161≅1082,76пирамидсм.
Объем данной пирамиды с точностью до сотых равен
1 082,76 см 3 .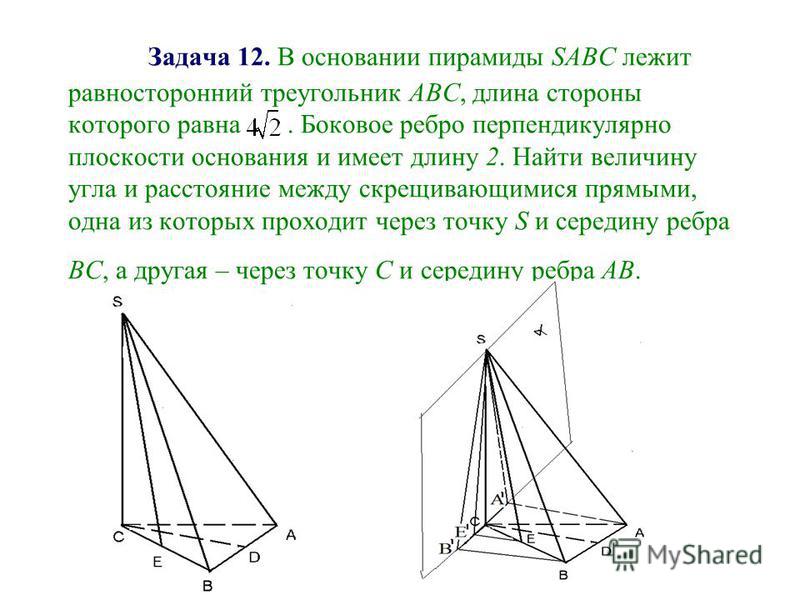
Пример 4. Нахождение объема правильной треугольной пирамиды
Найдите объем следующей правильной пирамиды, округленный до сотых.
Ответ
В вопросе у нас правильная пирамида, значит, все стороны основания (здесь треугольник) имеют одинаковую длину. Следовательно, основание пирамиды равностороннее. треугольник со стороной 14 см, как указано на схеме. Также указана высота пирамиды. (17 см). Помните, что объем пирамиды определяется как 𝑉=13(𝐴×ℎ).pyramidbase
Следовательно, здесь нам нужно найти площадь треугольного основания, которая определяется выражением 𝐴=12𝑏×ℎ,базовый треугольник
, где 𝑏 — основание, а ℎтреугольник — высота треугольника.
Поскольку основание равностороннего треугольника, мы можем найти его высоту, применив
Теорема Пифагора в прямоугольном треугольнике, образованном высотой треугольника
катет и одна из его сторон в качестве гипотенузы, как показано на схеме.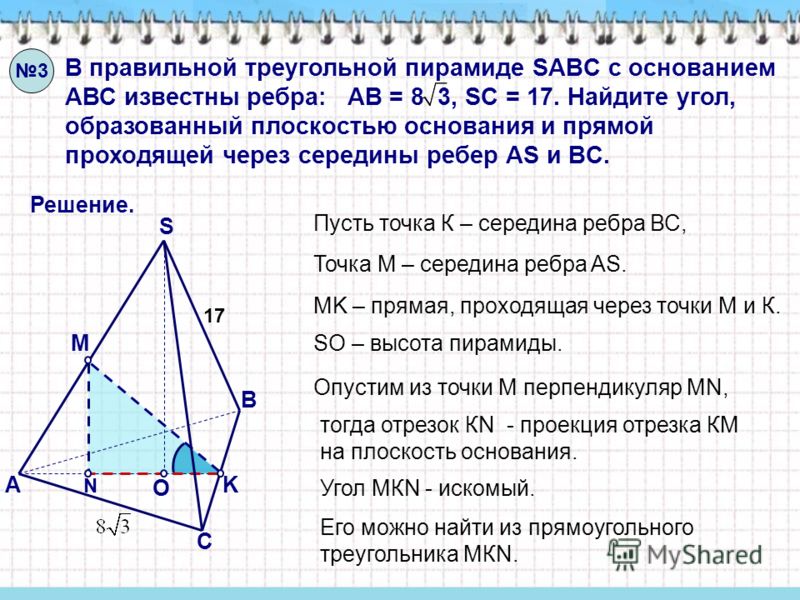
Находим, что ℎ+7=14;треугольник, то есть ℎ+49=196.triangle
Вычитая 49 с каждой стороны, мы получаем ℎ=196−49=147.triangle
Извлечение квадратного корня из обеих сторон дает ℎ=√147.triangle
Подставляя это в наше уравнение для площадь треугольного основания, находим, что 𝐴=1214×√147, основания и подставляя это в наше уравнение для объема пирамиды, получаем 𝑉=131214×√147×17.pyramid
Будьте осторожны, не перепутайте высоту пирамиды с высотой основания. Мы теперь можно вычислить объем пирамиды с помощью калькулятора, округлив результат до ближайшая сотая. Находим 𝑉≅480,93.pyramidcm
Объем пирамиды, округленный до сотых, равен 480,93 см 3 .
Пример 5. Нахождение высоты пирамиды по ее объему и площади основания
Найдите высоту правильной пирамиды, объем которой равен
196 см 3 и площадь основания
42 см 2 .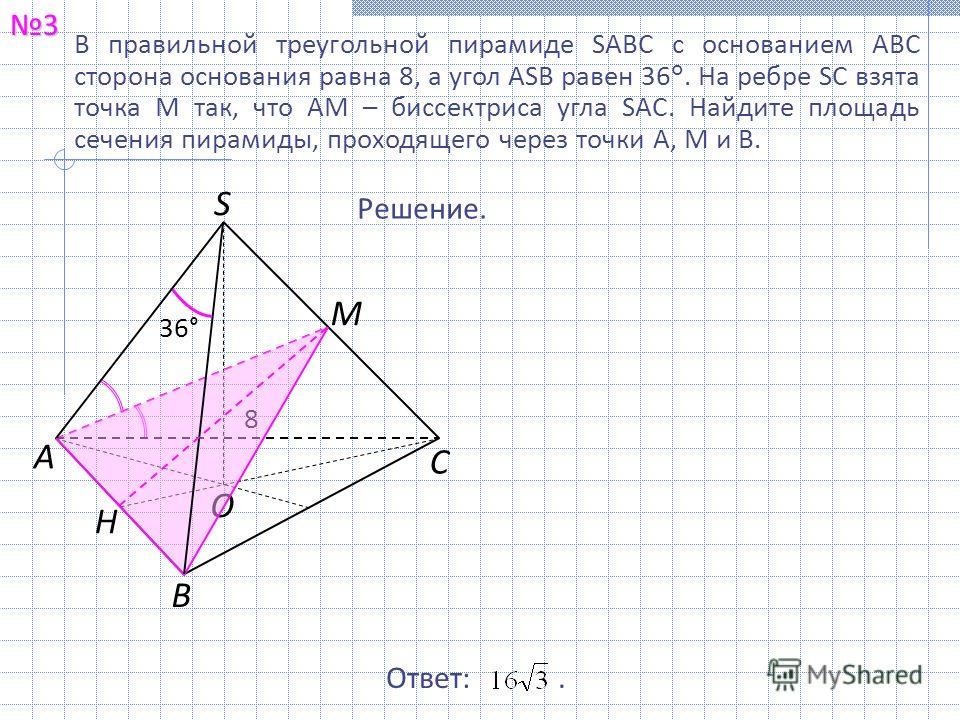
Ответ
В этом вопросе нам даны объем и площадь основания правильной пирамиды, и нам нужно найти его высоту.
Мы знаем, что эти три параметра связаны уравнением 𝑉=13(𝐴×ℎ)основание пирамиды.
Здесь ℎ — это неизвестное, поэтому нам нужно изменить наше уравнение, чтобы сделать ℎ тема:
Убедившись, что объем пирамиды и площадь ее основания даны в единицы, происходящие от одной и той же единицы длины (здесь сантиметры), мы можем подставить их значения в уравнение
Находим
Высота данной пирамиды равна 14 см.
Ключевые точки
- Пирамиды — это трехмерные геометрические фигуры или твердые объекты, основанием которых является многоугольник (треугольник, квадрат, прямоугольник, пятиугольник и т.д.) и все остальные стороны треугольники которые встречаются в вершине или вершине.
- Прямоугольная пирамида — это пирамида, вершина которой лежит выше центра тяжести основания.

- Правильная пирамида — это правильная пирамида, основание которой представляет собой правильный многоугольник: все стороны основание равной длины, а все боковые ребра пирамиды равны длина.
- Объем пирамиды составляет одну треть объема призмы с тем же основанием и высота:
Кто-нибудь может мне помочь?? Не знаю, как начать
Метод вычисления объема диска
Диана Р.
спросил 06.07.21Докажите, что пирамида высотой 90 182 h 90 183, основанием которой является равносторонний треугольник со стороной 90 182 s 90 183, имеет объем √3/12 hs 2
Подписаться І 2
Подробнее
Отчет
4 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Ефим С. ответил 06.07.21
ответил 06.07.21
Репетитор
5 (20)
Репетитор по математике с опытом
Смотрите таких репетиторов
Смотрите таких репетиторов
V = 1/3Bh, где B — площадь основания. B = s 2 √3/4 (площадь равностороннего треугольника со стороной s)
Итак, V = 1/3s 2 h√3/4 = s 2 h√3/12.
Голосовать за 1 Понизить
Подробнее
Отчет
Дуг С. ответил 06.07.21
Репетитор
5,0 (1392)
Репетитор по математике с репутацией, чтобы объяснить сложные понятия
Смотрите таких репетиторов
Смотрите таких репетиторов
Вот несколько предложений.
Вы знаете, как сделать объем путем нарезки? ∫ A(x) dx, где A(x) — формула площади среза.
Если представить пирамиду, лежащую горизонтально вдоль оси x с основанием в точке x = h, то типичными срезами вдоль оси x будут равносторонние треугольники, подобные основанию. Вы можете установить соотношение: h/s = x/v, где v — длина стороны типичного среза. Решите для v, чтобы получить v = xs/h, помня, что s и h являются константами.
Найдите формулу площади равностороннего треугольника в зависимости от длины стороны. Подставьте xs/h в эту формулу, затем проинтегрируйте от 0 до h относительно x, где A(x) — это формула, которую вы получите, когда сделаете замену.
Голосовать за 1 Понизить
Подробнее
Отчет
Раймонд Б. ответил 10.07.21 92/4кв3
Голосовать за 0 Понизить
Подробнее
Отчет
Адам Б. ответил 06.07.21
ответил 06.07.21
Репетитор
5,0 (380)
«Молодой» профессор математики, недавно вышедший на пенсию
Об этом репетиторе ›
Об этом репетиторе ›
Здесь нужно применить метод нарезки. Нарисуйте треугольную пирамиду с основанием в виде равностороннего треугольника
ABC и назовите вершину O.
На отдельном чертеже равностороннего треугольника ABC нарисуйте высоту AK треугольника, которая также является медианой
. Теперь посмотрим на прямоугольный треугольник АКБ.
AB = с, KB = с/2.
Тогда по теореме Пифагора AK = (s√3)/2
Следовательно, площадь треугольника равна (s 2 √3)/4.
Теперь, если бы проблема была просто базовой задачей геометрии, вычисление объема пирамиды было бы
легко найти, поскольку V = 1/3 (площадь основания) (высота) = (1/3) ( с 2 √3)/4 Н = (1/12)(с 2 √3)Н.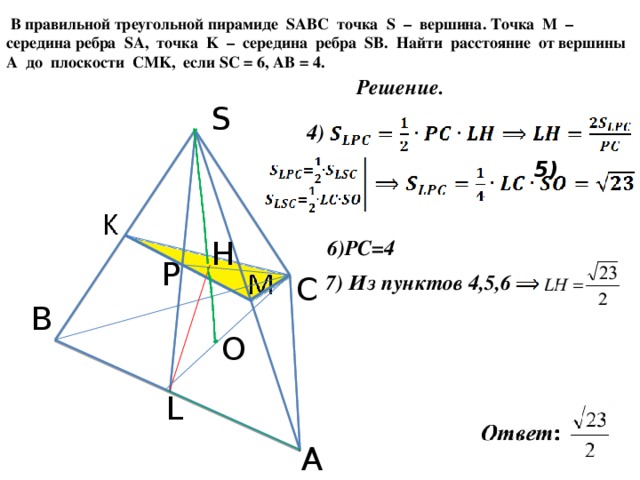
Но нам нужно использовать Исчисление, чтобы получить тот же результат.
Назад к пирамиде OABC.
Введем прямоугольную систему координат, в которой ось Y проходит через вершину пирамиды
и перпендикулярна основанию , а ось x проходит через центр основания, скажем G, перпендикулярно стороне равностороннего треугольника и содержит AK.
При любом y в интервале [0,H] на оси y поперечное сечение, перпендикулярное оси y, представляет собой равносторонний треугольник .
Если мы обозначим через a длину этого треугольника , то подобными треугольниками
s/a =H/(H-y) ⇒a = (H-y)(s/h)
Тогда площадь Ω(y ) поперечного сечения в y . Затем
Ω(y)=(a 2 √3)/4 = [(H-y) 2 с 2 √3]/(4H 2 )
и объем пирамиды равен
V = ∫ H 0 ω (y) dy =
∫ H 0 [(H-Y) 2 S 2 √3]/(4H 2 ) Dy =
9000 2 √3]/(4H 2 ).

 5 класс.
5 класс.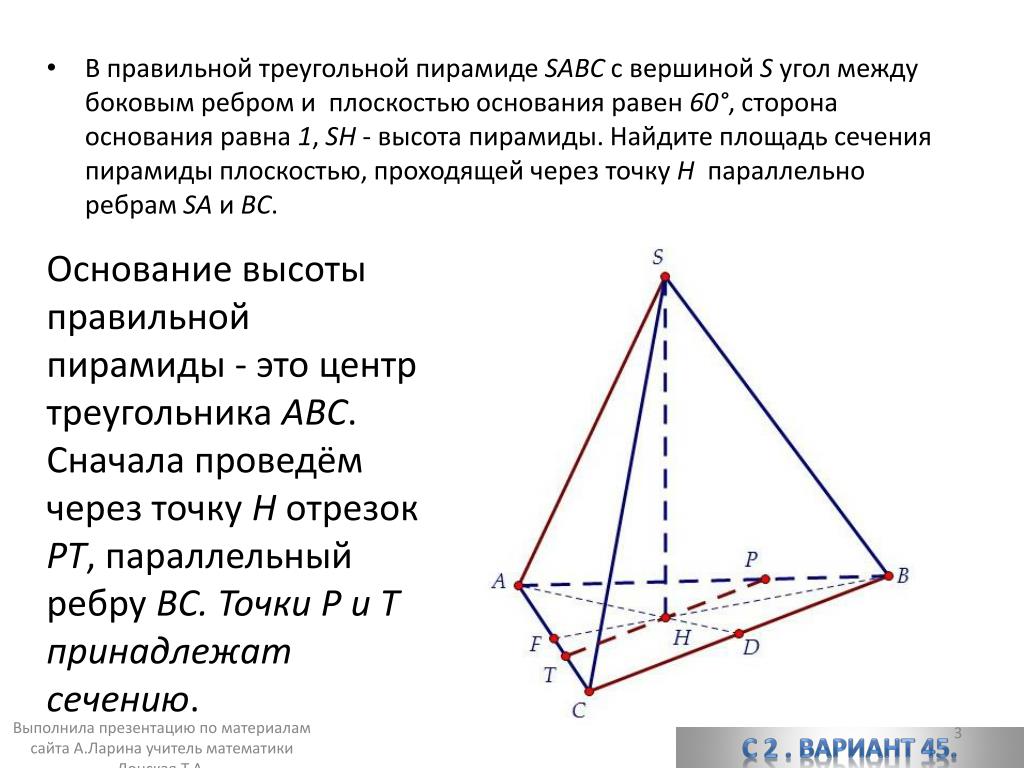 10 — 11 класс.
10 — 11 класс.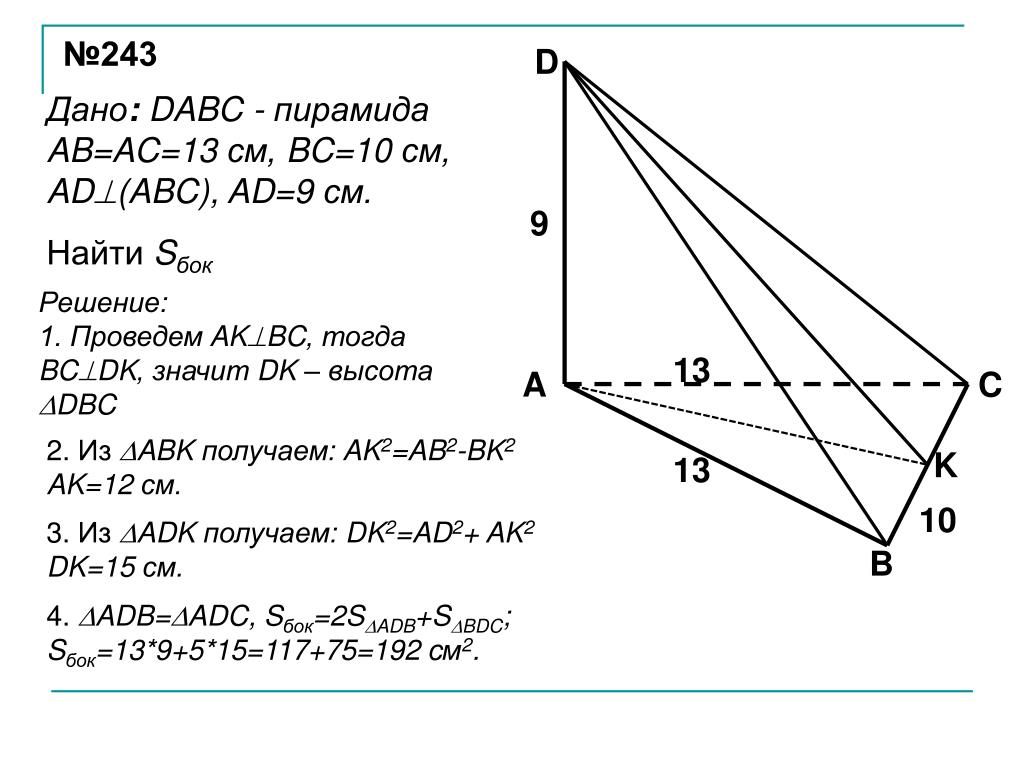
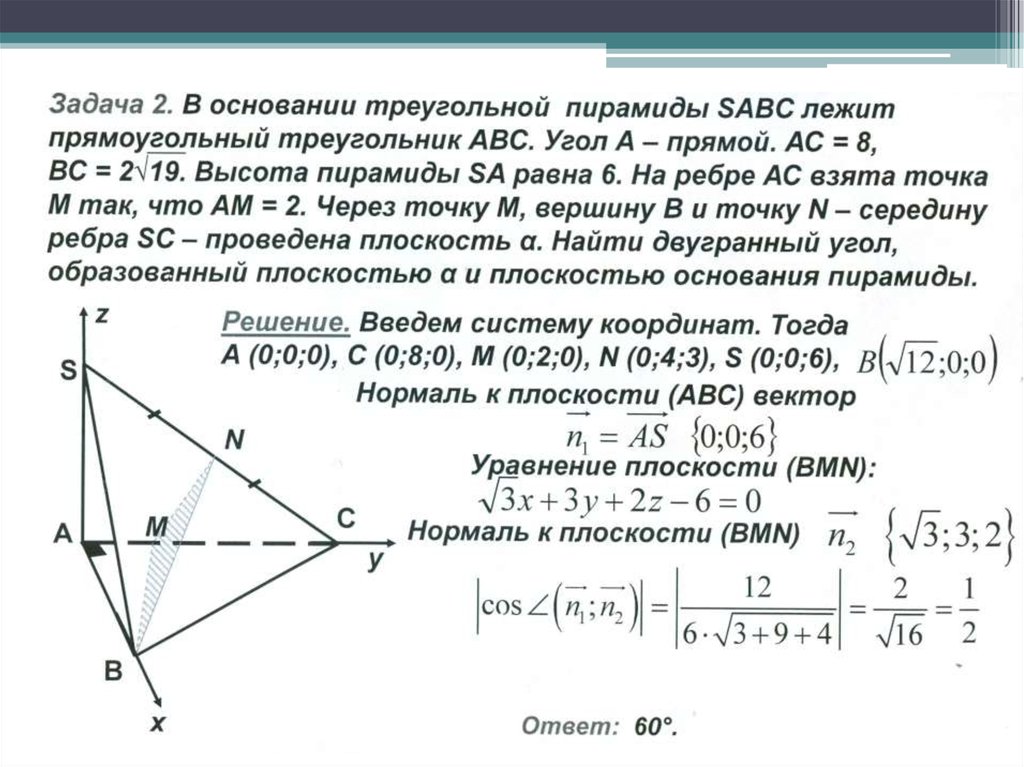

Leave A Comment