Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v
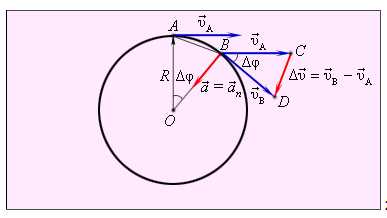
Разница векторов есть . Так как , получим
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
fizmat.by
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
∆l=R∆φ
Если угол поворота мал, то ∆l≈∆s.
Проиллюстрируем сказанное:
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω, то есть скорости изменения угла поворота.
Определение. Угловая скоростьУгловая скорость в данной точке траектории — предел отношения углового перемещения ∆φ к промежутку времени ∆t, за которое оно произошло. ∆t→0.
ω=∆φ∆t, ∆t→0.
Единица измерения угловой скорости — радиан в секунду (радс).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
ω=vR
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
an=∆v→∆t, ∆t→0
Модуль центростремительного ускорения можно вычислить по формуле:
an=v2R=ω2R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v→ за малый промежуток времени ∆t. ∆v→=vB→-vA→.
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a→=∆v→∆t, ∆t→0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что OAAB=BCCD.
Если значение угла ∆φ мало, расстояние AB=∆s≈v·∆t. Принимая во внимание, что OA=R
zaochnik.com
Равномерное движение по окружности. Скорость, ускорение
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.
Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:
. (1)
Частота обращения — это величина, обратная периоду:
.
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).
Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).
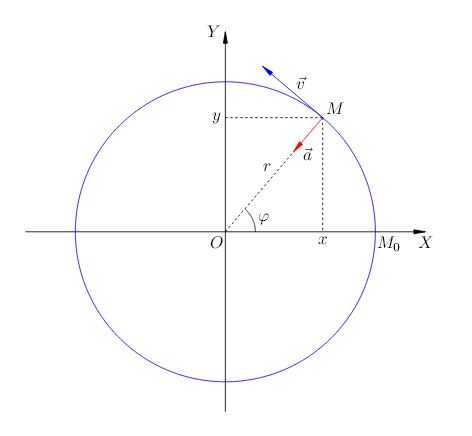 |
| Рис. 1. Равномерное движение по окружности |
Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .
Отношение угла поворота ко времени называется угловой скоростью
. (2)
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому
. (3)
Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:
. (4)
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что
.
Но из формулы (2) имеем: . Следовательно,
. (5)
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):
С учётом формул (5) имеем:
(6)
Полученные формулы (6) можно записать в виде одного векторного равенства:
(7)
где — радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
(8)
Выразим угловую скорость из (4)
и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:
.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
1.1.8 Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Видеоурок: Движение по окружности
Лекция: Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Движение по окружности
Траектория движения — окружность.
Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.
Любое криволинейное движение можно свести к нескольким движениям по окружности. Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое.Основные характеристики движения
1. Линейная скорость
 Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.
Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.Так как траектория движения точки — окружность, то в качестве пути в числителе находится формула длины перемещения.
Поэтому формула мгновенной скорости приобретает следующий вид, где Т — период:
2. Центростремительное ускорение
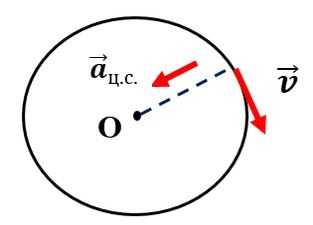 Направлено перпендикулярно к линейной скорости на протяжении всего движения.
Направлено перпендикулярно к линейной скорости на протяжении всего движения.Центростремительное ускорение определяется по формуле:
3. Период вращения
Период вращения — это величина, определяющая время, за которое тело делает одно полное вращение.
Период — это скалярная величина. Основной единицей периода является [Т]=1с.
Период определяется по формуле:
где N — количество оборотов, t — время, за которое они были совершены.
4. Частота вращения
Определяет, насколько часто совершаются обороты в единицу времени.
Частота — скалярная величина. Измеряется в [n] = 1с-1.
Частота определяется по формуле:
5. Угловое перемещение
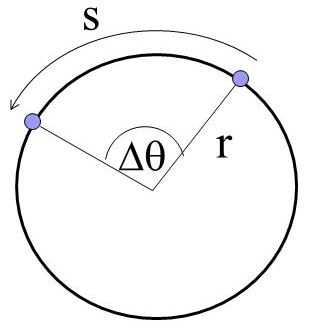
Угловое перемещение — величина, которая определяется углом поворота радиуса, соединяющего центр описываемой окружности, с точкой, где находится тело, относительно начального его положения.
Данная величина может измеряться в градусной или радианной мере углов.
6. Угловая скорость
Это значение, которое определяет, насколько изменяется угловое перемещение со временем.
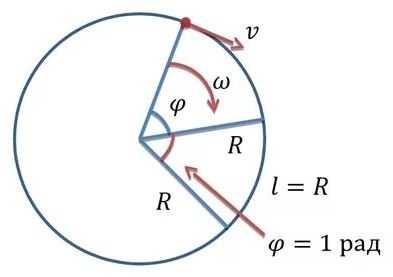 Измеряется в 1 рад/с.Определяется по формуле:
Измеряется в 1 рад/с.Определяется по формуле:где
— угловая скорость материальной точки, 1/с
— угол поворота радиус — вектора, рад- промежуток времени, с
Угловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой:
cknow.ru
Движение по окружности-Теория.Скорость в физике
На главную Теория Задачи Учёные Интересные статьи Шкала скоростейKинематика равномерного вращения по окружности
При движении по окружности с
постоянной по величине линейной
скоростью v тело испытывает
направленное к центру окружности
постоянное центростремительное
ускорение
aц = v2/R,
где R — радиус окружности.
Вывод формулы для центростремительного ускорения
По определению
На рисунке треугольники,
образованные векторами перемещений
и скоростей, подобны. Учитывая, что
|r1| = |r2| = R и |v1| = |v2| = v, из
подобия треугольников находим:
откуда
Поместим начало координат в
центр окружности и выберем
плоскость, в которой лежит
окружность, за плоскость (x, y).
Положение точки на окружности в
любой момент времени однозначно
определяется полярным углом j,
измеряемым в радианах (рад), причем
x = R cos(j + j0), y = R sin(j + j0),
где j0 определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).
В случае равномерного вращения
угол j, измеряемый в радианах,
линейно растет со временем:
j = wt,
где w называется циклической (круговой) частотой. Размерность циклической частоты: [w] = c-1 = Гц.
Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью.
Зависимость координат точки на
окружности от времени в случае
равномерного вращения с заданной
частотой можно записать в виде:
x = R cos(wt + j0),
y = R sin(wt + j0).
Время, за которое совершается один оборот, называется периодом T.
Частота
n = 1/T.
Размерность частоты: [n] = с-1 = Гц.
Связь циклической частоты с
периодом и частотой: 2p = wT, откуда
w = 2p/T = 2pn.
Связь линейной скорости и угловой
скорости находится из равенства:
2pR = vT, откуда
v = 2pR/T = wR.
Выражение для
центростремительного ускорения
можно записать разными способами,
используя связи между скоростью,
частотой и периодом:
aц = v2/R = w2R = 4p2n2R = 4p2R/T2.
Связь поступательного и вращательного движений
Основные кинематические
характеристики движения по прямой с
постоянным ускорением: перемещение
s, скорость v и ускорение a.
Соответствующие характеристики при
движении по окружности радиусом R:
угловое перемещение j, угловая
скорость w и угловое ускорение a (в
случае, если тело вращается с
переменной скоростью). Из
геометрических соображений
вытекают следующие связи между
этими характеристиками:
перемещение sугловое перемещение j = s/R;
скорость vугловая скорость w = v/R;
ускорение aугловое ускорение a = a/R.
Все формулы кинематики
равноускоренного движения по прямой
могут быть превращены в формулы
кинематики вращения по окружности,
если сделать указанные замены.
Например:
s = vtj = wt,
v = v0 + atw = w0 + at.
Связь между линейной и угловой
скоростями точки при вращении по
окружности можно записать в
векторной форме. Действительно,
пусть окружность с центром в начале
координат расположена в плоскости
(x, y). В любой момент времени вектор
R, проведенный из начала координат в
точку на окружности, где находится
тело, перпендикулярен вектору
скорости тела v, направленному по
касательной к окружности в этой
точке. Определим вектор w, который
по модулю равен угловой скорости w и
направлен вдоль оси вращения в
сторону, которая определяется
правилом правого винта: если
завинчивать винт так, чтобы
направление его вращения совпадало с
направлением вращения точки по
окружности, то направление движения
винта показывает направление
вектора w. Тогда связь трех взаимно
перпендикулярных векторов R, v и w
можно записать с помощью векторного
произведения векторов:
v = wR.Задачи на эту тему
gym1517.narod.ru
Вращательное движение (движение тела по окружности) | Формулы и расчеты онлайн
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
\[ φ = \frac{s}{r} \]
Соотношение между единицами угла
\[ \frac[-1.35]{φ_{рад}}{φ_{°}} = \frac[-1.2]{π}{180°} \]
$ 1 рад = 57.3° $ | $ 1° = 17.45 мрад $ | $ 1´ = 291 мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
\[ [n] = [f] = \frac{Обороты}{Секунда} = \frac{(об)}{с} = \frac{1}{c} = Герц \]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
\[ T = \frac{1}{f} = \frac{1}{n} \]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
\[ φ = 2 π N \]
Угловая скорость
Из формулы для одного оборота следует:
\[ ω = 2 π f = \frac{2π}{T} \]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
В помощь студенту
Вращательное движение (движение тела по окружности) |
стр. 421 |
|---|
www.fxyz.ru
Равномерное движение по окружности, формулы и примеры
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.
В окружающем нас мире мы часто сталкиваемся с подобным движением — при любом вращении твердого тела вокруг некоторой закрепленной оси все точки этого тела движутся по окружностям.
Основные характеристики и формулы
Пусть материальная точка движется по окружности радиуса (рис.1). Начало декартовой системы координат поместим в центр окружности. Тогда положение точки на окружности однозначно определяется углом поворота между осью и радиус-вектором точки.
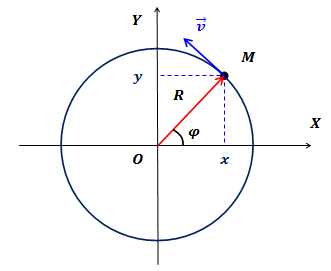
Рис.1. Равномерное движение тела по окружности
Условились положительным считать направление вращения против часовой стрелки.
Декартовые координаты точки однозначно определяются углом поворота точки:
При движении точки по окружности ее координата, то есть угол поворота , изменяется или становится функцией времени. Поэтому закон движения в этом случае — это зависимость угла поворота от времени: .
Единицей измерения угла поворота в системе СИ является радиан.
Период вращения — это время, за которое точка совершает один полный оборот по окружности, т.е. поворачивается на угол .
Частота вращения — это число полных оборотов, совершаемых точкой при равномерном движении по окружности, в единицу времени:
В системе СИ частота измеряется в
Частота и период связаны между собой формулой:
Примеры решения задач
ru.solverbook.com

Leave A Comment