Задачи на движение по окружности с решением
Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только.
Движение по окружности: определение, примеры
Движение по окружности – самый простой случай криволинейного движения.
Примеры движения по окружности:
- грузовик движется по мосту с радиусом кривизны R;
- атлет крутит шар в руке, перед тем как бросить его;
- космическая станция летает по кругу над поверхностью Земли;
- катафот вращается на раскрученном колесе велосипеда.
Приведем ниже кинематические соотношения для поступательного и вращательного движений:
Вопросы на движение по окружности
Вопрос 1. Как направлено центростремительное ускорение?
Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.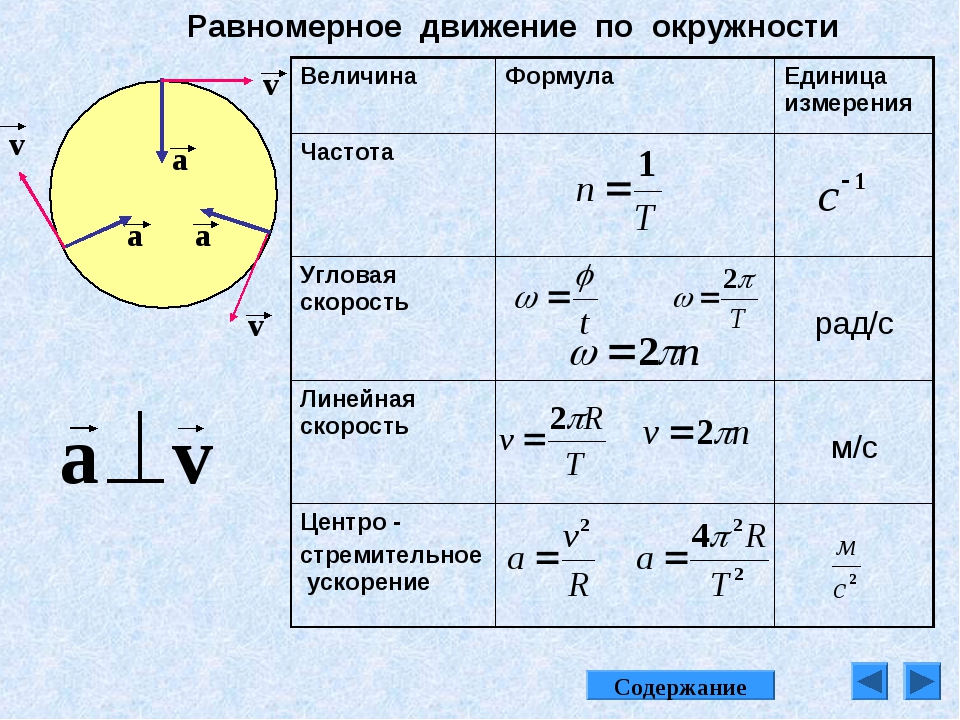
Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?
Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.
Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?
Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.
Вопрос 4. Что такое линейная и угловая скорость?
Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.
Вопрос 5. При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?
Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.
Задачи на движение по окружности
Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задача №1. Нахождение линейной скорости при движении по окружности
Условие
Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?
Решение
В данном случае ввиду имеется нормальное ускорение.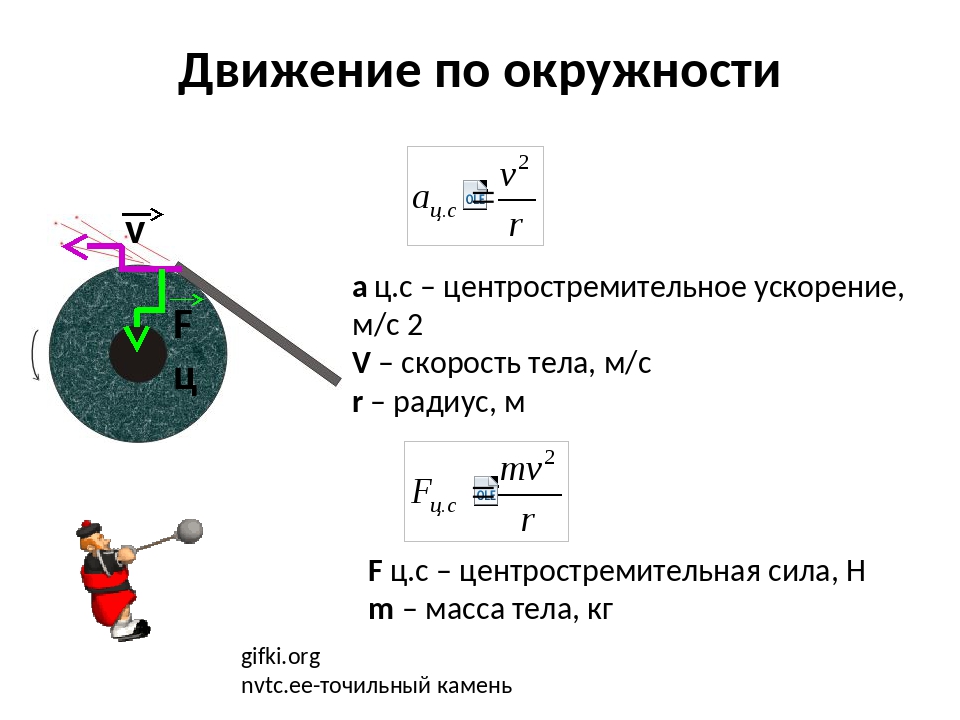
Ответ: 10,9 м/с.
Задача №2. Нахождение углового ускорения
Условие
Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
Решение
Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:
Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:
Ответ: 3,2 радиан на секунду в квадрате.
Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.Задача №3. Нахождение скорости движения по окружности
Условие
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Решение
Две точки вращаются на одном колесе, а значит, с одинаковой частотой. 2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.
2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.
Решение
Полное ускорение – векторная сумма нормального и тангенциального ускорений.
Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:
Подставляем значение t из условия и вычисляем:
Ответ: 1,65 метра в секунду.
Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.
Урок 4. равномерное движение точки по окружности — Физика — 10 класс
Физика, 10 класс
Урок 04.Равномерное движение точки по окружности
Перечень вопросов, рассматриваемых на уроке:
- Равномерное движение точки по окружности и его характеристики.
- Центростремительное ускорение.
Глоссарий по теме
Криволинейное движение – это движение по дугам окружностей разных радиусов.
Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0
Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.
Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.
Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.
При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.
Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.
Возьмем разные точки на линии и нарисуем векторы скорости . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.
Векторы и не лежат на одной прямой, угол между ними не равен нулю.
Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.
Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.
2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.
Равномерное движение точки по окружности — это движение точки с постоянной по модулю скоростью (v = const) по траектории, представляющей собой окружность. Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение
Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.
Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.
Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была.
Модули скоростей равны:
но вектора скоростей не равны.
Поэтому построим вектор для тела, движущегося по окружности. Перенесем вектор в начало вектораи найдем разность векторов.
направлен в сторону.
Вспомним, что векторнаправлен по касательной, а касательная перпендикулярна радиусу окружности. Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Что можно сказать об угле между векторами ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.
Рассмотрим равнобедренный треугольник со сторонами , . Углы у основания равны.
Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 900
Вектор будет перпендикулярен вектору в пределе, а значит вектор ускорения тоже перпендикулярен т. е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением
е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением
Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.
Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Длина дуги АВ это путь, пройденный точкой от А до В,
тогда запишем:
Умножим наи получим:
В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:
Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными
- Криволинейное движение — это движение по дугам окружностей разных радиусов.

А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.
Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т.е. перпендикуляр.
Основные выводы:
— движение криволинейное, так как траекторией является окружность;
— движение равномерное, так как модуль скорости не меняется;
— вектор скорости направлен по касательной к окружности;
-вектор ускорения направлен к центру окружности;
— модуль центростремительного ускорения равен:
Примеры и разбор решения заданий
1. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением
где R = 50 м; υ= км/ч = 10 м/с.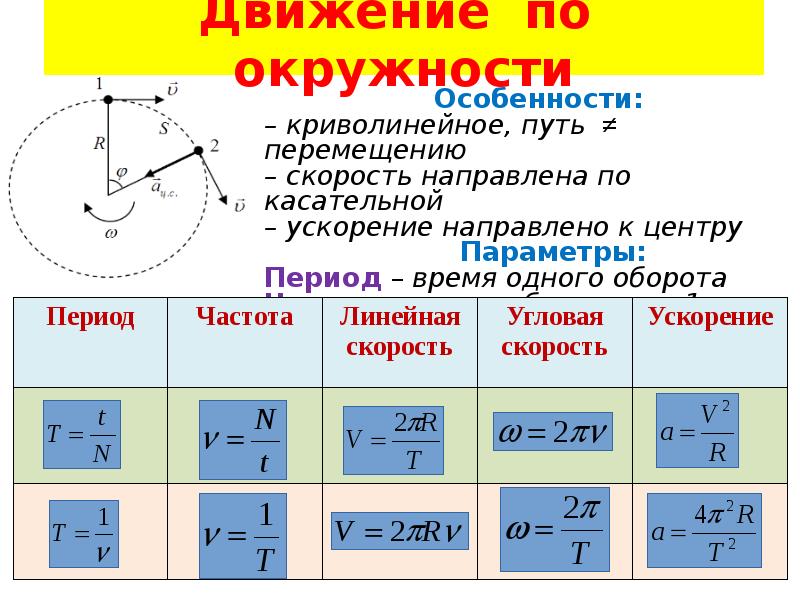
Тогда ac = (10 м/с)2 / 50 м = 2 м/с2.
Ответ: 2 м/с2
2. Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
Дано:
R1 =10см = 0,10 м
R2 = 30см = 0,30 м
Найти —
Задано два объекта:
1) материальная точка, которая движется по окружности R1;
2) материальная точка, которая движется по окружности R2.
При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением
Для тела 1 уравнение (1) примет вид:
для тела 2:
Тогда
Центростремительное ускорение тела (2) меньше ускорения тела (1) в 3 раза.
11. Задача про движение материальной точки по окружности
Теперь воспользуемся полученными выше знаниями для решения красивой классической задачи про движение материальной точки по окружности.
Материальная точка двигается равномерно по окружности. В первом приближении похоже на движение Земли вокруг Солнца или Луны вокруг Земли.
Тогда мы можем записать уравнения движения в прямоугольной инерциальной системе координат XYZ. Причем, пусть движение происходит в плоскости XY, тогда координата Z(t) всегда равна 0:
где φ(t) функция зависимости угла между радиус вектором точки, проведенным из начала координат, и осью X от времени. При равномерном движении этот угол изменяется с постоянной угловой скоростью ω [радиан/с].Найдем функции скорости и ускорения для данной материальной точки.
Находим первые, а затем и вторые производные по времени. Первые производные по времени от функций координат будут являться функциями зависимости компонентов скоростей по соответствующим координатам материальной точки от времени.
С помощью таблиц производных тригонометрических функций (или с помощью онлайн системы вычисления производных в интернете) находим что производные синуса и косинуса равны
Из формул (23), (28), (29) получаем дифференцированием по t:
Соответственно, модуль вектора скорости V(t) равен корню квадратному из суммы квадратов компонент. Надеюсь, все помнят, как находить длину гипотенузы прямоугольного треугольника из длин катетов!
Скорость, действительно, постоянна по модулю!
А ускорение?
Дифференцируем функции скоростей по времени t, получаем функции компонентов ускорений по соответствующим осям координат:
Следовательно, модуль вектора ускорения аналогично предыдущему равен:
Из формул (45), (46) и (47) видно, что ускорение всегда направлено к центру. Догадайтесь почему? И оно, ускорение, тоже постоянно по модулю. А так как масса тела у нас постоянна, то значит, и сила притяжения к центру при таком движении так же должна быть постоянна по модулю.
А так как масса тела у нас постоянна, то значит, и сила притяжения к центру при таком движении так же должна быть постоянна по модулю.
На этом можно было бы остановиться. Мы вывели уравнения для скорости и ускорения, которые описывают равномерное движение материальной точки по окружности. К тому же определили, что скорость и ускорение по модулю являются постоянными. И зависят от радиуса окружности R, и некой постоянной 𝛚.
Но что такое эта самая постоянная 𝛚? Это угловая скорость.
Это скорость обращения в радианах?! Знаете, что такое радиан? Что такое радиан, можно посмотреть в интернете. Это угол, измеренный в радиусах, отложенных по окружности.
В 180 градусах умещается π радианов = 3,14…… радианов. Радиан – безразмерная величина, типа доли. Просто столько-то радианов. Если умножим на величину радиуса окружности в метрах, получим длину дуги нашей окружности (величиной в столько-то радианов) в метрах.
Размерность нашего 𝛚 – [1/с].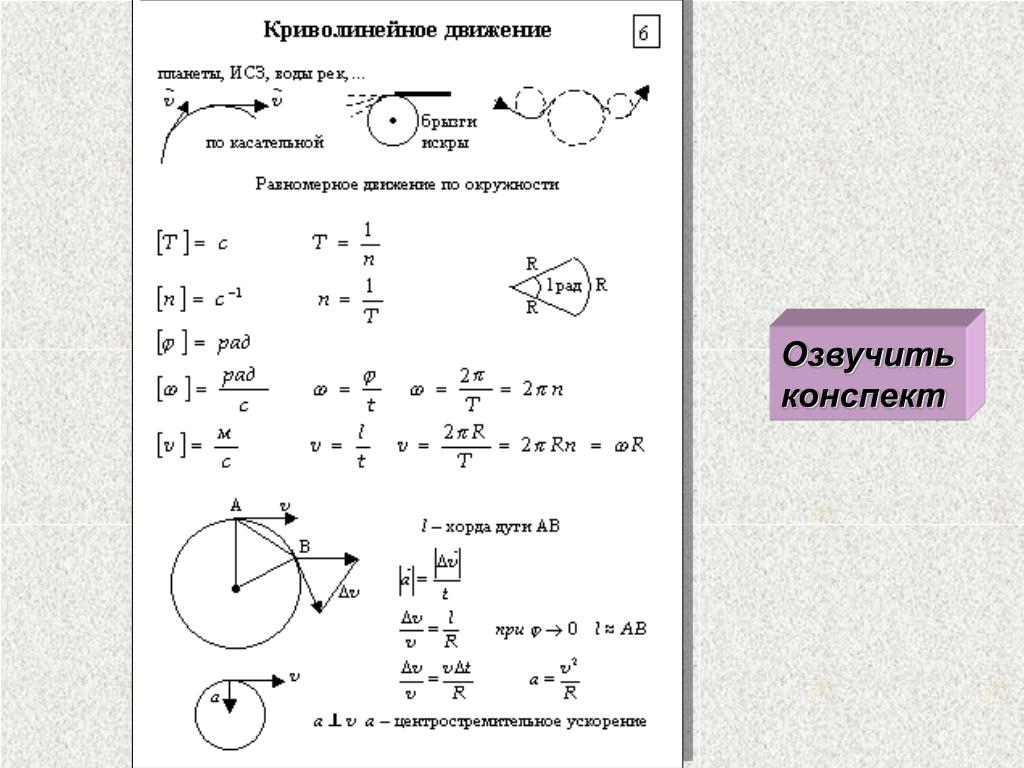 Правильно! В формуле (46) размерность у ускорения – [м/с2].
Правильно! В формуле (46) размерность у ускорения – [м/с2].
У чего еще есть размерность [1/с]? У частоты вращения γ – столько-то оборотов в секунду. Легко заметить, что если частота равна одному обороту в секунду γ = 1, то так как в полной окружности 2π радиан, следовательно
Подставляем в (49), получаем:
Мы продолжим рассмотрение кругового движения в последующих главах. Пока же ограничимся еще одной формулой. Вы, надеюсь, знаете, что период T обращения есть величина обратная частоте T = 1 / γ [в секундах]
Так? Тогда из (51) следует
Мы «убрали» зависимость от времени у модуля ускорения, поскольку оно по модулю не зависит от времени.
Заметим так же, что формулы (50) — (53) скалярные, а не векторные.
Предлагаю вам самостоятельно вывести формулу зависимости модуля ускорения a от модуля линейной скорости V и радиуса R.
Заметьте, мы вывели формулы аналитически. Просто из заданных уравнений движения (X(t),Y(t), Z(t)). Мы задали зависимость координат от времени и простым дифференцированием нашли зависимости от времени скоростей и ускорений. Точнее, установили их независимость от времени. Мы с вами аналитически вывели, что для равномерного движения по окружности телу (материальной точке) нужно придать ускорение, постоянное по величине и направленное к центру окружности, вдоль которой движется тело. Но самое главное, мы вывели уравнения зависимости периода обращения такого тела (материальной точки), ускорения и радиуса орбиты. И оказалось, что действительно период обращения космического корабля вокруг Земли, например, зависит только от радиуса орбиты и ускорения, придаваемого кораблю Землей.
Теперь решим красивую задачу.
Задача: «Нам нужно запустить на орбиту спутник-шпион, который будет следить за конкретным неподвижным объектом на поверхности Земли, например, за военной базой. Вопрос, каковы параметры орбиты такого спутника?»
Решение: Используем уравнение (53). Для того, чтобы спутник мог круглосуточно наблюдать на поверхности Земли за военной базой, он должен все время находиться в пределах видимости объекта. Если мы запустим спутник, период обращения которого вокруг Земли будет равен периоду обращения самой Земли вокруг своей оси, а орбита будет лежать в плоскости экватора, то такой спутник будет все время висеть над одной точкой. С Земли он будет казаться неподвижно висящим над экватором.
Какие параметры имеет такая орбита? Берем формулу (53). Смотрим, что у нас известно и неизвестно. Известен период обращения. Неизвестен радиус орбиты. А ускорение? Оно, как мы знаем, зависит от радиуса орбиты. На уровне поверхности Земли ускорение равно g ≅ 9,8 м/с2. Если радиус орбиты больше радиуса Земли в два раза, то ускорение меньше в 4 раза. Надеюсь, все помнят формулу закона всемирного тяготения.
Если радиус орбиты больше радиуса Земли в два раза, то ускорение меньше в 4 раза. Надеюсь, все помнят формулу закона всемирного тяготения.
У поверхности земли ускорение свободного падения
На орбите ускорение свободного падения
Тогда у нас получается
Подставляем в уравнение (50), получаем
Теперь выразим Rорбиты из формулы (56)
Проверяем размерности получившейся формулы
Правильная формула!
Теперь подставляем в нее известные численные значения. Период обращения – 24 часа = 24 * 60 * 60 сек. Радиус Земли приблизительно = 6 300 000 м. Ускорение у поверхности = 9,8 м/с2. Подставляем. Посчитайте сами и проверьте результат!
Получаем около 42 000 км. Таким образом спутник будет висеть над одной точкой экватора приблизительно на высоте около 36 000 км. над поверхностью Земли. Это правильный результат! Так называемые «геостационарные» (стационарные относительно поверхности Земли) спутники имеют такие параметры орбиты.
Урок физики «Равномерное движение по окружности», 10 класс, ФГОС
10 класс Раздел «Кинематика»
Урок №
Тема урока: Равномерное движение по окружности
Цель урока: ознакомить учащихся с равномерным движением по окружности и физическими величинами, характеризующими это движение
Задачи урока: Образовательная — сформировать у учащихся представления о характеристиках равномерного движения по окружности.
Развивающие: формировать умение определять вид движения тела; сравнивать, анализировать, обобщать данные о движении тела; умение
развивать способность структурировать информацию в рамках поставленной задачи;
формировать умения использовать основные понятия, формулы и физические законы движения тела при движении по окружности;
развивать физическое мышление учащихся через практическую деятельность.
Воспитывающие: потребность познания окружающего мира, любознательность, внимательность и трудолюбие.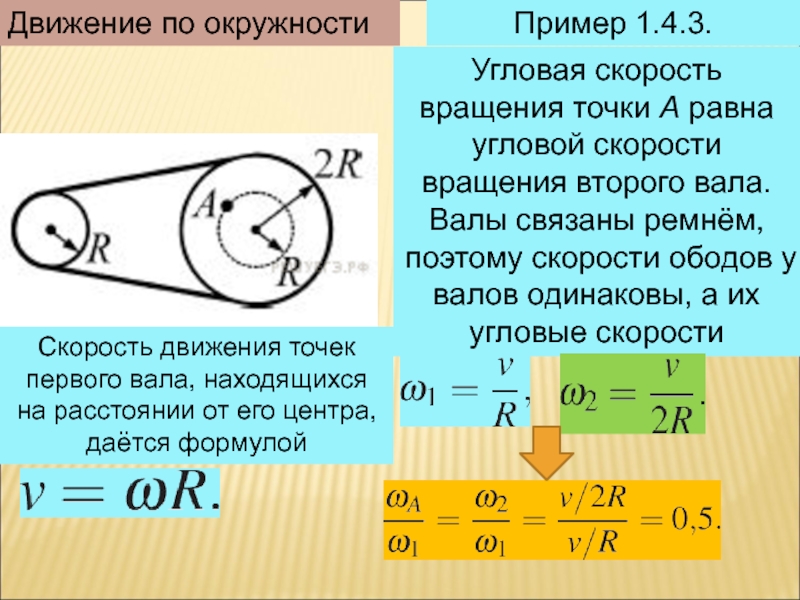
Планируемые результаты: Предметные: знать — определения и формулы периода, частоты, линейной и угловой скорости, центростремительного ускорения; уметь — применять формулы кинематики криволинейного движения при решении задач.
Личностные: формирование умений управлять своей учебной деятельностью, формирование интереса к физике при анализе явлений формирование мотивации постановкой познавательных задач.
Метапредметные: применять знания законов движения по окружности в повседневной жизни.
Тип урока: изучение нового материала
Ход урока
1.ОРГАНИЗАЦИОННЫЙ МОМЕНТ
Проверка наличия домашнего задания.
2. АКТУАЛИЗАЦИЯ ЗНАНИЙ А) и Б) выполняем одновременно.
А) В начале занятия давайте проведем физическую разминку в виде физического футбола по темам: «Равноускоренное прямолинейное движение. Свободное падение». Первый учащийся задаёт вопрос по теме и говорит кому направляет этот пас. Второй отвечает. Задает свой вопрос и т.д.
Второй отвечает. Задает свой вопрос и т.д.
Б) написать формулы на доске по теме свободное падение. Дополнительный вопрос. С какого этажа дома упал предмет без начальной скорости, если он находился в полете 2 с?
3.ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Криволинейное движение в природе и технике более распространено, чем прямолинейное. Примеры: движение лыжника с горки на горку, движение человека на карусели, движение стержня ручки во время письма, движение частей станка при обработки детали(шлифование), полет волейбольного мяча после удара и тому подобное.
Любое криволинейное движение можно представить как последовательность движений по дугам окружностей различных радиусов.
Рассмотрим частный случай криволинейного движения — движение по окружности, которое в окружающем мире распространено: движение стрелки часов, движение искусственных спутники Земли, зубчатые колесики в велосипеде; движение автомобиля и поезда на выпуклых мостах.
Движение по окружности – это вращательное движение.
Демонстрация. Шарик на нити.
Вращательным движением тела называется такое движение, при котором все точки описывают окружности, центры которых находятся на одной прямой, называемой осью вращения.
Нарисуем окружность укажем в некоторых точках направление вектора мгновенной скорости.
Мгновенная скорость тела, движущегося по окружности, направлена по касательной к ней в этой точке.
Наблюдая движение брызг грязи из-под колес автомобиля, что буксует мы в этом можем убедиться.
(см. рис учебника). По касательной также разлетаются раскаленные частицы металла отрываются от стального резца, если коснуться им поверхности вращающегося точильного камня.
Величина | обозначение | Единица измерения | Формула |
Период | Т | с | Т=t/n; T=2πr/v |
Частота | υ | Гц | υ =n/t=1/Т |
Линейная скорость | v | м/с | v=2πr/T=ωr; v=Δl/Δt |
Угловая скорость | ω | рад/с | ω=v/r=2π/T= Δφ/Δt |
Ускорение | а | м/с2 | a=v2/r= ω2r |
Мы будем изучать движение точки по окружности с постоянной по модулю скоростью. Его называют равномерным движением по окружности.
Его называют равномерным движением по окружности.
Составим таблицу характеристик этого движения. Учащиеся по очереди выходят заполнять таблицу, руководствуясь учебником.
Скорость точки, движущейся по окружности, называют линейной скоростью.
Линейная скорость v — это физическая величина, характеризующая криволинейное движение и равна отношению пути Δl, пройденного телом по криволинейной траектории за малый промежуток времени Δt, к величине этого промежутка
Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за который тело совершает один полный оборот.
Период вращения Т — это физическая величина, равная времени одного полного оборота.
Единица периода вращения в СИ — секунда ([Т] = с).
Частота вращения — это физическая величина, численно равна числу полных оборотов за единицу времени.
Угловая скорость — это физическая величина, равная отношению угла поворота радиуса, проведенного к телу от центра круга, по которому движется тело, к промежутку времени, в течение которого этот поворот осуществлялся.
Основная задача механики для равномерного движения по окружности состоит так же в определении положения тела в любой момент времени.
Поскольку движение по кругу происходит в одной плоскости, то для описания движения можно воспользоваться двухмерной системой координат. Если связать точку начала координат с центром круга, по которому движется тело, а начальное положение тела соединить с точкой пересечения окружности и оси Ох, то координаты х и можно вычислить по формулам: х=Rсоsφ; y=Rsinφ.
Поскольку угол φ меняется с течением времени по закону φ = ωt, то уравнение координаты для равномерного движения по окружности имеет следующий вид: х=Rсоs ωt;y=Rsin ωt.
ЗАКРЕПЛЕНИЕ. РЕШЕНИЕ ЗАДАЧ У ДОСКИ. Вызываю 3 ученика.
1. Кабинка карусели движется по окружности радиусом 24 м. Период его вращения равен 30с. Чему равна скорость движения кабинки?
Дано:
R=24м
Т=30с v=2πR/T v=2*π*24м /30с=48 π /30м/с=5 м/с
v-? Ответ: 5 м/с
Вопрос к классу
Чему равен период вращения часовой стрелки часов? минутной? секундной?
Тм=1ч=3600с;
Тс=1мин=60с;
Тч=12ч=12*3600с=43200с.
2. Во сколько раз скорость конца минутной стрелки башенных часов Биг-Бен в Лондоне больше скорости конца минутной стрелки наручных часов, если длина стрелки башенных часов — 4,2 м, а длина стрелки наручных часов — 1,5 см?
Справка. Часы на башне Биг-Бен в Лондоне до настоящего времени являются самыми большими в мире. Диаметр циферблата – 7 метров. Длина стрелок – 2,7 и 4,2 метра. Часовой механизм считается эталоном надежности, общий вес его составляет 5 тонн.
Дано:
Rб=4,2м Тмб = Тмр =1ч=3600с v=2πr/T
Rр=1,5 см = 1,5*10-2 м vб/ vб =(2*π*4,2м / 3600с/)*(3600с/2*π*1,5*10-2 м )=280 раз
vб/ vб -? Ответ: 280 раз
3.Напишите уравнение движения материальной точки, движущейся по дуге радиусом 5 м с угловой скоростью π/4 рад/с. Какими будут координаты точки через 3 с после начала отсчета времени?
Дано:
R=5м х=Rсоs ωt; y=Rsin ωt
ω= π/4 рад/с
х(t)-? х=5соs π/4t; y=5sin π/4t
y (t)-?
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ.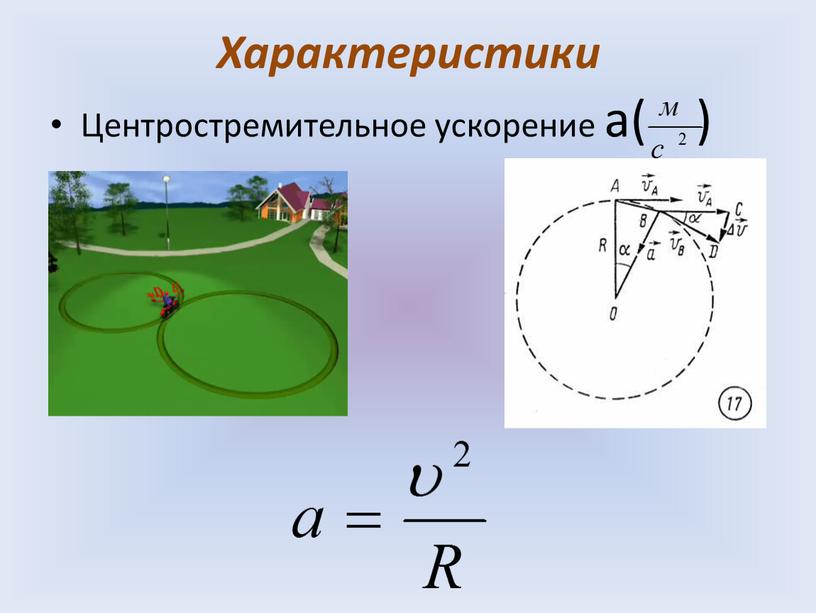 РАБОТА ПО КАРТОЧКЕ.
РАБОТА ПО КАРТОЧКЕ.
Детская карусель за одну минуту совершает 4 оборота. Найти период и частоту, с которой она вращается.
Дано:
N=4об
T=1мин 60с Т=t/N T=60с/4=15с υ=N/t υ=4/60=1/15=0.067Гц
T-?
υ -? Ответ: 15 с,15 Гц
РЕФЛЕКСИЯ
Что нового узнали? Сложно ли использовать формулы при решении задач?
ДОМАШНЕЕ ЗАДАНИЕ
1. Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский Физика 10 –М.: Просвещение, 2017.
§ 15,16 читать, учить определения, формулы. Выполнить с.61 А1-А4.
2.Проект в виде буклета «Равномерное движение по окружности» (по желанию)
Движение по окружности | LAMPA
Найдем угловую скорость. Известно, что ω=φt\omega=\frac{\varphi}{t}ω=tφ. В качестве угла φ\varphiφ можно взять полный оборот, то есть угол 2π2\pi2π радиан, а в качестве времени — время одного полного оборота, то есть период TTT. Поэтому
Поэтому
ω=2πT,\omega=\frac{2\pi}{T}{,}ω=T2π,ω=2πT=2π⋅1T=2πν.\omega=\frac{2\pi}{T}=2\pi\cdot\frac{1}{T}=2\pi\nu{.}ω=T2π=2π⋅T1=2πν.
Эти формулы мы тоже рекомендуем запомнить. Это будет полезно.
Единица измерения угловой скорости [ω]=радс[\omega]=\frac{\text{рад}}{\text{с}}[ω]=срад.
Оказывается, что линейная скорость VVV и угловая скорость ω\omegaω связаны друг с другом. Рассмотрим пример из жизни. На детских площадках наверняка все видели карусель. Представьте, что карусель вращается. Вы сами сидите на сиденьи этой карусели, а ваш друг не стал сидеть на сиденьи, а «пролез» поближе к центру карусели.
Поскольку каждый из вас поворачивается вокруг карусели на один и тот же угол за то же время, то угловые скорости у вас равны: ωвы=ωдруг\omega_{вы}=\omega_{друг}ωвы=ωдруг. Но вот линейные скорости у вас не равны: Vвы≠VдругV_{вы}\neq V_{друг}Vвы≠Vдруг. Это нам подсказывает наш жизненный опыт. Тот, кто сидит поближе, двигается медленнее.
Но вот линейные скорости у вас не равны: Vвы≠VдругV_{вы}\neq V_{друг}Vвы≠Vдруг. Это нам подсказывает наш жизненный опыт. Тот, кто сидит поближе, двигается медленнее.
Чем ближе к центру находится тело — тем меньше его линейная скорость VVV. И наоборот: чем дальше от центра (чем больше расстояние от центра), тем больше скорость VVV.
Линейная скорость VVV также будет больше и в том случае, если будет больше быстрота поворота вокруг оси, то есть угловая скорость ω\omegaω.
По-простому: чем дальше сидишь от оси (чем больше RRR) и чем быстрее вращается тело (чем больше ω\omegaω), тем больше линейная скорость VVV.
Линейную скорость VVV можно пойти по формуле:
V=ω⋅R.V=\omega\cdot R{.}V=ω⋅R.
Эту формулу можно вывести строго. Возьмем уже известные нам формулы:
V=2πR⋅νV=2\pi R\cdot \nuV=2πR⋅ν и ω=2π⋅ν\omega=2\pi\cdot \nuω=2π⋅ν.
Из них видно, что в первой формуле вместо 2πν2\pi\nu2πν можно подставить ω\omegaω:
V=2πR⋅ν=2πνR=(2πν)⋅R=ω⋅RV=2\pi R\cdot \nu=2\pi\nu R=(2\pi\nu)\cdot R=\omega\cdot RV=2πR⋅ν=2πνR=(2πν)⋅R=ω⋅R.
Мы получили формулу V=ω⋅RV=\omega\cdot RV=ω⋅R.
Дополнительные главы физики: кинематика. 9 класс: Участники курса
Курс ориентирован на слушателей, владеющих школьной программой по физике 9 класса. В процессе обучения учащиеся познакомятся с основными принципами и методами кинематики, увидят, как довольно сложные движения можно свести к комбинации более простых, и научатся решать разнообразные задачи.
Курс состоит из 10 обязательных и 2 лекционных модулей, 51 видеолекций с конспектами, 181 обязательных упражнений и факультативных задач для самостоятельного решения.
Учебные модули
— Геометрия и физика
— Описание движения
— Ускорение
— Движение по окружности
— Малые приращения физических величин
— Движение тела, брошенного под углом к горизонту
— Криволинейное движение
— Кинематика плоского движения твердого тела
— Комбинация прямолинейных движений
— Кинематические связи
— Выбор системы отсчета
— Комбинация вращения и прямолинейного движения
Внутри каждого модуля есть:
— видео с кратким конспектом, где обсуждается теория и разбираются примеры решения задач,
— упражнения с автоматической проверкой, позволяющие понять, как усвоена теория,
— задачи для самостоятельного решения, которые не учитываются в прогрессе и не идут в зачет по модулю, но позволяют качественно повысить свой уровень.
Каждый ученик самостоятельно определяет для себя темп и удобное время учебы. Часть модулей открыта сразу, следующие модули открываются после того, как получен зачет по предыдущим. В каждом разделе есть ответы на популярные вопросы, где можно уточнить свое понимание теории или условия задачи, но нельзя получить подсказки по решению.
По итогам обучения выдается электронный сертификат. Для его получения необходим зачет по всем учебным модулям, кроме лекционных. Условие получения зачета по модулю — успешное выполнение не менее 70% упражнений. Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Если ученик не успеет получить зачет по отдельным модулям, то он не сможет получить сертификат, но сможет возобновить обучение, когда курс стартует в следующий раз. При этом выполнять пройденные модули заново не потребуется (но может быть предложено, если соответствующие учебные материалы обновятся).
В следующий раз курс будет открыт осенью 2020 года.
Решение задач. Движение тела по окружности
Цель: научить решать задачи на движение тела по окружности.
Ход урока
I. Повторение. Беседа
1. Точка движется равномерно по окружности. Постоянна ли ее скорость?
2. Есть ли ускорения у точки, которая движется по окружности?
3. Куда направлено ускорение?
4. Что такое период? Частота?
5. Как связаны между собой ускорение, скорость и радиус при равномерном движении тела по окружности.
6. Что называется осью вращения твердого тела?
7. Что такое угловая скорость?
8. Как связаны между собой угловая и линейная скорости? Угловая скорость и центростремительное ускорение?
II. Решение задач
I группа
1. Скорость точек рабочей поверхности наждачного круга диаметром 300 мм не должна превышать 35 м/с. Допустима ли посадка круга на вал электродвигателя, совершающего 1400 об/мин, 2800 об/мин? (Да, нет.)
2. Частота вращения воздушного винта самолета 1500 об/мин. Сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч? (45 000)
Сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч? (45 000)
3. Период вращения платформы карусельного станка 4 с. Найти скорость крайних точек платформы, удаленных от оси вращения на 2 м. (3,14 м/с)
4. Скорость точек экватора Солнца при его вращении вокруг своей оси 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек экватора. (253 сут., 5,7 мм/с?)
II группа
1. Минутная стрелка в 1,5 раза длиннее часовой. Определите, во сколько раз скорость конца часовой стрелки меньше скорости конца минутной стрелки. (В 18 раз)
2. Определите центростремительное ускорение точек колеса автомобиля, соприкасающихся с дорогой, если автомобиль движется со скоростью 36 км/ч и при этом частота вращения колеса равна 4е-1. (251,2 м/с?)
3. Две материальные точки движутся по окружности радиусами R1 и R2 причем R1 = 2R2. Сравните их центростремительные ускорения, если равны их периоды обращения. (2:1)
(2:1)
4. Минутная стрелка часов в 2 раза длиннее секундной. Найдите отношение скоростей концов стрелок. (1:30)
III группа
1. Чему равен радиус вращающегося колеса, если известно, что скорость точки, лежащей на ободе, в 2,5 раза больше скорости точки, лежащей на расстоянии 5 см ближе к оси колеса? (8,5 см)
2. Найдите линейную скорость и центростремительное ускорение точек на широте 60°. Радиус Земли равен 6400 км. (233 м/с, 1,7410-2 м/с?)
3. Небольшое тело движется по окружности радиуса R со скоростью, которая линейно увеличивается со временем по закону v = kt. Найдите зависимость полного ускорения тела от времени.
4. Какое расстояние пройдет велосипедист при 60 оборотах педалей, если диаметр колеса 70 см, ведущая зубчатка имеет 48 зубцов, а ведомая -18 зубцов? (352 м)
Домашнее задание
П. 20,21, задачи на стр. 51.
Математика кругового движения
При анализе движения объектов по кругу нас будут интересовать три математические величины.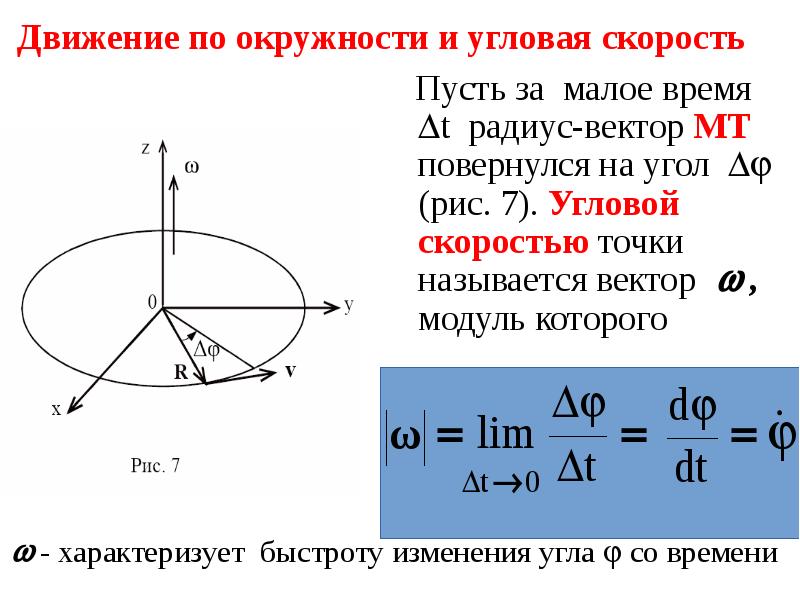 Эти три величины — скорость, ускорение и сила. Скорость объекта, движущегося по кругу, определяется следующим уравнением.
Эти три величины — скорость, ускорение и сила. Скорость объекта, движущегося по кругу, определяется следующим уравнением.Ускорение объекта, движущегося по кругу, можно определить с помощью двух из следующих уравнений.
Уравнение справа (вверху) получено из уравнения слева путем подстановки выражения для скорости.
Чистая сила ( F net ), действующая на объект, движущийся по кругу, направлена внутрь. Хотя на объект может воздействовать более одной силы, их векторная сумма должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если таковая имеется), так что внешняя сила компенсируется, и неуравновешенная сила направлена в направлении центра круга. Суммарная сила связана с ускорением объекта (как всегда) и, таким образом, определяется следующими тремя уравнениями:
Уравнения в середине (вверху) и справа (вверху) получены из уравнения слева путем подстановки выражений для ускорения.
Этот набор уравнений кругового движения можно использовать двумя способами:
Эти два способа показаны ниже.
Уравнения как руководство к мышлениюУравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение второго закона Ньютона определяет, как ускорение связано с чистой силой и массой объекта.
Соотношение, выражаемое уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается. Фактически, если бы чистая сила была увеличена в 2 раза, уравнение предсказало бы, что ускорение увеличится в 2 раза. Точно так же, если бы чистая сила была уменьшена в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза.
Уравнение второго закона Ньютона также показывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше будет значение ускорения. По мере увеличения массы ускорение уменьшается. Фактически, если бы масса была увеличена в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса была уменьшена в 2 раза, уравнение предсказало бы, что ускорение будет увеличиваются в 2 раза.
Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше будет значение ускорения. По мере увеличения массы ускорение уменьшается. Фактически, если бы масса была увеличена в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса была уменьшена в 2 раза, уравнение предсказало бы, что ускорение будет увеличиваются в 2 раза.
Как упоминалось ранее, уравнения позволяют делать прогнозы о влиянии изменения одной величины на вторую величину. Поскольку уравнение второго закона Ньютона показывает три величины, каждая из которых возведена в первую степень, предсказательная способность уравнения довольно проста. Прогностическая способность уравнения усложняется, когда одна из величин, включенных в уравнение, возводится в степень. Например, рассмотрим следующее уравнение, связывающее чистую силу ( F net ) со скоростью ( v ) объекта, движущегося с равномерным круговым движением.
Это уравнение показывает, что чистая сила, необходимая объекту для движения по кругу, прямо пропорциональна квадрату скорости объекта. При постоянной массе и радиусе сеть F пропорциональна скорости 2 .
Фактор, на который изменяется чистая сила, является квадратом фактора, на который изменяется скорость. Впоследствии, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза.А если скорость объекта уменьшается вдвое (уменьшается в 2 раза), требуемая полезная сила уменьшается в 4 раза.
Уравнения как рецепт решения проблем Математические уравнения, представленные выше для движения объектов по кругу, могут использоваться для решения задач кругового движения, в которых необходимо определить неизвестную величину. Процесс решения задачи о круговом движении очень похож на любую другую задачу в классе физики. Процесс включает в себя внимательное прочтение проблемы, идентификацию известной и необходимой информации в переменной форме, выбор соответствующего уравнения (й), замену известных значений в уравнение и, наконец, алгебраическую обработку уравнения для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам кругового движения.
Процесс включает в себя внимательное прочтение проблемы, идентификацию известной и необходимой информации в переменной форме, выбор соответствующего уравнения (й), замену известных значений в уравнение и, наконец, алгебраическую обработку уравнения для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам кругового движения.
| Пример задачи № 1 Автомобиль массой 900 кг, движущийся со скоростью 10 м / с, делает разворот по окружности с радиусом 25.0 мин. Определите ускорение и чистую силу, действующую на автомобиль. |
Решение этой проблемы начинается с выявления известной и запрашиваемой информации.
Известная информация: м = 900 кг | Запрошенная информация: а = ???? |
Для определения ускорения автомобиля используйте уравнение a = v 2 / R. Решение следующее:
Решение следующее:
a = (10,0 м / с) 2 / (25,0 м)
a = (100 м 2 / с 2 ) / (25,0 м)
a = 4 м / с 2
Чтобы определить чистую силу, действующую на автомобиль, используйте уравнение F net = m • a. Решение следующее.
F net = m • aF нетто = (900 кг) • (4 м / с 2 )
F нетто = 3600 N
| Пример задачи № 2 Полузащитник весом 95 кг делает разворот на футбольном поле.Полузащитник прокладывает путь, представляющий собой часть круга радиусом 12 метров. Полузащитник совершает четверть оборота по кругу за 2,1 секунды. Определите скорость, ускорение и чистую силу, действующую на полузащитника. |
Решение этой проблемы начинается с выявления известной и запрашиваемой информации.
Известная информация: м = 95.0 кг | Запрошенная информация: v = ???? |
Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d составляет одну четвертую окружности, а время равно 2.1 с. Решение следующее:
v = d / tv = (0,25 • 2 • pi • R) / т
v = (0,25 • 2 • 3,14 • 12,0 м) / (2,1 с)
v = 8,97 м / с
Чтобы определить ускорение полузащитника, используйте уравнение a = v 2 / R. Решение следующее:
а = v 2 / Ra = (8,97 м / с) 2 / (12,0 м)
а = (80. 5 м 2 / с 2 ) / (12,0 м)
5 м 2 / с 2 ) / (12,0 м)
a = 6,71 м / с 2
Чтобы определить чистую силу, действующую на полузащитника, используйте уравнение F net = m • a. Решение следующее.
F нетто = m * aF нетто = (95,0 кг) * (6,71 м / с 2 )
F нетто = 637 N
В Уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены, чтобы объяснить и проанализировать различные сценарии реального движения, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.
Хотим предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства Uniform Circular Motion Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Проверьте свое понимание
Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Проверьте свое понимание 1. Анна Литикал практикует демонстрацию центростремительной силы дома. Она наполняет ведро водой, привязывает его к прочной веревке и вращает по кругу. Анна вращает ведро, когда оно наполовину наполнено водой, а когда оно на четверть. В каком случае, чтобы вращать ведро по кругу, требуется больше силы? Объясните, используя уравнение как «руководство к размышлениям».
2.Lincoln Continental и Yugo делают поворот. Линкольн в четыре раза массивнее Юго. Если они совершают поворот с одинаковой скоростью, тогда как сравнивать центростремительные силы, действующие на две машины? Объяснять.
3. Cajun Cliffhanger в Great America — это аттракцион, в котором пассажиры выстраиваются по периметру цилиндра и вращаются по кругу с высокой скоростью поворота. Когда цилиндр начинает очень быстро вращаться, пол убирается из-под ног гонщиков.Какое влияние удвоение скорости оказывает на центростремительную силу? Объяснять.
Cajun Cliffhanger в Great America — это аттракцион, в котором пассажиры выстраиваются по периметру цилиндра и вращаются по кругу с высокой скоростью поворота. Когда цилиндр начинает очень быстро вращаться, пол убирается из-под ног гонщиков.Какое влияние удвоение скорости оказывает на центростремительную силу? Объяснять.
4. Определите центростремительную силу, действующую на ребенка весом 40 кг, который совершает 10 оборотов вокруг Клиффхэнгера за 29,3 секунды. Радиус ствола — 2,90 метра.
Веб-сайт класса физики
Круговое движение и гравитация: набор задач
Задача 1:
Во время экскурсии по физике в парк развлечений Тайлер и Мария взяли наездника на Вирлигиге.Поездка на Whirligig состоит из длинных качелей, которые вращаются по кругу на относительно высоких скоростях. В рамках своей лаборатории Тайлер и Мария подсчитали, что всадники проходят круг радиусом 6,5 м и делают один поворот каждые 5,8 секунды. Определите скорость всадников на Whirligig.
В рамках своей лаборатории Тайлер и Мария подсчитали, что всадники проходят круг радиусом 6,5 м и делают один поворот каждые 5,8 секунды. Определите скорость всадников на Whirligig.
Задача 2:
Самое высокое колесо обозрения в мире находится в Сингапуре. Колесо обозрения высотой 42 этажа и вместимостью до 780 пассажиров имеет диаметр 150 метров и совершает полный круг за 30 минут.Определите скорость гонщиков (в м / с и миль / час) на Singapore Flyer. ( GIVEN : 1,00 м / с = 2,24 миль / ч)
Задача 3:
Во время цикла отжима стиральной машины одежда прилипает к внешней стенке бочки, поскольку она вращается со скоростью до 1800 оборотов в минуту. Радиус ствола — 26 см.
а. Определите скорость одежды (в м / с), которая находится на стенке вращающегося цилиндра.
г. Определите ускорение одежды.
Задача 4:
Эльмира, штат Нью-Йорк, может похвастаться самой быстрой в мире каруселью. Карусель в парке Элдридж берет райдеров на скорость 18 миль / час (8,0 м / с). Радиус круга, по которому передвигаются внешние всадники, составляет примерно 7,4 м.
Карусель в парке Элдридж берет райдеров на скорость 18 миль / час (8,0 м / с). Радиус круга, по которому передвигаются внешние всадники, составляет примерно 7,4 м.
а. Определяет время для внешних гонщиков, чтобы сделать один полный круг.
г. Определите ускорение гонщиков.
Задача 5:
Производитель приводов CD-ROM утверждает, что проигрыватель может вращать диск с частотой до 1200 оборотов в минуту.
а. Если вращается с такой скоростью, какова скорость внешней строки данных на диске; этот ряд расположен в 5,6 см от центра диска?
г. Каково ускорение внешней строки данных?
Задача 6:
В витрине магазина игрушек в местном торговом центре самолет с батарейным питанием подвешен на веревке и летит по горизонтальному кругу. Самолет весом 631 грамм делает полный круг каждые 2,15 секунды. Радиус круга равен 0.950 м. Определите скорость, ускорение и результирующую силу, действующую на самолет.
Задача 7:
Доминик — звездный метатель диска в университетской команде по легкой атлетике Юга. В прошлогодних региональных соревнованиях Доминик развернул диск весом 1,6 кг по кругу радиусом 1,1 м, в конечном итоге достигнув скорости 52 м / с перед стартом. Определите чистую силу, действующую на диск в моменты перед запуском.
Задача 8:
Лэндон и Джоселин — партнеры по парному катанию.В минувшие выходные они усовершенствовали элемент смертельной спирали для включения в свои предстоящие соревнования. Во время этого маневра Лэндон держит Джоселин за руку и раскачивает ее по кругу, в то время как она удерживает лезвия на льду, вытянутые в почти горизонтальном положении. Определите чистую силу, которая должна быть приложена к Джоселин (m = 51 кг), если ее центр масс вращается по кругу с радиусом 61 см каждые 1,9 секунды.
Задача 9:
Стремясь разогнать об / мин до своего класса, Mr.H проводит демонстрацию с ведром с водой, привязанным к веревке длиной 1,3 метра. Ведро и вода имеют массу 1,8 кг. Г-н Н вращает ковш по вертикальному кругу так, чтобы его скорость составляла 3,9 м / с в верхней части петли и 6,4 м / с в нижней части петли.
Ведро и вода имеют массу 1,8 кг. Г-н Н вращает ковш по вертикальному кругу так, чтобы его скорость составляла 3,9 м / с в верхней части петли и 6,4 м / с в нижней части петли.
а. Определите ускорение ковша в каждом месте.
г. Определите чистую силу, испытываемую ковшом в каждом месте.
г. Нарисуйте схему свободного тела ковша для каждого местоположения и определите силу натяжения струны для этих двух местоположений.
Задача 10:
Пилот весом 76 кг на авиашоу выполняет петлю со своим самолетом. Внизу петли радиусом 52 м самолет движется со скоростью 48 м / с. Определите нормальную силу, действующую на пилота.
Задача 11:
Алексис едет на своей Toyota Camry и пытается свернуть на скоростную автомагистраль со скоростью 19,0 м / с. Радиус поворота горизонтальной кривой составляет 35,0 м. Ее машина имеет массу 1240 кг. Определите ускорение, чистую силу и минимальное значение коэффициента трения, которые необходимы для удержания автомобиля на дороге.
Задача 12:
Шейла (m = 62 кг) катается на американских горках «Демон». Радиус поворота верха петли — 12 м. Шейла находится вверх ногами в верхней части петли и испытывает нормальную силу, равную половине ее веса. Нарисуйте схему свободного тела и определите скорость Шейлы.
Задача 13:
В 2002 году профессиональный скейтбордист Боб Бернквист стал первым, кто успешно прошел полный поворот на 360 °. Определите минимальную скорость, которая потребуется в верхней части круговой петли, чтобы пройти через 1.Труба радиусом 8 м.
Задача 14:
Джастин едет на своем 1500-кг Camaro по горизонтальному повороту на ровной дороге со скоростью 23 м / с. Радиус поворота по кривой 65 м. Определите минимальное значение коэффициента трения, которое потребуется для удержания машины Джастина на повороте.
Задача 15:
Петлевая трасса построена для автомобиля массой 938 кг. Это полностью круглая петля — 14,2 м высотой в самой высокой точке. Водитель успешно завершает цикл со скоростью входа (внизу) 22.1 м / с.
Водитель успешно завершает цикл со скоростью входа (внизу) 22.1 м / с.
а. Используя функцию энергосбережения, определите скорость автомобиля на вершине петли.
г. Определите ускорение автомобиля на вершине петли.
г. Определите нормальную силу, действующую на автомобиль в верхней части петли.
Задача 16:
Тайрон и Миа имеют массу 84 кг и 59 кг соответственно. Они сидят на расстоянии 1,0 м друг от друга в передней части класса физики мистера Х. В течение некоторого времени каждый из них ощущал своего рода электричество в своих растущих отношениях.И вот, пройдя шесть единиц курса физики, они узнали, что их притягивает друг к другу гравитационное притяжение. Определите величину этой силы гравитационного притяжения.
Задача 17:
Определите силу гравитационного притяжения между Землей и Луной. Их массы составляют 5,98 x 10 24 кг и 7,26 x 10 22 кг соответственно. Среднее расстояние, разделяющее Землю и Луну, составляет 3,84 x 10 8 м. Определите силу гравитационного притяжения между Землей и Луной.
Среднее расстояние, разделяющее Землю и Луну, составляет 3,84 x 10 8 м. Определите силу гравитационного притяжения между Землей и Луной.
Задача 18:
Определите силу гравитационного притяжения между Землей и Солнцем. Их массы составляют 5,98 x 10 24 кг и 1,99 x 10 30 кг соответственно. Среднее расстояние между Землей и Солнцем составляет 1,50 x 10 11 м. Определите силу гравитационного притяжения между Землей и Солнцем.
Задача 19:
Определите ускорение Луны относительно Земли. (ДАННО: M Земля = 5.98 x 10 24 кг и расстояние Земля-Луна = 3,84 x 10 8 м)
Задача 20:
Определите ускорение Земли относительно Солнца. (ДАННЫЕ: M солнце = 1,99 x 10 30 кг и расстояние Земля-солнце = 1,50 x 10 11 м)
Задача 21:
Используйте закон всемирного тяготения Ньютона для определения ускорения 85-кг астронавта на Международной космической станции (МКС), когда МКС находится на высоте 350 км над поверхностью Земли. Радиус Земли — 6,37 х 10 6 м. (ДАННЫЕ: M Земля = 5,98 x 10 24 кг)
Радиус Земли — 6,37 х 10 6 м. (ДАННЫЕ: M Земля = 5,98 x 10 24 кг)
Задача 22:
Определите орбитальную скорость Международной космической станции, находящейся на высоте 350 км над поверхностью Земли. Радиус Земли — 6,37 х 10 6 м. (ДАННЫЕ: M Земля = 5,98 x 10 24 кг)
Задача 23:
Определите орбитальную скорость Земли, вращающейся вокруг Солнца.(ДАННЫЕ: M солнце = 1,99 x 10 30 кг и расстояние Земля-солнце = 1,50 x 10 11 м)
Задача 24:
Геркулес надеется вывести на орбиту бейсбольный мяч, бросив его горизонтально (по касательной к Земле) с вершины горы Ньютон — 97 км над поверхностью Земли. С какой скоростью он должен бросить мяч, чтобы вывести его на орбиту? (ДАННЫЕ: M Земля = 5,98 x 10 24 кг; R Земля = 6,37 x 10 6 м)
Задача 25:
Ученые определяют массы планет, наблюдая за влиянием гравитационного поля этих планет на близлежащие объекты — в основном на их луны. Измеряя период обращения и радиус обращения луны вокруг планеты, законы движения Ньютона можно использовать для определения массы планеты. Фобос, спутник планеты Марс, был открыт в 1877 году. Радиус его орбиты составляет 9380 км, а период обращения — 0,319 суток (2,77 x 10 4 секунд). Определите массу Марса на основе этих данных.
Измеряя период обращения и радиус обращения луны вокруг планеты, законы движения Ньютона можно использовать для определения массы планеты. Фобос, спутник планеты Марс, был открыт в 1877 году. Радиус его орбиты составляет 9380 км, а период обращения — 0,319 суток (2,77 x 10 4 секунд). Определите массу Марса на основе этих данных.
Задача 26:
Геостационарные спутники — это спутники, которые вращаются вокруг Земли над экватором и совершают один полный оборот каждые 24 часа.Поскольку их орбитальный период синхронизирован с периодом вращения Земли, геостационарный спутник всегда можно найти в одном и том же положении на небе относительно наблюдателя на Земле. (ДАННЫЕ: M Земля = 5,98 x 10 24 кг)
а. Определите радиус орбиты геостационарного спутника.
г. Определите орбитальную скорость геостационарного спутника.
г. Определите ускорение геостационарного спутника.
Задача 27:
В 2009 году космический корабль НАСА «Посланник» стал вторым космическим кораблем, совершившим оборот вокруг планеты Меркурий. Космический корабль находился на высоте 125 миль над поверхностью Меркурия. Определите орбитальную скорость и период обращения Посланника. (ДАННЫЕ: R Меркурий = 2,44 x 10 6 м; M Меркурий = 3,30 x 10 23 кг; 1 миля = 1609 м)
Вернуться к обзору
См. Аудиогид решения проблемы:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 274.4 Равномерное круговое движение — Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Найдите центростремительное ускорение объекта, движущегося по круговой траектории.
- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.

- Объясните разницу между центростремительным ускорением и тангенциальным ускорением, возникающим в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорение при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по кругу с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах действительно ускоряются, хотя скорость вращения постоянна.Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по искривленной траектории, такой как окружность. В этом случае вектор скорости меняется, или dv → / dt ≠ 0. Dv → / dt ≠ 0. Это показано на рисунке 4.18. Поскольку частица движется против часовой стрелки за время ΔtΔt по круговой траектории, ее вектор положения перемещается от r → (t) r → (t) к r → (t + Δt).r → (t + Δt). Вектор скорости имеет постоянную величину и касается пути при изменении от v → (t) v → (t) к v → (t + Δt), v → (t + Δt), изменяя только свое направление. Поскольку вектор скорости v → (t) v → (t) перпендикулярен вектору положения r → (t), r → (t), треугольники, образованные векторами положения и Δr →, Δr →, и векторами скорости и Δv → Δv → аналогичны. Кроме того, поскольку | r → (t) | = | r → (t + Δt) || r → (t) | = | r → (t + Δt) | и | v → (t) | = | v → (t + Δt) |, | v → (t) | = | v → (t + Δt) |, два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
В этом случае вектор скорости меняется, или dv → / dt ≠ 0. Dv → / dt ≠ 0. Это показано на рисунке 4.18. Поскольку частица движется против часовой стрелки за время ΔtΔt по круговой траектории, ее вектор положения перемещается от r → (t) r → (t) к r → (t + Δt).r → (t + Δt). Вектор скорости имеет постоянную величину и касается пути при изменении от v → (t) v → (t) к v → (t + Δt), v → (t + Δt), изменяя только свое направление. Поскольку вектор скорости v → (t) v → (t) перпендикулярен вектору положения r → (t), r → (t), треугольники, образованные векторами положения и Δr →, Δr →, и векторами скорости и Δv → Δv → аналогичны. Кроме того, поскольку | r → (t) | = | r → (t + Δt) || r → (t) | = | r → (t + Δt) | и | v → (t) | = | v → (t + Δt) |, | v → (t) | = | v → (t + Δt) |, два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
Δvv = ΔrrΔvv = Δrr или Δv = vrΔr.Δv = vrΔr.
Рис. 4.18 (a) Частица движется по кругу с постоянной скоростью, с векторами положения и скорости в моменты времени tt и t + Δt. t + Δt. (б) Векторы скорости, образующие треугольник. Два треугольника на рисунке похожи. Вектор Δv → Δv → указывает на центр окружности в пределе Δt → 0. Δt → 0.
t + Δt. (б) Векторы скорости, образующие треугольник. Два треугольника на рисунке похожи. Вектор Δv → Δv → указывает на центр окружности в пределе Δt → 0. Δt → 0.Мы можем найти величину ускорения из
a = limΔt → 0 (ΔvΔt) = vr (limΔt → 0ΔrΔt) = v2r.a = limΔt → 0 (ΔvΔt) = vr (limΔt → 0ΔrΔt) = v2r.Направление ускорения также можно определить, отметив, что когда ΔtΔt и, следовательно, ΔθΔθ приближаются к нулю, вектор Δv → Δv → приближается к направлению, перпендикулярному v →.v →. В пределе Δt → 0, Δt → 0, Δv → Δv → перпендикулярно v → .v →. Поскольку v → v → касается окружности, ускорение dv → / dtdv → / dt указывает на центр окружности. Таким образом, частица, движущаяся по кругу с постоянной скоростью, имеет ускорение с величиной
. Направление вектора ускорения — к центру круга (рисунок 4.19). Это радиальное ускорение, которое называется центростремительным ускорением, поэтому мы даем ему индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (означает «искать») и, таким образом, принимает значение «поиск центра». ”
”
Рис. 4.19. Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении. Также показан вектор скорости, касающийся окружности.
Давайте рассмотрим несколько примеров, которые иллюстрируют относительные величины скорости, радиуса и центростремительного ускорения.
Пример 4.10
Создание ускорения 1
г Самолет летит со скоростью 134,1 м / с по прямой и разворачивается по круговой траектории на уровне земли.Каким должен быть радиус окружности для создания центростремительного ускорения 1 g на пилоте и самолете по направлению к центру круговой траектории?Стратегия
Учитывая скорость струи, мы можем найти радиус окружности в выражении для центростремительного ускорения.Решение
Установите центростремительное ускорение равным ускорению свободного падения: 9,8 м / с2 = v2 / r. 9,8 м / с2 = v2 / r.
9,8 м / с2 = v2 / r.Решая для радиуса, находим
r = (134,1 м / с) 29,8 м / с2 = 1835 м = 1.835 км.р = (134,1 м / с) 29,8 м / с2 = 1835 м = 1,835 км.Значение
Чтобы создать у пилота большее ускорение, чем g , струе придется либо уменьшить радиус своей круговой траектории, либо увеличить свою скорость по существующей траектории, либо и то, и другое.Проверьте свое понимание 4.5
Радиус маховика 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение 900,0 см / с2? 900,0 см / с2?
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны круговой траектории.Типичные центростремительные ускорения приведены в следующей таблице.
| Объект | Центростремительное ускорение (м / с 2 или коэффициент г ) |
|---|---|
| Земля вокруг Солнца | 5,93 × 10–35,93 × 10–3 |
| Луна вокруг Земли | 2,73 × 10–32,73 × 10–3 |
| Спутник на геостационарной орбите | 0,233 |
| Внешний край компакт-диска при воспроизведении | 5.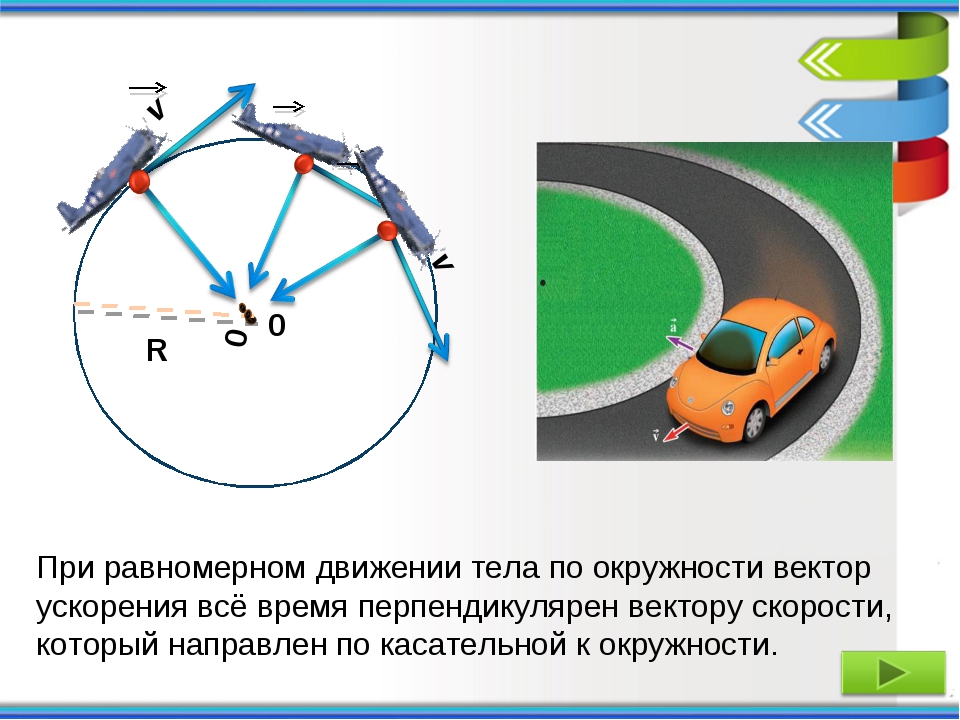 785,78 785,78 |
| Струя в бочке рулона | (2–3 г ) |
| Американские горки | (5 г ) |
| Электрон, вращающийся вокруг протона в простой модели атома Бора | 9,0 × 10 22 9,0 × 1022 |
Таблица 4.1 Типичные центростремительные ускорения
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана ее вектором положения r → (t).r → (t). На рис. 4.20 показана частица, совершающая круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения сметает угол θθ с осью x- . ..
..
4,28
Здесь ωω — постоянная, называемая угловой частотой частицы. Угловая частота измеряется в радианах (рад) в секунду и представляет собой просто количество радианов угловой меры, через которую проходит частица за секунду. Угол θθ, который имеет вектор положения в любой конкретный момент времени, равен ωtωt.
Если T — период движения или время, чтобы совершить один оборот (2π2π рад), то
Рис. 4.20. Вектор положения частицы, движущейся по кругу, с ее компонентами по осям x и y ..4,30
Из этого уравнения мы видим, что вектор ускорения имеет величину Aω2Aω2 и направлен против вектора положения, к началу координат, поскольку a → (t) = — ω2r → (t) .a → (t) = — ω2r → (t ).
Пример 4.11
Круговое движение протона
Протон имеет скорость 5 × 106 м / с5 × 106 м / с и движется по кругу в плоскости xy с радиусом r = 0,175 м. Каково его положение в плоскости xy в момент времени t = 2,0 × 10–7 с = 200 нс? T = 2,0 × 10–7 с = 200 нс? При t = 0 положение протона равно 0.м.
Каково его положение в плоскости xy в момент времени t = 2,0 × 10–7 с = 200 нс? T = 2,0 × 10–7 с = 200 нс? При t = 0 положение протона равно 0.м.Из этого результата мы видим, что протон расположен немного ниже оси x . Это показано на рисунке 4.21.
Рисунок 4.21. Вектор положения протона при t = 2,0 × 10–7 с = 200 нс. T = 2,0 × 10–7 с = 200 нс. Показана траектория протона. Угол, под которым протон движется по окружности, составляет 5,712 рад, что немного меньше одного полного оборота.Значение
Мы выбрали начальное положение частицы по оси x- . Это было совершенно произвольно.Если бы была дана другая начальная позиция, у нас была бы другая конечная позиция на t = 200 нс.Неравномерное круговое движение
Круговое движение не обязательно должно иметь постоянную скорость. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а круг имеет фиксированный радиус. Если скорость частицы тоже меняется, то мы вводим дополнительное ускорение в направлении, касательном к окружности.Такие ускорения происходят в точке на вершине, которая изменяет скорость вращения, или в любом ускоряющем роторе. В работе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы изменяется, то она имеет тангенциальное ускорение, которое представляет собой временную скорость изменения величины скорости:
aT = d | v → | dt.aT = d | v → | dt.4,31
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения радиально внутрь к центру окружности.Таким образом, частица, движущаяся по кругу с тангенциальным ускорением, имеет полное ускорение, которое является векторной суммой центростремительного и тангенциального ускорений:
а → = а → с + а → Т. а → = а → с + а → Т.
а → = а → с + а → Т.4,32
Векторы ускорения показаны на рисунке 4.22. Обратите внимание, что два вектора ускорения a → ca → c и a → Ta → T перпендикулярны друг другу, причем a → ca → c в радиальном направлении и a → Ta → T в тангенциальном направлении. Общее ускорение a → a → указывает под углом между a → ca → c и a → T.а → Т.
Рис. 4.22. Центростремительное ускорение указывает на центр круга. Тангенциальное ускорение является касательным к окружности в месте расположения частицы. Общее ускорение — это векторная сумма тангенциального и центростремительного ускорений, которые перпендикулярны.
Пример 4.12
Полное ускорение при круговом движении
Частица движется по окружности радиуса r = 2,0 м. За промежуток времени от t до = 1.От 5 с до т = 4,0 с его скорость меняется со временем в зависимости от v (t) = c1-c2t2, c1 = 4,0 м / с, c2 = 6,0 м · с. v (t) = c1-c2t2, c1 = 4,0 м / с, c2 = 6,0 м · с.
v (t) = c1-c2t2, c1 = 4,0 м / с, c2 = 6,0 м · с.Каково полное ускорение частицы при t = 2,0 с?
Стратегия
Нам даны скорость частицы и радиус круга, поэтому мы можем легко вычислить центростремительное ускорение. Направление центростремительного ускорения — к центру круга. Мы находим величину тангенциального ускорения, взяв производную по времени от | v (t) || v (t) | используя уравнение 4.31 и оценивая его как t = 2,0 с. Мы используем это и величину центростремительного ускорения, чтобы найти полное ускорение.Решение
Центростремительное ускорение v (2,0 с) = (4,0-6,0 (2,0) 2) м / с = 2,5 м / с v (2,0 с) = (4,0-6,0 (2,0) 2) м / с = 2,5 м / с ac = v2r = (2,5 м / с) 22,0 м = 3,1 м / с2 ac = v2r = (2,5 м / с) 22,0 м = 3,1 м / с2направлено к центру круга. Касательное ускорение
aT = | dv → dt | = 2c2t3 = 12,0 (2,0) 3 м / с2 = 1,5 м / с2. aT = | dv → dt | = 2c2t3 = 12,0 (2,0) 3 м / с2 = 1,5 м / с2.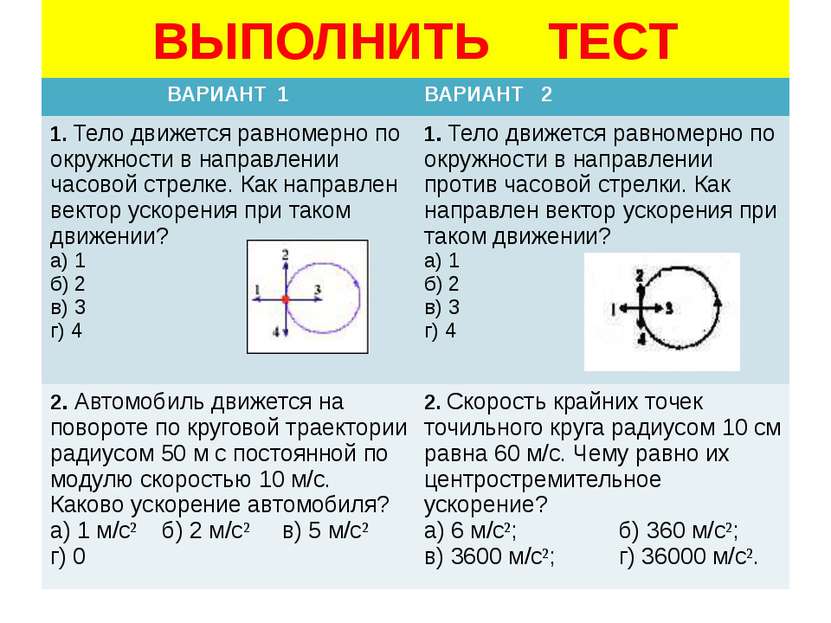
Суммарное ускорение
| а → | = 3.12 + 1,52 м / с2 = 3,44 м / с2 | a → | = 3,12 + 1,52 м / с2 = 3,44 м / с2и θ = tan − 13.11.5 = 64 ° θ = tan − 13.11.5 = 64 ° от касательной к окружности. См. Рисунок 4.23.
Рис. 4.23. Векторы тангенциального и центростремительного ускорения. Чистое ускорение a → a → — это векторная сумма двух ускорений.Значение
Направления центростремительного и тангенциального ускорений можно описать более удобно в терминах полярной системы координат с единичными векторами в радиальном и тангенциальном направлениях.Эта система координат, которая используется для движения по криволинейным траекториям, подробно обсуждается далее в книге.6.2 Равномерное круговое движение — Физика
Задачи обучения секции
К концу этого раздела вы сможете делать следующее:
- Описывать центростремительное ускорение и связывать его с линейным ускорением
- Опишите центростремительную силу и свяжите ее с линейной силой
- Решение проблем, связанных с центростремительным ускорением и центростремительной силой
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.
 Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.
- (D) вычислить влияние сил на объекты, включая закон инерции, соотношение между силой и ускорением и характер пар сил между объектами.
Кроме того, Руководство лаборатории по физике для старших классов рассматривает содержание этого раздела лаборатории под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.
Раздел Основные термины
Центростремительное ускорение
Поддержка учителя
Поддержка учителя
[BL] [OL] Проверьте равномерное круговое движение.Попросите учащихся привести примеры кругового движения. Проверьте линейное ускорение.
В предыдущем разделе мы определили круговое движение. Простейшим случаем кругового движения является равномерное круговое движение, когда объект движется по круговой траектории с постоянной скоростью . Обратите внимание, что, в отличие от скорости, линейная скорость объекта при круговом движении постоянно меняется, потому что он всегда меняет направление. Из кинематики мы знаем, что ускорение — это изменение скорости либо по величине, либо по направлению, либо по обоим направлениям.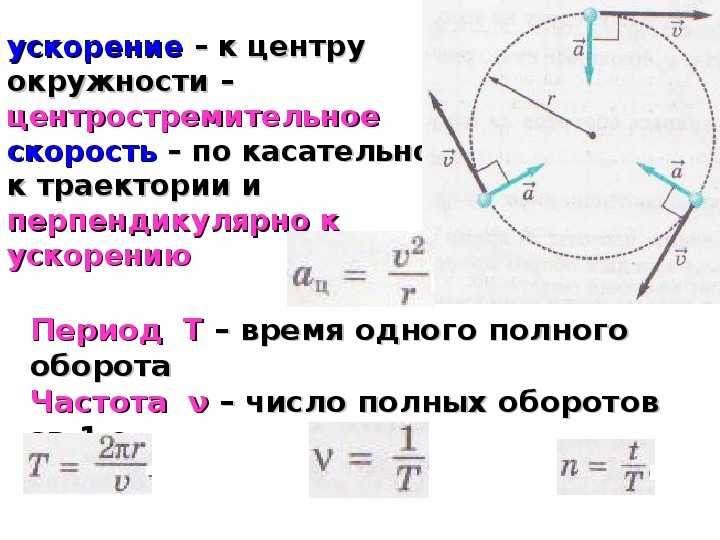 Следовательно, объект, совершающий равномерное круговое движение, всегда ускоряется, даже если величина его скорости постоянна.
Следовательно, объект, совершающий равномерное круговое движение, всегда ускоряется, даже если величина его скорости постоянна.
Вы сами испытываете это ускорение каждый раз, когда едете в машине на повороте. Если во время поворота удерживать рулевое колесо неподвижно и двигаться с постоянной скоростью, вы совершаете равномерное круговое движение. Вы замечаете ощущение скольжения (или отбрасывания, в зависимости от скорости) от центра поворота. На вас действует не настоящая сила — это происходит только потому, что ваше тело хочет продолжать движение по прямой линии (согласно первому закону Ньютона), в то время как машина сворачивает с этой прямой линии.Внутри машины создается впечатление, что вас оттесняют от центра поворота. Эта фиктивная сила известна как центробежная сила. Чем резче кривая и чем выше ваша скорость, тем заметнее становится этот эффект.
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Продемонстрируйте круговое движение, привязывая груз к веревке и вращая ее. Спросите студентов, что произойдет, если вы внезапно перережете веревку? В каком направлении движется объект? Почему? Что это говорит о направлении ускорения? Попросите студентов привести примеры, когда они столкнулись с центростремительным ускорением.
Спросите студентов, что произойдет, если вы внезапно перережете веревку? В каком направлении движется объект? Почему? Что это говорит о направлении ускорения? Попросите студентов привести примеры, когда они столкнулись с центростремительным ускорением.
На рис. 6.7 показан объект, движущийся по круговой траектории с постоянной скоростью. Направление мгновенной тангенциальной скорости показано в двух точках на пути. Ускорение происходит в направлении изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре круговой траектории). Если мы представим, что ΔsΔs становится все меньше и меньше, тогда ускорение будет указывать точно на в сторону центра вращения, но этот случай трудно изобразить.Мы называем ускорение объекта, движущегося в равномерном круговом движении, центростремительным ускорением a c , потому что центростремительное означает поиск центра .
Поддержка учителей
Поддержка учителей
Обратите внимание на рисунок 6.7. На рисунке показан объект, движущийся по круговой траектории с постоянной скоростью, и направление мгновенной скорости двух точек на траектории. Ускорение происходит в направлении изменения скорости и указывает на центр вращения. Это строго верно только при стремлении ΔsΔs к нулю.
Теперь, когда мы знаем, что центростремительное ускорение направлено к центру вращения, давайте обсудим величину центростремительного ускорения. Для объекта, движущегося со скоростью v по круговой траектории с радиусом r , величина центростремительного ускорения составляет
Для объекта, движущегося со скоростью v по круговой траектории с радиусом r , величина центростремительного ускорения составляет
Центростремительное ускорение больше на высоких скоростях и на крутых поворотах (меньший радиус), как вы могли заметить при вождении автомобиля, потому что автомобиль фактически толкает вас к центру поворота.Но немного удивительно, что a c пропорционально квадрату скорости. Это означает, например, что при повороте на 100 км / ч ускорение в четыре раза больше, чем при 50 км / ч.
Мы также можем выразить a c через величину угловой скорости. Подставляя v = rωv = rω в приведенное выше уравнение, получаем ac = (rω) 2r = rω2ac = (rω) 2r = rω2. Следовательно, величина центростремительного ускорения с точки зрения величины угловой скорости составляет
Советы для успеха
Уравнение, выраженное в форме a c = rω 2 , полезно для решения задач, где вам известна угловая скорость, а не тангенциальная скорость.
Виртуальная физика
Движение божьей коровки в 2D
В этом моделировании вы экспериментируете с положением, скоростью и ускорением божьей коровки при круговом и эллиптическом движении. Переключите тип движения с линейного на круговое и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.
Проверка захвата
Какой угол между ускорением и скоростью при равномерном круговом движении? Какое ускорение испытывает тело при равномерном круговом движении?
- Угол между ускорением и скоростью равен 0 °, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью равен 0 °, и тело испытывает центростремительное ускорение.
- Угол между ускорением и скоростью составляет 90 °, и тело испытывает линейное ускорение.

- Угол между ускорением и скоростью составляет 90 °, и тело испытывает центростремительное ускорение.
Центростремительная сила
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Используя ту же демонстрацию, что и раньше, попросите учащихся предсказать взаимосвязь между величинами угловой скорости, центростремительного ускорения, массы, центростремительной силы.Предложите студентам поэкспериментировать, используя веревки разной длины и веса.
Поскольку объект, находящийся в равномерном круговом движении, испытывает постоянное ускорение (за счет изменения направления), мы знаем из второго закона движения Ньютона, что на объект должна действовать постоянная чистая внешняя сила.
Любая сила или комбинация сил могут вызвать центростремительное ускорение. Вот лишь несколько примеров: натяжение веревки на тросе, сила притяжения Земли на Луне, трение между дорогой и шинами автомобиля при движении по кривой или обычная сила американских горок. следите за тележкой во время петли.
следите за тележкой во время петли.
Любая чистая сила, вызывающая равномерное круговое движение, называется центростремительной силой. Направление центростремительной силы — к центру вращения, такое же, как и для центростремительного ускорения. Согласно второму закону движения Ньютона, чистая сила вызывает ускорение массы согласно F net = м a . Для равномерного кругового движения ускорение является центростремительным: a = a c . Следовательно, величина центростремительной силы F c равна Fc = macFc = mac.
Используя две разные формы уравнения для величины центростремительного ускорения, ac = v2 / rac = v2 / r и ac = rω2ac = rω2, мы получаем два выражения, включающих величину центростремительной силы F c . Первое выражение относится к тангенциальной скорости, второе — к угловой скорости: Fc = mv2rFc = mv2r и Fc = mrω2Fc = mrω2.
Обе формы уравнения зависят от массы, скорости и радиуса круговой траектории. Вы можете использовать любое более удобное выражение для центростремительной силы.Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и чистая сила. По определению центростремительная сила направлена к центру вращения, поэтому объект также будет ускоряться к центру. Прямая линия, проведенная от кругового пути к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание: если вы решите первое выражение для r , вы получите
Из этого выражения мы видим, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть резкую кривую.
Рисунок 6.8 На этом рисунке сила трения f служит центростремительной силой F c . Центростремительная сила перпендикулярна тангенциальной скорости и вызывает равномерное круговое движение. Чем больше центростремительная сила F c , тем меньше радиус кривизны r и тем круче кривизна. Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F c дает меньший радиус r’r ‘.
Чем больше центростремительная сила F c , тем меньше радиус кривизны r и тем круче кривизна. Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F c дает меньший радиус r’r ‘.Watch Physics
Центростремительная сила и ускорение Intuition
В этом видео объясняется, почему центростремительная сила создает центростремительное ускорение и равномерное круговое движение. Он также охватывает разницу между скоростью и скоростью и показывает примеры равномерного кругового движения.
Поддержка учителей
Предупреждение о неправильном представлении
Поддержка учителей
Некоторые студенты могут запутаться между центростремительной силой и центробежной силой. Центробежная сила — это не реальная сила, а результат ускоряющейся системы отсчета, такой как вращающийся автомобиль или вращающаяся Земля. Центробежная сила относится к вымышленному центру , убегающему от силы .
Центробежная сила относится к вымышленному центру , убегающему от силы .
Проверка захвата
Представьте, что вы качаете йо-йо по вертикальному кругу по часовой стрелке перед собой, перпендикулярно направлению, в котором вы смотрите. А теперь представьте, что струна рвется, когда йойо достигает самого нижнего положения, ближайшего к полу. Что из следующего описывает путь йо-йо после разрыва струны?
- Йо-йо полетит вверх в направлении центростремительной силы.
- Йо-йо полетит вниз в направлении центростремительной силы.
- Йо-йо полетит влево в направлении тангенциальной скорости.
- Йойо полетит вправо в направлении тангенциальной скорости.
Решение проблем центростремительного ускорения и центростремительной силы
Чтобы получить представление о типичных величинах центростремительного ускорения, мы проведем лабораторию по оценке центростремительного ускорения теннисной ракетки, а затем, в нашем первом рабочем примере, сравним центростремительное ускорение автомобиля, огибающего кривую, с ускорением свободного падения. Для второго рабочего примера мы вычислим силу, необходимую для поворота автомобиля на повороте.
Для второго рабочего примера мы вычислим силу, необходимую для поворота автомобиля на повороте.
Snap Lab
Оценка центростремительного ускорения
В этом упражнении вы будете измерять качание клюшки для гольфа или теннисной ракетки, чтобы оценить центростремительное ускорение конца клюшки или ракетки. Вы можете сделать это в замедленном режиме. Напомним, что уравнение для центростремительного ускорения имеет вид ac = v2rac = v2r или ac = rω2ac = rω2.
- Одна теннисная ракетка или клюшка для гольфа
- Один таймер
- Одна линейка или рулетка
Порядок действий
- Работа с партнером.Стойте на безопасном расстоянии от вашего партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.
- Опишите движение качелей — это равномерное круговое движение? Почему или почему нет?
- Постарайтесь сделать свинг как можно ближе к равномерному круговому движению.
 Какие корректировки пришлось внести вашему партнеру?
Какие корректировки пришлось внести вашему партнеру? - Измерьте радиус кривизны. Что вы измерили физически?
- Используя таймер, найдите либо линейную, либо угловую скорость, в зависимости от того, какое уравнение вы решите использовать.
- Каково примерное центростремительное ускорение на основе этих измерений? Как вы думаете, насколько они точны? Почему? Как вы и ваш партнер можете сделать эти измерения более точными?
Поддержка учителя
Поддержка учителя
Удар клюшки или ракетки может быть очень близок к равномерному круговому движению. Для этого человек должен перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки — это радиус кривизны.Точность измерения угловой скорости и углового ускорения будет зависеть от разрешения используемого таймера и ошибки наблюдения человека. Размах клюшки или ракетки может быть очень близок к равномерному круговому движению.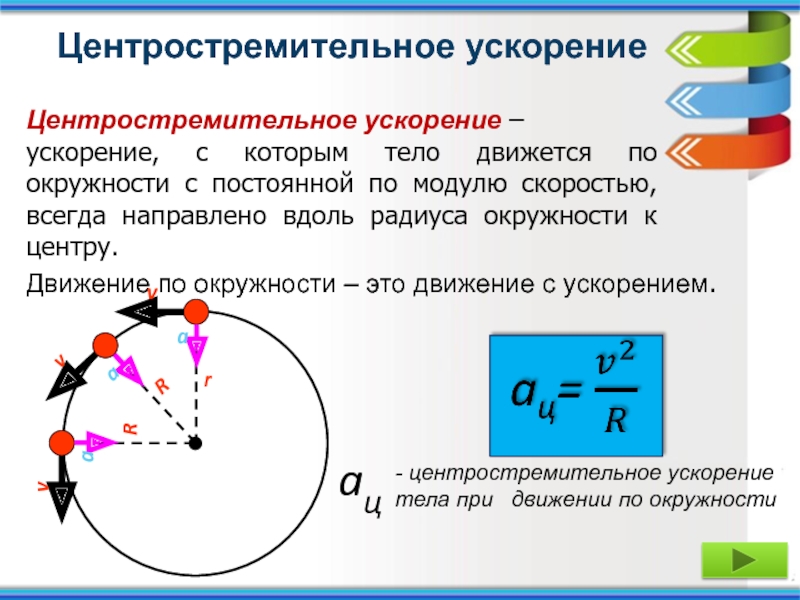 Для этого человек должен перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки — это радиус кривизны. Точность измерения угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки наблюдения человека.
Для этого человек должен перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки — это радиус кривизны. Точность измерения угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки наблюдения человека.
Проверка захвата
Было ли более полезным использовать в этом упражнении уравнение ac = v2rac = v2r или ac = rω2ac = rω2? Почему?
- Должно быть проще использовать ac = rω2ac = rω2, потому что измерение угловой скорости путем наблюдения было бы проще.
- Должно быть проще использовать ac = v2rac = v2r, потому что измерение тангенциальной скорости посредством наблюдения было бы проще.
- Должно быть проще использовать ac = rω2ac = rω2, потому что измерение угловой скорости путем наблюдения было бы затруднительно.
- Должно быть проще использовать ac = v2rac = v2r, потому что измерение тангенциальной скорости посредством наблюдения было бы затруднительно.

Рабочий пример
Сравнение центростремительного ускорения автомобиля, огибающего кривую, с ускорением под действием силы тяжести
Автомобиль следует по кривой радиусом 500 м со скоростью 25,0 м / с (около 90 км / ч). Какова величина центростремительного ускорения автомобиля? Сравните центростремительное ускорение для этой довольно пологой кривой, снятой на скорости шоссе, с ускорением свободного падения ( g ).
Стратегия
Поскольку дана линейная, а не угловая скорость, наиболее удобно использовать выражение ac = v2rac = v2r, чтобы найти величину центростремительного ускорения.
Решение
Ввод данных значений v = 25,0 м / с и r = 500 м в выражение для a c дает
ac = v2r = (25,0 м / с) 2500 м = 1,25 м / с 2. ac = v2r = (25,0 м / с) 2500 м = 1,25 м / с2.
Обсуждение
Для сравнения с ускорением свободного падения ( g = 9.80 м / с 2 ), берем соотношение ac / g = (1,25 м / с2) / (9,80 м / с2) = 0,128 ac / g = (1,25 м / с2) / (9,80 м / с2) = 0,128. Следовательно, ac = 0,128gac = 0,128g, что означает, что центростремительное ускорение составляет примерно одну десятую ускорения свободного падения.
Рабочий пример
Сила трения на шинах автомобиля, огибающих кривую
- Рассчитайте центростремительную силу, действующую на автомобиль массой 900 кг, который движется по кривой радиусом 600 м на горизонтальной поверхности со скоростью 25,0 м / с.
- Статическое трение предотвращает скольжение автомобиля.Найдите величину силы трения между шинами и дорогой, которая позволяет автомобилю обогнуть поворот, не соскальзывая по прямой.

Стратегия и решение для (а)
Мы знаем, что Fc = mv2rFc = mv2r. Следовательно,
Fc = mv2r = (900 кг) (25,0 м / с) 2600 м = 938 Н. Fc = mv2r = (900 кг) (25,0 м / с) 2600 м = 938 Н.Стратегия и решение для (b)
На изображении выше показаны силы, действующие на автомобиль при повороте кривой. На этой схеме автомобиль движется по странице, как показано, и поворачивает налево.Трение действует влево, ускоряя автомобиль к центру поворота. Поскольку трение — единственная горизонтальная сила, действующая на автомобиль, в этом случае оно обеспечивает всю центростремительную силу. Следовательно, сила трения в этой ситуации является центростремительной силой и направлена к центру кривой.
Обсуждение
Поскольку мы нашли силу трения в части (b), мы также можем решить для коэффициента трения, поскольку f = μsN = μsmgf = μsN = μsmg.
Практические задачи
9.Каково центростремительное ускорение объекта со скоростью 12 м / с, движущегося по траектории радиусом 2,0 м?
- 6 м / с
- 72 м / с
- 6 м / с2
- 72 м / с2

Вычислить центростремительное ускорение объекта, движущегося по траектории с радиусом кривизны 0,2 м и угловой скоростью 5 рад / с.
- 1 м / с
- 5 м / с
- 1 м / с 2
- 5 м / с 2
Проверьте свое понимание
11.Что такое равномерное круговое движение?
- Равномерное круговое движение — это когда объект ускоряется по круговой траектории с постоянно увеличивающейся скоростью.
- Равномерное круговое движение — это когда объект движется по круговой траектории с переменным ускорением.
- Равномерное круговое движение — это когда объект движется по круговой траектории с постоянной скоростью.
- Равномерное круговое движение — это когда объект движется по круговой траектории с переменной скоростью.

Что такое центростремительное ускорение?
- Ускорение объекта, движущегося по круговой траектории и направленного радиально к центру круговой орбиты
- Ускорение объекта, движущегося по круговой траектории и тангенциально направленного по круговой траектории
- Ускорение объекта, движущегося по линейной траектории и направленного в направлении движения объекта
- Ускорение объекта, движущегося по линейной траектории и направленного в направлении, противоположном движению объекта
Существует ли чистая сила, действующая на объект при равномерном круговом движении?
- Да, объект ускоряется, поэтому на него должна действовать чистая сила.
- Да потому что разгона нет.
- Нет, потому что ускорение есть.
- Нет, потому что разгона нет.
Укажите два примера сил, которые могут вызвать центростремительное ускорение.
- Сила притяжения Земли на Луну и нормальная сила
- Сила притяжения Земли на Луну и натяжение веревки на вращающемся тезерболе
- Нормальная сила и сила трения, действующие на движущийся автомобиль
- Нормальная сила и натяжение веревки на тезерболе
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, усвоили ли учащиеся учебные цели этого раздела.Если учащимся не удается решить конкретную задачу, формирующая оценка поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
Круговое движение — Высшая школа физики
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Практические задачи: решения для равномерного кругового движения C
Практические задачи: решения для равномерного кругового движения
1. (средний) Гоночный автомобиль, движущийся с постоянной тангенциальной скоростью 60 м / с, делает один круг по круговой трассе за 50 секунд.Определите величину ускорения автомобиля.
(средний) Гоночный автомобиль, движущийся с постоянной тангенциальной скоростью 60 м / с, делает один круг по круговой трассе за 50 секунд.Определите величину ускорения автомобиля.
a = v 2 / r
T = 2πr / v ….. r = Tv / 2π
объединить … a = v 2 / (Tv / 2π) = v / (T / 2π)
a = (60) / (50 / 6,28) = 7,5 м / с 2
2. (умеренный) Объект, который движется равномерно по кругу, имеет центростремительное ускорение 13 м / с. 2 . Если радиус движения 0,02 м, какова частота движения?
a = v 2 / r
13 = v 2 / 0,02
v = 0.51 м / с
v = 2πr / T
0,51 = 6,28 (0,02) / T
T = 0,25 с
f = 1 / T
f = 1 / (0,25) = 4 Гц
3. (легко) Найдите центростремительное ускорение для объекта на поверхности планеты (на экваторе) со следующими характеристиками: радиус = r = 4×10 6 м и 1 день = 100000 секунд.
a = v 2 / r = (2πr / T) 2 / r = 4π 2 r / T 2
a = 4 (3,14) 2 (4×10 6 ) / (100000 ) 2 = 0,016 м / с 2
4. (умеренно) Для объекта, находящегося в равномерном круговом движении, ранжируют изменения, перечисленные ниже как
(умеренно) Для объекта, находящегося в равномерном круговом движении, ранжируют изменения, перечисленные ниже как
в отношении влияния каждого из них на величину центростремительного ускорения объекта
? Предположим, что все остальные параметры остаются неизменными
, за исключением указанного в описании изменения.
Изменение A: скорость объекта удваивается
Изменение B: радиус движения увеличивается втрое
Изменение C: масса объекта увеличивается в три раза
Изменение D: радиус движения становится вдвое меньше
Изменение E: масса объекта объект становится вдвое меньше
Изменение F: скорость объекта становится вдвое меньше
Поскольку a = v 2 / r, масса не влияет на величину ускорения
, пока скорость и радиус остаются равными одно и тоже.Конечно, объект
нужно было бы заставить по-другому, чтобы сохранить скорость такой же, если масса изменится.
Мы обсудим эту концепцию, когда рассмотрим закон Ньютона 2 и .
Изменение A: ускорение увеличивается в четыре раза
Изменение B: ускорение становится на 1/3 меньше
Изменение C: ускорение не изменяется
Изменение D: ускорение удваивается
Изменение E: ускорение не изменяется
Изменение F: Ускорение становится в четыре раза меньше
Изменение F <Изменение B <Изменение C = Изменение E <Изменение D <Изменение A
5.(умеренный) Опишите процедуру, с помощью которой можно определить центростремительное ускорение автомобиля, движущегося с постоянной скоростью по круговой гоночной трассе. Составьте список стандартных лабораторных устройств, необходимых для проведения измерений, и вычислений, которые студент может сделать с измерениями для определения ускорения. Кроме того, определите диапазон ошибок, внесенных в окончательный ответ, если каждое измерение может иметь ошибку 10%. Этот тип вопросов очень важен для подготовки к экзамену. Пожалуйста, не торопитесь и ответьте на него полностью.
Необходимые измерительные приборы:
Длинная измерительная лента
Секундомер
Шаг 1: Используйте измерительную ленту, чтобы определить радиус (r) траектории автомобиля
на круговой гоночной трассе. Смоделируйте автомобиль как точечную частицу. Используйте геометрический центр автомобиля
Смоделируйте автомобиль как точечную частицу. Используйте геометрический центр автомобиля
в качестве местоположения этой точки.
Шаг 2: Используйте секундомер, чтобы определить время (T), необходимое автомобилю, чтобы один раз пройти
по трассе.
Расчеты:
скорость = v = 2πr / T
Определите ускорение: a = v 2 / r = (2πr / T) 2 / r = 4π 2 r / T 2
Поскольку каждое измерение имеет возможную ошибку 10%, в наихудшем случае
будет, если измерение радиуса будет на 10% больше, а время измерения
будет на 10% меньше.
Пример:
Если фактический радиус составляет 10,0 м, а измерение радиуса составляет 11,0 м
Если фактическое время составляет 10,0 с, а измерение времени составляет 9,0 с
Фактическое ускорение = a = 4π 2 (10,0) / (10,0) 2 = 0,40π 2 м / с 2
Измеренное ускорение = a м = 4π 2 (11,0) / (9,0) 2 = 0,54π 2 м / с 2
% Ошибка = [(Измеренное — Фактическое) / Фактическое] 100%%
Ошибка = [(0. 54π 2 — 0.40π 2 ) /0.40π 2 ] 100% = +35%
54π 2 — 0.40π 2 ) /0.40π 2 ] 100% = +35%
В результате этих измерений ответ будет на 35% больше. Это самая большая ожидаемая ошибка
, которая слишком велика.
Однако можно определить и слишком низкий ответ. Это происходит на максимальном уровне, когда радиус на 10% меньше, а измерение времени на 10% больше:
Пример:
Если фактический радиус составляет 10,0 м, а измерение радиуса составляет 9,0 м
Если фактическое время составляет 10,0 с а измерение времени — 11.0 с
Фактическое ускорение = a = 4π 2 (10,0) / (10,0) 2 = 0,40π 2 м / с 2
Измеренное ускорение = a м = 4π 2 (9,0) /(11.0) 2 = 0,30π 2 м / с 2
% Погрешность = [(Измеренное — Фактическое) / Фактическое] 100%
% Погрешность = [(0,30π 2 — 0,40π 2 ) /0,40π 2 ] 100% = -25%
Когда встречаются другие крайние значения, ошибка в% находится между расчетами, указанными выше
.
Пример:
Если фактический радиус составляет 10,0 м, а измерение радиуса составляет 11,0 м
Если фактическое время составляет 10,0 с, а измерение времени составляет 11,0 с
Фактическое ускорение = a = 4π 2 (10,0) / (10,0) 2 = 0,40π 2 м / с 2
Измеренное ускорение = a м = 4π 2 (11,0) / (11,0) 2 = 0,36π 2 м / с 2
% Ошибка = [(Измеренное — Фактическое) / Фактическое] 100%
% Ошибка = [(0,36π 2 — 0.40π 2 ) /0,40 2 ] 100% = -10%
Пример:
Если фактический радиус составляет 10,0 м, а измерение радиуса составляет 9,0 м.
Если фактическое время составляет 10,0 с, а измерение времени составляет 9,0 с.
Фактическое ускорение = a = 4π 2 (10,0) / (10,0) 2 = 0,40π 2 м / с 2
Измеренное ускорение = a м = 4π 2 (11,0) / ( 11,0) 2 = 0,44π 2 м / с 2
% Ошибка = [(Измеренное — Фактическое) / Фактическое] 100%
% Ошибка = [(0. 44π 2 — 0,40π 2 ) /0,40π 2 ] 100% = +10%
44π 2 — 0,40π 2 ) /0,40π 2 ] 100% = +10%
Когда измерения не достигают крайних значений, ошибка в% снова упадет в
между максимальным положительным и максимальным отрицательным значениями.
Пример:
Если фактический радиус составляет 10,0 м, а измерение радиуса составляет 10,5 м
Если фактическое время составляет 10,0 с, а измерение времени составляет 9,5 с
Фактическое ускорение = a = 4π 2 (10,0) / (10,0) 2 = 0,40π 2 м / с 2
Измеренное ускорение = a м = 4π 2 (10.5) / (9,5) 2 = 0,47π 2 м / с 2
% Ошибка = [(Измеренное — Фактическое) / Фактическое] 100%
% Погрешность = [(0,47π 2 — 0,40π 2 ) /0,40π 2 ] 100% = +18%
6. (средний) Частица движется с постоянной скоростью по круговой траектории с центром в начале системы координат xy. В одной точке (x = 4 м, y = 0 м) частица имеет скорость -5,0 Дж м / с. Определите скорость и ускорение, когда частица находится в точке:
Определите скорость и ускорение, когда частица находится в точке:
a.x = 0, y = -4 м
Скорость всегда касается траектории.
v = -5 i м / с (поскольку круговое движение по системе осей происходит по часовой стрелке)
a = v 2 / r = 5 2 /4 = 6,25 м / с 2
a = 6,25 j м / с 2 (всегда направлено к центру)
b. x = -4 м, y = 0
v = 5 j м / с
Величина ускорения постоянна, поэтому мы все еще имеем a = 6,25 м / с 2
a = 6.25 i м / с 2 (всегда направлено к центру)
c. x = 0, y = 4 м
v = 5 i м / с
a = -6,25 j м / с 2
d. x = -2,83, y = 2,83 м
Скорость по-прежнему будет иметь величину 5 м / с и по-прежнему будет касательной к траектории.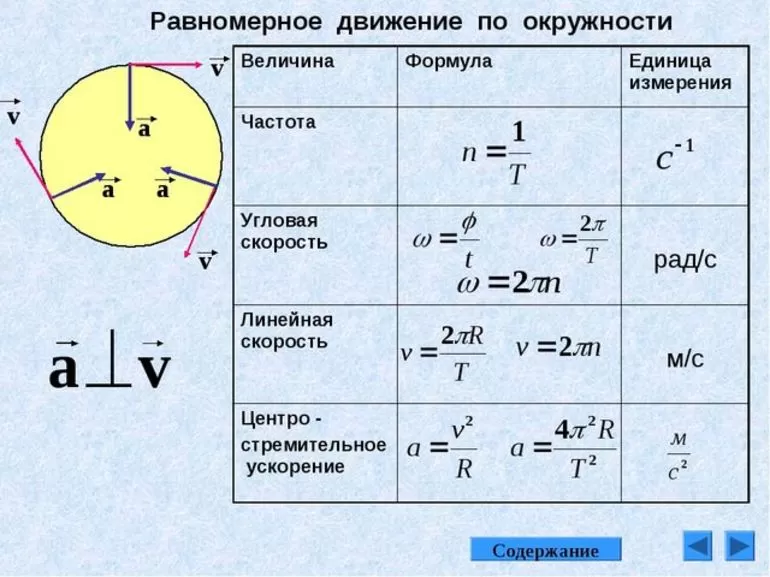 В указанной точке угол касательной составляет 45 °.
В указанной точке угол касательной составляет 45 °.
v = 5 м / с (cos45 i + sin45 j )
v = 3.54 i +3,54 j м / с
Ускорение по-прежнему будет иметь ту же величину, и опять же, оно должно быть направлено к центру. В данном случае под углом 315 °.
a = 6,25 м / с 2 (cos315 i + sin315 j )
a = 4,42 i — 4,42 j м / с 2
7. (средний) Каскадер выполняет на самолете круговую траекторию с постоянной скоростью. Начальная скорость (в м / с) самолета равна v o = 2500 i + 3000 j .Через минуту скорость самолета составит v = -2500 i — 3000 j . Найдите величину ускорения.
Сначала найдите скорость:
v = (2500 2 + 3000 2 ) ½ = 3905 м / с
Для равномерного кругового движения:
a = v 2 / r и T = 2πr / v
Объедините, чтобы показать, что a = 2πv / T
Поскольку T — это период движения, и данные сообщают, что для изменения скорости требуется одна минута (компоненты поменялись местами), период составляет 2 минуты (120 с).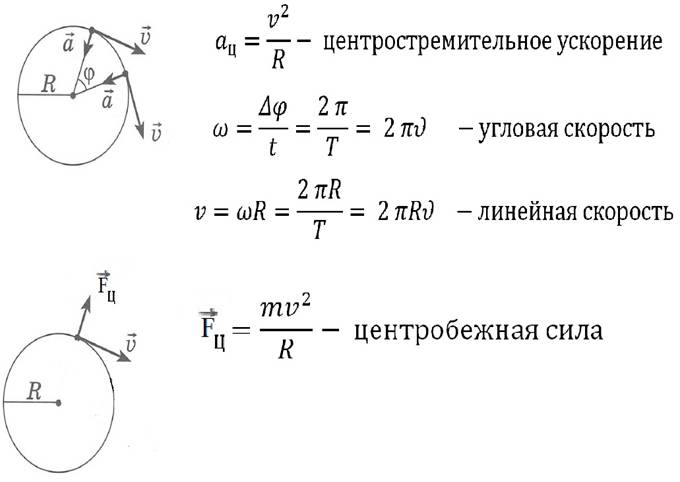
a = 2π (3905) / 120
a = 204 м / с 2
8. (умеренно) Эта проблема не относится к объекту, находящемуся в равномерном круговом движении, но имеет дело с движением в двух измерениях. Скорость (в м / с) частицы, движущейся в плоскости x-y, определяется выражением:
v = (6.0t — 4.0t 2 ) i + 8.0 j
a. Какое ускорение при t = 3,0 секунды?
a = d v / dt
a = (6.0 — 8.0t) i
a = (6.0 — 24,0) i = -18,0 i м / с 2
b. Когда, если вообще, будет нулевое ускорение?
a = 0 = 6,0 — 8,0 т
6,0 = 8,0 т
t = 6,0 / 8,0 = 0,75 с
c. Когда, если вообще, скорость будет нулем?
Скорость никогда не может быть нулевой, потому что всегда есть составляющая скорости в направлении j .
Сила и ускорение при круговом движении
Введение
Ускорение — это скорость изменения скорости во времени.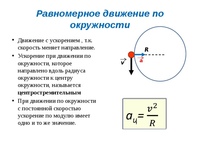 Поскольку скорость является вектором, она может изменяться двумя способами: ее величина может изменяться и ее направление может изменяться. Любое изменение вызывает ускорение. При круговом движении с постоянной скоростью скорость всегда тангенциальна к круговой траектории, и поэтому ее направление постоянно меняется, даже если ее величина постоянна. Следовательно, у объекта есть ускорение. Можно показать, что величина ускорения a c для равномерного кругового движения со скоростью v по траектории радиуса R равна, а направление ускорения — внутрь к центру круговой траектории. .Это показано на рисунке 1. Второй закон Ньютона требует, чтобы на объект действовала результирующая сила, равная по величине ma c , а в направлении a c . Круговое движение со скоростью v по траектории радиуса R имеет период (время на один оборот) T и частоту (оборотов / с)
Поскольку скорость является вектором, она может изменяться двумя способами: ее величина может изменяться и ее направление может изменяться. Любое изменение вызывает ускорение. При круговом движении с постоянной скоростью скорость всегда тангенциальна к круговой траектории, и поэтому ее направление постоянно меняется, даже если ее величина постоянна. Следовательно, у объекта есть ускорение. Можно показать, что величина ускорения a c для равномерного кругового движения со скоростью v по траектории радиуса R равна, а направление ускорения — внутрь к центру круговой траектории. .Это показано на рисунке 1. Второй закон Ньютона требует, чтобы на объект действовала результирующая сила, равная по величине ma c , а в направлении a c . Круговое движение со скоростью v по траектории радиуса R имеет период (время на один оборот) T и частоту (оборотов / с) f = 1 / T.
a c = 4 π 2 f 2 р.
Схема эксперимента показана на рис. 2. Когда пластиковая трубка перемещается по небольшому кругу над вашей головой, ракетка движется по горизонтальному кругу на конце струны, которая проходит через трубку и имеет подвес для массы с на его нижнем конце подвешены щелевые массы. ПрименениеΣF = ma
к неподвижному подвесу массы даетF струна = Mg,
, где F струна — натяжение струны, а M — сумма масс подвеса массы и массы помещенные на него щелевые массы.Из-за направленной вниз силы тяжести на мяч, когда мяч движется по горизонтальному кругу, струна находится под углом θ ниже горизонтали, как показано на рисунке 3. На рисунке L — длина струна, измеренная от центра трубки до центра шара.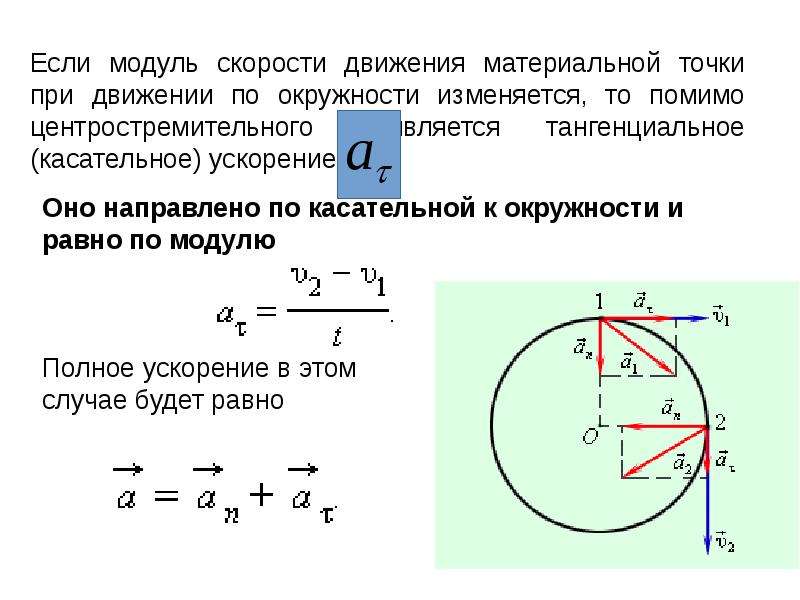 Радиус R круговой траектории шара равен
Радиус R круговой траектории шара равенR = L cos θ .
Силы, действующие на мяч, — это сила тяжести и натяжение струны. Натяжение струны направлено вдоль струны, а сила тяжести направлена прямо вниз.Схема свободного тела движущегося шара приведена на рисунке 4. Поскольку мяч движется по горизонтальной окружности, его ускорение является горизонтальным. Поэтому удобно использовать горизонтальные и вертикальные координаты, и на диаграмме сил F струна разложена на ее горизонтальную и вертикальную составляющие.ΣF x = ma x
даетF строка cos θ = ma c = m4 π 2 f 2 R.
R = L cos θ
, поэтомуF строка = m4 π 2 f 2 L.
И, начиная сF строка = Mg,
, затемMg = m4 π 2 f 2 L.
Перестановка дает следующее уравнение. f 2 =
f 2 =Цель
В этом эксперименте мы проверим выражение для ускорения объекта, движущегося равномерно по кругу.Аппарат
- Ракетбол с прикрепленной веревкой и зажимом из кожи аллигатора
- Пластиковая трубка
- Набор масс с прорезями и подвеска
- Баланс
- Секундомер
- Метрическая палочка
Обсуждение
Как обсуждалось во введении к этому эксперименту, применение второго закона Ньютона в экспериментальной установке дает следующее.(1)
f 2 = Обратите внимание, что угол θ , который струна образует с горизонталью, не появляется в уравнении.(1). Вывод уравнения. (1) предполагает, что ускорение объекта, движущегося с постоянной скоростью v по круговой траектории с радиусом R , имеет величину и направление, которые радиально внутрь к центру круговой траектории. В этом эксперименте мы измерим f для нескольких значений M и L . Мы будем использовать эти данные для проверки уравнения. (1), и, таким образом, проверить выражение для a c и наше приложение
Обратите внимание, что угол θ , который струна образует с горизонталью, не появляется в уравнении.(1). Вывод уравнения. (1) предполагает, что ускорение объекта, движущегося с постоянной скоростью v по круговой траектории с радиусом R , имеет величину и направление, которые радиально внутрь к центру круговой траектории. В этом эксперименте мы измерим f для нескольких значений M и L . Мы будем использовать эти данные для проверки уравнения. (1), и, таким образом, проверить выражение для a c и наше приложениеΣF = ma.
Мы сделаем это, построив график f 2 и проверив, хорошо ли представлены наши данные прямой линией с нулевыми интерцепциями y . Мы также будем использовать наклон линии и измерение массы м вращающегося объекта, чтобы вычислить г и посмотреть, насколько хорошо полученное таким образом значение согласуется с фактическим значением г .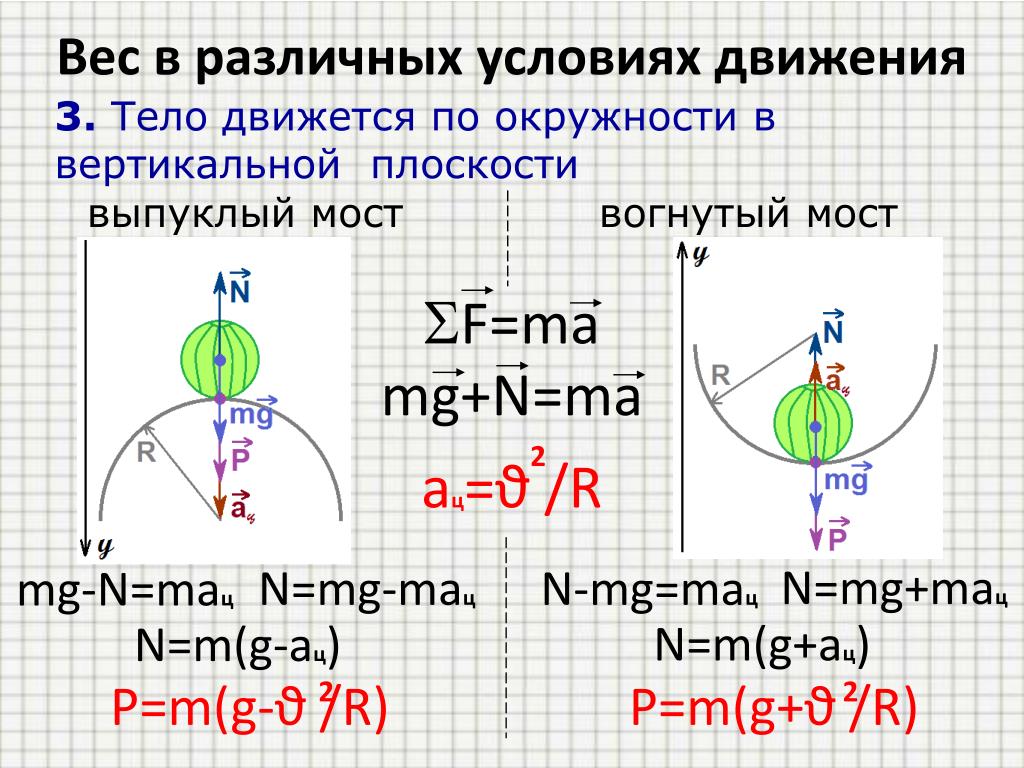
Процедура
Распечатайте лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.1
Для практики поместите гирю в 100 грамм с прорезью на подвес для масс на нижнем конце струны и покрутите ракетку над головой, удерживая струну под трубкой. Потренируйтесь вращать мяч над головой, сохраняя при этом путь мяча полностью горизонтальным, пока вы не сможете отпустить струну под трубкой и поддерживать такое же движение, пока масса не поднимается и не опускается. Это упражнение должен выполнять каждый партнер по лаборатории.2
Протяните струну через трубку так, чтобы длина L составляла 50.0 см. Напомним, что L — это расстояние от центра верхней части трубки до центра шара. Прикрепите зажим из крокодила к веревке примерно на 1 см ниже пластиковой трубки, чтобы он служил маркером, чтобы вы могли поддерживать постоянство L при вращении шара. Вращая мяч по горизонтальному кругу, следите за тем, чтобы веревка или зажим из крокодиловой кожи не касались вашей руки или руки. Перед измерением времени убедитесь, что мяч вращается по горизонтальной окружности.Затем попросите вашего партнера по лаборатории измерить время t 20 (1) , которое требуется, чтобы мяч совершил 20 оборотов. Поменяйте местами завихритель и таймер и повторите измерение, чтобы получить время t 20 (2) . Повторяйте измерения, пока не получите пару раз, которые отличаются менее чем на 2,0 секунды.
Перед измерением времени убедитесь, что мяч вращается по горизонтальной окружности.Затем попросите вашего партнера по лаборатории измерить время t 20 (1) , которое требуется, чтобы мяч совершил 20 оборотов. Поменяйте местами завихритель и таймер и повторите измерение, чтобы получить время t 20 (2) . Повторяйте измерения, пока не получите пару раз, которые отличаются менее чем на 2,0 секунды.3
Введите свои значения t 20 (1) и t 20 (2) в столбец дляM = 150 граммов
в таблице 1.Обратите внимание на это и позвольте заполнить оставшуюся часть столбца. Повторите процедуру для других наборов значений M и L . Помните, что M — это общая масса подвешенного к струне, масса подвески плюс масса грузов с прорезями, размещенных на подвеске.4
Откройте Excel и постройте график f 2 (для f в об / с) в зависимости от кг / м. Используйте Excel, чтобы найти уравнение прямой линии, которое лучше всего подходит для ваших данных.Все ваши точки данных должны находиться близко к этой линии, а пересечение линии y должно быть близко к нулю. Если одно или оба из них не соответствуют действительности, вы допустили ошибку при сборе, записи или графическом отображении ваших данных. Если вы и ваш партнер по лаборатории не можете найти, что не так, обратитесь за помощью к своему техническому специалисту.
Используйте Excel, чтобы найти уравнение прямой линии, которое лучше всего подходит для ваших данных.Все ваши точки данных должны находиться близко к этой линии, а пересечение линии y должно быть близко к нулю. Если одно или оба из них не соответствуют действительности, вы допустили ошибку при сборе, записи или графическом отображении ваших данных. Если вы и ваш партнер по лаборатории не можете найти, что не так, обратитесь за помощью к своему техническому специалисту.5
Запишите наклон линии, который лучше всего соответствует вашим данным.6
Используйте весы, чтобы измерить массу мяча. Запишите свои результаты.7
Используйте уравнение.(1) f 2 =8
Если фактическое значение г принято равным 9,80 м / с 2 , какова процентная разница между вашим экспериментальным результатом и фактическим значением г ? В расчетах оставьте достаточно значащих цифр, чтобы избежать ошибки округления.



 Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
 Какие корректировки пришлось внести вашему партнеру?
Какие корректировки пришлось внести вашему партнеру?

Leave A Comment