PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.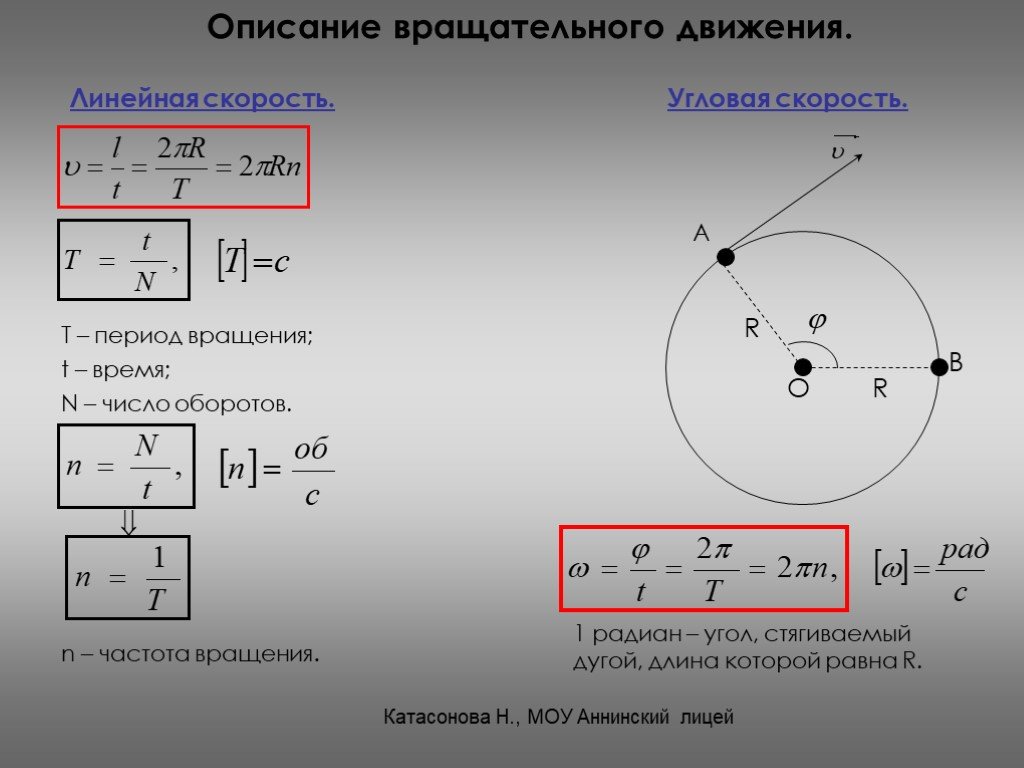
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Конспект лекции «Равнормерное6 движение точки по окружности»
«Круговое движение первичнее прямолинейного, поскольку оно проще и
более совершенно, ведь перемещаться бесконечно по прямой линии нельзя.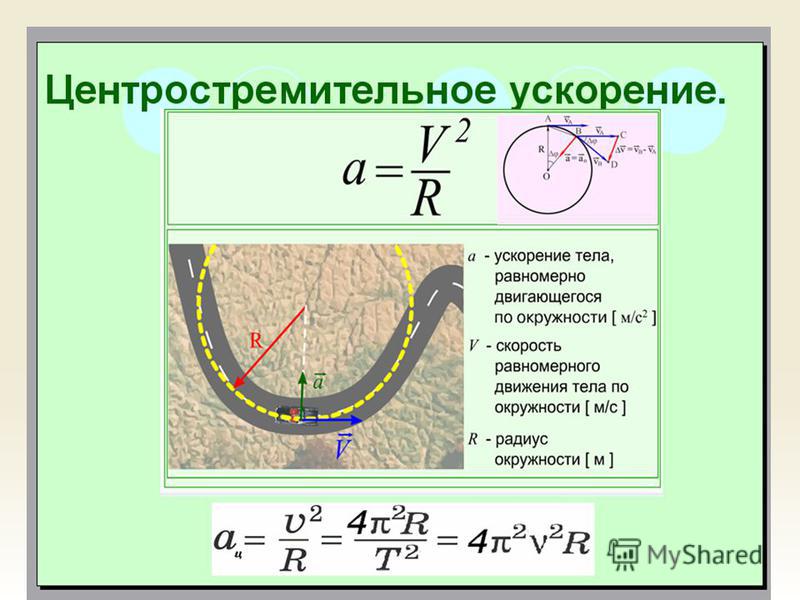
Аристотель,
древнегреческий философ,
(384-322 до н. э.)
РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
План лекции:
1. Криволинейное движение
2. Движение по окружности как периодическое движение
3. Угловая и линейная скорости
4. Центростремительное ускорение
5. Закон движения
Ранее мы рассматривали равноускоренное движение, траекторией
которого была прямая. При таком движении изменяется значение скорости, а ее
направление остается неизменным. В жизни чаще встречаются криволинейные
движения (орбитальное движение планет, повороты транспорта на дороге, карусели и т. п.), во время которых
происходят изменения направления скорости движения. Здесь проявляется векторный
характер ускорения.
По форме траектории криволинейное движение может быть достаточно разнообразным. Однако его всегда можно представить в виде последовательных участков, состоящих из отрезков прямых и дуг окружностей различного диаметра. Т. е. любое криволинейное движение является комбинацией прямолинейного движения и движения тела по окружности.
Криволинейное движение — движение, при котором траектория движущейся материальной точки в данной системе отсчета является кривой линией. В каждой точке скорость направлена по касательной к траектории. Скорость в общем случае — функция от времени и изменяется как по величине, так и по направлению (рис. 1).
В общем случае ускорение направлено под углом к скорости и также изменяется как по величине, так и по направлению. Ускорение по правилам действия над векторами можно разложить на две составляющие: в направлении скорости () и в перпендикулярном направлении (). Из рис. 1 следует, что и
Составляющую ускорения , направленную вдоль
скорости, называют тангенциальным
ускорением.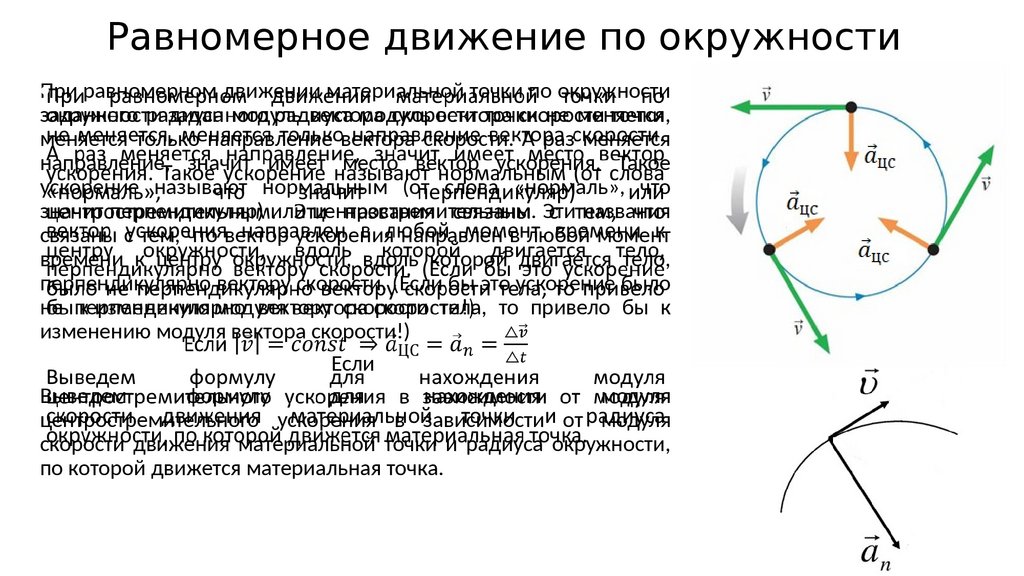 Тангенциальное
ускорение характеризует изменение скорости по величине (по модулю). Составляющую ускорения , направленную к центру кривизны
траектории, т. е. перпендикулярно скорости, называют нормальным ускорением. Нормальное ускорение характеризует изменение
скорости по направлению.
Тангенциальное
ускорение характеризует изменение скорости по величине (по модулю). Составляющую ускорения , направленную к центру кривизны
траектории, т. е. перпендикулярно скорости, называют нормальным ускорением. Нормальное ускорение характеризует изменение
скорости по направлению.
Движение тела по окружности довольно часто встречается в повседневной жизни. Взять хотя бы движение Земли вокруг своей оси или вокруг Солнца. Кроме этого существуют ещё сотни примеров: вращение колеса автомобиля, вращение электронов вокруг ядра атома, движение стрелок часов и многое другое.
Движение по окружности является простейшим примером периодического движения.
Периодическое движение — это движение, повторяющееся через определенный промежуток времени. Например, вращение Земли вокруг собственной оси, вращение Земли вокруг Солнца.
При
прямолинейном движении мы говорили о том, что тело совершает одинаковые
перемещения за равные промежутки времени.
Рассмотрим равномерное движение материальной точки по окружности. Пусть она равномерно движется по окружности радиуса и за некоторое время перемещается из точки в точку (рис. 2). Угол, который при этом описывает радиус, называется угловым перемещением.
Угловое перемещение обозначают греческой буквой (фи») и в СИ измеряют в радианах (рад). 1
Движение точки по окружности характеризуют также период вращения и
частота вращения. Период
вращения — это время, в течение которого материальная
точка совершает полный оборот по окружности, т. е. поворот на угол рад: , где — время вращения, — количество совершенных оборотов. В СИ период вращения измеряется
в секундах ().
В СИ период вращения измеряется
в секундах ().
Период вращения Земли вокруг собственной оси — 1 сутки, т. е. 24 ч. . Вследствие того, что Земля вращается вокруг собственной оси, происходит смена времени суток. Вокруг собственной оси вращаются также Луна, Солнце и планеты.
Период вращения Земли вокруг Солнца составляет 1 год, т.е. . Вследствие того, что Земля вращается вокруг Солнца, происходит смена времени года.
Частота вращения характеризует количество оборотов тела или материальной точки вокруг центра вращения за 1 секунду: , где — количество оборотов, совершенных за время . В СИ частота вращения измеряется в оборотах за секунду (об/с).
Между частотой и периодом вращения существует взаимообратная зависимость: и .
3. Угловая и линейная скоростиДля определения быстроты движения точки по окружности используют
понятие угловой скорости. Это физическая величина, равная отношению
углового перемещения к интервалу времени t, в
течение которого данное перемещение происходило: .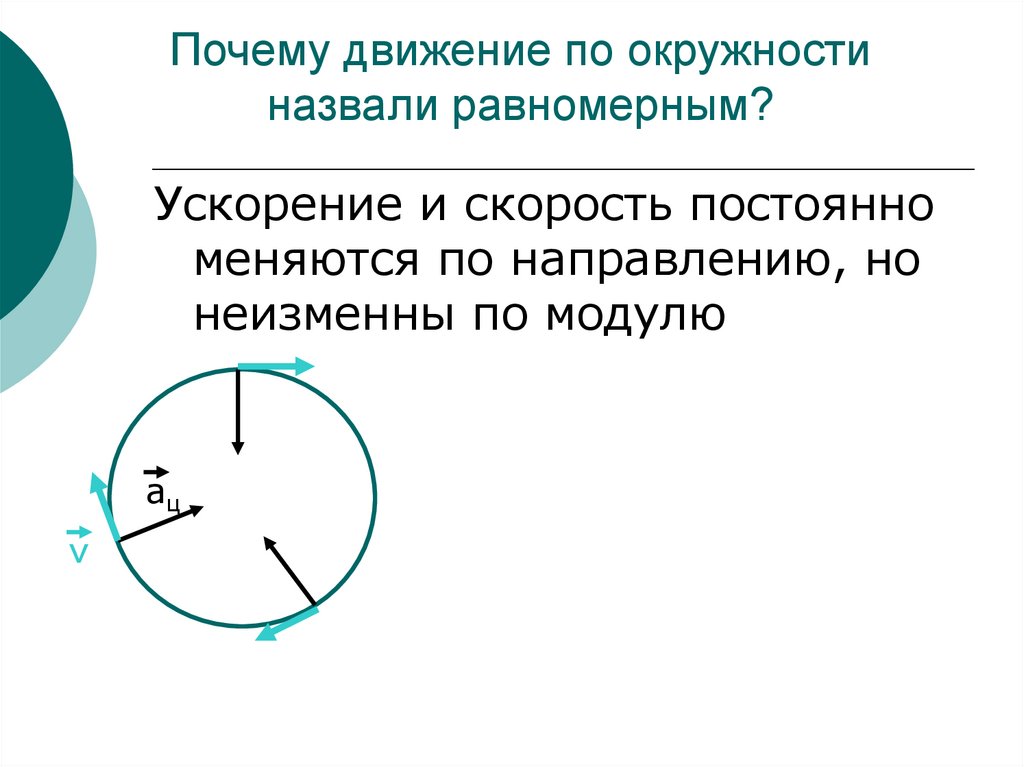 В СИ
угловая скорость измеряется в радианах за секунду (рад/с). 1 рад/с
равен угловой скорости такого равномерного движения точки по окружности, при
котором за совершается угловое перемещение 1 рад.
В СИ
угловая скорость измеряется в радианах за секунду (рад/с). 1 рад/с
равен угловой скорости такого равномерного движения точки по окружности, при
котором за совершается угловое перемещение 1 рад.
Поскольку за период угловое перемещение равно рад, то угловая скорость может быть определена через период и частоту вращения: или
Равномерное движение материальной точки по окружности характеризуется специфическими кинематическими величинами, благодаря которым его описывают при помощи соответствующих уравнений. Это — угловое перемещение и угловая скорость, период и частота вращения. Наряду с ними применяется и привычное для нас понятие скорости, которое в данном случае называют линейной скоростью.
Во время равномерного движения точки по окружности значение ее
линейной скорости остается неизменным , однако
направление вектора скорости все время меняется (рис. 3). Поэтому линейную
скорость можно характеризовать как скорость тела в некоторой точке. Она
направлена по касательной к дуге в данной точке (точка и
точка ). В этом можно убедиться, приложив к точильному камню стальной
нож: искры от него летят по касательной к поверхности камня в том месте, куда
поднесли нож.
В этом можно убедиться, приложив к точильному камню стальной
нож: искры от него летят по касательной к поверхности камня в том месте, куда
поднесли нож.
Поскольку в данном случае линейная скорость по модулю не изменяется, то из формулы скорости равномерного движения можно найти выражение для линейной скорости вращательного движения: . Или, учитывая, что , получим: .
Сравнивая формулы линейной скорости с угловой , благодаря несложным преобразованиям, получаем: , и
Итак, мгновенная скорость направлена по касательной к траектории движения. Значит, при движении тела по окружности, его скорость будет направлена по касательной к этой окружности в данной точке. При этом, модуль скорости, так же, как и модуль ускорения остаётся постоянным, в то время как их направления постоянно меняются.
Из этого можно сделать вывод, что любое криволинейное движение является ускоренным, даже если модуль скорости остаётся постоянным.
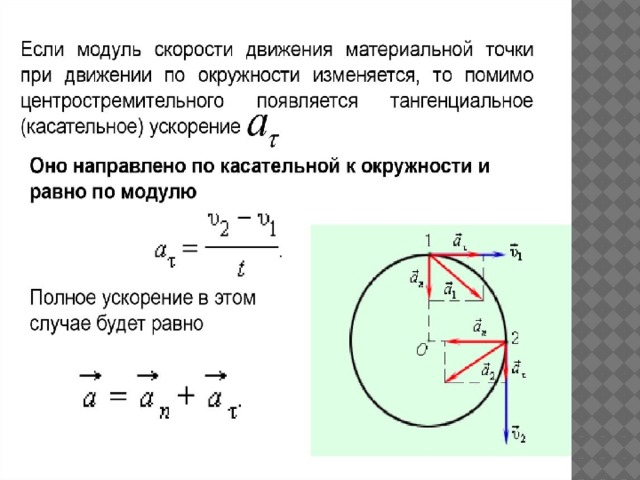
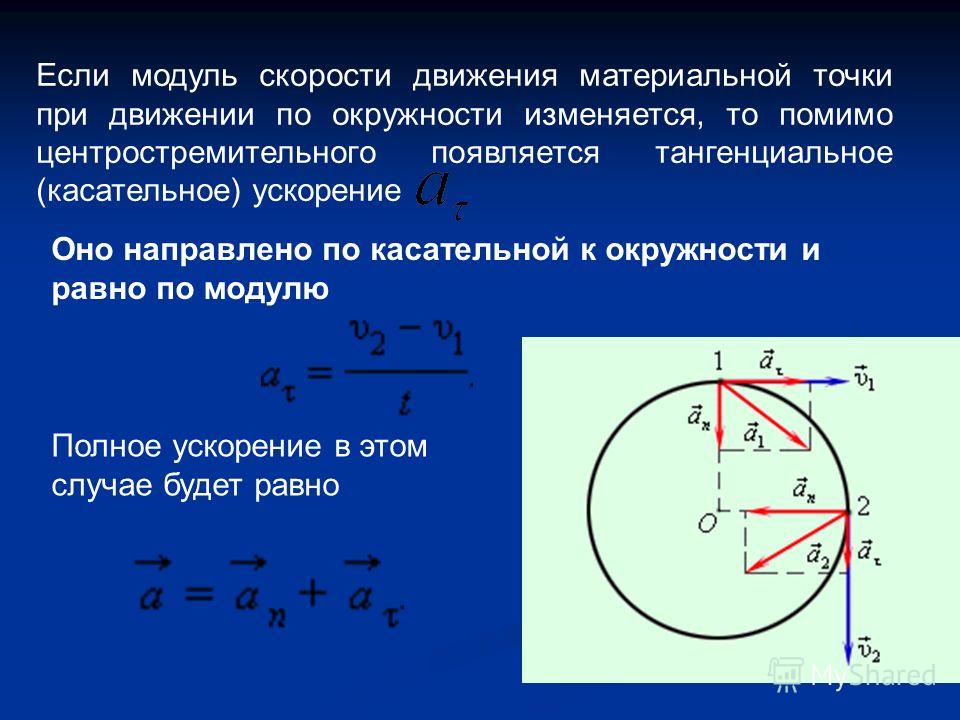
4. Центростремительное ускорениеИзменение направления вектора скорости вызывает
ускорение, ведь как векторная величина оно равно . Из
этой формулы следует, что вектор ускорения направлен
так же, как и вектор изменения скорости .
Построение вектора изменения скорости показано
на рис. 5 для какого-то промежутка времени . Если
уменьшать промежуток времени , то при этом точка станет приближаться к точке и будет
уменьшаться угол между радиусами и ,
следовательно и между векторами и . При этом вектор поворачивается
так, что приближается к радиусу, соединяющему центр окружности с точкой , то есть вектор оказывается направленным к центру
окружности. Значит, и вектор ускорения направлен к центру окружности.
Поэтому «стремящееся к центру» ускорение называют центростремительным и обозначают . Значение
центростремительного ускорения определяют по формуле . Центростремительное ускорение равно отношению квадрата скорости
материальной точки к радиусу окружности, по которой она движется.
Из
этой формулы следует, что вектор ускорения направлен
так же, как и вектор изменения скорости .
Построение вектора изменения скорости показано
на рис. 5 для какого-то промежутка времени . Если
уменьшать промежуток времени , то при этом точка станет приближаться к точке и будет
уменьшаться угол между радиусами и ,
следовательно и между векторами и . При этом вектор поворачивается
так, что приближается к радиусу, соединяющему центр окружности с точкой , то есть вектор оказывается направленным к центру
окружности. Значит, и вектор ускорения направлен к центру окружности.
Поэтому «стремящееся к центру» ускорение называют центростремительным и обозначают . Значение
центростремительного ускорения определяют по формуле . Центростремительное ускорение равно отношению квадрата скорости
материальной точки к радиусу окружности, по которой она движется.
Принимая во внимание, что , получаем .
5. Закон движенияРассмотрим
равномерное вращение точки в декартовой системе координат.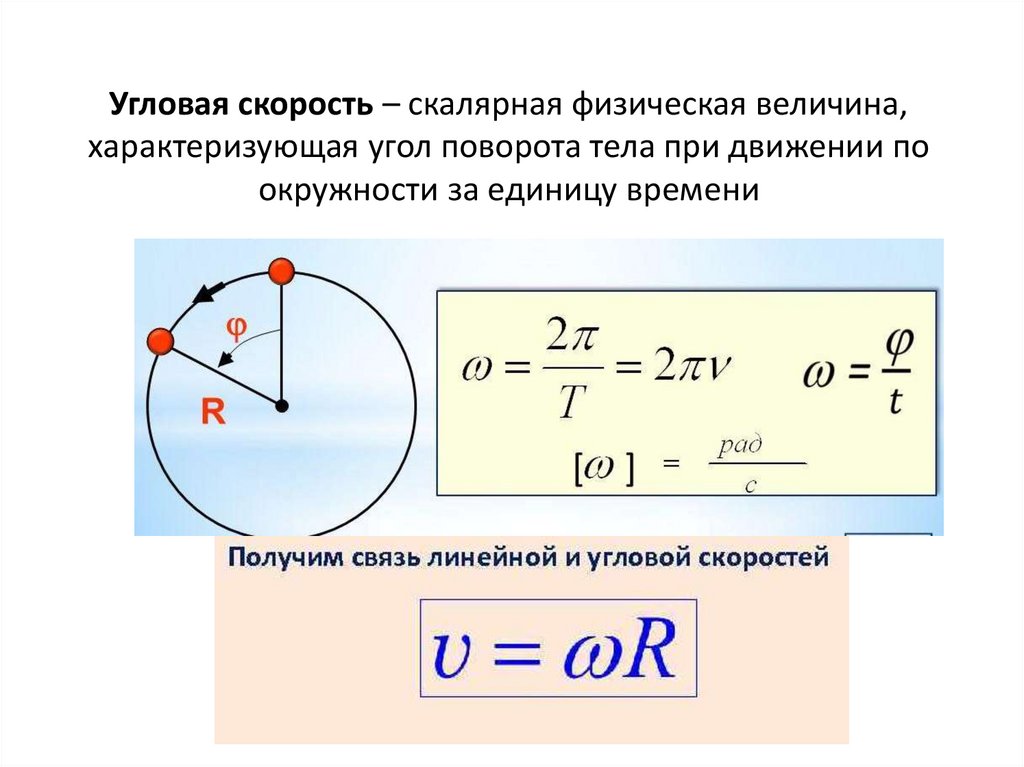 Поместим начало
координат в центре окружности. Видим из рисунка, что .
Но , следовательно,
Поместим начало
координат в центре окружности. Видим из рисунка, что .
Но , следовательно,
.
Последние формулы являются решением основной задачи механики для равномерного движения точки по окружности.
Примеры решения задач
Задача 1. Земля делает один оборот вокруг своей оси за 24 ч. Вычислить угловую и линейную скорости вращения точек поверхности Земли, которые находятся на экваторе. Радиус Земли равен 6400 км. Считайте, что ось вращения проходит сквозь полюсы.
Задача 2. Велосипедист едет по дороге со скоростью 10 м/с. Сколько оборотов за секунду делают колёса велосипеда, если они не скользят? Какое центростремительное ускорение точки обода колеса, если его радиус 35 см?
Задача 3. Спидометр автомобиля показывает 90 км/ч, а тахометр — 2400 об/мин. Чему равен радиус колеса в таком случае?
Задача 4. Землю, движущуюся вокруг Солнца, можно рассматривать как материальную
точку, так как радиус Земли ( м) много меньше
среднего расстояния от Земли до Солнца.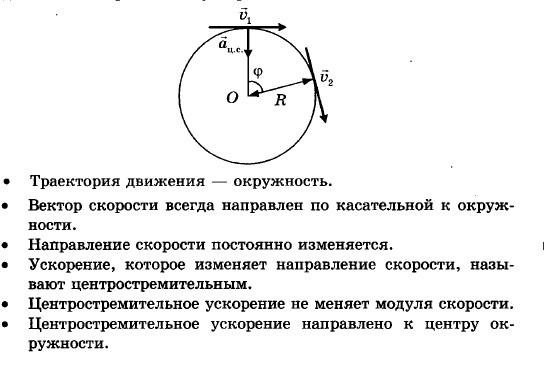 Среднее расстояние от Земли до Солнца
называют одной астрономической единицей ().
м. Траектория движения Земли вокруг
Солнца — эллипс, но фокусы эллипса близко расположены друг к другу, поэтому
можно считать, что Земля вокруг Солнца движется по окружности радиуса м. Определить линейную скорость
Земли.
Среднее расстояние от Земли до Солнца
называют одной астрономической единицей ().
м. Траектория движения Земли вокруг
Солнца — эллипс, но фокусы эллипса близко расположены друг к другу, поэтому
можно считать, что Земля вокруг Солнца движется по окружности радиуса м. Определить линейную скорость
Земли.
За один оборот, т. е. за время, равное периоду , Земля проходит путь, равный длине окружности , двигаясь с линейной скоростью :
Контрольные вопросы
1. Какое движение называют периодическим? Что такое период обращения?
2. Какую физическую величину называют частотой обращения?
3. Как связаны частота и период обращения?
4. Какие параметры характеризуют положение точки на окружности?
5. Какую физическую величину называют угловой скоростью? В каких единицах её выражают?
6. Какова зависимость между линейной и угловой скоростями точки при её движении по окружности?
7. Почему равномерное движение по окружности является ускоренным? Куда
направлен вектор центростремительного ускорения?
Почему равномерное движение по окружности является ускоренным? Куда
направлен вектор центростремительного ускорения?
8. Как можно вычислить модуль центростремительного ускорения?
9. Точка движется по криволинейной траектории с постоянной по модулю скоростью. Имеет ли эта точка ускорение?
10. Может ли точка иметь ускорение, если её скорость в данный момент времени равна нулю?
11. По какой формуле можно найти скорость тела, движущегося с постоянным ускорением?
Упражнения1. Конькобежец движется со скоростью 12 м/с по окружности радиусом 50 м. Каково центростремительное ускорение при движении конькобежца? Ответ указать с точностью до сотых, в м/с2 (Отв. 2,88)
2. Шлифовальный камень радиусом 30 см совершает один оборот за 0,6 с. Где расположены точки, имеющие наибольшую линейную скорость, и чему они равны? Ответ указать с точностью до сотых, в м/с. (Отв. 3,14)
3. Угловая
скорость лопастей вентилятора рад/с. Найдите число оборотов за 10 минут. (Отв. 6000)
Найдите число оборотов за 10 минут. (Отв. 6000)
4. Точка движется по окружности с постоянной по модулю скоростью, равной 1,5 м/с. Определите центростремительное ускорение (см/с2) точки, если за время 2,5 с направление вектора ее скорости изменяется на (Отв. 60)
5. Определить частоту обращения минутной стрелки часов (в Мс-1) (Отв. 280)
6. Продолжительность года на Земле 365 суток. Земля удалена от Солнца на расстояние м. Найти орбитальную скорость (в км/с) движения Земли (Отв. 30).
7. Линейная скорость точек обода вращающегося колеса равна 50 см/с, а линейная скорость его точек, находящихся на 3 см ближе к оси вращения, равна 40 см/с. Определите радиус (в см) колеса (Отв. 15).
8. Минутная стрелка часов на 20% длиннее секундной. Во сколько раз линейная скорость конца секундной стрелки больше, чем конца минутной стрелки? (Отв. 50)
9. Точка
движется по окружности с постоянной по модулю скоростью. За какую долю периода
обращения модуль перемещения точки будет равен радиусу окружности? Ответ
указать с точностью до сотых (Отв.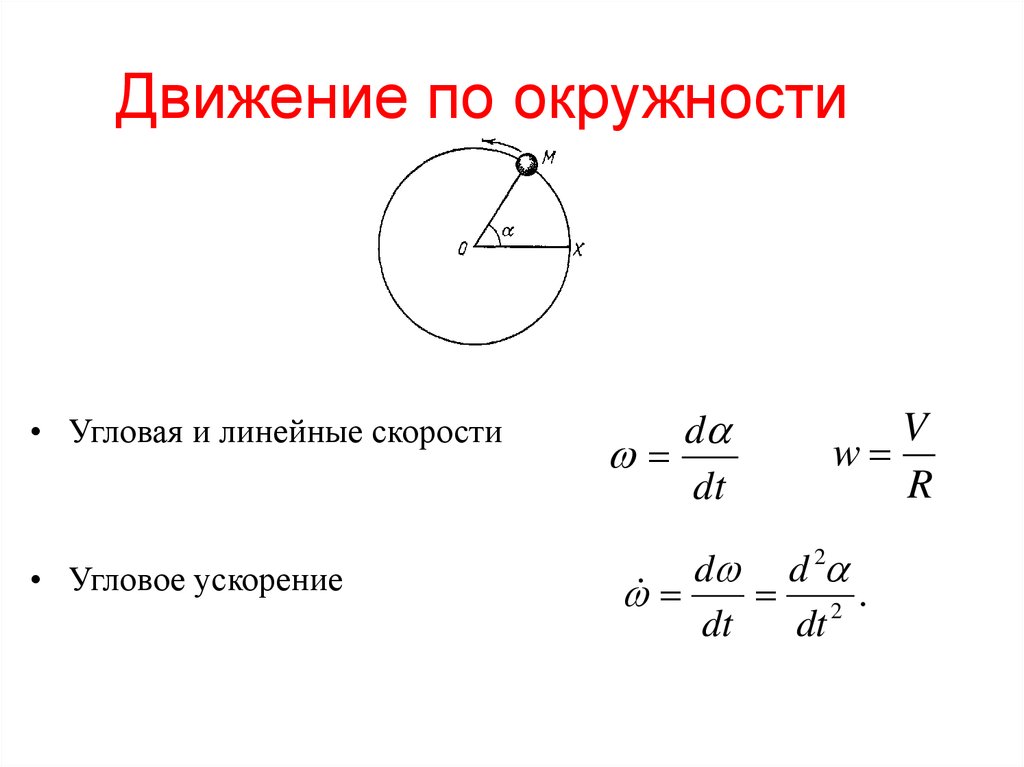 0,17).
0,17).
10. Материальная точка движется по окружности с постоянной по модулю скоростью 2 м/с. Определить центростремительное ускорение движения точки, если за 1,6 с вектор скорости изменяет свое направление на противоположное (Отв. 3,9).
11. Какую поступательную скорость (км/ч) имеют верхние точки обода велосипедного колеса, если велосипедист едет со скоростью 20 км/ч? (Отв. 40).
12. Во сколько раз линейная скорость точки поверхности Земли, лежащей на широте 600, меньше линейной скорости точки, лежащей на экваторе? (Отв. 2).
13. Маленький шарик, подвешенный к нити длиной 1м, равномерно двигается по горизонтальной окружности, образуя с вертикалью угол равный рад. Определить линейную скорость (м/с) шарика, если его период 0,5с, . (Отв. 6).
14. Самолет
летит со скоростью 360 км/ч. Пропеллер самолета диаметром 200 см вращается с
частотой 1800 об/мин. Определить скорость (м/с) конца пропеллера относительно
неподвижного наблюдателя на земле. (Отв. 213).
15. Волчок, вращающийся с угловой скоростью 62,8 рад/с, свободно падает со стола высотой 1 м. Какое число оборотов совершит волчок за время падения? (Отв. 4,5).
16. Мальчик вращает камень, привязанный к веревке длиной 0,5 м в вертикальной плоскости, так, что частота равна 3 об/с. На какую высоту (м) взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх? (Отв. 4,5).
17. Первая в мире орбитальная космическая станция двигалась со скоростью 7,3 км/с и имела период обращения 88,85 мин. Считая ее орбиту круговой, найти высоту (км) станции над поверхностью Земли. Радиус Земли принять равным 6400 км (Отв. 220).
18. Круглая горизонтальная платформа вращается вокруг своей оси с частотой 30 мин-1. Шар катится в направлении АО со скоростью 7 м/с. Найти скорость (м/с) шара относительно платформы в момент, когда АО = 8 м. (Отв. 26).
Литература1. Мякишев Г. Я., Физика 10 класс, 2014 год, стр. 55-57
55-57
2. Дмитриева В.Ф., Физика для профессий и специальностей технического профиля, 2017 год, стр.34-37
3. Фирсов А. В., Физика для профессий и специальностей технического и естественнонаучного профилей, 2013 год, стр. 22-24.
4. Тихомирова С. А. Физика. 10 класс, 2012 год, стр. 33-37.
Интернет-ресурсы1. http://fizmat.by/kursy/kinematika/okruzhnost
2. http://surl.li/aupfh
3. http://msk.edu.ua/ivk/Fizika/Internet-uroki/Mehanika/Dvizheniye_tela_po_krivolineynoy_trayektorii_Dvizheniye_po_okruzhnosti.mp4
Равномерное круговое движение
Равномерное круговое движениеОбзор:
Объект, движущийся по окружности радиусом r
с постоянной скоростью v ускоряется.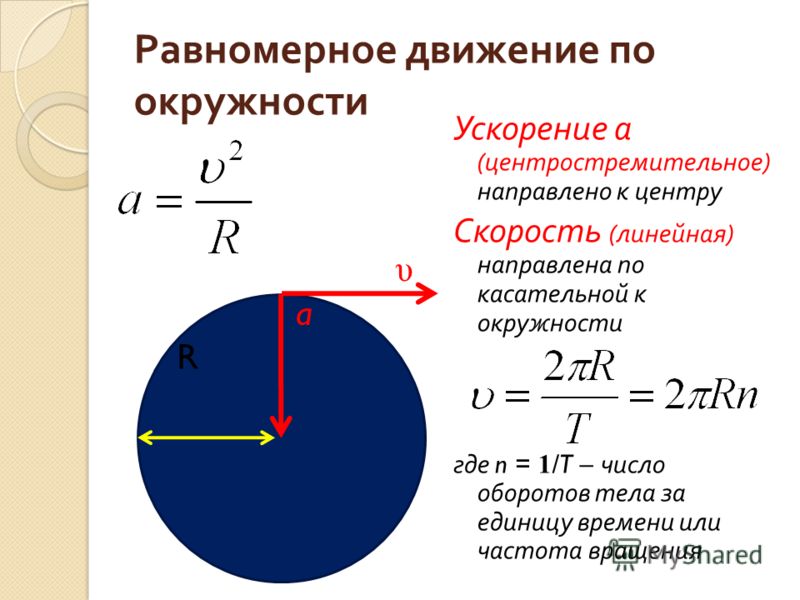 направление вектора его скорости все время меняется, но величина
вектор скорости остается постоянным. Вектор ускорения не может иметь
компонента в направлении вектора скорости, так как такая компонента
вызвать изменение скорости. Поэтому вектор ускорения должен быть
перпендикулярно вектору скорости в любой точке окружности. Этот
ускорение называется радиальным ускорением
или центростремительное ускорение, и оно указывает
к центру круга. Величина центростремительной
вектор ускорения равен с = v 2 /r.
направление вектора его скорости все время меняется, но величина
вектор скорости остается постоянным. Вектор ускорения не может иметь
компонента в направлении вектора скорости, так как такая компонента
вызвать изменение скорости. Поэтому вектор ускорения должен быть
перпендикулярно вектору скорости в любой точке окружности. Этот
ускорение называется радиальным ускорением
или центростремительное ускорение, и оно указывает
к центру круга. Величина центростремительной
вектор ускорения равен с = v 2 /r.
Какова сила при различных обстоятельствах?
Исследуя этот вопрос, решим несколько задач.
Проблема:
Груз массой 3 кг, прикрепленный к легкой нити, вращается по горизонтальной поверхности без трения. стол. Радиус окружности равен 0,8 м, а струна может выдержать массу 25 кг до разрыва. Какой диапазон скоростей может иметь масса перед струной перерывы?
Решение:
- Обоснование:
Масса, прикрепленная к нити, вращается по горизонтали, стол без трения.
Предположим, что масса вращается с постоянной скоростью. Это ускорение. Направление ускорения в сторону центр круга, а его величина v 2 /r. В струне есть напряжение. Нить натягивает массу с силой F, направленной к центру окружности. Этот сила F отвечает за центростремительное ускорение, F = мв 2 /р.
Струна может выдержать до разрыва массу 25 кг, т.е. может позволить массе до 25 кг висеть на веревке рядом с поверхность земли. Максимальное натяжение струны поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н.
Учитывая F max = 245 Н и F = mv 2 /r, мы можем найти v max . - Детали расчета:
v max 2 = F макс. об/мин = (250 Н)(0,8 м)/(3кг). v max = 8,1 м/с.
Проблема:
Монета, помещенная на расстоянии 30 см от центра вращающегося горизонтального поворотного стола
когда его скорость 50 см/с.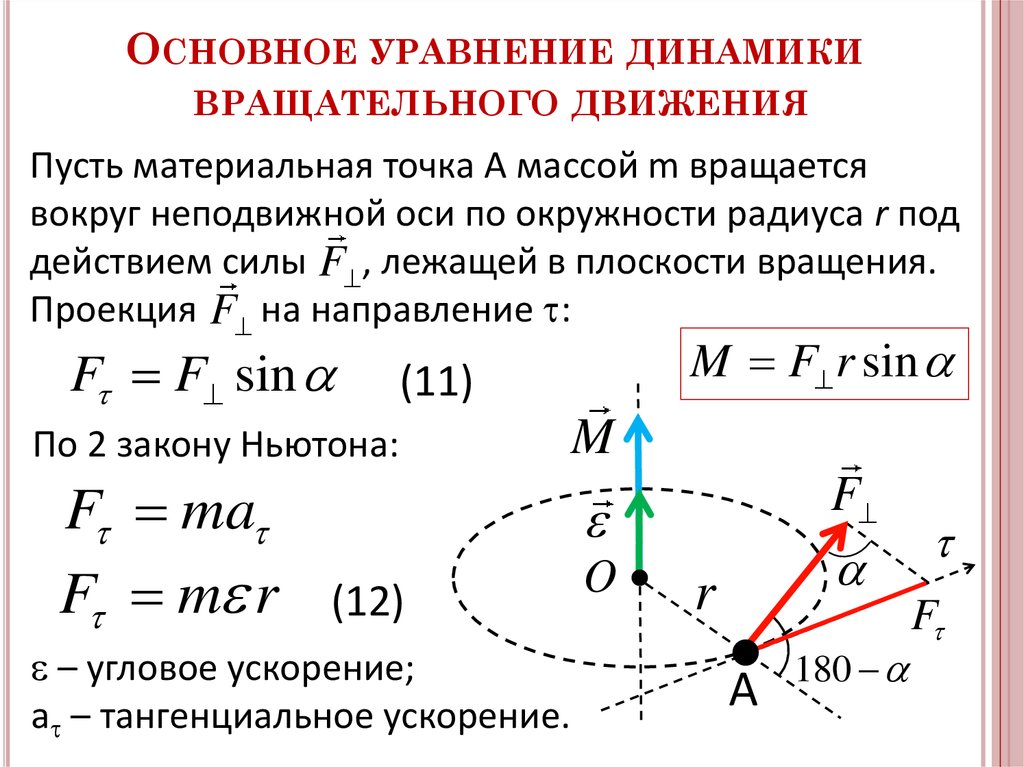
а) Какая сила обеспечивает центростремительное ускорение, когда монета неподвижна?
относительно поворотного стола?
б) Каков коэффициент статического трения между монетой и поворотным столом?
Решение:
- Обоснование:
Когда монета покоится относительно вращающегося поворотного стола, сила статическое трение между монетой и поворотным столом обеспечивает центростремительное ускорение.
Сила трения покоя имеет максимальное значение f с = μ с Н = μ с мг.
Настройка μ с мг = mv 2 /r, мы можем решить для μ s . - Детали расчета:
(а) Сила трения покоя между монетой и поворотным столом обеспечивает центростремительное ускорение.
(b) Величина максимального сила трения покоя равна f с = μ с Н. Это максимальная сила трения покоя равна mv 2 /r при v = 0,5 м/с. Имеем µ с N = µ с mg = mv 2 /r,
или мк с = v 2 /(rg) = (0,5 м/с) 2 /(0,3 м 9,8 м/с 2 ) = 0,085.
Проблема:
Рассмотрим конический маятник с грузом массой 80 кг на 10-метровом проводе, образующем угол.
θ = 5 o с вертикалью. Определить
(а) горизонтальная и вертикальная составляющая силы, действующей со стороны проволоки на
маятник и
(b) центростремительное ускорение боба.
Решение:
- Обоснование:
Диаграмма свободного тела боба показана справа.
Боб не меняет своего вертикального положения, y = константа, v y = a y = 0. Вертикальный компонент T должен иметь величина мг.
Горизонтальная составляющая Т обеспечивает центростремительное (радиальное) ускорение а р . - Детали расчета:
(a) Вертикальный компонент T должен иметь величина мг.
Tcos(5 o ) = мг, T = (80 кг 9,8 м/с 2 )/cos(5 или ) = 787 N
Величина горизонтальной составляющей T равна Tsin(5 o ) = 68,6 Н. Горизонтальная составляющая силы направлена к центру
круг.
Горизонтальная составляющая силы направлена к центру
круг.(b) Tsin(5 o ) = ma r , a r = (68,6 Н)/(80 кг) = 0,857 м/с 2 .
Скорость боба находится из a r = v 2 /r, v = (a r r) ½ .
Поскольку r = (10 м)*sin(5 o ), имеем v = 0,86 м/с.
Проблема:
Автомобиль массой 1800 кг преодолевает неровность на дороге, идущей по дуге окружности.
радиусом 42 м.
а) С какой силой дорога действует на автомобиль при прохождении автомобиля?
наивысшая точка горки, если автомобиль движется со скоростью 16 м/с?
б) С какой максимальной скоростью может двигаться автомобиль, проезжая через этот горб?
потеря связи с дорогой?
Решение:
- Обоснование:
Показана схема свободного кузова автомобиля.Единственными силами, действующими на автомобиль, движущийся с постоянной скоростью, являются сила тяжести и нормальная сила, действующая на дорогу.
 Если эти силы
равны по величине, автомобиль не разгоняется. Если автомобиль движется по
дуга окружности, то она ускоряется. Ускорение равно r =
v 2 /р. Следовательно, гравитационная сила должна иметь большую
величины, чем нормальная сила.
Если эти силы
равны по величине, автомобиль не разгоняется. Если автомобиль движется по
дуга окружности, то она ускоряется. Ускорение равно r =
v 2 /р. Следовательно, гравитационная сила должна иметь большую
величины, чем нормальная сила. - Детали расчета:
Нам нужно
мг — n = mv 2 /r, или n = m(g — v 2 /r).
n = (1800 кг)(9,8 м/с 2 — (16 м/с) 2 /(42 m)) = 6669 N(b) Автомобиль теряет контакт с дорогой, когда n становится равным нулю. Тогда дорога больше не поддерживает машину. Это происходит, когда g — v 2 /r = 0, или v 2 = gr = 411,6 м 2 /с 2 , v = 20,3 РС.
Модуль 5: Вопрос 1
Чувствуете ли вы, что вас бросает в обе стороны, когда вы преодолеваете поворот, который идеально накрен для скорости вашего автомобиля? Как направлена сила, приложенная на вас возле автокресла?
Обсудите это со своими однокурсниками на форуме!
Гравитация
Массивные объекты обладают инерцией. Требуется сила, чтобы изменить их состояние
движение. Все массивные объекты взаимодействуют через сила гравитации . Частица массой m 1 действует с силой
F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
Требуется сила, чтобы изменить их состояние
движение. Все массивные объекты взаимодействуют через сила гравитации . Частица массой m 1 действует с силой
F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
F 12 = (-G м 1 м 2 /r 12 2 )
( р 12 /р 12 ).
Здесь r 12 — расстояние между частицами 1
и 2, и ( р 12 /r 12 ) является единичный вектор , указывающий от частицы 1 к частице
2.
G — гравитационная постоянная, G = 6,67*10 -11 Нм 2 /кг 2 .
Сила F 21 , действующая на частицу массой m 2 действует на частицу массой m 1 , равно — F 12 ,
по третьему закону Ньютона. Сила тяжести всегда
привлекательный.
Точка в объекте, от которой расстояние r 12 равно измеряется его центр масс. Масса m 1 тянет массу m 2 , и масса m 2 тянет на массу m 1 . Центр масса каждого тела притягивается к центру масс другого объект.
Взвешивание земли
Радиус Земли R = 6368 км. Если вы подниметесь на гору высотой 1000 м,
ваше расстояние от центра земли изменится на (1/6368) * 100 % = 0,016 %
а величина гравитационной силы, действующей на вас, изменится на (1/6368) 2 *100
% = 2,4*10 -6 %. Для всех объектов вблизи поверхности земли
расстояние от центра почти постоянно, а величина
Поэтому вектор гравитационной силы приблизительно постоянен. За малым
расстояния, когда кривизной земной поверхности можно пренебречь,
направление вектора гравитационной силы также почти постоянно. Это указывает
прямо вниз к центру земли.
Сила тяжести, действующая на тело массой m на поверхности земли, равна
величина F = мг. Используя закон всемирного тяготения Ньютона, мы пишем GMm/R 2 =
мг, где М — масса Земли. Таким образом, мы имеем M = gR 2 /G.
Используя закон всемирного тяготения Ньютона, мы пишем GMm/R 2 =
мг, где М — масса Земли. Таким образом, мы имеем M = gR 2 /G.
Используя R = 6,4*10 6 м, находим M = (9,8 м/с 2 )(6,4*10 6 м) 2 /(6,67*10 -11 Н·м 2 /кг 2 ) =
6*10 24 кг.
Орбита
Гравитационное притяжение между объектом и землей притягивает объект к центру земли. Когда объект вращается вокруг Земли, направление силы тяжести на объекте постоянно меняется. радиус Земли настолько велик, что Земля кажется в некоторых местах плоской наблюдатель, стоящий на поверхности. Когда проблема касается только расстояний, которые намного меньше радиуса Земли, мы часто пренебрегаем кривизной земной поверхности и предположим, что сила гравитации направлена в одну и ту же направление вниз везде.
Ссылка: Спутник как снаряд
Предположим, что вблизи поверхности земли в
x-направление, как показано на рисунке выше. Первоначально он ускоряется только в
Y-направление. Но по мере движения объекта направление ускорения
изменения. Если начальная скорость объектов достаточно высока, мы должны принять
изменение направления силы учитывать при расчете объектов
траектория. Объект на круговой орбите вокруг Земли находится
постоянно падает к центру земли. Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Первоначально он ускоряется только в
Y-направление. Но по мере движения объекта направление ускорения
изменения. Если начальная скорость объектов достаточно высока, мы должны принять
изменение направления силы учитывать при расчете объектов
траектория. Объект на круговой орбите вокруг Земли находится
постоянно падает к центру земли. Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Сила тяжести всегда направлена к центру объекта. круговой орбите и отвечает за центростремительное ускорение объект.
F = mv 2 /r
Для объекта вблизи поверхности земли F = mg и r = 6,4*10 6 м. Скорость орбитального объекта находится из mg = mv 2 /r, v 2 = gr = (9,8 м/с 2 )(6,4*10 6 м). У нас v = 7919 м/с,
или примерно 8000 м/с. Требуется объект t = 2πr/v = (6,28*6,4*10 6 м)/(7919 м/с) = 5075 с = 84 мин, чтобы совершить полный оборот.
Если тот же объект двигался по круговой орбите с большим радиусом, сила силы тяжести на объекте будет меньше. Поскольку мы удваиваем расстояние от центра земли сила тяжести уменьшается в 1/4 раза. центростремительное ускорение v 2 /r уменьшается в 1/4 раза. Этот означает, что v 2 должен уменьшиться в 1/2 раза. Имеем v = 5600 м/с а для совершения оборота по орбите требуется 14355 с = 240 мин.
Объектов на геосинхронных орбитах совершить полный оборот за 24 часа или 86400 с. Следовательно, их скорость равна v =
2πr/(86400 с). Запись GMm/r 2 = mv 2 /r = m(2πr/(86400 с)) 2 /r,
или r 3 = GM(86400s) 2 /(4π). мы можем решить это
уравнение для радиуса геосинхронной орбиты. При М = 6*10 24 кг имеем r=42260 км. Геосинхронный спутник вращается вокруг 42260
км — 6400 км = 35860 км над поверхностью земли. Радиус его орбиты
в 6,6 раза больше радиуса Земли.
Луна делает один оборот вокруг Земли за 27,3 дня. Мы можем найти расстояние до Луну таким же образом мы нашли расстояние до геосинхронного спутника. Расстояние от Земли до Луны 384400 км.
Проблема:
Когда падающий метеор находится на расстоянии над земной поверхностью в 3 раза больше Радиус Земли, каково ускорение ее свободного падения под действием силы тяжести приложенная к нему сила?
Решение:
- Обоснование:
Сила, действующая на метеор, равна F = ma = GMm/r 2 . Следовательно, a = GM/r 2 . - Детали расчета:
a = GM/r 2 , a = (6,67*10 -11 Н·м 2 /кг 2 )*(6*10 24 кг)/(4*6,4*10 6 м) 2 = 0,61 м/с 2 .
(Метеор находится на 3 земных радиуса над земной поверхностью, значит, это 4 земных радиуса от его центра.)
Для получения дополнительной информации о равномерном круговом движении изучите это
материал из «Кабинета физики».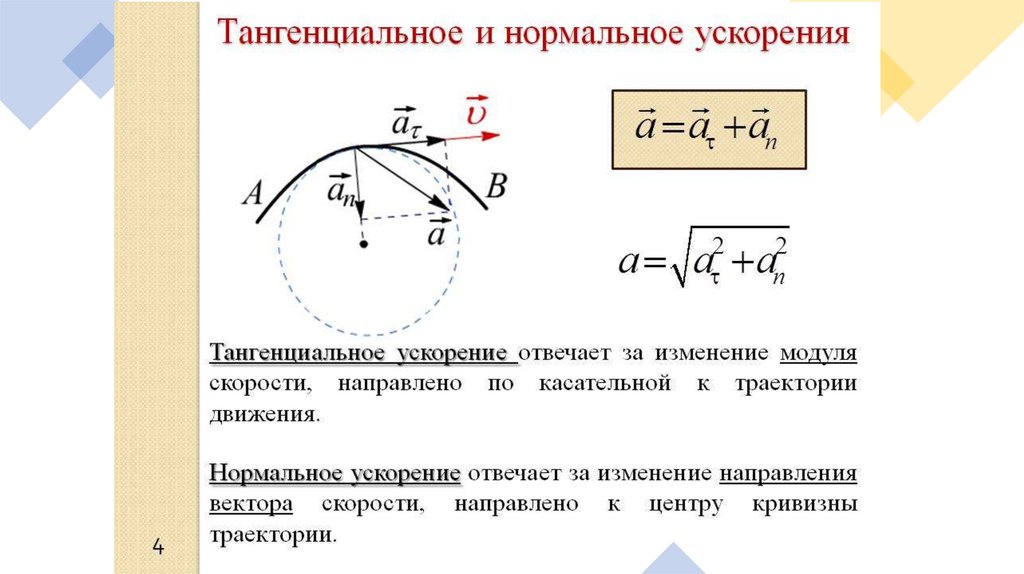
Ссылка: Движение Характеристики кругового движения
- Скорость и скорость
- Ускорение
- Требование к центростремительной силе
- Запретное F-слово
- Математика кругового движения
Ссылка: Применение кругового движения
- Второй закон Ньютона — Новый взгляд на
- Парк развлечений Физика
- Легкая атлетика
1.4: Скорость и угловая скорость
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7100
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley5 State University
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе.
 Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы. - Что такое длина дуги?
- В чем разница между линейной скоростью и угловой скоростью?
- Какие формулы связывают линейную скорость с угловой скоростью?
Начальное занятие
- Какова формула длины окружности \(C\) круга, радиус которого равен \(r\)?
- Предположим, что человек \(A\) идет по окружности с радиусом 10 футов, а человек B идет по окружности с радиусом 20 футов. Кроме того, предположим, что обоим \(A\) и \(B\) требуется 1 минута, чтобы пройти четверть окружности их соответствующих кругов (четверть полного оборота). Кто прошел наибольшее расстояние?
- Предположим, что оба человека продолжают идти с той же скоростью, что и в первую минуту. Сколько полных оборотов по кругу совершит каждый человек за 8 минут? Через 10 минут?
Длина дуги на окружности
В разделе 1.
 3 мы узнали, что мера угла в радианах равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Будут времена, когда также будет полезно знать длину дуг на других окружностях, которые опираются на тот же самый угол.
3 мы узнали, что мера угла в радианах равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Будут времена, когда также будет полезно знать длину дуг на других окружностях, которые опираются на тот же самый угол.Рисунок \(\PageIndex{1}\): Дуги, опирающиеся на угол в 1 радиан.
На рисунке \(\PageIndex{1}\) внутренний круг имеет радиус 1, внешний круг имеет радиус \(r\), а показанный угол имеет меру \(\theta\ ) радианы. Таким образом, длина дуги на единичной окружности, опирающейся на угол, равна \(\theta\), и мы использовали s для представления длины дуги на окружности радиуса \(r\), опирающейся на угол.
Напомним, что длина окружности радиуса \(r\) равна \(2\pi r\), а длина окружности радиуса 1 равна \(2\pi\). Следовательно, отношение длины дуги \(s\) на окружности радиуса \(r\), которая образует угол \(\тета\) радиан, к соответствующей дуге на единичной окружности, равно \(\dfrac{2 \pi r}{2\pi} = r\).
 Отсюда следует, что
Отсюда следует, что\[\dfrac{s}{\theta} = \dfrac{2\pi r}{\pi}\]
\[s = r\theta\]
Определение
На окружности радиуса \ (r\), длина дуги s, пересекаемая центральным углом в радианах, равна
\[s = r\theta\]
Примечание
Важно помнить, что для вычисления длины дуги мы должны измерить центральную угол в радианах.
(Непонятно, почему буква \(s\) обычно используется для обозначения длины дуги. Одно из объяснений состоит в том, что дуга «стягивает» угол.)
Упражнение \(\PageIndex{1}\)
Использование окружностей в начальном упражнении для этого раздела:
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 10 футов, которая тянется центральный угол \(\dfrac{\pi}{2}\) радиан. Результат равен одной четверти длины окружности?
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 20 футов, образующей центральный угол \(\dfrac{\pi}{2}\) радиан.
 Результат равен одной четверти длины окружности? 9\circ}) = \dfrac{11\pi}{90}\), и \[s = r\theta = (3ft)\dfrac{11\pi}{90}\] \[s = \dfrac{11 \pi}{30}\] Длина дуги составляет \(\dfrac{11\pi}{30}\) футов или около \(1,1519\) футов.
Результат равен одной четверти длины окружности? 9\circ}) = \dfrac{11\pi}{90}\), и \[s = r\theta = (3ft)\dfrac{11\pi}{90}\] \[s = \dfrac{11 \pi}{30}\] Длина дуги составляет \(\dfrac{11\pi}{30}\) футов или около \(1,1519\) футов.
Почему радианы?
Градусная мера привычна и удобна, так почему же мы вводим единицу измерения радиан? Это хороший вопрос, но с тонким ответом. Как мы только что видели, длина \(s\) дуги на окружности радиуса \(r\), опирающейся на угол \(\theta\) радиан, определяется выражением \(s = r\theta\), поэтому \(\тета = \dfrac{s}{r}\). В результате радиан представляет собой отношение двух длин (отношение длины дуги к радиусу окружности), что делает радиан безразмерной величиной. Таким образом, измерение в радианах можно рассматривать как действительное число. Это удобно для работы с длиной дуги (и угловой скоростью, как мы скоро увидим), а также будет полезно при изучении периодических явлений в главе 2. По этой причине радианная мера повсеместно используется в математике, физике и технике как в отличие от степеней, потому что, когда мы используем градусную меру, мы всегда должны учитывать градусную размерность в вычислениях.
 Это означает, что мера в радианах на самом деле более естественна с математической точки зрения, чем градусная мера.
Это означает, что мера в радианах на самом деле более естественна с математической точки зрения, чем градусная мера.Линейная и угловая скорость
Связь между дугой на окружности и углом, который она образует, измеряемым в радианах, позволяет нам определять величины, связанные с движением по окружности. Объекты, движущиеся по круговым траекториям, обладают двумя типами скорости: линейной и угловой скоростью. Подумайте о вращении на карусели. Если вы уроните камешек с края движущейся карусели, камешек не упадет прямо вниз. Вместо этого он будет продолжать двигаться вперед со скоростью, которую карусель имела в момент выпуска камешка. Это линейная скорость камня. линейная скорость измеряет изменение длины дуги во времени.
Рассмотрим точку \(P\), движущуюся с постоянной скоростью по окружности радиуса \(r\). Это называется равномерным круговым движением . Предположим, что P перемещается на расстояние s единиц за время \(t\).
 Линейная скорость v точки \(P\) равна пройденному ею расстоянию, деленному на прошедшее время. То есть \(v = \dfrac{s}{t}\). Расстояние s — это длина дуги, и мы знаем, что \(s = r\theta\).
Линейная скорость v точки \(P\) равна пройденному ею расстоянию, деленному на прошедшее время. То есть \(v = \dfrac{s}{t}\). Расстояние s — это длина дуги, и мы знаем, что \(s = r\theta\).Определение: линейная скорость
Рассмотрим точку \(P\), движущуюся с постоянной скоростью по окружности радиуса \(r\). линейная скорость \(v\) точки \(P\) определяется выражением
\[v = \dfrac{s}{t} = \dfrac{r\theta}{t}\]
где \(\theta\), измеренный в радианах, представляет собой центральный угол, опирающийся на дугу длины \(s\).
Другой способ измерения скорости движения объекта с постоянной скоростью по круговой траектории называется угловой скоростью. В то время как линейная скорость измеряет, как длина дуги изменяется с течением времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол с течением времени.
Определение: угловая скорость
Рассмотрим точку P, движущуюся с постоянной скоростью по окружности радиуса r по дуге, соответствующей центральному углу измерения \(\theta\) (в радианах).
 Угловая скорость \(\omega\) точки равна отношению угла \(\theta\) в радианах к времени t, которое требуется, чтобы выметать этот угол. Это
Угловая скорость \(\omega\) точки равна отношению угла \(\theta\) в радианах к времени t, которое требуется, чтобы выметать этот угол. Это\[\omega = \dfrac{\theta}{t}.\]
Примечание
Символ \(\omega\) — это строчная греческая буква «омега». Также обратите внимание, что угловая скорость не зависит от радиуса r.
Это несколько специальное определение угловой скорости, которое немного отличается от общего термина, используемого для описания скорости вращения точки по окружности. Этот термин составляет оборота в минуту или об/мин . Иногда используется единица оборота в секунду . Лучший способ представить число оборотов в минуту — использовать «долю единицы измерения» \(\dfrac{rev}{min}\). Поскольку 1 оборот равен \(2\pi\) радианам, мы видим, что если объект min движется со скоростью x оборотов в минуту, то
\[\omega = x \dfrac{об} {мин} \cdot \dfrac{2\pi рад}{об} = x(2\pi)\dfrac {рад}min}.
 \]
\]Упражнение \(\PageIndex{2}\)
Предположим, что круглый диск вращается со скоростью 40 оборотов в минуту. Мы хотим определить линейную скорость v (в футах в секунду) точки, которая находится в 3 футах от центра диска.
- Определите угловую скорость \(\omega\) точки в радианах в минуту. Подсказка : используйте формулу \[\omega = x \dfrac{rev}{min} \cdot \dfrac{2\pi rad}{rev}.\]
- Теперь мы знаем \(\omega = \dfrac{\theta}{t}\). Поэтому используйте формулу \(v = \dfrac{r\theta}{t}\), чтобы определить \(v\) в футах в минуту.
- Наконец, преобразуйте линейную скорость v в футах в минуту в футы в секунду.
- Ответить
1. Мы видим, что
\[\omega = 40\dfrac{об} {мин} \times \dfrac{2\pi\space рад}{об}\]
\[\omega = 80\pi\dfrac{rad}{мин}\ ]2. Результат пункта (а) дает
\[v = r(\dfrac{\theta}{r}) = r\omega\]
\[v = (3ft) \times 80\pi\dfrac{rad}{min}\]
\[v = 240\pi\dfrac{ft}{мин}\]3.
 Теперь мы конвертируем футы в минуту в футы в секунду.
Теперь мы конвертируем футы в минуту в футы в секунду.\[v = 240\pi\dfrac{ft}{min} \times \dfrac{1\space min}{60\space sec}\]
\[v = 4\pi\dfrac{ft}{sec} \приблизительно 12,566\dfrac{ft}{sec}\]
Обратите внимание, что в упражнении 1.18, как только мы определили угловую скорость, мы смогли определить и линейную скорость. То, что мы сделали в данном конкретном случае, мы можем сделать в целом. Существует простая формула, напрямую связывающая линейную скорость с угловой скоростью. Наша формула для линейной скорости: \(v =\dfrac{s}{t} \dfrac{r\theta}{t}\). Обратите внимание, что мы можем записать это как \(v = r\dfrac{\theta}{t}\). То есть \(v = r\omega\)
Примечание
Рассмотрим точку \(P\), движущуюся с постоянной (линейной) скоростью \(v\) по окружности радиуса \(r\). Если угловая скорость равна \(\omega\), то
\[v = r\omega\]
Итак, в упражнении 1.18, как только мы определили, что \(\omega = 80\pi \dfrac{rad}{min }\), мы могли бы определить v следующим образом:
\[v = r\omega = (3\space ft)(80\pi\dfrac{rad}{min} = 240\pi\dfrac{ft}{min }).
 \]
\]Обратите внимание, что, поскольку радианы «безразмерны», мы можем их опускать при работе с уравнениями, подобными предыдущему.
Пример \(\PageIndex{1}\): линейная и угловая скорость
LP (long play) или виниловая пластинка со скоростью вращения 331 об/мин представляет собой аналоговый носитель для хранения звука и долгое время использовался для прослушивания музыки. LP обычно имеет диаметр 12 или 10 дюймов. Чтобы работать с нашими формулами для линейной и угловой скорости, нам нужно знать угловую скорость в радианах в единицу времени. Для этого мы преобразуем \(33\dfrac{1}{3}\) оборотов в минуту в радианы в минуту. Мы будем использовать тот факт, что \(33\dfrac{1}{3} = \dfrac{100}{3}\)
\[\omega = \dfrac{100}{3}\dfrac{об} {мин} \times \dfrac{2\pi \space rad}{1\space rev} = \dfrac{200\pi}{ 3}\dfrac{rad}{min}\]
Теперь мы можем использовать формулу v D r! для определения линейной скорости точки на краю 12-дюймового LP. Радиус равен 6 дюймов, поэтому
\[v = r\omega = (6\space дюймов)(\dfrac{200\pi}{3}\dfrac{rad}{min}) = 400\pi \dfrac{ дюймы}{мин}\]
Может быть удобнее выразить это как десятичное значение в дюймах в секунду.
 Итак, мы получаем
Итак, мы получаем\[v = 400\pi \dfrac{дюймы}{мин} \times \dfrac{1\space min}{60 \space sec} \приблизительно 20,944\dfrac{дюймы}{sec}\]
Линейная скорость составляет примерно 20,944 дюйма в секунду.
Упражнение \(\PageIndex{3}\)
Для этих задач предположим, что Земля представляет собой сферу с радиусом 3959 миль. Поскольку Земля вращается вокруг своей оси, человек, стоящий на Земле, будет двигаться по кругу, перпендикулярному оси.
- Земля совершает оборот вокруг своей оси каждые \(24\) часа. Определить угловую скорость Земли в радианах в час. (Оставьте свой ответ в терминах числа ��\(\pi\).) 9\circ\) на север будет двигаться по кругу радиусом 2800 миль. Определите линейную скорость этого человека в милях в час и футах в секунду.
- Ответить
- Один оборот соответствует \(2\pi\) радианам. Итак, \[\omega = \dfrac{2\pi\space rad}{24\space hr} = \dfrac{\pi\space rad}{12\space hr}.
 \]
\] - Для определения линейной скорости используем формулу \(v = r\omega\) \[v = r\omega = (3959mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{3959\pi}{12}\dfrac{mi}{hr}\] Линейная скорость составляет примерно 1036,5 миль в час.
- Для определения линейной скорости используем формулу \(v = r\omega\) \[v = r\omega = (2800mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{2800\pi}{12}\dfrac{mi}{hr}\] Линейная скорость составляет примерно 733,04 мили в час. Чтобы преобразовать это в футы в секунду, мы используем тот факт, что в одной миле 5280 футов, в часе 60 минут, а в минуте 60 секунд. Итак,
\[v = (\dfrac{2800\pi}{12}\dfrac{mi}{hr})(\dfrac{5280\space ft}{1\space mi})(\dfrac{1\space hr }{60\пробел мин})(\dfrac{1\пробел мин}{60\пробел сек}) = \dfrac{(2800\pi)(5280)}{12\cdot 60\cdot 60}\dfrac{ft {сек}\]
Таким образом, линейная скорость приблизительно равна \(1075,1\) футов в секунду.
- Один оборот соответствует \(2\pi\) радианам. Итак, \[\omega = \dfrac{2\pi\space rad}{24\space hr} = \dfrac{\pi\space rad}{12\space hr}.
Резюме
В этом разделе мы изучили следующие важные концепции и идеи:
- На окружности радиуса \(r\) длина дуги \(s\), пересекаемая центральным углом с мера радиана равна \[s = r\theta\]
- Равномерное круговое движение – это когда точка движется с постоянной скоростью по окружности.
 линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки есть мера угла в радианах, деленная на время, которое требуется, чтобы этот угол опустить.
линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки есть мера угла в радианах, деленная на время, которое требуется, чтобы этот угол опустить. - Для точки \(P\), движущейся с постоянной (линейной) скоростью v по окружности окружности радиуса \(r\), имеем \[v = r\omega\], где \(\omega\) есть угловая скорость точки.
Эта страница под названием 1.4: Velocity and Angular Velocity используется в соответствии с лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстромом и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент. это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.


 2 Термодинамика
2 Термодинамика
 3 Фотометрия
3 Фотометрия

 Горизонтальная составляющая силы направлена к центру
круг.
Горизонтальная составляющая силы направлена к центру
круг. Если эти силы
равны по величине, автомобиль не разгоняется. Если автомобиль движется по
дуга окружности, то она ускоряется. Ускорение равно r =
v 2 /р. Следовательно, гравитационная сила должна иметь большую
величины, чем нормальная сила.
Если эти силы
равны по величине, автомобиль не разгоняется. Если автомобиль движется по
дуга окружности, то она ускоряется. Ускорение равно r =
v 2 /р. Следовательно, гравитационная сила должна иметь большую
величины, чем нормальная сила. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.  3 мы узнали, что мера угла в радианах равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Будут времена, когда также будет полезно знать длину дуг на других окружностях, которые опираются на тот же самый угол.
3 мы узнали, что мера угла в радианах равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Будут времена, когда также будет полезно знать длину дуг на других окружностях, которые опираются на тот же самый угол.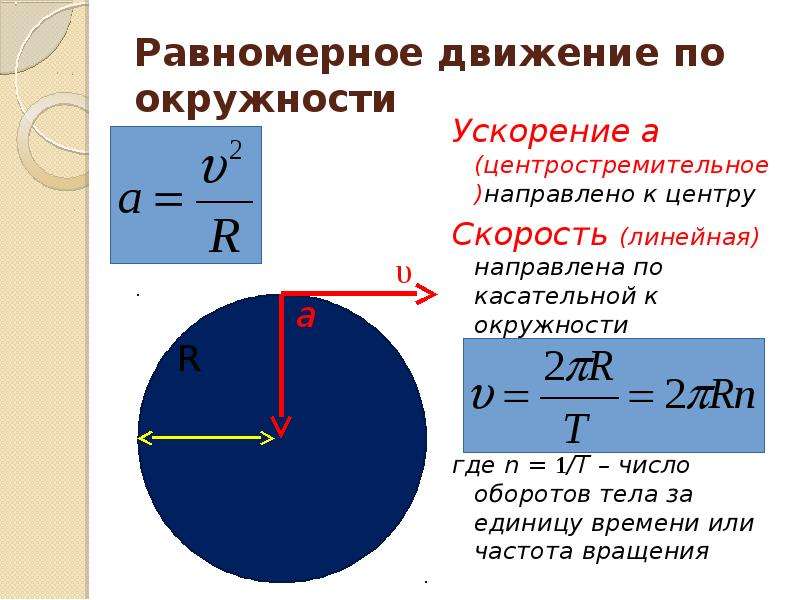 Отсюда следует, что
Отсюда следует, что Результат равен одной четверти длины окружности? 9\circ}) = \dfrac{11\pi}{90}\), и \[s = r\theta = (3ft)\dfrac{11\pi}{90}\] \[s = \dfrac{11 \pi}{30}\] Длина дуги составляет \(\dfrac{11\pi}{30}\) футов или около \(1,1519\) футов.
Результат равен одной четверти длины окружности? 9\circ}) = \dfrac{11\pi}{90}\), и \[s = r\theta = (3ft)\dfrac{11\pi}{90}\] \[s = \dfrac{11 \pi}{30}\] Длина дуги составляет \(\dfrac{11\pi}{30}\) футов или около \(1,1519\) футов.
Leave A Comment