Самостоятельная работа «Задачи стереометрии. Куб, параллелепипед, призма.» Подготовка к ЕГЭ.
С.Р. 1 (ЕГЭ №16 база), куб, параллелепипед, призма
Вариант 1.
1. Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 9 и 6. Объем параллелепипеда равен 756. Найдите площадь его поверхности и диагональ.
3. В прямоугольном параллелепипеде рёбра и диагональ равны соответственно и . Найдите объём параллелепипеда .
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы и площадь ее поверхности .
Вариант 2.
Ящик, имеющий форму куба с ребром 20 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 4. Объем параллелепипеда равен 240. Найдите площадь его поверхности и диагональ .
В прямоугольном параллелепипеде рёбра , и диагональ равны соответственно , и . Найдите объём параллелепипеда
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 8, боковое ребро равно 5. Найдите объем призмы и площадь ее поверхности .
Вариант 3.
Плоскость, проходящая через три точки A, B и C, разбивает куб на два многогранника. Сколько граней у многогранника, у которого больше граней?
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 9 и 5. Объем параллелепипеда равен 540. Найдите площадь его поверхности и диагональ .
Найдите площадь его поверхности и диагональ .
3. В прямоугольном параллелепипеде рёбра и диагональ равны соответственно и . Найдите объём параллелепипеда .
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы и площадь ее поверхности .
Вариант 4.
1.Аквариум имеет форму куба со стороной 40 см. Сколько л литров составляет объём аквариума? В одном литре 1000 к кубических сантиметров.
2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 10 и 2. Объем параллелепипеда равен 100. Найдите площадь его поверхности и диагональ .
3. В прямоугольном параллелепипеде рёбра , и диагональ равны соответственно , и . Найдите объём параллелепипеда .
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 8, боковое ребро равно 6. Найдите объем призмы и площадь ее поверхности.
Найдите объем призмы и площадь ее поверхности.
Вариант 5.
1. 1.Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
2.Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 5. Объем параллелепипеда равен 30. Найдите площадь его поверхности и диагональ .
3. В прямоугольном параллелепипеде рё ребра и диагональ равны соответственно 6 и . Найдите объём параллелепипеда .
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 7 и 8, боковое ребро равно 5. Найдите объем призмы и площадь ее поверхности .
Вариант 6.
1.Ящик, имеющий форму куба с ребром 20 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.
2.Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 2. Объем параллелепипеда равен 144. Найдите площадь его поверхности и диагональ .
3.В прямоугольном параллелепипеде рёбра , и диагональ равны соответственно , и . Найдите объём параллелепипеда
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 5, боковое ребро равно 6. Найдите объем призмы и площадь ее поверхности .
Вариант 7.
Плоскость, проходящая через три точки A, B и C, разбивает куб на два многогранника. Сколько граней у многогранника, у которого больше граней?
2.Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 4. Объем параллелепипеда равен 528. Найдите площадь его поверхности и диагональ .
3. В прямоугольном параллелепипеде рёбра и диагональ равны соответственно и . Найдите объём параллелепипеда .
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 5, боковое ребро равно 6. Найдите объем призмы и площадь ее поверхности .
Вариант 8.
1.Аквариум имеет форму куба со стороной 40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
2.Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 11 и 5. Объем параллелепипеда равен 440. Найдите площадь его поверхности и диагональ .
3.В прямоугольном параллелепипеде рёбра , и диагональ равны соответственно , и . Найдите объём параллелепипеда .
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 7, боковое ребро равно 6. Найдите объем призмы и площадь ее поверхности.
Найдите объем призмы и площадь ее поверхности.
Вариант 9.
1. Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 2. Объем параллелепипеда равен 112. Найдите площадь его поверхности и диагональ .
3.В прямоугольном параллелепипеде рёбра , и диагональ равны соответственно , и . Найдите объём параллелепипеда .
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5, боковое ребро равно 4. Найдите объем призмы и площадь ее поверхности.
Тренажёр по решению задания ЕГЭ №8 | Консультация по геометрии (11 класс) на тему:
Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию. Основания являются прямоугольниками.
Основания являются прямоугольниками.
Параллелепипед АВСDА1В1С1D1 – прямоугольный (рис. 1), если:
1. АА1⊥ АВСD (боковое ребро перпендикулярно плоскости основания, то есть параллелепипед прямой).
2. ∠ВАD = 90°, т. е. в основании лежит прямоугольник.
Рис. 1 Прямоугольный параллелепипед
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда. Но есть дополнительные свойства, которые выводятся из определения прямоугольного параллелепипеда.
Итак, прямоугольный параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию. Основание прямоугольного параллелепипеда — прямоугольник.
1. В прямоугольном параллелепипеде все шесть граней прямоугольники.
АВСD и А1В1С1D1 – прямоугольники по определению.
2. Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольного параллелепипеда — прямоугольники.
3. Все двугранные углы прямоугольного параллелепипеда прямые.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Примечание. Длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда, являются измерениями прямоугольного параллелепипеда. Их иногда называют длина, ширина, высота.
Диагонали прямоугольного параллелепипеда равны.
Обозначим измерения параллелепипеда АВС как a, b, c (см. рис. 62, тогда АС1 = СА1 = В1D = DВ1 =
Рис. 2
Прямоугольный параллелепипед
Задание №8
1.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Решение.
Площадь поверхности параллелепипеда с ребрами а1, а2, а3 дается формулой Пусть неизвестное ребро равно x. Подставляя известные величины из условия, получаем:
Ответ: 5.
Решите самостоятельно:
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 6. Площадь поверхности этого параллелепипеда равна 138.
 Найдите третье ребро, выходящее из той же вершины.
Найдите третье ребро, выходящее из той же вершины. - Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 5. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Площадь поверхности этого параллелепипеда равна 136. Найдите третье ребро, выходящее из той же вершины.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 8. Площадь поверхности этого параллелепипеда равна 246. Найдите третье ребро, выходящее из той же вершины.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 5. Площадь поверхности этого параллелепипеда равна 328. Найдите третье ребро, выходящее из той же вершины.
2.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Решение.
Пусть длина третьего ребра, исходящего из той же вершины, равна , тогда площадь поверхности параллелепипеда даётся формулой По условию площадь поверхности равна 16, тогда откуда
Длина диагонали прямоугольного параллелепипеда равна квадратному корню из суммы квадратов его измерений, поэтому
Ответ: 3.
Решите самостоятельно:
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 48 и 12. Площадь поверхности параллелепипеда равна 3072. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 2. Площадь поверхности параллелепипеда равна 64. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 9 и 12. Площадь поверхности параллелепипеда равна 1728. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 72 и 18. Площадь поверхности параллелепипеда равна 6912.
 Найдите его диагональ.
Найдите его диагональ. - Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 24 и 72. Площадь поверхности параллелепипеда равна 6912. Найдите его диагональ.
3.
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Решение.
Высота и рёбра такого параллелепипеда равны диаметру сферы, поэтому это куб с ребром 2. Площадь его поверхности равна 6 · 4 = 24.
Ответ: 24.
4. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Решение.
Объем прямоугольного параллелепипеда равен , где — площадь грани, а — высота перпендикулярного к ней ребра. Имеем
Ответ: 48.
Решите самостоятельно:
- Площадь грани прямоугольного параллелепипеда равна 15. Ребро, перпендикулярное этой грани, равно 2. Найдите объем параллелепипеда.
- Площадь грани прямоугольного параллелепипеда равна 12.
 Ребро, перпендикулярное этой грани, равно 5. Найдите объем параллелепипеда.
Ребро, перпендикулярное этой грани, равно 5. Найдите объем параллелепипеда. - Площадь грани прямоугольного параллелепипеда равна 21. Ребро, перпендикулярное этой грани, равно 3. Найдите объем параллелепипеда.
- Площадь грани прямоугольного параллелепипеда равна 14. Ребро, перпендикулярное этой грани, равно 5. Найдите объем параллелепипеда.
- Площадь грани прямоугольного параллелепипеда равна 20. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
5.
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Решение.
Объем прямоугольного параллелепипеда равен , где — площадь грани, а — высота перпендикулярного к ней ребра. Тогда площадь грани
Ответ: 8.
Решите самостоятельно:
- Объем прямоугольного параллелепипеда равен 105. Одно из его ребер равно 7. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.

- Объем прямоугольного параллелепипеда равен 72. Одно из его ребер равно 4. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
- Объем прямоугольного параллелепипеда равен 75. Одно из его ребер равно 5. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
- Объем прямоугольного параллелепипеда равен 90. Одно из его ребер равно 5. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
- Объем прямоугольного параллелепипеда равен 42. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
6.
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Решение.
Объем прямоугольного параллелепипеда равен , где — площадь грани, а — высота перпендикулярного к ней ребра. Тогда
Ответ: 5.
Решите самостоятельно:
- Объем прямоугольного параллелепипеда равен 144.
 Площадь одной его грани равна 18. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Площадь одной его грани равна 18. Найдите ребро параллелепипеда, перпендикулярное этой грани. - Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 15. Найдите ребро параллелепипеда, перпендикулярное этой грани.
- Объем прямоугольного параллелепипеда равен 48. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
- Объем прямоугольного параллелепипеда равен 105. Площадь одной его грани равна 21. Найдите ребро параллелепипеда, перпендикулярное этой грани.
- Объем прямоугольного параллелепипеда равен 72. Площадь одной его грани равна 24. Найдите ребро параллелепипеда, перпендикулярное этой грани.
7.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Решение.
Объем прямоугольного параллелепипеда равен произведению его измерений. Поэтому, если x — искомое ребро, то 2 · 6 · x = 48, откуда x = 4.
Ответ: 4.
Решите самостоятельно:
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 3. Объем параллелепипеда равен 180. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 9 и 5. Объем параллелепипеда равен 540. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 9. Объем параллелепипеда равен 1404. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 9 и 7. Объем параллелепипеда равен 189. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 10 и 9. Объем параллелепипеда равен 450. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

8.
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Решение.
Объем куба V = a3 равен объему параллелепипеда
Значит для ребра куба имеем:
Ответ: 6.
Решите самостоятельно:
- Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 12 и 18. Найдите ребро равновеликого ему куба.
- Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 6 и 36. Найдите ребро равновеликого ему куба.
- Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 3 и 24. Найдите ребро равновеликого ему куба.
- Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 1 и 729. Найдите ребро равновеликого ему куба.
- Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4 и 27. Найдите ребро равновеликого ему куба.
9.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Решение.
Длина диагонали параллелепипеда равна
Длина третьего ребра тогда Получим, что объем параллелепипеда
Ответ: 32.
Решите самостоятельно:
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 72 и 18. Диагональ параллелепипеда равна 78. Найдите объем параллелепипеда.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 10 и 5. Диагональ параллелепипеда равна 15. Найдите объем параллелепипеда.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 2. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 36 и 9. Диагональ параллелепипеда равна 39. Найдите объем параллелепипеда.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 24 и 16.
 Диагональ параллелепипеда равна 34. Найдите объем параллелепипеда.
Диагональ параллелепипеда равна 34. Найдите объем параллелепипеда.
10.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Решение.
Объем параллелепипеда равен
Отсюда найдем третье ребро:
Длина диагонали параллелепипеда равна
Ответ: 7.
Решите самостоятельно:
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 24 и 32. Объем параллелепипеда равен 32256. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 10 и 5. Объем параллелепипеда равен 500. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 12. Объем параллелепипеда равен 864. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 16. Объем параллелепипеда равен 9216.
 Найдите его диагональ.
Найдите его диагональ. - Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 27 и 36. Объем параллелепипеда равен 23328. Найдите его диагональ.
11.
Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол 45°. Найдите объем параллелепипеда.
Решение.
Ребро параллелепипеда напротив угла в равно , поскольку образует с заданной диагональю и диагональю одной из граней равнобедренный треугольник. Два другие ребра по построению лежат в прямоугольных треугольниках напротив угла в и равны, поэтому половине диагонали. Тогда объем параллелепипеда:
Ответ: 4.
Решите самостоятельно:
- Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна 2 и образует с плоскостью этой грани угол 30°. Найдите объем параллелепипеда.
12.
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Найдите его площадь поверхности.
Решение.
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме попарных произведений его измерений
Ответ: 22.
Решите самостоятельно:
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3 и 7. Найдите его площадь поверхности.
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 4 и 5. Найдите его площадь поверхности.
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 7 и 9. Найдите его площадь поверхности.
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 5 и 8. Найдите его площадь поверхности.
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 4 и 6. Найдите его площадь поверхности.
13.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Найдите площадь поверхности параллелепипеда.
Решение.
Обозначим известные ребра за и , а неизвестное за Площадь поверхности параллелепипеда выражается как
Диагональ параллелепипеда находится как
Выразим :
Тогда площадь поверхности
Ответ: 64.
Решите самостоятельно:
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 42 и 24. Диагональ параллелепипеда равна 58. Найдите площадь поверхности параллелепипеда.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 2. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 3. Диагональ параллелепипеда равна 13. Найдите площадь поверхности параллелепипеда.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 18 и 24. Диагональ параллелепипеда равна 34.
 Найдите площадь поверхности параллелепипеда.
Найдите площадь поверхности параллелепипеда. - Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 24 и 6. Диагональ параллелепипеда равна 26. Найдите площадь поверхности параллелепипеда.
14.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Решение.
Найдем третье ребро из выражения для объема:
Площадь поверхности параллелепипеда
Ответ: 22.
Решите самостоятельно:
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 2. Объем параллелепипеда равен 112. Найдите площадь его поверхности.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 7. Объем параллелепипеда равен 616. Найдите площадь его поверхности.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 6. Объем параллелепипеда равен 144.
 Найдите площадь его поверхности.
Найдите площадь его поверхности. - Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 10 и 8. Объем параллелепипеда равен 640. Найдите площадь его поверхности.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 2. Объем параллелепипеда равен 312. Найдите площадь его поверхности.
15.
Объем параллелепипеда равен 4,5. Найдите объем треугольной пирамиды
Решение.
Искомый объем равен разности объемов параллелепипеда со сторонами a, b и c и четырех пирамид, основания которых являются гранями данной треугольной пирамиды. Объём каждой из этих пирамид равен одной трети произведения площади основания на высоту, а площадь основания вдвое меньше площади основания параллелепипеда:
Ответ: 1,5.
Решите самостоятельно:
- Объем параллелепипеда равен Найдите объем треугольной пирамиды
- Объем параллелепипеда равен 2,7.
 Найдите объем треугольной пирамиды
Найдите объем треугольной пирамиды - Объем параллелепипеда равен Найдите объем треугольной пирамиды
- Объем параллелепипеда равен Найдите объем треугольной пирамиды
16.
Найдите объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда , у которого , ,
Решение.
Из рисунка видно, что многогранник является половиной данного прямоугольного параллелепипеда. Следовательно, объём искомого многогранника дается формулой:
Ответ: 30.
Решите самостоятельно:
- Найдите объем многогранника, вершинами которого являются точки , , , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , , , параллелепипеда , у которого , ,
17. Задание 8 № 245336
Задание 8 № 245336
Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , ,
Решение.
Площадь основания пирамиды в два раза меньше площади основания пареллелепипеда, а высота у них общая. Поэтому
Ответ: 8.
Решите самостоятельно:
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
18.
Найдите объем многогранника, вершинами которого являются точки , , , , прямоугольного параллелепипеда , у которого , ,
Решение.
Основанием пирамиды, объем которой нужно найти, является боковая грань параллелепипеда, а ее высотой является ребро Поэтому
Ответ: 16.
Решите самостоятельно:
- Найдите объем многогранника, вершинами которого являются точки , , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , , параллелепипеда , у которого , ,
19.
Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , ,
Решение.
Площадь основания пирамиды в два раза меньше площади основания пареллелепипеда, а высота у них общая. Поэтому
Поэтому
Ответ: 6.
Решите самостоятельно:
- Найдите объем многогранника, вершинами которого являются точки параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
- Найдите объем многогранника, вершинами которого являются точки , , , параллелепипеда , у которого , ,
20.
Найдите угол прямоугольного параллелепипеда, для которого , , Дайте ответ в градусах.
Решение.
В прямоугольнике отрезок является диагональю, По теореме Пифагора
Прямоугольный треугольник равнобедренный: , значит, его острые углы равны
Ответ: 45.
Решите самостоятельно:
- Найдите угол прямоугольного параллелепипеда, для которого , , Ответ дайте в градусах.

- Найдите угол прямоугольного параллелепипеда, для которого , , Ответ дайте в градусах.
- Найдите угол прямоугольного параллелепипеда, для которого , , Ответ дайте в градусах.
- Найдите угол прямоугольного параллелепипеда, для которого , , Ответ дайте в градусах.
- Найдите угол прямоугольного параллелепипеда, для которого , , Ответ дайте в градусах.
21.
В прямоугольном параллелепипеде ребро , ребро , ребро Точка — середина ребра Найдите площадь сечения, проходящего через точки и
Решение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому четырехугольник — параллелограмм. Кроме того, ребро перпендикулярно граням и , поэтому углы и — прямые. Следовательно, сечение — прямоугольник.
Из прямоугольного треугольника по теореме Пифагора найдем
Тогда площадь прямоугольника равна:
Ответ:5.
Решите самостоятельно:
- В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро BC = 4, ребро ребро BB1 = 4.
 Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K.
Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K. - В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро CD = 2, ребро ребро CC1 = 2. Точка K — середина ребра DD1. Найдите площадь сечения, проходящего через точки C1, B1 и K.
- В прямоугольном параллелепипеде известны длины рёбер: = 3, = 6, = 8. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
- В прямоугольном параллелепипеде известны длины рёбер: = 9, = 9, = 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
- В прямоугольном параллелепипеде известны длины рёбер: = 15, = 12, = 16. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
Задача по математике: Прямоугольный параллелепипед — вопрос № 74824, алгебра, выражение переменной из формулы
Прямоугольный параллелепипед имеет объем 768 см 3 , а ребра, отмеченные х, равны по длине. Вычислите значение x
Вычислите значение x
Правильный ответ:
Нашли ошибку или неточность? Не стесняйтесь
напишите нам. Спасибо!
Советы по использованию соответствующих онлайн-калькуляторов
Совет: конвертер единиц объема поможет вам преобразовать единицы объема.
Для решения этой задачи по математике необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы
- арифметика 900 24
- кубический корень
- объемная геометрия
- кубоид
Единицы физических величин:
- объем
Уровень задачи:
- практика для 13-летних
- Вычислить 67794
Вычислить объем прямоугольного параллелепипеда в заданных единицах, если известны длины его ребер. A) a = 20 см, b = 3 см, c = 7 см, (длина) B) a = 10 мм, b = 8 мм, c = 9 мм, (мл) C) a = 30 см, b = 5 см, c = 8 см, (l) D) a = 300 мм, b = 4 м, c = 7 дм, (hl) - Рассчитать 7653
Объем блока 900см 3 , а поверхность 600см². Площадь одной стены 60 см². Вычислите длины ребер a, b и c.
Площадь одной стены 60 см². Вычислите длины ребер a, b и c. - Прямоугольник
Прямоугольник с ребром a=6 см и диагональю пространства u=31 см имеет объем V=900 см³. Вычислите длину других ребер. - Объем трех прямоугольных параллелепипедов
Вычислите суммарный объем всех прямоугольных параллелепипедов, у которых размеры ребер относятся как 1:2:3, а одно из ребер имеет размер 6 см. - Сантиметры 4091
Вычислите длину диагонали тела бруска, два ребра которого имеют длину 2 см и 7 см, а объем равен 49 кубическим сантиметрам. - Размеры 15133
Аквариум имеет размеры a = 250 см b = 50 см c = 60 см вода наливается в аквариум до 45 см. Вы подсчитали, сколько литров воды в аквариуме? - Прямоугольный параллелепипед — пропорции
Размеры ребер прямоугольного параллелепипеда находятся в соотношении 2:3:5. Самая маленькая стена имеет площадь 54 см². Вычислите площадь поверхности и объем этого прямоугольного параллелепипеда. - Ребра прямоугольного параллелепипеда
Вычислите объем и поверхность прямоугольного параллелепипеда, длины ребер которого относятся к 2:3:4, а самое длинное ребро имеет длину 10 см.
- Кубик 5916
Эрик убирает после игры с кубом с ребром 14 см. Он убирает их в три коробки. Сколько кубиков может поместиться в: 1) прямоугольный параллелепипед со сторонами 4,2 дм, 5,6 дм и 7 дм? 2) куб с ребром 560 мм? 3) прямоугольный с ребрами 0,92. Длины двух его ребер равны a = 3 см, b = 5 см. Вычислите длину его третьего ребра. Скажем: по формуле для поверхности блока сначала вычислите c. - Соотношение сторон
Размеры прямоугольного параллелепипеда находятся в соотношении 3:1:2. Диагональ тела имеет длину 28 см. Найдите объем прямоугольного параллелепипеда. - Прямоугольный параллелепипед
Сумма длин трех ребер прямоугольного параллелепипеда, исходящих из одной вершины, равна 210 см. Соотношение длин ребер 7:5:3. Рассчитаем длину ребер. - Последовательные элементы
Блок имеет объем 1728 см³. Определить длины ребер a, b и c блоков, для которых a < b < c и a + b + c = 38 см и числовые значения которых в см представляют собой три последовательных члена геометрической прогрессии.
- Прямоугольник и отношение
Прямоугольник имеет объем 810 см³. Длины ребер из одной вершины относятся как 2:3:5. Найдите размеры прямоугольного параллелепипеда. - Размеры 47111
Размеры блока 9: 5: 4. Определить его объем, если известно, что сумма самого длинного и самого короткого ребра равна 65 см. - Сантиметры 21193
Какова высота бруска, у которого длина ребер основания 12 см, а длина 6 см, если его объем 360 кубических сантиметров? - Ребра прямоугольного параллелепипеда
Длины ребер прямоугольного параллелепипеда относятся как 2:3:4. Найдите их длину, если известно, что поверхность прямоугольного параллелепипеда равна 468 м².
Математическая задача: пропорциональный кубоид — вопрос № 5486, алгебра, уравнение
Длины ребер прямоугольного параллелепипеда относятся как 2:3:6. Диагональ его тела составляет 14 см в длину. Вычислите объем и площадь поверхности прямоугольного параллелепипеда.
Правильный ответ:
V = 288 см 3S = 288 см 2
Пошаговое объяснение:
a: b:c = 2:3:6 a= 2x b = 3x c = 6x u=14 см u = a2+b2+c2
u = (2x)2+(3x)2+(6x)2
u = 4×2+9×2+36×2
u2 = 4×2+9×2+36×2 x=u/4+9+36
=14/4+9+36
=2 см =12 см u2=a2+b2+c2
=42+62+122
=14 V=a⋅ b⋅ c=4⋅ 6⋅ 12=288 см3
S=2⋅ (a⋅ b+b⋅ c+a⋅ c)=2⋅ (4⋅ 6+6⋅ 12+4⋅ 12)=288 см2
Нашли ошибку или неточность? Не стесняйтесь
напишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Воспользуйтесь нашим калькулятором коэффициентов.
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
Совет: конвертер единиц объема поможет вам перевести единицы объема.
См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Для решения этой задачи по математике необходимо знать следующие знания:
- алгебра
- уравнение
- выражение переменной из формулы
- твердое тело геометрия
- прямоугольный параллелепипед
- пространственная диагональ
- площадь поверхности
- планиметрика
- теорема Пифагора
- прямоугольный треугольник
- треугольник
- основные функции
- отношение 9003 9
- Объем
- практика для 14-летних
- средняя школа
- Ребра прямоугольного параллелепипеда
Вычислите объем и поверхность прямоугольного параллелепипеда, длины ребер которого относятся к 2:3:4, а самое длинное ребро имеет длину 10 см.
- Диагонали прямоугольного параллелепипеда
Прямоугольный параллелепипед имеет размеры 15, 20 и 40 см. Вычислите его объем и поверхность, длину диагонали тела и длины всех трех диагоналей стенок. - Прямоугольный параллелепипед — ребра
Прямоугольный параллелепипед имеет размеры в соотношении 4:3:5. Длина самого короткого края 12 см. Найти: Длины остальных ребер Поверхность прямоугольного параллелепипеда Объем прямоугольного параллелепипеда 92. Длины двух его ребер равны a = 3 см, b = 5 см. Вычислите длину его третьего ребра. Скажем: по формуле для поверхности блока сначала вычислите c. - Призма Ниццы
Рассчитайте поверхность прямоугольного параллелепипеда, если сумма его ребер равна a + b + c = 19 см, а размер диагонали тела u = 13 см. - Рассчитать 62864
Объем блока 1440 см 3 , его поверхность 792 см 2 , площадь одной из его стен 92 см². Вычислите длины его сторон. - Четырехугольник 70294
Длины ребер четырехугольной призмы находятся в соотношении a:b:c = 2:4:5. Поверхность призмы 57 см². Рассчитайте объем.
Поверхность призмы 57 см². Рассчитайте объем. - Прямоугольник 7768
Основой прямоугольного параллелепипеда является прямоугольник. Отношение его длины к ширине 3:2. Длина прямоугольника основания находится в отношении 4:5 к высоте блока. Сумма длин всех ребер блока равна 2,8м. Найдите: а) поверхность - Отношение ребер
Размеры прямоугольного параллелепипеда находятся в соотношении 3:1:2. Диагональ тела имеет длину 28 см. Найдите объем прямоугольного параллелепипеда. - Ребра куба в соотношении
Длины ребер куба в соотношении 2:4:6. Вычислите их длины, зная, что объем прямоугольного параллелепипеда равен 24576 см³. - Диагональ тела
Найдите длину диагонали тела прямоугольного параллелепипеда с длинами ребер 16 см, 7 см и 4 см. - Сантиметры 4091
Вычислите длину диагонали тела бруска, два ребра которого имеют длину 2 см и 7 см, а объем равен 49 кубическим сантиметрам. - Прямоугольный параллелепипед — пропорции
Размеры ребер прямоугольного параллелепипеда находятся в соотношении 2:3:5.
Единицы физических величин:
Класс слова задача:
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: видео1 видео2

 Найдите третье ребро, выходящее из той же вершины.
Найдите третье ребро, выходящее из той же вершины. Найдите его диагональ.
Найдите его диагональ. Ребро, перпендикулярное этой грани, равно 5. Найдите объем параллелепипеда.
Ребро, перпендикулярное этой грани, равно 5. Найдите объем параллелепипеда.
 Площадь одной его грани равна 18. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Площадь одной его грани равна 18. Найдите ребро параллелепипеда, перпендикулярное этой грани.
 Диагональ параллелепипеда равна 34. Найдите объем параллелепипеда.
Диагональ параллелепипеда равна 34. Найдите объем параллелепипеда. Найдите его диагональ.
Найдите его диагональ. Найдите площадь поверхности параллелепипеда.
Найдите площадь поверхности параллелепипеда. Найдите площадь его поверхности.
Найдите площадь его поверхности. Найдите объем треугольной пирамиды
Найдите объем треугольной пирамиды 
 Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K.
Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K.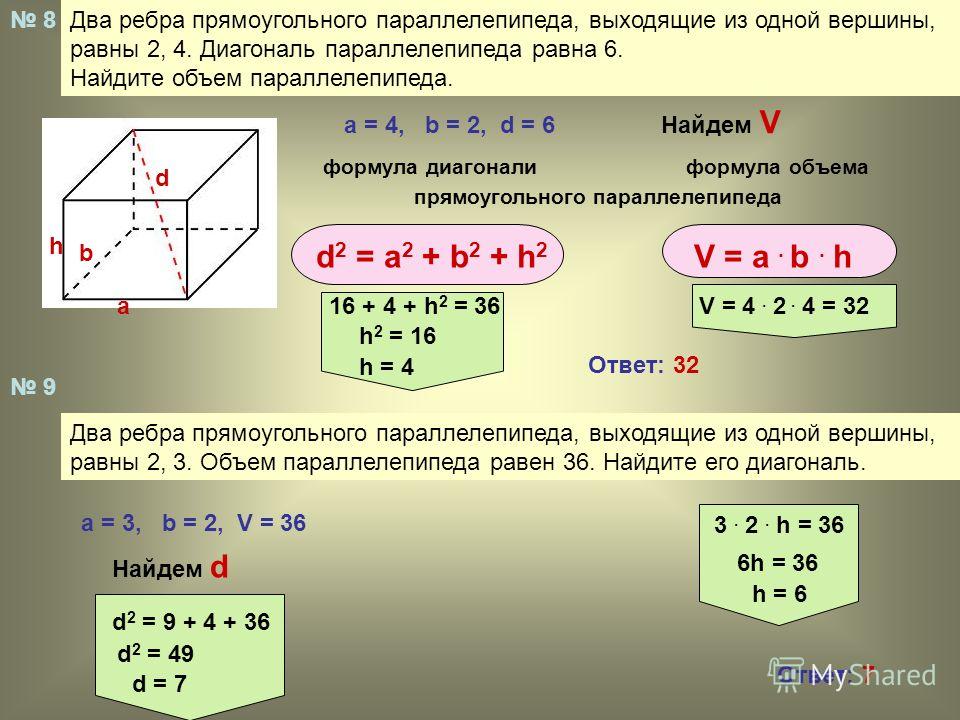 Площадь одной стены 60 см². Вычислите длины ребер a, b и c.
Площадь одной стены 60 см². Вычислите длины ребер a, b и c.

 Поверхность призмы 57 см². Рассчитайте объем.
Поверхность призмы 57 см². Рассчитайте объем.
Leave A Comment