Корень из 3 умножить на корень из 27: Решить sqrt[3]{27*8/256} | Microsoft Math Solver

{2}\]

Степень корня указывается над знаком корня слева. \[\sqrt[x]{a}\], в данном примере х — степень. Если запись не имеет такого обозначения, значит перед нами корень квадратный.

Умножение корней

Существует несколько вариантов умножения корней, это умножение с множителем, без множителя и с разными показателями.

Умножение без множителей

Первым делом рассмотри, как умножаются корни без множителя.

Убедившись, что корни, с которыми необходимо произвести действие имеют одинаковые степени. Например квадратный корень из числа а, можно умножать на квадратный корень из d.

Рассмотрим правило на двух примерах произведения двух квадратных и двух кубических корней.

Примеры:

\[\sqrt{2} * \sqrt{6}=\] первый пример умножение квадратных корней.

\[\sqrt[3]{3} * \sqrt[3]{18}=\] второй пример умножение кубических корне.

Решение:

Для того чтобы решить данные примеры необходимо произвести умножение под корнем. {2} * 3}=2 \sqrt{3}\], в данном примере число 12 можно разложить на произведение чисел 4 и 3, где 4 равно двум в квадрате.  Поэтому 2 выносим за приделы корня и упрощаем выражение.

\[\sqrt[3]{54}=\sqrt[3]{27 * 2}=\sqrt[3]{(3 * 3 * 3) * 2}=3 \sqrt[3]{2}\] в данном случае получившееся подкоренное число 54 можно разложить на произведение двух чисел 27 и 2 , где 27 = 3³, тройку выносим за корень кубический, тем самым мы упростили выражение.

Точно также производится умножение корней других степеней, при этом не важно количество умножаемых корней, правило не изменится.

Умножение корней с множителями

В данном случае мы так же рассматриваем примеры умножения корней с одинаковыми степенями. Множителем является число, стоящее перед корнем. Если при написании множитель отсутствует, то он равен единице. Умножить корень на число значит умножить число на множитель перед корнем. Для того чтобы произвести умножение с такими корнями, необходимо перемножить множители.

Пример умножения корней:

\[2 \sqrt{6} * \sqrt{6}=2 \sqrt{6 * 6}=2 \sqrt{36}=2 * 6=12\] в данном примере мы сначала произвели умножение множителей 1 и 2 , затем воспользовавшись первым правилом умножения корней, произвели умножение под знаком корня чисел 6 и 6.

Следующим шагом упрощаем выражение, корень из 36, равен целому числу 6. последним действием умножаем его на полученный множитель 2. и получаем ответ 12.

Пример 2.

\[2 \sqrt{6} * 3 \sqrt{3}=2 * 3 \sqrt{6 * 3}=6 \sqrt{18}=6 \sqrt{9 * 2}=6 * 3 \sqrt{2}=18 \sqrt{2}\]

В приведённом примере, мы также в начале производим умножение множителей 2 и 3, затем производим умножение подкоренных чисел 6 и 3, в результате получаем 6 корней из 18.

 После производим упрощение выражения под знаком корня, для этого разложили его на множители, таким образом чтобы одно из чисел можно было вынести за пределы знака корень такими числами стали 9 и 2, в результате получилось, что вынесенное число равно трём, так как 9 = \[3^{2}\] .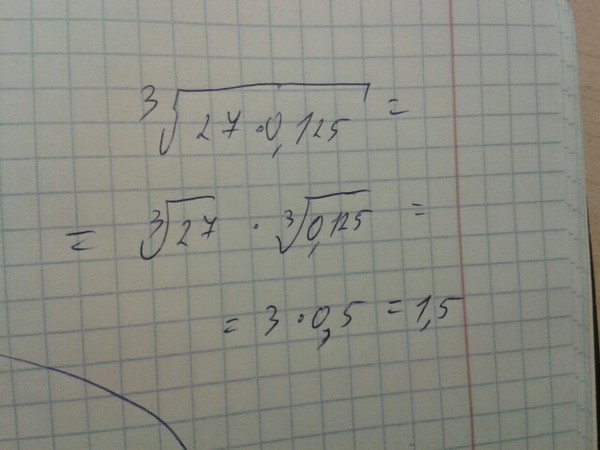

Теперь умножим получившийся ранее множитель 6 на вынесенное из под корня число 3, и получим ответ 18 корней из двух.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Умножение корней с разными показателями

Теперь разберём, как умножить корни если их показатели степени разные. Для этого необходимо найти наименьшее общее кратное число для этих показателей.  Таким числом является наименьшее число, которое можно разделить на оба эти показателя. Для того чтобы разобраться лучше в данном методе, приведём пример.

Пример:

\[\sqrt[2]{2} * \sqrt[3]{5}=\]

Сначала необходимо найти наименьшее общее кратное, наименьшим в данном случае является произведение 2*3 = 6. Значит для того чтобы произвести умножение корней необходимо привести их к показателю шестой степени.

Записываем новое полученное выражение \[\sqrt[6]{2} * \sqrt[6]{5}=\]

Теперь находим числа на которые нужно умножить показатели, чтобы найти наименьшее общее кратное

Для первого корня это деление 6\2 = 3, для второго 6\3 =2

Следующим шагом нужно возвести подкоренное число в степень, которая ровна числам найденным ранее, при нахождении НОК, то есть \[\sqrt[6]{2^{3}} * \sqrt[6]{5^{2}}=\]

Далее имея одинаковые показатели производим действия по умножению корней, так как делали это в предыдущих правилах. {2}}=\sqrt[6]{8 * 25}=\sqrt[6]{200}\]

Если полученное выражение можно упростить, то упрощаем его. В данном случае это невозможно.

Как мы видим произвести умножение корней не так и сложно, главное запомнить основные правила и формулы умножения корней и пользоваться ними.

Определение корня n-ой степени. Свойства арифметического корня n-ой степени 9 класс онлайн-подготовка на Ростелеком

Тема 15.

Определение корня n-ой степени. Свойства арифметического корня n-ой степени.

Давай вспомним, что квадратным корнем из числа а называется такое число, квадрат которого равен а. Аналогично определяется корень любой натуральной степени n.

Итак, корнем n-ой степени из числа а называется такое число, n-ая степень которого равна а.

Например, корнем пятой степени из 32 является число 2, так как 2⁵=32, корнем четвертой степени из 81 является каждое из чисел 3 и -3, так и 3⁴=81 и (-3)⁴=81.

Корень второй степени принято называть квадратным корнем, а корень третьей степени – кубическим корнем.

Если n — нечетное число, то выражение an имеет смысл при любом a; если n — четное число, то выражение an имеет смысл при a≥0.

Из определения корня n-ой степени следует, что при всех значениях а, при которых выражение anимеет смысл, верно равенствоann=a.

Определение: Арифметическим корнем n-ой степени из неотрицательного числа а называется неотрицательное число, n-ая степень которого равна а.

Корень нечетной степени из отрицательного числа можно выразить через арифметический корень. Например,

-83=-83=-2

Значит, при любом положительном a и нечетном n верно равенство:

-an=-an

Решим уравнение: x⁶ = 7. Корнями уравнения служат числа, шестая степень которых равна 7. И таких чисел два: 76 и -76.

Решим уравнение x³ = 27. Уравнение имеет единственный корень, это число, третья степень которого равна 27, то есть 273=3.

Рассмотрим свойства арифметического корня n-ой степени.

1. Если a≥0 и b≥0, то abn=anbn

Корень из неотрицательных множителей равен произведению корней из этих множителей.

Например, найдем значение выражения 16∙814=164∙814=2∙3=6

2. Если a≥0 и b>0, то abn=anbn

Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

Например, найдем значение выражения 210273=64273=643273=43=113.

3. Если n и k – натуральные числа и a≥0, то akn=ank
4. Если n,k и m – натуральные числа и a≥0, то amknk=amn

Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.

Рассмотрим некоторые примеры.

Вычислим значение выражения:

1353∙253=135∙253=27∙5∙253=27∙1253=3∙5=15

5106212∙526=510∙212∙526=512∙2126=10126=102=100

8-373∙8+373=8-378+373=64-373=273=3

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Квадратный корень из 27 — Как найти квадратный корень из 27?

LearnPracticeDownload

Знаете ли вы, что число 27 — единственное натуральное число, которое в 3 раза больше суммы своих цифр? Число 27 также называют троицей троиц, потому что это куб из 3. В этой главе мы вычислим квадратный корень из 27 методом деления в длинную сторону вместе с решенными примерами и интерактивными вопросами.
Давайте посмотрим, что такое квадратный корень из 27.

• Квадратный корень из 27 : √ 27 = 5,196152
• Квадрат 27: 27 ² = 729

1.	Чему равен квадратный корень из 27?
2.	Является ли квадратный корень из 27 рациональным или иррациональным?
3.	Как найти квадратный корень из 27?
4.	Важные примечания
5.	Нестандартное мышление!
6.	Часто задаваемые вопросы о квадратном корне из 27

Чему равен квадратный корень из 27?

Квадратный корень из числа — это число, которое умножается на само себя, чтобы получить исходное число. Неквадратные числа также имеют квадратный корень, просто они не являются целыми числами. Квадратный корень из 27 в радикальной форме представлен как √ 27, а в экспоненциальной форме он выражается как 27 ^1/2 . Квадратный корень из 27, округленный до 6 знаков после запятой, равен 5,196152.

Является ли квадратный корень из 27 рациональным или иррациональным?

Рациональное число — это число, имеющее вид p/q, где:

• p и q — целые числа
• q не равно 0

Число, которое нельзя выразить как отношение двух целых чисел, является иррациональным числом. Неконечные десятичные числа, имеющие повторяющиеся числа после запятой, являются рациональными числами. Теперь давайте посмотрим на квадратный корень из 27. 
√ 27 = 5,196152.
Как вы думаете, десятичная часть останавливается после 5.196152? Нет, она бесконечна. Следовательно, это неконечная десятичная дробь с неповторяющимися числами.
Число 5,1961524227.

.. нельзя записать в форме p/q. Итак, √ 27 — иррациональное число.

Как найти квадратный корень из 27?

Квадратные корни можно вычислить двумя способами:

1. Путем упрощения радикала чисел, которые являются полными квадратами
2. С помощью метода деления в длину для полных и несовершенных квадратов

Квадрат числа 5 равен 5 × 5 = 25, а квадрат числа 6 равен 6 × 6 = 36. Число 27 лежит между 25 и 36, поэтому 27 не является полным квадратом целого числа. Таким образом, для вычисления квадратного корня из 27 используется метод длинного деления.

Упрощенная радикальная форма квадратного корня из 27

Чтобы упростить квадратный корень из 27, сначала представим 27 как произведение его простых множителей. Простая факторизация числа 27 – это 3 × 3 × 3. Следовательно, √ 27 можно еще упростить как √ 3 × 3 × 3 = 3 √ 3. Таким образом, мы выразили квадратный корень из 27 в простейшей радикальной форме как 3 √ 3. Можете ли вы попробовать выразить квадратный корень из 20 аналогичным образом?

Извлечение квадратного корня из 27 методом деления в длину

Выполните приведенные ниже действия, чтобы найти корень квадратный из 27 путем деления в длину.

• Шаг 1. Сгруппируйте цифры 2 и 7 в пару, поместив над ними черту. Поскольку наше число равно 27, давайте представим его внутри символа деления.
• Шаг 2. Найдите наибольшее число, произведение которого при умножении на само себя меньше или равно 27. Мы знаем, что 5 × 5 = 25, а 25 меньше 27. 
• Шаг 3: Расставим пары десятичной точки и нулей и продолжим деление. Теперь умножьте частное на 2, и произведение станет начальной цифрой нашего следующего делителя.
• Шаг 4. Выберите наибольшее число вместо единицы для нового делителя, чтобы его произведение с числом было меньше или равно 200. Мы знаем, что 0 находится в разряде десятков, а наше произведение должно быть 200 и ближайшим умножение 102 × 2 = 204. Но 204 больше, чем 200. Поэтому используйте число 1 в разряде единиц, что дает 101 × 1 = 101
• . Шаг 5. Сократите следующую пару нулей и умножьте частное 51 (без учета десятичной дроби) на 2, то есть на 102, и на начальную цифру нового делителя. Обратите внимание, что квадратный корень из 27 — иррациональное число, т. е. бесконечное. Итак, остановите процесс после еще 2 или 3 итераций, повторив шаги 3 и 4, и вы получите квадратный корень из 27 методом деления в большую сторону.

Изучение квадратных корней с помощью иллюстраций и интерактивных примеров

• Квадратный корень из 22
• Квадратный корень из 26
• Квадратный корень из 28
• Квадратный корень из 29
• Квадратный корень из 30

Важные примечания:

• Квадратный корень из 27 в подкоренной форме выражается как 3 √ 3.
• В форме экспоненты квадратный корень из 27 записывается как 27 ^1/2 .
• Десятичное представление √ 27 равно 5,196125….
.

Think Tank:

• Можете ли вы придумать квадратное уравнение, корни которого равны √27?
• Поскольку (-√27) ²  = 27, можем ли мы сказать, что -√27 также является квадратным корнем из 27?

 

 

Как ваш ребенок может освоить математические понятия?

Мастерство в математике приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.

Забронировать бесплатный пробный урок

 

перейти к слайдуперейти к слайдуперейти к слайду

 

Часто задаваемые вопросы О квадратном корне из 27

Чему равен квадратный корень из 27?

Квадратный корень из 27 равен 3√3.

Как упростить квадратный корень из 27?

Запишите 27 как произведение его простых множителей. Таким образом, 27 = 3 × 3 × 3,
. Затем поступаем следующим образом: √27 = √3 × 3 × 3 = 3√3

Рационален ли квадратный корень из 27?

Нет, квадратный корень из 27 нерационален.