Диагонали ромба
Каким способом высчитать диагональ:
Выберите способчерез сторону и другую диагональчерез сторону и уголчерез вторую диагональ и уголчерез площадь и диагональСпособ расчёта
Введите размеры:
Выберите способ
расчёта
Результат:
Решение:
Отправить ссылку в:
# Теория
Ромб — это параллелограмм у которого все стороны равны.
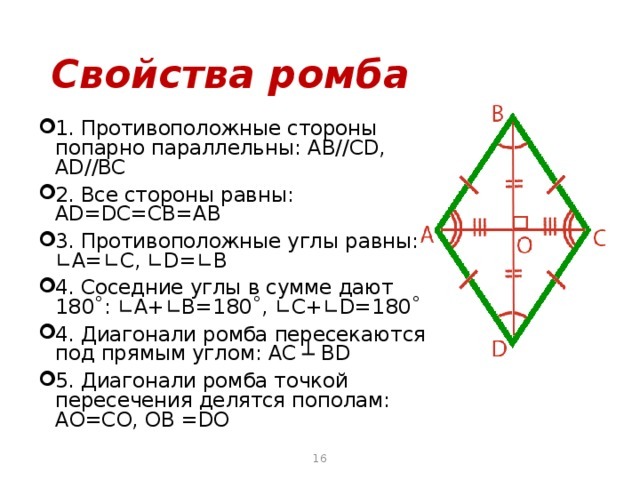
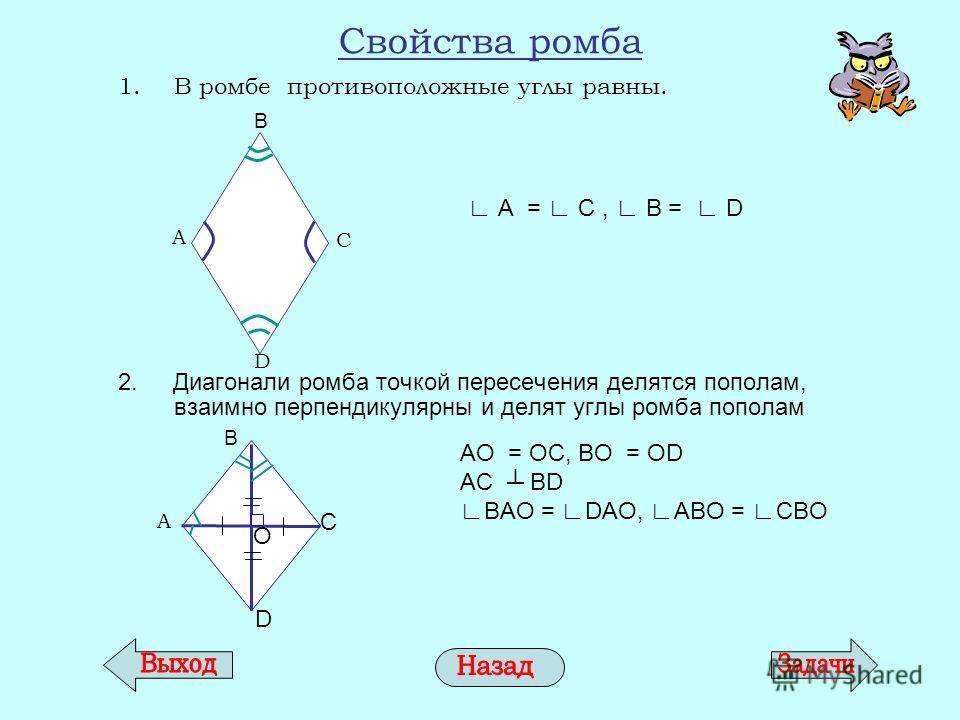
Свойства ромба:
- Диагонали ромба делят его углы пополам.
- Cумма углов прилежащих к одной стороне равна 180°.
- Диагонали ромба пересекаются под прямым углом (90°).
- Диагонали ромба в точке пересечения делятся попалам.
- Диагонали ромба являются биссектрисами его углов.

- D — большая диагональ ромба
- d — меньшая диагональ ромба
- a — сторона ромба
Через сторону и угол
Ddaaaaαβ- D — большая диагональ
- d — меньшая диагональ ромба
- a — сторона ромба
- α — острый угол ромба (от 0° до 90°)
- β — тупой угол ромба (от 90° до 180°)
D = a \sqrt{2 + 2 \cdot \cos \alpha}
D = a \sqrt{2 — 2 \cdot \cos \beta}
d = a \sqrt{2 + 2 \cdot \cos \beta}
Через угол и вторую диагональ
D = d \cdot \tg ( \dfrac{\beta}{2} )
d = D \cdot \tg ( \dfrac{\alpha}{2} )
- D — большая диагональ ромба
- d — меньшая диагональ ромба
- α — острый угол ромба (от 0° до 90°)
- β — тупой угол ромба (от 90° до 180°)
Через площадь и вторую диагональ
D = \dfrac{2 \cdot S}{d}
d = \dfrac{2 \cdot S}{D}
- D — большая диагональ ромба
- d — меньшая диагональ ромба
Похожие калькуляторы:
Площадь ромба
Сторона ромба через диагонали
Войдите чтобы писать комментарии
Из вершины тупого угла ромба проведён перпендикуляр к стороне.
 Под ка…
Под ка…Ответы
Оксана
29. 
Михаил Александров
от 0 p.
Читать ответы Андрей Андреевич
от 70 p.

Читать ответы Eleonora Gabrielyan
от 0 p.

Читать ответы Посмотреть всех экспертов из раздела Учеба и наука
Похожие вопросы задача по предмету «Аудит»
Аудиторская организация впервые проводит аудит…
Тетушка Леонсия большая любительница кошек и математики когда у нее спрашивать Сколько у неё кошек она хитро улыбается отвечает меня пять шестых моих кошек плюс 5 шестых кошки сколько кошек у тетушки
Решено
Однородный шар массой 5 кг скатывается без скольжения по наклонной плоскости, образующей угол 30° с горизонтом.

Решено
Первую половину пути автомобиль проехал со скоростью 69 км/ч а вторую половину 111км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути
Пользуйтесь нашим приложением
Какой угол образуется при пересечении диагоналей ромба?
Измерение — это раздел математики, который занимается измерением двумерных (2D) и трехмерных (3D) геометрических фигур и их параметров, таких как длина, форма, площадь поверхности, площадь боковой поверхности, объем и т. д. В простом Другими словами, в нем изложены принципы расчета на основе алгебраических уравнений, математических формул, а также свойства различных геометрических фигур. Круги, треугольники, четырехугольники и пятиугольники являются примерами двухмерных геометрических фигур, а сферы, кубы, призмы, цилиндры и т.
 д. являются примерами трехмерных геометрических фигур. Архимед известен как отец измерения.
д. являются примерами трехмерных геометрических фигур. Архимед известен как отец измерения.Ромб
В евклидовой геометрии ромб — это четырехугольник, противоположные стороны которого параллельны друг другу, а длины всех четырех сторон равны. Ромб — это особый вид параллелограмма, диагонали которого пересекаются пополам и пересекаются друг с другом под прямым углом, т. е. под углом 90°. Противоположные внутренние углы ромба равны, а сумма четырех углов ромба равна 360°. Ромб имеет форму ромба, поэтому его еще называют ромбом. Квадрат является частным случаем ромба, так как он также имеет четыре равные стороны с диагоналями, делящими друг друга пополам под прямым углом. Кроме того, четыре внутренних угла квадрата прямые.
Диагонали ромба
Диагональ — это отрезок, соединяющий противоположные вершины многоугольника. У ромба две диагонали пересекаются пополам под прямым углом, т. е. под углом 90°, и, таким образом, образуются четыре конгруэнтных прямоугольных треугольника.
 Давайте посмотрим на некоторые свойства диагоналей ромба.
Давайте посмотрим на некоторые свойства диагоналей ромба.- Диагонали ромба делятся пополам под прямым углом.
- Диагонали ромба делят противоположные углы ромба пополам.
- Длина диагоналей ромба может быть или не быть равной.
- Длину диагоналей можно найти по различным формулам, т. е. площадь ромба, теорема Пифагора.
- Другой ромб можно составить из ромба, соединив середины половин диагоналей.
Площадь ромба
Площадь, покрытая ромбом в двумерной плоскости, называется площадью ромба. Формула площади ромба равна произведению длин диагоналей, деленному на 2.
Площадь ромба = (d 1 × d 2 )/2 квадратных единиц
Где d 1 и d 2 — длины диагоналей.
Периметр ромба
Периметр ромба – это сумма всех четырех сторон или общая длина его границ. Формула периметра ромба равна четырехкратной длине его стороны.

Периметр ромба = 4а ед.
Где а — длина стороны ромба.
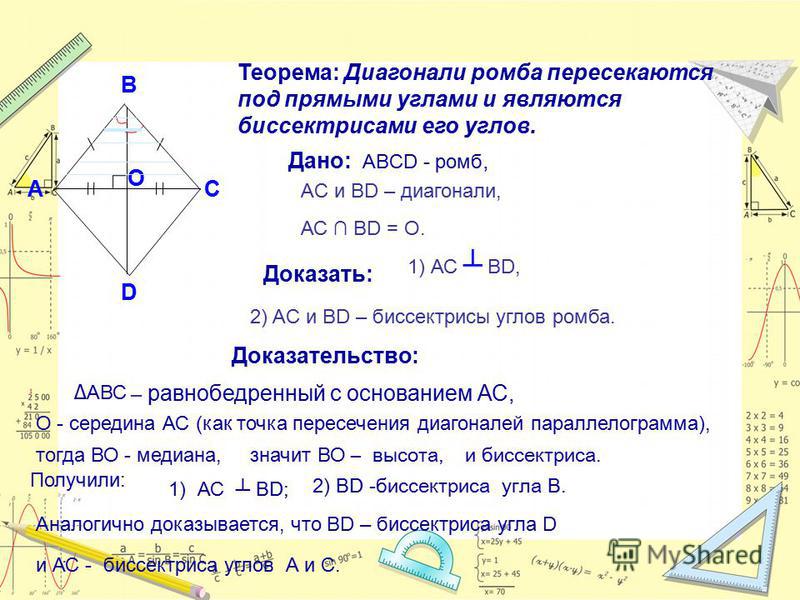
Угол, образованный при пересечении диагоналей ромба
Будем считать ромб ABCD и O точкой пересечения диагоналей AC и BD.
Теперь рассмотрим ΔAOB и ΔAOD
OB = OD [Поскольку диагонали ромба делят пополам]
OA = OA [Общая сторона обоих треугольников]
AB = DA [Поскольку стороны ромба равны]
Следовательно, по теореме SSS (сторона, сторона, сторона), ΔAOB и ΔAOD конгруэнтны.
Поскольку ΔAOB и ΔAOD равны, все соответствующие стороны и углы должны быть равны.
Следовательно, ∠AOB = ∠AOD.
Поскольку BD — прямая, сумма углов ∠AOB и ∠AOD должна быть равна 180°.
Итак, ∠AOB + ∠AOD = 180°
⇒ 2 ∠AOD = 180°
⇒ ∠AOD = 180°/2 = 90°
⇒ 003AOB = 90°003AOB = 90°003AOB = 90°003AOB угол, образованный при пересечении диагоналей ромба, прямой, т.
 е. 90°.
е. 90°.Примеры задач
Задача 1. Найдите диагональ ромба, если его площадь равна 150 см 2 , а длина наименьшей диагонали равна 10 см.
Решение:
Данные,
Площадь ромба = 150 см
Длина кратчайшей диагонали = 10 см.
Мы знаем, что
Площадь ромба = ½ d 1 d 2 квадратных единиц
⇒ 150 = (d 1 × 10)/2
⇒ 300 = d 1 × 10 ⇒ d 1 = 30 см
Следовательно, длина наибольшей диагонали ромба равна 30 см.
Задача 2: Найдите периметр ромба, если длина каждой стороны 11 см.
Решение:
Приведенные данные,
Длина стороны ромба = 11 см.
Мы знаем, что
Периметр ромба = 4а единиц
= 4 × 11 = 11 единиц.
Следовательно, периметр ромба равен 44 см.
Задача 3: Найдите значение x, если AO = 4x-7 и OC = 3x+11, где AC — диагональ ромба, а O — его центр.

Решение:
Даны данные,
AO = 4x-7 и OC = 3x + 11
Мы знаем, что
Диагонали ромба делят пополам.
Следовательно, AO = OC
⇒ 4x – 7 = 3x + 11
⇒ 4x – 3x = 11 + 7
⇒ x = 18
Следовательно, значение x = 18
Задача 4: Найдите значение y на рисунке ниже.
Решение:
При данных данных
∠OCD = 41° и ∠CDO = y
Мы знаем, что угол, образованный при пересечении диагоналей, равен i. , 90°.
Следовательно, треугольник ΔDOC прямоугольный.
⇒ ∠DOC = 90°
Мы знаем, что сумма углов треугольника равна 180°.
⇒ ∠OCD + ∠DOC + ∠CDO = 180°
⇒ 41° + 90° + y = 180°
⇒ y = 180° – 90° – 41° = 49°
9002, Отсюда значение у = 49°.Задача 5: Найдите площадь ромба, если его периметр равен 60 см, а длина одной из его диагоналей 18 см.

Решение:
Данные,
Пусть «а» — каждая сторона ромба
Периметр ромба = 60 см 8 диагонали
3
3
Мы знаем, что
Периметр ромба = 4а
⇒ 4а = 60 ⇒ а = 60/4
⇒ а = 15 см ромб — прямой угол, т. е. 90°.
Итак, рассмотрим прямоугольный треугольник BOC
Мы знаем, что диагонали ромба делят друг друга пополам.
Итак, OB = BD/2 = 9 см
По теореме Пифагора,
BC 2 = OB 2 + OC 2
⇒ OC 2 = BC 2 — OB 2
= (15) — 9 = 225 — 81 = 144
⇒ OC = √144 ⇒ OC = 12 см.
Итак, AC = 2 × OC = 2 × 12 = 24 см.
Мы знаем, что
Площадь ромба (A) = (d 1 × d 2 )/2 квадратных единицы
⇒ A = (24 × 18)/2 = 432/2 = 216 кв.см
Отсюда площадь данного ромба = 216 кв.см
Задача 6: Найти значение y на приведенном ниже рисунке.

Решение:
При данных данных
∠OAB = 36 и ∠OBC = x
Мы знаем, что угол, образованный при пересечении диагоналей ромба, ibus.e. 90°.
Следовательно, ΔAOB — прямоугольный треугольник.
⇒ ∠AOB = 90°
Мы знаем, что сумма углов треугольника равна 180°.
⇒ ∠OAB + ∠AOB + ∠ABO = 180°
⇒ 36° + 90° + ∠ABO = 180°
⇒ ∠ABO = 180° – 90° – 36° = 54°
Мы знаем, что диагонали ромба делят пополам противоположные углы ромба.
Итак, ∠ABO = ∠OBC = 54°
Следовательно, значение x равно 54°.
Задача 7: Найдите площадь ромба, если длина каждой стороны 10 см, а длина одной диагонали 16 см.
Решение:
Приведенные данные,
Длина каждой стороны ромба = 10 см
Длина одной диагонали = 16 см
Мы знаем, что угол, образованный при пересечении диагоналей ромба, является прямым, т.
 е. равен 90°.
е. равен 90°.Рассмотрим прямоугольный треугольник OAB
Мы знаем, что диагонали ромба делят друг друга пополам.
AB = 10 см
OA = AC/2 = 16/2 = 8 см
по теореме Pythagorean,
AB 2 = OA 2 + OB 2
⇒ OB 2 = = = = = = = =. АВ 2 – ОА 2
= (10) 2 – 8 2 = 100 – 64 = 36
⇒ OB = √36 ⇒ OB = 6 см
Теперь BD = 2 × OB = 2 × 6 = 12 см
3
0 Мы знаем, что Площадь ромба (A) = (d 1 × d 2 )/2⇒ A = (16 × 12)/2 = 192/2 = 96 кв. см
Отсюда площадь ромба заданный ромб = 96 кв. см
Диагонали параллелограммов, прямоугольников и ромбов (видео и практика)
TranscriptPractice
Привет, и добро пожаловать на это видео о диагоналях! Сегодня мы собираемся исследовать диагонали параллелограммов, прямоугольников, ромбов и квадратов и посмотреть, как эти фигуры соотносятся друг с другом в целом.
 Давайте начнем!
Давайте начнем!Все фигуры, которые мы сегодня рассмотрим, являются четырехугольниками , то есть все они являются четырехсторонними многоугольниками. Многоугольник — это фигура с несколькими сторонами.
Типы четырехугольников
Свойства параллелограмма
Параллелограмм — это четырехугольник, у которого два набора параллельных сторон. Синие стрелки обозначают, какие стороны параллельны друг другу. Противоположные стороны параллелограмма, отмеченные зелеными галочками, конгруэнтны, что означает, что они имеют одинаковую меру.
Свойства прямоугольника
Прямоугольник — это форма, которую мы все хорошо знаем, поскольку она так часто встречается в реальном мире. Но одна вещь, о которой мы обычно не задумываемся, это то, что прямоугольники — это просто особый вид параллелограмма. Это означает, что противоположные стороны параллельны и конгруэнтны, как и в нашем первом параллелограмме. Что делает прямоугольник специальным параллелограммом , так это то, что его внутренние углы одинаковы.
 На самом деле они все прямые углы , что означает, что они измеряют 90 градусов.
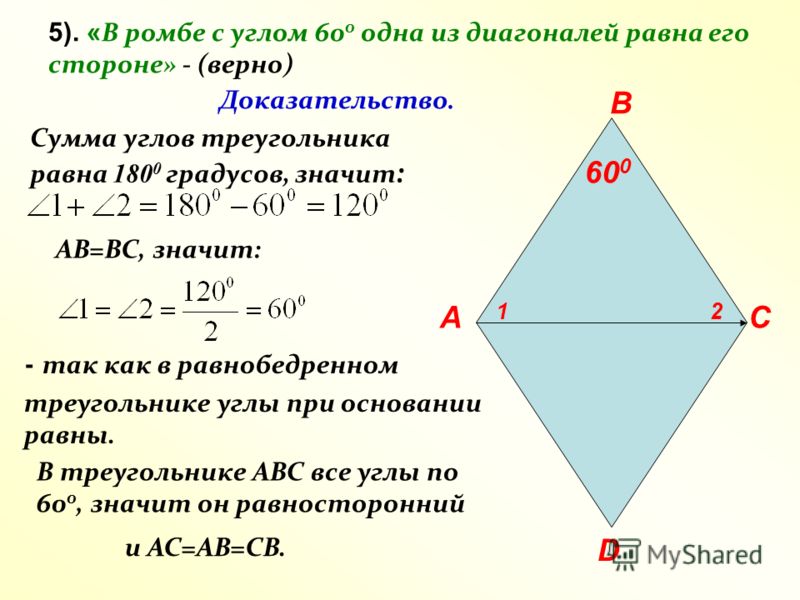
На самом деле они все прямые углы , что означает, что они измеряют 90 градусов.Свойства ромба
Другой особый параллелограмм — ромб. Он обладает всеми свойствами параллелограмма, но все стороны ромба равны. Обратите внимание, что все деления одинаковые, что говорит нам о том, что все стороны имеют одинаковую длину.
Свойства квадрата
Наш последний специальный параллелограмм является прямоугольником и ромбом одновременно, поэтому он имеет прямые углы прямоугольника и конгруэнтные стороны ромба. Это еще одна форма, которую мы все хорошо знаем: квадрат!
Как видите, противоположные стороны параллельны, все углы прямые и все стороны равны.
Итак, давайте вспомним наши четырехугольники, прежде чем мы начнем исследовать их диагонали:
Здесь мы расположили наши четырехугольники в виде «дерева», начиная с квадрата в качестве ствола. Каждый квадрат — это ромб, а каждый ромб — параллелограмм. Каждый квадрат также является прямоугольником, а каждый прямоугольник является параллелограммом.
 Вот как это работает, поднимаясь по дереву. Но спуститься не получится. Не каждый параллелограмм является прямоугольником и не каждый ромб является квадратом.
Вот как это работает, поднимаясь по дереву. Но спуститься не получится. Не каждый параллелограмм является прямоугольником и не каждый ромб является квадратом.Хорошо, теперь давайте исследуем диагонали этих четырех четырехугольников. Диагональ — это отрезок, соединяющий противоположные вершины или углы четырехугольника.
Диагонали параллелограмма
Вот наш обычный неспециальный параллелограмм с показанными диагоналями:
Как видите, диагонали параллелограмма делят друг друга пополам. Другими словами, они разрезают друг друга пополам. Мы могли бы добавить несколько цифр, чтобы лучше проиллюстрировать это…
, или мы могли бы использовать галочки, чтобы показать, что диагонали были разделены пополам:
Поскольку все три специальных четырехугольника, о которых мы говорим, являются параллелограммами, все они будут иметь диагонали, делящие пополам.
Диагонали прямоугольника
Теперь давайте посмотрим на прямоугольник.
 Вот прямоугольник с его диагоналями:
Вот прямоугольник с его диагоналями:Диагонали прямоугольника конгруэнтны, и, опять же, поскольку прямоугольник является параллелограммом, диагонали делят друг друга пополам, делая каждую половину одинаковой длины:
Каждая диагональ прямоугольника также делит прямоугольник на два конгруэнтных прямоугольных треугольника:
Это означает, что при желании мы могли бы вычислить длину диагонали, используя Теорему Пифагора .
Диагонали ромба
Теперь, когда мы разобрались с прямоугольниками, давайте посмотрим, что происходит с другим специальным параллелограммом, ромбом:
Опять же, поскольку каждый ромб является параллелограммом, его диагонали делят друг друга пополам. Однако диагонали НЕ одинакового размера, так что же в этом особенного? Посмотрите на углы, под которыми пересекаются диагонали. Эти углы выглядят так, как будто все они могут быть одинаковыми, и поскольку здесь четыре угла, это должно означать…
Каждый угол равен 90 градусов! Это означает, что диагонали ромба перпендикулярны друг другу 90 493 в дополнение к тому, что 90 494 делят друг друга пополам.

Диагонали квадрата
Итак, остался только один четырехугольник, квадрат. Помните, что квадрат является параллелограммом, прямоугольником и ромбом, поэтому он должен обладать всеми свойствами этих фигур:
- Диагонали делят друг друга пополам.
- Диагонали будут одинаковой длины.
- Диагонали будут перпендикулярны друг другу.
Посмотрим, правы ли мы:
Мы были правы! Если мы посмотрим внимательно, то также увидим, что две диагонали делят квадрат на четыре конгруэнтных равнобедренных прямоугольных треугольника.
Обзор
Теперь, когда мы рассмотрели наши четыре параллелограмма и их диагонали, давайте закончим обзор, чтобы посмотреть, что вы можете вспомнить.
Какое из следующих утверждений неверно?
- Каждый прямоугольник является параллелограммом.
- Каждый ромб является квадратом.
- Каждый квадрат является прямоугольником.
- Диагонали параллелограмма делятся пополам.

- Диагонали ромба пересекаются под прямым углом.
- Диагональ прямоугольника делит его на два равных прямоугольных треугольника.
- Диагонали прямоугольника имеют одинаковую длину.
- Четырехугольник, диагонали которого делятся пополам, пересекаются под прямым углом и равны, должен быть квадратом.
Спасибо за просмотр и приятного изучения!
Практические вопросы
Вопрос № 1:
Какое утверждение относительно диагональных линий, проведенных через квадрат, неверно?Диагональные линии будут одинаковой длины.
Получится четыре конгруэнтных равнобедренных прямоугольных треугольника.
Диагональные линии разделят друг друга пополам.
Будут сформированы четыре разносторонних треугольника.
Показать ответ
Ответ:
Когда диагональные линии проведены через квадрат, будут верны три вещи: диагональные линии будут пересекаться пополам в своих серединах, диагональные линии будут иметь одинаковую длину, а диагональные линии образуют четыре равные треугольники, все из которых являются прямоугольными равнобедренными треугольниками.

Скрыть ответ
Вопрос №2:
Какое утверждение верно?Параллелограмм всегда является прямоугольником.
Прямоугольник всегда является квадратом.
Ромб всегда является параллелограммом.
Параллелограмм всегда является ромбом.
Показать Ответ
Ответ:
Верно, что ромб всегда является параллелограммом. У ромба длины сторон равны, а диагональные линии перпендикулярны друг другу. Каждый квадрат — ромб, но не всякий ромб — квадрат.
Скрыть ответ
Вопрос № 3:
Какое определение не является точным для фигуры ниже?Прямоугольник
Четырехугольник
Ромб
Параллелограмм
Показать Ответ
Ответ:
Эта форма может быть классифицирована как прямоугольник или параллелограмм.
 Однако это не ромб. У ромба длины всех сторон равны.
Однако это не ромб. У ромба длины всех сторон равны.Скрыть ответ
Вопрос № 4:
Дом мальчиков сэра Джона — историческое здание в Кентербери. Сейчас это здание известно своей красной входной дверью с уникальным наклоном. Плотник хочет задокументировать некоторые размеры двери. Какое утверждение будет верным в отношении двух диагональных линий, идущих от угла к углу?Обе диагональные линии будут одинаковой длины.
Диагональные линии будут пересекаться пополам в середине каждой линии.
Диагональные линии разделятся пополам, образуя углы в 90 градусов.
Диагональные линии образуют четыре прямоугольных треугольника.
Показать Ответ
Ответ:
Диагонали параллелограмма пересекаются пополам в середине каждой прямой. Это означает, что каждая строка будет разрезана пополам другой строкой.



 Под ка…
Под ка…


 д. являются примерами трехмерных геометрических фигур. Архимед известен как отец измерения.
д. являются примерами трехмерных геометрических фигур. Архимед известен как отец измерения. Давайте посмотрим на некоторые свойства диагоналей ромба.
Давайте посмотрим на некоторые свойства диагоналей ромба.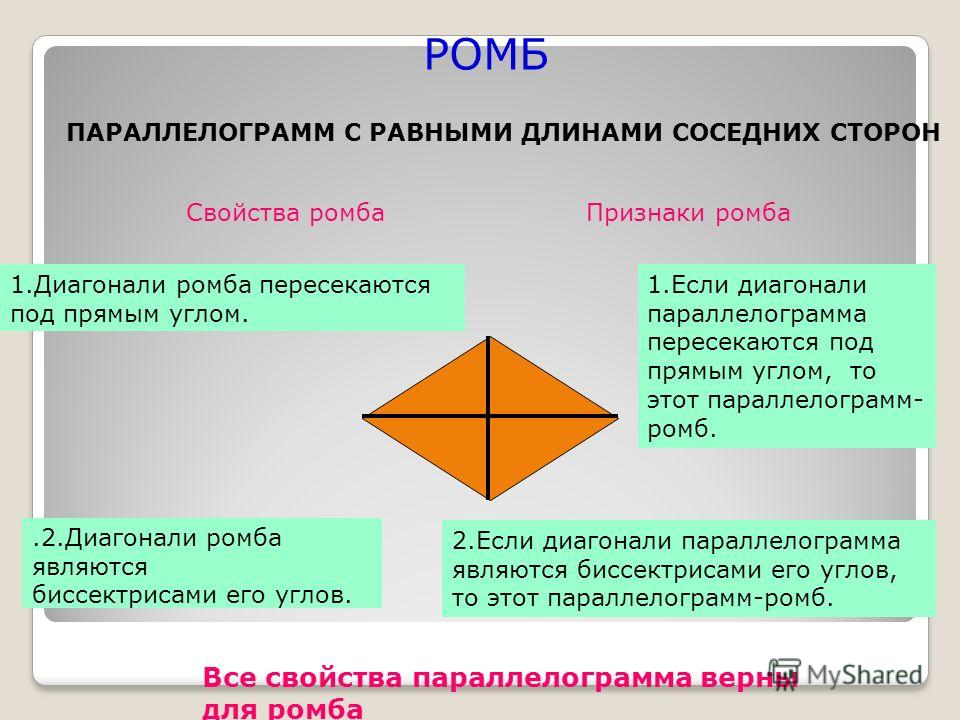
 е. 90°.
е. 90°.

 е. равен 90°.
е. равен 90°.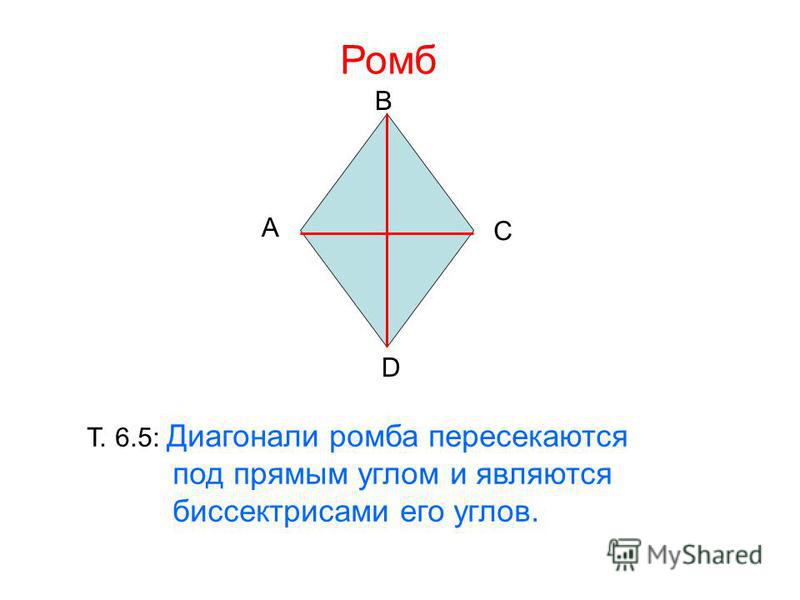 Давайте начнем!
Давайте начнем!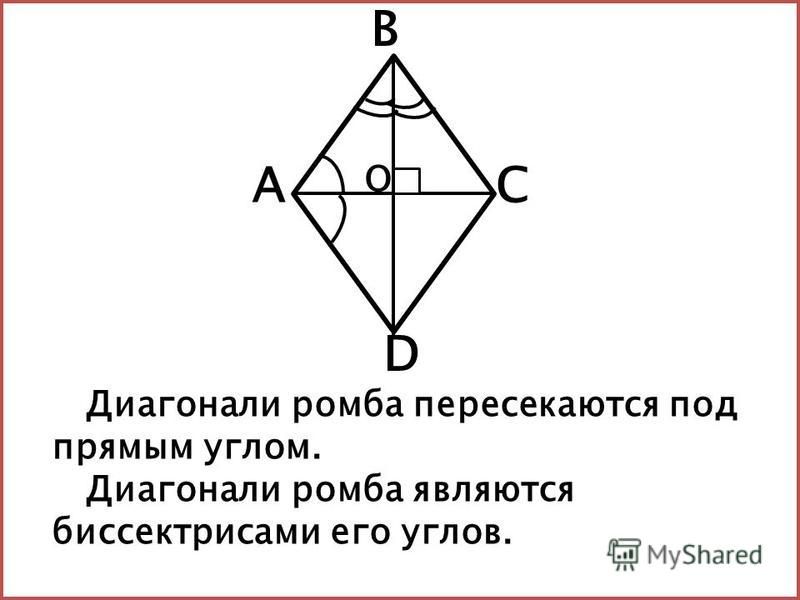 На самом деле они все прямые углы , что означает, что они измеряют 90 градусов.
На самом деле они все прямые углы , что означает, что они измеряют 90 градусов.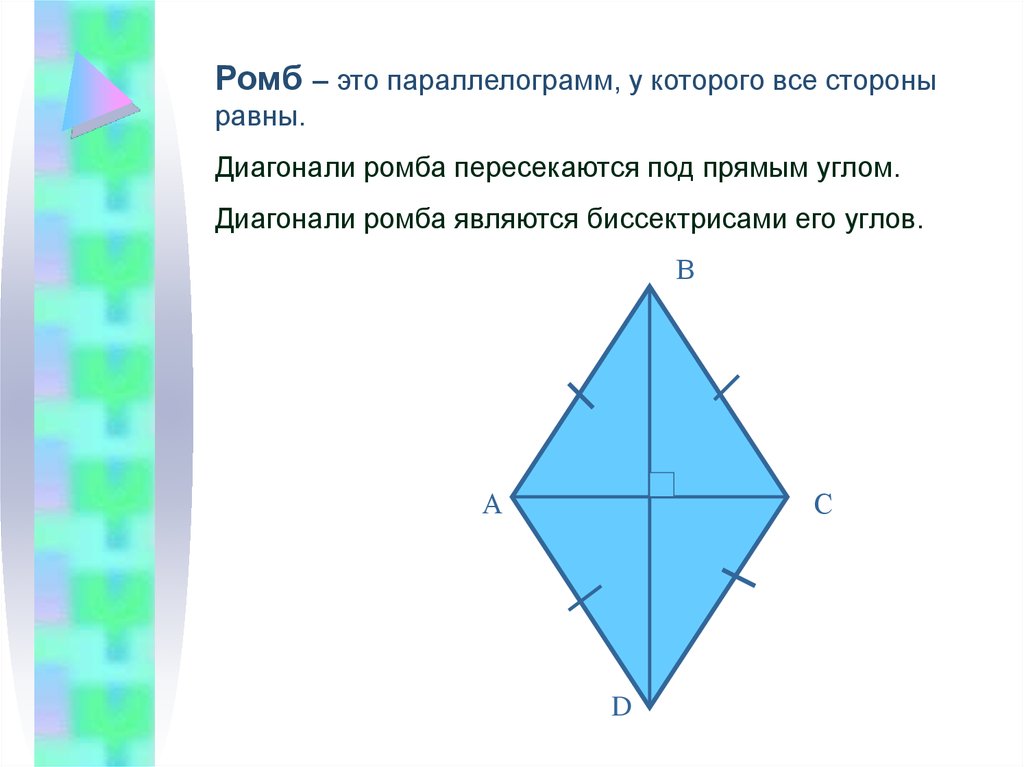 Вот как это работает, поднимаясь по дереву. Но спуститься не получится. Не каждый параллелограмм является прямоугольником и не каждый ромб является квадратом.
Вот как это работает, поднимаясь по дереву. Но спуститься не получится. Не каждый параллелограмм является прямоугольником и не каждый ромб является квадратом.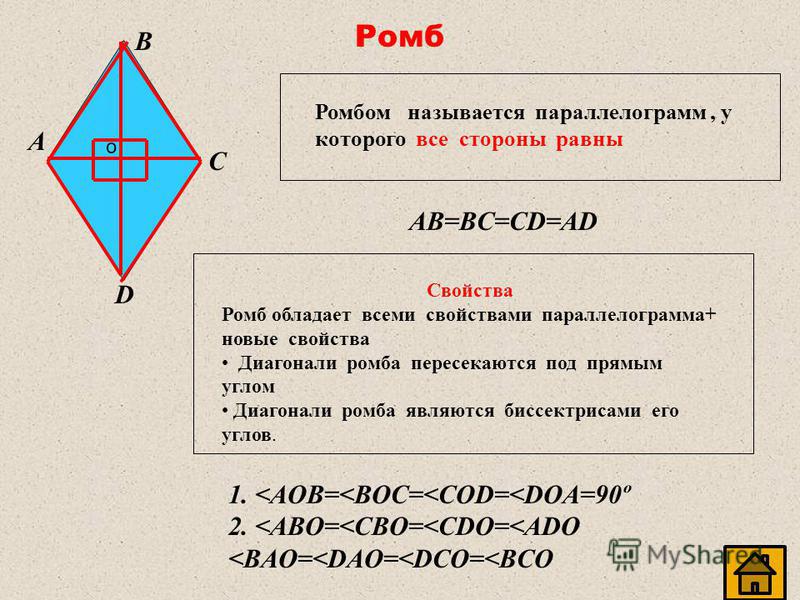 Вот прямоугольник с его диагоналями:
Вот прямоугольник с его диагоналями:

 Однако это не ромб. У ромба длины всех сторон равны.
Однако это не ромб. У ромба длины всех сторон равны.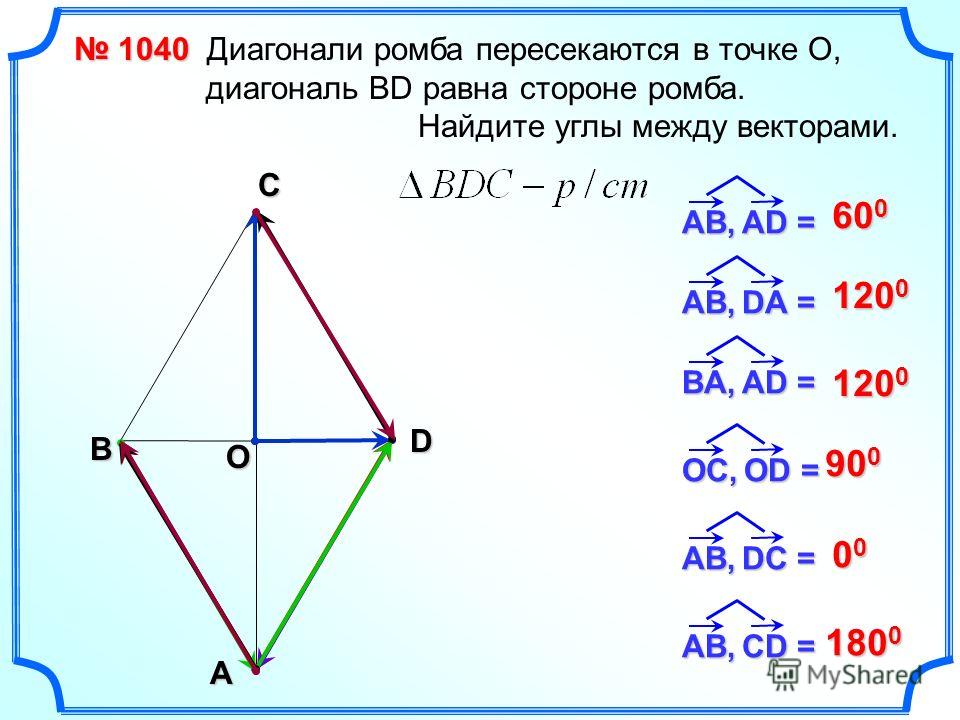
Leave A Comment