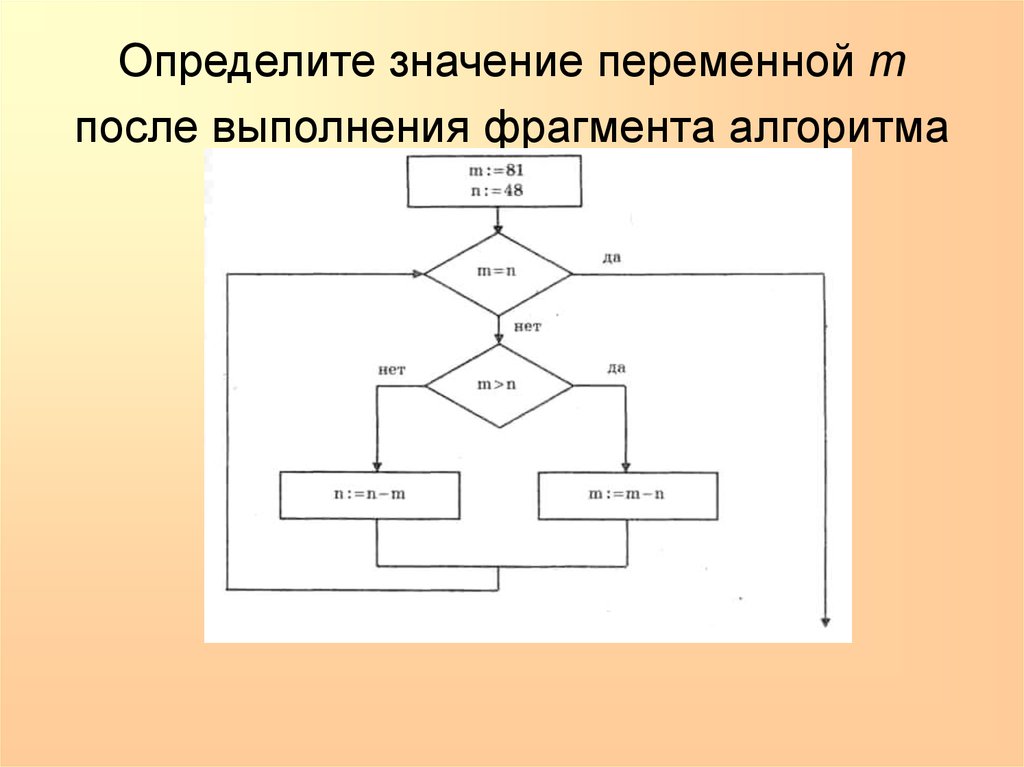
Python: 19x — Линейные программы. Переменные (ОГЭ)
1. Определите значение переменной aпосле выполнения алгоритма: a = 4 В ответе укажите одно целое число – значение переменной a. |
| Ответ: |
2. Определите значение переменной апосле выполнения данного алгоритма: a = 3 В ответе укажите одно целое число – значение переменной а. |
| Ответ: |
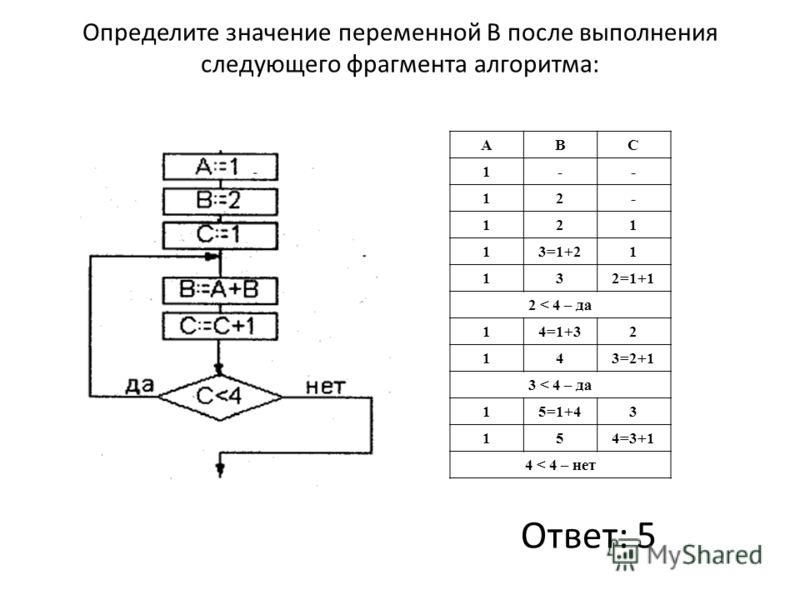
3. Определите значение переменной а после исполнения данного алгоритма. a = 12 В ответе укажите одно число — значение переменной а. |
| Ответ: |
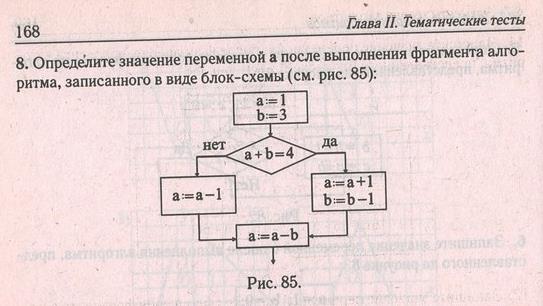
4. Определите значение переменной bпосле выполнения данного алгоритма: a = 4 В ответе укажите одно целое число – значение переменной b. |
| Ответ: |
5. Определите значение переменной eпосле выполнения данного алгоритма: f = 21 В ответе укажите одно целое число – значение переменной e. |
| Ответ: |
6. Определите значение переменной апосле выполнения данного алгоритма: a = 20 В ответе укажите одно целое число – значение переменной а. |
| Ответ: |
7. Определите значение переменной bпосле выполнения данного алгоритма: a = 14 В ответе укажите одно целое число – значение переменной b. |
| Ответ: |
8. Определите значение переменной bпосле выполнения данного алгоритма: b = 5 В ответе укажите одно целое число – значение переменной b. |
| Ответ: |
9. Определите значение переменной bпосле выполнения данного алгоритма: a = 7 В ответе укажите одно целое число – значение переменной b. |
| Ответ: |
10. Определите значение переменной bпосле выполнения данного алгоритма: a = 3 В ответе укажите одно целое число – значение переменной b. |
| Ответ: |
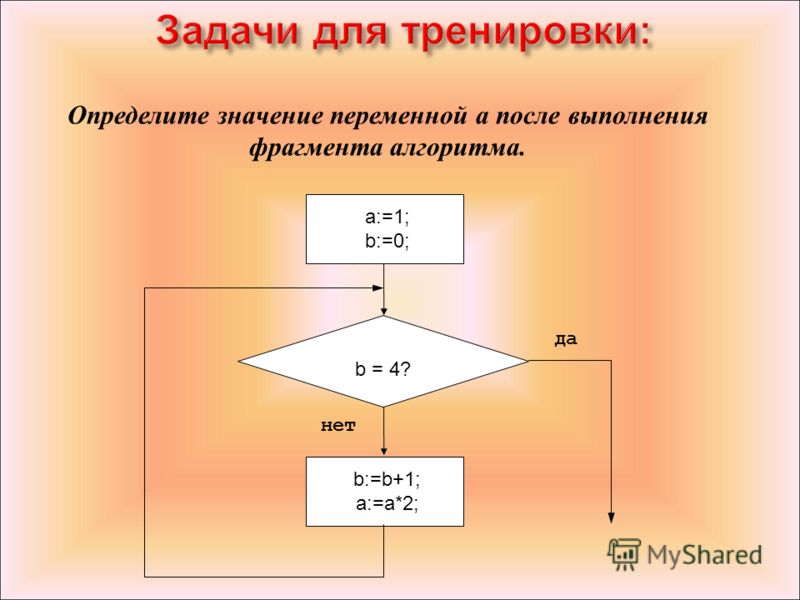
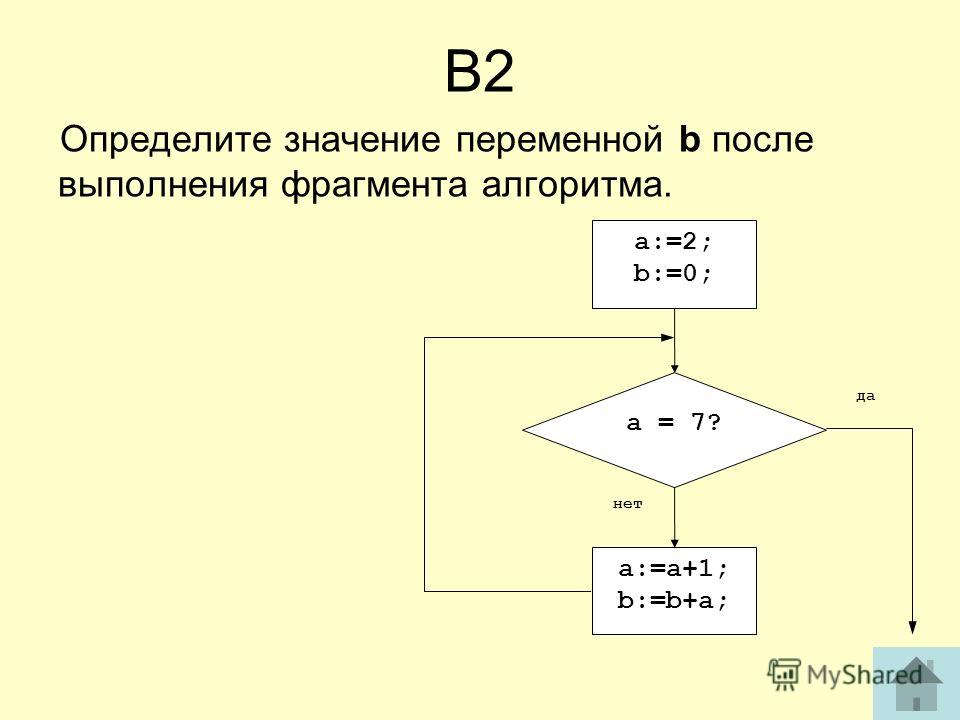
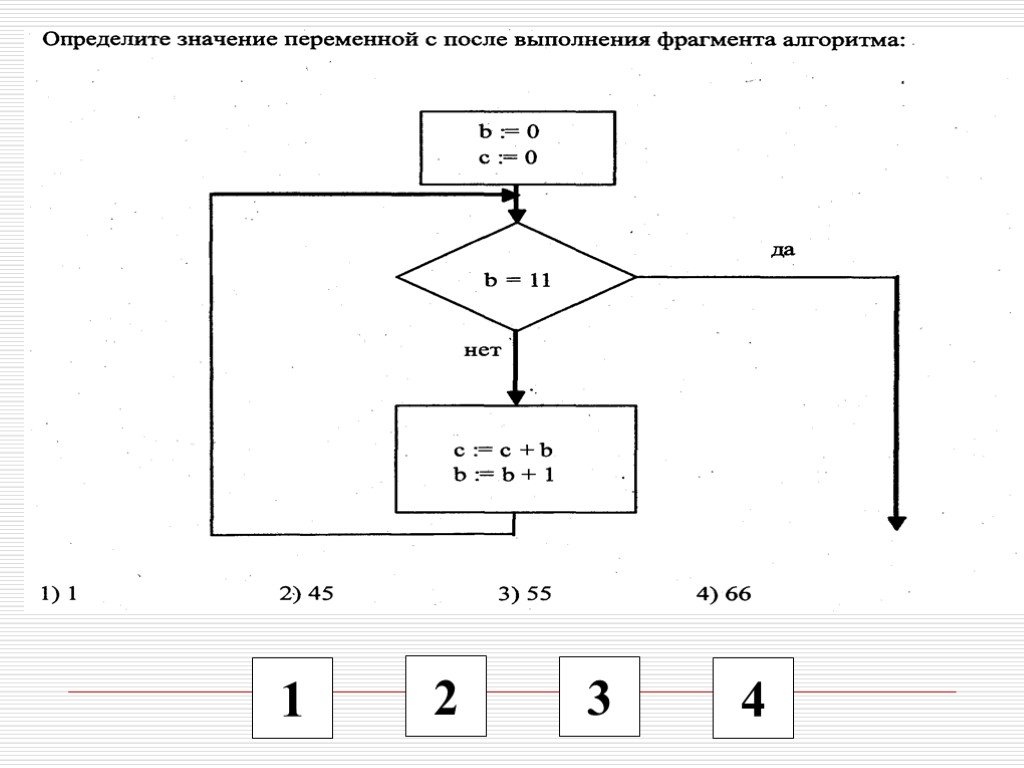
Задания по линейным алгоритмам
Задания 8. Линейный алгоритм, записанный на алгоритмическом языке
1. Задание 8 № 8. В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — операции сложения, вычитания, умножения и деления. Правила и порядок выполнения операций соответствуют правилам арифметики. Определите значение переменной b после выполнения алгоритма:
Задание 8 № 8. В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — операции сложения, вычитания, умножения и деления. Правила и порядок выполнения операций соответствуют правилам арифметики. Определите значение переменной b после выполнения алгоритма:
а := 2
b := 4
а := 2*а + 3*b
b := a/2*b В ответе укажите одно целое число — значение переменной b.
2. Задание 8 № 28. Определите значение переменной b после выполнения алгоритма:
а := 5
b := 4
а := 2*а + 3*b
b := a/2*b В ответе укажите одно целое число — значение переменной b.
3. Задание 8 № 48. Определите значение переменной b после выполнения алгоритма:
а := 4
b := 4
а := 2*а + 3*b
b := a/2*b В ответе укажите одно целое число — значение переменной b.
4. Задание 8 № 68. Определите значение переменной b после выполнения алгоритма:
а := 6
b := 4
а := 2*а + 3*b
b := a/2*b В ответе укажите одно целое число — значение переменной b.
5. Задание 8 № 88. Определите значение переменной b после выполнения алгоритма:
а := 7
b := 4
а := 2*а + 3*b
b := a/2*b В ответе укажите одно целое число — значение переменной b.
6. Задание 8 № 108. Определите значение переменной b после выполнения алгоритма:
а := 3
b := 4
а := 2*а + 3*b
b := a/2*b В ответе укажите одно целое число — значение переменной b.
7. Задание 8 № 128. Определите значение переменной b после выполнения алгоритма:
а := 1
b := 4
а := 2*а + 3*b
b := a/2*b В ответе укажите одно целое число — значение переменной b.
8. Задание 8 № 148. Определите значение переменной b после выполнения алгоритма:
а := 4
b := 2
b := a/2*b
a := 2*а + 3*b В ответе укажите одно целое число — значение переменной a.
9. Задание 8 № 168. Определите значение переменной b после выполнения алгоритма:
а := 6
b := 1
b := a/2*b
a := 2*а + 3*b В ответе укажите одно целое число — значение переменной a.
10. Задание 8 № 188. Определите значение переменной b после выполнения алгоритма:
а := 8
b := 2
b := a/2*b
a := 2*а + 3*b В ответе укажите одно целое число — значение переменной a.
11. Задание 8 № 208. Определите значение переменной b после выполнения алгоритма:
а := 10
b := 1
b := a/2*b
a := 2*а + 3*b В ответе укажите одно целое число — значение переменной a.
12. Задание 8 № 228. Определите значение переменной b после выполнения алгоритма:
а := 2 b := 4 b := a/2*b a := 2*а + 3*b
В ответе укажите одно целое число — значение переменной a.
Задания 8. Линейный алгоритм, записанный на алгоритмическом языке
13. Задание 8 № 248. В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной b после выполнения:
а := 4
b := 4
b := a/2*b
a := 2*а + 3*b В ответе укажите одно целое число — значение переменной a.
14. Задание 8 № 268. Определите значение переменной b после выполнения алгоритма:
а := 6
b := 2
b := a/2*b
a := 2*а + 3*b В ответе укажите одно целое число — значение переменной a.
15. Задание 8 № 288. Определите значение переменной b после выполнения алгоритма:
а := 6
b := 4
b := a/2*b
a := 2*а + 3*b В ответе укажите одно целое число — значение переменной a.
16. Задание 8 № 308. Определите значение переменной b после выполнения алгоритма:
а := 8
b := 3
b := a/2*b
a := 2*а + 3*b В ответе укажите одно целое число — значение переменной a.
17. Задание 8 № 328. Определите значение переменной b после выполнения алгоритма:
а := 4
b := 10
а := b — a*2
b := 24/a*4 В ответе укажите одно целое число — значение переменной b.
18. Задание 8 № 349. Определите значение переменной а после выполнения алгоритма:
а := 5
b := 4
b := 100 — a*b
a := b/16*a В ответе укажите одно целое число — значение переменной a.
19. Задание 8 № 369. Определите значение переменной а после выполнения алгоритма:
a := 10
b := 5
b := 100 + a/b
a := b/6*a В ответе укажите одно целое число — значение переменной a.
20. Задание 8 № 389. Определите значение переменной а после выполнения алгоритма:
а := 10
b := 110
b := 110 + b/a
a := b/11*a В ответе укажите одно целое число — значение переменной a.
21. Задание 8 № 409. Определите значение переменной а после выполнения алгоритма:
а := 0
b := 2
b := 2 + a + 4*b
a := b/2*a В ответе укажите одно целое число — значение переменной a.
22. Задание 8 № 429. Определите значение переменной b после выполнения алгоритма:
а := 3
b := 5
a := 6 + a*b
b := b + a/3 В ответе укажите одно целое число — значение переменной b.
23. Задание 8 № 449. Определите значение переменной a после выполнения алгоритма:
а := 17
b := 23
b := а + b + 1
а := b + а В ответе укажите одно целое число — значение переменной a.
24. Задание 8 № 469. Определите значение переменной a после выполнения алгоритма:
а := 100
b := 50
b := а — b/2 а := a/5 + b/3 В ответе укажите одно целое число — значение переменной a.
Задания 8. Линейный алгоритм, записанный на алгоритмическом языке
25. Задание 8 № 489. В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» —операции сложения, вычитания, умножения и деления.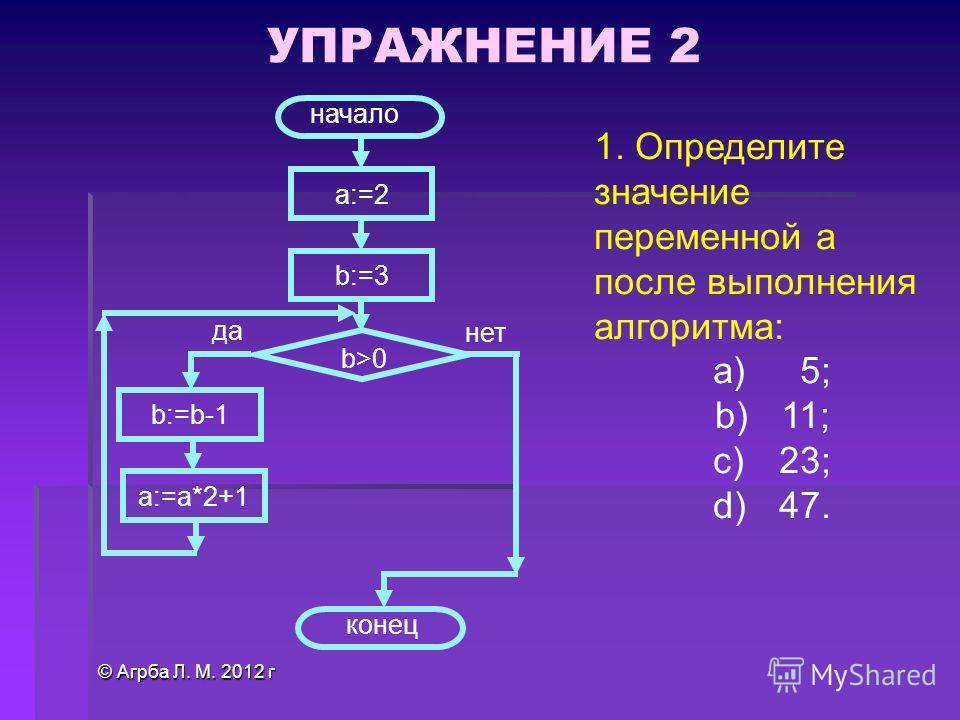 Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной b после выполнения:
Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной b после выполнения:
а := 1
b := 2
b := 3 + a*b
а := b/5*a*4 В ответе укажите одно целое число — значение переменной a.
26. Задание 8 № 509. Определите значение переменной b после выполнения алгоритма:
а := 1
b := 2 + a
b := a + b
а := b/2*2*a — 3 В ответе укажите одно целое число — значение переменной a.
27. Задание 8 № 529. Определите значение переменной b после выполнения алгоритма:
а := 5
b := 2 + a
а := a*b
b := 2*a — b В ответе укажите одно целое число — значение переменной b.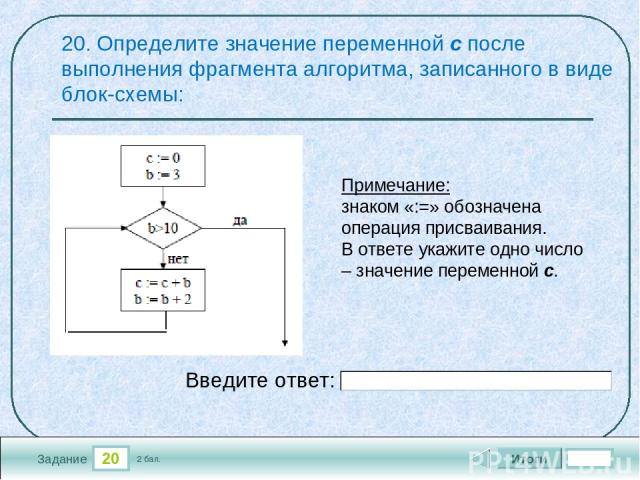
28. Задание 8 № 549. Определите значение переменной b после выполнения алгоритма:
a := 4
b := 5
a := b + 15
b := 100/a*4 В ответе укажите одно целое число — значение переменной b.
29. Задание 8 № 569.. Определите значение переменной a после выполнения алгоритма:
b := 8
a := 10
b := b + a*2
a := 29 — a В ответе укажите одно целое число — значение переменной a.
30. Задание 8 № 589. Определите значение переменной b после выполнения алгоритма:
а := 7
b := 5
а := b*4 — a*2
b := а*4 — 4 В ответе укажите одно целое число — значение переменной b.
31. Задание 8 № 609. Определите значение переменной b после выполнения алгоритма:
а := 7
b := 2
а := b*4 + a*3
b := 30 — a В ответе укажите одно целое число — значение переменной b.
32. Задание 8 № 629. Определите значение переменной b после выполнения алгоритма:
а := 3
b := 8
а := b — a*2
b := 24/a*4 В ответе укажите одно целое число — значение переменной b.
33. Задание 8 № 649. Определите значение переменной b после выполнения алгоритма:
а := 2
b := 20
а := b + a/2
b := 24 — a В ответе укажите одно целое число — значение переменной b.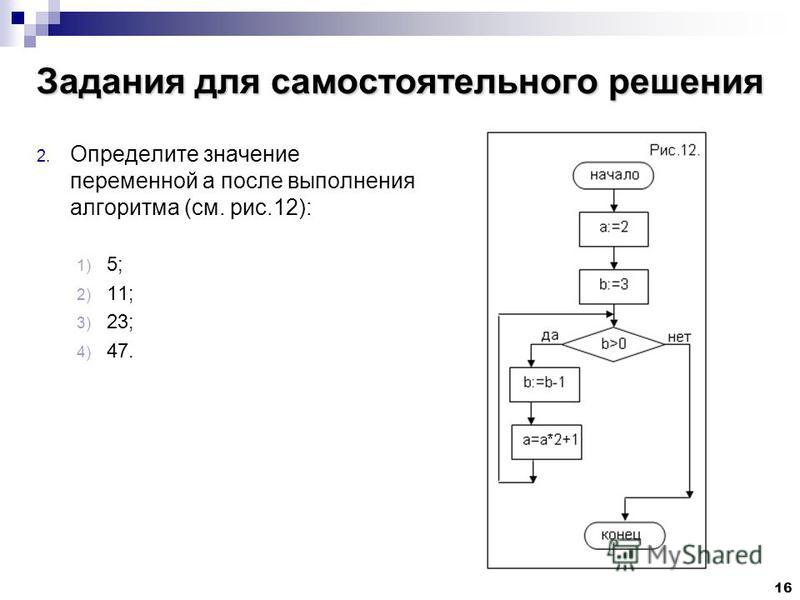
34. Задание 8 № 669. Определите значение переменной b после выполнения алгоритма:
b := -5
a := 2
а := 11 — 2*a — b
b := a/3 — 3*b В ответе укажите одно целое число — значение переменной b.
35. Задание 8 № 689. Определите значение переменной a после выполнения алгоритма:
b := 4
a := -3
b := 7 — 2*a — b
a := b/3 — a В ответе укажите одно целое число — значение переменной a.
36. Задание 8 № 709. Определите значение переменной a после выполнения алгоритма:
а := 6
b := 2 b := a/2*b a := 2*a + 3*b В ответе укажите одно целое число — значение переменной a.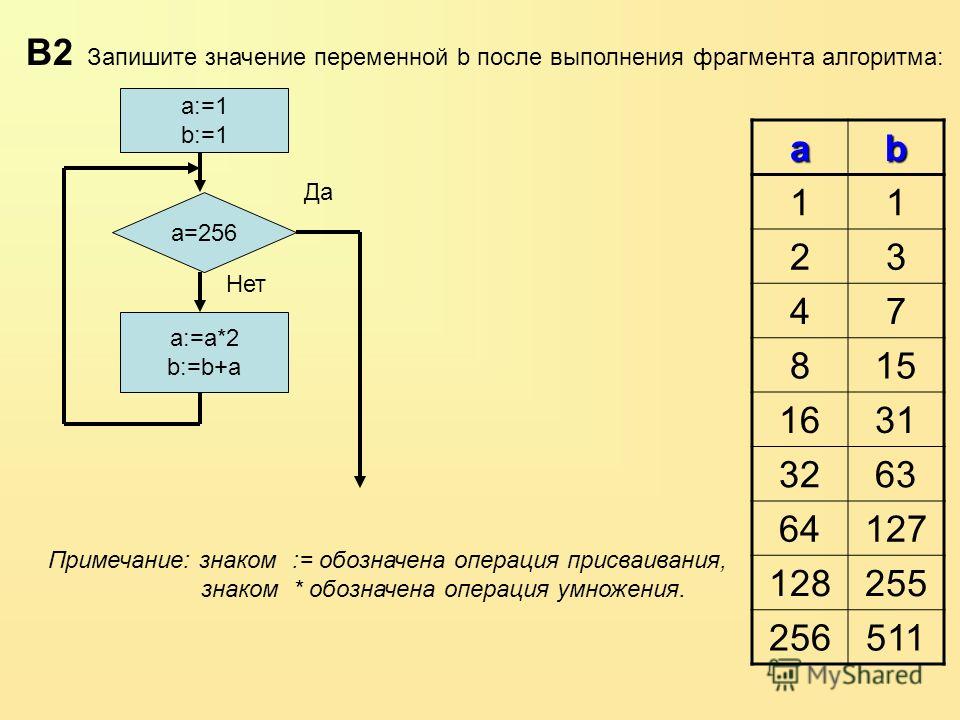
Задания 8. Линейный алгоритм, записанный на алгоритмическом языке
37. Задание 8 № 752. В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной b после выполнения:
а := 1
b := 27
a := b/a*2
b := a*2 — 8 В ответе укажите одно целое число — значение переменной b.
38. Задание 8 № 772. Определите значение переменной a после выполнения алгоритма:
b := 6
a := 30
b := b*4–21
a := 100–a–b В ответе укажите одно целое число — значение переменной a.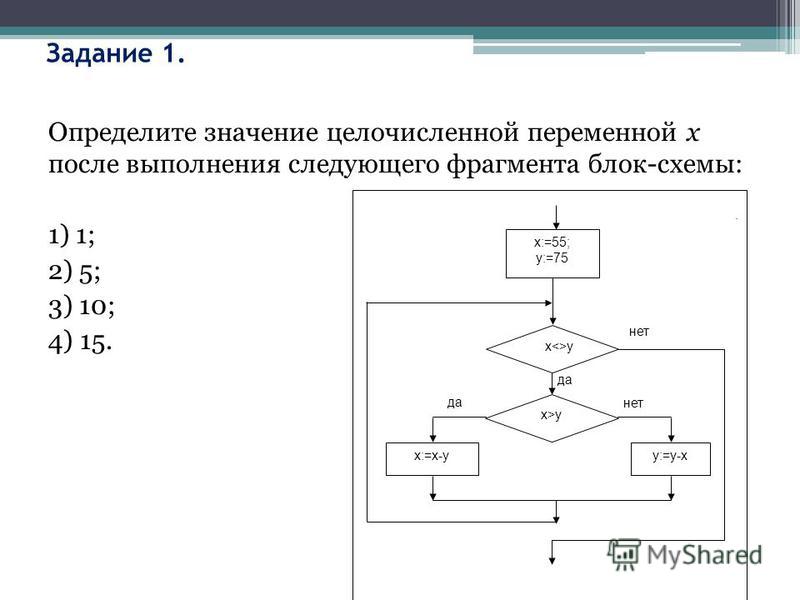
39. Задание 8 № 804. Определите значение переменной n после выполнения алгоритма:
v := 4
n := 13
v := n–v*3
n := v*14–n В ответе укажите одно целое число — значение переменной n.
40. Задание 8 № 824. Определите значение переменной n после выполнения алгоритма:
v := 1
n := 24
v := n–v*4
n := v*2–n В ответе укажите одно целое число — значение переменной n.
41. Задание 8 № 846. Определите значение переменной a после выполнения алгоритма:
a := 4
b := 6
a := ( a / 2 ) * ( b / 2 )
a := 2 * a + b В ответе укажите одно целое число — значение переменной a.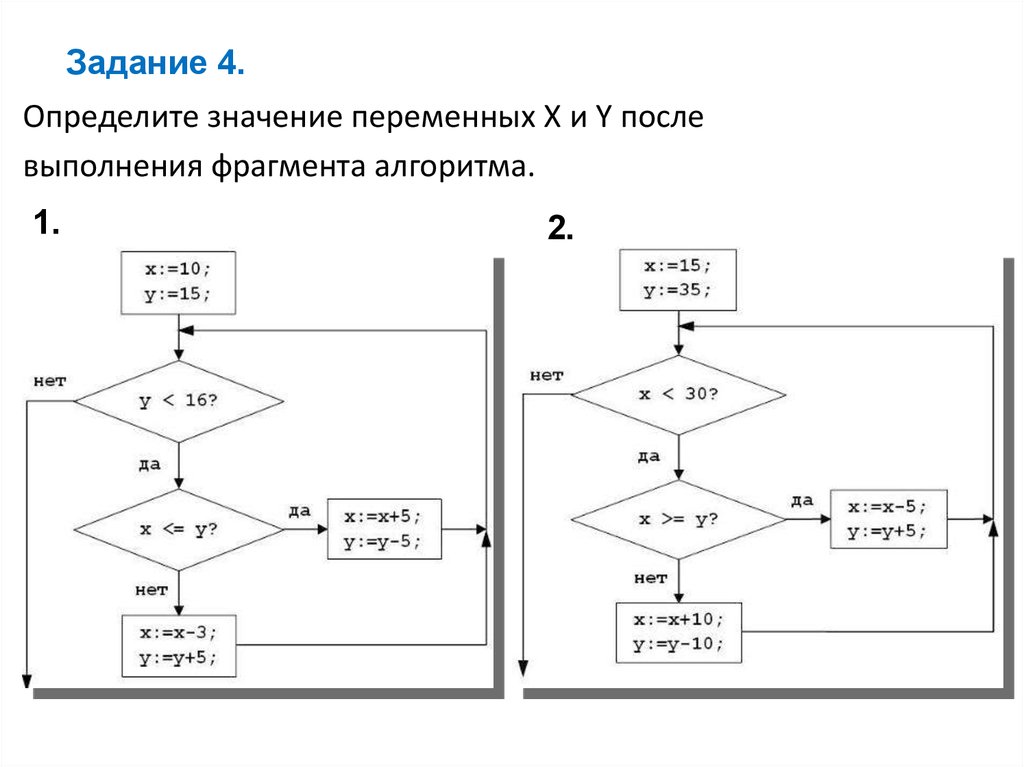
42. Задание 8 № 866. Определите значение переменной b после выполнения алгоритма:
a := 8
b := 3
a := 3 * a – b
b := ( a / 3 ) * ( b + 2 ) В ответе укажите одно целое число — значение переменной b.
43. Задание 8 № 887. Определите значение переменной m после выполнения алгоритма:
k := 5
m := 90
k := m-k*2
m := k*3-m В ответе укажите одно целое число — значение переменной m.
44. Задание 8 № 907. Определите значение переменной m после выполнения алгоритма:
k := 3
m := 30
k := m-k*3
m := k*10-m В ответе укажите одно целое число — значение переменной m.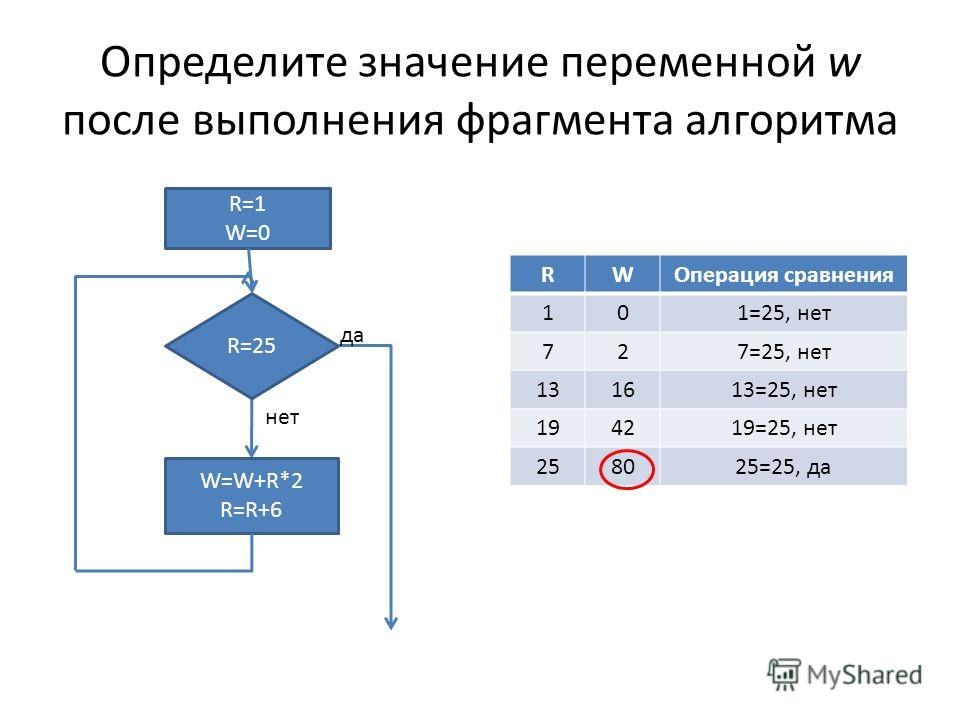
45. Задание 8 № 927. Определите значение переменной b после выполнения алгоритма:
a := 100
b := 400
a := 2*a+50
b := a*2–b В ответе укажите одно целое число – значение переменной b.
46. Задание 8 № 947. Определите значение переменной b после выполнения алгоритма:
a := 100
b :=240
a := 3*a+20
b := a*2–b В ответе укажите одно целое число — значение переменной b.
47. Задание 8 № 1019. Определите значение переменной e после выполнения алгоритма:
f := 100
e := 25
f := 2*f+50
e := f–150–e*2 В ответе укажите одно целое число — значение переменной e.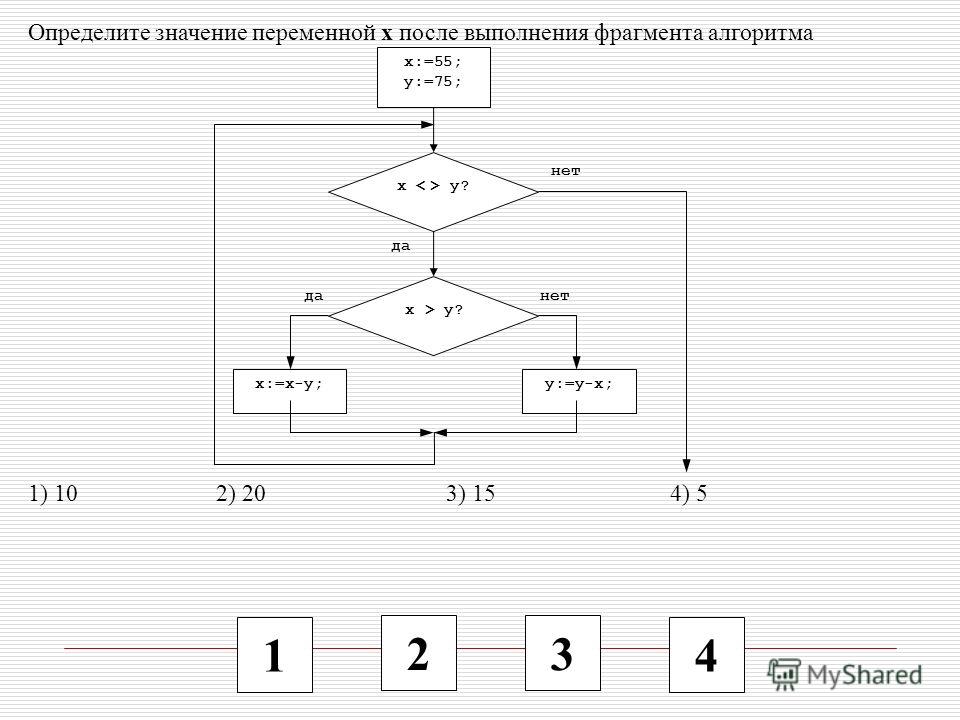
48. Задание 8 № 1039. Определите значение переменной e после выполнения алгоритма:
f := 21
e := 10 f := 5*f+5 e := f–10–e*5 В ответе укажите одно целое число — значение переменной e.
Задания 8. Линейный алгоритм, записанный на алгоритмическом языке
49. Задание 8 № 1059. В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики.Определите значение переменной a после выполнения:
a := 3
b := 7
b := 9+a*b
a := b/5*a В ответе укажите одно целое число — значение переменной a.
50. Задание 8 № 1079. Определите значение переменной a после выполнения алгоритма:
a := 7
с := 3
с := 3 + a * с
a := с / 3 * a В ответе укажите одно целое число — значение переменной a.
51. Задание 8 № 1102. Определите значение переменной a после выполнения алгоритма:
a := 4
b := 8+2*a
a := b/2*a В ответе укажите одно целое число — значение переменной a.
52. Задание 8 № 1122. . Определите значение переменной b после выполнения алгоритма:
a := 1
b := 4
a := 2*a+3*b
b := a/2*b В ответе укажите одно целое число — значение переменной b.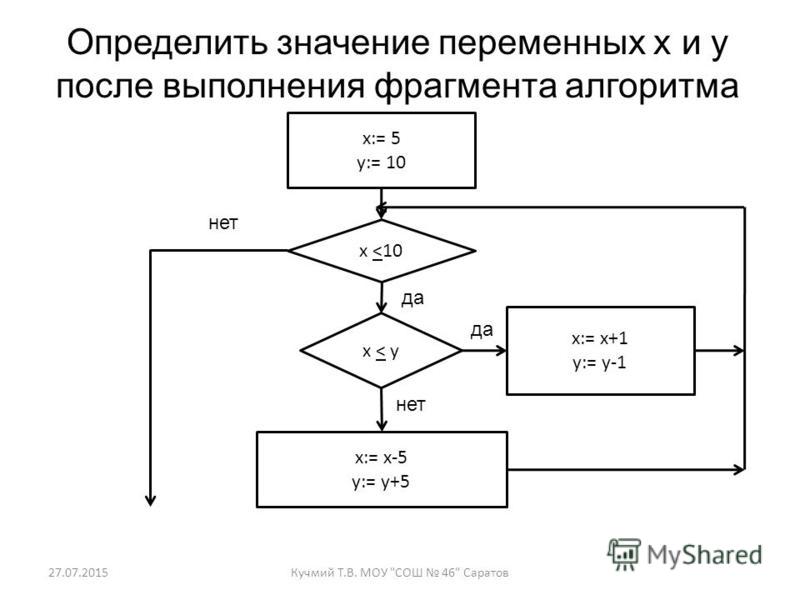
53. Задание 8 № 1142. Определите значение переменной a после выполнения алгоритма:
a := 4
b := 9
b := 6 * b – a
a := b / 5 * 3 – a В ответе укажите одно целое число — значение переменной a.
54. Задание 8 № 1162. Определите значение переменной b после выполнения алгоритма:
a := 4
b := 15
a := b-a*3
b := 24/a*4 В ответе укажите одно целое число — значение переменной b.
55. Задание 8 № 1241. Определите значение переменной a после выполнения алгоритма:
a := 12
b := 8 + a / 2
a := a – b / 2 В ответе укажите одно число — значение переменной а.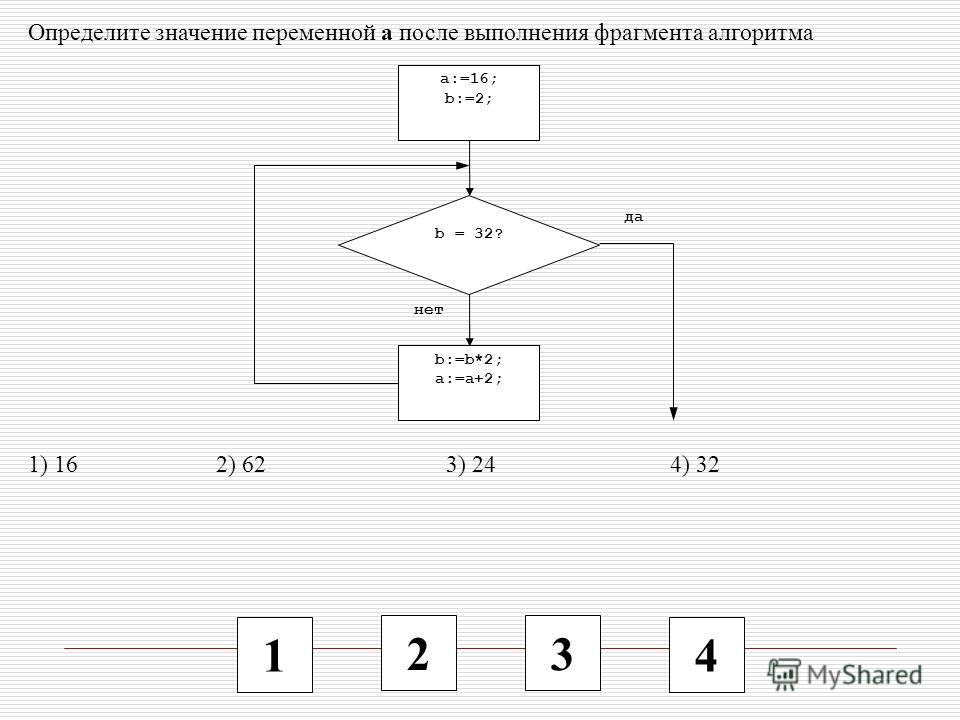
56. Задание 8 № 1261. Определите значение переменной a после выполнения алгоритма:
a := 2
b := 6
b := 12+a*b
a := b/4*a В ответе укажите одно целое число – значение переменной а.
Learning with Python, документация 2-го издания
6.1. Множественное присвоение
Как вы, возможно, уже поняли, законно выполнять более одного присвоения та же переменная. Новое присваивание заставляет существующую переменную ссылаться на новое значение (и перестать ссылаться на старое значение).
Брюс = 5 распечатать брюс, Брюс = 7 распечатать Брюс
Вывод этой программы 5 7, потому что в первый раз Брюс
напечатано, его значение равно 5, а во второй раз его значение равно 7. Запятая в конце
конец первого оператора печати подавляет новую строку после вывода,
вот почему оба выхода появляются в одной строке.
Вот как множественное назначение выглядит на диаграмме состояний:
При множественном назначении особенно важно различать операция присваивания и оператор равенства. Поскольку Python использует равные знак (=) для присваивания, заманчиво интерпретировать оператор как a = b как утверждение о равенстве. Это не!
Во-первых, равенство симметрично, а присваивание — нет. Например, в математика, если а = 7, то 7 = а. Но в Python оператор a = 7 допустимо, а 7 = a — нет.
Кроме того, в математике утверждение о равенстве всегда истинно. Если а = б теперь, тогда a всегда будет равно b. В Python оператор присваивания может сделать две переменные равны, но они не должны оставаться такими:
а = 5 b = a # a и b теперь равны a = 3 # a и b больше не равны
Третья строка изменяет значение a, но не изменяет значение
б, так что они уже не равны. (В некоторых языках программирования
для присваивания используется символ, например <- или :=, чтобы избежать путаницы.
6.2. Обновление переменных
Одной из наиболее распространенных форм множественного присвоения является обновление, при котором значение переменной зависит от старого.
х = х + 1
Это означает получение текущего значения x, добавление единицы, а затем обновление x новым значением. ценить.
Если вы попытаетесь обновить несуществующую переменную, вы получите сообщение об ошибке, потому что Python оценивает выражение в правой части оператора присваивания прежде чем он присвоит результирующее значение имени слева:
>>> х = х + 1 Traceback (последний последний вызов): Файл "", строка 1, в NameError: имя «x» не определено
Прежде чем вы сможете обновить переменную, вы должны
>>> x = 0 >>> х = х + 1 >>>
Обновление переменной путем добавления 1 называется приращением ; вычитание 1 равно
называется декрементом .
6.3. Оператор while
Компьютеры часто используются для автоматизации повторяющихся задач. Повторение идентичных или подобные задачи без ошибок — это то, с чем компьютеры справляются хорошо и люди плохо работают.
Повторное выполнение набора операторов называется итерацией . Потому что итерация настолько распространена, что Python предоставляет несколько языковых функций, чтобы сделать ее Полегче. Первая функция, которую мы собираемся рассмотреть, — это оператор while.
Вот функция обратного отсчета, которая демонстрирует использование в то время как оператор:
обратный отсчет (n):
при n > 0:
напечатать п
п = п-1
печатать "Отрыв!"
Вы можете читать инструкцию while почти так, как если бы она была написана на английском языке. Это значит, Пока n больше 0, продолжайте отображать значение n, а затем уменьшая значение n на 1. Когда вы дойдете до 0, отобразите слово Взлетать!
Более формально, вот последовательность выполнения оператора while:
- Вычислить условие, выдав False или True.

- Если условие ложно, выйти из оператора while и продолжить выполнение на следующем операторе.
- Если условие истинно, выполнить каждый из операторов в теле и затем вернитесь к шагу 1.
Тело состоит из всех операторов под заголовком с тем же отступ.
Этот тип потока называется цикл , потому что третий шаг повторяется наверх. Обратите внимание, что если условие ложно в первый раз через цикл, операторы внутри цикла никогда не выполняются.
Тело цикла должно изменить значение одной или нескольких переменных так, чтобы в конце концов условие становится ложным, и цикл завершается. В противном случае цикл будет повторяться вечно, что называется бесконечным циклом
В случае обратного отсчета мы можем доказать, что цикл завершается, потому что мы
знаем, что значение n конечно, и мы можем видеть, что значение n
становится меньше с каждым разом в цикле, поэтому в конце концов мы должны добраться до 0. В
другие случаи, это не так легко сказать. Посмотрите на следующую функцию,
определено для всех положительных целых чисел n:
В
другие случаи, это не так легко сказать. Посмотрите на следующую функцию,
определено для всех положительных целых чисел n:
def sequence(n):
в то время как n != 1:
напечатать п,
если n % 2 == 0: # n четно
п = п / 2
иначе: # n нечетно
п = п * 3 + 1
Условие для этого цикла n != 1, поэтому цикл будет продолжаться до тех пор, пока n равно 1, что сделает условие ложным.
Каждый раз в цикле программа выводит значение n, а затем проверяет, четное оно или нечетное. Если оно четное, значение n делится на 2. Если оно нечетное, значение заменяется на n * 3 + 1. Например, если начальное значение (аргумент, переданный в sequence) равно 3, в результате последовательность 3, 10, 5, 16, 8, 4, 2, 1.
Поскольку n иногда увеличивается, а иногда уменьшается, нет очевидного
доказательство того, что n когда-либо достигнет 1 или что программа завершится. Для некоторых
конкретных значений n, мы можем доказать терминацию. Например, если
начальное значение является степенью двойки, тогда значение n будет четным каждый
время в цикле, пока не достигнет 1. Предыдущий пример заканчивается таким
последовательность, начиная с 16.
Например, если
начальное значение является степенью двойки, тогда значение n будет четным каждый
время в цикле, пока не достигнет 1. Предыдущий пример заканчивается таким
последовательность, начиная с 16.
Помимо конкретных значений, интересен вопрос, можем ли мы доказать, что эта программа завершает на все значения n. Пока никому не удалось чтобы доказать это
6.4. Отслеживание программы
Чтобы писать эффективные компьютерные программы, программист должен развить способность к отслеживать выполнение компьютерной программы. Трассировка включает в себя становление компьютер и следуя за потоком выполнения через пример запуска программы, запись состояния всех переменных и любых выходных данных, которые программа генерирует после каждая инструкция выполняется.
Чтобы понять этот процесс, давайте проследим вызов sequence(3) из
предыдущий раздел. В начале трассировки у нас есть локальная переменная n
(параметр) с начальным значением 3.
Чтобы следить за всем этим, пока вы вручную трассируете программу, создайте заголовок столбца на лист бумаги для каждой переменной, созданной во время работы программы, и еще один для вывода. Наша трассировка пока будет выглядеть примерно так:
н выход -- ------ 3 3 10
Поскольку 10 != 1 оценивается как True, снова выполняется тело цикла, и напечатано 10. 10 % 2 == 0 истинно, поэтому ветвь if выполняется, и n становится равным 5. К концу трассировки мы имеем:
n выходных данных -- ------ 3 3 10 10 5 5 16 16 8 8 4 4 2 2 1
Трассировка может быть немного утомительной и подверженной ошибкам (вот почему мы заставляем компьютеры выполнять
это в первую очередь!), но это важный навык для программиста
иметь. Из этой трассировки мы можем многое узнать о том, как работает наш код.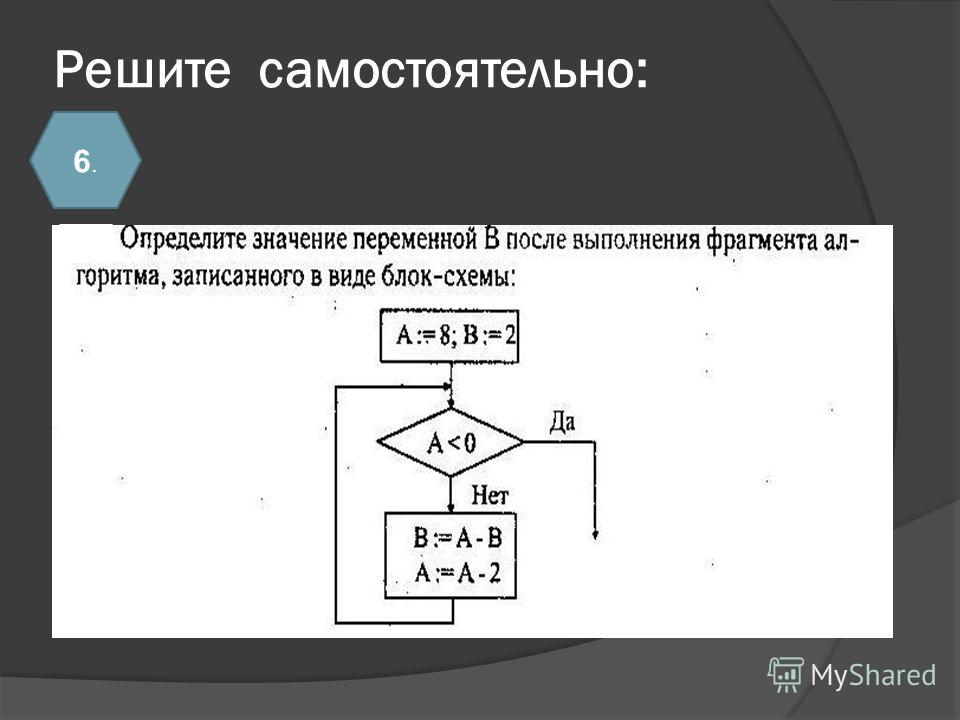 Мы
можно заметить, что как только n станет степенью двойки, например, программа
потребуется журнал 2 (n) выполнение тела цикла для завершения. Мы можем
также обратите внимание, что последняя 1 не будет напечатана в качестве вывода.
Мы
можно заметить, что как только n станет степенью двойки, например, программа
потребуется журнал 2 (n) выполнение тела цикла для завершения. Мы можем
также обратите внимание, что последняя 1 не будет напечатана в качестве вывода.
6.5. Подсчет цифр
Следующая функция подсчитывает количество десятичных цифр в положительном целое число, выраженное в десятичном формате:
def num_digits(n):
количество = 0
в то время как н:
количество = количество + 1
п = п / 10
количество возвратов
Вызов num_digits(710) вернет 3. Проследите выполнение этого вызов функции, чтобы убедиться, что она работает.
Эта функция демонстрирует другую схему вычислений, называемую счетчиком .
Переменная count инициализируется 0, а затем увеличивается каждый раз, когда
выполняется тело цикла. Когда цикл завершается, count содержит результат –
общее количество выполнений тела цикла, которое совпадает с
количество цифр.
Если бы мы хотели подсчитывать только цифры, равные 0 или 5, добавление условного перед увеличением счетчика добьется цели:
def num_zero_and_five_digits(n):
количество = 0
в то время как н:
цифра = п % 10
если цифра == 0 или цифра == 5:
количество = количество + 1
п = п / 10
количество возвратов
Подтвердите, что num_zero_and_five_digits(1055030250) возвращает 7.
6.7. Таблицы
Циклы хорошо подходят для создания табличных данных. До компьютеры были легко доступны, люди должны были вычислять логарифмы, синусы и косинусы и другие математические функции вручную. Чтобы сделать это проще, книги по математике содержали длинные таблицы со значениями этих функций. Создание таблиц было медленным и скучным, и они, как правило, были полны ошибок.
Когда на сцене появились компьютеры, одной из первых реакций было: «Это
большой! Мы можем использовать компьютеры для создания таблиц, так что не будет
ошибки.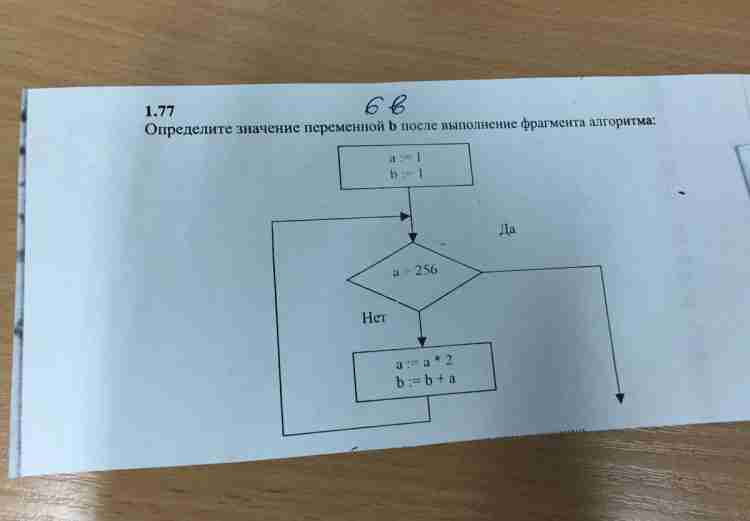 Это оказалось правдой (в основном), но недальновидно. Вскоре после этого,
компьютеры и калькуляторы были настолько распространены, что таблицы устарели.
Это оказалось правдой (в основном), но недальновидно. Вскоре после этого,
компьютеры и калькуляторы были настолько распространены, что таблицы устарели.
Ну, почти. Для некоторых операций компьютеры используют таблицы значений, чтобы получить приблизительный ответ, а затем выполнить вычисления, чтобы улучшить приближение. В некоторых случаях в базовых таблицах были ошибки, наиболее известные из которых в таблице Intel Pentium используется для выполнения деления с плавающей запятой.
Хотя таблица журнала уже не так полезна, как когда-то, она по-прежнему полезна. пример итерации. Следующая программа выводит последовательность значений в левый столбец и 2 в степени этого значения в правом столбце:
x = 1
пока х < 13:
напечатать х, '\t', 2**х
х += 1
Строка '\t' представляет собой символ табуляции . Символ обратной косой черты в
'\t' указывает на начало управляющей последовательности . Escape-последовательности
используются для представления невидимых символов, таких как табуляция и новая строка.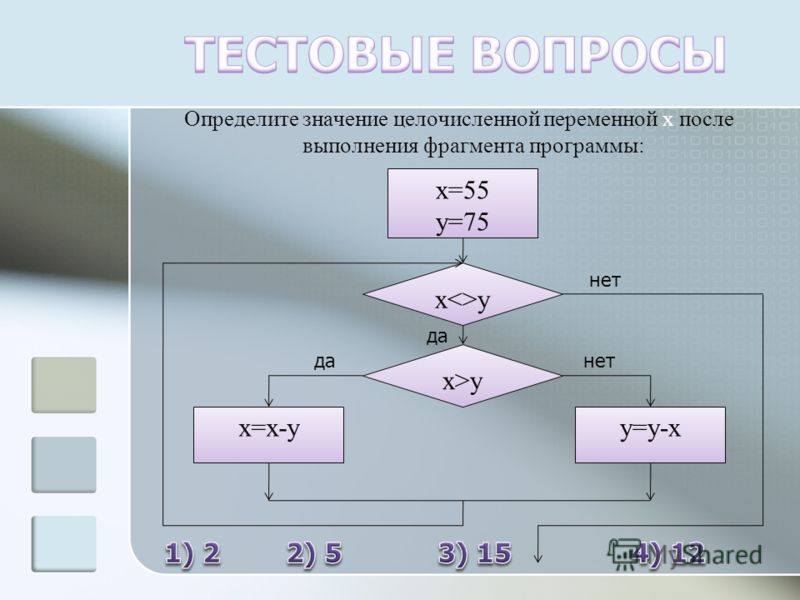 Последовательность
\n представляет новая строка .
Последовательность
\n представляет новая строка .
Управляющая последовательность может появляться в любом месте строки; в этом примере вкладка escape-последовательность — это единственное, что есть в строке. Как вы думаете, вы представляете обратная косая черта в строке?
Когда символы и строки отображаются на экране, невидимый маркер называемый курсор отслеживает, куда пойдет следующий символ. После оператор печати, курсор обычно переходит в начало следующего линия.
Символ табуляции перемещает курсор вправо до тех пор, пока он не достигнет одного из табуляция останавливается. Вкладки полезны для выравнивания столбцов текста, как в выводе. предыдущей программы:
1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1024 11 2048 12 4096
Из-за символов табуляции между столбцами положение второго столбца не зависит от количества цифр в первом столбце.
6.8. Двумерные таблицы
Двумерная таблица — это таблица, в которой вы считываете значение на пересечении
строки и столбца.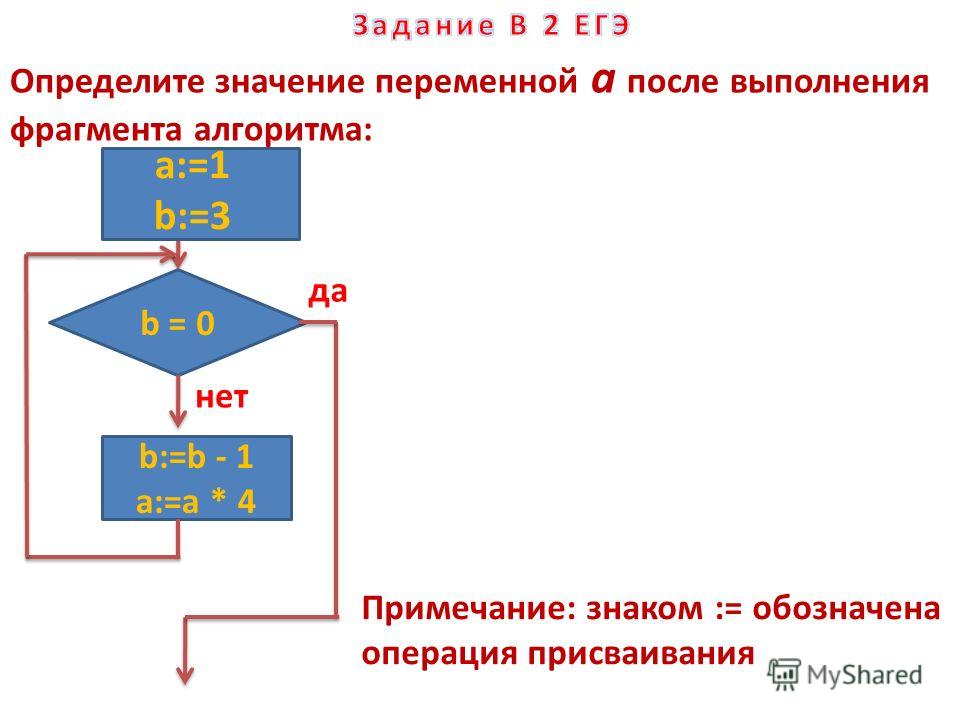 Таблица умножения является хорошим примером. Скажем, вы
хотите напечатать таблицу умножения для значений от 1 до 6.
Таблица умножения является хорошим примером. Скажем, вы
хотите напечатать таблицу умножения для значений от 1 до 6.
Хороший способ начать — написать цикл, который печатает числа, кратные 2, все на одна строка:
я = 1
пока я <= 6:
напечатать 2 * я, ' ',
я += 1
Распечатать
Первая строка инициализирует переменную с именем i, которая действует как счетчик или переменная цикла . По мере выполнения цикла значение i увеличивается с 1 до 6. Когда i равно 7, цикл завершается. Каждый раз через цикл он отображает значение 2 * i, за которым следуют три пробела.
Опять же, запятая в операторе печати подавляет новую строку. После цикл завершается, второй оператор печати начинает новую строку.
Вывод программы:
2 4 6 8 10 12
Пока все хорошо. Следующий шаг — инкапсулировать и обобщить .
6.9. Инкапсуляция и обобщение
Инкапсуляция — это процесс помещения фрагмента кода в функцию,
позволяя вам воспользоваться всеми преимуществами функций.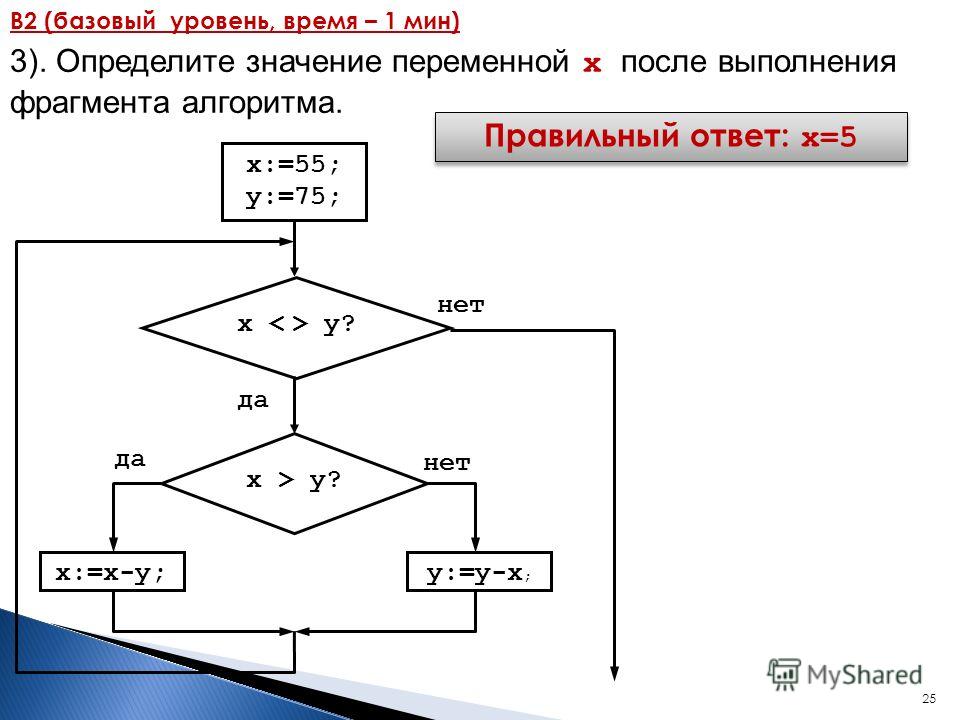 Ты
вы уже видели два примера инкапсуляции: print_parity в главе 4;
и is_divisible в главе 5.
Ты
вы уже видели два примера инкапсуляции: print_parity в главе 4;
и is_divisible в главе 5.
Обобщение означает взятие чего-то конкретного, например печать кратных из 2, и сделать его более общим, например, распечатать кратные любому целое число.
Эта функция инкапсулирует предыдущий цикл и обобщает его для печати кратно n:
def print_multiples(n):
я = 1
пока я <= 6:
выведите n * i, '\t',
я += 1
Распечатать
Для инкапсуляции все, что нам нужно было сделать, это добавить первую строку, которая объявляет имя функции и список параметров. Обобщая, все, что нам нужно было сделать было заменить значение 2 параметром n.
Если мы вызовем эту функцию с аргументом 2, мы получим тот же результат, что и раньше. С аргументом 3 вывод:
3 6 9 12 15 18
С аргументом 4 вывод:
4 8 12 16 20 24
Теперь вы, наверное, догадались, как распечатать таблицу умножения — по
многократный вызов print_multiples с разными аргументами.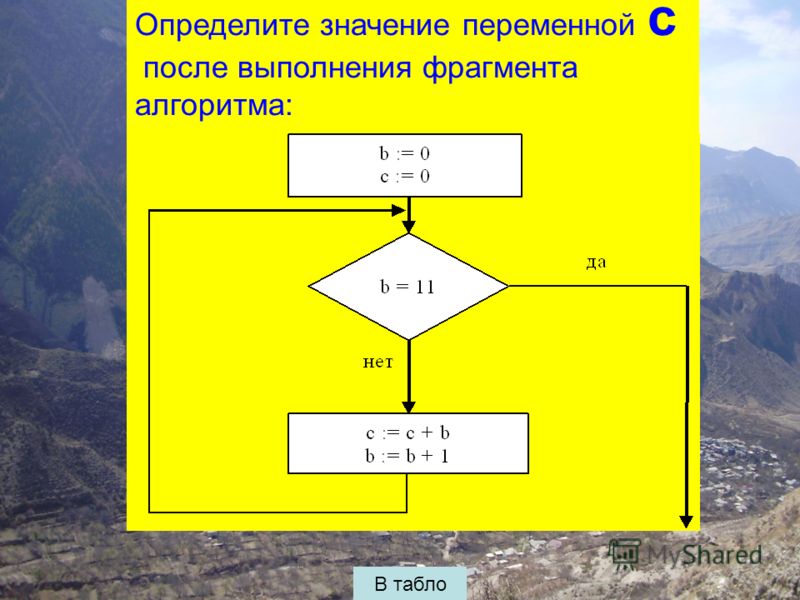 На самом деле мы
можно использовать другой цикл:
На самом деле мы
можно использовать другой цикл:
i = 1
пока я <= 6:
print_multiples (я)
я += 1
Обратите внимание, насколько этот цикл похож на цикл внутри print_multiples. Все мы сделал, заменил оператор печати вызовом функции.
Результатом работы этой программы является таблица умножения:
1 2 3 4 5 6 2 4 6 8 10 12 3 6 9 12 15 18 4 8 12 16 20 24 5 10 15 20 25 30 6 12 18 24 30 36
6.10. Подробнее об инкапсуляции
Чтобы еще раз продемонстрировать инкапсуляцию, возьмем код из последнего раздела. и заверните его в функцию:
определение print_mult_table():
я = 1
пока я <= 6:
print_multiples (я)
я += 1
Этот процесс является общим планом разработки . Мы разрабатываем код, написав строки кода вне какой-либо функции или ввода их в интерпретатор. Когда мы получим код работает, мы извлекаем его и заворачиваем в функцию.
Этот план развития особенно полезен, если вы не знаете, как разделить
программу в функции, когда вы начинаете писать.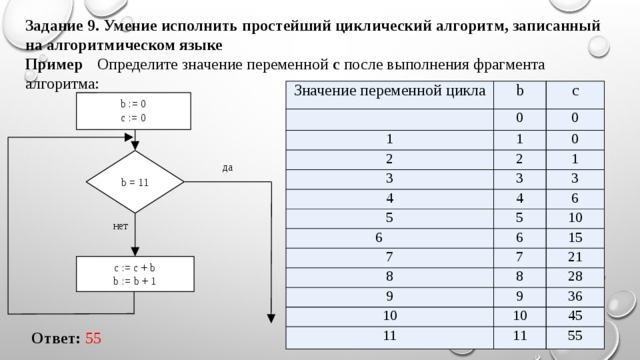 Этот подход позволяет вам
дизайн, как вы идете вперед.
Этот подход позволяет вам
дизайн, как вы идете вперед.
6.11. Локальные переменные
Вам может быть интересно, как мы можем использовать одну и ту же переменную i в обоих print_multiples и print_mult_table. Не вызывает ли это проблем, когда одна из функций изменяет значение переменной?
Нет, потому что i в print_multiples и i в print_mult_table - это , а не одна и та же переменная.
Переменные, созданные внутри определения функции, являются локальными; вы не можете получить доступ к локальная переменная из-за пределов своей домашней функции. Это означает, что вы можете иметь несколько переменных с одним и тем же именем, если они не находятся в одном и том же функция.
Диаграмма стека для этой программы показывает, что две переменные с именем i не одна и та же переменная. Они могут относиться к разным значениям, и изменение одного не влияет на другое.
Значение i в print_mult_table изменяется от 1 до 6. На диаграмме это
оказывается 3. В следующий раз через цикл это будет 4. Каждый раз через
цикл, print_mult_table вызывает print_multiples с текущим значением
я в качестве аргумента. Это значение присваивается параметру n.
В следующий раз через цикл это будет 4. Каждый раз через
цикл, print_mult_table вызывает print_multiples с текущим значением
я в качестве аргумента. Это значение присваивается параметру n.
Внутри print_multiples значение i изменяется от 1 до 6. В диаграмме, это 2. Изменение этой переменной не влияет на значение из i в print_mult_table.
Общепринято и совершенно законно иметь разные локальные переменные с то же имя. В частности, такие имена, как i и j, часто используются как переменные цикла. Если вы избегаете их использования в одной функции только потому, что использовали их в другом месте, вы, вероятно, затрудните чтение программы.
6.12. Больше обобщений
В качестве еще одного примера обобщения представьте, что вам нужна программа, которая напечатать таблицу умножения любого размера, а не только таблицу шесть на шесть. Ты можно добавить параметр в print_mult_table:
def print_mult_table(high):
я = 1
в то время как я <= высокий:
print_multiples (я)
я += 1
Мы заменили значение 6 параметром high.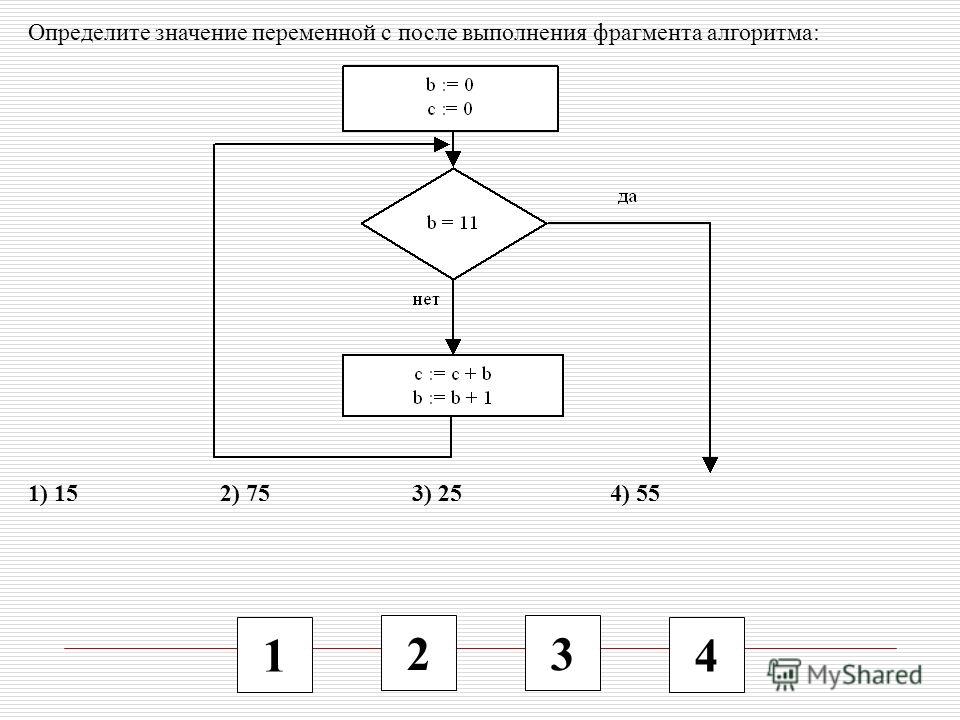 Если мы позвоним
print_mult_table с аргументом 7 выводит:
Если мы позвоним
print_mult_table с аргументом 7 выводит:
1 2 3 4 5 6 2 4 6 8 10 12 3 6 912 15 18 4 8 12 16 20 24 5 10 15 20 25 30 6 12 18 24 30 36 7 14 21 28 35 42
Это нормально, за исключением того, что мы, вероятно, хотим, чтобы таблица была квадратной — с одинаковое количество строк и столбцов. Для этого добавим еще один параметр в print_multiples, чтобы указать, сколько столбцов должно быть в таблице.
Просто чтобы не раздражать, мы называем этот параметр высоким, демонстрируя, что разные функции могут иметь параметры с одинаковыми именами (так же, как локальные переменные). Вот и вся программа:
по умолчанию print_multiples(n, high):
я = 1
в то время как я <= высокий:
выведите n*i, '\t',
я += 1
Распечатать
def print_mult_table (высокий):
я = 1
в то время как я <= высокий:
print_multiples (я, высокий)
я += 1
Обратите внимание: когда мы добавили новый параметр, нам пришлось изменить первую строку
функцию (заголовок функции), а также пришлось изменить место, где
функция вызывается в print_mult_table.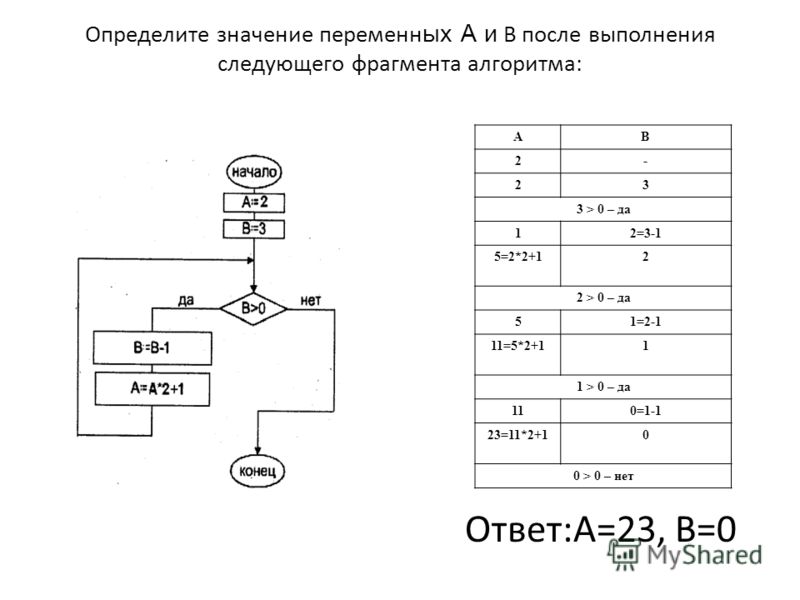
Как и ожидалось, эта программа создает квадратную таблицу семь на семь:
1 2 3 4 5 6 7 2 4 6 8 10 12 14 3 6 9 12 15 18 21 4 8 12 16 20 24 28 5 10 15 20 25 30 35 6 12 18 24 30 36 42 7 14 21 28 35 42 49
Когда вы соответствующим образом обобщаете функцию, вы часто получаете программу с возможности, которые вы не планировали. Например, вы можете заметить, что поскольку ab = ba все записи в таблице появляются дважды. Вы можете сэкономить чернила, распечатав только половина стола. Для этого вам нужно всего лишь изменить одну строку print_mult_table. Изменить
print_multiples(i, высокий)от
до
print_multiples(i, i)
и вы получите:
1 2 4 3 6 9 4 8 12 16 5 10 15 20 25 6 12 18 24 30 36 7 14 21 28 35 42 49
6.13. Функции
Несколько раз мы упоминали обо всем, для чего нужны функции. К Теперь вам может быть интересно, что именно это за вещи. Вот некоторые из их:
- Присвоение имени последовательности операторов упрощает чтение программы.
 и отлаживать.
и отлаживать. - Разделение длинной программы на функции позволяет разделить части программы, отлаживать их по отдельности, а затем составлять из них единое целое.
- Функции облегчают использование итерации.
- Хорошо продуманные функции часто полезны для многих программ. Как только вы напишете и отладить один, вы можете использовать его повторно.
6.14. Метод Ньютона
Циклы часто используются в программах, которые вычисляют численные результаты, начиная с приблизительным ответом и итеративным его улучшением.
Например, одним из способов вычисления квадратных корней является метод Ньютона. Предполагать что вы хотите знать квадратный корень из n. Если начать почти с любого приближение, вы можете вычислить лучшее приближение с помощью следующего формула:
лучше = (приблизительно + n/приблизительно)/2
Повторно применяя эту формулу до тех пор, пока лучшее приближение не будет равно предыдущий, мы можем написать функцию для вычисления квадратного корня:
def sqrt(n):
приблизительно = n/2,0
лучше = (приблизительно + n/приблизительно)/2,0
а лучше != приблизительно:
приблизительно = лучше
лучше = (приблизительно + n/приблизительно)/2,0
вернуться примерно
Попробуйте вызвать эту функцию с 25 в качестве аргумента, чтобы убедиться, что она возвращает 5. 0.
0.
6.15. Алгоритмы
Метод Ньютона является примером алгоритма : это механический процесс для решения категории задач (в данном случае для вычисления квадратных корней).
Определить алгоритм непросто. Это может помочь начать с чего-то это не алгоритм. Когда вы научились умножать однозначные числа, Вы, наверное, выучили таблицу умножения. По сути, вы запомнили 100 конкретные решения. Такое знание не является алгоритмическим.
Но если вы были ленивы, вы, вероятно, обманули, изучив несколько трюков. Для например, чтобы найти произведение n и 9, вы можете написать n - 1 как первую цифру а 10 - n как вторая цифра. Этот трюк является общим решением для умножение любого однозначного числа на 9. Это алгоритм!
Точно так же методы сложения с переносом, вычитания, которые вы изучили
с заимствованием и делением в длину — все это алгоритмы. Один из
особенностью алгоритмов является то, что они не требуют никакого интеллекта для
выполнять. Это механические процессы, в которых каждый шаг вытекает из
последние по простому набору правил.
По нашему мнению, стыдно, что люди так много времени проводят в школе научиться выполнять алгоритмы, которые буквально не требуют интеллекта.
С другой стороны, процесс разработки алгоритмов интересен, интеллектуально сложной и центральной частью того, что мы называем программированием.
Некоторые вещи, которые люди делают естественно, без затруднений или сознательно мысли труднее всего выразить алгоритмически. Понимание естественного язык является хорошим примером. Мы все это делаем, но пока никому не удалось объяснить как мы это делаем, по крайней мере не в виде алгоритма.
6.16. Глоссарий
- алгоритм
- Пошаговый процесс решения категории проблем.
- корпус
- Операторы внутри цикла.
- счетчик
- Переменная, используемая для подсчета чего-либо, обычно инициализируется нулем и увеличивается в теле цикла.
- курсор
- Невидимый маркер, который отслеживает, где будет следующий символ.
 быть напечатаны.
быть напечатаны. - уменьшение
- Уменьшить на 1.
- план развития
- Процесс разработки программы. В этой главе мы продемонстрировали стиль разработки, основанный на разработке кода для выполнения простых, конкретных вещи, а затем инкапсулировать и обобщать.
- инкапсулировать
- Чтобы разделить большую сложную программу на компоненты (например, функции) и изолировать компоненты друг от друга (используя локальные переменные, для пример).
- управляющая последовательность
- Управляющий символ \, за которым следует один или несколько печатных символов. используется для обозначения непечатаемого символа.
- обобщить
- Чтобы заменить что-то излишне конкретное (например, постоянное значение) с чем-то подходящим общим (например, с переменной или параметром). Обобщение делает код более универсальным, более вероятным для повторного использования и иногда даже проще написать.
- приращение
- Как существительное, так и глагол, приращение означает увеличение на 1.

- бесконечный цикл
- Цикл, в котором условие завершения никогда не выполняется.
- инициализация (переменной)
- Инициализировать переменную означает присвоить ей начальное значение, обычно в контекст многократного присвоения. Поскольку в Python переменных не существует пока им не будут присвоены значения, они инициализируются, когда они созданный. В других языках программирования это не так, и переменные могут быть созданы без инициализации, и в этом случае они либо по умолчанию, либо мусор значения.
- итерация
- Повторное выполнение набора операторов программирования.
- петля
- Оператор или группа операторов, которые выполняются многократно до тех пор, пока условие завершения выполнено.
- переменная цикла
- Переменная, используемая как часть условия завершения цикла.
- множественное присвоение
- Выполнение более одного присвоения одной и той же переменной во время
выполнение программы.

- новая строка
- Специальный символ, который заставляет курсор перемещаться в начало следующая строка.
- вкладка
- Специальный символ, который заставляет курсор перемещаться на следующую позицию табуляции на текущей строке.
- трассировка
- Следить за ходом выполнения программы вручную, записывая изменение состояния переменных и любого произведенного вывода.
6.17. Упражнения
Напишите одну строку, которая:
производит этот выход.
Добавьте оператор печати в функцию sqrt, определенную в разделе 6.14, которая печатает лучше каждый раз, когда он вычисляется. Назовите свой измененный функцию с 25 в качестве аргумента и запишите результаты.
Отследить выполнение последней версии print_mult_table и рисунка как это работает.
Напишите функцию print_triangular_numbers(n), которая выводит первое n треугольных чисел. Вызов print_triangular_numbers(5) произвести следующий вывод:
1 1 2 3 3 6 4 10 5 15
(подсказка : используйте веб-поиск, чтобы узнать, что такое треугольное число.
 )
)Откройте файл с именем ch06.py и добавьте следующее:
, если __name__ == '__main__': импортировать доктест doctest.testmod()Напишите функцию is_prime, которая принимает один целочисленный аргумент. и возвращает True, если аргументом является простое число и False в противном случае. Добавляйте doctests в свою функцию по мере ее разработки.
Что вернет num_digits(0)? Измените его, чтобы вернуть 1 для этого случай. Почему вызов num_digits(-24) приводит к бесконечному циклу (подсказка : -1/10 равно -1 )? Измените num_digits, чтобы он работал корректно с любым целочисленным значением. Добавьте следующее в ch06.py файл, который вы создали в предыдущем упражнении:
по определению num_digits(n): """ >>> число_цифр (12345) 5 >>> число_цифр (0) 1 >>> число_цифр (-12345) 5 """Добавьте тело функции в num_digits и подтвердите, что оно проходит доктесты.

Добавьте в ch06.py следующее:
по определению num_even_digits(n): """ >>> число_четных_цифр (123456) 3 >>> число_четных_цифр (2468) 4 >>> число_четных_цифр (1357) 0 >>> число_четных_цифр (2) 1 >>> число_четных_цифр (20) 2 """Напишите тело для num_even_digits, чтобы оно работало должным образом.
Добавьте в ch06.py следующее:
по определению print_digits(n): """ >>> print_digits(13789) 9 8 7 3 1 >>> print_digits(39874613) 3 1 6 4 7 8 9 3 >>> print_digits(213141) 1 4 1 3 1 2 """Напишите тело для print_digits, чтобы оно прошло заданные doctests.
Напишите функцию sum_of_squares_of_digits, которая вычисляет сумму квадратов цифр переданного ему целого числа. Например, sum_of_squares_of_digits(987) должен вернуть 194, так как 9**2 + 8**2 + 7**2 == 81 + 64 + 49 == 194.
по определению sum_of_squares_of_digits(n): """ >>> сумма_квадратов_цифр(1) 1 >>> сумма_квадратов_цифр(9) 81 >>> сумма_квадратов_цифр (11) 2 >>> сумма_квадратов_цифр (121) 6 >>> сумма_квадратов_цифр (987) 194 """Проверьте свое решение на соответствие doctests выше.

Что такое переменная в компьютерном программировании?
Переменные используются для хранения информации, на которую можно ссылаться и которой можно манипулировать в компьютерной программе. Они также предоставляют способ маркировки данных описательным именем, чтобы наши программы могли быть более понятными читателю и нам самим. Полезно думать о переменных как о контейнерах, содержащих информацию. Их единственная цель — маркировать и хранить данные в памяти. Затем эти данные можно использовать во всей вашей программе.
Именование переменных известно как одна из самых сложных задач в компьютерном программировании. Когда вы даёте имена переменным, хорошо подумайте об именах. Приложите все усилия, чтобы убедиться, что имя, которое вы присваиваете своей переменной, точно описательно и понятно другому читателю. Иногда этот другой читатель — это вы сами, когда вы пересматриваете программу, написанную месяцами или даже годами ранее.
При присвоении переменной используется символ = . Имя переменной идет слева, а значение, которое вы хотите сохранить в переменной, идет справа.
Имя переменной идет слева, а значение, которое вы хотите сохранить в переменной, идет справа.
irb :001 > first_name = 'Джо' => "Джо"
Здесь мы присвоили значение 'Джо' , которое является строкой, переменной first_name . Теперь, если мы хотим сослаться на эту переменную, мы можем это сделать.
irb :002 > имя_имя => "Джо"
Как видите, теперь мы сохранили строку 'Joe' в памяти для использования во всей программе.
Примечание. Убедитесь, что вы не путаете оператор присваивания ( = ) с оператором равенства ( == ). Отдельный символ = присваивает значение, а символ == проверяет, равны ли две вещи.
Давайте попробуем кое-что. Посмотрите на следующий сеанс irb.
ирб :001 > а = 4 => 4 ирб :002 > б = а => 4 ирб :003 > а = 7 => 7
Каково значение b на данный момент? Попробуйте предположить, а затем введите этот сеанс в irb, чтобы узнать.
Вы заметите, что значение b остается 4, а и были переназначены на 7. Это показывает, что переменные указывают на значения в памяти и не сильно связаны друг с другом. Если это сбивает с толку, не волнуйтесь, у нас есть много упражнений для вас, чтобы сделать эту информацию ясной и очевидной. А если сомневаетесь, всегда пробуйте в irb.
До сих пор вы могли назначать данные переменным только из программы. Однако на практике вам нужно, чтобы другие люди могли интересным образом взаимодействовать с вашими программами. Для этого мы также должны позволить пользователю хранить информацию в переменных. Затем мы можем решить, что нам делать с этими данными.
Один из способов получить информацию от пользователя — вызвать метод gets . получает означает «получить строку», и это очень весело. Когда вы используете его, программа ждет, пока пользователь 1) введет информацию и 2) нажмет клавишу ввода. Давайте попробуем. Введите эти примеры в irb, чтобы получить представление и немного поэкспериментировать с ними, если хотите.
Введите эти примеры в irb, чтобы получить представление и немного поэкспериментировать с ними, если хотите.
irb :001 > имя = получает Боб => "Боб\n"
После кода name = gets компьютер ждал, пока мы введем некоторую информацию. Мы набрали «Боб», а затем нажали ввод, и программа вернула 9.0497 "Боб\n" . \n в конце является символом «новой строки» и представляет собой клавишу ввода. Но мы не хотим, чтобы это было частью нашей строки. Мы будем использовать chomp , связанную с gets , чтобы избавиться от этого — вы можете поместить .chomp после любой строки, чтобы удалить символы возврата каретки в конце.
irb :001 > имя = gets.chomp Боб => "Боб"
Ну вот! Это намного красивее. Теперь мы можем использовать переменную name по своему усмотрению.
irb :001 > имя = gets.chomp Боб => "Боб" irb :002 > имя + 'супер здорово!' => "Боб просто супер!"
Область действия переменной определяет, где в программе переменная доступна для использования. Область действия переменной определяется тем, где переменная инициализируется или создается. В Ruby область действия переменной определяется определением метода или блоком .
У них разное поведение, когда дело доходит до области видимости переменных.
Область действия переменной определяется тем, где переменная инициализируется или создается. В Ruby область действия переменной определяется определением метода или блоком .
У них разное поведение, когда дело доходит до области видимости переменных.
Определения области видимости переменных и методов
Мы узнаем о методах в следующей главе. На данный момент вы можете думать о методах как о фрагментах многократно используемого кода, которые ваша программа может выполнять много раз во время своего выполнения. Определения методов выглядят следующим образом:
имя = 'Кто-то еще' def print_full_name(first_name, last_name) имя = имя_имя + ' ' + фамилия ставит имя конец
Как только мы определили метод, мы можем вызывать его столько раз, сколько нам нужно, с разными значениями для first_name и last_name :
print_full_name 'Питер', 'Генри' # печатает Питера Генри print_full_name 'Линн', 'Блейк' # печатает Линн Блейк print_full_name 'Kim', 'Johansson' # печатает Ким Йоханссон вставляет имя # печатает Somebody Else
С точки зрения переменной области действия, методы имеют автономную область действия. Это означает, что из тела метода можно ссылаться или изменять только переменные, инициализированные в теле метода. Кроме того, переменные, инициализированные внутри тела метода, недоступны вне тела метода. Это немного похоже на непроницаемый пузырь. Таким образом, в приведенном выше коде мы не можем использовать или изменить
Это означает, что из тела метода можно ссылаться или изменять только переменные, инициализированные в теле метода. Кроме того, переменные, инициализированные внутри тела метода, недоступны вне тела метода. Это немного похоже на непроницаемый пузырь. Таким образом, в приведенном выше коде мы не можем использовать или изменить name переменная из строки 1 из метода print_full_name . Однако мы можем создать и использовать другую переменную имени , которая локально привязана к методу. Вот почему строки 4 и 5 работают без изменения значения name из строки 1.
Область действия переменных и блоки
Блок — это фрагмент кода, который следует за вызовом метода, разделенный фигурными скобками {} или сделать/завершить :
всего = 0
[1, 2, 3].каждый { |число| всего += число }
ставит тотал # 6
всего = 0 [1, 2, 3].each do |number| всего += число конец ставит тотал # 6
В приведенных выше примерах { |число| . — это блок, как и  .. }
.. } do |number| ... конец . Хотя они выглядят по-разному, поведение идентично. В обоих случаях код может получать доступ и изменять переменные, определенные вне блока. Таким образом, оба блока могут получить доступ и изменить всего . Однако любые переменные, инициализированные внутри блока (например, номер ) не может быть доступен с помощью внешнего кода.
Для блоков одно правило, которое мы хотим подчеркнуть, заключается в следующем: Внутренняя область может обращаться к переменным, инициализированным во внешней области, но не наоборот.
Взглянув на код, вы проясните это. Допустим, у нас есть файл с именем scope.rb .
#scope.rb a = 5 # переменная инициализируется во внешней области видимости 3.раз сделать |n| # вызов метода с блоком a = 3 # доступен здесь, во внутренней области видимости? конец ставит
Каково значение a при выводе на экран? Попробуйте.
Значение a равно 3. Это связано с тем, что a доступно для внутренней области видимости, созданной 3.times do ... end , что позволило коду переназначить значение a . На самом деле три раза переназначал на 3.
Попробуем что-нибудь другое. Мы изменим исходный код scope.rb :
# scope.rb а = 5 3.раз сделать |n| # вызов метода с блоком а = 3 b = 5 # b инициализируется во внутренней области видимости конец ставит puts b # доступен ли b здесь, во внешней области видимости?
Какой результат вы получили при запуске этой программы? Вы должны были получить сообщение об ошибке примерно такого содержания:
scope.rb:11:in `': неопределенная локальная переменная или метод `b' для main:Object (ИмяОшибка)
Это связано с тем, что переменная b недоступна вне вызова метода с блоком, в котором она инициализирована. Когда мы вызываем , помещаем b , он недоступен в этой внешней области.
Прежде чем двигаться дальше, вы должны знать, что существует пять типов переменных. Константы, глобальные переменные, переменные класса, переменные экземпляра и локальные переменные. Хотя вам пока не следует слишком сильно беспокоиться об этих темах, вот краткое описание каждой из них.
Константы объявляются путем написания каждой буквы в имени переменной заглавной в соответствии с соглашением Ruby. Они используются для хранения данных, которые никогда не нужно изменять. В то время как большинство языков программирования не позволяют изменять значение, присвоенное константе, Ruby позволяет. Однако он выдаст предупреждение, информирующее вас о том, что для этой переменной было предыдущее определение. То, что вы можете, не означает, что вы должны изменить значение. На самом деле, вы не должны. Константы не могут быть объявлены в определениях методов и доступны во всех областях вашего приложения.
Пример объявления константы:
MY_CONSTANT = 'Я доступен во всем вашем приложении.'
Глобальные переменные объявляются, когда имя переменной начинается со знака доллара ( $ ). Эти переменные доступны во всем приложении, переопределяя все границы области. Рубисты стараются держаться подальше от глобальных переменных, так как при их использовании могут возникнуть неожиданные сложности.
Пример объявления глобальной переменной:
$var = 'Я также доступен в вашем приложении.'
Переменные класса объявляются путем начала имени переменной с двух знаков @ . Эти переменные доступны экземплярам вашего класса, а также самому классу. Когда вам нужно объявить переменную, связанную с классом, но каждому экземпляру этого класса не требуется собственное значение для этой переменной, вы используете переменную класса. Переменные класса должны быть инициализированы на уровне класса, вне каких-либо определений методов. Затем их можно изменить с помощью определений методов класса или экземпляра.
Пример объявления переменной класса:
@@instances = 0
Переменные экземпляра объявляются путем начала имени переменной с одного знака @ .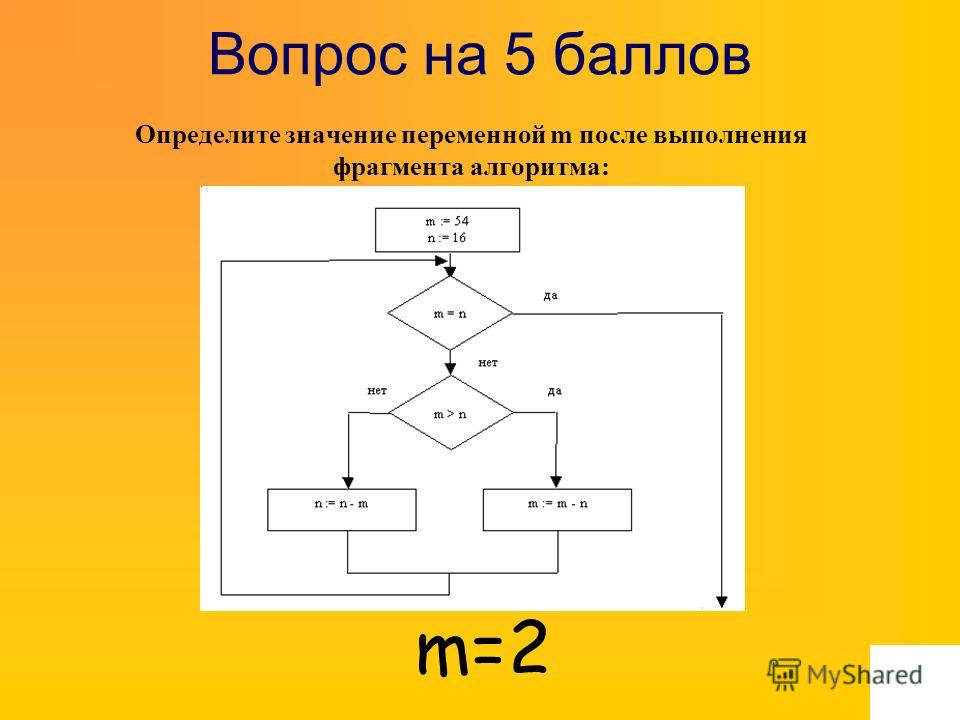 Эти переменные доступны во всем текущем экземпляре родительского класса. Переменные экземпляра могут пересекать некоторые границы области, но не все из них. Вы узнаете об этом больше, когда доберетесь до тем ООП, и не должны использовать переменные экземпляра, пока не узнаете о них больше.
Эти переменные доступны во всем текущем экземпляре родительского класса. Переменные экземпляра могут пересекать некоторые границы области, но не все из них. Вы узнаете об этом больше, когда доберетесь до тем ООП, и не должны использовать переменные экземпляра, пока не узнаете о них больше.
Пример объявления переменной экземпляра:
@var = 'Я доступен во всем текущем экземпляре этого класса.'
Локальные переменные — это наиболее распространенные переменные, с которыми вы столкнетесь, и они подчиняются всем границам области видимости. Эти переменные объявляются, начиная имя переменной ни с $ , ни с @ , а также не используя заглавные буквы во всем имени переменной.
Пример объявления локальной переменной:
var = 'Я должен пройти через границы области видимости.'
В этой главе мы говорили о том, как использовать переменные для хранения информации для последующего использования и как получить информацию от пользователя.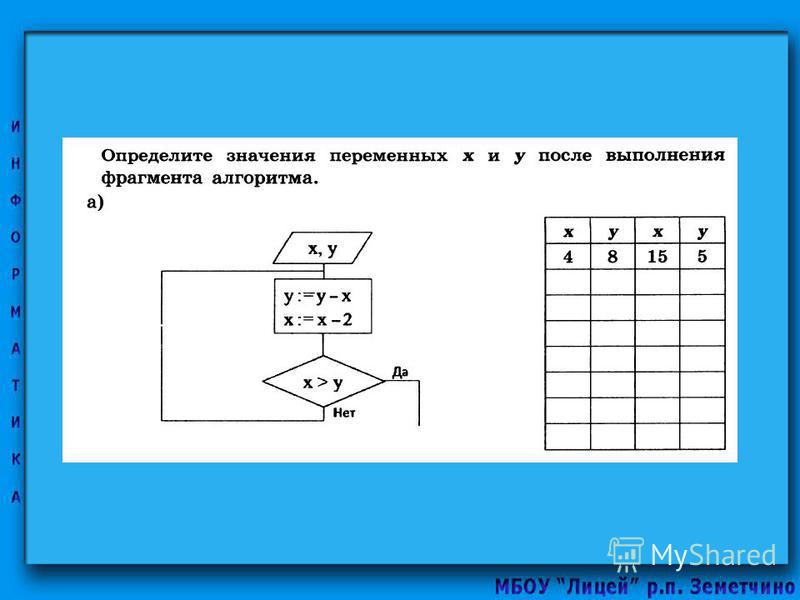


 и отлаживать.
и отлаживать. быть напечатаны.
быть напечатаны.
 )
)
 '
'
Leave A Comment