Прямоугольник. Формулы и свойства прямоугольника
Навигация по странице: Определение прямоугольника Основные свойства прямоугольника Стороны прямоугольника (длина и ширина прямоугольника) Диагональ прямоугольника Периметр прямоугольника Площадь прямоугольника Окружность описанная вокруг прямоугольника Угол между стороной и диагональю прямоугольника Угол между диагоналями прямоугольника
Определение.
Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Рис. 1 1 |
Рис.2 |
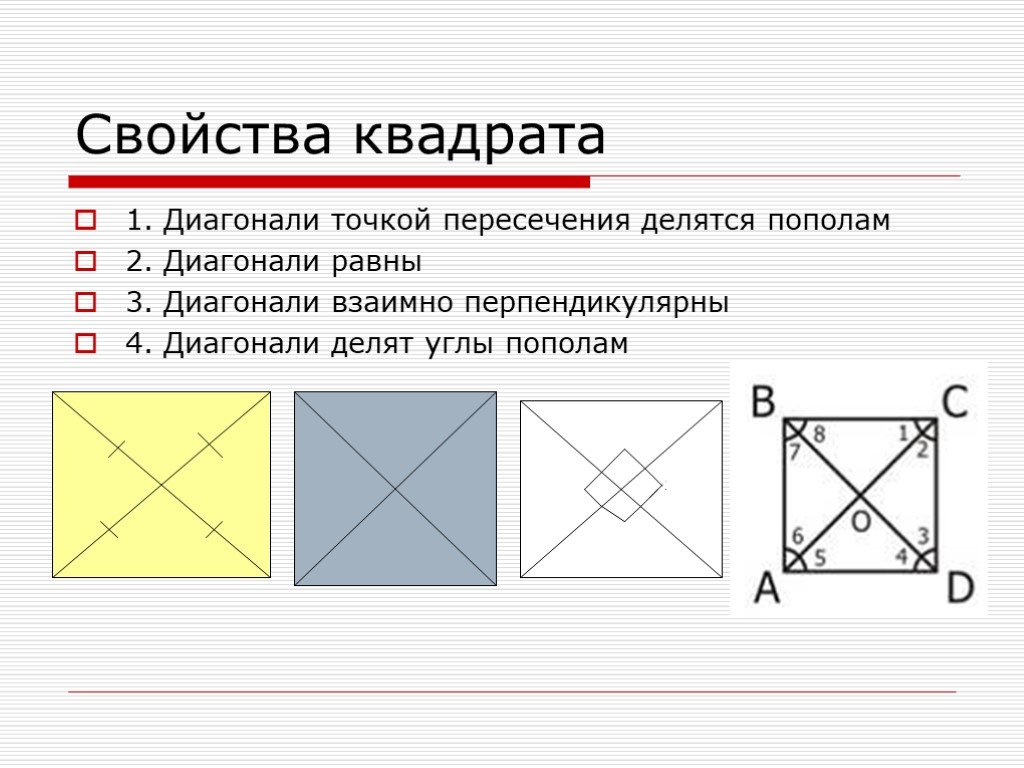
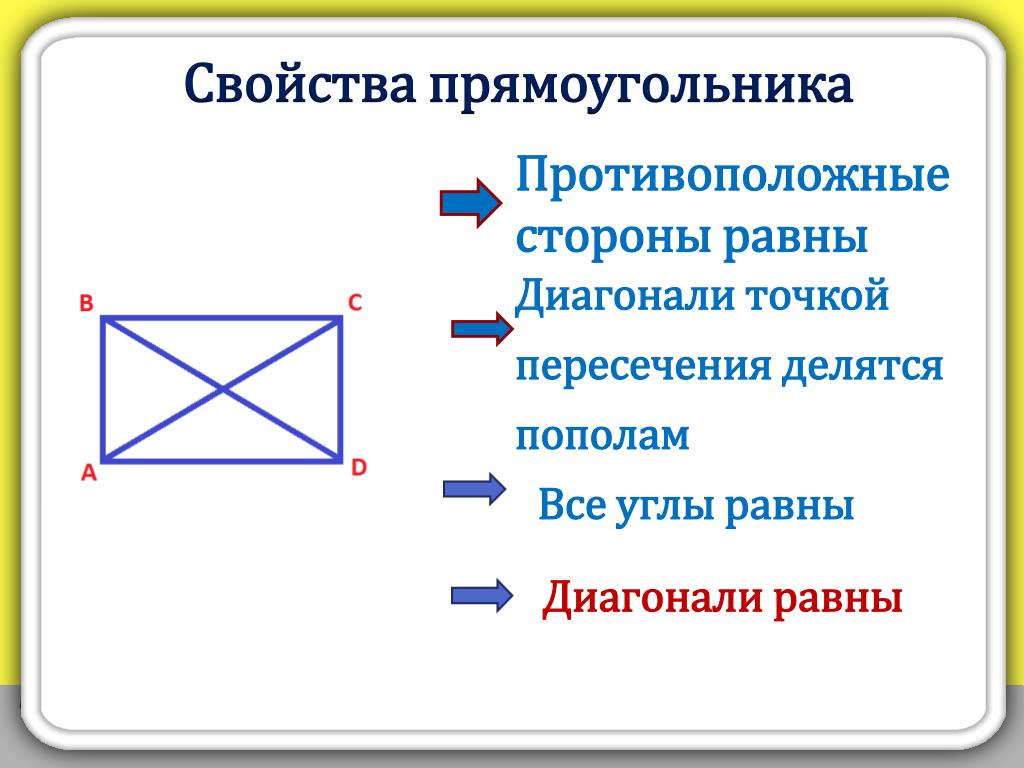
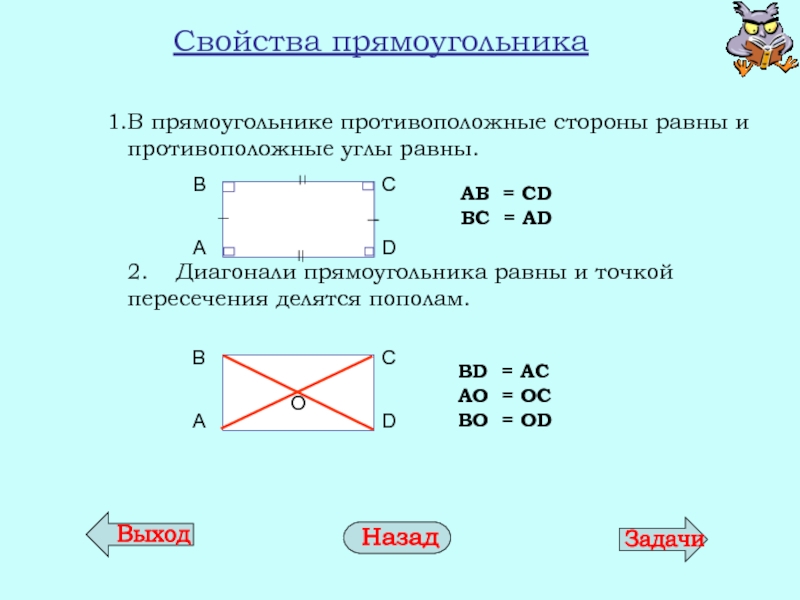
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
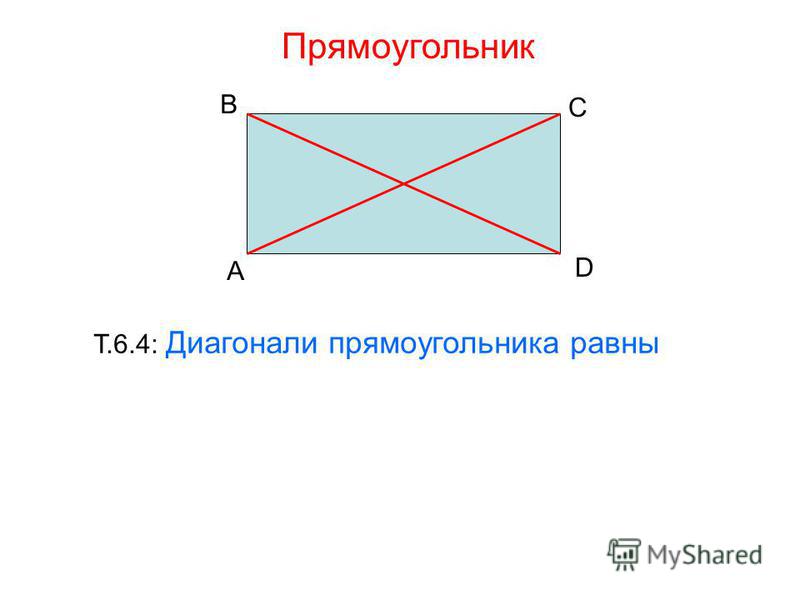
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
| AO = BO = CO = DO = | d | ||
| 2 |
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 — b2
b = √d2 — a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
| a = | S |
| b |
| b = | S |
| a |
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
| a = | P — 2b |
| 2 |
| b = | P — 2a |
| 2 |
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
| a = d sin | β |
| 2 |
| b = d cos | β |
| 2 |
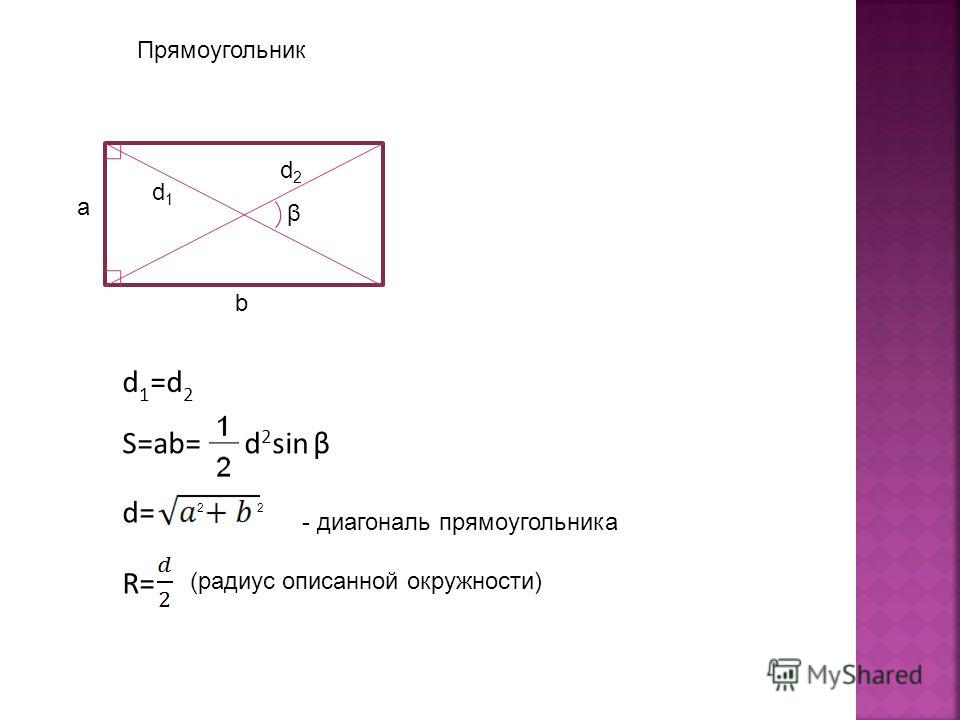
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3.
| d = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
| d = | a |
| sin α |
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
| d = | b |
| cos α |
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 — a2) = 2(b + √d2 — b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 — a2) = 2(b + √4R2 — b2
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 — a2) = 2(b + √Do2 — b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa — 2a2 | = | Pb — 2b2 |
| 2 | 2 |
S = a√d2 — a2 = b√d2 — b2
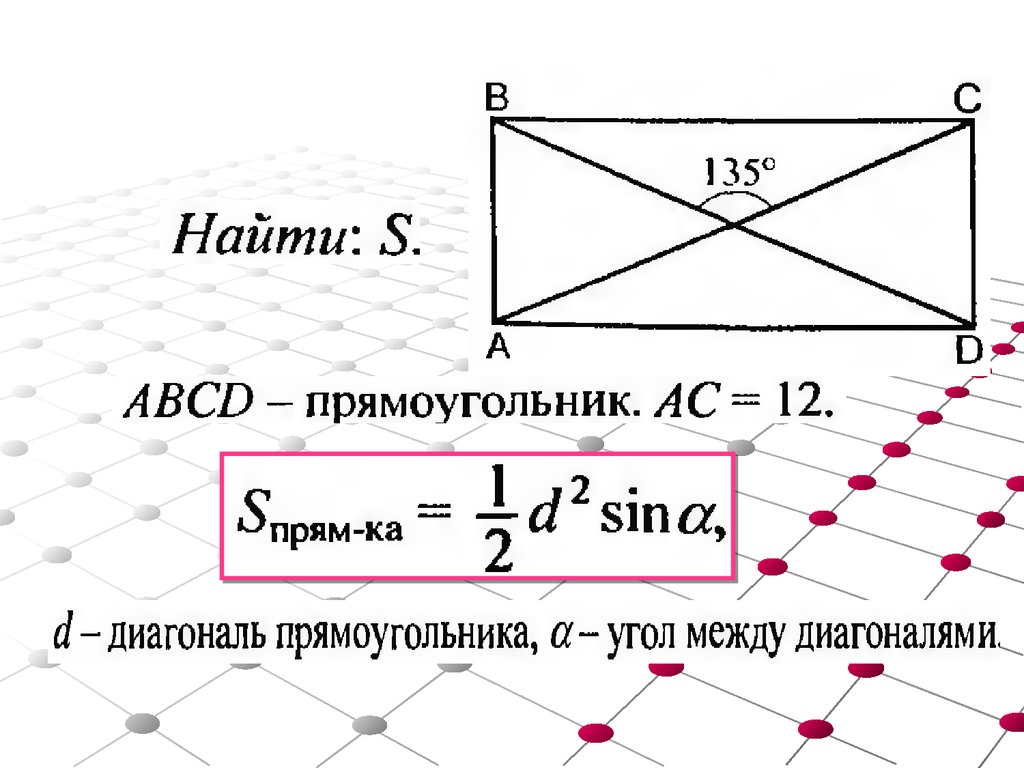
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
| S = | d2 · sin β |
| 2 |
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 — a2 = b√4R2 — b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 — a2 = b√Do2 — b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
| R = | √a2 + b2 |
| 2 |
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
| R = | d |
| 2 |
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
| R = | Dо |
| 2 |
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
| R = | a |
| 2sin α |
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
| R = | b |
| 2cos α |
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
| R = | √2S : sin β |
| 2 |
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
| sin α = | a |
| d |
| cos α = | b |
| d |
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
| α = | β |
| 2 |
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
| sin β = | 2S |
| d2 |
Все таблицы и формулы
Разница между прямоугольником и параллелограммом
Прямоугольник и параллелограмм являются четырехугольниками и двумерными фигурами. Прямоугольники представляют собой особый тип параллелограмма.
Прямоугольники представляют собой особый тип параллелограмма.
Образовательная викторина
Проверьте свои знания по темам, связанным с образованием
1 / 10
Цель оценки состоит в том, чтобы вынести суждение об образовании…
Количество
Качество
Период времени
Возраст
2 / 10
Какой раздел математики занимается изучением форм и размеров предметов?
Алгебра
Геометрия
Тригонометрия
Исчисление
3 / 10
Как называется наука о психике и поведении человека?
социология
Психология
Антропология
Политическая наука
4 / 10
Как называется стандартизированный тест, используемый при поступлении в колледжи в США?
Сб
GRE
ПОСЛЕДНИЙ
MCAT
5 / 10
Кого называют отцом современной физики?
Исаак Ньютон
Альберт Эйнштейн
Stephen Hawking
Галилео Галилей
6 / 10
В чем основное различие между государственным и частным университетом?
Местоположение
Финансирование
Размер
Предлагаемые программы на получение степени
7 / 10
Доктор Люк посещает эмоционально неуравновешенных студентов.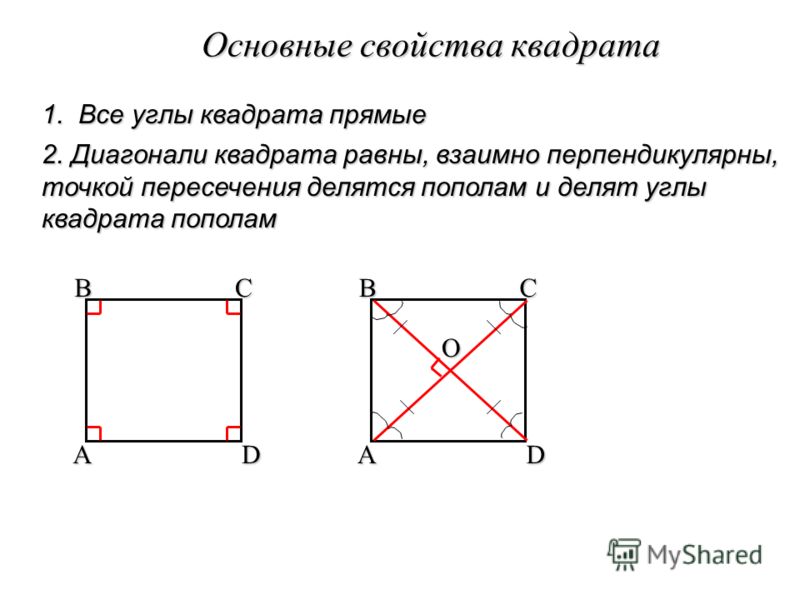 Какие услуги предоставляет доктор Люк?
Какие услуги предоставляет доктор Люк?
Служба инвентаризации
Информационная служба
Служба размещения
Консультационная служба
8 / 10
Какая столица страны Франция?
Париж
Марсель
Лион
Toulouse
9 / 10
Кто изобрел лампочку?
Томас Эдисон
Никола Тесла
Александр Грэхем Белл
Генри Форд
10 / 10
Как называется первый в мире университет?
Болонский университет
Оксфордский университет
Парижский университет
Александрийский университет
ваш счет
Даже если это подтип, чем прямоугольник отличается от параллелограмма?
Площадь четырехугольника можно вычислить по формуле (основание) х (высота). Но интересен тот факт, что площадь тоже можно вычислить.
Прямоугольник против параллелограммаОсновные выводы
- Прямоугольник – это параллелограмм с четырьмя прямыми углами, характеризующийся прямыми параллельными сторонами и равными противоположными углами.
- Параллелограммы — это четырехугольники с двумя парами параллельных сторон, включая различные формы, такие как прямоугольники, ромбы и квадраты.
- Основное различие между прямоугольниками и параллелограммами заключается в том, что прямоугольники представляют собой особую категорию параллелограммов, характеризующуюся четырьмя прямыми углами. Напротив, параллелограммы охватывают более широкий диапазон форм с параллельными сторонами.
Разница между прямоугольником и параллелограммом заключается в том, что хотя противоположные стороны обоих параллельны и равны, все углы прямоугольника равны 90 градусов. В то время как у параллелограмма противоположные углы равны, а смежные углы смежны.
Если внутренние углы параллелограмм стать 90 градусов, это дало бы нам прямоугольник.
Хотите сохранить эту статью на потом? Нажмите на сердечко в правом нижнем углу, чтобы сохранить в свой собственный блок статей!
Прямоугольники – это четырехугольники, у которых четыре стороны, а противоположные стороны равны. Все четыре внутренних угла равны и дополняют друг друга, т. е. 90 градусов.
е. 90 градусов.
С Пифагором теорема, мы можем вычислить стороны прямоугольников. Распространенными примерами вещей, имеющих прямоугольную форму, являются стол вершин, обложки книг и ноутбуков.
Параллелограммы — это также четырехугольники, у которых четыре стороны, а противоположные стороны равны. Противоположные стороны параллельны друг другу, отсюда и название.
Противоположные внутренние углы равны, а прилежащие внутренние углы смежные.
Сравнительная таблица
| Параметры сравнения | Прямоугольные | Параллелограмм |
|---|---|---|
| Углы | Все углы равны 90 градусов. | Противолежащие внутренние углы равны, а прилежащие углы смежные |
| Длина диагонали | Длины диагоналей равны | Диагонали различаются по длине. |
| Угол пересечения | Диагонали пересекаются под прямым углом | Диагонали пересекаются так, что образующиеся прилежащие углы являются дополнительными. |
| Симметрия | Имеет вращательную и отражательную симметрию | Имеет только степень вращения порядка 2 |
| Диагональное деление пополам | Диагонали делятся пополам, образуя прямоугольные треугольники | Диагонали делятся пополам, образуя равнобедренные треугольники |
Что такое прямоугольник?
Прямоугольники — это особый вид параллелограмм. Как и параллелограмм, прямоугольники также имеют равные и параллельные противоположные стороны.
Они имеют равные противолежащие внутренние углы и имеют смежные углы в качестве дополнительных.
Прямоугольники отличаются от параллелограммов тем, что все внутренние углы прямоугольника равны 90 градусам. Диагонали равны и даже пересекаются в середине, образуя прямоугольные треугольники.
Стороны прямоугольника можно вычислить, если известны значения диагоналей. Это можно сделать по теореме Пифагора, так как треугольники, образованные на пересечении диагоналей, прямоугольные.
Типичными примерами прямоугольников являются книги, шкафы и т. д.
Что такое параллелограмм?
Параллелограммы — это четырехугольники, у которых порядок симметрии равен 2. Они называются параллелограммами, потому что противоположные стороны этих четырехугольников параллельны, как в случае прямоугольника.
Противоположные внутренние углы параллелограмма равны, а прилежащие углы дополнительные, т.е. сумма прилежащих углов должна быть равна 180 градусам. Когда углы параллелограмма равны 90 градусов, он образует прямоугольник.
Диагонали параллелограмма не равны, но их середины делят пополам. Площадь пересечения образует равнобедренный треугольник.
Параллелограммы следуют закону параллелограмма, который гласит, что сумма квадратов сторон равна сумме квадратов их диагоналей. Этот закон можно применить для вычисления сторон параллелограмма.
любимая сладость Индии кая катли является примером параллелограмма.
Основные различия между прямоугольником и параллелограммом
- Основное отличие прямоугольника от параллелограмма, делающее прямоугольник частным случаем параллелограмма, заключается в том, что все углы прямоугольника равны 90 градусам.
 В параллелограмме это не так, потому что смежные углы только дополняют друг друга.
В параллелограмме это не так, потому что смежные углы только дополняют друг друга. - Даже если диагонали пересекаются друг с другом в середине, диагонали прямоугольника равны, но это не так в случае параллелограмма.
- Угол пересечения диагоналей в случае прямоугольника равен 90 градусов. Но это не обязательно в случае параллелограмма. Смежные углы, образованные при пересечении, считаются дополнительными.
- Симметрия для обеих двумерных структур различна. Это связано с тем, что симметрия прямоугольника может быть получена как из его вершин, так и из его сторон. Это означает, что прямоугольник имеет как вращательную, так и отражательную симметрию, в отличие от параллелограмма, который имеет только вращательную симметрию.
- Поскольку диагонали прямоугольника делят друг друга пополам под прямым углом, площадь, образованная пересечением, является прямоугольным треугольником. В случае параллелограмма площадь, образованная под пересечением диагоналей, представляет собой равнобедренный треугольник.

Рекомендации
- https://dl.acm.org/doi/pdf/10.1145/220279.220338
- https://www.tandfonline.com/doi/abs/10.1080/14794802.2014.933711
Один запрос?
Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы предоставить вам ценность. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/родными. ДЕЛИТЬСЯ ♥️
Эмма Смит
Эмма Смит имеет степень магистра английского языка в колледже Ирвин-Вэлли. Она работает журналистом с 2002 года, пишет статьи об английском языке, спорте и праве. Подробнее обо мне на ней био страница.
Диагональ прямоугольника — определение, свойства, вывод, примеры
Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины прямоугольника. Диагональ прямоугольника делит прямоугольник на два равных прямоугольных треугольника. Прямоугольник — это двумерная фигура с четырьмя сторонами, четырьмя вершинами и четырьмя углами. Две диагонали прямоугольника имеют одинаковую длину.
Две диагонали прямоугольника имеют одинаковую длину.
В этой статье мы поймем понятие диагонали прямоугольника и метод расчета его длины. Мы исследуем свойства, формулу и вывод формулы для вычисления длины диагонали прямоугольника. Давайте узнаем больше о диагоналях прямоугольника, их формуле и решим несколько примеров.
| 1. | Что такое диагонали прямоугольника? |
| 2. | Свойства диагоналей прямоугольника |
| 3. | Диагональ прямоугольника Формула |
| 4. | Диагональ производного прямоугольника |
| 5. | Углы диагоналей прямоугольника |
| 6. | Часто задаваемые вопросы о диагоналях прямоугольника |
Что такое диагональ прямоугольника?
Диагональ прямоугольника — это отрезок, соединяющий любые две его несмежные вершины. У прямоугольника две диагонали, каждая из которых делит прямоугольник на два прямоугольных треугольника, диагональ которых является гипотенузой. Диагонали делят друг друга пополам, образуя один угол тупой, а другой острый. Два треугольника, образованные диагональю прямоугольника, равны.
У прямоугольника две диагонали, каждая из которых делит прямоугольник на два прямоугольных треугольника, диагональ которых является гипотенузой. Диагонали делят друг друга пополам, образуя один угол тупой, а другой острый. Два треугольника, образованные диагональю прямоугольника, равны.
Свойства диагоналей прямоугольника
Диагональ прямоугольника — это отрезок, проведенный между противоположными вершинами прямоугольника. Свойства диагоналей прямоугольника следующие:
- Две диагонали прямоугольника конгруэнтны. Другими словами, длины диагоналей равны.
- Две диагонали делят друг друга пополам и делят прямоугольник на две равные части.
- Длину диагонали прямоугольника можно получить по теореме Пифагора.
- Когда диагонали делятся пополам, углы прямоугольника в центре становятся одним тупым углом, а другим острым углом.
- Когда две диагонали пересекаются пополам под углом 90°, это называется квадратом.

- Поскольку диагональ прямоугольника делит прямоугольник на два прямоугольных треугольника, она считается гипотенузой этих треугольников.
Диагональ прямоугольника Формула
Формула диагонали прямоугольника помогает найти длину и ширину прямоугольника. В следующем прямоугольнике AC и BD — диагонали. Вы можете видеть, что длины как AC, так и BD одинаковы. Диагональ делит прямоугольник на 2 прямоугольных треугольника, у которых стороны равны сторонам прямоугольника и с гипотенузой. Эта гипотенуза и есть диагональ.
Таким образом, для вычисления длин диагоналей прямоугольника используется формула: d = √( l 2 + w 2 )
Где,
- d = диагональ прямоугольника
- l = длина прямоугольника
- w = ширина прямоугольника
Диагональ производного прямоугольника
Формула диагонали прямоугольника выводится с помощью теоремы Пифагора. Рассмотрим прямоугольник, указанный выше. Рассмотрим прямоугольник длины «l» и ширины «w». Пусть длина каждой диагонали равна «d».
Рассмотрим прямоугольник длины «l» и ширины «w». Пусть длина каждой диагонали равна «d».
Applying Pythagoras theorem to the triangle BCD,
d 2 = l 2 + w 2
Taking square root on both sides,
d = √( l 2 + w 2 )
Таким образом, формула диагонали прямоугольника:
d = √( l 2 + w 2 )
Где
- l = длина прямоугольника
- w = ширина прямоугольника
Углы диагонали прямоугольника
Диагонали прямоугольника имеют одинаковую длину и делятся пополам, но не образуют прямого угла в центре. Они образуют линейные пары углов, такие как тупой угол + острый угол на каждой из диагоналей. Прямоугольник называется квадратом, если его диагонали делят друг друга пополам под прямым углом, так как диагонали прямоугольника не делят пополам соответствующие углы при вершинах на равные углы.
Диагональ делит прямоугольник на два конгруэнтных треугольника, которые также являются прямоугольными треугольниками с одинаковыми гипотенузами. Каждая диагональ действует как гипотенуза для образованных таким образом прямоугольных треугольников. Применяя теорему Пифагора к образованному таким образом треугольнику, d 2 = l 2 + w 2 , где d — диагональ, l — длина, а w — ширина прямоугольника. Извлекая квадратный корень с обеих сторон, √(d 2 ) = √(l 2 + w 2 ). Таким образом, формула диагонали прямоугольника равна: √( l 2 + w 2 ).
Каждая диагональ действует как гипотенуза для образованных таким образом прямоугольных треугольников. Применяя теорему Пифагора к образованному таким образом треугольнику, d 2 = l 2 + w 2 , где d — диагональ, l — длина, а w — ширина прямоугольника. Извлекая квадратный корень с обеих сторон, √(d 2 ) = √(l 2 + w 2 ). Таким образом, формула диагонали прямоугольника равна: √( l 2 + w 2 ).
Важные замечания о диагонали прямоугольника
- Диагональ прямоугольника представляет собой отрезок, соединяющий несмежные вершины.
- Длину диагонали прямоугольника можно рассчитать по формуле: d = √( l 2 + w 2 ).
- Две диагонали прямоугольника делят друг друга пополам.
Похожие статьи
- Свойства прямоугольника
- Углы прямоугольника
- Прямоугольник
Часто задаваемые вопросы о диагоналях прямоугольника
Что такое диагональ прямоугольника?
Диагональ прямоугольника — это отрезок, проведенный из противоположных вершин прямоугольника и делящий другую диагональ пополам. Две диагонали прямоугольника имеют одинаковую длину и делят прямоугольник на две равные части. Диагональ прямоугольника делит прямоугольник на два прямоугольных треугольника с гипотенузой.
Две диагонали прямоугольника имеют одинаковую длину и делят прямоугольник на две равные части. Диагональ прямоугольника делит прямоугольник на два прямоугольных треугольника с гипотенузой.
Что такое диагональная формула прямоугольника?
Формула для вычисления диагонали прямоугольника помогает найти длину диагонали. Формула:
d = √( l 2 + w 2 )
Где,
- d = диагональ прямоугольника
- l = длина прямоугольника
- w = ширина прямоугольника
Каковы свойства диагонали прямоугольника?
Свойства диагонали прямоугольника:
- Длина двух диагоналей одинакова.
- Две диагонали делят друг друга пополам и делят прямоугольник на две равные части.
- Длину диагоналей можно получить с помощью теоремы Пифагора.
- Когда диагонали делятся пополам, углы в центре прямоугольника становятся одним тупым углом, а другим острым.
- Когда две диагонали пересекаются пополам под углом 90°, это называется квадратом.

Диагонали прямоугольника равны?
Диагонали прямоугольника делятся пополам и равны. Так как прямоугольник является четырехугольником, то все углы прямые. Прямоугольник также является параллелограммом, у которого противоположные стороны равны.
Диагонали прямоугольника делятся пополам под углом 90°?
Диагонали прямоугольника делят друг друга пополам, но не под углом 90 градусов.
Как определить площадь прямоугольника, зная диагональ прямоугольника?
Мы можем вычислить площадь (A) прямоугольника, если его диагональ (d) и длина (l) заданы по формуле Площадь = l × √(d 2 — l 2 ).
Как найти длину прямоугольника, зная диагональ прямоугольника?
Мы можем рассчитать длину прямоугольника (l), если его диагональ (d) и ширина (w) заданы по формуле l = √(d 2 — w 2 ).
Диагонали прямоугольника
Прямоугольник — это четырехсторонняя фигура с двумя парами противоположных параллельных сторон. Все прямоугольники имеют четыре прямых угла. Диагонали прямоугольника — это отрезки, соединяющие противоположные углы прямоугольника. Другими словами, диагонали прямоугольника делят его на четыре равные части.
Все прямоугольники имеют четыре прямых угла. Диагонали прямоугольника — это отрезки, соединяющие противоположные углы прямоугольника. Другими словами, диагонали прямоугольника делят его на четыре равные части.
Диагонали прямоугольника перпендикулярны друг другу. Это означает, что они образуют две пары конгруэнтных углов. Каждый угол равен 90 градусов. Диагонали прямоугольника также делят друг друга пополам. Это значит, что они делят друг друга на две равные части.
Длину диагоналей прямоугольника можно найти по теореме Пифагора. Эта теорема утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух других сторон. В прямоугольнике гипотенуза всегда является одной из диагоналей. Две другие стороны — это длины сторон прямоугольника. Следовательно, чтобы найти длину диагонали, нам нужно сначала найти длину одной стороны и одной диагонали.
Допустим, у нас есть прямоугольник со сторонами 3 дюйма и 4 дюйма. Мы можем использовать эти измерения, чтобы найти длину одной диагонали, используя теорему Пифагора. Во-первых, нам нужно возвести в квадрат и 3, и 4, чтобы получить 9 и 16 соответственно. Затем нам нужно добавить 9 + 16, чтобы получить 25. Наконец, нам нужно извлечь квадратный корень из 25, чтобы получить 5 дюймов, что и является нашим ответом!
Мы можем использовать эти измерения, чтобы найти длину одной диагонали, используя теорему Пифагора. Во-первых, нам нужно возвести в квадрат и 3, и 4, чтобы получить 9 и 16 соответственно. Затем нам нужно добавить 9 + 16, чтобы получить 25. Наконец, нам нужно извлечь квадратный корень из 25, чтобы получить 5 дюймов, что и является нашим ответом!
Заключение
Диагональ — это отрезок, соединяющий две несмежные вершины (углы) многоугольника (фигуры с прямыми сторонами). В прямоугольнике есть две диагонали, которые пересекают его центр и делят пополам (делят на две равные части) его длину и ширину! Эти диагонали также образуют две пары конгруэнтных углов (45°). Вы можете использовать теорему Пифагора, чтобы определить их длину, если вы заранее знаете размер стороны или одной диагонали!
Часто задаваемые вопросы
Что такое диагонали прямоугольника?
Прямоугольник — это четырехсторонняя фигура с двумя парами противоположных параллельных сторон.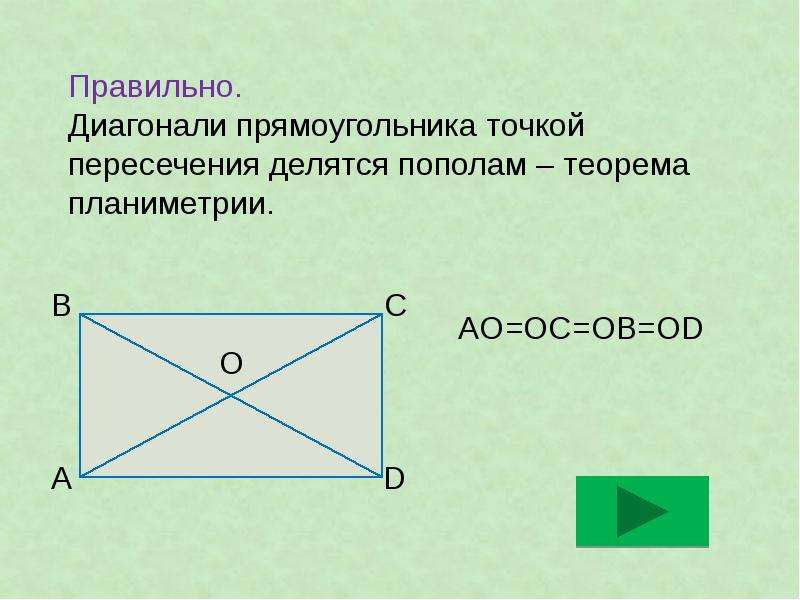

 В параллелограмме это не так, потому что смежные углы только дополняют друг друга.
В параллелограмме это не так, потому что смежные углы только дополняют друг друга.

Leave A Comment