Задачи 8 ЕГЭ профильная математика
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ

посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ

посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ

посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Найдите тангенс угла ABB3.
Найдите тангенс угла ABB3.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых ребер.
Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых ребер.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и C.
Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и C.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Найдите площадь сечения, проходящего через середины четырех его ребер.
Найдите площадь сечения, проходящего через середины четырех его ребер.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Задача 16 ЕГЭ математика база
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 В воду полностью погрузили деталь объемом 1500 см3,
при этом уровень жидкости в сосуде поднялся на 12 см. Какой уровень воды в сантиметрах был до погружения детали?
В воду полностью погрузили деталь объемом 1500 см3,
при этом уровень жидкости в сосуде поднялся на 12 см. Какой уровень воды в сантиметрах был до погружения детали?
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 25 см. Чему равен объем детали? Ответ выразите в см3.
При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 25 см. Чему равен объем детали? Ответ выразите в см3.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Найдите площадь поверхности параллелепипеда.
Найдите площадь поверхности параллелепипеда.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
посмотреть ответ
Подборка задач по стереометрии для подготовке к ЕГЭ
Комбинации тел
1.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
3.
В куб вписан шар радиуса 1. Найдите объем куба.
4.
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
5.
В основании прямой призмы лежит квадрат со стороной 2.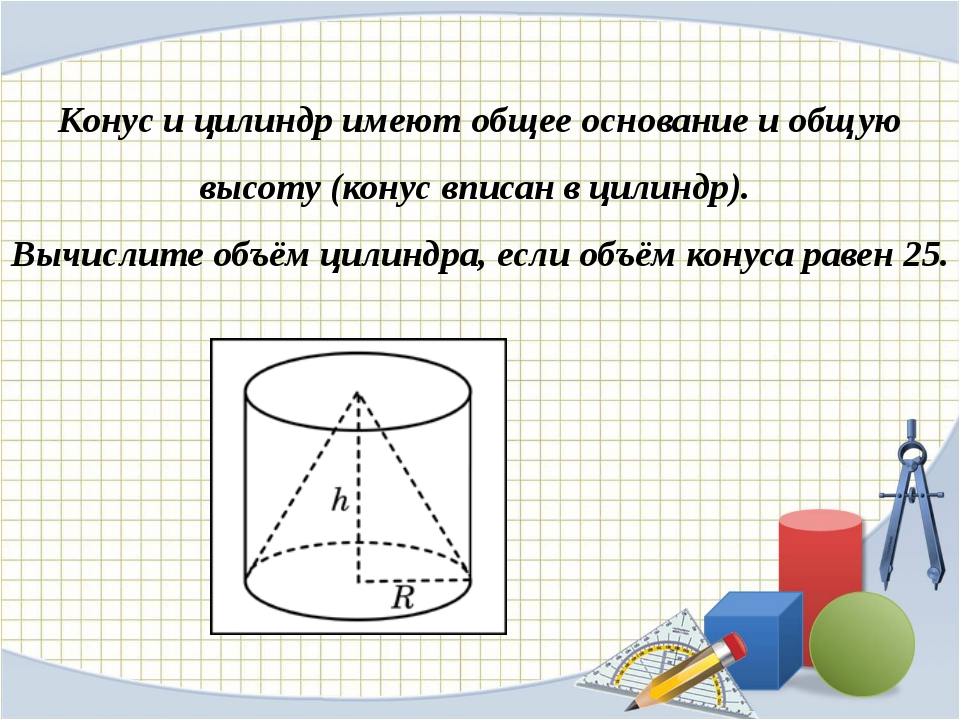 Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
6.
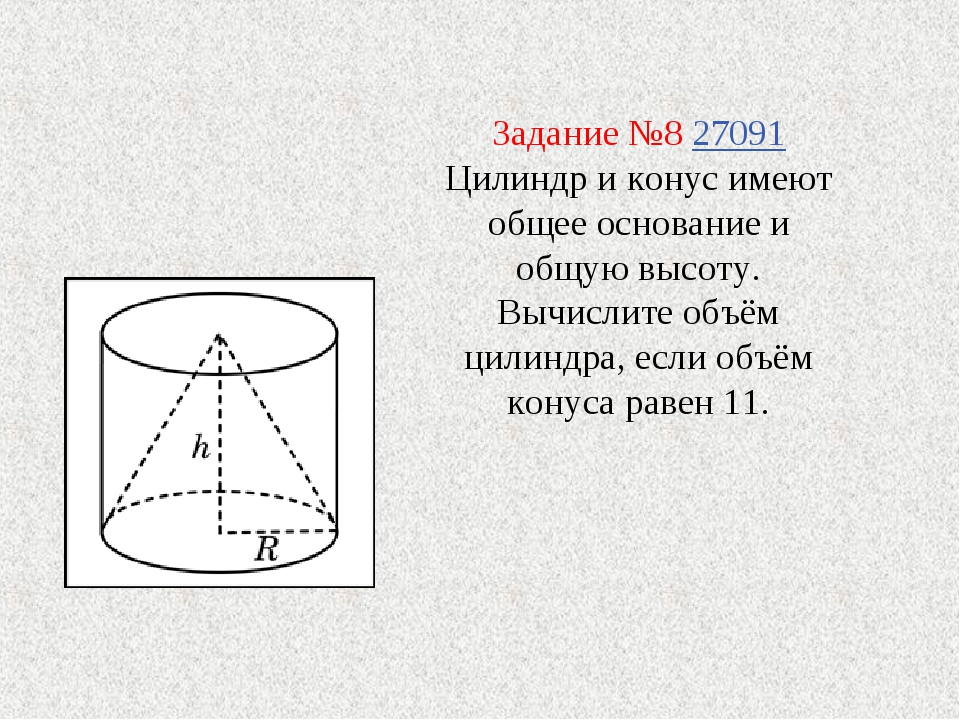
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
7.
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
8.
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
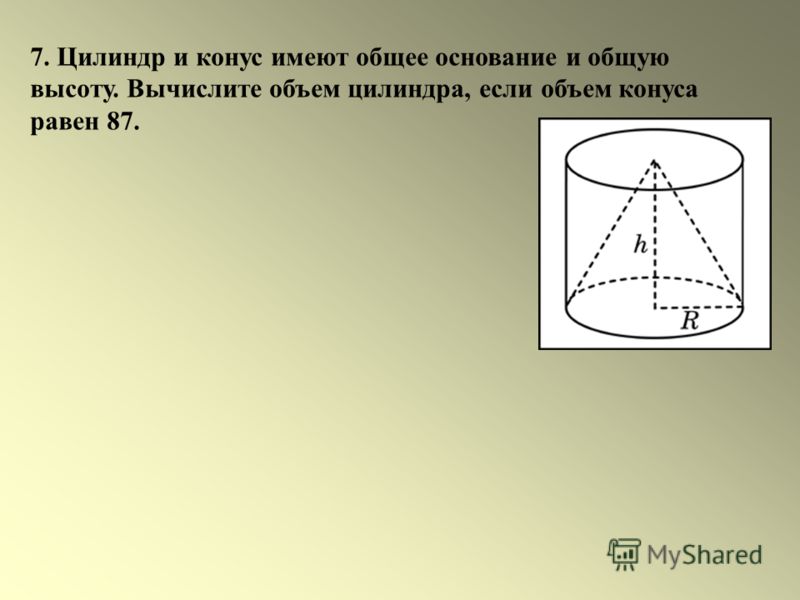
9. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
10.
Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
11
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
12.
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
13.
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на
14.
Около куба с ребром описан шар. Найдите объем этого шара, деленный на
15.
Вершина A куба с ребром 1,6 является центром сферы, проходящей через точку A1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину
16.
Середина ребра куба со стороной 1,9 является центром шара радиуса 0,95. Найдите площадь части поверхности шара, лежащей внутри куба. В ответе запишите
17.
Объём тетраэдра равен 19. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.
18.
Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
19. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
20.
Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Объем шара равен 24. Найдите объем цилиндра.
21.
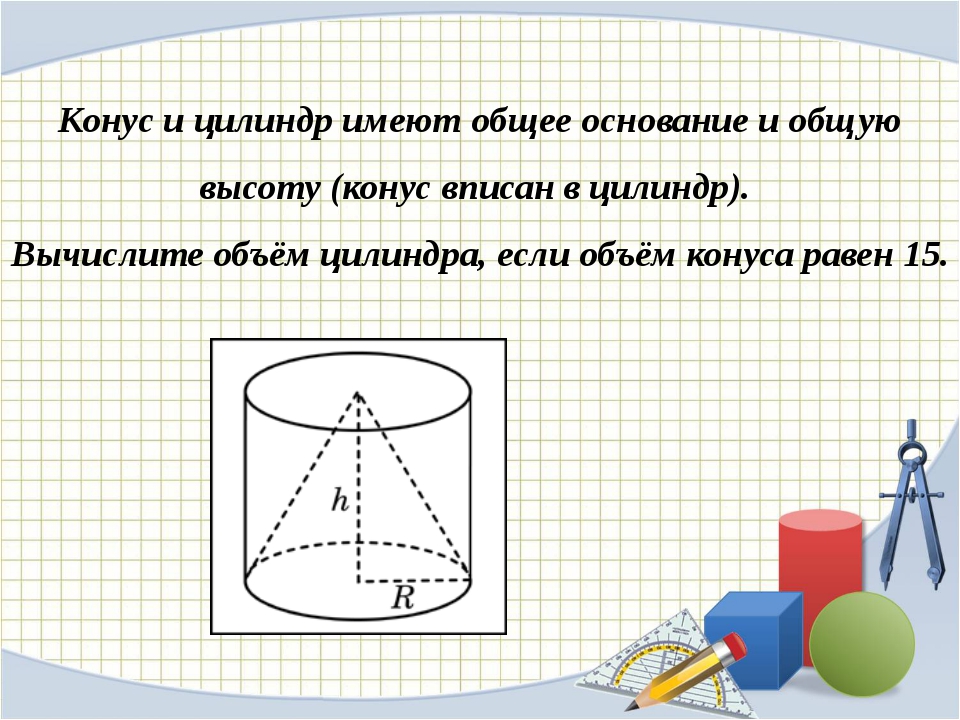
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 5.
22.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
23.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
24. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
25.
Куб вписан в шар радиуса Найдите объем куба.
26.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна Найдите радиус сферы.
27.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину).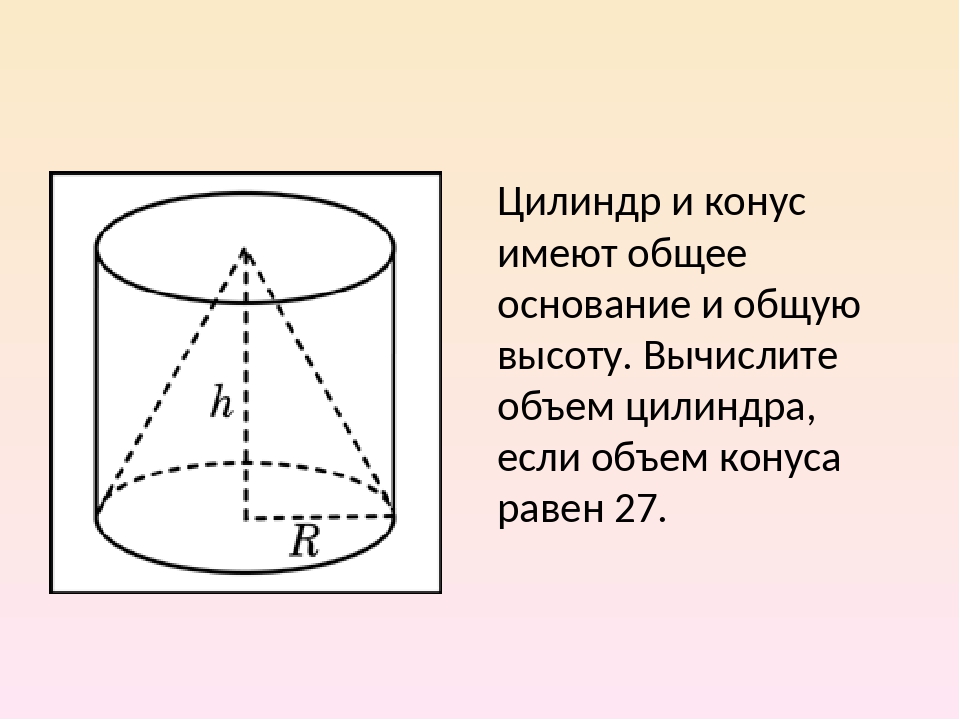 Центр сферы находится в центре основания конуса. Радиус сферы равен Найдите образующую конуса.
Центр сферы находится в центре основания конуса. Радиус сферы равен Найдите образующую конуса.
28.
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
29.
Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.
30. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.
31.
Прямоугольный параллелепипед описан около сферы радиуса 17. Найдите его объём.
32.
Куб описан около сферы радиуса 6. Найдите объём куба.
33.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
34.
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2.
35.
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна 2.
36.
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2.
37. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности конуса равна Найдите площадь боковой поверхности цилиндра.
Цилиндр
1.
В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
2.
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.
3. Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
4.
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на
5. В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.
6.
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
7.
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
8.
Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на
9.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
В ответе укажите
10.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
11.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
12. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
13.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
14.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
15.
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
16.
Площадь боковой поверхности цилиндра равна , а диаметр основания — 1. Найдите высоту цилиндра.
17. Площадь боковой поверхности цилиндра равна , а высота — 1. Найдите диаметр основания.
18. Объём первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м3).
Найдите объём второго цилиндра (в м3).
19.
Шар, объём которого равен 60, вписан в цилиндр. Найдите объём цилиндра.
Конус
1.
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
2.
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите
3.
Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
4.
Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней?
5.
Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на
6.
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.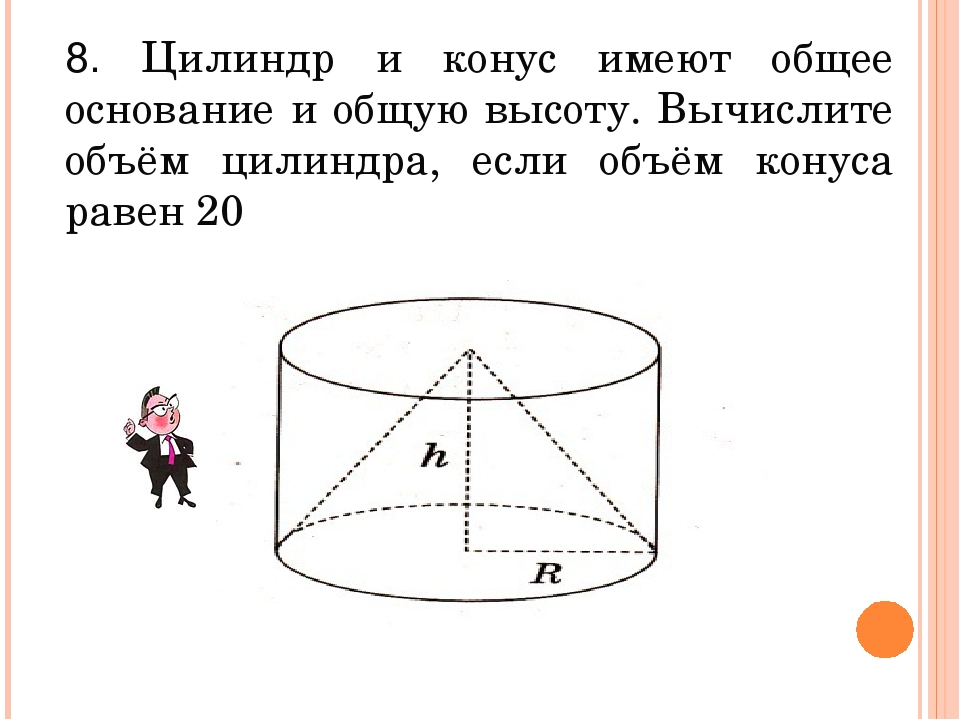
7.
Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 6. Найдите его объем, деленный на
8.
Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
9.
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
10.
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
11.
Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на
12.
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
13.
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса.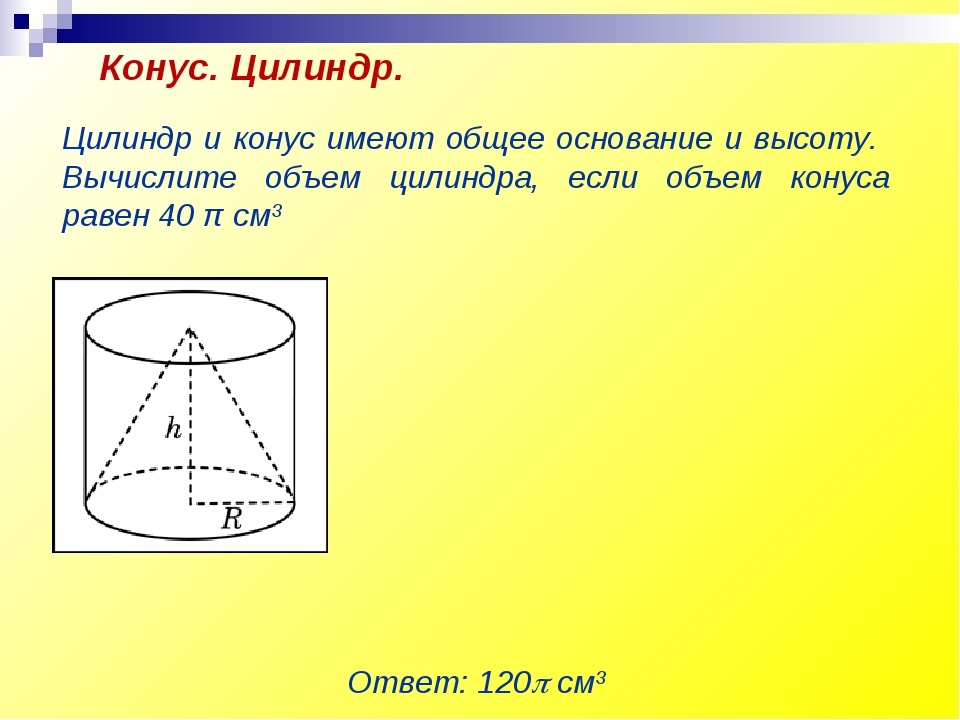 Найдите площадь полной поверхности отсечённого конуса.
Найдите площадь полной поверхности отсечённого конуса.
14.
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на
15.
Найдите объем части конуса, изображенной на рисунке. В ответе укажите
16.
Найдите объем части конуса, изображенной на рисунке. В ответе укажите
17.
Найдите объем части конуса, изображенной на рисунке. В ответе укажите
18.
Найдите объем части конуса, изображенной на рисунке. В ответе укажите
19. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
20. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
21. Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
22.
В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
23. Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса.
Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса.
24. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
25. Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
26. Диаметр основания конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
27
Найдите площадь осевого сечения конуса, радиус основания которого равен 3, а образующая равна 5.
28.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен Найдите образующую конуса.
29.
Площадь основания конуса равна 45. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 4 и 8, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Найдите площадь сечения конуса этой плоскостью.
Шар
1. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
2.
Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
3.
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
4. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
5. Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
6.
Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
7. Объем шара равен 288 Найдите площадь его поверхности, деленную на
8.
Площадь поверхности шара равна 24. Найдите площадь большого круга шара.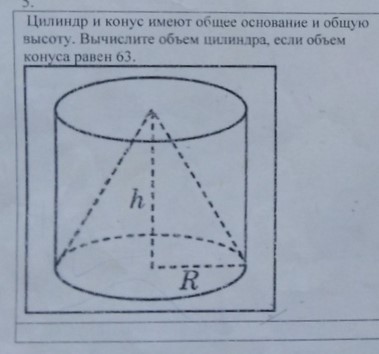
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/414609-podborka-zadach-po-stereometrii-dlja-podgotov
ЕГЭ по математике 2019, Ященко 20 вариантов, решение заданий 8 (тематическая рабочая тетрадь) — Решения вариантов ЕГЭ по математике: 2017, 2018, 2019, 2020
Подготовительные задания
Задачи из книжки https://yadi.sk/i/NZcoB3vn4T_c5w или https://yadi.sk/i/05jYXhJFpGw-9w (то же самое)
ЗАДАЧА 8
Подготовительные задания
1. 3.
3.
4. В цилиндрическом сосуде уровень жидкости достигает 54 см. На ка-
кой высоте будет находиться уровень жидкости, если ее перелить во
второй цилиндрический сосуд, диаметр которого в 3 раза больше
диаметра первого? Ответ выразите в сантиметрах.
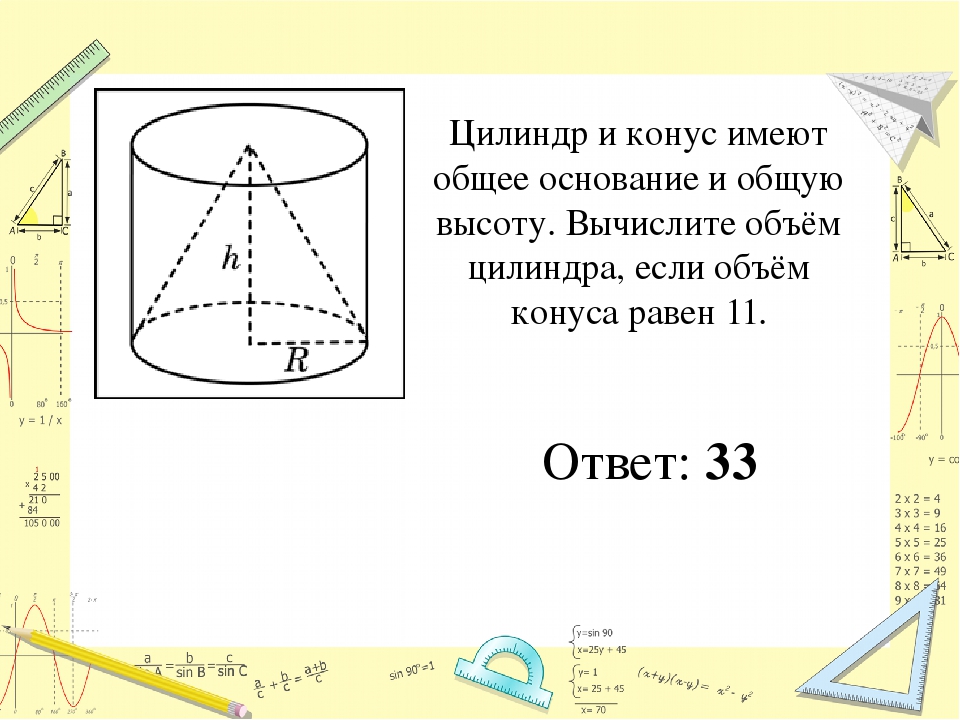
5. Цилиндр и конус имеют общие основание и высоту. Объём конуса
равен 60. Найдите объём цилиндра.
6. Во сколько раз увеличится объем конуса, если радиус его основания
увеличится в 3 раза, а высота останется прежней?
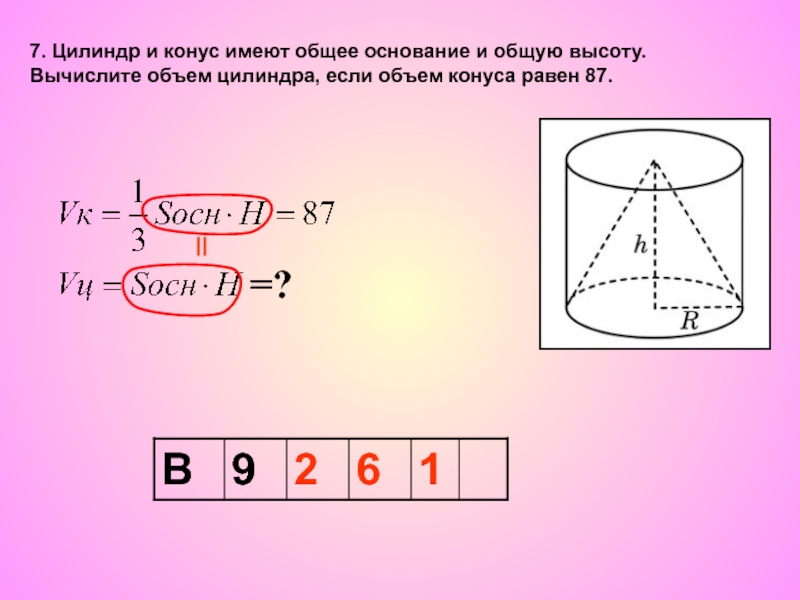
7. Цилиндр и конус имеют общие основание и высоту. Объём цилиндра
равен 153. Найдите объём конуса.
8. Объём куба, описанного около сферы, равен 2744. Найдите радиус
сферы.
9. Через среднюю линию основания треугольной призмы, объём кото-
рой равен 6, проведена плоскость, параллельная боковому ребру.
Найдите объём отсеченной треугольной призмы.
10. Объём куба равен 68. Найдите объём треугольной призмы, отсекае-
мой от него плоскостью, проходящей через середины двух рёбер, вы-
ходящих из одной вершины, и параллельной третьему ребру, выхо-
дящему из этой же вершины.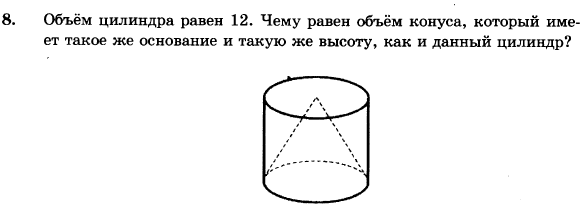
11. Найдите объем многогранника, вершинами которого являются точ-
ки А, В, С, D, А1, D1, параллелепипеда АВСDA1B1C1D1‚ у которого
АВ=4, АD=4, АА1=9.
12. Найдите объем многогранника, вершинами которого являются точ-
ки В, С, D, С1, D1, параллелепипеда АВСDA1B1C1D1, у которого
АВ=3, АD=З, АА1=7.
13.Найдите объем многогранника, вершинами которого являются точ-
ки А, В, D, А1, параллелепипеда АВСDA1B1C1D1, у которого АВ=8,
АD=5, АА1=6.
14. Найдите объем многогранника, вершинами которого являются точ-
ки С, А1, В1, С1, правильной треугольной призмы. АВСА1В1С1, пло-
щадь основания которой равна 5, а боковое ребро равно 9.
15. Цилиндр, объём которого равен 69, описан около шара. Найдите
объём шара.
16. Конус и цилиндр имеют общее основание и общую высоту (конус
вписан в цилиндр). Вычислите объём цилиндра, если объём конуса
равен 35.
17. Шар вписан в цилиндр. Площадь поверхности шара равна 132. Най-
дите площадь полной поверхности цилиндра.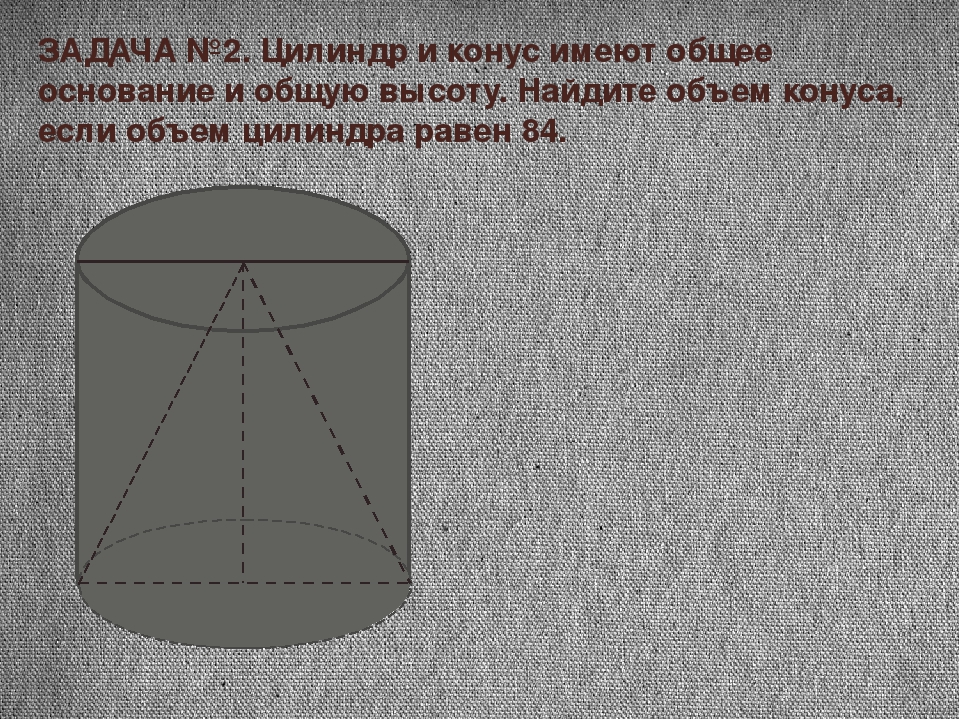
18. В правильной треугольной призме АВСА1В1С1, все ребра которой
равны 2, найдите угол между прямыми АА1 и ВС1. Ответ дайте в
градусах.
19. В правильной четырёхугольной призме АВСDA1B1C1D1, известно, что
D1В=2*АВ. Найдите угол между диагоналями ВD1 и СА1 . Ответ дай-
те в градусах.
20. Шар, объём которого равен 7л ‚, вписан в куб. Найдите объём куба.
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки «Ященко 36 вариантов 2019»,
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео.
 Нажимай!
Нажимай! C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru
Задачи ЕГЭ на объем конуса и цилиндра на 2 варианта с ответами | Материал для подготовки к ЕГЭ (ГИА) по геометрии (11 класс) на тему:
ВАРИАНТ 1
1.В цилиндрический сосуд налили воды. Уровень воды при этом достигает высоты 15 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 12 см. Чему равен объем детали? Ответ выразите в .
2.Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27.
3.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
4.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
5.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
6.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
В ответе укажите .
7.Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
8.Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 114.
9.Найдите объем V конуса, образующая которого равна 3 и наклонена к плоскости основания под углом 30. В ответе укажите .
10.Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 20 раз?
11.Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 22 раз?
12.Высота конуса равна 3, образующая равна 9. Найдите его объем, деленный на .
13.Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
ВАРИАНТ 2
1.В цилиндрический сосуд налили воды. Уровень воды при этом достигает высоты 16 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Чему равен объем детали? Ответ выразите в .
2.Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 23.
Вычислите объем цилиндра, если объем конуса равен 23.
3.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
4.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
5.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
6.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
7.Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
8.Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 63.
9.Найдите объем V конуса, образующая которого равна 11 и наклонена к плоскости основания под углом 30. В ответе укажите .
10.Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 22 раза?
11.Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 40 раза?
12.Высота конуса равна 4, образующая равна 10. Найдите его объем, деленный на .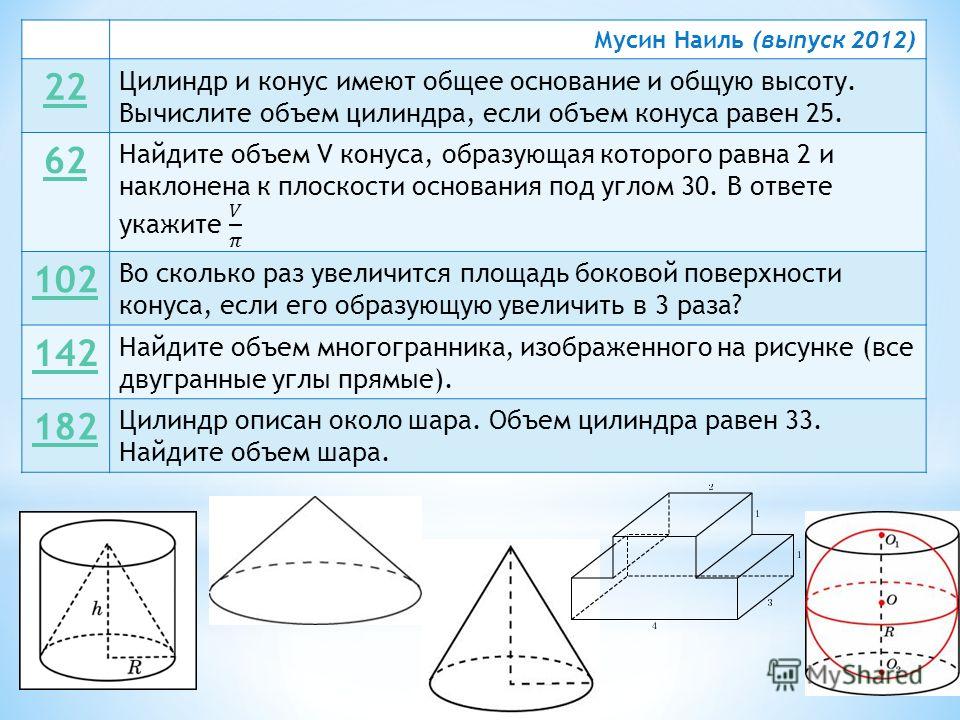
13.Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
ОТВЕТЫ.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
1вар | 960 | 81 | 32 | 15 | 8 | 120 | 648 | 38 | 3,375 | 20 | 484 | 72 | 243 |
2вар | 2275 | 69 | 3,75 | 144 | 56 | 96 | 2970 | 21 | 166,375 | 22 | 1600 | 112 | 263,25 |
3.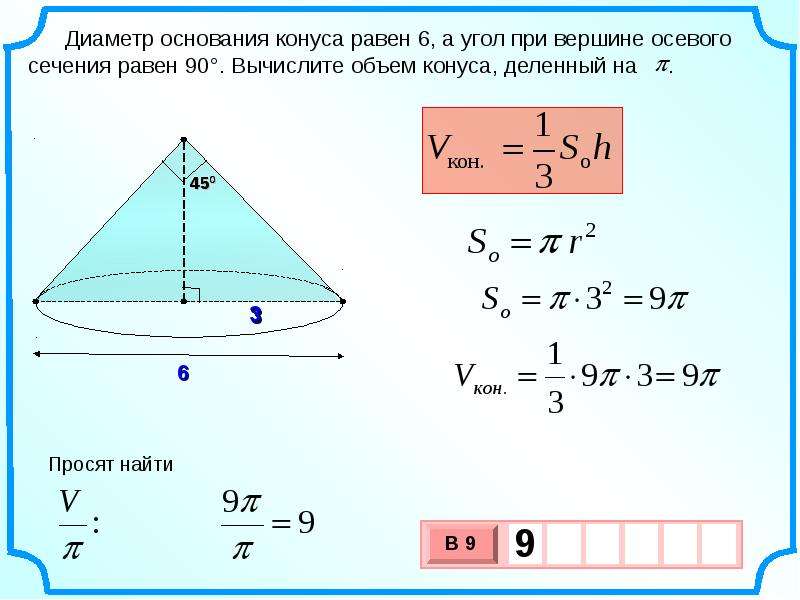 В цилиндрический сосуд налили воды. Уровень воды при этом достигает высоты 20 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 16 см. Чему равен объем детали? Ответ выразите в .
В цилиндрический сосуд налили воды. Уровень воды при этом достигает высоты 20 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 16 см. Чему равен объем детали? Ответ выразите в .
4.В цилиндрический сосуд налили воды. Уровень воды при этом достигает высоты 19 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 8 см. Чему равен объем детали? Ответ выразите в .
5.В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в сантиметрах.
6.В цилиндрическом сосуде уровень жидкости достигает 8 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в сантиметрах.
7.В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого? Ответ выразите в сантиметрах.
8.В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 4 раза больше первого? Ответ выразите в сантиметрах.
9.В цилиндрическом сосуде уровень жидкости достигает 32 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 4 раза больше первого? Ответ выразите в сантиметрах.
10.В цилиндрическом сосуде уровень жидкости достигает 36 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого? Ответ выразите в сантиметрах.
13.Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 18.
14.Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.
15.Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 16.
17.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
20.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
21.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
22.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
24.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
25.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
28.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
30.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
32.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
33.Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
34.Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .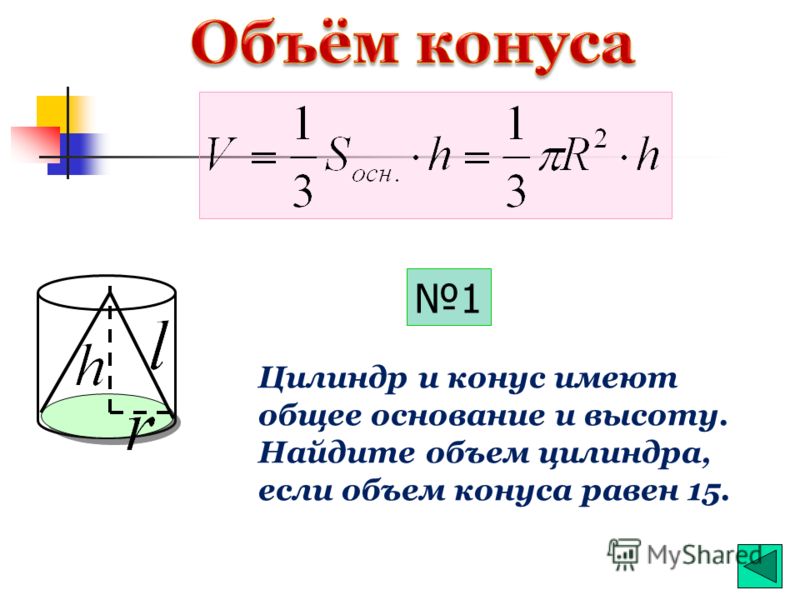
37.Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
42.Найдите объем V конуса, образующая которого равна 27 и наклонена к плоскости основания под углом 30. В ответе укажите .
43.Найдите объем V конуса, образующая которого равна 51 и наклонена к плоскости основания под углом 30. В ответе укажите .
44.Найдите объем V конуса, образующая которого равна 7 и наклонена к плоскости основания под углом 30. В ответе укажите .
45.Найдите объем V конуса, образующая которого равна 12 и наклонена к плоскости основания под углом 30. В ответе укажите .
46.Найдите объем V конуса, образующая которого равна 19 и наклонена к плоскости основания под углом 30. В ответе укажите .
47.Найдите объем V конуса, образующая которого равна 31 и наклонена к плоскости основания под углом 30. В ответе укажите .
48.Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 18,5 раза?
51.Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 16,5 раза?
52. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 6 раз?
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 6 раз?
53.Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 15 раз?
54.Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 6,5 раза?
57.Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 14 раз?
58.Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 4,5 раза?
59.Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 26 раз?
60.Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 3 раза?
61.Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 17 раз?
62.Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 9 раз?
65.Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 45.
66.Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 159.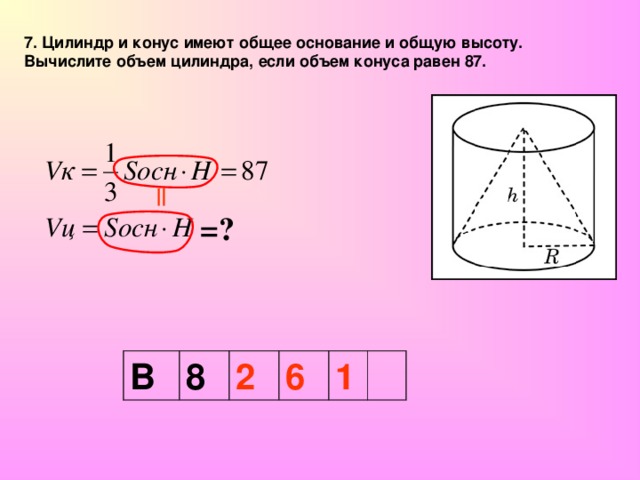
67.Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 129.
68.Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 84.
69.Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 90.
70.Высота конуса равна 3, образующая равна 6. Найдите его объем, деленный на .
71.Высота конуса равна 12, образующая равна 14. Найдите его объем, деленный на .
74.Высота конуса равна 2, образующая равна 4. Найдите его объем, деленный на .
75.Диаметр основания конуса равен 66, а угол при вершине осевого сечения равен . Вычислите объем конуса, деленный на .
76.Диаметр основания конуса равен 36, а угол при вершине осевого сечения равен . Вычислите объем конуса, деленный на .
77.Диаметр основания конуса равен 12, а угол при вершине осевого сечения равен . Вычислите объем конуса, деленный на .
78.Диаметр основания конуса равен 18, а угол при вершине осевого сечения равен . Вычислите объем конуса, деленный на .
Вычислите объем конуса, деленный на .
79.Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен . Вычислите объем конуса, деленный на .
Стереометрия: комбинации тел. — PDF Free Download
Все прототипы задания В9 (2013)
Все прототипы задания В9 (2013) ( 245359) Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. ( 245360) Найдите расстояние между вершинами и прямоугольного параллелепипеда,
ПодробнееПрямоугольный параллелепипед
ЗАДАНИЕ 10 Стереометрия Куб 1. Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.
Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.
Все прототипы В года
1. Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние
ПодробнееТригонометрические уравнения
Тригонометрические уравнения С б) Укажите корни, принадлежащие отрезку. а) Решите уравнение б) Укажите корни уравнения, принадлежащие отрезку а) Решbте уравнение. б) Укажите корни этого уравнения, принадлежащие
ПодробнееЗадание 16 Задачи по стереометрии
Задание 16 Задачи по стереометрии Куб 1. Диагональ куба равна 12. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30
Диагональ куба равна 12. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30
Задание 8 Стереометрия.
Задание 8 Стереометрия. Куб 1. Площадь поверхности куба равна 18. Найдите его диагональ. 2. Объем куба равен 8. Найдите площадь его поверхности. 3. Если каждое ребро куба увеличить на 1, то его площадь
ПодробнееВсе прототипы задания В11 (2013)
Все прототипы задания В11 (2013) ( 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). ( 25561) Найдите площадь поверхности многогранника, изображенного
ПодробнееЗадание 13. Задачи по стереометрии
Задание 13 Задачи по стереометрии 1.Диагональ куба равна Куб. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см
Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см
Все прототипы заданий В года
1. Прототип задания B13 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий
ПодробнееСтартовая контрольная работа
Стартовая контрольная работа Контрольная работа 1(на 20 мин) 1. Найдите координаты вектора АВ, если А (5; 1; 3), В (2; 2; 4). 2. Даны векторы b (3; 1; 2) и c 2b c (1; 4; 3). Найдите. 3. Изобразите систему
ПодробнееВсе прототипы заданий В года
1. Прототип задания B13 ( 27054) выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Все прототипы заданий В13
Найдите третье ребро, выходящее из той же вершины. Все прототипы заданий В13
Все прототипы заданий года
1. Прототип задания 12 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий 12
ПодробнееСтереометрия: пирамиды.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: пирамиды. 27069. Стороны основания правильной
ПодробнееЗадачи по с т е р е о м е т р и и
Задачи по с т е р е о м е т р и и Ермак Елена Анатольевна, доктор педагогических наук, профессор кафедры математического анализа и методики обучения математике Псковского государственного университета
ПодробнееСтереометрия: призма.

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: призма. 27047. В сосуд, имеющий форму
ПодробнееСтереометрия: конус, цилиндр.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: конус, цилиндр. 27052. Объем конуса равен
Подробнее7. Задачи по стереометрии
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 7 Задачи по стереометрии методические указания для абитуриентов физического факультета Ростов-на-Дону 00 Печатается по решению учебнофакультета РГУ методической комиссии
ПодробнееКуб. Прямоугольный параллелепипед
Куб 1. Задание 16 27098. Диагональ куба равна. Найдите его объем. О т в е т : 8 2. Задание 16 500957. Во сколько раз увеличится объем куба, если все его рѐбра увеличить в 5 раз? О т в е т : 1 2 5 3. Задание
Задание 16 27098. Диагональ куба равна. Найдите его объем. О т в е т : 8 2. Задание 16 500957. Во сколько раз увеличится объем куба, если все его рѐбра увеличить в 5 раз? О т в е т : 1 2 5 3. Задание
Подготовка к ЕГЭ по математике
2015 2016 Подготовка к ЕГЭ по математике Прототипы задач из открытого банка заданий ЕГЭ по математике (профильный уровень) http://mathege.ru Стереометрия. Параллелепипед. Куб. Александр и Наталья Крутицких
ПодробнееПланиметрия: комбинации фигур.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: комбинации фигур. 27624. Периметр треугольника
Подробнее А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.
Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.
ID_7154 1/10 neznaika.pro
1 Задачи по стереометрии Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Найдите объём
Подробнее1 Расстояние от точки до прямой
1 Расстояние от точки до прямой 1 1 1 1 1.1. В единичном кубе 1 1 1 1 найдите расстояние от точки до прямой 1. 1 1.2. В правильной треугольной призме 1 1 1, все ребра которой равны 1, найдите расстояние
ПодробнееТест по теме «Задачи стереометрии»
Тест по теме «Задачи стереометрии» Тест составлен на основе учебника «Геометрия, 10-11 класс (базового и профильного уровней ) / Л. С. Атанасян и др. — М.: «Просвещение», 2010. Аннотация: Задачи теста соответствуют
С. Атанасян и др. — М.: «Просвещение», 2010. Аннотация: Задачи теста соответствуют
Геометрия. Тренировочный вариант 1
Геометрия. Тренировочный вариант 1 1. Найдите площадь трапеции, изображённой на рисунке. 2. Около треугольника MNP описана окружность с центром О. Найдите угол РОМ, если угол PNM равен 17. Ответ дайте
ПодробнееКуб. 3. Найдите объем многогранника, вершинами которого являются точки,,,,, прямоугольного параллелепипеда, у которого,,.
Куб. 1. Диагональ куба равна. Найдите его объем. 2.Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить
ПодробнееЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ
ЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ Инструкция. Решите задание. Дайте краткий ответ. 1. Апофема правильной треугольной пирамиды 4 см, а сторона основания 8 см. Найдите площадь боковой поверхности пирамиды.
Решите задание. Дайте краткий ответ. 1. Апофема правильной треугольной пирамиды 4 см, а сторона основания 8 см. Найдите площадь боковой поверхности пирамиды.
УДК 373:51 ББК 22.1я72 С50
УДК 373:5 ББК 22.я72 С50 Смирнов В. А. ЕГЭ 205. Математика. Задача 2. Геометрия: объем, площадь поверхности. Рабочая тетрадь Под ред. И. В. Ященко Электронное издание М.: МЦНМО, 205 64 с. ISN 978-5-4439-24-3
ПодробнееЕГЭ Математика Задача 16
ГОТОВИМСЯ К ЕГЭ В. А. Смирнов ЕГЭ 05. Математика Задача 6 Геометрия. Стереометрия Под редакцией И. В. Ященко Электронное издание Москва Издательство МЦНМО 05 УДК 373:5 ББК.я7 С50 Смирнов В. А. ЕГЭ 05.
ПодробнееОсновные определения, теоремы и формулы планиметрии.
Основные определения, теоремы и формулы планиметрии. Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне
Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне
Тела вращения. Конус, цилиндр, шар. — Математика
Файл к занятию 12
Цилиндр
Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. Прямая, проходящая через центры оснований, называется осью цилиндра, отрезок, соединяющий окружности оснований и перпендикулярный им, — образующей цилиндра, а перпендикуляр, опущенный из какой-либо точки одного основания на другое основание, — высотой цилиндра. Высота цилиндра равна его образующей. Пусть h — высота цилиндра, r — радиус цилиндра, Sбок — площадь боковой поверхности цилиндра, Sосн — площадь основания цилиндра, Sполн — площадь полной поверхности цилиндра, V — объем цилиндра. |
V=
Конус
Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет. Пусть h — высота конуса, r — радиус основания конуса, l — образующая конуса, Sбок — площадь боковой поверхности конуса, Sосн – площадь основания конуса, Sполн — площадь полной поверхности конуса, V — объем конуса. Тогда имеют место следующие соотношения: |
V=
Задание 1.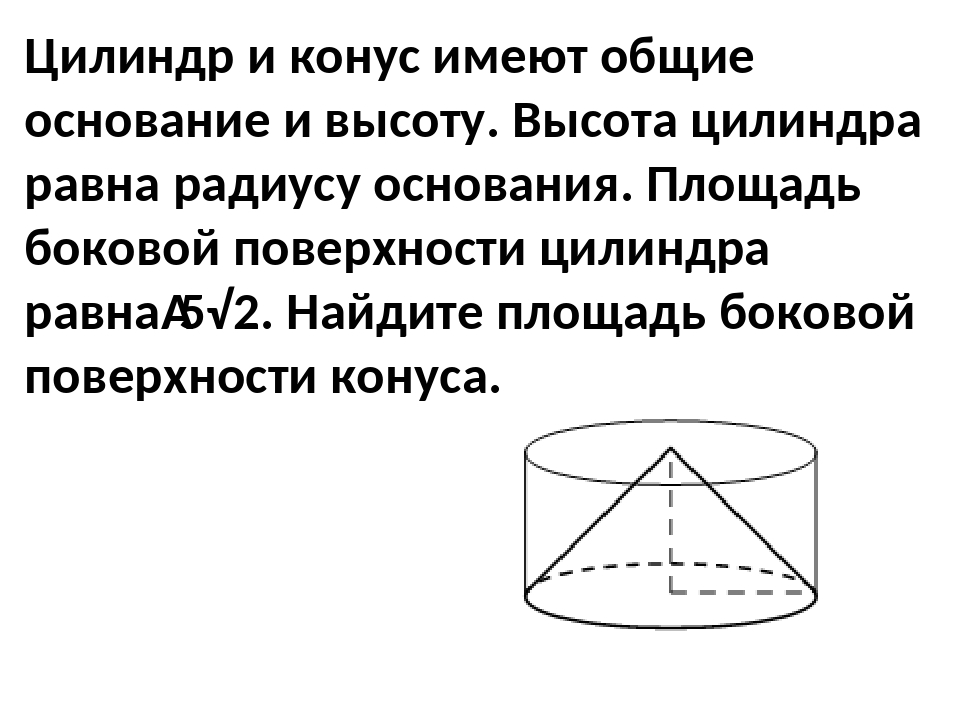 Высота конуса равна 24, а диаметр основания равен 90. Найдите образующую конуса. Ответ: 51
Высота конуса равна 24, а диаметр основания равен 90. Найдите образующую конуса. Ответ: 51
Задание 2. Высота конуса равна 9, а длина образующей равна 41. Найдите диаметр основания конуса. Ответ:80
Задание 3. Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса. Ответ: 24.
Задание 4. Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения. Ответ: 252
Задание 5. Площадь боковой поверхности цилиндра равна 24 π, а диаметр основания равен 8. Найдите высоту цилиндра. Ответ: 3
Задание 6. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2. Во сколько раз объём первого цилиндра больше объёма второго? Ответ: 2
Задание 7. В цилиндрическом сосуде уровень жидкости достигает 16 см.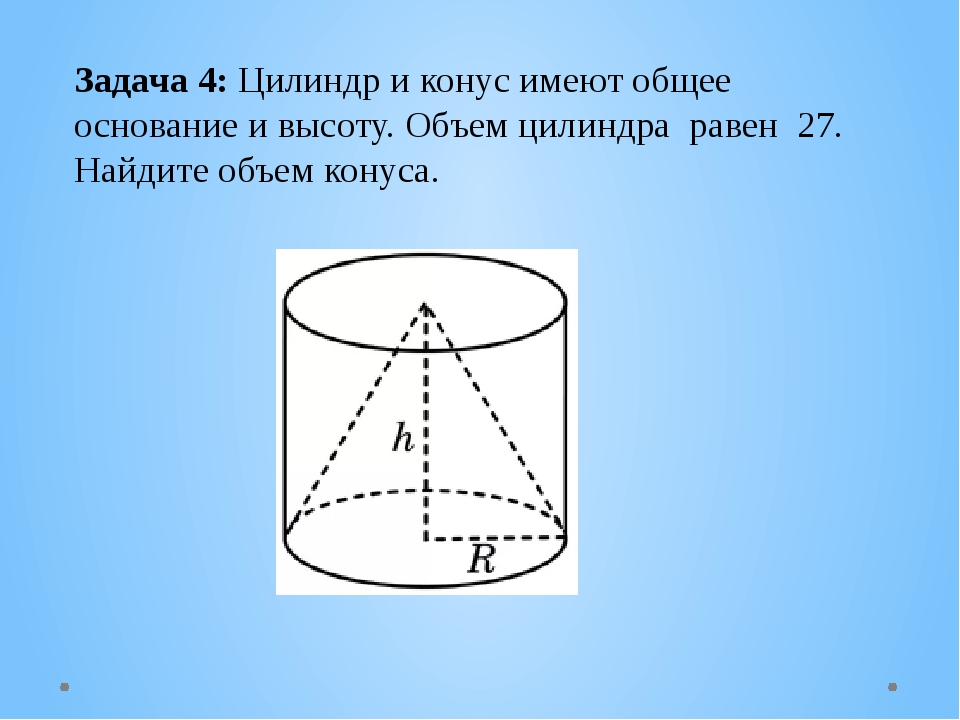 На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см. Ответ: 4.
На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см. Ответ: 4.
Задание 8. Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой. Ответ:4,5
Задание 9. В цилиндрический сосуд, в котором находится 10 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,6 раза. Чему равен объём детали? Ответ выразите в дм3. Ответ: 6
Задание 10. В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ выразите в см3. Ответ: 1000.
Задание 11. Объём конуса равен 60π, а его высота равна 5. Найдите радиус основания конуса. Ответ:6
Объём конуса равен 60π, а его высота равна 5. Найдите радиус основания конуса. Ответ:6
Задание 12. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π. Ответ: 24
Задание 13. Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 5 раз, а высоту оставить прежней? Ответ: 25
Сечение конуса плоскостью, параллельной основанию
Сечение конуса плоскостью, параллельной его основанию (перпендикулярной высоте), делит высоту и образующие конуса на пропорциональные отрезки.
Площади сечений конуса, параллельных его основанию, относятся как квадраты их расстояний от вершины конуса.
Задание 14. Площадь полной поверхности конуса равна 16. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсечённого конуса.
Решение: 1 способ:
Площадь полной поверхности конуса вычисляется по формуле
Так как сечение делит высоту конуса пополам, значит, радиус основания и образующая отсеченного конуса в 2 раза меньше радиуса основания и образующей исходного конуса.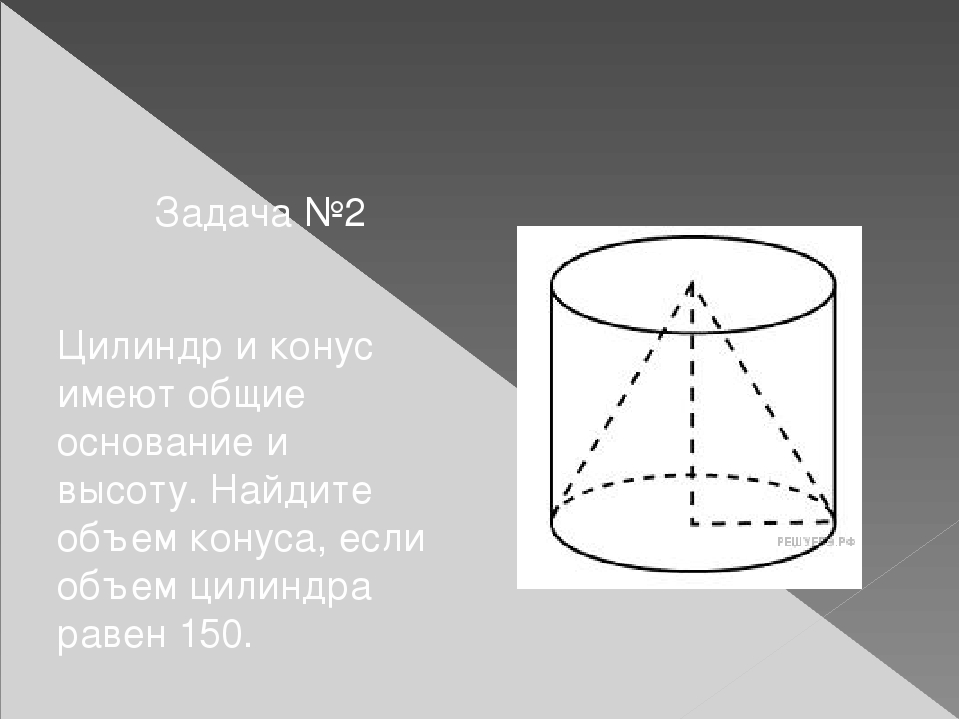 Следовательно, площадь поверхности отсеченного конуса
Следовательно, площадь поверхности отсеченного конуса
Площадь поверхности отсеченного конуса равна 16/4=4.
2 способ: Исходный и отсеченный конус являются подобными телами. Следовательно, площади их поверхности относятся как коэффициент подобия в квадрате.
k=;
Ответ:4
Задание 15. Площадь полной поверхности конуса равна 35. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 3:2, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса. Ответ: 12,6
Задание 16. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 54 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение.
Меньший конус подобен большему с коэффициентом k=. Объемы подобных тел относятся как куб коэффициента подобия.. Поэтому объем большего конуса в 8 раз больше объема меньшего конуcа. V= 54 мл. Значит, необходимо долить 432 − 54 = 378 мл жидкости. Ответ: 378.
Объемы подобных тел относятся как куб коэффициента подобия.. Поэтому объем большего конуса в 8 раз больше объема меньшего конуcа. V= 54 мл. Значит, необходимо долить 432 − 54 = 378 мл жидкости. Ответ: 378.
Задание 17. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 25 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? Ответ:175
Шар и сфера. Площадь поверхности и объем.
Шаром называется фигура, полученная при вращении полукруга вокруг оси, содержащей его диаметр. Сферой называется поверхность шара.
Пусть R — радиус шара, D=2R — его диаметр, S — площадь ограничивающей шар сферы, V — объем шара, тогда имеют место следующие соотношения:
Задание 18. Даны два шара с радиусами 8 и 2.
Даны два шара с радиусами 8 и 2.
1)Во сколько раз объём большего шара больше объёма другого? Ответ: 64.
2) Во сколько раз площадь поверхности большего шара больше площади поверхности другого? Ответ:16
Задание 19. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 42.
Решение.
Объем цилиндра равен произведению площади основания на высоту, а объем конуса равен одной трети произведения площади основания на высоту. Так как они имеют общее основание и высоту, объем цилиндра в три раза больше объема конуса. Ответ: 126.
Задание 20. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10. Найдите образующую конуса. Ответ: 20
Ответ: 20
Задание 21. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса
равна 11 . Найдите радиус сферы. Ответ:11
Задание 22. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Решение.
Высота цилиндра равна диаметру шара, а радиус основания цилиндра равен радиусу шара. Площадь основания цилиндра:
Площадь боковой поверхности цилиндра:
=
Площадь полной поверхности цилиндра:
Так как площадь поверхности шара вычисляется по формуле
,
Найдем отношение площади поверхности цилиндра к площади поверхности шара.
Имеем:
. Ответ:166,5.
Задание 23. Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра. Ответ: 72
Задание 24. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра. Ответ: 36
Задание 25. Цилиндр описан около шара. Объём шара равен 50. Найдите объём цилиндра. Ответ:75
Объем конуса
А конус представляет собой трехмерную фигуру с одним круглым основанием. Изогнутая поверхность соединяет основание и вершину.
В объем из
3
-размерное твердое тело — это объем занимаемого пространства. Объем измеряется в кубических единицах (
в
3
,
футов
3
,
см
3
,
м
3
,
и так далее). Перед вычислением объема убедитесь, что все измерения относятся к одной и той же единице.
Перед вычислением объема убедитесь, что все измерения относятся к одной и той же единице.
Громкость V конуса с радиус р составляет одну треть площади основания B раз больше высоты час .
V знак равно 1 3 B час или же V знак равно 1 3 π р 2 час , куда B знак равно π р 2
Примечание : Формула объема наклонного конуса такая же, как и у правого.
Объемы конуса и
цилиндр
связаны так же, как и
объемы пирамиды
и
призма
относятся к. Если высота конуса и цилиндра равны, то объем цилиндра в три раза больше объема конуса.
Пример:
Найдите объем показанного конуса. Округлите до ближайшей десятой доли кубического сантиметра.
Решение
Из рисунка радиус конуса равен 8 см и высота 18 см.
Формула для определения объема конуса:
V знак равно 1 3 π р 2 час
Заменять 8 за р и 18 за час .
V знак равно 1 3 π ( 8 ) 2 ( 18 )
Упрощать.
V знак равно 1 3 π ( 64 ) ( 18 ) знак равно 384 π ≈ 1206,4
Следовательно, объем конуса составляет около 1206.4 кубические сантиметры.
Калькулятор конуса
Форма конуса
r = радиус
h = высота
s = наклонная высота
В = объем
L = площадь боковой поверхности
B = площадь основания
A = общая площадь поверхности
π = пи = 3.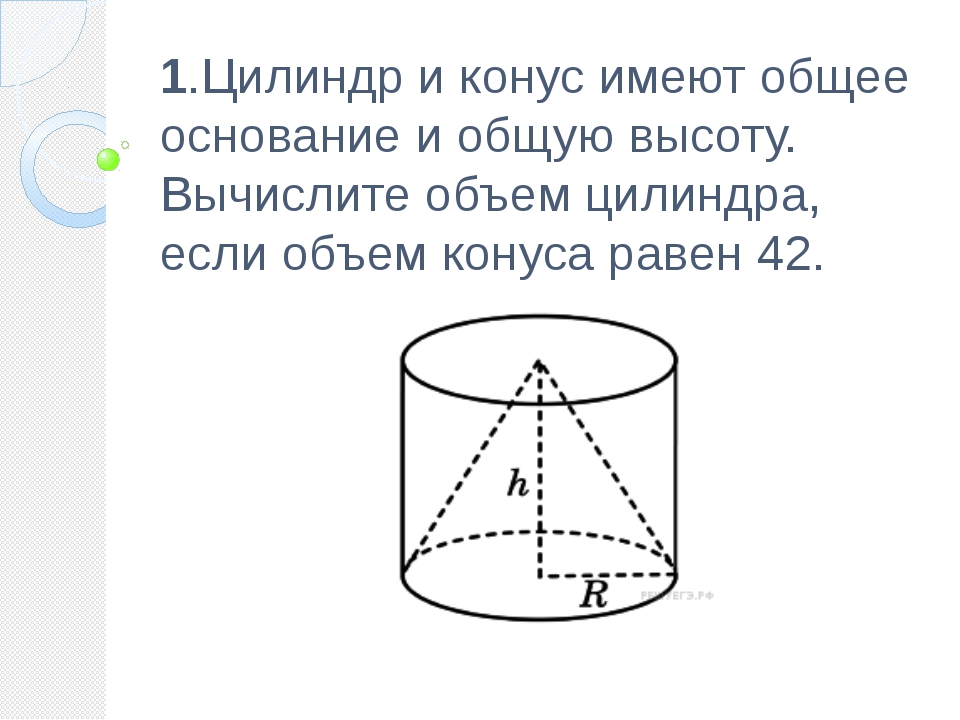 1415926535898
1415926535898
√ = квадратный корень
Использование калькулятора
Этот онлайн-калькулятор рассчитает различные свойства правильного кругового конуса с учетом любых двух известных переменных. Термин «круглая» поясняет эту форму как пирамиду с круглым поперечным сечением. Термин «справа» означает, что вершина конуса центрируется над основанием. Сам по себе термин «конус» часто означает правильный круговой конус.
Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на вычисления. Имеются единицы измерения, указывающие порядок результатов, например футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты приведут к s в мм, V в мм 3 , L в мм 2 , B в мм 2 и A в мм 2 .
Ниже приведены стандартные формулы для конуса.Вычисления основаны на алгебраическом манипулировании этими стандартными формулами.
Формулы кругового конуса для радиуса r и высоты h:
- Объем конуса:
- Наклонная высота конуса:
- Площадь боковой поверхности конуса:
- L = πrs = πr√ (r 2 + h 2 )
- Площадь основания конуса (кружка):
- Общая площадь конуса:
- A = L + B = πrs + πr 2 = πr (s + r) = πr (r + √ (r 2 + h 2 ))
Расчет круглого конуса:
Используйте следующие дополнительные формулы наряду с формулами выше.
- По заданным радиусу и высоте рассчитайте наклонную высоту, объем, площадь боковой поверхности и общую площадь поверхности.
Для заданных r, h найти s, V, L, A - По заданному радиусу и наклонной высоте рассчитайте высоту, объем, площадь боковой поверхности и общую площадь поверхности.
Для данного r, s найти h, V, L, A - По заданному радиусу и объему рассчитайте высоту, наклонную высоту, площадь боковой поверхности и общую площадь поверхности.
Для данного r, V найти h, s, L, A - По заданному радиусу и площади боковой поверхности рассчитайте высоту, наклонную высоту, объем и общую площадь поверхности.
Для данного r, L найти h, s, V, A- с = L / (πr)
- h = √ (с 2 — r 2 )
- По заданному радиусу и общей площади поверхности рассчитайте высоту, наклонную высоту, объем и площадь боковой поверхности.

Для данного r, A найти h, s, V, L- s = [A — (πr 2 )] / (πr)
- h = √ (с 2 — r 2 )
- Зная высоту и наклонную высоту, рассчитайте радиус, объем, площадь боковой поверхности и общую площадь поверхности.
По заданному h, s найти r, V, L, A - По заданной высоте и объему рассчитайте радиус, наклонную высоту, площадь боковой поверхности и общую площадь поверхности.
Для заданных h, V найти r, s, L, A- r = √ [(3 * v) / (π * h)]
- Зная наклонную высоту и площадь боковой поверхности, рассчитайте радиус, высоту, объем и общую площадь поверхности.
Дано s, L найти r, h, V, A- r = л / (π * с)
- h = √ (с 2 — r 2 )
Список литературы
Вайсштейн, Эрик В. «Конус». Из MathWorld — Интернет-ресурс Wolfram.
«Конус». Из MathWorld — Интернет-ресурс Wolfram.
http://mathworld.wolfram.com/Cone.html
Объем конуса и цилиндра
Представьте себе прямоугольник, разделенный диагональю на два прямоугольных треугольника. Как площадь прямоугольного треугольника, образованного диагональю, связана с площадью прямоугольника? Площадь любого прямоугольника равна произведению его ширины и длины.Например, если прямоугольник имеет ширину 3 дюйма и длину 5 дюймов, его площадь составляет 15 квадратных дюймов (длина, умноженная на ширину). На рисунке ниже показан прямоугольник, «разделенный» по диагонали, демонстрируя, что прямоугольник можно представить как два равных прямоугольных треугольника, соединенных вместе. Площади прямоугольников и прямоугольных треугольников пропорциональны друг другу: прямоугольник имеет вдвое большую площадь, чем прямоугольный треугольник, образованный его диагональю.
Точно так же объемы конуса и цилиндра, имеющие одинаковые основания и высоту, пропорциональны.Если конус и цилиндр имеют основания (показаны цветом) с равными площадями и оба имеют одинаковую высоту, то объем конуса составляет одну треть объема цилиндра.
Представьте себе, что конус на рисунке перевернут вверх дном, острием вниз. Если бы рожок был полым с открытым верхом, его можно было бы заполнить жидкостью, как рожок мороженого. Чтобы заполнить цилиндр, нужно было бы трижды наполнить и вылить содержимое конуса в цилиндр.
На рисунке выше также показаны термины высота и радиус для конуса и цилиндра.Основание конуса — окружность радиуса r . Высота конуса равна длине h прямой линии от вершины конуса до центра его круглого основания. Оба конца цилиндра представляют собой окружности радиусом r каждый. Высота цилиндра равна длине х между центрами двух концов.
Соотношение объемов между этими конусами и цилиндрами с одинаковыми основаниями и высотой можно выразить математически. Объем объекта — это количество пространства, заключенного в нем.Например, объем куба — это площадь одной стороны, умноженная на его высоту. На рисунке ниже изображен куб. Цветом обозначена площадь его основания. Умножение этой (цветной) площади на высоту L куба дает его объем. И поскольку все измерения (длина, ширина и высота) куба идентичны, его объем составляет L × L × L или L 3 , где L — длина каждой стороны.
Объем объекта — это количество пространства, заключенного в нем.Например, объем куба — это площадь одной стороны, умноженная на его высоту. На рисунке ниже изображен куб. Цветом обозначена площадь его основания. Умножение этой (цветной) площади на высоту L куба дает его объем. И поскольку все измерения (длина, ширина и высота) куба идентичны, его объем составляет L × L × L или L 3 , где L — длина каждой стороны.
Ту же процедуру можно применить для определения объема цилиндра.То есть площадь основания цилиндра, умноженная на высоту цилиндра, дает его объем. Основания цилиндра и конуса, показанные ранее, представляют собой круги. Площадь круга равна π r 2 , где r — радиус круга. Следовательно, объем V cyl определяется уравнением: V cyl π r 2 h (площадь его круглого основания, умноженная на его высоту), где r — радиус цилиндр и х его высота. Объем конуса ( V конус ) составляет одну треть от объема цилиндра с таким же основанием и высотой:.
Объем конуса ( V конус ) составляет одну треть от объема цилиндра с таким же основанием и высотой:.
Конусы и цилиндры, показанные ранее, являются правильными круговыми конусами и правильными круговыми цилиндрами, что означает, что центральная ось каждого перпендикулярна основанию. Существуют и другие типы цилиндров и конусов, и пропорции и уравнения, которые были разработаны выше, также применимы к этим другим типам цилиндров и конусов.
Филип Эдвард Кот с
Уильям Артур Аткинс
Библиография
Abbott, P. Геометрия. Нью-Йорк: Дэвид Маккей Ко., Инк., 1982.
Интернет-ресурсы
Метод Архимеда. Американское математическое общество.
% PDF-1.4
%
1150 0 объект
>
endobj
xref
1150 327
0000000016 00000 н.
0000008295 00000 н.
0000008384 00000 п.
0000008633 00000 п.
0000011937 00000 п.
0000011987 00000 п. 0000012036 00000 п.
0000012085 00000 п.
0000012134 00000 п.
0000012183 00000 п.
0000012232 00000 п.
0000012282 00000 п.
0000012332 00000 п.
0000012381 00000 п.
0000012431 00000 п.
0000012481 00000 п.
0000012531 00000 п.
0000012586 00000 п.
0000012637 00000 п.
0000012693 00000 п.
0000012743 00000 п.
0000013057 00000 п.
0000013342 00000 п.
0000013638 00000 п.
0000013717 00000 п.
0000013794 00000 п.
0000014171 00000 п.
0000014797 00000 п.
0000015175 00000 п.
0000015224 00000 п.
0000015275 00000 п.
0000015324 00000 п.
0000015373 00000 п.
0000015422 00000 п.
0000015473 00000 п.
0000015523 00000 п.
0000031745 00000 п.
0000032170 00000 п.
0000032954 00000 п.
0000033063 00000 п.
0000033675 00000 п.
0000033788 00000 п.
0000033941 00000 п.
0000034300 00000 п.
0000034653 00000 п.
0000035619 00000 п.
0000035924 00000 п.
0000036295 00000 п.
0000036373 00000 п.
0000036449 00000 п.
0000036722 00000 п.
0000036761 00000 п.
0000037062 00000 п.
0000037756 00000 п.
0000012036 00000 п.
0000012085 00000 п.
0000012134 00000 п.
0000012183 00000 п.
0000012232 00000 п.
0000012282 00000 п.
0000012332 00000 п.
0000012381 00000 п.
0000012431 00000 п.
0000012481 00000 п.
0000012531 00000 п.
0000012586 00000 п.
0000012637 00000 п.
0000012693 00000 п.
0000012743 00000 п.
0000013057 00000 п.
0000013342 00000 п.
0000013638 00000 п.
0000013717 00000 п.
0000013794 00000 п.
0000014171 00000 п.
0000014797 00000 п.
0000015175 00000 п.
0000015224 00000 п.
0000015275 00000 п.
0000015324 00000 п.
0000015373 00000 п.
0000015422 00000 п.
0000015473 00000 п.
0000015523 00000 п.
0000031745 00000 п.
0000032170 00000 п.
0000032954 00000 п.
0000033063 00000 п.
0000033675 00000 п.
0000033788 00000 п.
0000033941 00000 п.
0000034300 00000 п.
0000034653 00000 п.
0000035619 00000 п.
0000035924 00000 п.
0000036295 00000 п.
0000036373 00000 п.
0000036449 00000 п.
0000036722 00000 п.
0000036761 00000 п.
0000037062 00000 п.
0000037756 00000 п. 0000038201 00000 п.
0000038858 00000 п.
0000039238 00000 п.
0000050700 00000 п.
0000059515 00000 п.
0000060048 00000 п.
0000060247 00000 п.
0000062727 00000 н.
0000063065 00000 п.
0000063426 00000 п.
0000063602 00000 п.
0000064269 00000 н.
0000064653 00000 п.
0000065187 00000 п.
0000065247 00000 п.
0000065887 00000 п.
0000066090 00000 н.
0000066387 00000 п.
0000066489 00000 н.
0000067592 00000 п.
0000067846 00000 п.
0000068192 00000 п.
0000068467 00000 п.
0000068833 00000 п.
0000068966 00000 п.
0000080696 00000 п.
0000091618 00000 п.
0000103944 00000 н.
0000116909 00000 н.
0000117172 00000 н.
0000117436 00000 н.
0000118217 00000 н.
0000130834 00000 н.
0000131790 00000 н.
0000132530 00000 н.
0000134430 00000 н.
0000134496 00000 н.
0000136758 00000 н.
0000142392 00000 н.
0000146292 00000 н.
0000149539 00000 н.
0000151329 00000 н.
0000154022 00000 н.
0000156928 00000 н.
0000158953 00000 н.
0000160791 00000 п.
0000161007 00000 н.
0000161239 00000 н.
0000038201 00000 п.
0000038858 00000 п.
0000039238 00000 п.
0000050700 00000 п.
0000059515 00000 п.
0000060048 00000 п.
0000060247 00000 п.
0000062727 00000 н.
0000063065 00000 п.
0000063426 00000 п.
0000063602 00000 п.
0000064269 00000 н.
0000064653 00000 п.
0000065187 00000 п.
0000065247 00000 п.
0000065887 00000 п.
0000066090 00000 н.
0000066387 00000 п.
0000066489 00000 н.
0000067592 00000 п.
0000067846 00000 п.
0000068192 00000 п.
0000068467 00000 п.
0000068833 00000 п.
0000068966 00000 п.
0000080696 00000 п.
0000091618 00000 п.
0000103944 00000 н.
0000116909 00000 н.
0000117172 00000 н.
0000117436 00000 н.
0000118217 00000 н.
0000130834 00000 н.
0000131790 00000 н.
0000132530 00000 н.
0000134430 00000 н.
0000134496 00000 н.
0000136758 00000 н.
0000142392 00000 н.
0000146292 00000 н.
0000149539 00000 н.
0000151329 00000 н.
0000154022 00000 н.
0000156928 00000 н.
0000158953 00000 н.
0000160791 00000 п.
0000161007 00000 н.
0000161239 00000 н. 0000161832 00000 н.
0000161923 00000 н.
0000162107 00000 н.
0000162170 00000 н.
0000162939 00000 н.
0000163192 00000 н.
0000163639 00000 н.
0000163702 00000 н.
0000163768 00000 н.
0000163831 00000 н.
0000163918 00000 н.
0000163984 00000 н.
0000164047 00000 н.
0000164116 00000 н.
0000164188 00000 п.
0000164257 00000 н.
0000164344 00000 н.
0000164540 00000 н.
0000164763 00000 н.
0000165001 00000 н.
0000165622 00000 н.
0000165814 00000 н.
0000165893 00000 н.
0000207290 00000 н.
0000207331 00000 н.
0000252154 00000 н.
0000252195 00000 н.
0000293592 00000 н.
0000293633 00000 н.
0000303461 00000 н.
0000309681 00000 п.
0000315867 00000 н.
0000322085 00000 н.
0000328345 00000 н.
0000334555 00000 н.
0000340754 00000 н.
0000346944 00000 н.
0000353163 00000 п.
0000359387 00000 н.
0000365590 00000 н.
0000365930 00000 н.
0000366079 00000 п.
0000372299 00000 н.
0000378522 00000 н.
0000384753 00000 п.
00003
0000161832 00000 н.
0000161923 00000 н.
0000162107 00000 н.
0000162170 00000 н.
0000162939 00000 н.
0000163192 00000 н.
0000163639 00000 н.
0000163702 00000 н.
0000163768 00000 н.
0000163831 00000 н.
0000163918 00000 н.
0000163984 00000 н.
0000164047 00000 н.
0000164116 00000 н.
0000164188 00000 п.
0000164257 00000 н.
0000164344 00000 н.
0000164540 00000 н.
0000164763 00000 н.
0000165001 00000 н.
0000165622 00000 н.
0000165814 00000 н.
0000165893 00000 н.
0000207290 00000 н.
0000207331 00000 н.
0000252154 00000 н.
0000252195 00000 н.
0000293592 00000 н.
0000293633 00000 н.
0000303461 00000 н.
0000309681 00000 п.
0000315867 00000 н.
0000322085 00000 н.
0000328345 00000 н.
0000334555 00000 н.
0000340754 00000 н.
0000346944 00000 н.
0000353163 00000 п.
0000359387 00000 н.
0000365590 00000 н.
0000365930 00000 н.
0000366079 00000 п.
0000372299 00000 н.
0000378522 00000 н.
0000384753 00000 п.
00003
- 00000 н.
0000397305 00000 н.
0000403593 00000 н.
- Цель использования
- Расчет объема в усеченном керамическом кувшине
- Цель использования
- Расчет приблизительного объема дерева твердых пород на дне бразильского озера.
- Цель использования
- Расчет объема формы для оценки веса набора дротиков со стальным наконечником.
- Цель использования
- Расчет потребности в листовом металле для редуктора
- Цель использования
- Расчет внутреннего объема Instant Pot
- Цель использования
- рассчитать объем кофейной чашки
- Цель использования
- Подсчитайте объем воды в коробке клапана в земле, чтобы я мог определить расход воды в землю.

- Цель использования
- Необходим для определения объема садового контейнера. А теперь посчитаем, сколько галлонов!
- Цель использования
- Производитель устриц, рассчитывающий размеры для изготовления корзин для устриц: 1 бушель, полтора бушеля
- Цель использования
- оценка вместимости деревянной урны, которую я делаю для умершего родственника
- Найдите объем и площадь поверхности прямоугольных тел
- Найдите объем и площадь поверхности сфер
- Найти объем и площадь цилиндров
- Найдите объем конусов
- Прочтите задачу и убедитесь, что вы понимаете все слова и идеи. Нарисуйте фигуру и напишите на ней указанную информацию.
- Определите , что вы ищете.
- Имя то, что вы ищете.Выберите переменную для представления этого количества.
- Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.

- ⓐ 792 куб. фут
- ⓑ 518 кв. Футов
- ⓐ 1,440 куб. фут
- ⓑ 792 кв. Фута
- ⓐ 216 куб. фут
- ⓑ 228 кв. Футов
- ⓐ 2,772 куб. дюймы
- ⓑ 1264 кв. Дюйма
- ⓐ 91,125 куб. м
- ⓑ 121.5 кв.м
- ⓐ 389.017 куб. ярд
- ⓑ 319.74 кв. Ярд.
- ⓐ 64 куб.фут
- ⓑ 96 кв. Футов
- ⓐ 4096 куб. дюймы
- ⓑ 1536 кв. Дюйм
- ⓐ 113,04 куб. размеры в см
- ⓑ 113.04 кв. См
- ⓐ 4,19 куб. фут
- ⓑ 12,56 кв. Фута
- ⓐ 3052,08 куб. дюймы
- ⓑ 1017,36 кв. Дюйма
- ⓐ 14,13 куб. фут
- ⓑ 28,26 кв. Фута
- ⓐ 351,68 куб. размеры в см
- ⓑ 276,32 кв. См
- ⓐ 100,48 куб. фут
- ⓑ 125,6 кв. Фута
- ⓐ 3 818,24 куб. размеры в см
- ⓑ 1356,48 кв. См
- ⓐ 91.5624 куб. фут
- ⓑ 113,6052 кв. Фута
- ⓐ 17,64 куб. ярд
- ⓑ 41.58 кв. Ярд.
- ⓐ 1,024 куб. фут
- ⓑ 640 кв. Футов
- ⓐ 3350,49 куб. размеры в см
- ⓑ 1622,42 кв. См
- ⓐ 125 куб. размеры в см
- ⓑ 150 кв. См
- ⓐ 1124,864 куб. футы
- ⓑ 648.96 кв. Фут
- ⓐ 262 144 куб. фут
- ⓑ 24 576 кв. Футов
- ⓐ 21,952 куб. м
- ⓑ 47,04 кв. М
- ⓐ 113,04 куб. размеры в см
- ⓑ 113.04 кв. См
- ⓐ 1,766,25 куб. фут
- ⓑ 706.5 кв. Футов
- ⓐ 14 130 куб. дюймы
- ⓑ 2 826 кв. Дюймов
- ⓐ 381,51 куб. размеры в см
- ⓑ 254,34 кв. См
- ⓐ 254.34 куб. фут
- ⓑ 226.08 кв. Фут
- ⓐ 29,673 куб. м
- ⓑ 53.694 кв.м
- ⓐ 1020,5 куб. размеры в см
- ⓑ 565,2 кв. См
- ⓐ 678,24 куб. дюймы
- ⓑ 508,68 кв. Дюйма
- ⓐ 31,4 куб. фут
- ⓑ 2,6 куб. фут
- ⓒ 28.8 куб. фут
- конус
- Конус — это сплошная фигура с одним круглым основанием и вершиной.
- куб
- Куб — это прямоугольное тело, длина, ширина и высота которого равны.
- цилиндр
- Цилиндр — это сплошная фигура с двумя параллельными кругами одинакового размера вверху и внизу.
- Вертикальная высота (или высота), которая представляет собой перпендикулярное расстояние от верха вниз до основания.
- Радиус круглого основания
- Наклонная высота, которая представляет собой расстояние от верха вниз по стороне до точки на основной окружности.
- Радиус r можно найти по формуле где s — наклонная высота, h — высота.
- Высоту h можно найти по формуле где s — высота наклона, r — радиус основания.
- На верхнем рисунке нажмите «скрыть детали».
- Перетащите оранжевые точки, чтобы установить радиус и высоту конуса.
- Рассчитайте наклонную высоту конуса по формуле
- Нажмите «показать подробности», чтобы проверить свой ответ.
 0000409887 00000 н.
0000416109 00000 н.
0000422268 00000 н.
0000428537 00000 п.
0000428874 00000 н.
0000429025 00000 н.
0000435292 00000 н.
0000441556 00000 н.
0000447839 00000 н.
0000454122 00000 н.
0000460387 00000 н.
0000466670 00000 н.
0000472962 00000 н.
0000479161 00000 н.
0000485460 00000 н.
0000491732 00000 н.
0000491999 00000 н.
0000492148 00000 н.
0000498426 00000 н.
0000504662 00000 н.
0000510930 00000 н.
0000517202 00000 н.
0000523468 00000 н.
0000529750 00000 н.
0000536029 00000 н.
0000542261 00000 н.
0000548478 00000 н.
0000554332 00000 н.
0000554754 00000 н.
0000554906 00000 н.
0000560755 00000 н.
0000566584 00000 н.
0000572432 00000 н.
0000578254 00000 н.
0000578681 00000 н.
0000578827 00000 н.
0000579265 00000 н.
0000579410 00000 п.
0000579823 00000 н.
0000579975 00000 н.
0000580047 00000 н.
0000580119 00000 п.
0000580195 00000 н.
0000580329 00000 н.
0000580480 00000 н.
00005 00000 н.
00005
0000409887 00000 н.
0000416109 00000 н.
0000422268 00000 н.
0000428537 00000 п.
0000428874 00000 н.
0000429025 00000 н.
0000435292 00000 н.
0000441556 00000 н.
0000447839 00000 н.
0000454122 00000 н.
0000460387 00000 н.
0000466670 00000 н.
0000472962 00000 н.
0000479161 00000 н.
0000485460 00000 н.
0000491732 00000 н.
0000491999 00000 н.
0000492148 00000 н.
0000498426 00000 н.
0000504662 00000 н.
0000510930 00000 н.
0000517202 00000 н.
0000523468 00000 н.
0000529750 00000 н.
0000536029 00000 н.
0000542261 00000 н.
0000548478 00000 н.
0000554332 00000 н.
0000554754 00000 н.
0000554906 00000 н.
0000560755 00000 н.
0000566584 00000 н.
0000572432 00000 н.
0000578254 00000 н.
0000578681 00000 н.
0000578827 00000 н.
0000579265 00000 н.
0000579410 00000 п.
0000579823 00000 н.
0000579975 00000 н.
0000580047 00000 н.
0000580119 00000 п.
0000580195 00000 н.
0000580329 00000 н.
0000580480 00000 н.
00005 00000 н.
0000500000 н. 0000591223 00000 н.
 0000591967 00000 н.
0000592112 00000 н.
0000598364 00000 н.
0000604596 00000 н.
0000610840 00000 п.
0000617117 00000 н.
0000623288 00000 н.
0000629447 00000 н.
0000635722 00000 н.
0000641870 00000 н.
0000648151 00000 н.
0000654344 00000 п.
0000654912 00000 н.
0000655063 00000 н.
0000661209 00000 н.
0000667401 00000 н.
0000673543 00000 н.
0000679731 00000 н.
0000685884 00000 н.
0000692062 00000 н.
0000698215 00000 н.
0000704427 00000 н.
0000710693 00000 п.
0000716948 00000 н.
0000717288 00000 н.
0000717437 00000 н.
0000723649 00000 н.
0000729927 00000 н.
0000736151 00000 п.
0000742368 00000 н.
0000748602 00000 н.
0000754855 00000 н.
0000761126 00000 н.
0000767305 00000 н.
0000773559 00000 н.
0000779843 00000 н.
0000780180 00000 н.
0000780331 00000 п.
0000786301 00000 п.
0000792555 00000 н.
0000798806 00000 п.
0000805062 00000 н.
0000811335 00000 н.
0000817613 00000 н.
0000823864 00000 н.
0000830115 00000 н.
0000836371 00000 п.
0000842621 00000 н.
0000591967 00000 н.
0000592112 00000 н.
0000598364 00000 н.
0000604596 00000 н.
0000610840 00000 п.
0000617117 00000 н.
0000623288 00000 н.
0000629447 00000 н.
0000635722 00000 н.
0000641870 00000 н.
0000648151 00000 н.
0000654344 00000 п.
0000654912 00000 н.
0000655063 00000 н.
0000661209 00000 н.
0000667401 00000 н.
0000673543 00000 н.
0000679731 00000 н.
0000685884 00000 н.
0000692062 00000 н.
0000698215 00000 н.
0000704427 00000 н.
0000710693 00000 п.
0000716948 00000 н.
0000717288 00000 н.
0000717437 00000 н.
0000723649 00000 н.
0000729927 00000 н.
0000736151 00000 п.
0000742368 00000 н.
0000748602 00000 н.
0000754855 00000 н.
0000761126 00000 н.
0000767305 00000 н.
0000773559 00000 н.
0000779843 00000 н.
0000780180 00000 н.
0000780331 00000 п.
0000786301 00000 п.
0000792555 00000 н.
0000798806 00000 п.
0000805062 00000 н.
0000811335 00000 н.
0000817613 00000 н.
0000823864 00000 н.
0000830115 00000 н.
0000836371 00000 п.
0000842621 00000 н. 0000842888 00000 н.
0000843037 00000 н.
0000849278 00000 н.
0000855547 00000 н.
0000861740 00000 н.
0000868000 00000 н.
0000874259 00000 н.
0000880537 00000 п.
0000886794 00000 н.
0000893064 00000 н.
0000899317 00000 н.
0000
0000842888 00000 н.
0000843037 00000 н.
0000849278 00000 н.
0000855547 00000 н.
0000861740 00000 н.
0000868000 00000 н.
0000874259 00000 н.
0000880537 00000 п.
0000886794 00000 н.
0000893064 00000 н.
0000899317 00000 н.
00003 00000 н. 0000
5 00000 н. 0000
7 00000 н. 0000912395 00000 н. 0000918653 00000 п. 0000924876 00000 н. 0000931143 00000 п. 0000937411 00000 п. 0000943620 00000 н. 0000949871 00000 п. 0000956124 00000 п. 0000962405 00000 п. 0000968603 00000 п. 0000969016 00000 н. 0000969168 00000 п. 0000975425 00000 н. 0000981694 00000 н. 0000987976 00000 н. 0000994185 00000 н. 0001000408 00000 п. 0001006677 00000 п. 0001012957 00000 п. 0001019257 00000 п. 0001025509 00000 п. 0001031786 00000 п. 0001031937 00000 п. 0001038218 00000 п. 0001044487 00000 п. 0001050746 00000 п. 0001056948 00000 п. 0001063212 00000 п. 0001069477 00000 п. 0001075744 00000 п. 0001081996 00000 п. 0001088250 00000 п. 0001094527 00000 п. 0001094876 00000 п. 0001095076 00000 п.
0001095317 00000 п.
0001095526 00000 п.
0001095731 00000 п.
0001095942 00000 п.
0001096164 00000 п.
0001096382 00000 п.
0001096629 00000 п.
0001098403 00000 п.
0001103339 00000 п.
0001105618 00000 п.
0001107491 00000 п.
0001107673 00000 п.
0001108613 00000 п.
0001108847 00000 п.
0001110436 00000 п.
0001125581 00000 п.
0001126803 00000 п.
0001127841 00000 п.
0001128094 00000 п.
0001128323 00000 п.
0001128580 00000 п.
0001130198 00000 п.
0001131410 00000 п.
0001134063 00000 п.
0001134224 00000 п.
0001134422 00000 п.
0001136744 00000 п.
0001137061 00000 п.
0001137593 00000 п.
0001137955 00000 п.
0001138145 00000 п.
0000006836 00000 н.
трейлер
] / Назад 3443661 >>
startxref
0
%% EOF
1476 0 объект
> поток
h U {PTe? DzOvp65KP D ޠ0 JC ր) 1 DM @ P-FILFfto70 ~ gνw {;
0001095076 00000 п.
0001095317 00000 п.
0001095526 00000 п.
0001095731 00000 п.
0001095942 00000 п.
0001096164 00000 п.
0001096382 00000 п.
0001096629 00000 п.
0001098403 00000 п.
0001103339 00000 п.
0001105618 00000 п.
0001107491 00000 п.
0001107673 00000 п.
0001108613 00000 п.
0001108847 00000 п.
0001110436 00000 п.
0001125581 00000 п.
0001126803 00000 п.
0001127841 00000 п.
0001128094 00000 п.
0001128323 00000 п.
0001128580 00000 п.
0001130198 00000 п.
0001131410 00000 п.
0001134063 00000 п.
0001134224 00000 п.
0001134422 00000 п.
0001136744 00000 п.
0001137061 00000 п.
0001137593 00000 п.
0001137955 00000 п.
0001138145 00000 п.
0000006836 00000 н.
трейлер
] / Назад 3443661 >>
startxref
0
%% EOF
1476 0 объект
> поток
h U {PTe? DzOvp65KP D ޠ0 JC ր) 1 DM @ P-FILFfto70 ~ gνw {;Вычислитель объема круглого усеченного конуса
[1] 2021/02/18 01:15 Женщина / Уровень 20 лет / Средняя школа / Университет / Аспирант / Полезно /
[2] 2021. 01.24 14:17 Женский / 20-летний уровень / Средняя школа / Университет / Аспирант / Очень /
01.24 14:17 Женский / 20-летний уровень / Средняя школа / Университет / Аспирант / Очень /
[3] 2021.01.15 01:52 Мужчина / Уровень 40 лет / Другое / Очень /
[4] 2021.01.12 20:40 Мужчина / Уровень 20 лет / Инженер / Очень /
[5] 2020/12/04 07:22 Мужчина / 50 лет / Пенсионер / Очень /
[6] 2020/11/13 08:39 Женский / До 20 лет / Старшая школа / Университет / Аспирантка / Очень /
[7] 2020/10/01 08:18 Мужчина / Уровень 30 лет / Инженер / Очень /
[8] 2020/09/27 03:51 Женщина / Уровень 40 лет / Домохозяйка / Полезно /
[9] 2020/09/05 19:49 Мужской / возраст 50 лет / Самозанятые лица / Очень /
[10] 2020/09/03 06:27 Мужчина / 60 лет и старше / Пенсионер / Очень /
Объем и площадь поверхности — Prealgebra
Цели обучения
К концу этого раздела вы сможете:
В этом разделе мы закончим изучение геометрических приложений. Находим объем и площадь некоторых трехмерных фигур. Поскольку мы будем решать приложения, мы еще раз покажем нашу стратегию решения проблем для геометрических приложений.
Находим объем и площадь некоторых трехмерных фигур. Поскольку мы будем решать приложения, мы еще раз покажем нашу стратегию решения проблем для геометрических приложений.
Стратегия решения проблем для геометрических приложений
Найти объем и площадь поверхности прямоугольных тел
Тренер по черлидингу приказывает команде красить деревянные ящики в цвета школы, чтобы на них стоять на играх.(См. (Рисунок)). Количество краски, необходимое для покрытия внешней стороны каждой коробки, — это площадь поверхности, квадратная мера общей площади всех сторон. Количество места внутри обрешетки — это объем, кубическая мера.
Деревянный ящик имеет форму прямоугольного твердого тела.
Каждый ящик имеет форму прямоугольного твердого тела. Его размеры — длина, ширина и высота. Прямоугольное тело, показанное на (Рисунок), имеет единицы измерения длины, ширины и высоты.Вы можете сказать, сколько всего кубических единиц? Давайте посмотрим слой за слоем.
Всего кубических единиц. Обратите внимание, что это
Объем любого прямоугольного твердого тела является произведением длины, ширины и высоты.
Мы также могли бы написать формулу объема прямоугольного твердого тела через площадь основания. Площадь базы, равна
Площадь базы, равна
Мы можем заменить в формуле объема, чтобы получить другую форму формулы объема.
Теперь у нас есть другая версия формулы объема для прямоугольных тел. Давайте посмотрим, как это работает с прямоугольным телом, с которого мы начали. См. (Рисунок).
Чтобы найти площадь поверхности прямоугольного твердого тела, подумайте о том, чтобы найти площадь каждой из его граней. Сколько граней у прямоугольного тела наверху? Вы можете увидеть три из них.
Обратите внимание, что для каждого из трех лиц, которые вы видите, есть идентичное противоположное лицо, которое не отображается.
Площадь поверхности прямоугольного твердого тела, показанного на (Рисунок), выражена в квадратных единицах.
В общем, чтобы найти площадь поверхности прямоугольного твердого тела, помните, что каждая грань представляет собой прямоугольник, поэтому его площадь является произведением его длины и ширины (см. (Рисунок)). Найдите площадь каждого лица, которое вы видите, а затем умножьте каждую площадь на два, чтобы учесть лицо на противоположной стороне.
(Рисунок)). Найдите площадь каждого лица, которое вы видите, а затем умножьте каждую площадь на два, чтобы учесть лицо на противоположной стороне.
Объем и площадь прямоугольного твердого тела
Для прямоугольного твердого тела длиной, шириной и высотой
Выполнение задания по манипуляции математикой «Раскрашенный куб» поможет вам лучше понять объем и площадь поверхности.
Для прямоугольного твердого тела длиной см, высотой см и шириной см найдите объема и ⓑ площади поверхности.
Найдите объем и ⓑ площадь поверхности прямоугольного твердого тела, используя следующие параметры: длина в футах, ширина в футах и высота в футах.
Найдите объем и ⓑ площадь поверхности прямоугольного твердого тела, используя следующие параметры: длина в футах, ширина в футах и высота в футах.
Прямоугольный ящик имеет длину в дюймах, ширину в дюймах и высоту в дюймы. Найдите его объем ⓐ и площадь поверхности ⓑ.
Прямоугольная коробка имеет длину в футах, ширину в футах и высоту в футах.Найдите его объем ⓐ и площадь поверхности ⓑ.
Прямоугольный чемодан имеет длину в дюймах, ширину в дюймах и высоту в дюймах. Найдите его объем ⓐ и площадь поверхности ⓑ.
Объем и площадь куба
Куб — это прямоугольное тело, длина, ширина и высота которого равны. См. Раздел «Объем и площадь поверхности куба» ниже.Подставляя s для длины, ширины и высоты в формулы для объема и площади поверхности прямоугольного твердого тела, получаем:
Итак, для куба формулы для объема и площади поверхности имеют вид и
Объем и площадь куба
Для любого куба с длиной сторон
Куб имеет дюймы с каждой стороны. Найдите его объем ⓐ и площадь поверхности ⓑ.
Найдите его объем ⓐ и площадь поверхности ⓑ.
Для куба со стороной 4,5 метра найдите объема и ⓑ площади поверхности куба.
Для куба со стороной 7,3 ярда найдите объема и ⓑ площади поверхности куба.
Кубик блокнота имеет дюймы с каждой стороны. Найдите его объем ⓐ и площадь поверхности ⓑ.
Упаковочная коробка — это куб, измеряющий ножки с каждой стороны. Найдите его объем ⓐ и площадь поверхности ⓑ.
Стена сложена из кирпича кубической формы. Каждый куб имеет дюймы с каждой стороны. Найдите объема и ⓑ площади поверхности каждого куба.
Найдите объем и площадь поверхности сфер
Сфера — это баскетбольный мяч, похожий на трехмерный круг. Как и в случае с кругом, размер сферы определяется ее радиусом, который представляет собой расстояние от центра сферы до любой точки на ее поверхности.Формулы для объема и площади поверхности сферы приведены ниже.
Как и в случае с кругом, размер сферы определяется ее радиусом, который представляет собой расстояние от центра сферы до любой точки на ее поверхности.Формулы для объема и площади поверхности сферы приведены ниже.
Показать, откуда взялись эти формулы, как мы это делали для прямоугольного твердого тела, выходит за рамки этого курса. Приближаемся к
Объем и площадь поверхности
Для сферы радиусом
Сфера имеет радиус в дюймах. Найдите его объем ⓐ и площадь поверхности ⓑ.
Найдите объем ⓐ и площадь поверхности сферы радиусом 3 сантиметра.
Найдите объем ⓐ и площадь поверхности каждой сферы радиусом фута
Земной шар имеет форму шара радиусом в сантиметрах. Найдите его объем ⓐ и площадь поверхности ⓑ. Округлите ответ до сотых.
Пляжный мяч имеет форму шара с радиусом в дюймах. Найдите его объем ⓐ и площадь поверхности ⓑ.
Найдите его объем ⓐ и площадь поверхности ⓑ.
Римская статуя изображает Атласа, держащего земной шар радиусом в фут. Найдите объема и ⓑ площади земного шара.
Найдите объем и площадь цилиндра
Если вы когда-нибудь видели банку газировки, вы знаете, как выглядит баллон. Цилиндр представляет собой сплошную фигуру с двумя параллельными кругами одинакового размера вверху и внизу.Верх и низ цилиндра называются основаниями. Высота цилиндра — это расстояние между двумя основаниями. Для всех цилиндров, с которыми мы будем работать здесь, стороны и высота будут перпендикулярны основанию.
Цилиндр имеет два круглых основания одинакового размера. Высота — это расстояние между основаниями.
Прямоугольные тела и цилиндры в чем-то похожи, потому что оба имеют два основания и высоту. Формула объема прямоугольного твердого тела также может использоваться для определения объема цилиндра.
Формула объема прямоугольного твердого тела также может использоваться для определения объема цилиндра.
Для прямоугольного твердого тела площадь основания является площадью прямоугольного основания, длина × ширина. Для цилиндра площадь основания — это площадь его круглого основания. (Рисунок) сравнивает, как формула используется для прямоугольных тел и цилиндров.
Увидев, как цилиндр похож на твердое тело прямоугольной формы, можно легче понять формулу объема цилиндра.
Чтобы понять формулу площади поверхности цилиндра, представьте банку с овощами.У него три поверхности: верхняя, нижняя и часть, образующая боковые стороны банки. Если аккуратно отрезать этикетку со стороны банки и развернуть ее, вы увидите, что это прямоугольник. См. (Рисунок).
Разрезав и развернув этикетку банки с овощами, мы можем увидеть, что поверхность цилиндра представляет собой прямоугольник. Длина прямоугольника — это окружность основания цилиндра, а ширина — это высота цилиндра.
Расстояние по краю банки — это длина окружности основания цилиндра, а также длина прямоугольной этикетки.Высота цилиндра равна ширине прямоугольной этикетки. Таким образом, площадь этикетки можно представить как
Чтобы найти общую площадь поверхности цилиндра, мы добавляем площади двух окружностей к площади прямоугольника.
Площадь цилиндра радиусом и высотой
Объем и площадь цилиндра
Для цилиндра с радиусом и высотой
Цилиндр имеет высоту в сантиметрах и радиус в сантиметрах.Найдите объем ⓐ и площадь поверхности ⓑ.
Найдите объем ⓐ и площадь поверхности цилиндра радиусом 4 см и высотой 7 см.
Найдите объем ⓐ и площадь поверхности цилиндра с заданным радиусом 2 фута и высотой 8 футов.
Найдите объема и ⓑ площади поверхности банки с газировкой. Радиус основания — сантиметры, а высота — сантиметры.Предположим, банка имеет форму цилиндра.
Радиус основания — сантиметры, а высота — сантиметры.Предположим, банка имеет форму цилиндра.
Найдите объем ⓐ и площадь поверхности банки с краской радиусом 8 см и высотой 19 см. Предположим, банка имеет форму цилиндра.
Найдите объем ⓐ и площадь поверхности цилиндрического барабана радиусом 2,7 фута и высотой 4 фута. Предположим, барабан имеет форму цилиндра.
Найдите объем конусов
Первое изображение, которое у многих из нас возникает, когда мы слышим слово «рожок», — это рожок мороженого. Есть много других применений рожков (но большинство из них не так вкусно, как рожки мороженого). В этом разделе мы увидим, как найти объем конуса.
В геометрии конус представляет собой твердую фигуру с одним круглым основанием и вершиной.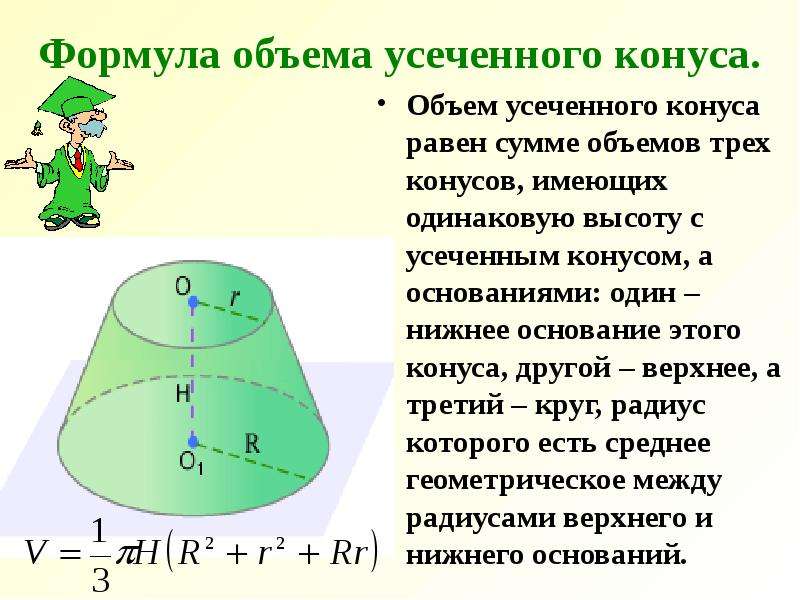 Высота конуса — это расстояние между его основанием и вершиной.Конусы, которые мы рассмотрим в этом разделе, всегда будут иметь высоту, перпендикулярную основанию. См. (Рисунок).
Высота конуса — это расстояние между его основанием и вершиной.Конусы, которые мы рассмотрим в этом разделе, всегда будут иметь высоту, перпендикулярную основанию. См. (Рисунок).
Высота конуса — это расстояние между его основанием и вершиной.
Ранее в этом разделе мы видели, что объем цилиндра равен. Мы можем представить себе конус как часть цилиндра. (Рисунок) показывает конус, помещенный внутри цилиндра той же высоты и того же основания. Если мы сравним объем конуса и цилиндра, то увидим, что объем конуса меньше объема цилиндра.
Объем конуса меньше объема цилиндра с таким же основанием и высотой.
Фактически, объем конуса составляет ровно одну треть объема цилиндра с тем же основанием и высотой. Объем конуса
Поскольку основание конуса — это круг, мы можем подставить формулу площади круга, вместо , чтобы получить формулу для объема конуса.
В этой книге мы найдем только объем конуса, но не площадь его поверхности.
Объем конуса
Для конуса с радиусом и высотой.
Найдите объем конуса с высотой в дюймах и радиусом его основания в дюймах.
Найдите объем конуса с высотой в дюймах и радиусом в дюймах
Найдите объем конуса высотой в сантиметрах и радиусом в сантиметрах
В любимом гастропабе Марти подают картофель фри в бумажной упаковке в форме конуса. Каков объем конической оболочки в дюймах в высоту и в дюймах в диаметре? Округлите ответ до сотых.
Сколько кубических дюймов конфет поместится в конусообразной пиньяте, имеющей длину в дюймах и дюймы в основании? Округлите ответ до сотых.
Каков объем шляпы для вечеринок в форме конуса, имеющей дюйм в высоту и дюйм в ширину у основания? Округлите ответ до сотых.
Сводка геометрических формул
В следующих таблицах представлены все формулы, рассматриваемые в этой главе.
Практика ведет к совершенству
Найти объем и площадь поверхности прямоугольных тел
В следующих упражнениях найдите ⓐ объем и ⓑ площадь поверхности прямоугольного твердого тела заданных размеров.
метра длины, метра ширины, метра высоты
длина футов, ширина футов, высота
футовярдов длины, ширины ярдов, высоты
ярдовдлина сантиметра, ширина сантиметра, высота сантиметра
В следующих упражнениях решите.
Транспортный фургон Прямоугольный передвижной фургон имеет длину ножек, ширину ножек и высоту ножек.Найдите его объем ⓐ и площадь поверхности ⓑ.
Подарочная коробка Прямоугольная подарочная коробка имеет длину в дюймах, ширину в дюймах и высоту в дюймах. Найдите его объем ⓐ и площадь поверхности ⓑ.
Коробка Коробка прямоугольной формы имеет длину см, ширину см и высоту см. Найдите его объем ⓐ и площадь поверхности ⓑ.
Транспортный контейнер Прямоугольный транспортный контейнер имеет длину в футах, ширину в футах и высоту в футах.Найдите его объем ⓐ и площадь поверхности ⓑ.
В следующих упражнениях найдите ⓐ объем и ⓑ площадь поверхности куба с заданной длиной стороны.
см
дюймов
футов
метра
В следующих упражнениях решите.
Научный центр Каждая сторона куба в научном центре Discovery в Санта-Ане имеет длину фута.Найдите его объем ⓐ и площадь поверхности ⓑ.
Музей Музей в форме куба имеет стороны метровой длины. Найдите его объем ⓐ и площадь поверхности ⓑ.
Найдите его объем ⓐ и площадь поверхности ⓑ.
Основание статуи Основание статуи представляет собой куб со сторонами метровой длины. Найдите его объем ⓐ и площадь поверхности ⓑ.
Коробка для салфеток Коробка для салфеток представляет собой куб со сторонами 4.5 дюймов в длину. Найдите его объем ⓐ и площадь поверхности ⓑ.
Найдите объем и площадь поверхности сфер
В следующих упражнениях найдите ⓐ объем и ⓑ площадь поверхности сферы с заданным радиусом. Округлите ответы до сотых.
см
дюймов
футов
ярдов
В следующих упражнениях решите.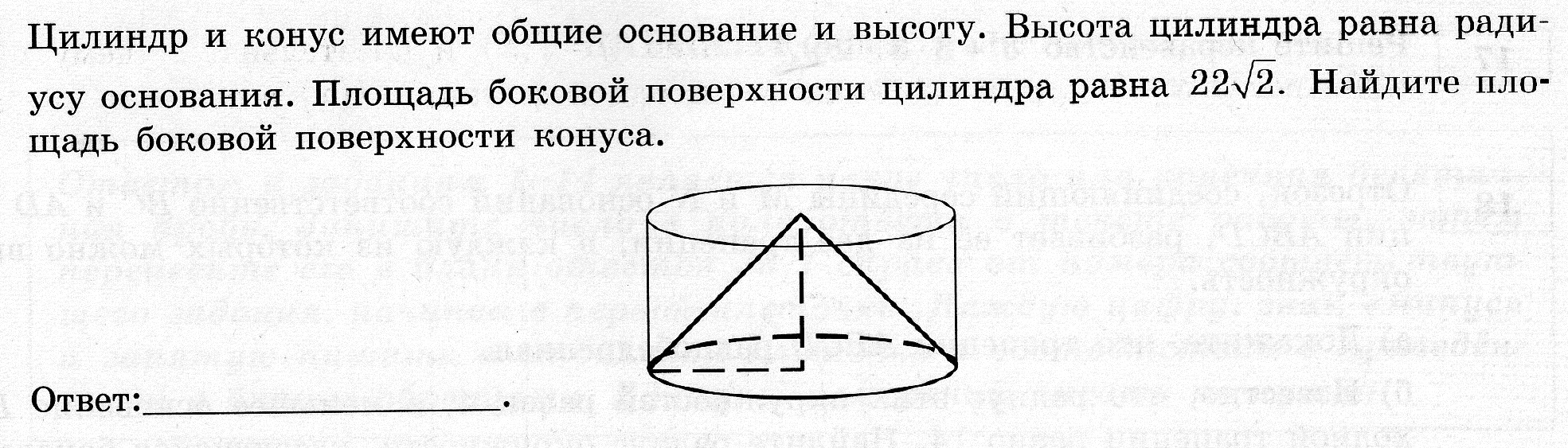 Округлите ответы до сотых.
Округлите ответы до сотых.
Мяч для упражнений Мяч для упражнений имеет радиус в дюймах. Найдите его объем ⓐ и площадь поверхности ⓑ.
Полет на воздушном шаре Большой воздушный шар в парке — это большая оранжевая сфера радиусом в фут. Найдите его объем ⓐ и площадь поверхности ⓑ.
Мяч для гольфа Мяч для гольфа имеет радиус сантиметра.Найдите его объем ⓐ и площадь поверхности ⓑ.
Бейсбол Бейсбольный мяч имеет радиус в дюймах. Найдите его объем ⓐ и площадь поверхности ⓑ.
Найдите объем и площадь поверхности цилиндра
В следующих упражнениях найдите ⓐ объем и ⓑ площадь поверхности цилиндра с заданными радиусом и высотой. Округлите ответы до сотых.
Округлите ответы до сотых.
футов, высота
футоврадиус сантиметра, высота
сантиметрарадиуса метров, высоты
метровярдов, высота
ярдовВ следующих упражнениях решите. Округлите ответы до сотых.
Банка для кофе Банка для кофе имеет радиус см и высоту см. Найдите его объем ⓐ и площадь поверхности ⓑ.
Пакет для снеков Пакет для снеков имеет форму цилиндра с радиусом см и высотой см. Найдите его объем ⓐ и площадь поверхности ⓑ.
Столб для парикмахерской Цилиндрический столб для парикмахерской имеет диаметр в дюймы и высоту в дюймы.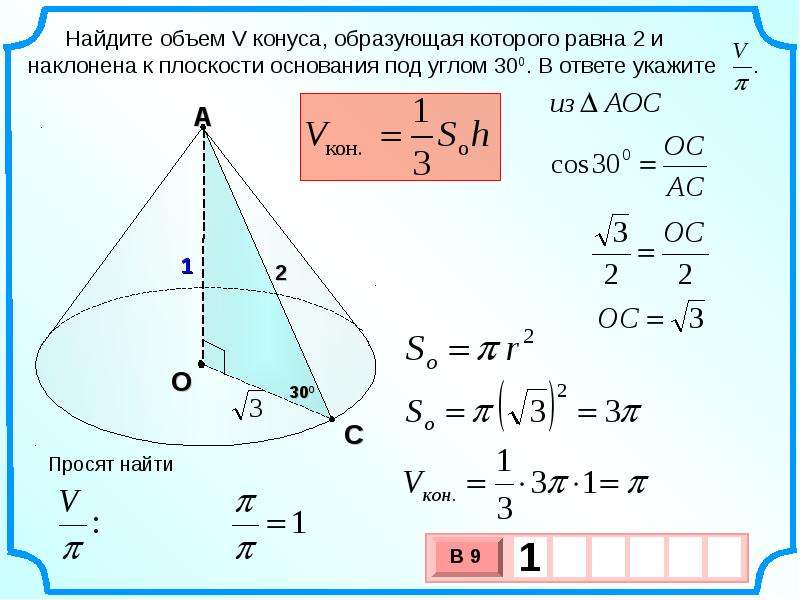 Найдите его объем ⓐ и площадь поверхности ⓑ.
Найдите его объем ⓐ и площадь поверхности ⓑ.
Архитектура Цилиндрическая колонна имеет диаметр футов и высоту футов.Найдите его объем ⓐ и площадь поверхности ⓑ.
Найдите объем конусов
В следующих упражнениях найдите объем конуса с заданными размерами. Округлите ответы до сотых.
футов высоты и радиуса
футовдюймов высоты и радиуса
дюймоввысота сантиметра и радиус см
метров высоты и радиуса
В следующих упражнениях решите. Округлите ответы до сотых.
Типи Каков объем конусообразной палатки-типи высотой в фут и шириной у основания?
Чашка для попкорна Каков объем конической чашки для попкорна, имеющей дюйм в высоту и дюйм в диаметре у основания?
Силос Каков объем силоса конической формы высотой в футах и шириной в футах у основания?
Куча песка Каков объем конической кучи песка метровой высоты и метровой ширины у основания?
Повседневная математика
Столб уличного фонаря Столб уличного фонаря имеет форму усеченного конуса, как показано на рисунке ниже. Это большой конус без верхнего конуса меньшего размера. Большой конус в фут с радиусом в основании. Меньший конус имеет высоту футов с радиусом основания футов. С точностью до десятых,
Это большой конус без верхнего конуса меньшего размера. Большой конус в фут с радиусом в основании. Меньший конус имеет высоту футов с радиусом основания футов. С точностью до десятых,
ⓐ найти объем большого конуса.
ⓑ найти объем маленького конуса.
ⓒ найдите объем столба, вычтя объем малого конуса из объема большого конуса.
Конусы для мороженого Обычный конус для мороженого имеет высоту 4 дюйма и диаметр в несколько дюймов. Вафельный рожок имеет высоту в дюймы и диаметр в дюймах. С точностью до сотых,
ⓐ найти объем обычного рожка мороженого.
ⓑ найти объем вафельного рожка.
ⓒ Насколько больше мороженого умещается в вафельном рожке по сравнению с обычным рожком?
Письменные упражнения
Формулы для объема цилиндра и конуса аналогичны. Объясните, как можно запомнить, какая формула сочетается с какой формой.
Объясните, как можно запомнить, какая формула сочетается с какой формой.
Что имеет больший объем: куб со сторонами стопы или сфера диаметром в стопу? Объясните свои рассуждения.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Глоссарий
Наклонная высота правого конуса
Наклонная высота правого конуса — Math Open Reference Определение:
Расстояние от вершины конуса вниз по краю до точки на краю основания.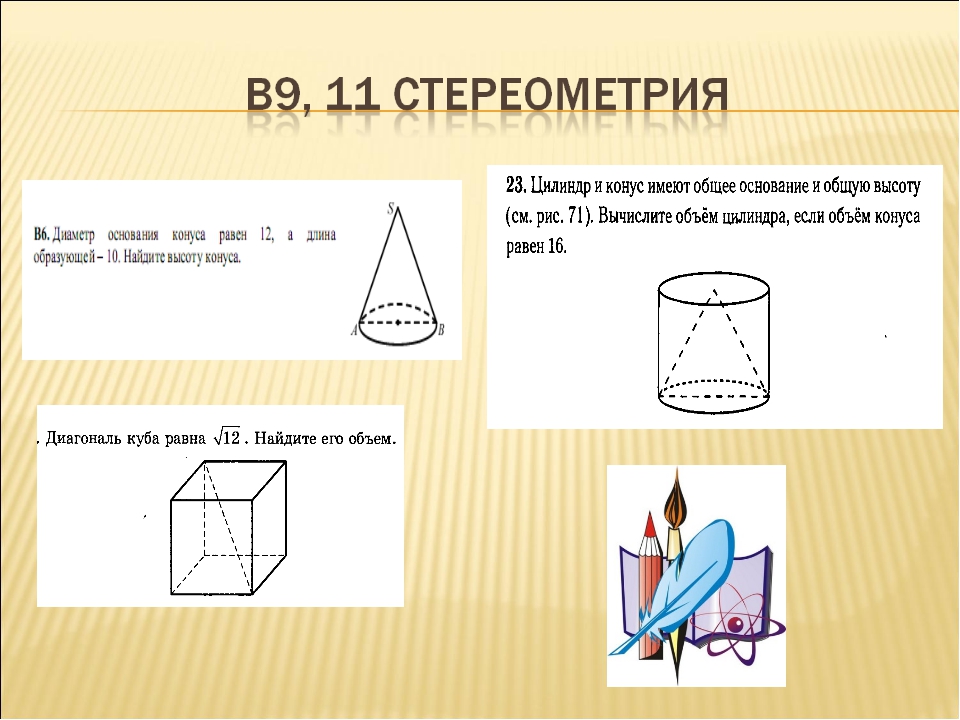
Попробуй это Перетащите оранжевые точки, чтобы настроить радиус и высоту конуса, и обратите внимание на изменение высоты наклона.
Есть три измерения конуса.
Эти три связаны, и нам нужны только любые два, чтобы определить конус.Затем мы можем найти третье недостающее измерение.
На рисунке выше мы видим, что три измерения образуют
прямоугольный треугольник,
с наклонной высотой как
гипотенуза
так что мы можем использовать
Теорема Пифагора для его решения *.
Перетащите любую оранжевую точку на верхнем рисунке и обратите внимание, как наклонная высота рассчитывается на основе радиуса и высоты.
* Фактически мы можем использовать любой метод решения этого треугольника, который нам нравится. Это просто зависит от того, что вам дают, и от личных предпочтений.См. Раздел Решение треугольника.
Это просто зависит от того, что вам дают, и от личных предпочтений.См. Раздел Решение треугольника.
Определение высоты наклона
Применяя теорему Пифагора, наклонная высота определяется по формуле: где r — радиус основания, h — высота.
Если вам задана высота уклона
Переставляя члены теоремы Пифагора, мы можем найти другую длину:
Что попробовать
Связанные темы
(C) Открытый справочник по математике, 2011 г.

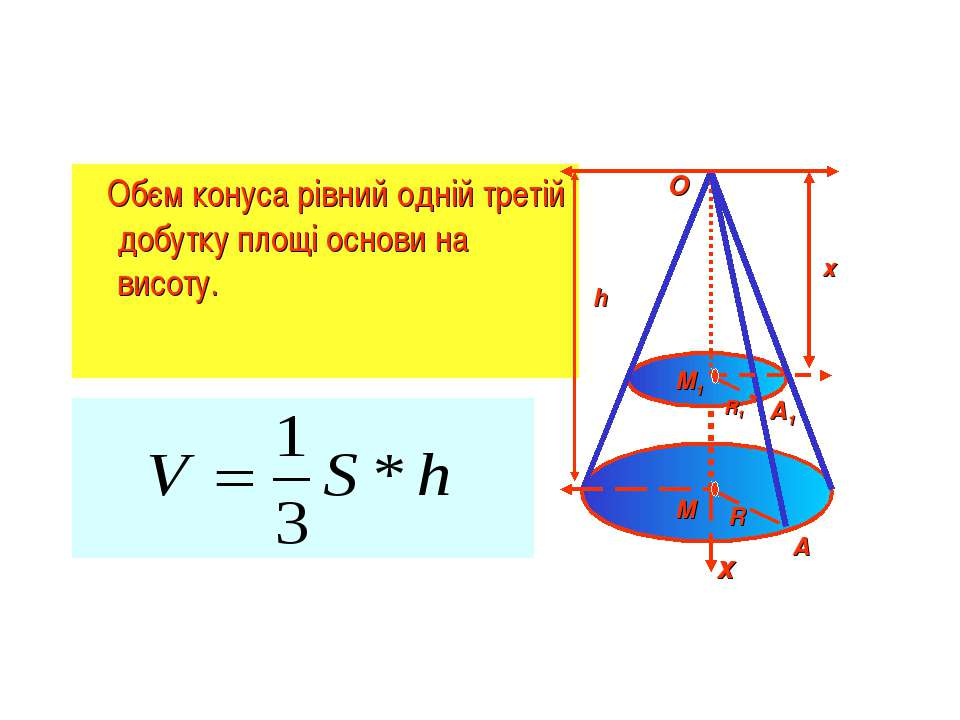 Тогда имеют место следующие соотношения:
Тогда имеют место следующие соотношения:

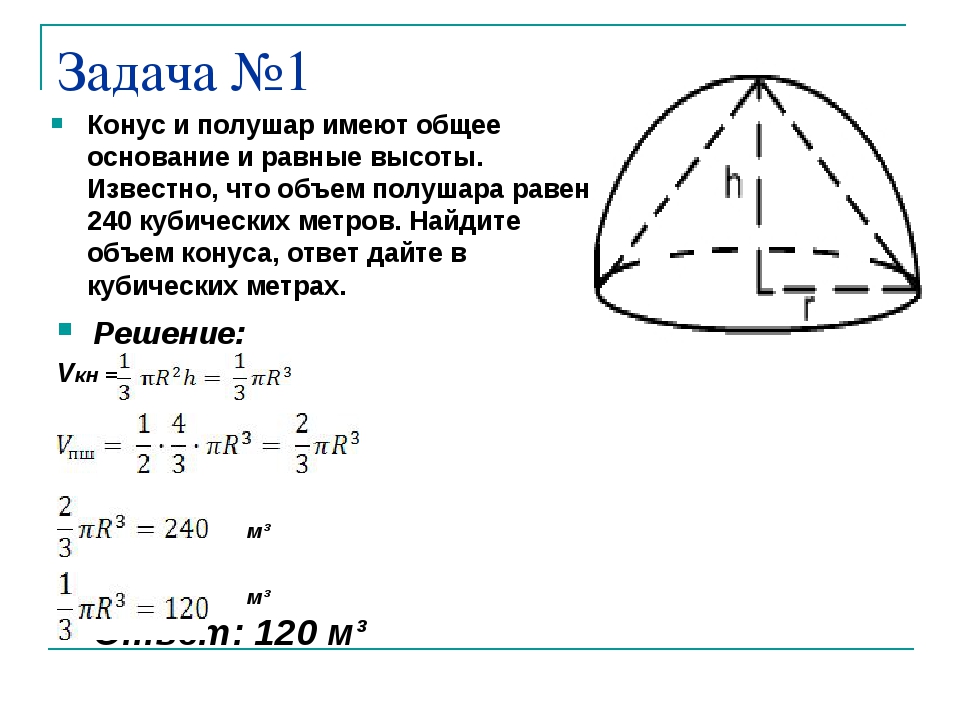
Leave A Comment