§ 6. Скорость прямолинейного равноускоренного движения. График скорости. —
Вопросы.1. Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю.
2. Что представляет собой график проекции вектора скорости равноускоренного движения при начальной скорости: а) равной нулю; б) не равной нулю?
3. Чем сходны и чем отличаются друг от друга движения, графики которых представлены на рисунках 11 и 12?
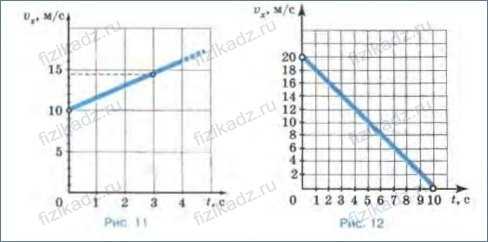
В обоих случаях движение происходит с ускорением, однако в первом случае ускорение положительно, а во-втором отрицательно.
Упражнения.
1. Хоккеист слегка ударил клюшкой по шайбе, придав ей скорость 2 м/с. Чему будет равна скорость шайбы через 4 с после удара, если в результате трения о лёд она движется с ускорением 0,25 м/с

2. Лыжник съезжает с горы из состояния покоя с ускорением, равным 0,2 м/с2. Через какой промежуток времени его скорость возрастёт до 2 м/с?

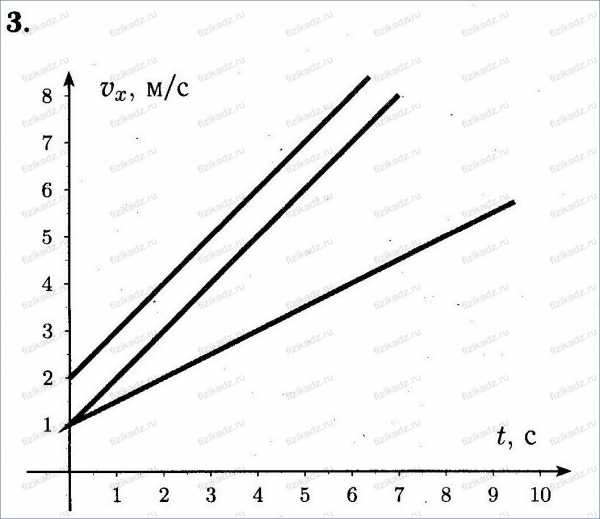
3. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v
Масштаб во всех случаях одинаков: 1см- 1м/с; 1см — 1с.
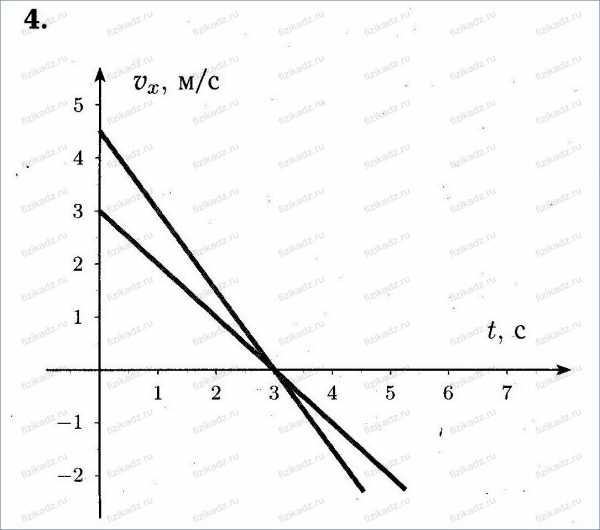
4. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v
Масштаб выберите сами.
5. На рисунке 13 представлены графики зависимости модуля вектора скорости от времени при прямолинейном движении двух тел. С каким по модулю ускорением движется тело I? тело II?
fizikadz.ru
Скорость прямолинейного равноускоренного движения: график скорости
Проекцию скорости на ось Ох при прямолинейном равноускоренном движении можно найти по следующей формуле:
Выразим из этой формулы, формулу для проекции скорости которую имело лвижущееся тело к концу некоторого промежутка времени t.
То есть, зная проекцию вектора начальной скорости V0x и проекцию вектора ускорения ax в любой момент времени можно вычислить проекцию вектора мгновенной скорости Vx, которую будет иметь тело в данной точке.
- Представим зависимость скорости от времени при равноускоренно движении в виде графика.
Графиком уравнения Vx=V0x+ax*t будет прямая линия. Расположение этой лини в системе координат будет определяться значениями ax b V0x.
График проекции скорости тела при нулевой начальной скорости
На следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел нулевую скорость, и двигалось равноускоренно и прямолинейно с ускорением ax=1,5 м/(с^2) в течение 40 секунд.
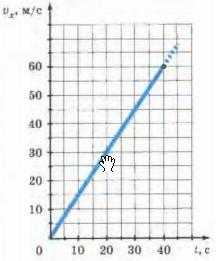
Так как изначально скорость была нулю, то уравнение примет следующий вид
Vx=ax*t.
Для построения графика достаточно взять пару точек. Выберем момент времени
t=0. Тогда Vx=0.
t=40, тогда Vx= ax*t =1,5*40 = 60
Отметим эти точки на графике и соединим их прямой.
Так как ускорение положительное, то график образует с осью Ох острый угол.
График проекции скорости тела при ненулевой начальной скорости
Теперь посмотрим, как будет выглядеть график вектора проекции скорости, при начальной скорости тела отличной от нуля.
В этом случае график будет описываться функцией Vx=V0x+ax*t.
На следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел скорость Vx=10, и двигалось равноускоренно и прямолинейно с ускорением ax=1,4 м/(с^2) в течение 4 секунд.
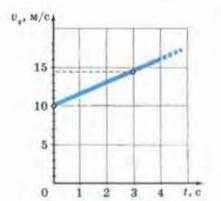
Для построения такого графика, также достаточно взять несколько значений переменной t и посчитать в них значение проекции скорости Vx. А потом соединить их прямой линией. Как видите, график имеет начальную точку не в нуле, в значении, которое имеет начальная скорость.
График проекции скорости тела при торможении
Если бы ускорение было отрицательным, то есть тело постепенно тормозило, то график составлял бы с положительным направлением оси Ох тупой угол.
Ниже представлен график такой ситуации.
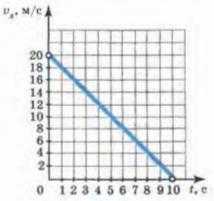
Из графика видно, что тело начинало свое движение со скоростью 20 м/с, и постепенно замедляло её. За 10 секунд, оно полностью остановилось.
Нужна помощь в учебе?
Предыдущая тема: Прямолинейное равноускоренное движение и ускорение
Следующая тема:   Перемещение при прямолинейном равноускоренном движении
Все неприличные комментарии будут удаляться.
www.nado5.ru
Графики равномерного, равноускоренного движения, сравнение. Линейная, квадратная зависимость. Правила определения параметров
Тестирование онлайн
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают
Графики равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) — прямая линия, параллельная оси времени.

Правило определения пути по графику v(t): Численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График s(t) — наклонная линия.
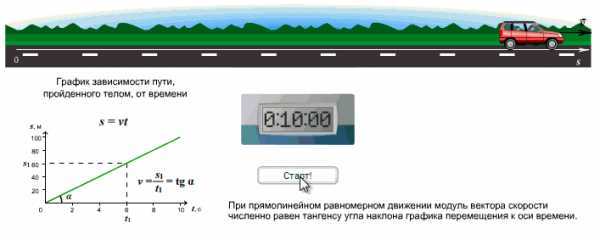
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.
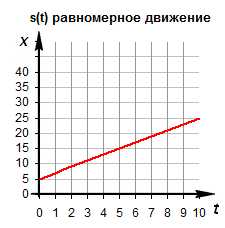
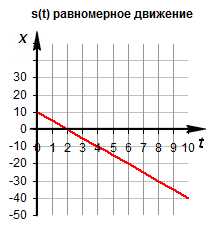
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
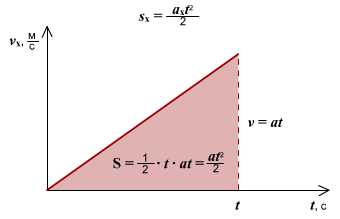
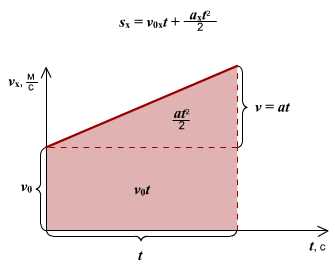
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.
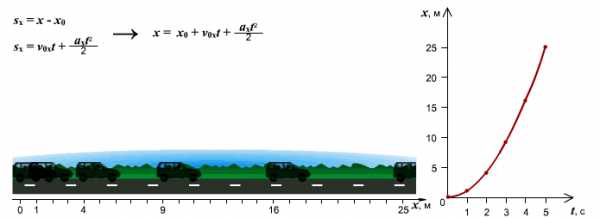
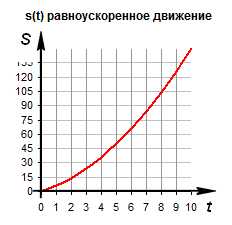
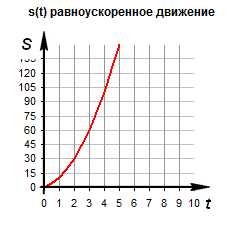
График движения при . График движения при
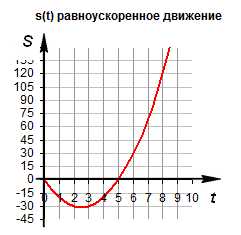
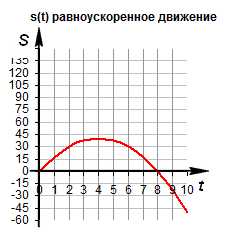
График движения при . График движения при
Сравнительная таблица графиков
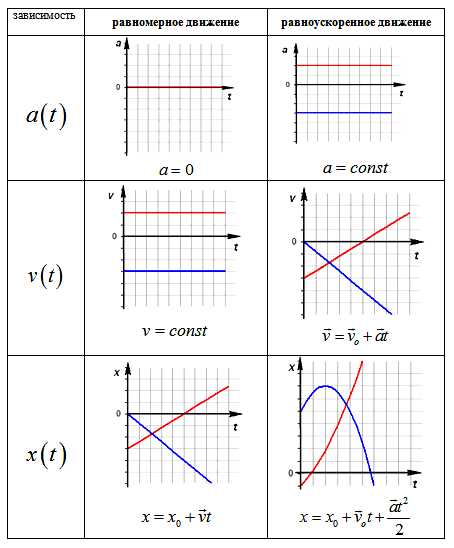
fizmat.by
Графики равноускоренного движения. Видеоурок. Физика 10 Класс
На прошлом уроке мы изучили основные законы и зависимости равноускоренного движения. На этом уроке мы научимся строить графики равноускоренного движения – это графики зависимости проекции скорости от времени, графики зависимости проекции перемещения от времени, графики зависимости координаты от времени, и анализировать эти графики. Также решим несколько типовых задач по этой теме.
Зависимость проекции скорости от времени является линейной, так как описывается следующим законом:
Из курса математики нам известно похожее уравнение:
Это уравнение прямой, следовательно, график зависимости проекции скорости от времени также будет иметь вид прямой. Нарисуем эту прямую на координатной сетке (рис. 1). Для этого выбираем произвольное значение и строим произвольную прямую.
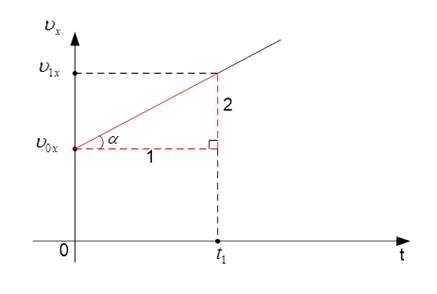
Рис. 1. График зависимости проекции скорости от времени
Проанализируем полученный график.
Видно, что скорость тела возрастала и в какой-то момент времени была равна . Это говорит о том, что проекция ускорения .
Рассмотрим прямоугольный треугольник (выделенный красным цветом). Длина катета 1 в этом треугольнике равна , а длина катета 2 равна . С помощью этих катетов найдем тангенс угла , то есть тангенс угла наклона построенной прямой:
Нам известно, что отношение изменения скорости ко времени, за которое оно произошло – это ускорение, следовательно:
Проанализируем график на рисунке 2.
Рис. 2. График зависимости проекции скорости от времени
Видно, что скорость тела не менялась и всегда оставалась равной , следовательно, проекция ускорения этого тела равно нулю . Такое движение является равномерным.
Проанализируем график на рисунке 3.
Рис. 3. График зависимости проекции скорости от времени
Видно, что проекция ускорения имеет знак минус . До момента времени модуль скорости уменьшался (тело тормозило), а далее модуль скорости увеличивался (тело разгонялось в противоположную сторону), следовательно, момент времени – это точка поворота (рис. 4).
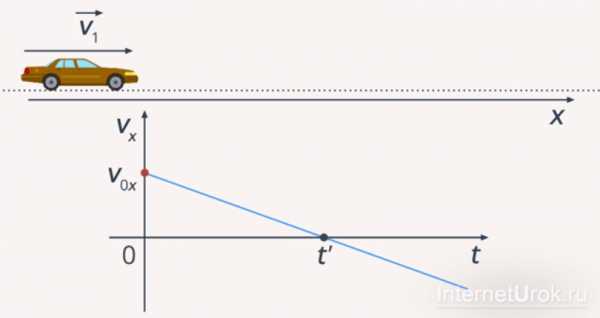
Рис. 4. Точка поворота
На рисунке 5 представлен график зависимости проекции скорости от времени для движущегося тела. По данному рисунку запишите эту зависимость аналитически.
Рис. 5. Иллюстрация к задаче
Решение
Зависимость является прямой, то есть тело двигалось равноускоренно. Зависимость скорости от времени при равноускоренном движении выглядит следующим образом:
Для того чтобы записать эту зависимость для данного тела, необходимо найти проекцию начальной скорости и проекцию ускорения .
Начальная скорость – это скорость в начальный момент времени, то есть при . На данном графике видно, что начальная скорость равна (цена одного деления на оси проекции скорости ).
Формула для нахождения проекции ускорения:
Начальная скорость нам известна, а определим в произвольный момент времени. В данном случае удобно определить скорость в точке пересечения прямой с осью времени. Скорость в этой точке равна нулю . Время, за которое скорость изменилась с до определим по графику. Это время равно (цена одного деления на оси времени ).
Подставляем полученные данные в формулу проекции ускорения:
Подставляем значение проекции начальной скорости и ускорения в закон изменения проекции скорости со временем:
Ответ:.
Зависимость проекции перемещения от времени имеет следующий вид:
Множитель t в этой зависимости стоит как в первой степени, так и во второй. С точки зрения математики такая зависимость называется квадратичной, а график ее – парабола.
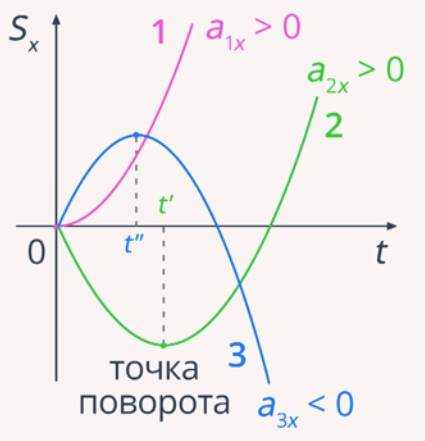
Рис. 6. Графики зависимости проекции перемещения от времени
На рисунке 6 изображены параболы.
Ветви параболы 1 направлены вверх, следовательно, коэффициент , то есть проекция ускорения положительная .
Для параболы 2 проекция ускорения также будет положительной . До момента времени тело двигалось в противоположную выбранной оси сторону; – точка поворота.
Ветви параболы 3 направлены вниз, следовательно, проекция ускорения меньше нуля . – точка поворота.
Зависимость координаты от времени имеет следующий вид:
Данная зависимость отличается от уравнения зависимости проекции перемещения от времени только слагаемым . Поэтому график также будет иметь вид параболы, которая сдвинута по оси ординат на величину начальной координаты () (рис. 7).
Рис. 7. Сдвиг графика
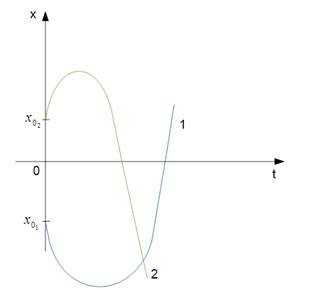
Рис. 8. Графики зависимости координаты от времени
На рисунке 8 изображены графики зависимости координаты от времени.
Парабола 1 имеет отрицательную начальную координату. Ветви этой параболы направлены вверх, следовательно, проекция ускорения будет больше нуля, .
У параболы 2 начальная координата больше нуля. Ветви этой параболы направлены вниз, следовательно, проекция ускорения будет меньше нуля, .
Модуль проекции ускорения будет больше во втором случае, так как координата (x) менялась быстрее.
На рисунке 9 представлен график зависимости для равноускоренно движущегося тела. Известно, что начальная координата тела составляла . По этим данным запишите аналитически зависимость , и , а также постройте график зависимости .
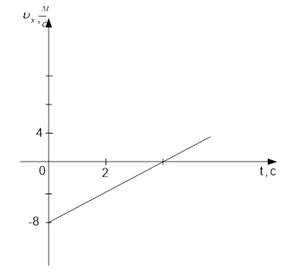
Рис. 9. Иллюстрация к задаче
Решение
1. Общий вид закона :
На графике видно, что проекция начальной скорости равна:
Формула для нахождения проекции ускорения:
В данном случае удобно определить скорость в точке пересечения прямой с осью времени. Скорость в этой точке равна нулю . Время, за которое скорость изменилась от начального значения до значения , определим по графику. Это время равно .
Подставляем значение проекции начальной скорости и ускорения в уравнение :
2. Общий вид закона :
Значение проекции начальной скорости и ускорения нам известны, поэтому подставляем их в уравнение:
3. Общий вид закона :
Значение проекции начальной скорости и ускорения, а также начальной координаты нам известны, поэтому подставляем их в уравнение:
4. По имеющейся зависимости построим график.
Для того чтобы построить график параболы, необходимо определить координаты вершины.
Координаты вершины параболы находятся по формулам:
;
Тогда,
Ординату вершины найдем, подставив значение абсциссы () в уравнение зависимости :
Также необходимо найти точки пересечения параболы с осями.
Из условия известна начальная координата. То есть при , . Вторую точку найдем, подставив 0 вместо в уравнение зависимости координаты от времени.
При решении данного квадратного уравнения получаем два корня и . Нам подходит положительный корень , так как мы считаем, что тело начало двигаться в момент времени . – момент времени за 2 с до начала наблюдения.
Следовательно, вторая точка имеет абсциссу , ординату .
По известным точкам строим параболу. Ветви данной параболы направлены вверх, так как в уравнении перед стоит знак плюс (рис. 10).
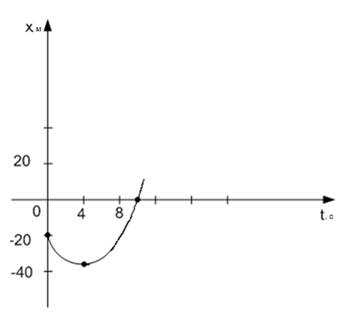
Рис. 10. Иллюстрация к задаче
Список литературы
- М.М. Балашов, А.И. Гомонова, А.Б. Долицкий. Физика: механика. 10. – М.: Дрофа, 2004.
- А.П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
- В.А. Касьянов. Физика 10 кл. – М.: Дрофа, 2000
- А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «ru.solverbook.com» (Источник)
- Интернет-портал «msk.edu.ua» (Источник)
- Интернет-портал «festival.1september.ru» (Источник)
Домашнее задание
- Задача 57, 58 (стр. 15) – А.П. Рымкевич. Физика. Задачник 10-11
- Нарисуйте график зависимости координаты от времени для прямолинейного движения, удовлетворяющего одновременно двум условиям: а) средняя скорость в промежутке времени от 2 до 6 с равна 5 м/с; б) максимальная скорость в том же промежутке равна 15 м/с.
- По графикам зависимости проекции скорости от времени (рис. 11) определите для каждого тела:
а) проекцию начальной скорости;
б) проекцию скорости через 2 с;
в) проекцию ускорения;
г) уравнение проекции скорости;
д) когда проекция скорости тел будет равна 6 м/с.
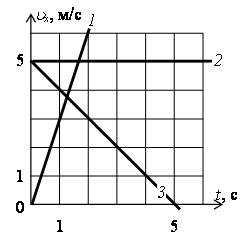
Рис. 11. Иллюстрация к задаче
interneturok.ru
Ł Скорость равноускоренного движения формула Проекции скорости и ускорения
КАБАРДИН О.Ф.
ФИЗИКА (справочные материалы), 1991
СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ
При движении тела по криволинейной траектории направление вектора скорости изменяется в процессе движения, вектор ускорения при этом может оказаться направлен под любым углом к вектору скорости (рис. 9).
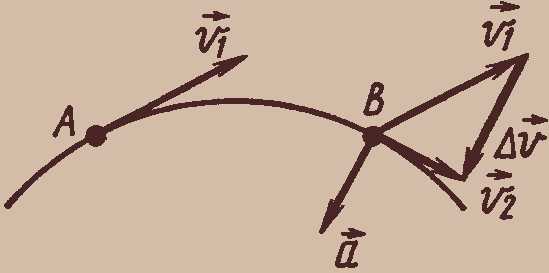
Рис. 9
Самый простой вид неравномерного движения — это равноускоренное движение. Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:
. (2.2)
Из формулы (2.1) следует, что при выражении скорости в метрах в секунду, а времени в секундах ускорение выражается в метрах на секунду в квадрате:
.
Метр на секунду в квадрате равен ускорению прямолинейно и равноускоренно движущейся точки, при котором за время 1 с скорость точки изменяется на 1 м/с.
Скорость равноускоренного движения. При равноускоренном движении с начальной скоростью ускорение равно
(2.3)
где — скорость в момент времени . Отсюда скорость равноускоренного движения равна
. (2.4)
Проекции скорости и ускорения. Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.
Векторы начальной скорости и ускорения могут иметь различные направления, поэтому переход от уравнения (2.4) в векторной форме к уравнениям в алгебраической форме может оказаться довольно сложной задачей. Задача нахождения модуля и направления скорости равноускоренного движения в любой момент времени может быть успешно решена следующим путем. Как известно, проекция1 суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось. Поэтому для нахождения проекции вектора скорости на произвольную ось OX нужно найти алгебраическую сумму проекций векторов и на ту же ось:
. (2.5)
Проекцию вектора на ось считают положительной, если от проекции начала к проекции конца вектора нужно идти по направлению оси, и отрицательной — в противоположном случае.
Так, в случае расположения векторов и , представленном на рисунке 10, их проекции и на ось OX положительны. В случае расположения векторов и , представленном на рисунке 11, проекция положительна, а проекция отрицательна.
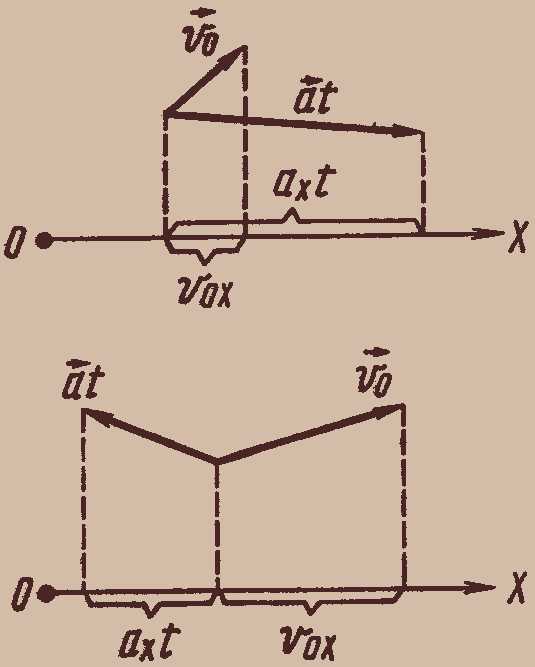
Рис. 10-11
График скорости. Из уравнения (2.5) следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось OX равна нулю ( ), то эта прямая проходит через начало координат (рис. 12).
Графики зависимости проекции скорости от времени для равноускоренных движений, происходящих с одинаковой начальной скоростью и различным ускорением , приведены на рисунке 13.
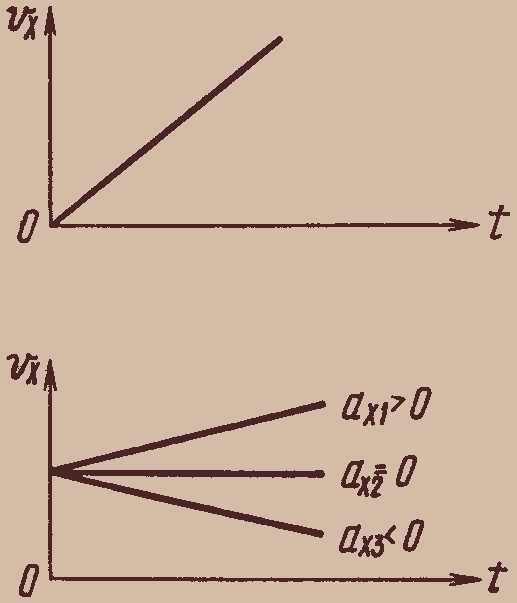
Рис. 12-13
Перемещение тела при равномерном движении. Установим связь проекции вектора перемещения на координатную ось OX при равномерном прямолинейном движении с проекцией вектора скорости на ту же ось и временем .
При равномерном прямолинейном движении график зависимости проекции скорости от времени является прямой, параллельной оси абсцисс (рис. 14).
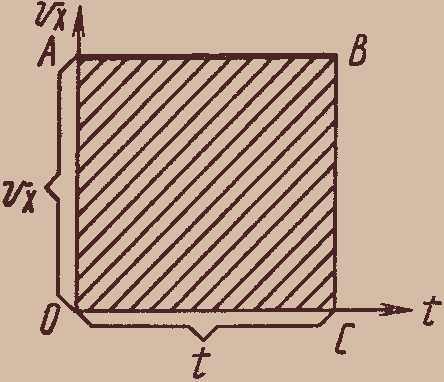
Рис. 14
Проекция перемещения тела за время при равномерном движении со скоростью (см. формулу 1.1) определяется выражением
. (2.6)
Длина стороны OA прямоугольника ОABC (см. рис. 14) пропорциональна проекции скорости , длина стороны ОС — времени движения . Следовательно, площадь прямоугольника ОABC прямо пропорциональна произведению или проекции перемещения .
⇦ Ctrl предыдущая страница / страница 3 из 140 / следующая страница Ctrl ⇨мобильная версия страницы Смотрите также на этом сайте:
ГАДАНИЯ, СОННИКИ, ЗАГОВОРЫ, НУМЕРОЛОГИЯ, ХИРОМАНТИЯ, ВУДУ, МАЯТНИК, ДЕНЕЖНАЯ МАГИЯ
ВЯЗАНИЕ НА СПИЦАХ, КРЮЧКОМ, ТУНИССКОЕ ВЯЗАНИЕ, МОДЕЛИ ВЯЗАНОЙ ОДЕЖДЫ; ШИТЬЕ; МАШИННОЕ ВЯЗАНИЕ
РАЗНООБРАЗНЫЕ КУЛИНАРНЫЕ РЕЦЕПТЫ; ГОРШОЧКИ, МИКРОВОЛНОВКА; КОНСЕРВИРОВАНИЕ
СПРАВОЧНИКИ ПО ФИЗИКЕ, МАТЕМАТИКЕ, АНГЛИЙСКОМУ ЯЗЫКУ; ПОХУДЕНИЕ, АКУПУНКТУРА; НЕИСПРАВНОСТИ АВТОМОБИЛЯ
МНОЖЕСТВО ИСТОРИЧЕСКИХ ФАКТОВ О СОБЫТИЯХ, ОРУЖИИ И ОБМУНДИРОВАНИИ ВТОРОЙ МИРОВОЙ ВОЙНЫ; АРМЕЙСКИЕ БОТИНКИ ВСЕХ ВРЕМЕН
ПОПУЛЯРНЫЕ ПЕСЕННИКИ 1963-1987 гг.; ТОСТЫ, РОЗЫГРЫШИ, КОНКУРСЫ
Пользуйтесь поиском вверху страницы! Все, что будет найдено со значком Ł — относится к данному сайту
cartalana.org
Равномерное прямолинейное движение
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:
vcp = vСкорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:
= / t
Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
= • t
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:
vx = v, то есть v > 0Проекция перемещения на ось ОХ равна:
s = vt = x – x0где x0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:
х = x0 + vtЕсли положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
х = x0 - vt
Зависимость скорости, координат и пути от времени
Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна
v = s1 / t1 = tg αгде α – угол наклона графика к оси времени. Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:
tg α = v
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что
tg α1 > tg α2следовательно, скорость тела 1 выше скорости тела 2 (v1 > v2).
tg α3 = v3 < 0Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть
х = х0
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.
av-physics.narod.ru

Leave A Comment