ЭДС. Закон Ома для полной цепи
Оглавление:
- Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
- Сторонняя сила
- Закон Ома для полной цепи
- КПД электрической цепи
- Закон Ома для неоднородного участка
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т. е. против направления тока).
е. против направления тока).
к оглавлению ▴
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
к оглавлению ▴
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).
Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и .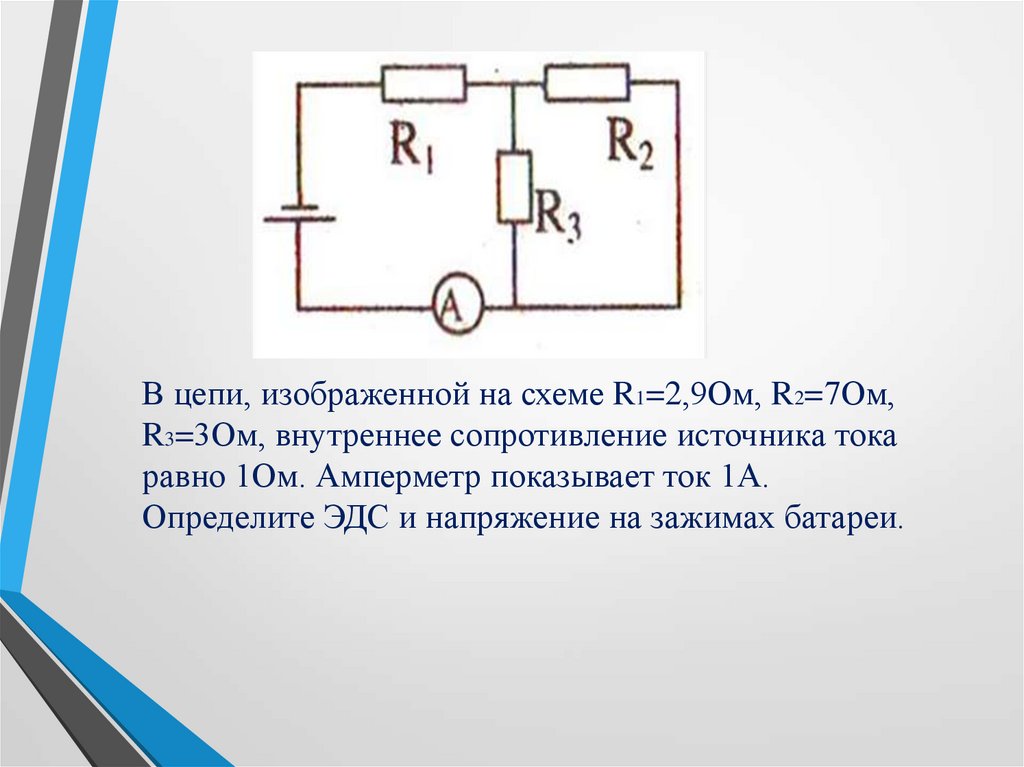 Данное количество теплоты определяется законом Джоуля–Ленца:
Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
к оглавлению ▴
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
к оглавлению ▴
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).
Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:
За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: .
Подставляем сюда выражения для , и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :
Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.
Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Повторим основные понятия и определения по теме «Закон Ома».
Напомним, что напряжение измеряется в вольтах.
Сила тока измеряется в амперах.
 Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.
Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.Основные определения, которые мы используем в решении задач:
Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.
Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.
Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.
Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.
По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).
Измеряется сила тока в амперах (А).
Сопротивление измеряют в омах (Ом).
Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).
Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:
- Сопротивление проводника тем больше, чем больше его длина.
- Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.
Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм2/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:
Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:
Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.
Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм
Решение:
Из закона Ома для проводника или участка цепи без источника следует:
По графику: при
Из формулы сопротивления выражаем и находим длину проводника:
Ответ: 10.
Задача 2. Через поперечное сечение проводников за 8 с прошло 1020 электронов. Какова сила тока в проводнике? Ответ дайте в амперах.
По определению силы тока:
Заряд всех электронов: где е — модуль заряда электрона, Кл.
Тогда
Ответ: 2.
Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)
Решение:
По закону Ома для полной цепи:
Тогда
Ответ: 0,07.
Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.
Решение:
Сила тока короткого замыкания определяется следующим образом:
Отсюда выражаем и находим внутреннее сопротивление источника:
При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:
Отсюда выражаем сопротивление резистора и находим его:
Ответ: 1,9.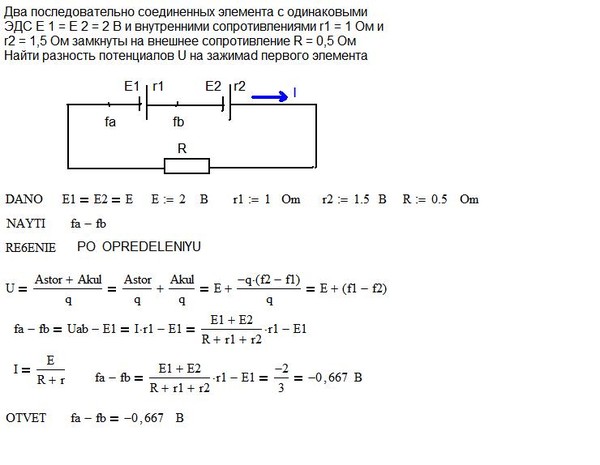
Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.
Решение:
Выражаем время в секундах: t = 10 минут = 600 с.
Определяем силу тока по закону Ома для полной цепи:
Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.
По определению силы тока:
Отсюда Кл.
Ответ: 1500.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 07.02.2023
Error
Skip to main content
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…ВведениеПрограмма обученияКинематикаДинамикаЗаконы сохраненияСтатикаГидростатикаОсновы мол_физикиОсновы термодинамикиВзаимные превращения газ, жидкость и твёрдое тело_телЭлектростатикаМагнитное поле Механические колебанияЭлектромагнитные колебанияГеометрическая оптикаВолновая оптикаКвантовая оптикаОсновы спец_теор_отнАтом и атомное ядро_ядроМетодические рекомендацииВарианты контрольных работ по физике для абитуриентов, выпускников школКонтрольные работы по физике для абитуриентов, выпускников техникумов. Краткая инструкция и константыВариант тестирования 1Вариант тестирования 2Вариант тестирования 3Вариант тестирования 4
Краткая инструкция и константыВариант тестирования 1Вариант тестирования 2Вариант тестирования 3Вариант тестирования 4
Drop the block here to make it dock
Skip NavigationHome
Site pages
Courses
Факультет довузовской подготовки (ФДП)
Довузовская подготовка
Предуниверсариум
Наследники Бетанкура
Профориентация 2021
Математика ФДП
Обществознание (ФДП)
Русский язык (ФДП)
Физика ФДП
Participants
General
Механика
Молекулярная физика и термодинамика
Электричество и магнетизм
Электростатика
Постоянный ток
Магнитное поле
Колебания и волны
Оптика
Атом и атомное ядро
Методические указания и контрольные работы по физи.
 ..
..Итоговое тестирование
Тренировочные тесты (абитуриенты)
Факультет «Автоматизация и интеллектуальные технол…
Факультет «Промышленное и гражданское строительство»
Факультет «Транспортное строительство»
Факультет «Транспортные и энергетические системы»
Факультет «Управление перевозками и логистика»
Факультет «Экономика и менеджмент»
Факультет безотрывных форм обучения
Центр компьютерного тестирования
Отдел аспирантуры
Институт непрерывного образования (ИНО)
Промышленный и городской транспорт (НОЦ ПГТ)
Студенческое научное общество
Центр русского языка
Вопросы и ответы
Великолукский филиал ПГУПС
Ярославский филиал ПГУПС
Научно-образовательный центр инновационного развит.
 ..
..Центр целевой контрактной подготовки
Ученый совет Университета
Открытый онлайн-курс «История транспорта»
Тестирование иностранных абитуриентов (Testing for…
27.
 02.03 Диагностическая работа
02.03 Диагностическая работа
Внутреннее сопротивление, ЭДС и электрический ток – Решенные практические задачи – Все различия
Внутреннее сопротивление – это сопротивление протеканию тока элементами и батареями. Это приводит к выработке тепла. Ом — это единица измерения внутреннего сопротивления.
Существуют различные формулы для определения внутреннего сопротивления. Мы можем найти ответы на любой вопрос, если мы обеспечены данными. Например, чтобы найти внутреннее сопротивление, мы используем эту формулу:
e = I (r + R)
В этой формуле e — ЭДС или электродвижущая сила, измеряемая в омах, I — ток, измеряемый в амперах (А), а R — сопротивление нагрузки, а r внутреннее сопротивление. Ом — это единица измерения внутреннего сопротивления.
Предыдущая формула преобразована в следующую форму:
- e = Ir+ IR
- e = V + Ir
В обозначается как разность потенциалов, приложенная к ячейке, а I представляет ток, протекающий через клетка.
Примечание: Электродвижущая сила (ЭДС) всегда больше разности потенциалов (В) ячейки.
Таким образом, зная одни параметры, мы можем найти другие. В этой статье я буду решать многие практические задачи, которые помогут вам узнать, как использовать физику в нашей повседневной жизни, а также способы расчета параметров вместе с формулами и описаниями. Просто будь со мной до конца.
При разомкнутой цепи разность потенциалов между клеммами аккумулятора составляет 2,2 вольта. Разность потенциалов уменьшается до 1,8 вольт при подключении через сопротивление 5 Ом. Что такое внутреннее сопротивление?
Это обрыв цепи. Внутреннее сопротивление батареи не имеет падения напряжения на ней при разомкнутой цепи. Когда образуется замкнутая цепь, ток протекает через внутреннее сопротивление, вызывая падение напряжения и понижая напряжение на батарее.
В этом случае необходимо определить внутреннее сопротивление. Вы измеряете напряжение в цепи, когда она открывается и закрывается, а также сопротивление нагрузки. Чтобы решить эту проблему, сначала нам нужно собрать данные, указанные в отчете, а затем предсказать, что нужно рассчитать.
Вы измеряете напряжение в цепи, когда она открывается и закрывается, а также сопротивление нагрузки. Чтобы решить эту проблему, сначала нам нужно собрать данные, указанные в отчете, а затем предсказать, что нужно рассчитать.
Данные: Разность потенциалов V = 2,2 В, сопротивление нагрузки Сопротивление = 5 Ом, падение разности потенциалов 1,8 В,
Найдите внутреннее сопротивление.
Чтобы найти это, нам нужно решить следующие шаги.
Сначала, , нам нужно найти ток нагрузки как ,
I = V/R, поэтому 1,8/5 = 0,36 А
Затем, Найти падение напряжения на внутреннем сопротивлении батареи: V=0,4 В
Итак, зная ток и напряжение внутреннего сопротивления:
R=V/I, 0,4/0,36 дает 1,1 Ом
Следовательно, внутреннее сопротивление равно 1,1 Ом.
В разомкнутой цепи разность потенциалов между выводами элемента составляет 2,2 вольта.
 Разность потенциалов на клеммах составляет 1,8 вольта при сопротивлении 5 Ом на клеммах ячейки. Чему будет равно внутреннее сопротивление элемента?
Разность потенциалов на клеммах составляет 1,8 вольта при сопротивлении 5 Ом на клеммах ячейки. Чему будет равно внутреннее сопротивление элемента?Это простой вопрос о двух резисторах, соединенных последовательно через источник 2,2 В, один из которых имеет сопротивление 5 Ом. Итак, вопрос в том, каково другое сопротивление в последовательной комбинации, внутреннее сопротивление батареи?
Это невероятно просто. Сначала нарисуйте ячейку на 2,2 В, затем R (внутренний резистор), внешний резистор на 5 Ом и, наконец, вернитесь к источнику.
На 5 Ом падение 1,8 В.
Что такое внутренний резистор, если ток, протекающий через него, I = 1,8/5 ампер = 0,36 А?
Давайте посмотрим на это,
R = E / I, таким образом (2,2 – 1,8)В / 0,36 А
= 0,4 / 0,36 и это равно 1,111 Ом
Здесь внутреннее сопротивление 1,11 Ом.
Существуют альтернативные способы решения этого вопроса, такие как:
Когда ячейка подключена к 5 Ом , ток, протекающий по цепи, равен I = 2,2/(5+r) А. Где r равно внутреннее сопротивление клетки. Падение напряжения на сопротивлении 5 Ом равно
Где r равно внутреннее сопротивление клетки. Падение напряжения на сопротивлении 5 Ом равно
5×2,2/(5+r)=2,2–1,8 и
11=2+0,4r,
, поэтому r=9/0,4 Ом.
Замкнутая цепь обеспечивает ток и проводимостьТретий и самый точный способ решения:
- Падение напряжения на внутреннем сопротивлении равно 2,2 – 1,8 = 0,4 В.
Когда два сопротивления соединены последовательно, через них будет течь одинаковый ток.
IR=0,40,36=1,11 Ом
Думаю, теперь вы знаете, как рассчитать внутреннее сопротивление аккумуляторов.
Рассмотрим две лампочки, одна на 50 Вт, а другая на 75 Вт, обе рассчитаны на 120 В. Какая лампочка обладает наибольшей устойчивостью? Какая лампочка имеет наибольший ток?
Ток должен быть больше, чтобы работать с большей мощностью при том же напряжении. Поскольку ток обратно пропорционален сопротивлению, лампочка с большей мощностью имеет меньшее сопротивление.

Глядя на уравнение, связывающее силу тока и сопротивление, можно прийти к такому же выводу:
P=U2/R
При измерении сопротивления лампы накаливания нужно быть осторожным: оно значительно изменится, когда нить холодная по сравнению с горячей. Когда лампа накаливания холодная, она почти полностью замыкается по сравнению с горячей.
Чем ниже сопротивление, тем выше потребляемая мощность (при одинаковом напряжении). Из-за более низкого сопротивления может протекать больший ток при том же электрическом напряжении (напряжении)
Используя формулу Мощность = V2 / R
288 Ом.
I=P/V = 50/120 = 0,417 Ампер потребляется 50-ваттной лампочкой.
Для лампы мощностью 75 Вт R=V2/P = 1202 / 75 = 192 Ом.
I=P/V = 75/120 = 0,625 Ампер потребляется 75-ваттной лампочкой.
Сопротивление 50-ваттной лампы самое высокое.
Наибольший ток несет 75-ваттная лампа.
Уравнение Эйнштейна — главное нововведение в физике12-вольтовая батарея была подключена к нагрузке 10 Ом.
 Потребляемый ток был 1,18 ампер. Каково было внутреннее сопротивление батареи?
Потребляемый ток был 1,18 ампер. Каково было внутреннее сопротивление батареи?Для начала вы должны принять, что напряжение или ЭДС батареи составляет ровно 12В. Теперь вы можете найти внутреннее сопротивление, используя закон Ома.
Rобщ. = 12 В / 1,18 А = 10,17 Ом Rобщ. = В/I = 12 В / 1,18 А = 10,17 Ом
Всего – Rнагрузка = 10,17 Ом – 10 Ом = 0,017 Ом
Мощность, рассеиваемая нагрузкой с известным сопротивлением, подключенной к известной разности потенциалов, может быть рассчитана по формуле… В течение одной минуты батарея 10 В обеспечивает резистивную нагрузку 10 Ом . Что именно? Аккумулятор на 24 вольта имеет внутреннее сопротивление 1 Ом в показанной цепи, а амперметр показывает силу тока 12 А.
Или можно сделать так
Ответ на этот вопрос можно найти непосредственно в омах Закон.
По закону Ома можно рассчитать напряжение, сопротивление и ток в последовательно соединенной цепи.
V=I⋅R
где V обозначает напряжение, I обозначает ток, а R обозначает сопротивление найти по пути.
 В этом случае у нас есть внешнее сопротивление (обозначенное R) и внутреннее сопротивление батареи (обозначенное r).
В этом случае у нас есть внешнее сопротивление (обозначенное R) и внутреннее сопротивление батареи (обозначенное r).Поскольку теперь мы знаем напряжение (12 В), ток (1,18 А) и внешнее сопротивление (10), мы можем решить следующее уравнение:
I⋅(R+r)=В
R+r= VI
r=VI−R
Подставим наши переменные действительными числами:
r=121,18−10≈0,1695 Ом
Посмотрите видео о Основах электричества и его элементахРазность потенциалов батареи равна 2 контактам. вольт при подключении к внешнему сопротивлению 20 Ом и 13,5 вольт при подключении к внешнему сопротивлению 45 Ом. Каковы ЭДС и внутреннее сопротивление батареи?
Пусть E — ЭДС батареи, а R — внутреннее сопротивление батареи, тогда для 20 Ом ток равен 12/20 = 0,6 А, а для 45 Ом ток равен 13,5/45 = 0,3 А, поэтому первое условие 0,6R+12=E и второе условие 0,3R+13,5=E, поэтому решение R= 5 Ом и E= 15 В.

E=15 В
r=5 Ом
Вот как это можно сделать:
Определите ток для каждой цепи,
I1=0,6[A] и I2=0,3[A]
Напишите уравнение для каждой цепи, используя уравнение U=E-I*r. Будет два уравнения и две переменные.
Вычислить E.
Вся физика связана с электрическими цепямиЧтобы найти r, подставьте найденное значение E обратно в любое уравнение.
При силе тока 1,5 А PD батареи составляет 10 В, а при токе 2,5 А PD составляет 8 В. Каково внутреннее сопротивление батареи?
Согласно постановке задачи
Vbat – Ix Ri = Pd
и предполагается, что
10 = Vbat – 1,5*Ri (уравнение 1)
и
8 = Vbat – 2,5*Ri 2)
У нас есть два линейных алгебраических уравнения первого порядка с двумя неизвестными, которые мы можем довольно легко решить подстановкой. Уравнение 1 преобразуется, чтобы дать
Vbat = 10, умноженное на 1,5 * Ri
, и подстановка его в уравнение 2 дает
8 = (10 + 1,5 Ri) минус 2,5 Ri
. Следовательно, –2,5) = 10
Следовательно, –2,5) = 10Итак, чтобы определить Ri,
-2 равняется -Ri
, в результате чего Ri = 2 Ом
Посмотрите видео о том, как узнать внутреннее сопротивление и ЭДС элементаВ чем разница между ваттами и вольтами?
Вольт — единица потенциальной энергии . Он указывает, сколько энергии может дать единица силы тока , а ампер — это единица измерения силы тока. Он говорит нам о количестве электронов, протекающих в секунду.
Ватт — это единица мощности, которая показывает, сколько энергии используется в единицу времени. Один ватт — это мощность, обеспечиваемая источником питания в один вольт при протекании тока в один ампер: 1 В 1 А равен 1 Вт
Чтобы рассчитать количество потребляемой энергии, умножьте количество ватт на время.
 Киловатт-час (кВтч) — это стандартная единица энергии, которая в 1000 раз превышает количество энергии, потребляемой при использовании одного ватта мощности в течение одного часа.
Киловатт-час (кВтч) — это стандартная единица энергии, которая в 1000 раз превышает количество энергии, потребляемой при использовании одного ватта мощности в течение одного часа.Думаю, вы хорошо знакомы с ваттами и вольтами и их различиями.
Вот таблица, показывающая стандартные электрические единицы измерения вместе с их символами
Стандартные международные единицы измерения электрического токаЭлектрические параметры SI unit of measurement Symbol Description Voltage Volt V or E Unit to measure Electrical Potential
V=I x RТок Ампер I или i Единицы измерения электрического тока
I = V/RСопротивление 4 OHMS R, ω Блок сопротивления DC
R = V/IWEOL WATTS W WATTS W WATTS W Ватт W ВАТТС W ВАТТ WELY . 
Conductance Siemen G or ℧ The inverse of resistance
G= 1/RCharge Coulomb Q Unit to measure electrical Charge
Q=C x VЗаключительные мысли
Внутреннее сопротивление — это сопротивление потоку тока, который проходит через элементы и батареи. Это сопротивление также приводит к выделению тепла. Различные параметры электрического тока помогают нам найти другие неизвестные параметры.
Различные практические задачи помогают нам лучше понять эти параметры. Ранее были решены различные проблемы, которые помогли нам найти электродвижущие силы (ЭДС), внутреннее сопротивление и ток.
Физика — это не просто понимание; это наука о физических параметрах нашей повседневной жизни.
 Он включает в себя ток, проводимость и различные законы физики.
Он включает в себя ток, проводимость и различные законы физики.Все, что вам нужно знать, это практиковать эти задачи и запоминать формулы, чтобы справиться с экзаменами и любыми числовыми задачами, с которыми вы сталкиваетесь в жизни.
Другие статьи
- Различия между мангой и ранобэ
- Копье и копье – в чем разница
- Индийцы против пакистанцев (основное отличие)
Решения для домашнего задания 5
Решения для домашнего задания 5Глава 19
Р52) На рис. 19-17а полное сопротивление равно 15 Ом, а ЭДС батареи составляет 24,0 В. Если измеренная постоянная времени равна 35 мкс, рассчитайте а) полную емкость цепи и б) время, за которое чтобы напряжение на резисторе достигло 16,0 В.
РЕШЕНИЕ:
(a) Поскольку мы знаем постоянную времени тау = RC =35 мкс
C = 35 x 10 -6 / 15000 Ом = 2,33 x 10 -9 F
(б)ток = I o e -t / RC , I o = 24 В / 15000 Ом = 1,6 мА
Напряжение на резисторе V = I o (15 кОм)e -t / RC = (24 В) e -t / 35 мкс
V = 16, если 16 = 24 e -t / 35 мкс
e -t / 35 мкс 9045,7 t / 35 мкс = ln(1,5), t = (35 мкс) ln(1,5) = 14,2 мксP57) Гальванометр имеет внутреннее сопротивление 30 Ом и отклоняет полная шкала для тока 50 мкА.
РЕШЕНИЕ: Опишите, как использовать это
гальванометр для изготовления (а) амперметра для измерения силы тока до 30 А и (б)
вольтметр для получения полного отклонения 1000 В.
Опишите, как использовать это
гальванометр для изготовления (а) амперметра для измерения силы тока до 30 А и (б)
вольтметр для получения полного отклонения 1000 В.
(a) Нам нужен шунтирующий резистор, чтобы амперметр имел максимальное отклонение при токе через шунт I = 50 мкА. Остальная часть тока идет по параллельному пути с резистором R.
итак, (30 А) (R) = (50 x 10 -6 ) (г) где г = 30 Ом.
R = (50/30) x 10 -6 x 30 Ом = 50 x 10 -6 Ом.
(b) Нам нужно последовательное сопротивление, чтобы общее напряжение на обоих резисторах R + r равно 1000 В
итак, 50 x 10 -6 (R + r) = 1000 Ом.
R + r = 20 мкОм, а поскольку rP69) Трехходовая лампочка может производить 50 Вт, 100 Вт или 150 Вт при напряжении 120 В. Такая лампочка содержит две нити накала, которые можно подключить к сети 120 В. по отдельности или параллельно. Опишите, как связаны эти два нити сделаны, чтобы дать каждую из трех ватт.
 Что должно быть
сопротивление каждой нити?
Что должно быть
сопротивление каждой нити?РЕШЕНИЕ:
P 1 = (120 В) 2 / R 1 = 50 Вт, значит, R 1 = 288 Ом.
P 2 = (120 В) 2 / R 2 = 100 Вт, т.е. R 2 = 144 Ом
P 3 = (120 В) 2 / (1/R 1 + 1/R 2 ) = 150 Вт, т.е.
.Глава 20
Q3) В каком направлении проходят силовые линии магнитного поля, окружающие прямую провод с током, который движется прямо на вас?
РЕШЕНИЕ:
P2) Провод длиной 1,5 м, по которому течет ток 6,5 А, ориентирован горизонтально. В этой точке земной поверхности угол наклона магнитное поле Земли составляет угол 40 o к проволока. Оцените магнитную силу, действующую на провод под действием Земли. магнитное поле 5,5 х 10 -5 Тл в этой точке.
РЕШЕНИЕ:
| Ф | = (I) (L) (| B |) sin(40 o ) = (6. 5)
(1,5) (5,5 х 10 -5 ) (0,643) N
5)
(1,5) (5,5 х 10 -5 ) (0,643) N
| Ф | = 3,45 x 10 -4 Н, сила в бумага.P9)Альфа-частицы с зарядом q = +2 e и массой m = 6,6 x 10 -27 кг выбрасывается из радиоактивного источника со скоростью 1,6 х 10 -7 м/с. Какой будет напряженность магнитного поля требуется, чтобы согнуть их в круговую траекторию радиуса r = 0,25 м?
РЕШЕНИЕ:
Сила = m a цент = m v 2 / r = q v B
B = (м v) / (q v) = (6,6 x 10 -27 кг)(1,6 х 10 7 м/с) / [(3,2 x 10 -19 C) (0,25 м)]
B = 1,32 TP31) Три длинных параллельных провода на расстоянии 38,0 см друг от друга. (Смотрящий вдоль них они находятся в трех углах равнобедренного треугольника.) ток в каждом проводе 8,00 А, а в проводе А противоположен что в проводах В и С (рис. 20-54). Определите магнитная сила на единицу длины на каждый провод из-за двух других.

РЕШЕНИЕ:
(a) | F до | на A из-за B и C :
| F 2 | / л = | F 3 | / л = [µ o I 1 I 2 ] / [2 (pi) r] = сила / длина
| F 2 | / L = (2 х 10 -7 )(8)(8) / (0,38) Н/м = 3,37 x 10 -5 Н/м
F to на A указывает вверх, так как боковые компоненты отменяются.
| Ф до | = 2 | F 2 | cos(30 o = 5,84 x 10 -5 N
(b) | F tot | на B из-за A и C :
По симметрии, | F до | 60 или ниже линии, соединяющей B и C
| F to | / L = (| F tot | y / L) sin(60 o ) / L
| F to | / Д = 3,4 х 10 -5 Н/м
(c)аналогично сила на C равна 60 o ниже линии, идущей от C и B ,
| F до | / L = 3,4 x 10 -5 Н/мP36)Соленоид длиной 30,0 см и диаметром 1,25 см должен создавать поле 0,385 Тл в его центре.


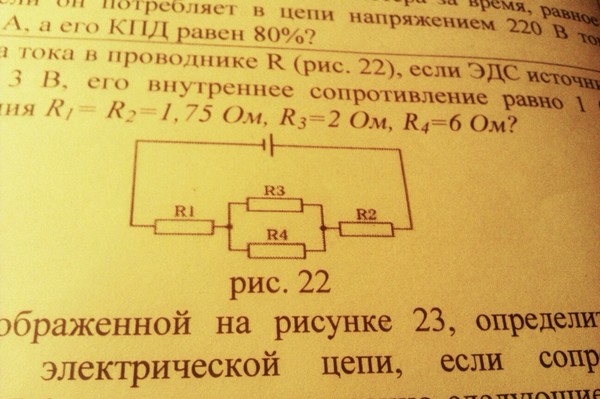 ..
.. ..
.. 02.03 Диагностическая работа
02.03 Диагностическая работа
 Потребляемый ток был 1,18 ампер. Каково было внутреннее сопротивление батареи?
Потребляемый ток был 1,18 ампер. Каково было внутреннее сопротивление батареи? В этом случае у нас есть внешнее сопротивление (обозначенное R) и внутреннее сопротивление батареи (обозначенное r).
В этом случае у нас есть внешнее сопротивление (обозначенное R) и внутреннее сопротивление батареи (обозначенное r).
 Следовательно, –2,5) = 10
Следовательно, –2,5) = 10 Киловатт-час (кВтч) — это стандартная единица энергии, которая в 1000 раз превышает количество энергии, потребляемой при использовании одного ватта мощности в течение одного часа.
Киловатт-час (кВтч) — это стандартная единица энергии, которая в 1000 раз превышает количество энергии, потребляемой при использовании одного ватта мощности в течение одного часа.
 Он включает в себя ток, проводимость и различные законы физики.
Он включает в себя ток, проводимость и различные законы физики. Опишите, как использовать это
гальванометр для изготовления (а) амперметра для измерения силы тока до 30 А и (б)
вольтметр для получения полного отклонения 1000 В.
Опишите, как использовать это
гальванометр для изготовления (а) амперметра для измерения силы тока до 30 А и (б)
вольтметр для получения полного отклонения 1000 В. Что должно быть
сопротивление каждой нити?
Что должно быть
сопротивление каждой нити? 5)
(1,5) (5,5 х 10 -5 ) (0,643) N
5)
(1,5) (5,5 х 10 -5 ) (0,643) N 

Leave A Comment