МБОУ Красненская СОШ — в10

Задание В10 Простейшие вероятностные задачи.

Задача1

На книжной полке Максима 25 книг: 12 детективов, 4 учебника по математике и 9 книг в жанре

«фэнтези», найдите вероятность того, что наудачу взятая с этой полки книга окажется учебником по математике.

РЕШЕНИЕ:

Вероятность того,  что наудачу взятвя с полки книга окажется учебником математике, равна 4:25= 0,16

Ответ: 0,16.

Задача 2

Юра дважды бросал кубик. Найдите вероятность того, что при втором броске у него выпало столько же очков, сколько и припервом.

Ответ округлите до сотых.

РЕШЕНИЕ: Так как броски кубика независимые события то вероятность того, что оба раза выпадет одинаковое количество очков равна 1/6= 0,17(если округлить до сотых)

Ответ: 0,17

Задача 3

Пете и Юре нужно написать реферат на одну и ту же тему. Ученики нашли в Интернете один и тот же набор из 10 рефератов на заланную тему, и каждый скачал наугад

выбранный реферат из этого набора. Какова вероятност того, что представленные рефераты оказались различными?

РЕШЕНИЕ:

Пусть Петя скачал наугад выбранный из 10 реферат. Вероятность скачивания Юрой того же рефератаравна 1/10 или 0,1.

Вероятность несовпадения рефератов равна 1 — 0,1 = 0,9.

Ответ: 0,9

 

Задача 4

Алексей подкидывает монету до тех пор, пока не выпадает решка. Какова вероятность того, что он сделает  ровно4 подбрасывания?

РЕШЕНИЕ:

4 подбрасывания означает, что при каждом из первых трёх подбрасываний выпадал орел, а в четвертом — решка. Вероятность появления заданного из двух

равновозможных исходов в одном испытании равна 1/2; по формуле произведения событий вычислим вероятность появления  заданного исхода

в каждом из 4-х подбрасываний: 1/2•1/2•1/2•1/ =1/16= 0,0625.

Ответ: 0,0625

 

Задача 5  

В мешке лежит пять неразличимых на  ощупь карточек с буквами А,Т,А,К,А. Какова вероятность того , что , наудачу извлекая по очереди карточки

и выкладывая их на столе  можно получить слово «АТАКА»?

РЕШЕНИЕ:

Буква  Т  в слове АТАКА стоит на втором месте, буква К стоит на четвертом. Буква Т с равной возможностью может занять любое из пяти мест,

вероятность её появления на втором месте равна 1/5. Вероятно появления буквы  К на нужном месте из оставшихся четырех равна 1/4. Искомая вероятность равна

1/5•1/4=1/20=0,05.

Ответ: 0,05.

 

Задача 6

Какова вероятность того, что наудачу взятое целое число из диапазона 0 — 999 больше 449?

РЕШЕНИЕ:

В указанном диапазоне 1000 целых чисел из них 999 — 449 = 550, 550 чисел больше 449. Наудачу взятое из указанного диапазона число будет

больше 449 с вероятностью  550/1000= 0.55.

Ответ: 0,55.

 

Задача 7

Карточки с цифрами от 1до  4 наудачу извлекают из мешка и кладут по порядку. Какова вероятность того, что карточку с цифрой 3 извлекут последней?

РЕШЕНИЕ:

Последне с равной вероятностью может оказаться любая их карточек, поэтому вероятность того, что последней будет карточка с цифрой 3

равна 1/4=0,25

Ответ: 0,25.

Задача 8

В книге 400 страниц , из них на 36 есть картинки. Школьник открывает книгу на наудачу выбранной странице. Какова вероятность того, что на

открытой странице не будет картинок?

РЕШЕНИЕ:

Картинок нет на 400 — 36 = 364 . Вероятность открыть книгу на одной из этих страниц равна 364/400=0,91.

ОТВЕТ: 0,91

 

Задача9

Готовяськ экзамену по ОБЖ , Влад выучил 16 билетов из 40. На экзамене он вытянул 1  билет наудачу. Какова вероятно того, что

это будет выученный билет?

РЕШЕНИЕ:

Вероятность вытянуть выученный билет равна 16/40=0,4

Ответ: 0,4

 

Задача 10.

В партии 1050 деталей, из них 630 типа А, а остальные —  типа Б .Какова вероятность того, что наудачу взятая детель — типа Б?

РЕШЕНИЕ:

В партии 1050 — 630 = 420 детелей типа  Б  . Искомая вероятность равна 420 : 1050 =0,4.

Ответ: 0,4.

 

Задача 11

В классе 20 учеников, из них 4 — Светы и 5- Дим. Директор вызвал наугад одного из учеников. Какова вероятность того,что вызванного

ученика зовут Света или Дима?

РЕШЕНИЕ:

Вероятность того, что директор вызовет  Свету или Диму (4+5) : 20 =0,45

Ответ: 0,45 

 

Задача12

В случае эксперимента симметричную монету бросают четырежды. Найдите вероятность тог , что орел выпадет ровно 1 раз?

РЕШЕНИЕ:

Выпадение орла или решки равновероятно т.е. по 50%. Найдем общее число исходов 2•2•2•2=16. 4 благоприятствуют событию

«орел выпал 1 раз». Искомая вероятность равна 4:16=0,25.

Ответ:0,25

 

Задача 13

В случае эксперимента бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 12 очков. Ответ округлите до сотых.

РЕШЕНИЕ:

Найдем общее количество исходов: 6•6•6=216

Найдем число благоприятных исходов: событию » в сумме выпало 12 очков» удовлетворяют исходы6

(1;5;6), (1;6;5) (2;4;6) (2;5;5) (2;6;4) (3;3;6) (3;4;5) (3;5;4)

(3;6;3)  (4;2;6) (4;3;5) (4;4;4) (4;5;3) (4;6;2) (5;1;6) (5;2;5)

(5;3;4)  (5;4;3) (5;5;2) (5;6;1) (6;1;5) (6;2;4) (6;3;3) (6;4;2) (6;5;1) всего таких исходов 25. Искомая вероятность равна 25:216=0,12…

Ответ: 0,12

 

Задача14

 На чемпионате мира п о фигурному катанию участвуют 75 спортсменов, среди них 12 — из России, 8 — из Китая. Порядок выступления

определяется жребием. Найдите вероятность того, что 13-м будет выступать спортсмен из России.

РЕШЕНИЕ:

13-ым может выступать оиз спортсменов. Вероятность выступления 13-м спортсмена из России равна 12:75=0,16.

Ответ:0,16

 

Задача 15

Ракета поражает цель с вероятностью 0,9. Какова вероятность того, что  цель не окажется пораженной после 4 запусков ракеты?

РЕШЕНИЕ:

Вероятность промаха при одном запуске равна 1- 0,9= 0,1.

 По формуле произведения событий вероятность промаха во всех четырех запусках равна 0,1•0,1•0,1•0,1=0,0001.

Ответ: 0,0001.

Задача16

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадает не менее 11 очков.

 Ответ округлите до сотых.

РЕШЕНИЕ:

Всего равновозможных исходов 6•6= 36.

Событию «в сумме выпало не менее 11 очков» благоприятствуют три исхода: (5;6),(6;5),(6,6).

Вероятность этого события равна 3:36= 0,08

Ответ:0,08

 

Задача 17

Из 75 парашютов 6 неисправных. Какова вероятность того, что наудачу взятый парашют исправен?

РЕШЕНИЕ:

Исправных парашютов 75 — 6 = 69.

Вероятность того, что наугад взятый парашют будет исправен 69 : 75 =0,92.

Ответ: 0,92

 

Задача 18

Мастер из 15 деталей сделал 8 бракованных. Комиссия взяла на проверку 2 наудачу выбранные детали.

Какова вероятностьо того, что хотя бы одна деталь окажется бракованной?

РЕШЕНИЕ:

Найдем сколько не бракованных деталей: 15-8 =7, Вероятность отсутствия брака в первой детали равна 7:15=7/15 т.е. семь пятнадцатых.

Если первая деталь исправна, то вторая деталь выбирается из 14-ти, среди которых 6 без брака.

Вероятность отсуствия брака во второй детали( при отсутствия брака в первой) равна 6:14=6/14 т. е. шесть четырнадцатых.

Вероятность исправности обеих деталей равна 7/15 •6/14 = 0,2( семь пятнадцатых умножить на шесть четырнадцатых).

Найдем вероятноть того, что хотя бы одна деталь окажется бракованной: 1 — 0,2 = 0,8.

Ответ: 0,8

Задача 19

У Григория в понедельник 6 уроков: 3  по математике и 3 по русскому языку.Он наудачу пропустил 2 из них ( необязательно подряд).

Какова вероятность того, что оба пропущенных   урока по математике?

РЕШЕНИЕ:

Вероятность того, что 1-ый пропущенный урок- математика 3: 6= 0,5.

Если 1-ый пропущенный урок математика, то остаётся 5 уроков и среди них 2 урока математики.

Вероятность пропуска 2-го урока математики равна 2 : 5=0,4.

Вероятность того, что оба пропущенных урока — по математике , равна 0,5 • 0,4 =0,2.

 

Ответ: 0,2

Задача  20

В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием.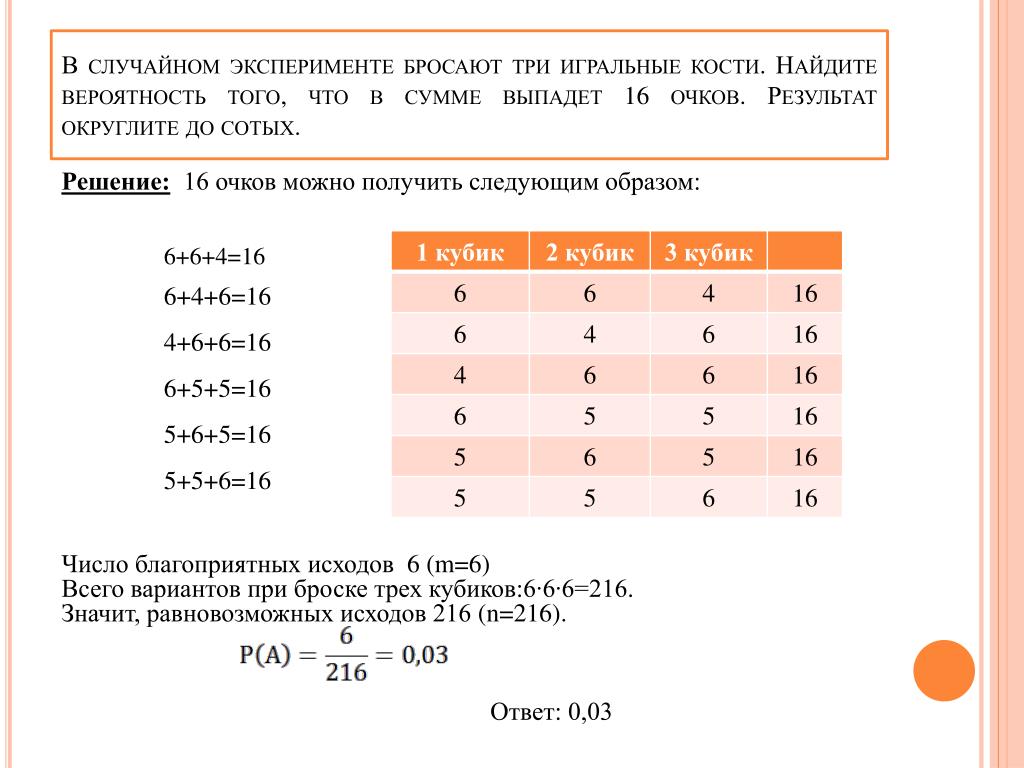

 Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.

РЕШЕНИЕ:

Определим сколько спортсменок из Китая: 20 -(8+7) =5 .

Всего исходов 20 (т.к. всего спортсменок 20). Благоприятных исходов для Китаянок — 5

Вероятность того, что спортсменкой , выступающей первой окажется из Китая равна: 5 : 20 =0,25.

Ответ:0,25

Задача 21

Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами.

Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

РЕШЕНИЕ:

На 100 сумок приходится 8 сумок с дефектами.

Если покупатель купит 108 сумок, то 100 сумок окажутся качественными, а 8 с дефектами.

Всего исходов 108

Благопритяных 100.Найдем вероятность того ,что купленная сумка окажется качественной  100:108 = 0,93

Ответ:0,93

Задача 22

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков.

Результат округлите до сотых.

РЕШЕНИЕ:

Всего исходов 6•6 = 36

Найдем  количество вариантов ( благоприятных исходов) когда в сумме выпадет 8 очков : (2 и 6), (3 и 5), (4 и4), (6и 2 ) , (5 и 3) всего 5 вариантов

Следовательно вероятность того, что в сумме выпадет 8 очков равна 5 : 36 =0,138… Округлим число 0.138.. до сотых и получим 0,14.

Ответ: 0,14

Задача 23

В случайном эксперименте симметричную монету бросают дважды.

Найдите вероятность того, что орел выпадет ровно один раз.

РЕШЕНИЕ:

Выпадение «орла» или «решки» равновероятно т.е. 50%.

Найдем общее число исходов (0 ,Р ),(О , О) (Р, О), (Р , Р) или ( 2•2=4)

Благоприятных исходов ( из общего числа исходов ), когда выпадает «орел» ровно один раз это (О,Р), (Р,О) — 2 благоприятных исхода.

Вероятность того, что «орел» выпадет ровно один раз 2:4=0,5

Ответ: 0,5.

Задача 24

В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии.  

Порядок, в котором выступают спортсмены, определяется жребием.

 Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.

РЕШЕНИЕ:

Найдем общее число спортсменов 4+ 7+9+5 =25

Определяется жребием — означает, что каждый  из выступающих спортсменов имеет шанс быть последним.

Общее число количества исходов равно 25. Благоприятных исходов для спортсменов из Швеции равно 9.

 Найдем вероятность того, что спортсмен, выступающий последним окажется из Швеции  9 : 25 = 0,36.

Ответ: 0,36.

Задача25

В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков.

 Результат округлите до сотых.

РЕШЕНИЕ:

Найдем общее число исходов: 6•6•6=216 (т.к.3 игральные кости)

Комбинаций, когда в сумме выпадает 6 очков: (1;2;3), (2;2;2), (1,1,4).

Найдем число благоприятных исходов:Составим комбинации когда выпадает 6 очков :(1;2;3) ,(2;1;3),(3;1;2),(3;2;1),(2;3;1), (1;3;2) — 6 исходов,

6 очков выпадает при комбинации (2;2;2) — 1 исход.   6 очков может выпасть при комбинации(1;1;4),(1;4;1),(4;1;1)- 3 исхода.

Таким образом благоприятных исходов:  6+1+3 = 10.

Найдем вероятность того, что в сумме выпадет 6 очков: 10:216 =0,046… .Округлим число 0,046 до сотых, получим 0,05.

Ответ: 0,05

Задача 26

В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет все три раза.

РЕШЕНИЕ:

При подбрасывании может выпасть «орел» или «решка», всего исходов 2 из них благоприятных 1.Вероятность, что выпадет «орел» равна 1/2 или 0,5.

Это независимые события, поэтому вероятность того, что орел выпадет все три раза найдем  по правилу произведения 0,5•0,5•0,5= 0,125.

Ответ: 0,125.

 Задача 27

В лотерее 100 билетов, из которых 10 выигрышных. Участник покупает три билета. Определить вероятность того, что хотя бы один билет будет выигрышным.

Решение:

Вероятность того,  что хотя бы один билет будет выигрышным найдем как  разность 1 — P, где Р -вероятность того, что ни один билет не будет выигрышным.

Найдем вероятность того,что  не будет выигрышным  1-ый билет 90:100=0,09.

Если взяли 1 билет, то останется 100-1= 99 билетов , невыигрышных будет 99 — 10 =89, вероятность того, что 2-ой билет невыигрышный 89:99=89/99.

Вероятность того, что 3-ий билет будет невыигрышным 88 :98 = 88/98.

Вероятность того, что все три билета не будут выигрышными  90/100•89/99•88/98 = 0,73(приблизительно).

Найдем вероятность того, что хотя бы один билет окажется выигрышным 1 — 0,73 =0,27

Ответ: 0,27.

Задача 28

В урне 8 шаров: 3 белых и 5 чёрных. Какова вероятность, что вынутые наугад два шара окажутся а) белые; б) чёрные; в) одного цвета

Решение:

а)Вероятность того, что 1-ый шар белый равна 3: 8=3/8 ( три восьмых)

Вероятность того, что 2-ой шар белый равна 2:7 =2/7 ( две седьмых) ( после того как один вынули из 8 шаров останется 7, из 3 белых шаров останется 2)

Вероятрость того,что оба шара белые: 3/8 •2/7=0,11(приблизительно)

б) Вероятность того, что 1-ый шар окажется черным равна 5:8=5/8

Вероятность того, что второй шар окажется черным 4:7=4/7

Таким образом вероятность того, что оба шара окажутся черными 5/8•4/7 =0,36( приблизительно).

в)Одного цвета. Либо 2 белых, либо 2 черных 0,11+0,36= 0,47.
Ответ: 0,11; 0,36; 0,47.

Задача 29

Из трёх орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,9, для второго и третьего орудий эти вероятности равны соответственно 0,5 и 0,8. Найти вероятность того, что а) только один снаряд попадёт в цель; б) все три снаряда попадут в цель.

РЕШЕНИЕ:

а)Вероятность того, что только один снаряд попадет в цель равна Р=Р¹+Р² +Р³, где Р¹,Р², Р³ — вероятности попадания 1-го , 2-го,3-его орудия.

Найдем вероятность того, что 1-ый попадетР¹= 0,9•(1-0,5)•(1-0,8)=0,09, где (1-0,5)-вероятность что не попадет 2-ое орудие, (1-0,8) — 3-ье орудие не попадет.

Аналогично для 2-го орудия:Р²=(1-0,9)•0,5•(1-0,8)=0,1•0,5•0,2=0,01.

 Р³=(1-0,9)•(1-0,5)•0,8=0,04. Найдем вероятность, что попадет только один снаряд 0,09+0,01+0,04=0,14.

б)Найдем вероятность того, что все три снаряда попадут в цель Р¹•р²•Р3 = 0,9•0,5•0,8 =0,38.

Ответ:а) 0,14;б) 0,38

Задача30

Студент знает 30 из 40 вопросов программы. Найти вероятность того, что студент знает два вопроса, содержащиеся в его экзаменационном билете( в билете 3 вопроса).

РЕШЕНИЕ:

Найдем вероятность того, что студент знает 1-ый, 2-ой вопрос, но не знает 3-ий:30/40•29/39•10/38=0,15

Найдем вероятность того, что студент знает1-ый , 3-ий вопрос,но не знает 2-ой: 30/40•10/39•29/38= 0,15

Найдем вероятность того,что знает2-ой,  3-ий, но не знает 1-ый вопрос:10/40•30/39•29/38=0,15

Таким образом вроятность  того что знает два вопроса из трех равна ),15+0,15+0,15= 0,45.

Ответ:0,45

ЕГЭ Профиль №3. Классическое определение вероятности — math200.ru

Skip to content

ЕГЭ Профиль №3. Классическое определение вероятностиadmin2022-08-28T09:46:26+03:00

Скачать файл в формате pdf.


ЕГЭ Профиль №3. Классическое определение вероятности

Задача 1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

Ответ

ОТВЕТ: 0,14.

Задача 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что разница выпавших очков равна 1 или 2.

Ответ

ОТВЕТ: 0,5.

Задача 3. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что сумма выпавших очков равна 16. Результат округлите до сотых.

Ответ

ОТВЕТ: 0,03.

Задача 4. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что сумма выпавших очков равна 14. Результат округлите до сотых.

Ответ

ОТВЕТ: 0,07.

Задача 5. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.

Ответ

ОТВЕТ: 0,25.

Задача 6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет все три раза.

Ответ

ОТВЕТ: 0,125.

Задача 7. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел выпадет ровно один раз.

Ответ

ОТВЕТ: 0,25.

Задача 8. В чемпионате по гимнастике участвуют 60 спортсменок: 17 из США, 28 из Мексики, остальные — из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.

Ответ

ОТВЕТ: 0,25.

Задача 9. При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.

Ответ

ОТВЕТ: 0,006.

Задача 10. Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.

Ответ

ОТВЕТ: 0,92.

Задача 11. В соревнованиях по толканию ядра участвуют 3 спортсмена из Македонии, 8 спортсменов из Сербии, 3 спортсмена из Хорватии и 6 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Сербии.

Ответ

ОТВЕТ: 0,4.

Задача 12. Научная конференция проводится в 4 дня. Всего запланировано 50 докладов — первые два дня по 11 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

Ответ

ОТВЕТ: 0,28.

Задача 13. Конкурс исполнителей проводится в 3 дня. Всего заявлено 40 выступлений — по одному от каждой страны. В первый день 10 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

Ответ

ОТВЕТ: 0,375.

Задача 14. На семинар приехали 3 ученых из Болгарии, 4 из Австрии и 5 из Финляндии. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из Болгарии.

Ответ

ОТВЕТ: 0,25.

Задача 15. Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 спортсменов, среди которых 13 участников из России, в том числе Владимир Егоров. Найдите вероятность того, что в первом туре Владимир Егоров будет играть с каким-либо спортсменом из России?

Ответ

ОТВЕТ: 0,48.

Задача 16. В сборнике билетов по химии всего 50 билетов, в 20 из них встречается вопрос по углеводородам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по углеводородам.

Ответ

ОТВЕТ: 0,4.

Задача 17. В сборнике билетов по математике всего 60 билетов, в 9 из них встречается вопрос по производной. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по производной.

Ответ

ОТВЕТ: 0,85.

Задача 18. На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 3 прыгуна из Украины и 8 прыгунов из Бразилии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двенадцатым будет выступать прыгун из Бразилии.

Ответ

ОТВЕТ: 0,32.

Задача 19. Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.

Ответ

ОТВЕТ: 0,25.

Задача 20. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:  1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.  Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

Ответ

ОТВЕТ: 0,25.

Задача 21. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?

Ответ

ОТВЕТ: 0,5.

Задача 22. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?

Ответ

ОТВЕТ: 0,3.

Задача 23. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?

Ответ

ОТВЕТ: 0,4.

Задача 24. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию    «А = сумма очков равна 5»?

Ответ

ОТВЕТ: 4.

Задача 25. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадает орёл, во второй — решка).

Ответ

ОТВЕТ: 0,25.

Задача 26. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.

Ответ

ОТВЕТ: 0,33.

Задача 27. В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков.
Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.

Ответ

ОТВЕТ: 0,498.

Задача 28. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.

Ответ

ОТВЕТ: 0,1.

Задача 29. На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

Ответ

ОТВЕТ: 0,04.

Задача 30. В классе 26 человек, среди них два близнеца  — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

Ответ

ОТВЕТ: 0,48.

Задача 31. В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрные с жёлтыми надписями на бортах, остальные  — жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.

Ответ

ОТВЕТ: 0,46.

Задача 32. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.

Ответ

ОТВЕТ: 0,2.

Задача 33. Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

Ответ

ОТВЕТ: 0,006.

Задача 34. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.

Ответ

ОТВЕТ: 0,035.

Задача 35. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 0С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 0С или выше.

Ответ

ОТВЕТ: 0,19.

Задача 36. В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».

Ответ

ОТВЕТ: 0,25.

Задача 37. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.

Ответ

ОТВЕТ: 0,25.

Задача 38. За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.

Ответ

ОТВЕТ: 0,25.

Задача 39. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Ответ

ОТВЕТ: 0,995.

Задача 40. Фабрика выпускает сумки. В среднем на 92 качественных сумки приходится 8 сумок, имеющих скрытые дефекты. Найдите вероятность того, что выбранная в магазине сумка окажется с дефектами.

Ответ

ОТВЕТ: 0,08.

Задача 41. Какова вероятность того, что две последние цифры телефонного номера различные?

Ответ

ОТВЕТ: 0,9.

Задача 42. Какова вероятность того, что номера двух случайно выбранных паспортов оканчиваются одной и той же цифрой?

Ответ

ОТВЕТ: 0,1.

Задача 43. В группе из девяти человек есть две подруги Даша и Диана. Группу случайным образом делят на три одинаковые по численности подгруппы. Найдите вероятность, что Даша и Диана окажутся в одной подгруппе.

Ответ

ОТВЕТ: 0,25.

Реклама

Поддержать нас

Q.4.3 Брошены три игральные кости. По предположению… [БЕСПЛАТНОЕ РЕШЕНИЕ]

Q.4.3 Брошены три игральные кости. По предположению… [БЕСПЛАТНОЕ РЕШЕНИЕ] | StudySmarter

Выберите язык

Предлагаемые языки для вас:

Немецкий (DE)

Дойч (Великобритания)

Европа

  • английский (DE)
  • английский (Великобритания)

Q. 4.3

Проверено экспертами

Найдено: Страница 163

Перейти к главе

Ответы без размытия.

Просто зарегистрируйтесь бесплатно, и вы в игре.

Зарегистрируйтесь бесплатно Я сделаю это позже

Краткий ответ

Брошены три игральные кости. Предполагая, что каждый из 63 = 216 возможных исходов равновероятен, найдите вероятности, связанные с возможными значениями, которые может принять X, где X — сумма 3 игральных костей.

Распределение вероятностей X может быть сведено в таблицу, как указано ниже:

См. пошаговое решение

Пошаговое решение

СОДЕРЖАНИЕ :

ОГЛАВЛЕНИЕ

    Шаг 1: Получение информации

    Брошены три игральные кости. Предполагая, что каждый из 63=216 возможных исходов равновероятен

    Шаг 2: Решение

    В случайном эксперименте по броску трех игральных костей одновременно возможны 63=216 возможных результатов. Пусть X — сумма чисел, выпавших на трех костях. Тогда потенциальные значения X могут варьироваться от 3 для исхода (1,1,1) до 18, то есть для произведения (6,6,6).

    Поскольку все 216 продуктов равновероятны, как и в случае задачи двух игральных костей, это также симметричное распределение. Исходы 3 и 18 имеют одинаковую вероятность, т.е. 1216.

    Аналогично исходы (4 и 17), (5 и 16), (6 и 15), (7 и 14), (8 и 13), (9 и 12) и (10 и 11) имеют одинаковые вероятности, которые нам нужно получить сейчас.

    Вероятность выпадения суммы 4 на трех кубиках есть не что иное, как получение любого из исходов (1,1,2),(1,2,1) и (2,1,1). Всего 3 исхода. Таким образом, вероятность равна 3216.

    Вероятность выпадения суммы 5 на трех кубиках есть не что иное, как получение любого из исходов (1,1,3), (1,3,1),(3,1,1),(1,2,2 ),(2,1,2) и (2,2,1). Всего 6 исходов. Таким образом, вероятность равна 6216.

    Вероятность выпадения суммы 6 при игре тремя кубиками есть не что иное, как получение любого из исходов (1,1,4),(1,4,1),(4,1,1) ,(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1) и (2,2,2). Всего 10 исходов. Итак, вероятность равна 10216.

    Вероятность выпадения суммы 7 на трех кубиках есть не что иное, как получение любого из исходов (1,1,5),(1,5,1),(5,1,1) ,(1,2,4),(1,4,2),(2,1,4),(2,4,1),(4,1,2),(4,2,1),( 1,3,3),(3,1,3),(3,3,1),(2,2,3),(2,3,2) и (3,2,2). Всего 15 исходов. Таким образом, вероятность равна 15216.

    Шаг 4: Окончательный расчет

    Вероятность выпадения суммы 8 на трех кубиках есть не что иное, как получение любого из исходов (1,1,6),(1,6,1),(6,1,1) ,(1,2,5),(1,5,2),(2,1,5),(2,5,1),(5,1,2),(5,2,1),( 1,3,4),(1,4,3),(3, 1,4),(3,4,1),(4,1,3),(4,3,1),(2, 2,4),(2,4,2),(4,2,2),(2,3,3),(3,2,3) и (3,3,2). Сумма 21 исхода. Следовательно, вероятность равна 21216.

    Вероятность выпадения суммы 9 при игре тремя кубиками есть не что иное, как получение любого из исходов (1,2,6),(1,6,2),(2,1,6) ,(2,6,1),(6,1,2),(6,2,1),(1,3,5),(1,5,3),(3,1,5),( 3,5,1),(5,1,3),(5,3,1),(1,4,4),(4,1,4),(4,4,1),(2, 2,5),(2,5,2),(5,2,2),(2,3,4),(2,4,3),(3,2,4),(3,4, 2),(4,2,3),(4,3,2) и (3,3,3). Сумма 25 исходов. Таким образом, вероятность равна 25216.

    Вероятность выпадения суммы 10 на трех кубиках есть не что иное, как получение любого из исходов (1, 3 ,6),(1,6,3),(3,1,6),(3,6,1 ),(6,1,3),(6,3,1),(1,4,5),(1,5,4),(4,1,5),(4,5,1), (5,1,4),(5,4,1),(2,2,6),(2,6,2),(6,2,2),(2,3,5),(2) ,5,3),(3,2,5),(3,5,2),(5,2,3),(5,3,2),(2,4,4),(4,2 ,4),(4,4,2),(3,3,4),(3,4,3) и (4,3,3). Сумма 27 исходов. Таким образом, вероятность равна 27216.

    Шаг 4: Окончательный ответ

    Распределение вероятности X может быть приведено в табличном виде, как указано ниже:

    Самые популярные вопросы для учебников по математике

    Рекомендуемые пояснения к учебникам по математике

    94% пользователей StudySmarter получают более высокие оценки.

    Бесплатная регистрация

    Вероятность того, что сумма трех игральных костей не больше 9

    спросил

    Изменено 4 года, 1 месяц назад

    Просмотрено 2к раз

    $\begingroup$

    Какова вероятность того, что сумма 3 неразличимых костей меньше или равна 9?

    Я пытался посчитать пары $X_1, X_2$ так, чтобы их сумма была меньше или равна 8, но, кажется, я пересчитал, потому что я получаю, что для каждой пары игральных костей у меня есть 46 возможностей, чтобы их сумма была меньше чем 8.

    • вероятность
    • кости

    $\endgroup$

    3

    $\begingroup$

    Рассмотрим сумму первых двух костей. Если сумма меньше или равна 3, третья кость может иметь любое значение. По мере того, как сумма увеличивается с 3 до 8, третья кость может выбросить меньше возможных значений. Поскольку количество способов выбросить сумму $n$ двумя костями равно $6 — |n — 7|$, общее количество способов выбросить 93 = 216$ способов бросить три кости, вероятность выпадения 9 или меньше равна:

    $$\frac{81}{216} = 0,375$$

    $\endgroup$

    $\begingroup$

    У вас есть $27$ комбинаций цифр $(1,2,3)$ плюс $15$ комбинаций, включающих $4$: $(1,1,4), (1,2,4), (2,2, 4), (1,3,4)$ и $(2,3,4)$ плюс комбинации $12$, которые включают $5$: $(1,1,5), (1,2,5), (2 ,2,5), (1,3,5)$ из возможных исходов $216$. Итак, 54/216 = 0,25 9 долларов.0005

    $\endgroup$

    2

    $\begingroup$

    «Неразличимая» часть может ввести в заблуждение. Если вам нужна вероятность события, полученного при броске трех игральных костей, вы должны пометить кости первой, второй и третьей.

    Количество способов, которыми кости могут сложить до 9$ или меньше, равно количеству способов, которыми вы можете составить сумму 9$ или меньше из трех положительных целых чисел в последовательности при условии, что ни одно целое не больше $6.$

    Если убрать условие «больше $6$», то количество способов составить сумму не более $9$ из трех положительных целых чисел будет равно количеству способов составить сумму ровно $10$ из четырех положительных чисел. целые числа. Хорошо известным способом вычисления этого числа является так называемый метод «звезд и полос». что говорит нам о том, что ответ $\binom93 = 84.