Боковая сторона равнобедренной трапеции равна 18: Решение №2473 Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании равен 60°, большее основание равно 28.

боковая сторона равнобедренной трапеции равна 18 см,а средняя линия-16 см.Найдите периметр трапеции. — Знания.site

Ответы 1

Средняя линия трапеции равна половине суммы оснований, таким образом сумма оснований трапеции равна двум средним линиям, таким образом, периметр трапеции будет равен: (18+16)·2= 68 (см).

• Автор:

  hope55

• Оценить ответ:

  0

Знаешь ответ? Добавь его сюда!

Последние вопросы

• Математика

  10 минут назад

  Для строительства детской площадки рабочие проводили измерительные работы. Они подготовили две площадки квадратной формы. Найди их периметр, если известно, что величина периметра каждого из них меньше 90 м. Если цифры в записи одного периметра поменять местами, то получится периметр второго участка. Как записать решение?

• Математика

  8 часов назад

  Запишите решение в столбик и ответ.

• Русский язык

  8 часов назад

  Рус.яз 9 класс

• Физика

  8 часов назад

  Металлический шар массой 880 грамм падает на земл с высоты 3м. Какую работу при этом совершает сила тяжести

• Физика

  8 часов назад

  Процесс появление электрической дуги, ее физическое явление, способы гашения дуги

• Математика

  8 часов назад

  Нужна формула расчета

• Русский язык

  8 часов назад

  Русский язык 8 класс

• Русский язык

  8 часов назад

  Вставте пропущенные буквы в словах

• Геометрия

  9 часов назад

  Задача по геометрии

• Биология

  9 часов назад

  Биология дз срочно

• Химия

  9 часов назад

  1. Назовите групповой реагент и перечислите катионы, входящие в IV группу. 2. Укажите цвет гидроксидов катионов IV

• История

  9 часов назад

  Что произошло в риме после смерти Цезаря

• География

  9 часов назад

  Расположите регионы России в той последовательности, в которой их жители встречают Новый год.

• Русский язык

  9 часов назад

  Подскажите пожалуйста с заданием по русскому языку, дать характеристику предложению

• География

  9 часов назад

  Расположите регионы россии в порядке уменьшения среднегодового количества осадков.

How much to ban the user?

1 hour 1 day 100 years

Самостоятельная работа средняя линия трапеции 25 вариантов | Материал для подготовки к ЕГЭ (ГИА) по геометрии (9 класс):

ВАРИАНТ 1

1.Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

2.Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

3.Боковые стороны трапеции равны 12 см и 16 см, а периметр равен 54 см. Найдите среднюю линию трапеции.

4.Дана равнобедренная трапеция АВСD. Перпендикуляр, проведенный из вершины  В к большему основанию АD, делит это основание на два отрезка, больший из которых равен 11 см. Найдите среднюю линию трапеции.

ВАРИАНТ 2

1.Большее основание трапеции равно 30 см, а средняя линия равна 25 см. Найдите меньшее основание трапеции

2.Средняя линия трапеции равна 12 см, а одно из оснований в 2 раза больше другого.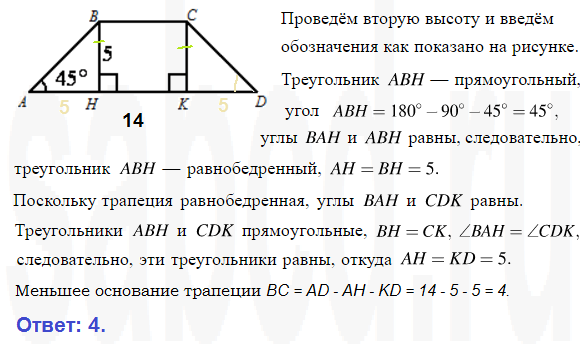 Найдите основания трапеции.

3.Боковые стороны трапеции равны 14 см и 18 см, а периметр равен 58 см. Найдите среднюю линию трапеции.угол =30.

4.Дана равнобедренная трапеция АВСD. Перпендикуляр, проведенный из вершины  В к большему основанию АD, делит это основание на два отрезка, больший из которых равен 15 см. Найдите среднюю линию трапеции.

ВАРИАНТ 3

1.НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ, ЕСЛИ ЕЕ ОСНОВАНИЯ РАВНЫ 30 И 16.

2.СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 15 СМ, А ОДНО ИЗ ОСНОВАНИЙ В 3 РАЗА БОЛЬШЕ ДРУГОГО. НАЙДИТЕ ОСНОВАНИЯ ТРАПЕЦИИ.

3.БОКОВЫЕ СТОРОНЫ ТРАПЕЦИИ РАВНЫ 16 СМ И 22 СМ, А ПЕРИМЕТР РАВЕН 74 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.УГОЛ =30.

4.В ПРЯМОУГОЛЬНОЙ ТРАПЕЦИИ МЕНЬШАЯ БОКОВАЯ СТОРОНА 12 СМ, А БОЛЬШАЯ СОСТАВЛЯЕТ С БОЛЬШИМ ОСНОВАНИЕМ УГОЛ 45О. НАЙДИТЕ ОСНОВАНИЕ ТРАПЕЦИИ, ЕСЛИ ЕЕ СРЕДНЯЯ ЛИНИЯ РАВНА 20 СМ.

ВАРИАНТ 4

1.Большее основание трапеции равно 40 см, а средняя линия равна 25 см. Найдите меньшее основание трапеции

2.В ТРАПЕЦИИ ABCD , БОКОВЫЕ СТОРОНЫ РАВНЫ 10 СМ И 12 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 8 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

3.ДАНА РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ АВСD. ПЕРПЕНДИКУЛЯР, ПРОВЕДЕННЫЙ ИЗ ВЕРШИНЫ  В К БОЛЬШЕМУ ОСНОВАНИЮ АD, ДЕЛИТ ЭТО ОСНОВАНИЕ НА ДВА ОТРЕЗКА, БОЛЬШИЙ ИЗ КОТОРЫХ РАВЕН 25 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ДИАГОНАЛЬ РАВНА 12 СМ И СОСТАВЛЯЕТ С ОСНОВАНИЕМ УГОЛ 45О. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 5

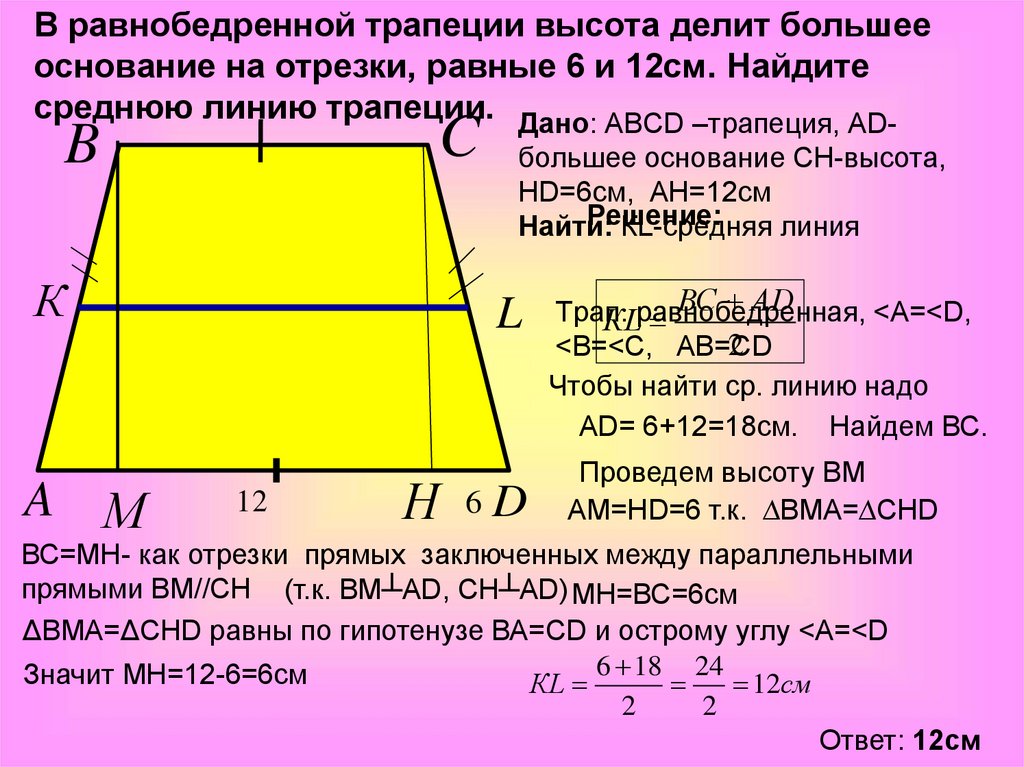
1.В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.

2.В равнобедренной трапеции  один из углов равен 60о, боковая сторона равна 8 см, а меньшее основание  7 см. Найдите среднюю линию трапеции.

3.В ТРАПЕЦИИ ABCD  AB = CD, ВЫСОТА ВН ДЕЛИТ ОСНОВАНИЕ НА ДВА ОТРЕЗКА, МЕНЬШИЙ ИЗ КОТОРЫХ РАВЕН 5 СМ. НАЙДИТЕ AD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 9 СМ.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.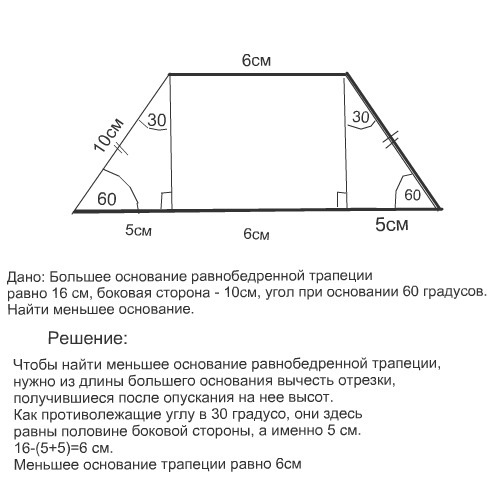  

ВАРИАНТ 6

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ВЫСОТА ДЕЛИТ БОЛЬШЕЕ ОСНОВАНИЕ НА ОТРЕЗКИ, РАВНЫЕ 15 СМ И 22 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

2.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ  ОДИН ИЗ УГЛОВ РАВЕН 60О, БОКОВАЯ СТОРОНА РАВНА 10 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ  17 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

3.В ТРАПЕЦИИ MNKP , БОКОВЫЕ СТОРОНЫ РАВНЫ 8 СМ И 10 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 5 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.ДАНА РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ АВСD. ПЕРПЕНДИКУЛЯР, ПРОВЕДЕННЫЙ ИЗ ВЕРШИНЫ  В К БОЛЬШЕМУ ОСНОВАНИЮ АD, ДЕЛИТ ЭТО ОСНОВАНИЕ НА ДВА ОТРЕЗКА, БОЛЬШИЙ ИЗ КОТОРЫХ РАВЕН 10 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 7

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ВЫСОТА ДЕЛИТ БОЛЬШЕЕ ОСНОВАНИЕ НА ОТРЕЗКИ, РАВНЫЕ 14 СМ И 19 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

2.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ  ОДИН ИЗ УГЛОВ РАВЕН 60О, БОКОВАЯ СТОРОНА РАВНА 18 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 4 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD СМ, А ВЫСОТА ТРАПЕЦИИ РАВНА 3 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.ДАНА РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ АВСD. ПЕРПЕНДИКУЛЯР, ПРОВЕДЕННЫЙ ИЗ ВЕРШИНЫ  В К БОЛЬШЕМУ ОСНОВАНИЮ АD, ДЕЛИТ ЭТО ОСНОВАНИЕ НА ДВА ОТРЕЗКА, БОЛЬШИЙ ИЗ КОТОРЫХ РАВЕН 22 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 8

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ БОКОВАЯ СТОРОНА РАВНА 15 СМ, А ЕЕ СРЕДНЯЯ ЛИНИЯ 22 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

2.Средняя линия трапеции равна 21, а меньшее основание равно 5. Найдите большее основание трапеции. 

2.В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 10 см и 17 см. Найдите среднюю линию трапеции. 

3.В ТРАПЕЦИИ ABCD , БОКОВЫЕ СТОРОНЫ РАВНЫ 14 СМ И 16 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 8 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ДИАГОНАЛЬ РАВНА 10 СМ И СОСТАВЛЯЕТ С ОСНОВАНИЕМ УГОЛ 45О. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 9

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ БОКОВАЯ СТОРОНА РАВНА 15 СМ, А ЕЕ СРЕДНЯЯ ЛИНИЯ 12 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.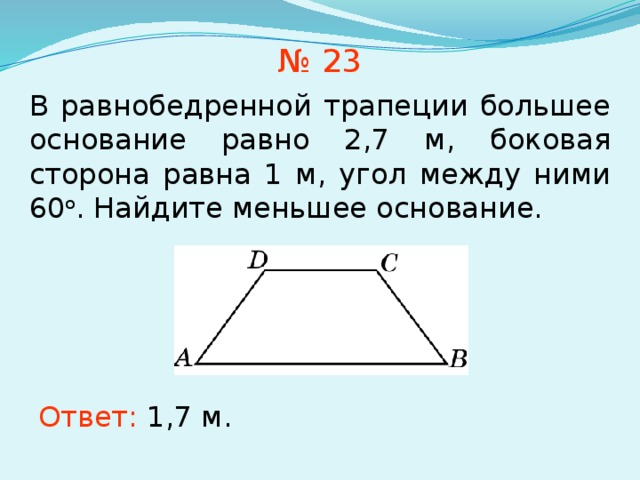

2.Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции. 

3.Средняя линия трапеции равна 8 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

4.В ТРАПЕЦИИ ABCD , БОКОВЫЕ СТОРОНЫ РАВНЫ 20 СМ И 22 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 10 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 10

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ БОКОВАЯ СТОРОНА РАВНА 18 СМ, А ЕЕ СРЕДНЯЯ ЛИНИЯ 10 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

2.Средняя линия трапеции равна 18, а меньшее основание равно 12. Найдите большее основание трапеции. 

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ДИАГОНАЛЬ РАВНА 14 СМ И СОСТАВЛЯЕТ С ОСНОВАНИЕМ УГОЛ 45О. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.В ПРЯМОУГОЛЬНОЙ ТРАПЕЦИИ МЕНЬШЕЕ ОСНОВАНИЕ РАВНО МЕНЬШЕЙ БОКОВОЙ СТОРОНЕ, ОДИН ИЗ УГЛОВ 45О, А СРЕДНЯЯ ЛИНИЯ 10 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

ВАРИАНТ 11

1.НАЙДИТЕ БОКОВУЮ СТОРОНУ РАВНОБЕДРЕННОЙ ТРАПЕЦИИ, ПЕРИМЕТР КОТОРОЙ РАВЕН 38, А СРЕДНЯЯ ЛИНИЯ РАВНА 9.

2.В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 3 см и 6 см. Найдите среднюю линию трапеции. 

3.В ТРАПЕЦИИ ABCD , БОКОВЫЕ СТОРОНЫ РАВНЫ 11 СМ И 13 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 17 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.В ПРЯМОУГОЛЬНОЙ ТРАПЕЦИИ МЕНЬШЕЕ ОСНОВАНИЕ В 2 РАЗА МЕНЬШЕ БОКОВОЙ СТОРОНЫ, ОДИН ИЗ УГЛОВ РАВЕН 125О, А СРЕДНЯЯ ЛИНИЯ РАВНА 14 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

ВАРИАНТ 12

1.Разность оснований трапеции равна 10 см, а средняя линия равна 22 см. Найдите основания этой трапеции.

2.В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 24.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 22, а меньшее основание BC равно 10

ВАРИАНТ 13

1.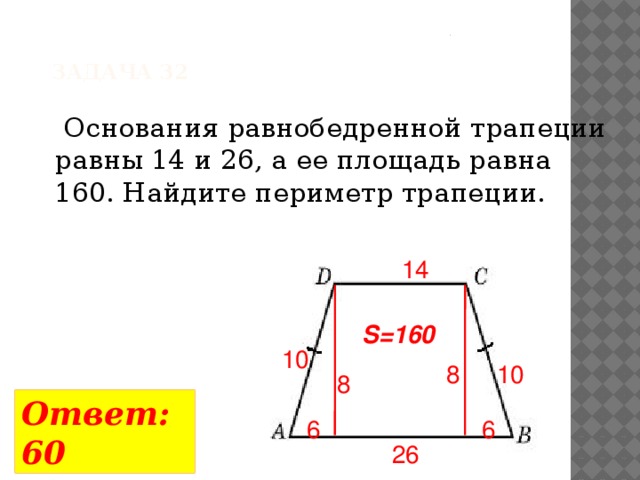 Боковые стороны равнобедренной трапеции равны по 15 см, а средняя линия этой трапеции 25 см. Найдите периметр этой трапеции.

2.В ТРАПЕЦИИ АВСD БОКОВЫЕ СТОРОНЫ AB И CD РАВНЫ, CH — ВЫСОТА, ПРОВЕДЁННАЯ К БОЛЬШЕМУ ОСНОВАНИЮ AD. НАЙДИТЕ ДЛИНУ ОТРЕЗКА HD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ KM ТРАПЕЦИИ РАВНА 12, А МЕНЬШЕЕ ОСНОВАНИЕ BC РАВНО 4.

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 14.

4. В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 18, а меньшее основание BC равно 10

ВАРИАНТ 14

1.Средняя линия трапеции равна 30 см, а одно из оснований в два раза меньше другого. Найдите основания трапеции.

2.В ТРАПЕЦИИ АВСD БОКОВЫЕ СТОРОНЫ AB И CD РАВНЫ, СН — ВЫСОТА, ПРОВЕДЁННАЯ К БОЛЬШЕМУ ОСНОВАНИЮ AD. НАЙДИТЕ ДЛИНУ ОТРЕЗКА HD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ KM ТРАПЕЦИИ РАВНА 16, А МЕНЬШЕЕ ОСНОВАНИЕ BC РАВНО 6.

3.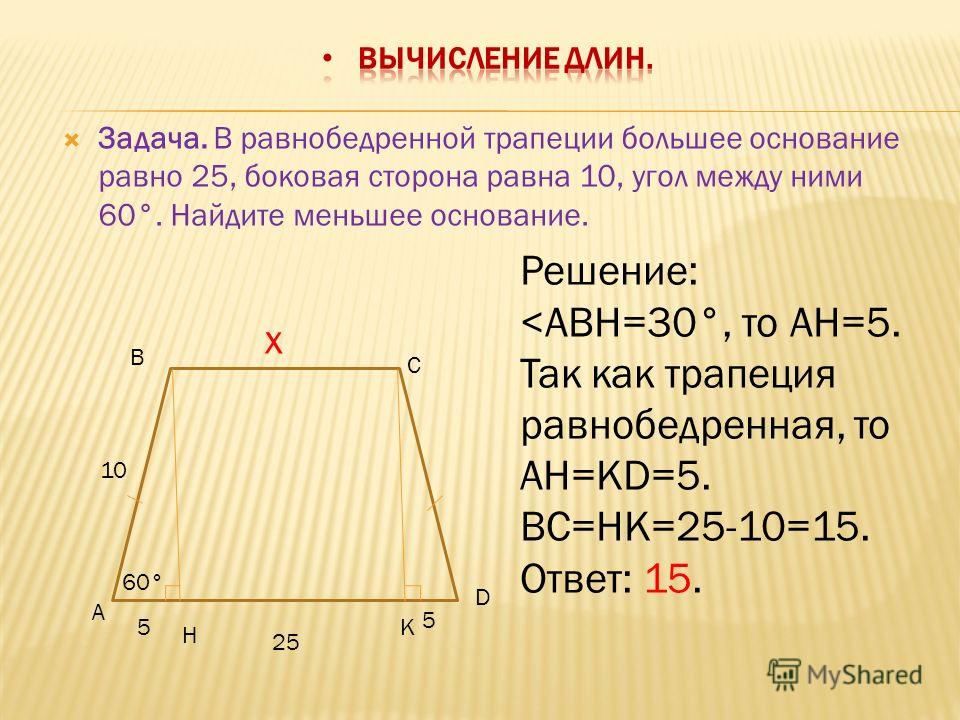 В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 14 см и 27 см. Найдите среднюю линию трапеции. 

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 18.

ВАРИАНТ 15

1.В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 4 см и 7 см. Найдите среднюю линию трапеции. 

2.Разность оснований трапеции равна 10 см, а средняя линия равна 12 см. Найдите основания этой трапеции.

3.В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 20, а меньшее основание BC равно 6.

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 16.

ВАРИАНТ 16

1.Средняя линия трапеции на 2 см меньше большего основания. Найдите среднюю линию трапеции, если меньшее основание равно 6 см. 

2.Разность оснований трапеции равна 12 см, а средняя линия равна 22 см. Найдите основания этой трапеции.

3.В ТРАПЕЦИИ АВСD БОКОВЫЕ СТОРОНЫ AB И CD РАВНЫ, СН — ВЫСОТА, ПРОВЕДЁННАЯ К БОЛЬШЕМУ ОСНОВАНИЮ AD. НАЙДИТЕ ДЛИНУ ОТРЕЗКА HD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ KM ТРАПЕЦИИ РАВНА 10, А МЕНЬШЕЕ ОСНОВАНИЕ BC РАВНО 5.

4.Средняя линия трапеции равна 16 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

ВАРИАНТ 17

1.Длина большего основания трапеции в 2 раза больше длины меньшего основания. Найдите длину меньшего основания, если длина средней линии равна 3 см. 

2.Боковые стороны равнобедренной трапеции равны по 25 см, а средняя линия этой трапеции 35 см. Найдите периметр этой трапеции.

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ СРЕДНЯЯ ЛИНИЯ РАВНА 10 СМ, А ПЕРИМЕТР 36 СМ. НАЙДИТЕ БОКОВЫЕ СТОРОНЫ ЭТОЙ ТРАПЕЦИИ.

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 20.

ВАРИАНТ 18

1.НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ, ЕСЛИ ЕЕ ОСНОВАНИЯ РАВНЫ 10СМ И 14СМ.

2.Боковые стороны равнобедренной трапеции равны по 15 см, а средняя линия этой трапеции 25 см. Найдите периметр этой трапеции.

3.В равнобедренной трапеции средняя линия равна 10 см, а периметр 36 см. Найдите боковые стороны этой трапеции.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4. 

ВАРИАНТ 19

1.СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 30 СМ, А ОДНО ИЗ ОСНОВАНИЙ В ДВА РАЗА БОЛЬШЕ ДРУГОГО. НАЙДИТЕ ОСНОВАНИЯ ТРАПЕЦИИ.

2.Разность оснований трапеции равна 8см, а средняя линия равна 20см. Найдите основания этой трапеции.

3.В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 2 см и 7 см. Найдите среднюю линию трапеции.  

4.Средняя линия трапеции равна 12 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

ВАРИАНТ 20

1.НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ, ЕСЛИ ЕЕ ОСНОВАНИЯ РАВНЫ 12СМ И 16СМ.

2.Боковые стороны равнобедренной трапеции равны по 14 см, а средняя линия этой трапеции 28 см. Найдите периметр этой трапеции.

3.Средняя линия трапеции равна 15 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

4.В равнобедренной трапеции ABCD с основаниями AD и BC

 DAC  45 .        Найдите среднюю линии трапеции, если высота трапеции равна 13.

ВАРИАНТ 21

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ СРЕДНЯЯ ЛИНИЯ РАВНА 20 СМ, А ПЕРИМЕТР 44 СМ. НАЙДИТЕ БОКОВЫЕ СТОРОНЫ ЭТОЙ ТРАПЕЦИИ.

2.Разность оснований трапеции равна 8см, а средняя линия равна 15см. Найдите основания этой трапеции.

3.Средняя линия трапеции равна 15 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

4.В равнобедренной трапеции ABCD с основаниями AD и BC

 DAC  45 .         Найдите среднюю линии трапеции, если высота трапеции равна 14.

ВАРИАНТ 22

1.Боковые стороны трапеции равны 18 см и 12 см, а периметр равен 50см. Найдите среднюю линию  трапеции.

2.Дана равнобедренная трапеция АВСД.  Перпендикуляр, проведённый из вершины В к большему основанию АД, делит это основание на  два отрезка, больший из которых равен 8 см. Найдите среднюю линию трапеции.

3.В равнобедренной трапеции ABCD с основаниями AD и ВС АВ = ВС = CD. Найдите среднюю линии трапеции, если AD = 18 и

 D  60 .

4.Средняя линия трапеции равна 20 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

ВАРИАНТ 23

1.Боковые стороны трапеции равны 24 см и 26 см, а периметр равен 70см. Найдите среднюю линию трапеции.

2.Дана равнобедренная трапеция АВСД. Перпендикуляр, проведённый из вершины В к большему основанию АД, делит это основание на два отрезка, больший из которых равен 9 см. Найдите среднюю линию трапеции

3.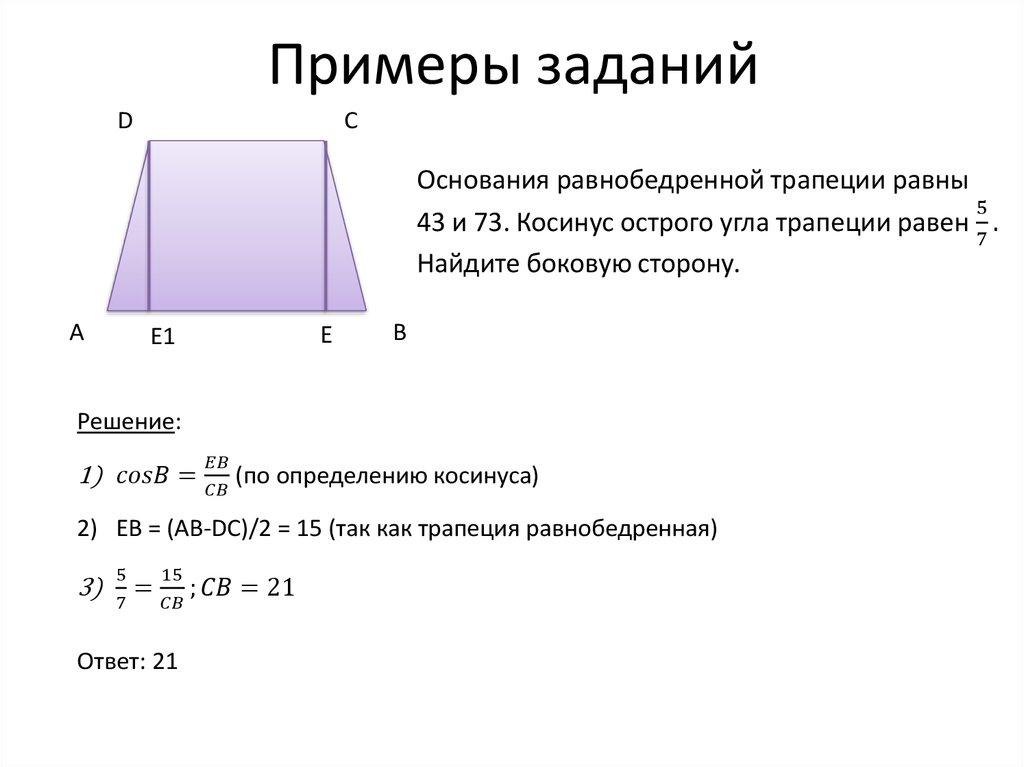 Средняя линия трапеции равна 10 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

4.В равнобедренной трапеции ABCD с основаниями AD и BC

 DAC  45 .        Найдите среднюю линии трапеции, если высота трапеции равна 10.

 ВАРИАНТ 24

1.СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 38, А МЕНЬШЕЕ ОСНОВАНИЕ РАВНО 18. НАЙДИТЕ БОЛЬШЕЕ ОСНОВАНИЕ ТРАПЕЦИИ.

2.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ  ОДИН ИЗ УГЛОВ РАВЕН 60О, БОКОВАЯ СТОРОНА РАВНА 8 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ  10 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

3.В ТРАПЕЦИИ ABCD  AB = CD, ВЫСОТА ВН ДЕЛИТ ОСНОВАНИЕ НА ДВА ОТРЕЗКА, МЕНЬШИЙ ИЗ КОТОРЫХ РАВЕН 5 СМ. НАЙДИТЕ AD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 9 СМ.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4. 

ВАРИАНТ 25

1.НАЙДИТЕ        ПЕРИМЕТР        РАВНОБЕДРЕННОЙ        ТРАПЕЦИИ        С        БОКОВЫМИ СТОРОНАМИ РАВНЫМИ 7 И СРЕДНЕЙ ЛИНИЕЙ РАВНОЙ 10

2.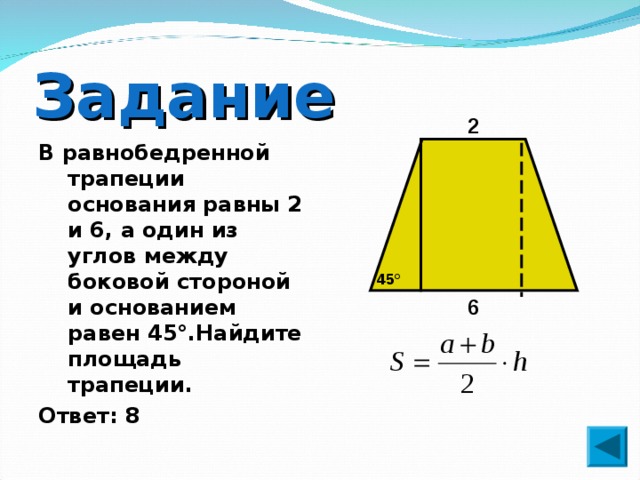 В равнобедренной трапеции  один из углов равен 60о, боковая сторона равна 18 см, а меньшее основание  17 см. Найдите среднюю линию трапеции.

3.В ТРАПЕЦИИ ABCD  AB = CD, ВЫСОТА ВН ДЕЛИТ ОСНОВАНИЕ НА ДВА ОТРЕЗКА, МЕНЬШИЙ ИЗ КОТОРЫХ РАВЕН 5 СМ. НАЙДИТЕ AD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 10 СМ.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 14. 

Как найти параллельную сторону равнобедренной трапеции?

Измерение влечет за собой процессы измерения и всех расчетов, относящихся к различным геометрическим формам, происходящие в математической теории, а также в нашей повседневной жизни. Изучение всех геометрических фигур подпадает под сферу измерения.

Трапеция

Такой выпуклый четырехугольник, у которого ровно одна пара параллельных сторон, называется трапецией или трапецией. Трапеция — это двумерная фигура, похожая на стол.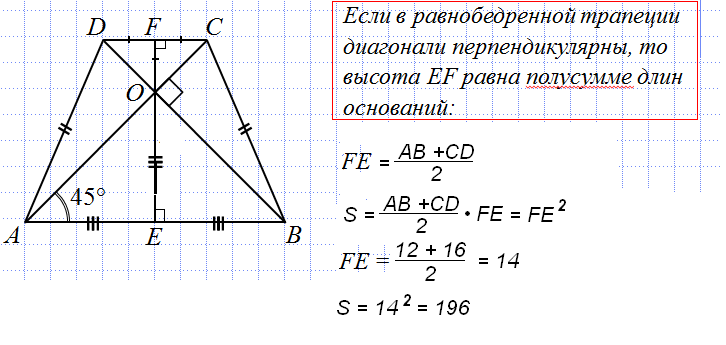 Как и у всех других четырехугольников, сумма всех внутренних углов трапеции также равна 360°. На следующем рисунке показана трапеция ABCD с параллельными сторонами AB и CD и непараллельными сторонами AD и BC.

Равнобедренная трапеция

Равнобедренная трапеция — это трапеция, имеющая ровно одну пару параллельных сторон, а непараллельные стороны равны по длине. Углы при основании также равны.

На приведенном выше рисунке изображена равнобедренная трапеция ABCD, у которой AB и CD — стороны основания, а AD и BC — непараллельные стороны, равные по длине. Углы при основании: ∠B = ∠A и ∠C = ∠D.

Свойства равнобедренной трапеции

• Равнобедренная трапеция – это трапеция, стороны которой параллельны.
• Стороны, кроме основных сторон, непараллельны и равны по длине.
• Длины диагоналей равнобедренной трапеции равны.
• Углы при основании равнобедренной трапеции равны.

Площадь равнобедренной трапеции

Площадь равнобедренной трапеции рассчитывается по следующей формуле:

A = (Высота × сумма параллельных сторон)/2

Как найти параллельную сторону равнобедренной трапеции?

Ответ:

Зная отношение параллельных сторон равнобедренной трапеции к ее площади, можно легко вычислить длины каждой стороны.

Пример: Допустим, отношение параллельных сторон равнобедренной трапеции равно 2:1. Площадь 90 единиц ² и высота 10 единиц.

Пусть длина более короткой параллельной стороны равна «х» единиц.

A = (высота × сумма параллельных сторон)/2

⇒ 90 = 10(x + 2x)/ 2

⇒ 18 = 3x

⇒ x = 6 единиц

Таким образом, длина более короткого сторона равна 6 единицам, а более длинная параллельная сторона — 12 единицам.

Аналогичные задачи

Вопрос 1: Найдите площадь равнобедренной трапеции, периметр которой равен 100 см, высота 10 см, а непараллельные стороны по 20 см каждая.

Решение:

Периметр = Сумма всех сторон = 100 см.

Пусть сумма параллельных сторон равна  a + b.

⇒ a + b + 20 + 20 = 100

⇒ a + b = 60 см

Теперь площадь = h(a + b)/ 2

= 10(60)/ 2

⇒ A = A 300 см ²

Вопрос 2: Найдите длины параллельных сторон равнобедренной трапеции, если их отношение равно 1:3, высота равна 5 единицам, а площадь равна 100 единицам ² .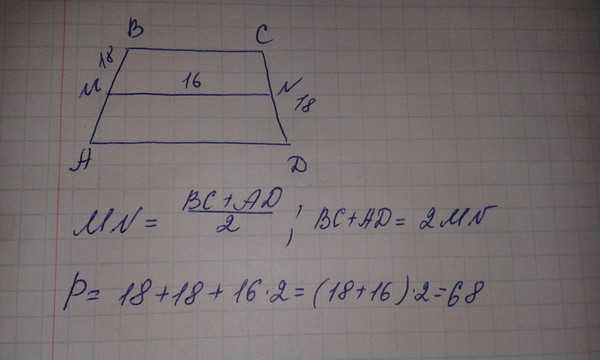

Решение:

Пусть длина более короткой параллельной стороны равна x единицам.

A = (высота × сумма параллельных сторон)/2

⇒ 100 = 5(x + 3x)/ 2

⇒ 40 = 4x

⇒ x = 10 единиц

сторона равна 10 единицам, а более длинная параллельная сторона равна 30 единицам.

Вопрос 3: Найдите длины параллельных сторон равнобедренной трапеции, если их отношение 1:4, высота 5 единиц, а площадь 100 единиц ² .

Решение:

Пусть длина более короткой параллельной стороны будет x единиц.

A = (высота × сумма параллельных сторон)/2

⇒ 100 = 5(x + 4x)/ 2

⇒ 40 = 5x

⇒ x = 8 единиц

Таким образом, длина более короткого сторона равна 8 единицам, а более длинная параллельная сторона — 32 единицам.

Вопрос 4: Найдите длины параллельных сторон равнобедренной трапеции, если их отношение 1:4, высота 5 единиц и площадь 50 единиц ² .

Решение:

Пусть длина более короткой параллельной стороны будет x единиц.

A = (высота × сумма параллельных сторон)/2

⇒ 50 = 5(x + 4x)/ 2

⇒ 20 = 5x

⇒ x = 4 единицы

Таким образом, длина более короткого сторона равна 4 единицам, а более длинная параллельная сторона — 16 единицам.

Вопрос 5: Найдите длины параллельных сторон равнобедренной трапеции, если их отношение равно 1:3, высота равна 2 единицам, а площадь равна 100 единицам ² .

Решение:

Пусть длина более короткой параллельной стороны будет x единиц.

A = (Высота × сумма параллельных сторон)/2

⇒ 100 = 2(x + 3x)/ 2

⇒ 100 = 4x

⇒ x = 25 единиц

Таким образом, длина меньшей сторона 25 единиц, а более длинная параллельная сторона 75 единиц.

Математическая задача: Равнобедренная трапеция — вопрос № 4962, алгебра

Какова высота равнобедренной трапеции, длина основания которой 11 см и 8 см, а длина катетов 2,5 см?

Правильный ответ:

Нашли ошибку или неточность? Не стесняйтесь

написать нам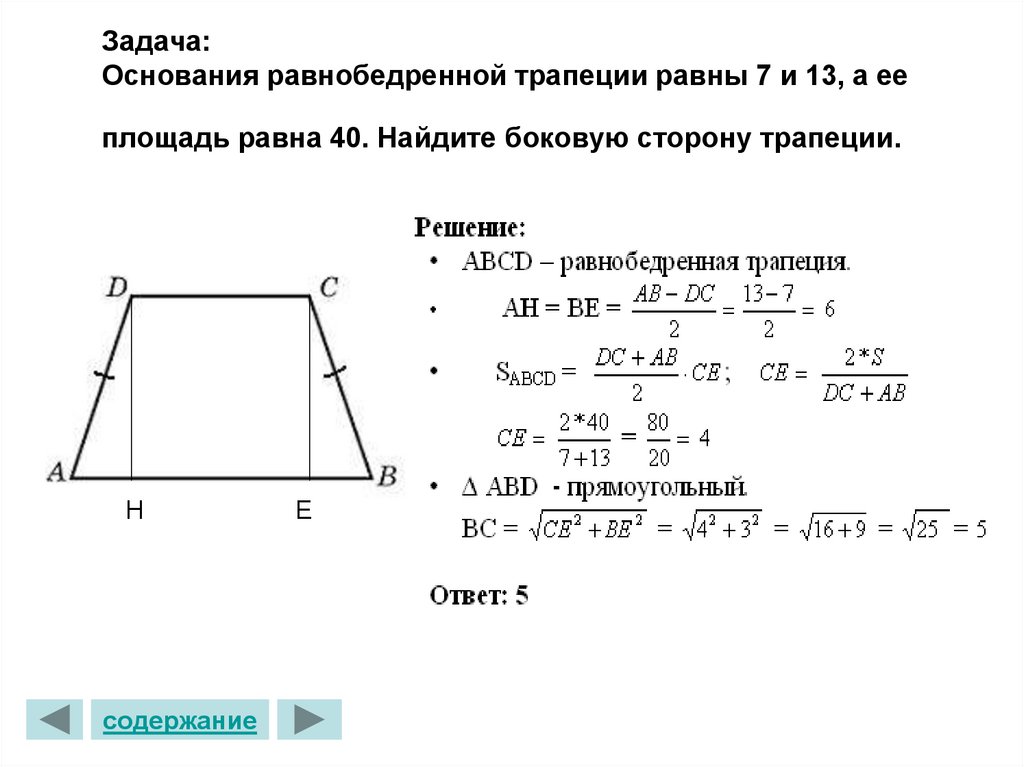

. Спасибо!

Советы по использованию связанных онлайн-калькуляторов

См. также наш калькулятор прямоугольного треугольника.
Расчет равнобедренного треугольника.
См. также наш калькулятор тригонометрического треугольника.

Для решения этой словесной задачи по математике необходимо знать следующие знания:

• алгебра
• выражение переменной из формулы
• планиметрия
• теорема Пифагора
• прямоугольный треугольник
• треугольник
• трапеция

степень словесной задачи для

8
лет 28

практика для 14-летних

 

Мы поощряем посмотрите это обучающее видео по этой математической задаче: видео1   видео2

• Равнобедренный 2
  Равнобедренный треугольный каркас имеет длину 72 метра по ножкам и 18 метров по основанию. Найдите периметр рамки.
• IS трапеция
  Вычислите длину диагонали u и высоту v равнобедренной трапеции ABCD, основания которой имеют длину a = |AB| = 37 см, с = |CD| = 29 см и ноги b = d = |BC| = |АД| = 28 см.
• Длина IT
  Найдите длину (окружность) равнобедренной трапеции, у которой длины оснований a, c и высота h заданы: a = 8 см c = 2 см h = 4 см.
• Равнобедренная трапеция
  Найдите площадь равнобедренной трапеции с основаниями 8 см и 72 мм. Высота трапеции равна трем четвертям большего основания.
• Трапеция
  Найдите высоту трапеции ABCD, площадь которой 77,5 см², а длина основания 16 см и 15 см.
• Трапециевидная призма
  Рассчитайте поверхность четырехугольной призмы ABCDA’B’C’D’ с трапециевидным основанием ABCD. Высота призмы 12 см; Данные трапеции ABCD: длина основания AB 8 см, длина основания CD 3 см, длина плеча BC 4 см, длина диагонали АС 7 см. L
• Трапеция 78904
  Рассчитайте среднюю перекладину трапеции, площадь которой 111,8 см², а высота 6,5 см.
• Сад
  Сад имеет форму равнобедренной трапеции с основаниями 64 м и длиной 24 м. Высота 25 м. На каком огородном участке можно выращивать овощи, если пятую часть площади занимают дача, газон и дорожка?
• Высота – 6183
  В равнобедренной трапеции ABCD длина основания равна а = 10 см, с = 6 см, а длина плеча равна 4 см. Вычислите его высоту — результат округлите до десятых.
• Площадь RT 2
  Вычислите площадь прямоугольного треугольника, катеты которого имеют длину 6,2 см и 90,8 см.
• Четырехугольник 24161
  Вычислите объем четырехугольной призмы, основанием которой является равнобедренная трапеция с основаниями 10 см и 4 см на расстоянии 6 см друг от друга. Высота призмы 25 см. Как можно вычислить площадь поверхности?
• Шоколадный рулет
  Кусочек шоколадного рулета длиной 5 см весит 30 г. Сколько калорий будет содержать одинаковый шоколадный валик в форме призмы длиной 0,5 м, сечение которого равнобедренной трапеции с основаниями 25 и 13 см и катетом 10 см? Вы знаете, что 100 г
• Равнобедренная трапеция
  Вычислить площадь равнобедренной трапеции, основания которой относятся как 4:3; ножка b = 13 см и высота = 12 см.
• Четырехугольная призма
  Четырехугольная призма имеет объем 648 см³. Трапеция, являющаяся ее основанием, имеет размеры основания: а = 10 см, с = 5 и высоту v = 6 см.