Решение задач ОГЭ по математике: вариант №5 задача №23
Сергей Ролев Нет комментариев 380 просмотров
Условие задачи
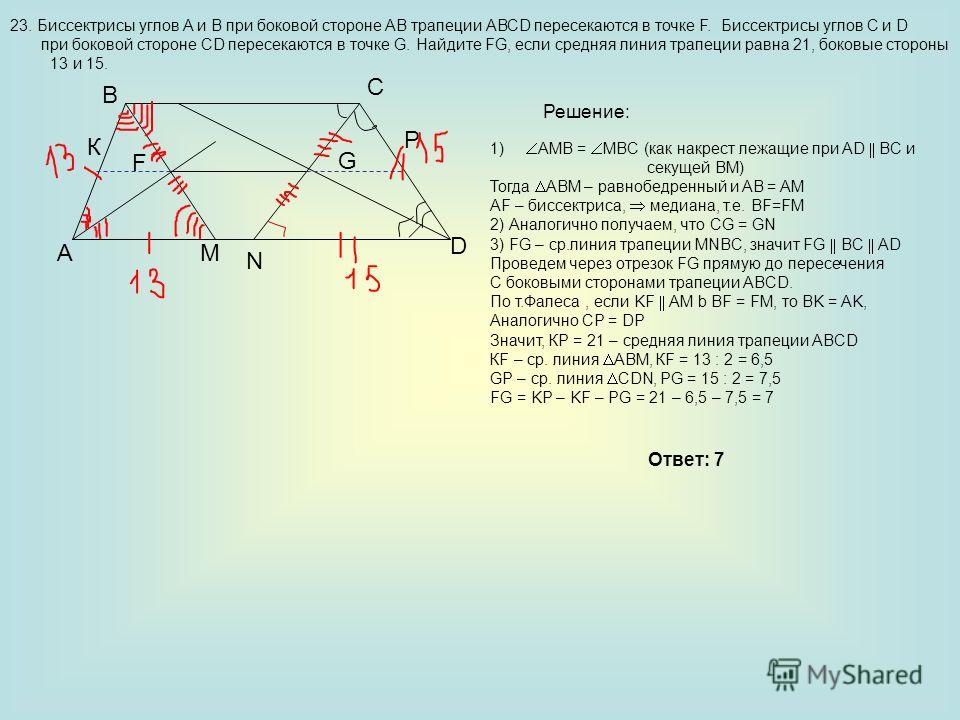
Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD пересекаются в точке F. Найдите АВ, если АF = 24, ВF = 18.
Решение
Изобразим трапецию АВСD на чертеже:
Углы А и В – внутренние односторонние углы при параллельных прямых, следовательно их сумма равна 180˚.
Рассмотрим треугольник АВF. Поскольку АF и ВF – биссектрисы,
∟ВАF+∟АВF=0,5∟ВАD+0.5∟АВC=0,5(∟ВАD + ∟АВC) = 0,5×180˚=90˚
Отсюда получаем, ∟АFВ = 180˚- 90˚=
90˚, то есть Δ АВF –
прямоугольный.
АВ² = АF² + ВF² = 24²+ 18² = 576 + 324 = 900 = 30²
Следовательно, АВ = 30
Ответ: 30
Основные выводы
Для решения этой задачи, надо знать
- свойства углов при параллельных прямых и секущей
- теорему Пифагора
- Очень полезен хороший чертёж
Желаю новых успехов в подготовке к ОГЭ!
Понравилась статья? Поделись!
- Вконтакте
- Одноклассники
- 552 Решение задач ОГЭ по математике: вариант №4 задача №25 1654884780 1654885631
- 574 Решение задач ОГЭ по математике: вариант №3 задача №25 1654709820 1654712779
- 731 Решение задач ОГЭ по математике: вариант №2 задача №25 1654284300 1654285218
- 567 Решение задач ОГЭ по математике: задачи №24 варианты № 9, 10, 12, 13, 14, 15, 16, 17, 18, 20, 21, 22, 23, 25, 26, 30, 33, 34, 35, 36, 37, 38 1654023120 1654023755
- 526 Решение задач ОГЭ по математике: вариант №32 задача №24 1653937380 1653938818
- 620 Решение задач ОГЭ по математике: вариант №31 задача №24 1653836220 1654021624
- 433 Решение задач ОГЭ по математике: вариант №28 задача №24 1653678900 1653679577
- 458 Решение задач ОГЭ по математике: вариант №27 задача №24 1653644340 1653644799
Пропорциональные отрезки problems & answers for quizzes and worksheets
Browse from millions of quizzes
QUIZ
Mathematics
76%
accuracy
3
plays
Татьяна Назаренко
3 years
Mathematics
Татьяна Назаренко
3
plays
7 questions
7 questions
Show Answers
See Preview
1.
 Multiple-choice
Multiple-choice1 minute
1 pt
Сторона ромба равна 10, а одна из диагоналей 16. Найдите расстояние от центра ромба до его стороны.
2. Multiple-choice
1 minute
1 pt
Биссектрисы углов при боковой стороне АВ трапеции ABCD пересекаются в точке К. Найдите расстояние от точки К до прямой АВ, если АК = 3\sqrt{3}3 , АВ = 2.
32\frac{\sqrt{3}}{2}23
22\frac{\sqrt{2}}{2}22
23\frac{\sqrt{2}}{3}32
3. Multiple-choice
1 minute
1 pt
В прямоугольном треугольнике АВС угол С прямой, СН — высота, АВ = 15, АН = 3. Найдите СН.
4.
 Multiple-choice
Multiple-choice1 minute
1 pt
Высота прямоугольного треугольника, проведенная к гипотенузе, равна 6, а проекция одного из катетов на гипотенузу равна 12. Найдите гипотенузу.
5. Multiple-choice
1 minute
1 pt
Вычислите высоту прямоугольного треугольника, проведенную к гипотенузе, если его катеты равны 3 и 4.
6. Multiple-choice
1 minute
В прямоугольном треугольнике отношение катетов равно 1 : 2. Найдите отношение проекций этих катетов на гипотенузу.
1 : 4.
7. Multiple-choice
1 minute
1 pt
В прямоугольном треугольнике АВС угол С прямой, СН — высота.
 Найдите АН, если АН : НВ = 1 : 8, АС = 9.
Найдите АН, если АН : НВ = 1 : 8, АС = 9.Expore all questions with a free account
Already have an account?
Треугольники C2.0
Треугольники C2.0Реклама
Верхний обрезанный слайд
Скачать для чтения офлайн
Образование
Треугольники Введение Сумма углов треугольника Типы треугольников Высота, медиана и биссектриса угла Конгруэнтность треугольников Стороны, противоположные конгруэнтным углам
Реклама
Реклама
Треугольники C2.0
- Глава 2 Треугольники
- ГЛАВА 2: ТРЕУГОЛЬНИКИ 2.1 Введение 2.2 Сумма углов треугольника 2.3 Типы треугольников 2.4 Высота, медиана и биссектриса угла 2.5 Конгруэнтность треугольников 2.6 Стороны, противоположные равным углам
- ГЛАВА 2: ТРЕУГОЛЬНИКИ
• 2.1 Введение
Как следует из названия треугольника, эта геометрическая фигура состоит из трех углов.

- 2.2 Сумма углов треугольника • Можно легко доказать, что сумма трех углов D равна 1800 ГЛАВА 2: ТРЕУГОЛЬНИКИ Рисунок 2.2 D ABC на рис. 2.2 представляет собой треугольник с линией l, параллельной отрезку. до н.э. и проходя через A. seg. АБ — это поперечные на двух параллельных прямых seg. PQ и сегмент BC. Следовательно, m PAB и m ABC равны, так как они являются альтернативными внутренними углами. Аналогично m QAC = m ACB. Теперь PAQ = m PAB + m BAC + m CAQ т. е. 1800 = m ABC + m BAC + m ACB м PAQ = 1800, потому что это прямая линия. Таким образом, сумма мер трех углов любого треугольника равна 1800.
- 2.3 Типы треугольников
• Треугольники подразделяются на
различных типов, используя два разных
параметры — длины их
стороны и мера их
углы.
• Длина стороны
а. Равносторонний треугольник: если длины
все три стороны треугольника равны
равны, то он называется равносторонним
треугольник.
 На рис. 2.3 показан
равносторонний треугольник.
Рисунок 2.3
На рис. 2.3 показан
равносторонний треугольник.
Рисунок 2.3 - Длина стороны б. Равнобедренный треугольник: если только два стороны треугольника равны в длина, называется равнобедренной треугольник. На рис. 2.4 показан равнобедренный треугольник. в. Разносторонний треугольник: если все стороны треугольника имеют разную длину называется разносторонним треугольником. Фигура 2.5 показан разносторонний треугольник. 2.3 Типы треугольников
- Углы • Остроугольный треугольник: треугольник, в котором все углы острые, (т.е. < 900) называется острым треугольник. На рис. 2.6 показан острый треугольник. Частным случаем остроугольного треугольника является когда все три острых угла равны равный. Этот D называется равносторонний треугольник. Рисунок 2.7 изображен равносторонний треугольник. 2.3 Типы треугольников
- 2.3 Типы треугольников
Углы
б. Тупоугольный треугольник: треугольник в
какой из углов тупой
называется тупоугольным треугольником. Фигура
2.8 изображен тупоугольный треугольник.
 в. Прямоугольный треугольник: это треугольник в
какой из углов прямой
угол. Рисунок 2.9показывает право
треугольник.
Поскольку KJL равно 900, можно сказать
что JKJL и JLK
дополняющий. В прямоугольном треугольнике
сторона, противоположная прямому углу,
называется гипотенузой.
в. Прямоугольный треугольник: это треугольник в
какой из углов прямой
угол. Рисунок 2.9показывает право
треугольник.
Поскольку KJL равно 900, можно сказать
что JKJL и JLK
дополняющий. В прямоугольном треугольнике
сторона, противоположная прямому углу,
называется гипотенузой. - 2.4 Высота, медиана и биссектриса угла Высота • Высота – это перпендикуляр упал из одной вершины в сторона (или ее продолжение), противоположная вершина. Он измеряет расстояние между вершиной и линия, которая является противоположной стороной. Так как в каждом треугольнике три вершины имеют три высоты. а. Высоты остроугольного треугольника: Для остроугольного треугольника 2.10 все высоты присутствуют в треугольнике.
- 2.4 Высота, медиана и биссектриса угла
б. Высоты для прямоугольного треугольника: • Для прямоугольного треугольника два из
высоты лежат по сторонам
треугольник, сегмент. АВ это высота
от А до сег. до н.э. и сег. ЦБ
высота от C до сегмента AB.
Оба они находятся по бокам
треугольник.
 Третья высота
сег. BD, то есть от B до AC.
точка пересечения сег. АВ, сег.
до н.э. и сег. BD есть B. Таким образом, для a
прямоугольный треугольник три высоты
пересекаются в вершине справа
угол.
Рисунок 2.11
Третья высота
сег. BD, то есть от B до AC.
точка пересечения сег. АВ, сег.
до н.э. и сег. BD есть B. Таким образом, для a
прямоугольный треугольник три высоты
пересекаются в вершине справа
угол.
Рисунок 2.11 - 2.4 Высота, медиана и биссектриса угла в. Высоты для тупоугольного треугольника: • D ABC — тупоугольный треугольник. Высота от линии А до пересечения содержащий seg.BC в D. Поэтому сег. AD – высота. Сходным образом seg.CE — высота на AB и BF высота на сегменте. переменного тока. Принадлежащий три высоты, присутствует только одна внутри треугольника. Два других находятся на продолжении линии содержащий противоположную сторону. Эти три высоты встречаются в точка P, которая находится вне треугольник. Рисунок 2.12
- 2.4 Высота, медиана и биссектриса угла
медиана
• Отрезок от вершины треугольника до середины стороны, противоположной
его называют медианой. Таким образом, каждый треугольник имеет три медианы. На рис. 2.13 показано
медианы остроугольного и тупоугольного треугольников.
 Все три медианы всегда пересекаются внутри треугольника, независимо от типа треугольника.
Все три медианы всегда пересекаются внутри треугольника, независимо от типа треугольника. - 2.4 Высота, медиана и биссектриса угла Биссектриса угла • Отрезок от вершины до противоположной стороны, делящий угол пополам. вершина называется биссектрисой угла. Таким образом, каждый треугольник имеет три биссектрисы угла. На рис. 2.14 показаны биссектрисы остроугольного и тупоугольного треугольников.
- 2.5 Конгруэнтность треугольников Два треугольника называются равными, если все соответствующие части равный. Для обозначения конгруэнтности используется символ @ и D PQR @ D STU. подразумевает, что а также т. е. соответствующие углы и соответствующие стороны равны.
- 2.5 Конгруэнтность треугольников С С С Постулат Если все стороны одного треугольника равны соответствующим сторонам другого треугольника, то эти треугольники равны (рис. 2.15). сег. АВ = сегмент. ПК, сег. БК = сег. QR-код и сег. СА = сегмент. РП D ABC @ D PQR от S S S.
- 2.5 Конгруэнтность треугольников
Постулат С А С
Если две стороны и угол, заключенный в одном треугольнике, равны
соответствующие две стороны и угол, заключенный в другом треугольнике, то
два треугольника равны (рис.
 2.16).
сег. АВ = сегмент. ПК, сег. БК = сег. QR-код
и
m ABC = m PQR
D ABC @ D PQR по постулату S A S.
2.16).
сег. АВ = сегмент. ПК, сег. БК = сег. QR-код
и
m ABC = m PQR
D ABC @ D PQR по постулату S A S. - 2.5 Конгруэнтность треугольников А С А постулат Если два угла одного треугольника и сторона, которую они образуют, равны соответствующие углы и сторона другого треугольника, эти два треугольника равны (рисунок 2.17). m B + m R m L = m P и сег. БК = сег. РП D ABC @ D QRP по постулату A S A.
- 2.5 Конгруэнтность треугольников Постулат АА S Если два угла треугольника и не заключенная в них сторона равны соответствующие углы и стороны другого треугольника, эти два треугольника равны конгруэнтны (рис. 2.18) m A = m P m B = m Q и АС = PR D ABC @ D PQR от AA S.
- 2.5 Конгруэнтность треугольников
Постулат HS
Этот постулат применим только к прямоугольным треугольникам. Если гипотенуза и любая
сторона прямоугольного треугольника равна гипотенузе и соответствующей стороне
другого прямоугольного треугольника, то эти два треугольника равны (рис.
 2.19).).
Тогда гипотенуза AC = гипотенуза PR.
Сторона AB = сторона PQ
D ABC @ D PQR по постулату HS.
2.19).).
Тогда гипотенуза AC = гипотенуза PR.
Сторона AB = сторона PQ
D ABC @ D PQR по постулату HS. - Упражнение 1: Назовите постулат, который будет использоваться для доказательства конгруэнтности следующих пар треугольников. а) б)
- Упражнение 1: Назовите постулат, который будет использоваться для доказательства конгруэнтности следующих пар треугольников. CD)
- Упражнение 1: Назовите постулат, который будет использоваться для доказательства конгруэнтности следующих пар треугольников. д) е)
- Упражнение 1: Назовите постулат, который будет использоваться для доказательства конгруэнтности следующих пар треугольников. г)
- Пример 1
На рис. 2.21 сег. МН @ сегмент. МО, секция. PN @ отд. PO, докажите, что MNP @MOP.
Рисунок 2.21
Решение:
Нарисуйте сегмент MP
В треугольнике MNP и MOP
сег. Миннесота в сегменте МО
сег. PN @ отд. ПО
сег. депутат @ сег. депутат
D MNP @ D MOP … (постулат S S S)
MNP @ MOP ….(поскольку они являются соответствующими углами
равные треугольники).

- Рисунок 2.21 Упражнение 2: На рис. 2.22 H и G — две точки на конгруэнтных сторонах DE и DF многоугольника D DEF, такие, что сег. DH @ сег. ДГ. Докажите, что сег. ВЧ @ сег. ГЭ.
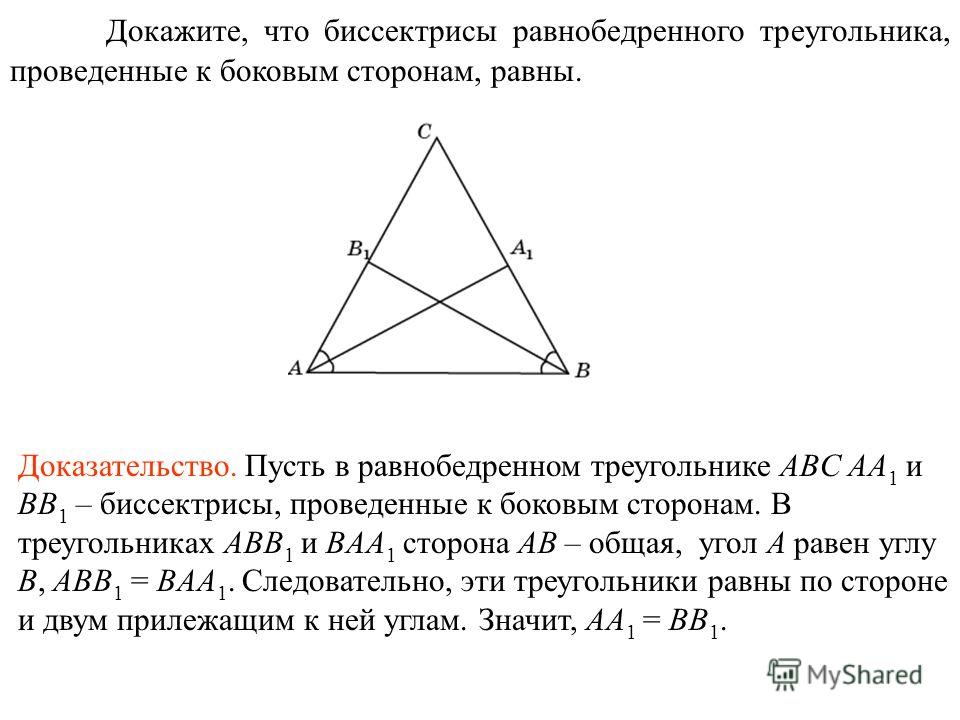
- 2.6 Стороны, противоположные конгруэнтным углам Теорема: Если две стороны треугольника равны, то противолежащие углы они также равны. Это можно доказать следующим образом: Рассмотрим D ABC, где AB = AC (рис. 2.23). Рисунок 2.23 Доказательство: Чтобы доказать, что m B = m C, опустите медиану из A в BC в точке P. Поскольку AP является медианой, BP = CP. В D ABP и D ACP сег. AB @ сег. АС (дано) сег. BP @ сегмент. CP (P — середина) сег. Точка доступа @сегмент. АП (та же линия) Следовательно, два треугольника конгруэнтны по постулату SSS. Д АД @ Д АКП m B = m C, поскольку они являются соответствующими углами конгруэнтных треугольников.
- 2.6 Стороны, противоположные конгруэнтным углам
Рисунок 2.24
Обратное утверждение этой теоремы также верно и может быть довольно легко доказано.
 Рассмотрим D ABC, где m B = m C (рис. 2.24).
Чтобы доказать, что AB = AC, опустим биссектрису угла AP на BC.
Поскольку AP — биссектриса m BAP = m CAP
m ABP = m ACP (дано)
сег. Точка доступа @сегмент. АП (та же сторона)
D ABP @ D ACP по постулату AAS.
Следовательно, соответствующие стороны равны.
сег. АВ = сегмент. переменный ток
Вывод: если два угла треугольника равны, то противолежащие им стороны
также равны.
Рассмотрим D ABC, где m B = m C (рис. 2.24).
Чтобы доказать, что AB = AC, опустим биссектрису угла AP на BC.
Поскольку AP — биссектриса m BAP = m CAP
m ABP = m ACP (дано)
сег. Точка доступа @сегмент. АП (та же сторона)
D ABP @ D ACP по постулату AAS.
Следовательно, соответствующие стороны равны.
сег. АВ = сегмент. переменный ток
Вывод: если два угла треугольника равны, то противолежащие им стороны
также равны. - конец
Реклама
Теорема о биссектрисе угла | Brilliant Math & Science Wiki
Тревор Араширо, Кханг Нгуен Тхань, Кристофер Бу, и
способствовал
Содержимое
- Определение
- Доказательство теоремы о биссектрисе угла
- Использование теоремы о биссектрисе угла
- Дополнительные проблемы
Разделить угол пополам означает разрезать его на две равные части или углы. Допустим, мы хотим разделить пополам угол в 50 градусов, тогда мы разделим его на два угла по 25 градусов.
Допустим, мы хотим разделить пополам угол в 50 градусов, тогда мы разделим его на два угла по 25 градусов.
Теорема о биссектрисе угла
На рисунке выше пусть \(x+y=c\big(=\lvert\overline{BA}\rvert\big),\) и пусть \(\lvert\overline{CD}\rvert=e\) — длина биссектрисы угла \(C\).
В своей простейшей форме теорема о биссектрисе угла утверждает, что
\[\begin{array} &\frac{a}{x}=\frac{b}{y} &\text{ or } &ay=bx.\qquad (1) \end{array}\]
Теорема о биссектрисе угла также утверждает, что \(e,\) длина биссектрисы угла \(\overline{CD},\) удовлетворяет 92=аб-ху. \qquad (2) \]
Доказательство (1):
Применение правила синусов к \(\треугольнику BCD\) и \(\треугольнику ACD\) дает
\[\dfrac{a}{\sin\angle BDC}=\dfrac{x}{\sin\angle BCD}, ~~~~~\dfrac{b}{\sin\angle ADC}=\dfrac{ y}{\sin\угол ACD}.\]
Используя равенства \(\sin\угол ADC=\sin\left(\pi-\угол BDC\right)=\sin\угол BDC\) и \(\angle BCD=\угол ACD\) \((\ )так как \(CD\) — биссектриса угла\(),\) получаем
\[\dfrac{a}{x}=\dfrac{\sin\angle BDC}{\sin\angle BCD}=\dfrac{\sin\angle ADC}{\sin\angle ACD}=\dfrac{b {у},\] 92x}{ab}}-xy\\ &=аб-ху.
\ _\квадрат \конец{выравнивание}\]
Другое доказательство (1):
Рассмотрим \(\треугольник ABC\) и пусть \(AE\) — биссектриса \(\угол A\).
Теперь продолжим \(AE\) до \(D\) так, чтобы \(CD\) был параллелен \(AB\).
Тогда \(\угол ABE\) = \(\угол DCE\) и \(\угол BAE\) = \(\угол CDE,\), откуда следует
\[\треугольник ABE\sim \треугольник DCE.\]
Итак,
\[\dfrac{c}{x} = \dfrac{a}{y}.\]
Поскольку \(\угол BAE\) = \(\угол CDE\) = \(\угол CAE,\) по свойству равнобедренности \(a = b,\), откуда следует
\[\dfrac{c}{x} = \dfrac{b}{y}. \ _\квадрат\]
В \(\triangle{ABC}\), \(\lvert\overline{AB}\rvert=10, \lvert\overline{BC}\rvert=8, \lvert\overline{AC}\rvert=12\) . Пусть \(D\) — точка на стороне \(\overline{AB}\) такая, что \(\overline{CD}\) делит пополам \(\угол C\). Тогда какова длина \(\overline{AD}?\)
Пусть \(\lvert\overline{AB}\rvert=c, \lvert\overline{BC}\rvert=a, \lvert\overline{AC}\rvert=b, \lvert\overline{AD}\rvert =y, \lvert\overline{BD}\rvert=x\), то теперь мы ищем \(y.
\)
Используя теорему о биссектрисе угла, \( \frac{y}{b}=\frac{x}{a}\implies \frac{y}{12}=\frac{x}{8}. \qquad (1 ) \)
Поскольку \(x+y=c\) или \(x=c-y,\) подставляется в \((1)\), мы получаем
\[\begin{выравнивание} \frac{y}{12}&=\frac{10-y}{8}\\\\ \Стрелка вправо y&=6. \ _\квадрат \конец{выравнивание}\]
Следующий пример аналогичен предыдущему, но вместо этого мы находим длину \(e\) биссектрисы угла \(\overline{CD}\).
В \(\triangle{ABC}\), \(\lvert\overline{AB}\rvert=10, \lvert\overline{BC}\rvert=8, \lvert\overline{AC}\rvert=12\) . Пусть \(D\) — точка на стороне \(\overline{AB}\) такая, что \(\overline{CD}\) делит пополам \(\угол C\), тогда какова длина \(\overline {CD}?\)
В нашем предыдущем примере мы уже нашли \(\lvert\overline{AD}\rvert=6\) и \(\lvert\overline{BD}\rvert=4\).
Таким образом,
\[\begin{выравнивание} е &=\sqrt{ab-xy}\\ &= \sqrt{(8)(12)-(4)(6)}\\ &=6\кварт{2}. \ _\квадрат \конец{выравнивание}\]
Нам дан треугольник со следующим свойством: один из его углов разделен на четыре части (делится на четыре равных угла) высотой, биссектрисой угла и медианой, проведенной из этой вершины.
Найдите градус четырехсекционной.
База разбита на четыре сегмента в соотношении \(x : x : y : 2x +y\).
Предположим, что длина левой стороны треугольника равна \(1\).
Тогда длина биссектрисы угла также равна \(1\).
Применяя теорему о биссектрисе угла к большому треугольнику, мы видим, что длина правой стороны равна\[\dfrac{2x+2y}{2x}=1+\dfrac{y}{x}.\]
Но если мы применим теорему о биссектрисе угла к левой половине треугольника, мы получим \(\frac{2x+y}{y}= 1+\frac{2x}{y}\) для той же длины. Следовательно,
\[\dfrac{y}{x}=\dfrac{2x}{y} \подразумевается x:y=1:\sqrt2.\] 9\круг\) треугольник.
Таким образом, четырехгранный угол прямой. \(_\квадрат\)
В \(\треугольнике ABC\), \(\угол ABC = 30°.\) на \(\overline{AC}\) выбраны точки \(P\) и \(Q\) такие, что \(AP+ ВС=АВ+СQ\). Биссектриса внутреннего угла \(\угол ABC\) пересекает \(\overline{AC}\) в точке \(R\).

 Multiple-choice
Multiple-choice Multiple-choice
Multiple-choice Найдите АН, если АН : НВ = 1 : 8, АС = 9.
Найдите АН, если АН : НВ = 1 : 8, АС = 9.
 На рис. 2.3 показан
равносторонний треугольник.
Рисунок 2.3
На рис. 2.3 показан
равносторонний треугольник.
Рисунок 2.3 в. Прямоугольный треугольник: это треугольник в
какой из углов прямой
угол. Рисунок 2.9показывает право
треугольник.
Поскольку KJL равно 900, можно сказать
что JKJL и JLK
дополняющий. В прямоугольном треугольнике
сторона, противоположная прямому углу,
называется гипотенузой.
в. Прямоугольный треугольник: это треугольник в
какой из углов прямой
угол. Рисунок 2.9показывает право
треугольник.
Поскольку KJL равно 900, можно сказать
что JKJL и JLK
дополняющий. В прямоугольном треугольнике
сторона, противоположная прямому углу,
называется гипотенузой. Третья высота
сег. BD, то есть от B до AC.
точка пересечения сег. АВ, сег.
до н.э. и сег. BD есть B. Таким образом, для a
прямоугольный треугольник три высоты
пересекаются в вершине справа
угол.
Рисунок 2.11
Третья высота
сег. BD, то есть от B до AC.
точка пересечения сег. АВ, сег.
до н.э. и сег. BD есть B. Таким образом, для a
прямоугольный треугольник три высоты
пересекаются в вершине справа
угол.
Рисунок 2.11 Все три медианы всегда пересекаются внутри треугольника, независимо от типа треугольника.
Все три медианы всегда пересекаются внутри треугольника, независимо от типа треугольника.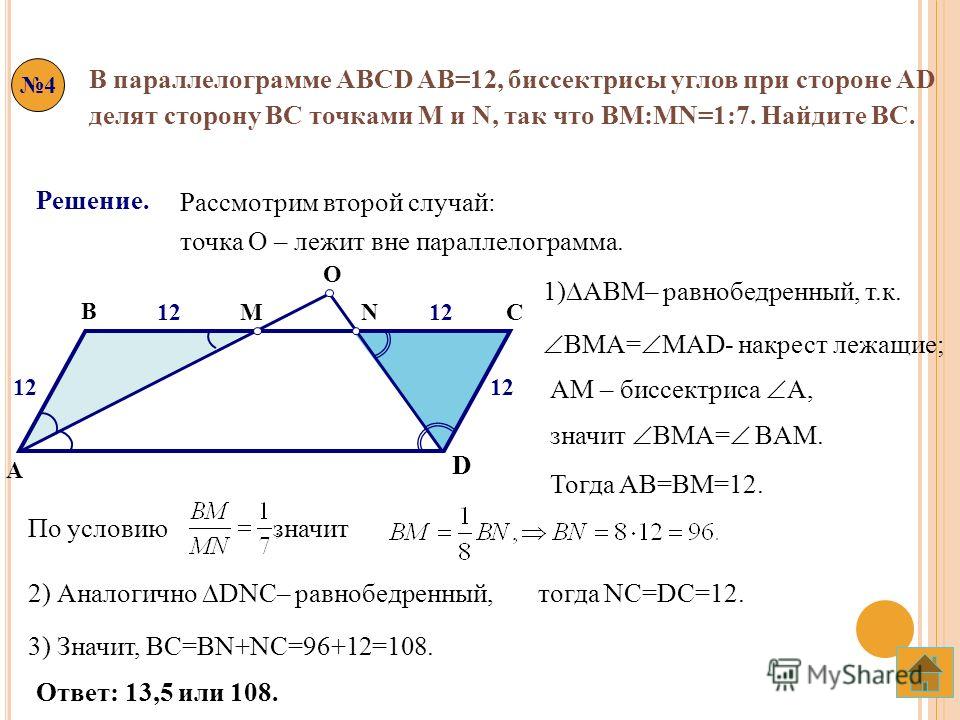 2.16).
сег. АВ = сегмент. ПК, сег. БК = сег. QR-код
и
m ABC = m PQR
D ABC @ D PQR по постулату S A S.
2.16).
сег. АВ = сегмент. ПК, сег. БК = сег. QR-код
и
m ABC = m PQR
D ABC @ D PQR по постулату S A S. 2.19).).
Тогда гипотенуза AC = гипотенуза PR.
Сторона AB = сторона PQ
D ABC @ D PQR по постулату HS.
2.19).).
Тогда гипотенуза AC = гипотенуза PR.
Сторона AB = сторона PQ
D ABC @ D PQR по постулату HS.
 Рассмотрим D ABC, где m B = m C (рис. 2.24).
Чтобы доказать, что AB = AC, опустим биссектрису угла AP на BC.
Поскольку AP — биссектриса m BAP = m CAP
m ABP = m ACP (дано)
сег. Точка доступа @сегмент. АП (та же сторона)
D ABP @ D ACP по постулату AAS.
Следовательно, соответствующие стороны равны.
сег. АВ = сегмент. переменный ток
Вывод: если два угла треугольника равны, то противолежащие им стороны
также равны.
Рассмотрим D ABC, где m B = m C (рис. 2.24).
Чтобы доказать, что AB = AC, опустим биссектрису угла AP на BC.
Поскольку AP — биссектриса m BAP = m CAP
m ABP = m ACP (дано)
сег. Точка доступа @сегмент. АП (та же сторона)
D ABP @ D ACP по постулату AAS.
Следовательно, соответствующие стороны равны.
сег. АВ = сегмент. переменный ток
Вывод: если два угла треугольника равны, то противолежащие им стороны
также равны. \ _\квадрат
\конец{выравнивание}\]
\ _\квадрат
\конец{выравнивание}\] \)
\)
Leave A Comment