Как обозначать числа с пи на числовой окружности?
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа \(2π\), \(π\), \(\frac{π}{2}\), \(-\frac{π}{2}\), \(\frac{3π}{2}\)
Как вы знаете из прошлой статьи, радиус числовой окружности равен \(1\). Значит, длина окружности равняется \(2π\) (вычислили по формуле \(l=2πR\)). С учетом этого отметим \(2π\) на числовой окружности. Чтобы отметить это число нужно пройти от \(0\) по числовой окружности расстояние равно \(2π\) в положительном направлении, а так как длина окружности \(2π\), то получается, что мы сделаем полный оборот. То есть, числу \(2π\) и \(0\) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.
Теперь обозначим на числовой окружности число \(π\). \(π\) – это половина от \(2π\). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от \(0\) в положительном направлении половину окружности.
Отметим точку \(\frac{π}{2}\). \(\frac{π}{2}\) – это половина от \(π\), следовательно чтобы отметить это число, нужно от \(0\) пройти в положительном направлении расстояние равное половине \(π\), то есть четверть окружности.
Обозначим на окружности точки \(-\)\(\frac{π}{2}\). Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.
Нанесем \(-π\). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.
Теперь рассмотрим пример посложнее. Отметим на окружности число \(\frac{3π}{2}\). Для этого дробь \(\frac{3}{2}\) переведем в смешанный вид \(\frac{3}{2}\)\(=1\)\(\frac{1}{2}\), т.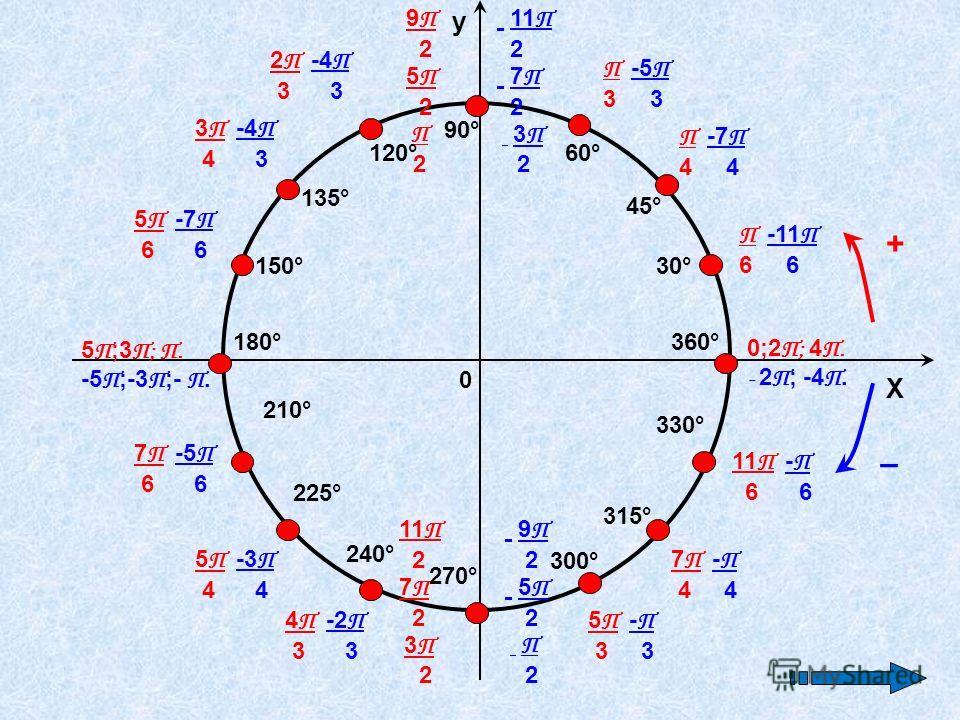 е. \(\frac{3π}{2}\)\(=π+\)\(\frac{π}{2}\). Значит, нужно от \(0\) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
е. \(\frac{3π}{2}\)\(=π+\)\(\frac{π}{2}\). Значит, нужно от \(0\) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
Задание 1. Отметьте на числовой окружности точки \(-2π\),\(-\)\(\frac{3π}{2}\).
Обозначаем числа \(\frac{π}{4}\), \(\frac{π}{3}\), \(\frac{π}{6}\)
Выше мы нашли значения в точках пересечения числовой окружности с осями \(x\) и \(y\). Теперь определим положение промежуточных точек. Для начала нанесем точки \(\frac{π}{4}\), \(\frac{π}{3}\) и \(\frac{π}{6}\).
\(\frac{π}{4}\) – это треть от \(π\) (иначе говоря,\(\frac{π}{3}\)\(=π:3\)), поэтому расстояние \(\frac{π}{3}\) – это треть от полукруга.
\(\frac{π}{6}\) – это половина \(\frac{π}{3}\) (ведь \(\frac{π}{6}\)\(=\)\(\frac{π}{3}\)\(:2\)) поэтому расстояние \(\frac{π}{6}\) – это половина от расстояния \(\frac{π}{3}\).
Вот так они расположены друг относительно друга:
Замечание: Расположение точек со значением \(0\), \(\frac{π}{2}\),\(π\), \(\frac{3π}{2}\), \(\frac{π}{4}\), \(\frac{π}{3}\), \(\frac{π}{6}\) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа \(\frac{7π}{6}\), \(-\frac{4π}{3}\), \(\frac{7π}{4}\)
Обозначим на окружности точку \(\frac{7π}{6}\), для этого выполним следующие преобразования: \(\frac{7π}{6}\)\(=\)\(\frac{6π + π}{6}\)\(=\)\(\frac{6π}{6}\)\(+\)\(\frac{π}{6}\)\(=π+\)\(\frac{π}{6}\).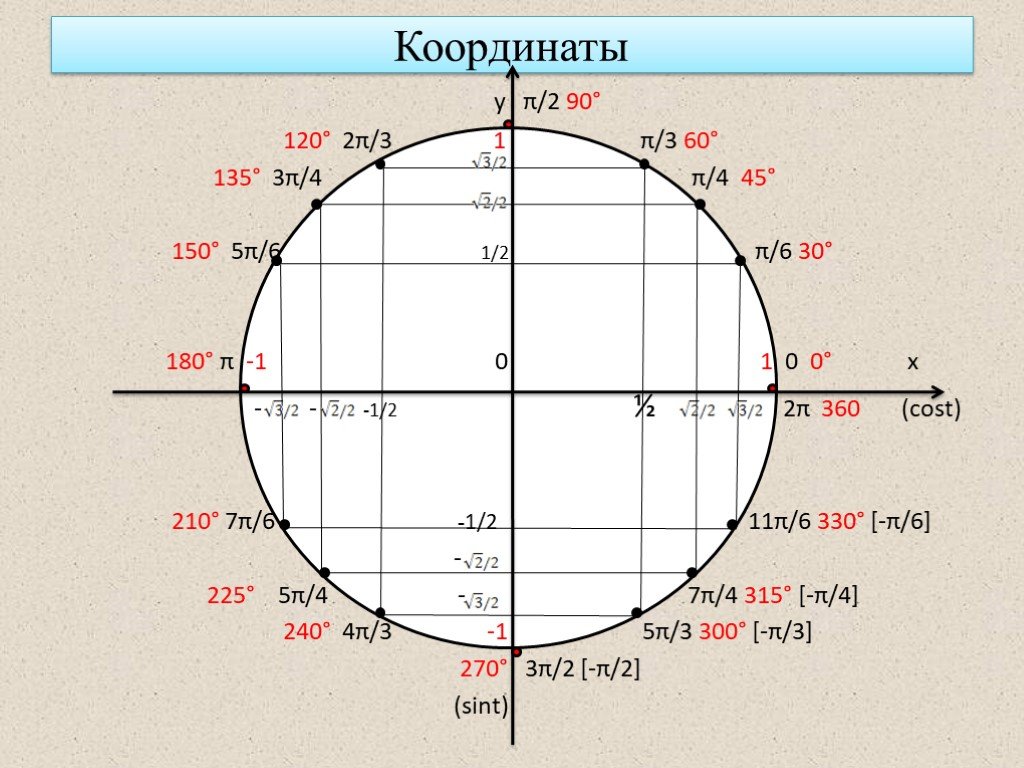 Отсюда видно, что от нуля в положительную сторону надо пройти расстояние \(π\), а потом еще \(\frac{π}{6}\).
Отсюда видно, что от нуля в положительную сторону надо пройти расстояние \(π\), а потом еще \(\frac{π}{6}\).
Отметим на окружности точку \(-\)\(\frac{4π}{3}\). Преобразовываем: \(-\)\(\frac{4π}{3}\)\(=-\)\(\frac{3π}{3}\)\(-\)\(\frac{π}{3}\)\(=-π-\)\(\frac{π}{3}\). Значит надо от \(0\) пройти в отрицательную сторону расстояние \(π\) и еще \(\frac{π}{3}\).
Нанесем точку \(\frac{7π}{4}\), для этого преобразуем \(\frac{7π}{4}\)\(=\)\(\frac{8π-π}{4}\)\(=\)\(\frac{8π}{4}\)\(-\)\(\frac{π}{4}\)\(=2π-\)\(\frac{π}{4}\). Значит, чтобы поставить точку со значением \(\frac{7π}{4}\), надо от точки со значением \(2π\) пройти в отрицательную сторону расстояние \(\frac{π}{4}\).
Задание 2. Отметьте на числовой окружности точки \(-\)\(\frac{π}{6}\),\(-\)\(\frac{π}{4}\),\(-\)\(\frac{π}{3}\),\(\frac{5π}{4}\),\(-\)\(\frac{7π}{6}\),\(\frac{11π}{6}\), \(\frac{2π}{3}\),\(-\)\(\frac{3π}{4}\).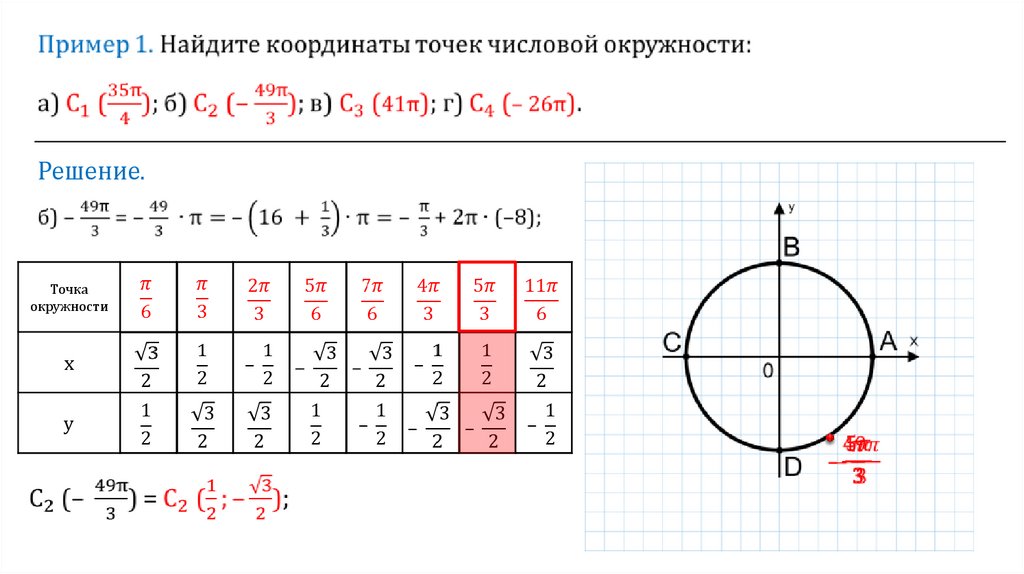
Обозначаем числа \(10π\), \(-3π\), \(\frac{7π}{2}\) ,\(\frac{16π}{3}\), \(-\frac{21π}{2}\), \(-\frac{29π}{6}\)
Запишем \(10π\) в виде \(5 \cdot 2π\). Вспоминаем, что \(2π\) – это расстояние равное длине окружности, поэтому чтобы отметить точку \(10π\), нужно от нуля пройти расстояние равное \(5\) окружностям. Нетрудно догадаться, что мы окажемся снова в точке \(0\), просто сделаем пять оборотов.
Из этого примера можно сделать вывод:
Числам с разницей в \(2πn\), где \(n∈Z\) (то есть \(n\) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше \(2π\) (или меньше \(-2π\)), надо выделить из него целое четное количество \(π\) (\(2π\), \(8π\), \(-10π\)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Еще один вывод:
Точке, которой соответствует \(0\), также соответствуют все четные количества \(π\) (\(±2π\),\(±4π\),\(±6π\)…).
Теперь нанесем на окружность \(-3π\). \(-3π=-π-2π\), значит \(-3π\) и \(–π\) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в \(-2π\)).
Кстати, там же будут находиться все нечетные \(π\).
Точке, которой соответствует \(π\), также соответствуют все нечетные количества \(π\) (\(±π\),\(±3π\),\(±5π\)…).
Сейчас обозначим число \(\frac{7π}{2}\). Как обычно, преобразовываем: \(\frac{7π}{2}\)\(=\)\(\frac{6π}{2}\)\(+\)\(\frac{π}{2}\)\(=3π+\)\(\frac{π}{2}\)\(=2π+π+\)\(\frac{π}{2}\). Два пи – отбрасываем, и получается что, для обозначения числа \(\frac{7π}{2}\) нужно от нуля в положительную сторону пройти расстояние равное \(π+\)\(\frac{π}{2}\) (т.е. половину окружности и еще четверть).
Отметим \(\frac{16π}{3}\). Вновь преобразования: \(\frac{16π}{3}\)\(=\)\(\frac{15π + π}{3}\)\(=\)\(\frac{15π}{3}\)\(+\)\(\frac{π}{3}\)\(=5π+\)\(\frac{π}{3}\)\(=4π+π+\)\(\frac{π}{3}\).
Нанесем на окружность число \(-\)\(\frac{21π}{2}\).
\(-\)\(\frac{21π}{2}\)\(= -\)\(\frac{20π}{2}\)\(-\)\(\frac{π}{2}\)\(=-10π-\)\(\frac{π}{2}\). Значит, место \(-\)\(\frac{21π}{2}\) совпадает с местом числа \(-\)\(\frac{π}{2}\).
Обозначим \(-\)\(\frac{29π}{6}\).
\(-\)\(\frac{29π}{6}\)\(=-\)\(\frac{30π}{6}\)\(+\)\(\frac{π}{6}\)\(=-5π+\)\(\frac{π}{6}\)\(=-4π-π+\)\(\frac{π}{6}\). Для обозначение \(-\)\(\frac{29π}{6}\), на числовой окружности надо от точки со значением \(–π\) пройти в положительную сторону \(\frac{π}{6}\).
Задание 3. Отметьте на числовой окружности точки \(-8π\),\(-7π\), \(\frac{11π}{4}\),\(-\)\(\frac{7π}{3}\),\(\frac{17π}{6}\),\(-\)\(\frac{20π}{3}\),\(-\)\(\frac{11π}{2}\).
Скачать статью
Окружность на координатной плоскости
☰
Если расположить единичную числовую окружность на координатной плоскости, то для ее точек можно найти координаты. Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0).
Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0).
Обычно на единичной числовой окружности отмечают точки соответствующие от начала отсчета на окружности
- четвертям — 0 или 2π, π/2, π, (2π)/3,
- серединам четвертей — π/4, (3π)/4, (5π)/4, (7π)/4,
- третям четвертей — π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.
На координатной плоскости при указанном выше расположении на ней единичной окружности можно найти координаты, соответствующие этим точкам окружности.
Координаты концов четвертей найти очень легко. У точки 0 окружности координата x равна 1, а y равен 0. Можно обозначить так A (0) = A (1; 0).
Конец первой четверти будет располагаться на положительной полуоси ординат. Следовательно, B (π/2) = B (0; 1).
Конец второй четверти находится на отрицательной полуоси абсцисс: C (π) = C (-1; 0).
Конец третьей четверти: D ((2π)/3) = D (0; -1).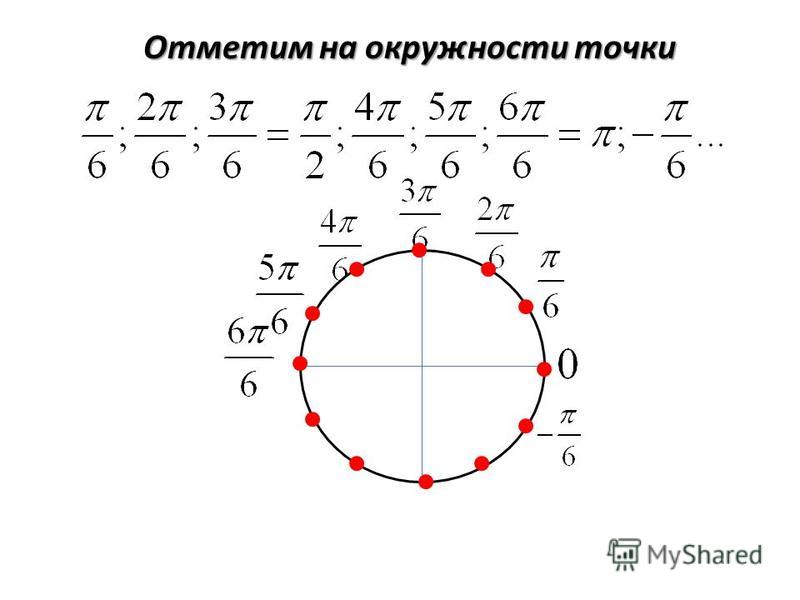
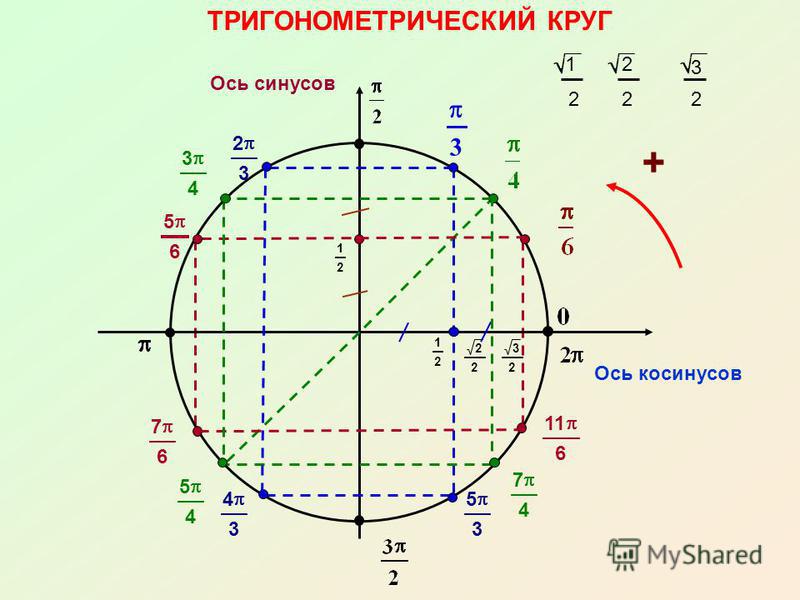
Но как найти координаты середин четвертей? Для этого строят прямоугольный треугольник. Его гипотенузой является отрезок от центра окружности (или начала координат) к точке середины четверти окружности. Это радиус окружности. Поскольку окружность единичная, то гипотенуза равна 1. Далее проводят перпендикуляр из точки окружности к любой оси. Пусть будет к оси x. Получается прямоугольный треугольник, длины катетов которого — это и есть координаты x и y точки окружности.
Четверть окружности составляет 90º. А половина четверти составляет 45º. Поскольку гипотенуза проведена к точке середины четверти, то угол между гипотенузой и катетом, выходящим из начала координат, равен 45º. Но сумма углов любого треугольника равна 180º. Следовательно, на угол между гипотенузой и другим катетом остается также 45º. Получается равнобедренный прямоугольный треугольник.
Из теоремы Пифагора получаем уравнение x2 + y2 = 12. Поскольку x = y, а 12 = 1, то уравнение упрощается до x2 + x2 = 1. Решив его, получаем x = √½ = 1/√2 = √2/2.
Решив его, получаем x = √½ = 1/√2 = √2/2.
Таким образом, координаты точки M1 (π/4) = M1 (√2/2; √2/2).
В координатах точек середин других четвертей будут меняться только знаки, а модули значений оставаться такими же, так как прямоугольный треугольник будет только переворачиваться. Получим:
M2 ((3π)/4) = M2 (-√2/2; √2/2)
M3 ((5π)/4) = M3 (-√2/2; -√2/2)
M4 ((7π)/4) = M4 (√2/2; -√2/2)
При определении координат третьих частей четвертей окружности также строят прямоугольный треугольник. Если брать точку π/6 и проводить перпендикуляр к оси x, то угол между гипотенузой и катетом, лежащим на оси x, составит 30º. Известно, что катет, лежащий против угла в 30º, равен половине гипотенузы. Значит, мы нашли координату y, она равна ½.
Зная длины гипотенузы и одного из катетов, по теореме Пифагора находим другой катет:
x2 + (½)2 = 12
x2 = 1 — ¼ = ¾
x = √3/2
Таким образом T1 (π/6) = T1 (√3/2; ½).
Для точки второй трети первой четверти (π/3) перпендикуляр на ось лучше провести к оси y. Тогда угол при начале координат также будет 30º. Здесь уже координата x будет равна ½, а y соответственно √3/2: T2 (π/3) = T2 (½; √3/2).
Для других точек третей четвертей будут меняться знаки и порядок значений координат. Все точки, которые ближе расположены к оси x будут иметь по модулю значение координаты x, равное √3/2. Те точки, которые ближе к оси y, будут иметь по модулю значение y, равное √3/2.
T3 ((2π)/3) = T3 (-½; √3/2)
T4 ((5π)/6) = T4 (-√3/2; ½)
T5 ((7π)/6) = T5 (-√3/2; -½)
T6 ((4π)/3) = T6 (-½; -√3/2)
T7 ((5π)/3) = T7 (½; -√3/2)
T8 ((11π)/6) = T8 (√3/2; -½)
CHHAYA PUBLICATION-CIRCLE-Exercise 3 (Quick Answer Type Questions)
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro и dekho sari videos bina kisi ad ки рукаават ке!
Обновлено: 27-06-2022
लिखित उत्तर
Ответ
Правильный ответ-x-3y = 5
Шаг за шагом от экспертов.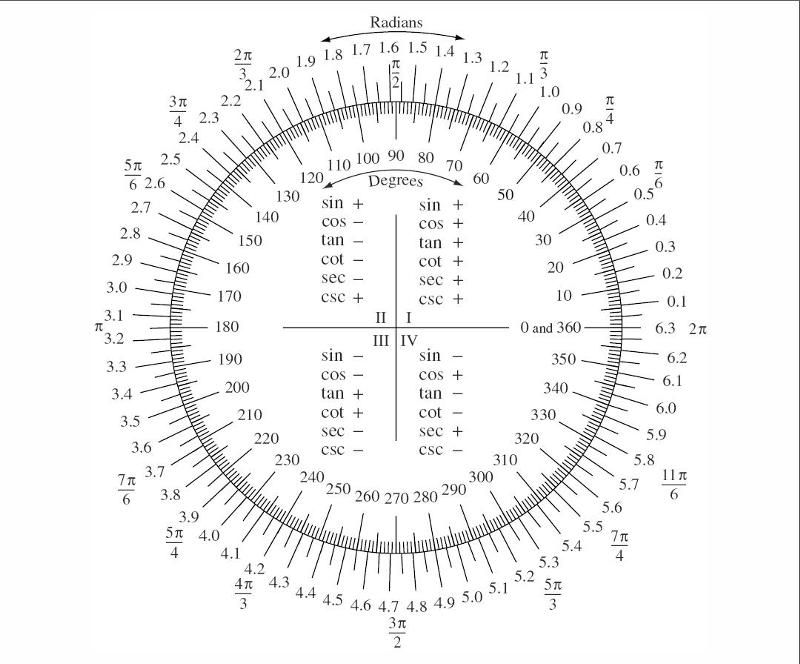 . 92 Орхонально, тогда уравнение локуса его центра:
. 92 Орхонально, тогда уравнение локуса его центра:
412661479
যদি x2+y2- (3p+4) x- (p — 2) y+10p = 0 বৃত্তটি (3,1) বিন্দুগামী হয়, তবে P এর মান হবে-
470819851
দেখাও যে, P- এর সব মানের জন্য x2+y2-x (3p+4) −y (p- 2)+10p = 0 বৃত্ত (3, 1) বিন্দু দিয়ে যায়। যদি P পরিবর্তনশীল হয়, তবে কেন্দ্রের সঞ্চারপথ নির্ণয় করো।।।।
470825732
Покажите, что геометрическое место центров окружностей, проходящих через точки пересечения окружностей x2+y2=1 и x2+y2−2x+y=0, равно x+2y=0 92=0, то существует окружность, проходящая через P,Q и (1,1) для
642548889
. Покажите, что для всех значений p окружность x2+y2−x(3p+4)−y(p−2 )+10p=0 проходит через точку (3,1). Если p меняется, найдите геометрическое место центра указанной выше окружности.
643970384
Если точка P такая, что отношение квадратов длин касательных от P к окружности S x2+y2+2x−4y−20=0 и x2+y2−4x+2y−44=0 равно 2:3, тогда геометрическое место P представляет собой окружность с центром
644181538
Геометрическое место центра окружности, проходящей через пересечение окружностей x2+y2=1 и x2+y2−2x+y=0, равно
644746879
для пересечения разностной границы
Когда люди нравятся друг другу, правила меняются
Три практики
Я буду необычайно интересоваться другими
Я останусь в комнате с отличием
Я перестану сравнивать свои лучшие качества с вашими худшими
Предстоящие круги
Обновления по электронной почте
Избранные видео
Пояснение к 3-м практическим кругам — за 100 секунд.
Тогда я понял, что моя раса имеет значение. Клип 3Practice Story Circle
Приходят ли незаслуженные привилегии к пробуждению белым в Америке?
Джим Хендерсон представляет 3 практики [любезно предоставлено Тедксом Эвереттом]
Цветные люди: Насколько вы можете доверять Белому союзнику… и как узнать?
3 практики . Краткое введение и история
Брайан Макларен о 3 тренировочных кругах с Джимом Хендерсоном и Джимом Хэнкоком
Питер Блок рассказывает о важности 3 тренировочных кружков
Купить на Амазонке
5-звездочные отзывы
***** Отличная маленькая книга. Легко читать. Но имеет глубокую проницательность и практическое применение
Мне нравится, как книга разбита на легко усваиваемые части, которые можно применять на практике в повседневном общении с другими, особенно с людьми, которые могут категорически не соглашаться с тобой more
***** Сообщение и инструменты, которые нам нужны
Хендерсон и Хэнкок доставили инструменты, в которых мы все нуждаемся. С какой бы стороны вы ни оказались (и вы обнаружите, что оказались на одной из сторон), вы захотите узнать о 3 практиках more
С какой бы стороны вы ни оказались (и вы обнаружите, что оказались на одной из сторон), вы захотите узнать о 3 практиках more
***** 5.0 из 5 звезд Спасательный круг в мутной воде
Мне понравилось это легкое чтение о том, как остаться в комнате с разницей. «Мне было бы любопытно узнать…» — прекрасный мостик для осознанного разговора. больше
Узнайте больше или оставьте свой отзыв на Amazon.com
W e тренируйте лидеров кругов в когортах, потому что в 3Practice Circles обретение ясности — это командный вид спорта.
Изучение вместе готовит нас к совместной работе в качестве главных судей и со-арбитров, когда мы начнем собирать и вести 3 практических кружка в реальном мире.
3Тренировочные круги волшебны, но не волшебны. Мы раскрываем секреты, благодаря которым Круги работают, на шести онлайн-тренировках в течение трех недель. Затем командный практикум — руководство 3Practice Workout Circles под руководством тренеров 3Practice — готовит нас к созыву и проведению реальных 3Practice Circles — лично и онлайн — в качестве сертифицированных руководителей 3Practice Circle.
Затем командный практикум — руководство 3Practice Workout Circles под руководством тренеров 3Practice — готовит нас к созыву и проведению реальных 3Practice Circles — лично и онлайн — в качестве сертифицированных руководителей 3Practice Circle.
Шесть живых учебных занятий
Сессии Сессии на Zoom — Около двух часов на класс
часы каждую пятницу 12P (или по примеру)
Занятие 01 — 3Руководство в практическом кружкеЗанятие 02 — 3Свертывание практического кружка
Занятие 03 — 3Роли практического кружка
Занятие 04 040087 – 3Правила тренировочного круга
Сессия 05 – 3Развертка тренировочного круга
Сессия 06 – 3Резонанс тренировочного круга
Мы записываем каждую тренировку. Если вы пропустите одно из них, вы можете посмотреть запись и обсудить ее с инструкторами в рабочее время.
После шести тренировочных занятий для руководителей 3-х тренировочных кружков формируются практические команды для раунда 3-х тренировочных кружков и коучинга, которые обычно завершаются примерно через месяц, во время которых каждый член команды по очереди выполняет функции главного судьи и Помощник судьи для всего круга.
3Инструкторы практического кружка наблюдают за кандидатами и тренируют их. По завершении тренировочных кружков и коучинга кандидаты получают сертификат 3Practice Circle Leaders.
If you want to talk about Circle Leader training, send us a note or email us: [email protected] or [email protected]
Open and Private 3Practice Когорты обучения руководителей кругов Самые эффективные Когорты 3Practice Circle Leaders проходят в течение шести двухчасовых сеансов Zoom в прямом эфире в течение трех недель, за которыми следуют практические занятия с тренером в группах по два человека.
Открытые когорты для отдельных лиц и небольших групп обычно проводятся с 4 до 6 часов по тихоокеанскому времени — понедельник + среда или вторник + четверг. Обычно мы планируем четыре или пять открытых когорт в год.
Частные когорты расписаны в соответствии с календарем и расписанием организаций и учреждений, которые заказывают обучение.
ЗАПИСАТЬСЯ НА СЛЕДУЮЩИЙ ТРЕНИНГ
СПРОСИТЕ О ПРЕДСТОЯЩЕМ ТРЕНИНГЕ ДЛЯ РУКОВОДИТЕЛЕЙ КРУГА
Пара часто задаваемых вопросов
Часто задаваемые вопросы: Что такое практикум по обучению руководителей кружков?После шестисеансовой серии онлайн-тренировок Zoom практические команды — обычно два человека — вместе работают над раундом из 3 практических тренировочных кружков и коучингом — в течение примерно четырех недель, — в течение которых каждый член команды по очереди выполняет функции главного судьи и Со-арбитр.
3Инструкторы практического кружка наблюдают за кандидатами и тренируют их на протяжении всего практического занятия.
Конечно. Если вы берете деньги за руководство 3Practice Circles, у нас есть для этого простое лицензионное соглашение.
Лицензионный сбор немного компенсирует нам текущую разработку и систему поддержки, которую мы предоставляем. И это помогает нам снизить плату за обучение на начальном этапе, что очень важно для нас.
Если вам нужны подробности, , пожалуйста, свяжитесь с нами .
Практика 1
Меня будут необычайно интересовать другие.
«Внимание — редчайшая и чистейшая форма щедрости».
— Симоне Вейл
человек, но его привычка, которая меня больше всего интересует, — это его любопытство. По радио Ира производит впечатление действительно любознательного человека. Я хотел знать, был ли он таким в реальной жизни, поэтому я спросил его.
«Ира засмеялась. «Конечно, мне любопытно! Я имею в виду, насколько фальшивым было бы для меня задавать вопросы, не имея их в виду? Как вы думаете, люди не поймут это?» Конечно, поймут».
Большинство из нас научились замечать фальшивый интерес за милю. Мы также учимся распознавать искренность. И нас тянет к тем, кто искренне хочет нас понять. В «Трех практиках» мы пытаемся начинать каждый вопрос со слов «Мне было бы любопытно узнать…».
Подумайте о тех случаях, когда вы получали положительное, конкретное, приветственное внимание… такое внимание, которое заставляло вас чувствовать себя в тот момент самым важным человеком в комнате — потому что кто-то задал вопрос в способ, который сделал вас единственным человеком, который мог ответить на него.
У большинства из нас нет переизбытка таких воспоминаний, поэтому те, которые у нас есть, остаются с нами навсегда — учитель, который подбадривал нас, родитель друга, который радушно принял нас, сосед по комнате в колледже, который познакомила нас со своими друзьями — все они были сложены в мысленную папку под названием «Невозможно забыть».
Джим Хендерсон говорит: «Айра Гласс — создатель и ведущий чрезвычайно популярного радиошоу и подкаста This American Life . Ира — очаровательная
Первая практика посвящена искреннему любопытству.
Вторая практика
Я останусь в комнате с разницей.«Когда вы обнаружите, что я голосовал не за того человека, значит ли это, что нам нужно расстаться?»
Но это чувство безопасности неизбежно проходит… сменяется подозрением, тревогой, страхом, гневом…. Не нужно большого воображения, чтобы понять, что быть разделенным вовсе не безопаснее.
Как выразилась Кэтрин Шульц: «Воображение — это то, что позволяет нам . . . наслаждайтесь историями, отличными от наших собственных. …Эмпатия — это то, что позволяет нам серьезно относиться к этим историям». Придумывать и практиковать новые способы преодоления Раздела Различий — и жить, чтобы рассказывать об этом — вот в чем суть 3-х практик.
Если бы 3 практики нужно было свести к одной идее, это была бы Пребывание в комнате с отличием.
Даже беглый взгляд на культурный ландшафт, вероятно, заставит людей чувствовать себя немного неуверенно в этом утверждении. Оставаться в комнате с отличием — это то, чего люди учатся избегать в изоляции сделанных на заказ эхо-камер социальных сетей и узконаправленных СМИ. Почему-то кажется, что безопаснее искать компанию себе подобных.
вторая практика — попасть в комнату и сделать все возможное, чтобы остаться в комнате.
Практика третья
Я перестану сравнивать свои лучшие качества с вашими худшими. «У меня нет времени знакомиться с каждым человеком, которого я встречаю в своей повседневной жизни. Так что, слава богу, в моем распоряжении есть удобное маленькое устройство, которое помогает мне понять, как бороться практически со всеми, с кем я сталкиваюсь: со стереотипами. Да, стереотипы реально экономят время!»
Да, стереотипы реально экономят время!»
— The Onion
3 Практика Закройте круг предложением поблагодарить кого-то из участников круга. Люди часто выражают благодарность за вежливые, наводящие на размышления вопросы, которые им задавали. А некоторые идут еще дальше — например, человек, который закончил свою благодарность словами: «Во время этой группы я понял, что иногда я думаю, что вещи — это факты, которые на самом деле могут вовсе не быть фактами. Мне нужно подумать об этом больше».
По сути, это говорит: «Позвольте мне встать там, где стоите вы, и посмотреть, увижу ли я то же самое. А потом мы поговорим об этом».
Неспособность видеть то, что другим кажется очевидным, само по себе не является моральным недостатком.
Слушая, как другой человек описывает то, что он видит, мы можем осознать, что, как он не видит того, что видим мы, так и мы не видим того, что видят они.
Это полезное напоминание о том, что то, что видят два человека, частично зависит от того, где они стоят, и повышает вероятность того, что 1) ни у одного из них не может быть совершенно беспрепятственного обзора, и 2) у одного может быть более четкий обзор или лучший угол чем другой.

Leave A Comment