3 x решение: Решение уравнений онлайн

Решение систем уравнений онлайн

Рассмотрим систему из двух нелинейных уравнений с двумя неизвестными:

x25y245y3x3

Перепишем уравнения системы в следующем виде:

x245y241y3x535

Тогда, первое уравнение системы представляет собой эллипс с большой полуосью равной 2 и малой полуосью равной 25 . Второе уравнение системы — это прямая линия с тангесом угла наклона равным 35 и величиной отрезка, отсекаемого на оси Oy равной 35 .

Изобразим вышесказанное на схематичном графике:

Точки пересечения прямой с эллипсом M₁(x₁,y₁) и M₂(x₂,y₂) являются решениями исходной системы уравнений. Поскольку прямая пересекает эллипс только в двух указанных выше точках, других решений нет.

Только что мы рассмотрели так называемый графический метод решения систем уравнений, который хорошо подходит для решения системы из двух уравнений с двумя неизвестными. При большем количестве неизвестных, решениями будут точки в многомерном пространстве, что существенно усложняет задачу.

Если для решения исходной системы использовать более универсальный метод подстановки, мы получим следующий результат:

x19235140.452122y135235700.871273×29235141.73784y235235700.442702

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, позволяет решать разнообразные типы систем уравнений.

Решить кубические уравнения онлайн

Часто при решении математических, статистических, инженерных задач приходится решать разные уравнения.

Уравнение 3-й степени — это кубическое уравнение вида ax

3 + bx² + cx + d = 0, где а не равно 0. Число х считается корнем уравнения, если при его подстановке получается верное равенство.

Для графического анализа уравнения используется кубическая парабола.

Имеются разные способы решения кубических уравнений, среди них: теорема Безу, формулы Кардано, Виета, метод возвратного уравнения.

Кубические уравнения вида: х³ = а имеют корень x = ³√a

В некоторых случаях при решении уравнений:

• в левой части уравнения можно сгруппировать слагаемые;
• разложить ее на множители;
• найти корни.

Решение уравнения методом Кардано начинается с приведения исходного кубического уравнения ax

3 + bx² + cx + d = 0 к более простому виду: y³ + py + q = 0, если заменить х неизвестным у при условии х = у — b / 3а.

В данном уравнении: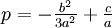
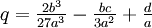Кубическое уравнение имеет 3 корня, разберем их с помощью дискриминанта:

Δ = — 4b³d + b²c² — 4ac³ + 18abcd — 27a²d²

• если дискриминант больше 0, уравнение имеет 3 вещественных корня;
• если меньше 0, 1 — вещественный корень и 2 комплексных;
• если меньше 0, тогда хотя бы 2 корня совпадают.

С помощью онлайн калькулятора можно намного быстрее решить кубическое уравнение, найти его корни.

Решение задач по математике онлайн

Данный сайт обращён к учащимся в том или ином объеме изучающим математику и/или геометрию и призван помочь школьникам и студентам в изучении курса математики, освободить их от многих рутинных вычислений, и подсказать метод решения.
Основу сайта составляют математические программы (калькуляторы) для решения задач онлайн.
Все вычисления производятся на сайте, программы не нужно скачивать и устанавливать на компьютер.

На каждую задачу приводится поэтапный процесс получения ответа, т.е. подробное решение с объяснениями этапов решения данной задачи.
Решение задач приводится в виде, принятом в большинстве школ и вузов, некоторые задачи решаются двумя способами.
Все математические программы (калькуляторы) бесплатные.
Полный список математических и геометрических задач для решения вы можете найти в меню справа.

Вычислить: $$x^2+2x-1=0$$ $$2\frac{1}{3} \cdot \left( 2\frac{3}{4}-1\frac{3}{8} \right) $$ Решение: $$2\frac{1}{3} \cdot \left( 2\frac{3}{4}-1\frac{3}{8} \right) = $$

Промежуточные результаты:

$$2\frac{3}{4}-1\frac{3}{8} = \frac{2\cdot(2\cdot4+3)-1\cdot8-3}{8} = \frac{11}{8}$$

$$ = 2\frac{1}{3} \cdot \frac{11}{8} = \frac{2\cdot3+1}{3} \cdot \frac{11}{8} = \frac{7}{3} \cdot \frac{11}{8} = \frac{77}{24} = 3\frac{5}{24} $$ Ответ: $$ 3\frac{5}{24} $$ Найти корни квадратного уравнения: $$x^2+2x-1=0$$ Решение.

Вычислим дискриминант.

$$D = b^2-4ac = 8$$ $$x_{1,2}= \frac{-b\pm\sqrt{D}}{2a} = \frac{-2\pm\sqrt{8}}{2} = \frac{-2\pm2\sqrt{2}}{2} $$ Ответ: $$ x_1 = -1+\sqrt{2},\; x_2 = -1-\sqrt{2} $$ Решить неравенство: $$\frac{4 x^2-7 x+3}{3 x-1} \geq x-1$$ Решение: $$\frac{4 x^2-7 x+3}{3 x-1} \geq x-1\Rightarrow $$ $$\frac{4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) }{3 x-1} \geq 0$$

Упрощение выражения \(4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) \)

$$4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) = $$ Раскрытие скобок: $$4 x^2-7 x+3+ \left( -x+1 \right) \left( 3 x-1 \right) = $$ Раскрытие скобок: $$4 x^2-7 x+3-3 x^2+x+3 x-1= $$ $$x^2-3 x+2$$ Ответ: \( x^2-3 x+2 \) Решим квадратное уравнение \( x^2-3 x+2= 0 \)

Решение квадратного уравнения \( x^2-3 x+2= 0 \)

Вычислим дискриминант. $$D = b^2-4ac = 1$$ $$x_{1,2}= \frac{-b\pm\sqrt{D}}{2a} = \frac{3\pm\sqrt{1}}{2} = \frac{3\pm1}{2} $$ Ответ: \( x_1 = 2,\; x_2 = 1 \)

Решение по теореме Виета

Т.к. \( \left| a \right|=1 \), то можно воспользоваться теоремой Виета: $$x^2+px+q=0 \Rightarrow \left\{\begin{array}{l} x_1+x_2=-p \\ x_1 \cdot x_2=q \end{array}\right.$$ $$\left\{\begin{array}{l} x_1+x_2=3 \\ x_1 \cdot x_2=2 \end{array}\right. \Rightarrow \left\{\begin{array}{l} x_1=2 \\ x_2=1 \end{array}\right.$$ Ответ: \( x_1= 2,\; x_2= 1 \) Корни квадратного уравнения: $$ x_1 = 1 ;\; x_2 = 2 $$ Решим линейное уравнение \( 3 x-1= 0 \) Корень линейного уравнения: \( x = \frac{1}{3}\)

$$ \frac{1}{3} $$

$$ 1 $$

$$ 2 $$

Ответ: $$ x \in \left( \frac{1}{3} ;\; 1 \right] \cup \left[ 2 ;\; +\infty \right) $$ или $$ \frac{1}{3}

Нахождение производной функции

Найти производную функции $$ f(x) = \left( 1+sin \left( 2 \cdot x\right) \right) ^{2}$$ Решение $$ f'(x) = \left( \left( 1+sin \left( 2 \cdot x\right) \right) ^{2}\right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot \left( 1+sin \left( 2 \cdot x\right) \right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot \left( sin \left( 2 \cdot x\right) \right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) \cdot \left( 2 \cdot x\right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) \cdot 2= $$ $$ = 4 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) $$ Ответ: $$ f'(x) = 4 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) $$

В разделе Книги вы найдете большой список книг, учебников, решебников, ГДЗ, тестов и контрольных работ с ответами по математике и геометрии для всех классов общеобразовательных школ.
Все книги в электронном виде и доступны для скачивания бесплатно.

Отдельно стоит упомянуть программу для построения графиков функций онлайн.
Программа работает в вашем браузере, её не нужно устанавливать на компьютер.
Запустить программу

Решить квадратное уравнение онлайн

Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить решение квадратного уравнения онлайн и разобраться, как они решаются, на понятных примерах.
Чтобы произвести решение квадратного уравнения онлайн, вначале приведите уравнение к общему виду:
ax² + bx + c = 0
Заполните соответственно поля формы:

Как решить квадратное уравнение

Как решить квадратное уравнение:	Виды корней:
1. Привести квадратное уравнение к общему виду: Общий вид Аx2+Bx+C=0 Пример : 3х — 2х2+1=-1 Приводим к -2х2+3х+2=0 2. Находим дискриминант D. D=B2-4*A*C . Для нашего примера D= 9-(4*(-2)*2)=9+16=25. 3. Находим корни уравнения. x1=(-В+D1/2)/2А . Для нашего случая x1=(-3+5)/(-4)=-0,5 x2=(-В-D1/2)/2А. Для нашего примера x2=(-3-5)/(-4)=2 Если В — четное число, то дискриманант и корни удобнее считать по формулам: D=К2-ac x1=(-K+D1/2)/А x2=(-K-D1/2)/А, Где K=B/2	1. Действительные корни. Причем. x1 не равно x2 Ситуация возникает, когда D>0 и A не равно 0. 2. Действительные корни совпадают. x1 равно x2 Ситуация возникает, когда D=0. Однако при этом, ни А, ни В, ни С не должны быть равны 0. 3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1)1/2 Ситуация возникает, когда D 4. Уравнение имеет одно решение. A=0, B и C нулю не равны. Уравнение становиться линейным. 5. Уравнение имеет бесчисленное множество решений. A=0, B=0, C=0. 6. Уравнение решений не имеет. A=0, B=0, C не равно 0.

Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений.

Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.
x² + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B²-4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число^1/2!
x1=(-В+D^1/2)/2А = (-3+7)/2 = 2
x2=(-В-D^1/2)/2А = (-3-7)/2 = -5

Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10

Пример 2. Решение квадратного уравнения с совпадением действительных корней.
х² – 8x + 16 = 0
А=1, B = -8, С=16
D = k² – AC = 16 – 16 = 0
X = -k/A = 4

Подставим
(x-4)*(x-4) = (x-4)2 = X² – 8x + 16

Пример 3. Решение квадратного уравнения с комплексными корнями.
13х² – 4x + 1 = 0
А=1, B = -4, С=9
D = b² – 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.

x1=(-В+D^1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13
x2=(-В-D^1/2)/2А = (4-6i)/(2*13) = 2/13-3i/13
, где I – это квадратный корень из -1

Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор окажется весьма полезным для вас.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Детские автокресла, коляски, коляски и мебель

С рождения до ок. 24 месяца

С рождения до ок.4 года

Прибл. От 9 месяцев до 12 лет

Прибл.От 3 до 12 лет

.

Решатель кубика Рубика — 𝗕𝗲𝘀𝘁 𝗙𝗿𝗲𝗲 𝗢𝗻𝗹𝗶𝗻𝗲 𝗔𝗽𝗽

Онлайн-решатель Кубик Рубика ™ вычисляет шаги, необходимые для решения зашифрованного кубика Рубика из любой допустимой начальной позиции. Введите цвета вашей головоломки и нажмите кнопку Решить . Подождите, пока программа найдет решение, затем следуйте инструкциям, чтобы собрать свой куб.

Как пользоваться?

Воспользуйтесь этим приложением, чтобы играть с кубиком Рубика онлайн. Нажмите кнопку Scramble и попытайтесь найти решение самостоятельно, вращая грани с помощью кнопок или клавиатуры.

Приложение использует алгоритм Kociemba с открытым исходным кодом, чтобы найти решение за 20 шагов для любого допустимого скремблирования. Для более медленных компьютеров программа автоматически снижает производительность вычислений, чтобы получить более длительное решение.

Как использовать решатель кубика Рубика?

1. Выберите вид

Начните с выбора наиболее подходящего для вас вида с помощью маленьких вкладок над кубом. Трехмерный вид по умолчанию можно настроить, установив прозрачные лицевые стороны или вы можете поднять скрытые грани.Вращайте куб с помощью стрелок или проводя по экрану.

Есть два развернутых вида, которые показывают каждую грань, что помогает настроить зашифрованную конфигурацию.

2. Установить скремблированный куб

Есть много способов установить скремблированный куб.

Самый простой способ — использовать палитру цветов . Выберите цвет на палитре и вставьте его на поверхность пазла. Щелкните поле более одного раза, чтобы отключить цветовую палитру, и циклически переключайте цвета, продолжая щелкать поля головоломки.

D : Вниз лицом по часовой стрелке

Сделайте поворота лица в головоломке, используя кнопки поворота или соответствующие кнопки на клавиатуре: L, R, U, D, F, B . Заглавные буквы обозначают вращение каждой грани по часовой стрелке: влево, вправо, вверх, вниз, вперед, назад. Он поворачивается против часовой стрелки, если за буквой следует апостроф.

Выполнить или воспроизвести алгоритм скремблирования в выделенном поле ввода.Скопируйте и вставьте список букв, потому что программа может выполнять повороты, когда вы вводите их прямо в поле. Обозначьте обратный поворот строчными буквами или одинарными кавычками (‘).

Заставьте программу сгенерировать случайный тасование с помощью кнопки Scramble или вернитесь в решенное положение в любое время, нажав Reset .

3. Вычислить решение кубика Рубика

Когда скремблированные цвета правильно настроены и соответствуют вашему кубику Рубика, щелкните команду Solve , чтобы получить решение.Решатель куба предупредит вас, если ваша конфигурация неверна.

Нажатие кнопки «Решить» оставит страницу шифрования открытой и откроет страницу решения в новой вкладке браузера. Это позволит вам вернуться и внести коррективы, если что-то не так.

Оставьте комментарий, поделитесь и лайк!

Эта головоломка, несомненно, является удивительным предметом. Узнайте больше об этом, просмотрев

.Решения

NCERT для математики класса 10 Глава 4 Квадратичные уравнения

Вы можете выбрать главу 4 — Решения NCERT по квадратичным уравнениям для PDF-файла по математике 10 класса для предстоящих экзаменов, а также найти решения для всех глав по математике ниже.

Решения NCERT для математики 10 класса

Глава 4 Квадратное уравнение 10 класса разделена на пять разделов и четыре упражнения. Первый раздел — это введение без упражнений.Второй и третий разделы объясняют два важных свойства, тогда как четвертый и пятый разделы возвращаются к темам, изучаемым в классе 9.

Список упражнений и тем, которые они охватывают:

Путешествие от полинома к квадратному уравнению

Каждое квадратное уравнение является полиномом. (второй степени) равен нулю. То есть, когда полином наивысшего значения показателя степени, равного двум, равен нулю, он становится квадратным уравнением. Например, когда многочлен второй степени, такой как 2 \ [x ^ {2} \] + 3x + 4, равен нулю (т.е.{2} \] + 3x + 4 = 0) оно называется квадратным уравнением.

Слово квадратное уравнение представляет собой комбинацию слова квадрат, означающего квадрат, и «уравнение», которое имеет знак равенства (=). Следовательно, квадратное уравнение всегда имеет вторую степень, то есть показатель степени возведен в квадрат и всегда равен нулю. Стандартная форма квадратного уравнения:

Здесь a, b и c — действительные числа, а ‘a’ не может быть равным нулю

Решения квадратного уравнения

Значения переменной, удовлетворяющей квадратному уравнению: называются нулями или корнями квадратного уравнения.2} \] — 3x + 1 = 0. Если мы поместим значение x как 1, тогда все уравнение станет нулевым, что фактически равно значению в правой части, то есть LHS = RHS.

График

Если вы рисуете график квадратного уравнения, вы всегда получите кривую, которая дважды касается оси x, потому что переменная возведена в степень 2 (возведена в квадрат). Например, если мы нарисуем кривую x2-8x + 12 = 0, тогда кривая встретится с осью x в двух точках (2,0) и (6,0). Итак, 2 и 6 — корни квадратного уравнения.{2} \] + bx + c = 0. Позже Шридхарачарья (1025 г. н.э.) вывел формулу, теперь известную как квадратная формула (цитируемая Бхаскарой II) для решения квадратного уравнения методом завершения квадрата. Арабский математик Аль-Хорезми (около 800 г. н.э.) также изучал квадратные уравнения разных типов. Авраам бар Хийя Ха-Наси в своей книге «Liber embadorum», опубликованной в Европе в 1145 году н. Э., Дал полные решения различных квадратных уравнений.

Лучше знать решения, чем все вопросы — Решения NCERT Веданту

Математика играет доминирующую роль в области науки и техники.Он стал основой современной жизни и незаменимым инструментом современного поколения. Веданту стремится сфабриковать решение глав, чтобы помочь вам понять концепцию без каких-либо сбоев. Подробные и пошаговые объяснения всех ответов на вопросы к упражнениям считаются очень полезными для тех, кто желает изучать математику в качестве предмета в своих старших классах. Vedantu сосредотачивается на корнях образования заслуживают плоды тяжелой работы и определения.

Математика — предмет с наибольшим количеством баллов, и его легко решить, когда все основные понятия ясны. Поэтому лучше практиковать некоторые решения как следует, чем просто знать все вопросы. Решения NCERT для 10-го класса, глава 4, прививают безупречные качества объективности, точности и аккуратности наряду с обострением вашего интеллекта. Решения строго соответствуют последней программе, предписанной CBSE.

.

Решатель и симулятор Pyraminx

Играйте в извилистую головоломку Pyraminx онлайн или рассчитайте ее решение с помощью этого бесплатного симулятора!
Pyraminx — вторая по популярности извилистая головоломка в мире, и ее решение, несомненно, проще, чем метод кубика Рубика, но все же не так очевидно, поэтому вам может понадобиться этот инструмент.

Как использовать?

На рисунке выше изображена развернутая головоломка Пираминкс, имеющая цветовую схему по умолчанию.Щелкайте стрелки, чтобы повернуть грани. Маленькие скручивают вершины, а большие стрелки захватывают два слоя одновременно. Если вы знакомы с решением Pyraminx, тогда вы знаете, что угловые элементы не мешают и могут быть решены простым поворотом, поэтому двухслойные повороты будут играть основную роль в решении.

Расчет решения

Нажмите кнопку Edit , чтобы вручную установить цвет пазла. Вершины и центральные части уже установлены, потому что они могут быть решены очень легко, а кромочные части остаются пустыми, потому что их решение является настоящей проблемой здесь.Начните с добавления трех синих стикеров, затем продолжайте зеленую, желтую и, наконец, красную. Программа будет пытаться угадать и заполнить цвета по мере продвижения вперед, поэтому она устанавливает первый и последний желтый, а все красные поля автоматически, не позволяя вам установить недопустимый скрембл.

Нажмите кнопку Решить , чтобы получить алгоритм решения и визуальное трехмерное представление шагов. Прежде чем приступить к вращению, убедитесь, что тетраэдр в ваших руках ориентирован правильно!

Реши сам

Создайте случайный тасование, нажав Scramble , и попробуйте решить головоломку самостоятельно, щелкая стрелки поворота.

Как решить пираминкс

Pyraminx — это официальное соревнование WCA, и самые быстрые спидкуберы могут пройти его менее чем за 2 секунды. Решение намного проще, чем метод кубика Рубика, и вы можете изучить решение Pyraminx здесь.

Оставьте сообщение ниже, если у вас есть какие-либо вопросы, предложения или просто хотите сказать привет!

.