| Прототипы задания №1 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №2 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №3 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №4 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №5 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №6 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №7 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №8 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №9 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №10 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №11 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №13 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №14 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №15 открытого банка ЕГЭ по математике (базовый уровень) new | |
| Прототипы задания №16 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №17 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №18 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №19 открытого банка ЕГЭ по математике (базовый уровень) | |
| Прототипы задания №20 открытого банка ЕГЭ по математике (базовый уровень) |
Какие ошибки допускали в этом году на ЕГЭ — Российская газета
Какие ошибки стали самыми «популярными» на ЕГЭ по русскому? Почему в «базовой» математике появилось больше троечников? Сколько школьников путают Госдуму и Правительство? Эксперты Федерального института педагогических измерений проанализировали типичные ошибки ЕГЭ-2019 и рассказали, что нужно подтянуть к следующему экзамену.
Русский язык
Это обязательный предмет: если его не сдашь, аттестат не получишь. Минимум — 24 балла. До «тройки» в этом году, так же как и в прошлом, не дотянули меньше одного процента выпускников.
Самой сложной орфограммой оказалось «Правописание личных окончаний глаголов и суффиксов причастий». Например, слово «тащАщий» — здесь участники ЕГЭ определяют спряжение по глаголу «таскать», а не «тащить». То есть смешивают виды глагола. «СутулЯщийся», «светИтся», «колЕтся»… Правильно подставить букву смогли только 38% «егэшников».
Вторыми по сложности оказались задания, проверяющие правописание суффиксов и приставок. Их выполнили в среднем 58% выпускников. «БеЗголосый», «череСчур»… Причина ошибок? Ребятам даже в 11-м классе по-прежнему сложно определить некоторые части речи. Отсюда и неправильные суффиксы и приставки, которые многим школьникам в итоге сильно «испортили» жизнь.
С правописанием -Н- и -НН- справляются чуть лучше (65% выпускников). «Тканый», «растрепанный», «лиственница». .. И примерно столько же ребят (65%) справляются с правописанием корней «гар/гор», «клан/клон», «бер/бир» — вариантов много.
.. И примерно столько же ребят (65%) справляются с правописанием корней «гар/гор», «клан/клон», «бер/бир» — вариантов много.
Пунктуация — тоже слабое звено. В 2019 году было введено новое задание на анализ небольшого текста. С ним справились только 32% выпускников. Остальные запутались в запятых, тире и двоеточиях.
У многих «егэшников» хромает и грамматика. Ошибки? На любой вкус: «более лучший, самый красивейший»; «много время», «превосходство перед другими», «по окончанию спектакля».
Математика
Это еще один обязательный предмет, но экзаменов по нему два: базовый (достаточно и «тройки» для получения аттестата) и профильный, результаты которого спрашивают вузы.
Что интересно? В этом году результаты «базы» по сравнению с прошлым годом серьезно изменились. «Троечников» стало намного больше. В 2018 году их было 13% от всех сдающих, а в 2019-м — уже 19,8%. Число отличников, наоборот, уменьшилось — с 48% в 2018 году до 39,9% — в 2019-м. Эксперты связывают это с тем, что впервые в 2019 году выпускник был обязан выбрать что-то одно: или «профиль», или «базу». А не все вместе, как многие делали раньше. В итоге самые подготовленные выпускники, которые раньше использовали «базу» как тренировку, массово перешли на «профиль».
А не все вместе, как многие делали раньше. В итоге самые подготовленные выпускники, которые раньше использовали «базу» как тренировку, массово перешли на «профиль».
На «базе» остались в основном гуманитарии. То есть те, кому математика для поступления в вуз не нужна. Что оказалось для них самым сложным? С трудом выпускникам далась стереометрия.
«В бак, имеющий форму правильной четырехугольной призмы, налито 10 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,6 раза. Найдите объем детали». С подобной задачкой справляются около 40% выпускников.
Еще хуже обстоят дела с умением строить простейшие математические модели.
«В доме всего 10 квартир с номерами от 1 до 10. В каждой живет не менее одного и не более трех человек. В квартирах с 1-й по 8-ю включительно суммарно живет 10 человек. А в квартирах с 7 по 10 включительно суммарно — тоже 10 жильцов. Вопрос: сколько человек живет в этом доме?» С этим заданием справляются менее трети ребят.
Профильная математика, наоборот, пошла «в рост». Почти половина всех сдающих набрала на этом экзамене более 61 балла. Для сравнения — в прошлом году таких ребят было всего 32%. Число «двоечников», наоборот, снизилось. Правда, и здесь самыми трудными остаются задания на геометрию и математические модели. Плюс матанализ.
Обществознание
Это самый популярный предмет: как экзамен по выбору его из года в год сдают примерно 50% выпускников. Но в итоге до «тройки» не дотягивает практически каждый пятый. Почему так много?
Некоторые ребята считают, что обществознание можно сдать легко и без труда, толком не готовятся. Рассматривают экзамен как «запасной вариант». Это самая фатальная ошибка.
Около 20% ребят, сдающих обществознание, толком не знают, чем занимается прокуратура и полиция. Считают, что правоохранительные органы принимают законы. 24% выпускников уверены, что трудовой договор может быть заключен устно: «Вот я сделаю, а ты мне заплати…»
30% не различают уголовное и гражданское право. И около 50% выпускников отмечают, что «Правительство РФ принимает законы». Кстати, эта ошибка была одной из самых «популярных» и в прошлом году.
И около 50% выпускников отмечают, что «Правительство РФ принимает законы». Кстати, эта ошибка была одной из самых «популярных» и в прошлом году.
Статистика показывает: выпускники 2019 года не разбираются в семейных делах и брачных отношениях. «В РФ признается только брак, зарегистрированный в ЗАГСе. Все остальные виды совместного проживания мужчины и женщины браком не являются. Необходимо акцентировать на этом внимание учеников», — замечают эксперты.
Фото: Инфографика «РГ» / Антон Переплетчиков / Ксения Колесникова
как сдать ЕГЭ по профильной математике — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
Что нужно делать школьнику, чтобы получить 100 баллов?
Чтобы получить 100 баллов, надо любить и понимать математику (быть математиком — по сути, по настроению, по образу жизни). Если школьник рассматривает математику как второстепенный предмет, как предмет, который просто необходимо сдать, например, когда речь идет о поступлении на экономические направления, он не сможет получить 100 баллов ни при каком раскладе.
По вашему опыту преподавания, какие разделы математики самые сложные и вызывают наибольшие затруднения?
Сегодня для школьника самое сложное — это геометрия. К сожалению, культура геометрии в школе просто отсутствует. И еще, конечно, задачи с параметрами. Старшеклассники их панически боятся. Но ученик, который понимает математику, и с этими задачами справляется. Для их решения требуется именно понимание, а все необходимые для этого знания изложены в курсе школьной математики.
А вообще, в любой теме есть простой материал (азы), который лежит в основе задач из первой части ЕГЭ, и сложный материал, который лежит в основе задач второй части. Думаю, что если есть желание, то каждый в состоянии освоить азы любой темы из школьной программы по математике, а вот более глубокое понимание этих тем и умение решать сложные задачи по силам не всем.
Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов
А какие темы можно назвать самыми простыми?
Обычно школьники легко решают линейные и квадратные уравнения, но только в том случае, если в них нет параметра. Так что по темам «Линейная функция» и «Квадратичная функция» есть простые задачи, а есть сложные. И так по любой теме. Можно сформулировать простую задачу, а можно такую, что никто не решит.
Простыми темами можно считать те, на большинство задач по которым можно школьника натаскать. Простая задача — это гарантированно правильно решенная. А про ЕГЭ (особенно про задачи первой части) так вообще нельзя говорить.
Присутствует ли на ЕГЭ по математике фактор везения? Возможно ли получить высокий балл, если знаешь предмет на более скромный результат?
Да, это возможно, но только если речь идет о результате в районе 75 баллов или меньше. Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов. Там нужно решать сложные задачи из второй части, а они требуют четкого обоснования решения, что для большинства является непосильным. Здесь должна быть стабильность.
А можно завалить экзамен, если знаешь предмет очень хорошо?
Элементарно. Арифметические ошибки, невнимательное чтение условия задачи и просто паника. Все это приводит талантливых учеников к более скромным результатам.
Что же делать? Есть «формула успеха», которая поможет подготовиться к ЕГЭ по математике?
Учить математику! Не натаскиваться по вариантам ЕГЭ, а систематически учить темы, разбираться, стараться понять. Тогда до многих задач школьник дойдет сам, своим умом, а это и есть залог успешной подготовки и высоких баллов. Математика — это, в первую очередь, понимание, а потом уже формулы и схемы решения. При подготовке методом натаскивания потолок — это 75 баллов. Одна и та же задача, сформулированная просто «с другого конца», натасканного ребенка деморализует. Он не может узнать знакомую задачу, а разобраться в «новой» сам не в состоянии.
Вот, например, задача № 17. Когда она появилась в вариантах диагностических работ, детям в школе начали давать формулы для ее решения. И школьники заучивали эти формулы, сопротивляясь попыткам учителей объяснить, откуда они взялись. Многие действовали методом «я знаю формулу и по ней буду решать». А на самом экзамене в условие внесли незначительное изменение, и ни одна из выученных формул не подходила.
Надо выбросить калькулятор и научиться считать без него
До ЕГЭ по математике осталось 3,5 месяца. Как вы посоветуете выпускникам распределить время, чтобы подготовиться наилучшим образом?
Во-первых, выбросить калькулятор и научиться считать без него. Во-вторых, повторить теорию и выучить формулы (именно сейчас, а не перед экзаменом): то есть подготовить базу, а дальше решать задачи. Можно решать из сборников вариантов ЕГЭ, но, к сожалению, там их не очень много и они часто повторяются.
Каждый ребенок ставит для себя определенную планку в зависимости от того, куда собирается поступать и как знает предмет. Если говорить о заданиях второй части ЕГЭ, то во время подготовки необходимо прежде всего обратить внимание на задачи № 13, № 15 и № 17. Их можно научиться решать. Если решение не вызывает проблем, можно переходить к задачам № 14 и № 16.
Если решение не вызывает проблем, можно переходить к задачам № 14 и № 16.
Задачи № 18 и № 19 — это, конечно, уже очень высокий уровень, но попробовать можно. Если эти задачи идут хорошо, то я не думаю, что надо тратить оставшееся время на курсы. Лучше решить больше задач самостоятельно. Если же возникают проблемы или неуверенность, что вы все решаете верно, не откладывая обращайтесь за помощью. Эффективная стратегия на этот период — решать, решать и решать!
Как готовиться к заданиям повышенной сложности
| Задание № 10 | Задача легкая. Здесь важно внимательно читать условие. Внимание на единицы измерения! Все величины подставлять в одних единицах измерения. |
| Задание № 11 | Текстовая задача. Не считаю ее сложной. Обратите внимание на вопрос задачи, что именно спрашивают в условии и в каких единицах измерения необходимо записать ответ. Часто школьники пишут скорость не того пешехода или производительность не той трубы. |
| Задания № 13, № 15 | Задания решаемые, но должна быть база по всем темам алгебры. Особенное внимание необходимо обратить на область определения (в особенности это касается логарифма, тангенса и котангенса). Нужно уметь применять те тождественные преобразования, которые помогут решить задачу, а не заведут в тупик, и знать все формулы наизусть. |
| Задания № 14, № 16 | Задачи по геометрии. Самое сложное в них — это умение доказать. Для этого школьник должен владеть всем материалом планиметрии и стереометрии, знать все теоремы и следствия из них, уметь их доказывать. И еще важен чертеж! Он может либо стать эффективным инструментом и подсказать правильный ход решения, либо, если сделан некорректно, помешать решению задачи. |
| Задание № 17 | Несложная задача. Это задание на умение формализовать текстовую задачу, то есть записать условие задачи в виде уравнений или неравенств (этого же требует и решение задачи № 11). На ЕГЭ под этим номером пока стабильно дают задачу на проценты. Теоретически может быть и задача на поиск оптимального решения, но такие варианты пока встречались только в диагностических работах. После формализации условия получается стандартная математическая задача о нахождении экстремума функции или на нахождение наибольшего (наименьшего) значения функции на отрезке (аналогично задаче № 12). Здесь важно не пользоваться готовыми формулами, а разбираться, почему в этой задаче так, а в другой иначе. Только тогда можно научиться переводить условие текстовой задачи на язык математики. На ЕГЭ под этим номером пока стабильно дают задачу на проценты. Теоретически может быть и задача на поиск оптимального решения, но такие варианты пока встречались только в диагностических работах. После формализации условия получается стандартная математическая задача о нахождении экстремума функции или на нахождение наибольшего (наименьшего) значения функции на отрезке (аналогично задаче № 12). Здесь важно не пользоваться готовыми формулами, а разбираться, почему в этой задаче так, а в другой иначе. Только тогда можно научиться переводить условие текстовой задачи на язык математики. |
| Задание № 18 | Для решения этой задачи необходимо отличное владение предметом. Поможет ее решить знание свойств элементарных функций, умение исследовать функции и строить их графики. Все это есть в школьном курсе математики. |
| Задание № 19 | Это задача для тех, кому интересна математика. В ходе решения может возникнуть необходимость обратиться к любому разделу предмета из программы любого класса. Нужно найти в своей голове и грамотно применить эти знания. В одной задаче может сочетаться арифметическая прогрессия со свойствами делимости чисел и нахождением наибольшего значения. Для решения этой задачи нужно понимать, когда достаточно привести пример, а когда необходимо строгое обоснование. Нужно найти в своей голове и грамотно применить эти знания. В одной задаче может сочетаться арифметическая прогрессия со свойствами делимости чисел и нахождением наибольшего значения. Для решения этой задачи нужно понимать, когда достаточно привести пример, а когда необходимо строгое обоснование. |
Подготовка к ЕГЭ и ОГЭ 2021 в СПб
Команда профессионалов
Наши преподаватели обладают всесторонними знаниями и высоким профессионализмом в сочетании с талантом общения. Они умеют так заинтересовывать учеников, что дети на урок приходят с удовольствием, а после уроков ждут следующих занятий. У отличного педагога ученики на уроках испытывают состояние счастья: они действуют, творят, ощущают, что их любят и желают им добра. В результате они начинают отлично понимать предмет и смело в нем ориентироваться.
В своей работе наши преподаватели придерживаются принципа: «Не навреди ученику, сделай всё от тебя зависящее, чтобы дать ему знания, чтобы он чувствовал себя личностью, не ущемляй его достоинства». У детей есть особое чутьё на педагога, и учатся они с большим увлечением у того учителя, который сам увлечён, любит свою профессию, который может их понять, который в душе, сколько бы ему ни было лет, остаётся молодым.
У детей есть особое чутьё на педагога, и учатся они с большим увлечением у того учителя, который сам увлечён, любит свою профессию, который может их понять, который в душе, сколько бы ему ни было лет, остаётся молодым.
Талант учителя заключается в умении передавать знания другому и в умении делать трудные задачи лёгкими. Понимать, что нет на свете неспособных детей. Увлекать, окрылять, вдохновлять, учить противостоять трудностям и побеждать!!!
Анненкова Ольга Мстиславовна
Окончила Ленинградский ветеринарный институт. Кандидат ветеринарных наук. Преподаватель анатомии, физиологии и патологии человека в Санкт-Петербургском государственном бюджетном ПОУ «Фельдшерский колледж».
Эксперт ГИА по биологии.
Педагогический стаж 17 лет.
Байбуз Дмитрий Викторович
Окончил Санкт-Петербургский государственный Университета.
Присуждена степень Магистра Физики по направлению «Физика».
Учитель математики высшей квалификационной категории в ГБОУ СОШ № 306 Адмиралтейского района Санкт-Петербурга. Педагогический стаж 6 лет.
Педагогический стаж 6 лет.
Стаж подготовки к ЕГЭ 6 лет.
Эксперт ГИА по математике.
Федоренко Даниил Александрович
Окончил 1995 г. Санкт-Петербургский государственный университет, физический факультет, кафедра Высшей математики и вычислительной физики.
Учитель физики высшей квалификационной категории в ГБОУ «Школа № 237 Красносельского района Санкт-Петербурга».
Педагогический стаж 12 лет.
Опыт подготовки к ЕГЭ 9 лет.
Эксперт ЕГЭ по физике.
Кубрина Марина Сергеевна
Окончила в 1982 г. Рязанский радиотехнический институт.
Факультет радиотехники.
Специальность – инженер-радиотехник.
Учитель информатики первой квалификационной категории в ГБОУ Вторая Санкт-Петербургская гимназия Адмиралтейского района Санкт-Петербурга.
Педагогический стаж 12 лет.
Стаж подготовки к ЕГЭ 10 лет.
Эксперт ЭГЭ/ОГЭ по информатике.
Подлесова Татьяна Алексеевна
Окончила в 1981 г. ЛФЭИ им. Вознесенского Н. А. по специальности «Экономист-переводчик».
Учитель английского языка высшей квалификационной категории в Гимназии № 171 Центрального района Санкт-Петербурга.
А. по специальности «Экономист-переводчик».
Учитель английского языка высшей квалификационной категории в Гимназии № 171 Центрального района Санкт-Петербурга.
Педагогический стаж 20 лет.
Стаж подготовки к ЕГЭ 9 лет.
Эксперт ЕГЭ по английскому языку.
Евстифеева Анастасия Михайловна
Окончила филологический факультет Российского Государственного Педагогического Университета им. Герцена по специальности «Русский язык и литература».
Учитель русского языка и литературы в Лицее № 470 Калининского района Санкт-Петербурга.
Педагогический стаж 20 лет.
Стаж подготовки к ЕГЭ 10 лет.
Эксперт ГИА по русскому языку.
Розмыслова Лариса Вадимовна
Окончила в 1996 г. Российский государственный педагогический университет им. А.И. Герцена.
Учитель литературы и русского языка высшей квалификационной категории в ГБОУ № 27 с углубленным изучением литературы им. И.А. Бунина в Выборгском районе Санкт-Петербурга.
Эксперт ОГЭ/ЕГЭ по литературе и русскому языку. Педагогический стаж 23 года.
Педагогический стаж 23 года.
Стаж подготовки к ОГЭ/ЕГЭ: 6 лет.
Победитель конкурса «Учитель года 2009»
Саморуков Валентин Владимирович
Закончил с отличием в 1998 г. Факультет социальных наук Российского Государственного Педагогического Университета им. А.И. Герцена по специальности «Учитель истории». Учитель истории и обществознания высшей квалификационной категории. Легко находит контакт с учениками, владеет эффективными методиками подготовки к ЕГЭ. Педагогический стаж 20 лет (Гимназия № 209, Физико-математический лицей № 366), стаж подготовки к ЕГЭ — более 12 лет. Эксперт ЕГЭ по истории и обществознанию с 2009 года. Организатор ЕГЭ с 2008 года.
Подробнее…Шевченко Людмила Ефимовна
Окончила в 1975 г. Ташкентский Государственный педагогический институт русского языка и литературы.
Учитель русского языка высшей квалификационной категории в ГБОУ ЦО № 133 Невского района Санкт-Петербурга. Педагогический стаж 40 лет. Стаж подготовки к ЕГЭ 6 лет. Эксперт ЕГЭ по русскому языку.
Эксперт ЕГЭ по русскому языку.
Победитель конкурса «Учитель года-1998 г.»
Власов Александр Сергеевич
Окончил 1995 г. Ленинградский государственный педагогический институт им. А.И. Герцена.
Учитель истории, обществознания и права высшей квалификационной категории в частной образовательной школе Невского района Санкт-Петербурга – «Санкт-Петербургская школа ТТИШБ» Педагогический стаж 22 года.
Эксперт ЕГЭ по истории, обществознанию и праву.
Волошинов Леонид Андреевич
Окончил Российский государственный педагогический университет им. А.И. Герцена. Магистр социальных наук.
Учитель обществознания и истории высшей квалификационной категории в ГБОУ № 306 и ГБОУ № 266 Адмиралтейского района СПб
Эксперт ОГЭ/ЕГЭ по обществознанию и истории
Педагогический стаж 15 лет
Стаж подготовки к ОГЭ/ЕГЭ 9 лет
Якжик Маргарита Валерьевна
Окончила в 1997 г. Брестский Государственный университет биологический факультет
о специальности – биология, химия.
Учитель биологии и химии высшей
квалификационной категории в ГБОУ СОШ № 306 Адмиралтейского района Санкт-Петербурга.
Педагогический стаж 28 лет.
Стаж подготовки к ЕГЭ 15 лет.
Эксперт ЕГЭ по биологии и химии.
Победитель районного конкурса педагогических достижений 2006 г. в номинации «Лучший классный руководитель»
Радионов Александр Павлович
Окончил в 2012 г. Таганрогский государственный Педагогический Институт им. А.П. Чехова.
Присуждена квалификация — Учитель математики по специальности «Математика».
Учитель математики в ГБОУ СОШ Приморского района Санкт-Петербурга.
Педагогический стаж 7 лет.
Стаж подготовки к ЕГЭ 7 лет.
Авдеенко Ольга Александровна
Окончила в 1984 г. Алма-Атинский энергетический институт по специальности инженер-преподаватель электро-энергетических дисциплин.
Учитель физики первой квалификационной категории в ГБОУ СОШ № 253 Приморского района Санкт-Петербурга.
Педагогический стаж 32 года.
Стаж подготовки к ЕГЭ/ОГЭ 15 лет.
Лашуков Михаил Сергеевич
Окончил 2016 г. Санкт-Петербургский государственный Университет.
Присуждена степень Бакалавра Химии по направлению «Химия».
Учитель химии и биологии в ГБОУ СОШ № 306 Адмиралтейского района Санкт-Петербурга.
Педагогический стаж 5 лет.
Стаж подготовки к ЕГЭ 5 лет.
»Плохой расчет целевой группы по математике
Количество поступающих в колледж студентов, которым требуется развивающая курсовая математика, является национальной проблемой. По данным Национального центра статистики образования, 42% студентов, впервые поступающих в колледж осенью 2003 г., прошли курс развивающей математики. В нашем учебном заведении, Вустерском государственном университете, 54% студентов, поступивших осенью 2004 года, изучали развивающую математику. Это огромная проблема по ряду причин; Студенты, которые должны посещать курсы, на которые им не предоставляется кредит, несут денежные затраты, а колледжи и университеты должны платить инструкторам за преподавание таких курсов. В этой статье мы исследуем изменение политики, недавно внедренное Советом по высшему образованию Массачусетса (MBHE), которое стремится решить эту проблему, радикально изменив способ размещения студентов в их первом классе математики на уровне колледжа.
В этой статье мы исследуем изменение политики, недавно внедренное Советом по высшему образованию Массачусетса (MBHE), которое стремится решить эту проблему, радикально изменив способ размещения студентов в их первом классе математики на уровне колледжа.
Текущий процесс размещения поступающих на первый курс математики был сформирован в соответствии с Общей политикой оценки Массачусетса, принятой MBHE в 1998 году, которая была основана на отчете Целевой группы по оценке математики. Все члены комитета имели образование в области математики, а половина членов занимала должности факультетов математики.Кроме того, в отчет были включены подробные протоколы всех собраний и всех голосований. Политика предписывала, что все поступающие студенты должны были сдавать экзамен по элементарной алгебре Accuplacer, который охватывает темы курса алгебры I (обычно сдают в восьмом или девятом классе). Кроме того, политика предписывает «сокращенный балл», который определяет, будет ли поступающий ученик зачислен на развивающий курс.
Решение об изменении этого процесса было принято в октябре 2013 года, когда MBHE решило реализовать четыре «основных и всеобъемлющих рекомендации», вынесенных Целевой группой по преобразованию развивающего математического образования.В отчете MBHE указано, что в рабочую группу входило 17 человек. В отличие от целевой группы 1998 года, только пять из членов указаны как имеющие текущие должности, которые включают обучение математике. Еще один член — бывший профессор математики. Напротив, в отчет не включены ни протоколы, ни записи голосований. Попытки получить их позволяют предположить, что таких записей нет.
Первая рекомендация целевой группы — это недавние выпускники средней школы с средним баллом 2.7 и выше освобождаются от начального вступительного экзамена (в настоящее время Accuplacer) и должны быть переведены непосредственно на самый низкий курс математики колледжа, соответствующий выбранной ими траектории обучения. Кроме того, выпускники средней школы, средний балл среднего успеваемости которых ниже 2,7, но выше 2,4 и которые успешно прошли четыре курса математики, включая математику в старшем классе, освобождаются от начального вступительного экзамена и должны быть переведены непосредственно на курс математики на уровне колледжа. подходит для выбранной ими области обучения.Чтобы уточнить, это относится к общему среднему баллу средней школы, а не только к среднему баллу по математике в средней школе. Мы категорически не согласны с этой рекомендацией.
подходит для выбранной ими области обучения.Чтобы уточнить, это относится к общему среднему баллу средней школы, а не только к среднему баллу по математике в средней школе. Мы категорически не согласны с этой рекомендацией.
Нашим первым предметом разногласий является позиция целевой группы в отношении курсовой работы по развитию. В отчете говорится, что «студенты, которые поступают на развивающие курсы, с меньшей вероятностью закончат обучение… эти студенты часто разочаровываются и никогда не достигают точки, когда они даже пытаются пройти курс начального уровня». Первая часть заявления никого не должна удивлять.Точно так же студенты первого курса, не прошедшие курс, с меньшей вероятностью закончат учебу. Должны ли мы бороться с этим, запретив студентам-первокурсникам плохие оценки?
Вторая часть утверждения предполагает, что лучший способ избавиться от уныния, которое испытывает ученик, столкнувшись с развивающей работой, — это позволить им автоматически зачислить на кредитный курс. В основе этого вывода лежит предположение, что такой студент преуспеет в этом курсе, даже если во многих случаях у него не будет жизненно важных базовых навыков, необходимых для успеха (навыков, которым они будут обучаться в курсе развивающей математики).Целевая группа не задумывается о том, насколько обескураживающим может быть для студента повторение несколько раз одного и того же курса, к которому он не подготовлен.
В основе этого вывода лежит предположение, что такой студент преуспеет в этом курсе, даже если во многих случаях у него не будет жизненно важных базовых навыков, необходимых для успеха (навыков, которым они будут обучаться в курсе развивающей математики).Целевая группа не задумывается о том, насколько обескураживающим может быть для студента повторение несколько раз одного и того же курса, к которому он не подготовлен.
Наша озабоченность по поводу учащихся, испытывающих трудности на курсах, к которым они не подготовлены, основана на опыте. Несколько лет назад наша администрация отменила требования к вступительным экзаменам для переводных студентов. Летом 2013 года у нас был студент, изучающий математику, который перешел на курс, эквивалентный колледжу алгебры, из местного колледжа.В соответствии со старой политикой этот студент все равно должен был бы принимать Accuplacer; однако в соответствии с новой политикой студенту разрешили зарегистрироваться для предварительного расчета. Этот студент много работал, задавал вопросы и набрал 4% на первом промежуточном экзамене. Впоследствии он отказался от курса. В беседе с ним мы предложили ему повторно пройти курс алгебры в колледже, потому что ему явно не хватало навыков, необходимых для преуспевания в предварительном исчислении. Вместо этого он решил снова попробовать предварительный расчет осенью.Он снова усердно работал, задавал вопросы и на этот раз набрал 6% в первом промежуточном экзамене. Он снова отказался от курса и, наконец, через год он согласился пойти на курс алгебры в колледже, чтобы повысить свои навыки. Этому студенту оказали невероятную медвежью услугу, посчитав подготовленным к курсу, к которому он был явно не готов. Он потратил впустую сотни долларов, и мы можем сказать из прямых разговоров, что он был невероятно обескуражен этим опытом. Мы понимаем, что этот анекдот конкретно не относится к развивающим курсам, но наша общая точка зрения заключается в том, что тесты по размещению служат жизненно важной цели, и когда студенты считаются подготовленными к выбранному ими классу без проверки их основных навыков, мы опасаемся, что такие ситуации могут возникнуть.
Этот студент много работал, задавал вопросы и набрал 4% на первом промежуточном экзамене. Впоследствии он отказался от курса. В беседе с ним мы предложили ему повторно пройти курс алгебры в колледже, потому что ему явно не хватало навыков, необходимых для преуспевания в предварительном исчислении. Вместо этого он решил снова попробовать предварительный расчет осенью.Он снова усердно работал, задавал вопросы и на этот раз набрал 6% в первом промежуточном экзамене. Он снова отказался от курса и, наконец, через год он согласился пойти на курс алгебры в колледже, чтобы повысить свои навыки. Этому студенту оказали невероятную медвежью услугу, посчитав подготовленным к курсу, к которому он был явно не готов. Он потратил впустую сотни долларов, и мы можем сказать из прямых разговоров, что он был невероятно обескуражен этим опытом. Мы понимаем, что этот анекдот конкретно не относится к развивающим курсам, но наша общая точка зрения заключается в том, что тесты по размещению служат жизненно важной цели, и когда студенты считаются подготовленными к выбранному ими классу без проверки их основных навыков, мы опасаемся, что такие ситуации могут возникнуть. гораздо чаще.
гораздо чаще.
Еще одним предметом разногласий, который у нас есть с рекомендациями целевой группы, является освобождение от тестирования всех поступающих студентов со средним академическим баллом 2,7 или выше (а в случае студентов, которые прошли четыре урока математики, включая один в старшем классе, средний балл средней школы 2,4 или выше). Мы снова обеспокоены тем, что такая политика приведет к тому, что множество учащихся окажутся крайне недостаточно подготовленными к своему первому уроку математики на уровне колледжа. В соответствии с этой политикой учащийся, получивший оценку D- на каждом уроке математики, который он посещал в старшей школе (и в первом случае, который даже не прошел курс математики в старшем классе), будет считаться готовым к математике на уровне колледжа. при условии, что его средний балл в средней школе равен 2.7. Любой, кто полагает, что ученик, получивший двойку на всех уроках математики в старшей школе и даже не посещавший математический класс в старшем классе, преуспеет в своем первом курсе уровня колледжа, либо сильно недооценивает строгость колледжа. уровень математики или ожидает, что стандарты на таких курсах будут снижены, чтобы приспособить такое количество плохо подготовленных студентов. Мы поговорили с несколькими членами целевой группы, чтобы попытаться определить исследовательскую базу для этой рекомендации.Никакой конкретной информации предоставлено не было. Ответы варьировались от «Я пропустил эту встречу» до «Спросите сотрудников DHE».
уровень математики или ожидает, что стандарты на таких курсах будут снижены, чтобы приспособить такое количество плохо подготовленных студентов. Мы поговорили с несколькими членами целевой группы, чтобы попытаться определить исследовательскую базу для этой рекомендации.Никакой конкретной информации предоставлено не было. Ответы варьировались от «Я пропустил эту встречу» до «Спросите сотрудников DHE».
В отчете о состоянии штата Массачусетс за 2013 год, подготовленном Советом колледжей, содержится информация о средних успеваемости учащихся старших классов средней школы. Средний балл предоставивших эту информацию составил 3,23. Только 13% указали, что у них средний балл ниже 2,7. Это говорит нам о том, что это чрезвычайно низкий порог.
У нас также есть серьезные сомнения в отношении очевидной исследовательской основы рекомендаций целевой группы, а именно «Прогнозирование успеха в колледже: важность вступительных тестов и академических справок».В докладе 2012 года Клайва Белфилда и Питера М. Кроста из Исследовательского центра общественных колледжей (CCRT) Педагогического колледжа Колумбийского университета были изучены только общественные колледжи, и не были включены данные из Содружества Массачусетс. Во-вторых, нас беспокоит то, как целевая группа интерпретировала документ. В своем проекте отчета целевая группа резюмирует документ следующим образом:
Кроста из Исследовательского центра общественных колледжей (CCRT) Педагогического колледжа Колумбийского университета были изучены только общественные колледжи, и не были включены данные из Содружества Массачусетс. Во-вторых, нас беспокоит то, как целевая группа интерпретировала документ. В своем проекте отчета целевая группа резюмирует документ следующим образом:
«В этом документе используются данные о студентах из системы общественных колледжей штата для проверки достоверности результатов тестов и информации о средней школе при прогнозировании оценок за курс и успеваемости в колледже.Авторы считают, что вступительные тесты не дают точных прогнозов относительно успеваемости учащихся в колледже. Напротив, средний балл средней школы полезен для прогнозирования многих аспектов успеваемости учащихся в колледже ».
Это вводящее в заблуждение резюме, поскольку целевая группа, кажется, путает предикторы успеха в колледже с точным размещением курса. Несмотря на то, что они связаны между собой, установочный тест не говорит о том, будет ли кто-то успешен на уроках математики в колледже, а скорее, если у него есть база знаний, чтобы добиться успеха.До того, как мы внедрили нашу текущую программу размещения в WSU, студенты могли записываться на уроки математики на уровне колледжа независимо от результатов их тестовых экзаменов. Неудивительно, что мы наблюдали очень высокий процент неудач среди этих студентов в самых разных классах.
Несмотря на то, что они связаны между собой, установочный тест не говорит о том, будет ли кто-то успешен на уроках математики в колледже, а скорее, если у него есть база знаний, чтобы добиться успеха.До того, как мы внедрили нашу текущую программу размещения в WSU, студенты могли записываться на уроки математики на уровне колледжа независимо от результатов их тестовых экзаменов. Неудивительно, что мы наблюдали очень высокий процент неудач среди этих студентов в самых разных классах.
Но, пожалуй, самое главное, авторы статьи CCRT признают, что их работа над показателями достоверности основана на экстраполяции. В частности, поскольку учащиеся, набравшие меньше баллов Accuplacer, помещаются в развивающий класс, нет прямых данных о том, как такие учащиеся были бы в классе колледжа, если бы они были непосредственно помещены в него.Таким образом, чтобы предсказать, как поступят такие студенты, если они будут непосредственно зачислены на курс уровня колледжа, необходимо использовать экстраполяцию (см. Приложение для гипотетических примеров).
Приложение для гипотетических примеров).
Согласно нашему первому гипотетическому примеру, мы можем линейно экстраполировать ниже сокращенной оценки, чтобы «сделать вывод», что 60% студентов, набравших 20 баллов на Accuplacer (для справки, сокращенная оценка составляет 82), пройдут свой первый курс математики на уровне колледжа. . Можно увидеть, как, если бы этот вывод был действительно верным, можно было бы привести аргумент в пользу исключения тестирования размещения.К сожалению, нет абсолютно никаких доказательств, подтверждающих кривую такой формы для оценок в тесте на размещение ниже оценки по разрезанию. Чтобы еще больше проиллюстрировать опасность экстраполяции, рассмотрим следующий набор диаграмм рассеяния в нашем Приложении, на которых изображены медианы роста мальчиков в возрасте от 2 до 20. Предположим, мы никогда не видели мальчика младше 15 лет, и у нас есть данные только для мальчиков в возрасте от 15 до 20 лет. Как и в нашей гипотетической вышеупомянутой гипотезе, мы можем экстраполировать возраст младше 15 лет, чтобы «сделать вывод», что двухлетний ребенок будет выше 5 футов!
Мы также задаемся вопросом, почему общественные колледжи и государственные университеты подчиняются одним и тем же рекомендациям.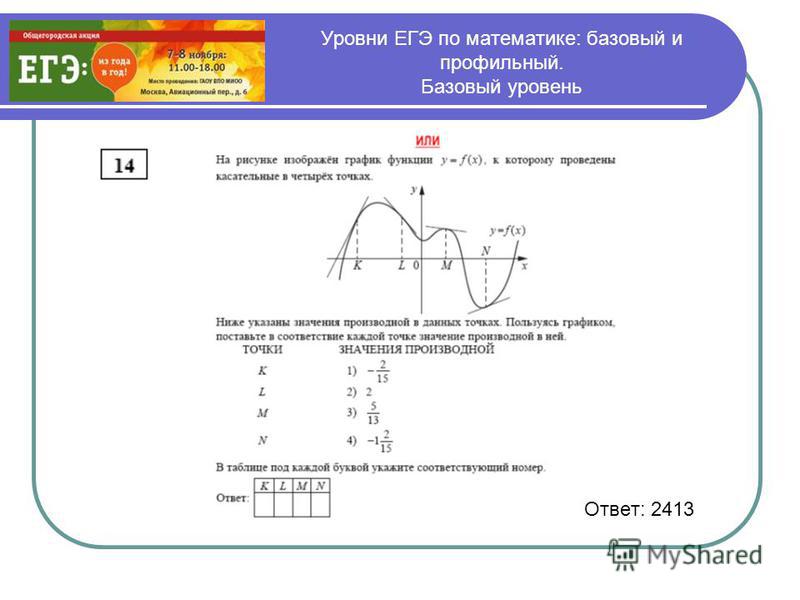 Государственные университеты и общественные колледжи имеют большие различия, начиная от заявлений о миссии и кончая студентами и демографическими данными. В частности, общественные колледжи предлагают открытый набор, что приводит к огромному количеству неподготовленных студентов по сравнению с государственными университетами. Согласно данным отчета целевой группы, осенью 2010 года 53% поступающих студентов общественных колледжей нуждались в развивающем математическом образовании по сравнению с 23% поступающих в государственные университеты. Также кажется, что состав целевой группы в значительной степени склоняется к точке зрения местного колледжа.Из 17 членов целевой группы более половины так или иначе связаны с общественным колледжем; с другой стороны, только один член в настоящее время является преподавателем математического факультета государственного университета.
Государственные университеты и общественные колледжи имеют большие различия, начиная от заявлений о миссии и кончая студентами и демографическими данными. В частности, общественные колледжи предлагают открытый набор, что приводит к огромному количеству неподготовленных студентов по сравнению с государственными университетами. Согласно данным отчета целевой группы, осенью 2010 года 53% поступающих студентов общественных колледжей нуждались в развивающем математическом образовании по сравнению с 23% поступающих в государственные университеты. Также кажется, что состав целевой группы в значительной степени склоняется к точке зрения местного колледжа.Из 17 членов целевой группы более половины так или иначе связаны с общественным колледжем; с другой стороны, только один член в настоящее время является преподавателем математического факультета государственного университета.
Кроме того, большинство исследований (девять из 17 статей), использованных для поддержки рекомендаций целевой группы, было проведено CCRT при Колумбийском университете. Фактически, даже несмотря на то, что целевая группа цитирует 17 ресурсов в поддержку своих рекомендаций, на самом деле они происходят только из трех источников: CCRT, Jobs for the Future и Complete College America.Мы, безусловно, понимаем необходимость реформы на уровне колледжей и ценим жизненно важную роль, которую играют колледжи. Однако мы очень обеспокоены тем, что государственные университеты подчиняются тем же рекомендациям, что и общественные колледжи, когда очевидно, что голоса из системы государственных университетов были в подавляющем меньшинстве в отношении членства в целевой группе и исследовательской базы.
Фактически, даже несмотря на то, что целевая группа цитирует 17 ресурсов в поддержку своих рекомендаций, на самом деле они происходят только из трех источников: CCRT, Jobs for the Future и Complete College America.Мы, безусловно, понимаем необходимость реформы на уровне колледжей и ценим жизненно важную роль, которую играют колледжи. Однако мы очень обеспокоены тем, что государственные университеты подчиняются тем же рекомендациям, что и общественные колледжи, когда очевидно, что голоса из системы государственных университетов были в подавляющем меньшинстве в отношении членства в целевой группе и исследовательской базы.
В разделе отчета целевой группы, озаглавленном «Поручение целевой группе по преобразованию развивающего математического образования», четыре области были упомянуты как выделенные в итоговом отчете Рабочей группы по уровням выпускников и успеваемости учащихся за 2011 год.В первом разделе, «Исследования и образование», указано: «Обзор инновационных практик, применяемых в настоящее время в колледжах в Массачусетсе и за его пределами, и создание инициатив, которые успешно распространяют передовой опыт в нескольких университетских городках». Однако успешная программа, которую мы проводим в штате Вустер, была проигнорирована в отчете оперативной группы. Почему? Как упоминалось выше, в 2004 году у нас была неудачная программа начального уровня: 54% поступающих учащихся были переведены на развивающую математику, и только 30% из этих студентов прошли курс развивающей математики.Тесно сотрудничая с нашей администрацией, мы приступили к изменению программы на основе данных, включая тщательный статистический анализ эффективности наших изменений. Благодаря усилиям по повышению осведомленности учащихся о процессе размещения, а также по улучшению их математической подготовки процент поступающих учащихся, нуждающихся в исправлении, снизился с 54% в 2004 году до 24% в 2006 году. Кроме того, в наших переработанных классах развивающей математики проходные баллы увеличился с 30% в 2004 г. до 80% в 2009 г., где они и остались.(Для получения более подробной информации о нашей программе см. «Успешная развивающая математика : модель« Обзор-предварительное тестирование-повторное тестирование »помогает студентам двигаться вперед» , опубликовано в журнале The New England Journal of Higher Education .
Однако успешная программа, которую мы проводим в штате Вустер, была проигнорирована в отчете оперативной группы. Почему? Как упоминалось выше, в 2004 году у нас была неудачная программа начального уровня: 54% поступающих учащихся были переведены на развивающую математику, и только 30% из этих студентов прошли курс развивающей математики.Тесно сотрудничая с нашей администрацией, мы приступили к изменению программы на основе данных, включая тщательный статистический анализ эффективности наших изменений. Благодаря усилиям по повышению осведомленности учащихся о процессе размещения, а также по улучшению их математической подготовки процент поступающих учащихся, нуждающихся в исправлении, снизился с 54% в 2004 году до 24% в 2006 году. Кроме того, в наших переработанных классах развивающей математики проходные баллы увеличился с 30% в 2004 г. до 80% в 2009 г., где они и остались.(Для получения более подробной информации о нашей программе см. «Успешная развивающая математика : модель« Обзор-предварительное тестирование-повторное тестирование »помогает студентам двигаться вперед» , опубликовано в журнале The New England Journal of Higher Education . Удивительно, что эта статья не была включена в список ссылка в отчете оперативной группы.)
Удивительно, что эта статья не была включена в список ссылка в отчете оперативной группы.)
Мы полагаем, что выполнение рекомендаций целевой группы приведет либо к понижению стандартов в начальных курсах математики, либо к увеличению числа студентов, не сдавших первый курс математики в колледже.Мы понимаем и одобряем стремление целевой группы улучшить развивающее образование, но мало доказательств того, что эти рекомендации будут иметь такой эффект.
Майк Виндерс — адъюнкт-профессор математики в Государственном университете Вустера. Ричард Биск — профессор математики в Государственном университете Вустера, заведующий кафедрой математики с 2004 по 2012 год.
Поделиться страницей
Комментарии закрыты.
«Давайте обсудим математику»; Влияние уроков по проблемам сдвига на математические дискуссии и повышение уровня в начальной алгебре
Дизайн
Мы использовали квазиэкспериментальный план исследования (до и после тестирования, контрольная группа), чтобы исследовать вопрос нашего исследования.
Интервенция
В обоих условиях студенты работали в течение 5 недель над серией уроков из 12 уроков по 60 минут на тему ранней алгебры. В условии проблемы смены мы заменили пять из этих уроков, которые подходили для адаптации, уроками задачи смены.Уроки по проблеме смены состояли из задач, которые были близки или адаптированы к классическим задачам из учебника в соответствии с последовательностью задач в учебнике (Moderne Wiskunde 1A 2012; Moderne Wiskunde 1B 2012). Поступая так, мы стремились приблизиться к учебной программе учителя. Мы разработали эти задачи в соответствии с принципами проектирования Palha et al. (2013).
Эти принципы проектирования:
- 1)
«проектировщик руководствуется учебной целью более глубокого понимания математики
- 2)
математика должна начинаться с уровня, который экспериментально реален для учащихся, а
- 3) Отражение
может быть вызвано математическими обсуждениями »(Palha et al.
 2013, стр. 148–149)
2013, стр. 148–149)
Ни в одном из условий учителям не давали предварительных инструкций о том, как поддерживать небольшие группы учеников. Учителя оказывали поддержку обычным способом (т.е. учителя в основном давали содержательную помощь или подсказки отдельным ученикам в группах).
В условиях обычного учебника ученики сидели вместе небольшими разнородными группами по три или четыре ученика (как обычно), и им разрешалось разговаривать друг с другом, но они работали индивидуально над обычными заданиями из обычного учебника математики в течение всех 12 уроков. .Каждый урок начинался с 15-минутного инструктажа учителя, после чего ученики выполняли задания из учебника в течение 45 минут.
В условно-посменном режиме студенты совместно работали в течение пяти уроков (урок 2, 4, 6, 11 и 12) на уроках, связанных со сменой. Каждый урок начинался с 15-минутного вступительного слова учителя, за которым следовали ученики, работающие над уроками по сменам в течение 45 минут. На оставшихся уроках ученики сидели в одних и тех же небольших разнородных группах и работали над обычными заданиями из учебника.
На оставшихся уроках ученики сидели в одних и тех же небольших разнородных группах и работали над обычными заданиями из учебника.
Урок задачи сдвига для ранней алгебры
Основная цель обучения на уроках проблемы сдвига — более глубокое понимание ранней алгебры, в частности, формул (принцип дизайна: «дизайнер руководствуется целью обучения — более глубоким пониманием математики »(Палха и др., 2013, с. 148–149)). Все возможные переходы к формулам представления и обратно связаны с этой целью обучения. Для достижения этой учебной цели серия уроков (уроки с проблемами смены плюс обычные разделы) в целом содержала упражнения, проверяющие все возможные переключения между представлениями Жанвье (1987).В частности, серия уроков содержала упражнения, включающие все шесть переходов к формулам представления и обратно. Если, например, конкретное переключение произошло только в одном направлении в обычной задаче, мы добавили соответствующий переключатель в противоположном направлении в уроке по задаче переключения. Приспосабливая стандартные задачи, мы остаемся близкими к опыту учащихся по математике (принцип дизайна: «математика должна начинаться с уровня, который экспериментально реален для учащихся» (Palha et al.2013, стр. 148–149)), как это сделал Палха с упражнениями по геометрии (Палха и др., 2013).
Приспосабливая стандартные задачи, мы остаемся близкими к опыту учащихся по математике (принцип дизайна: «математика должна начинаться с уровня, который экспериментально реален для учащихся» (Palha et al.2013, стр. 148–149)), как это сделал Палха с упражнениями по геометрии (Палха и др., 2013).
Для примера рассмотрим задание по ранней алгебре из обычного учебника (см. Рис. 1).
Рис. 1Обычная задача по настройке таблицы
Эта условная задача уже содержит моделирование навыков перевода (переход от ситуации к формулам). Мы адаптировали задачу, добавив к ней распознавание параметра навыков перевода (переключение от формул к ситуации), так что распознавание и моделирование параметров навыков перевода можно изучать попарно, как было предложено Janvier (1987).Столы и стулья, которые являются частью обычного задания, также были распечатаны в цвете и разрезаны на отдельные фигуры столов и стульев, чтобы студенты могли работать с конкретным материалом. На рисунке 2 показана адаптированная задача.
На рисунке 2 показана адаптированная задача.
Адаптированное задание по настройке стола с конкретным материалом
Учителя в обоих условиях реализовали уроки, как предполагалось (оказали поддержку, как обычно). Проверка выполнения проводилась первым автором во время и после уроков (уточняйте у учителя и смотрите видеозаписи уроков).
Участников
Участниками были 160 учеников в возрасте от 12 до 15 лет ( M = 12,87, SD = 0,54) из 6 классов седьмого класса ( M = 26,67, SD = 0,52) и 6 учителей (5 мужчин, 1 женщина) одной школы в пригороде Амстердама, Нидерланды, в этнически неоднородном пригороде. Первый автор — учитель в этой школе.
Двадцать семь процентов студентов говорили дома по крайней мере на одном иностранном языке, помимо голландского.Восемь процентов студентов из числа этнических меньшинств вообще не говорили дома по-голландски. В начальной школе учащимся давали советы по отслеживанию: от профессионального до довузовского. В отличие от обычной практики в Нидерландах, в соответствии с рекомендациями начальной школы, школа откладывает поток учеников на 2 года. Семидесяти процентам участвовавших студентов были даны советы по профессиональному обучению и 30% студентов — доуниверситетскому уровню. Учащиеся разного происхождения и разного уровня подготовки были равномерно распределены по классам школой.Подобно Palha et al. (2014), в данном исследовании мы сосредоточились на гетерогенных группах. Все студенты (оба условия) работали в небольших разнородных группах (34 группы по четыре студента и восемь групп по три студента). Студенческие группы были сформированы на основе результатов предварительного теста по математике, измеренного с помощью предварительного теста математических знаний по ранней алгебре. Студенты были разделены на три категории в зависимости от их успеваемости: слабые, средние и сильные. Группы состояли из одного слабого ученика, двух средних учеников и одного сильного ученика (Webb et al.1998).
В отличие от обычной практики в Нидерландах, в соответствии с рекомендациями начальной школы, школа откладывает поток учеников на 2 года. Семидесяти процентам участвовавших студентов были даны советы по профессиональному обучению и 30% студентов — доуниверситетскому уровню. Учащиеся разного происхождения и разного уровня подготовки были равномерно распределены по классам школой.Подобно Palha et al. (2014), в данном исследовании мы сосредоточились на гетерогенных группах. Все студенты (оба условия) работали в небольших разнородных группах (34 группы по четыре студента и восемь групп по три студента). Студенческие группы были сформированы на основе результатов предварительного теста по математике, измеренного с помощью предварительного теста математических знаний по ранней алгебре. Студенты были разделены на три категории в зависимости от их успеваемости: слабые, средние и сильные. Группы состояли из одного слабого ученика, двух средних учеников и одного сильного ученика (Webb et al.1998). В идеале студенты работали в группах по четыре человека, но из-за ограничений в размере класса было сформировано восемь групп по три человека.
В идеале студенты работали в группах по четыре человека, но из-за ограничений в размере класса было сформировано восемь групп по три человека.
Учителя вызвались участвовать в этом исследовании. Каждый учитель вел свой класс. Учителя были разделены на три пары в зависимости от возраста и опыта преподавания (6, 13 и 33 года опыта преподавания). Для каждой пары один учитель был отнесен к экспериментальным условиям, а другой — к контрольным (три учителя с 17 группами по четыре ученика и четыре группы по три ученика в каждом состоянии, два мужчины и одна женщина в экспериментальных условиях и три мужчины. в контрольном состоянии).Один из учителей — первый автор этой статьи.
Сбор данных / инструменты / анализ
Математические дискуссии
В каждом классе (оба условия) случайным образом была выбрана одна группа для видеозаписи. Данные из одной группы в условиях обычного учебника отсутствовали, в результате чего всего три группы находились в состоянии проблемы смены и две группы в условии обычного учебника. Перед сбором данных каждую группу снимали на видео во время одного урока, чтобы студенты могли привыкнуть к камере.
Перед сбором данных каждую группу снимали на видео во время одного урока, чтобы студенты могли привыкнуть к камере.
Групповое взаимодействие было записано на видео в уроке 3. Урок 3 по проблеме смены был выбран из-за его четкого применения принципов проектирования, лежащих в основе уроков по проблеме смены.
Процессы взаимодействия были записаны и проанализированы с использованием программы Multiple Episode Protocol Analysis (Erkens 2002). Взаимодействие закодировано на уровне высказываний. Вслед за Van Boxtel et al. (2000) мы определяем высказывание как «отдельную единицу сообщения, которая отличается от другого высказывания« ощутимой »паузой, запятой или точкой» (Van Boxtel et al.2000, стр. 317–318). Чтобы получить общее представление о процессах взаимодействия, мы сначала закодировали все высказывания на уровне актов задания. Акты задачи относятся к функции высказываний по отношению к выполнению задачи (Ван Дри и др., 2005). Мы выделили семь основных категорий; четыре категории по измерению высказываний при выполнении задания и три категории высказываний вне задания (см. Таблицу 3). На втором этапе высказывания, которые были закодированы как разговор о содержании задачи, были разделены на беседы о содержании задачи с учителем и математические обсуждения (обсуждение содержания задачи с другими учениками в группе).Наконец, на третьем этапе высказывания, закодированные как математические дискуссии на втором этапе, были разделены на семь подкатегорий в соответствии с регулирующими и ключевыми действиями Модели процесса (Dekker and Elshout-Mohr 2004): попросите показать работу, попросите объяснить работать, критиковать работу, рассказывать / показывать работу, объяснять работу, оправдывать работу и восстанавливать работу (см. Таблицу 4). В разделе «Два примера математических обсуждений в условиях проблемы сдвига» мы приводим два примера анализа типичных математических дискуссий в условиях проблемы сдвига.
Таблицу 3). На втором этапе высказывания, которые были закодированы как разговор о содержании задачи, были разделены на беседы о содержании задачи с учителем и математические обсуждения (обсуждение содержания задачи с другими учениками в группе).Наконец, на третьем этапе высказывания, закодированные как математические дискуссии на втором этапе, были разделены на семь подкатегорий в соответствии с регулирующими и ключевыми действиями Модели процесса (Dekker and Elshout-Mohr 2004): попросите показать работу, попросите объяснить работать, критиковать работу, рассказывать / показывать работу, объяснять работу, оправдывать работу и восстанавливать работу (см. Таблицу 4). В разделе «Два примера математических обсуждений в условиях проблемы сдвига» мы приводим два примера анализа типичных математических дискуссий в условиях проблемы сдвига.
Межэкспертная надежность между двумя кодировщиками, первым автором и научным сотрудником, была рассчитана по трем случайно выбранным протоколам (сумма 1236 высказываний) для всех трех шагов кодирования. Межэкспертная надежность была хорошей (согласие 82% и каппа Коэна 0,76) для кодирования на первом этапе (говорить о содержании задачи, думать вслух о содержании задачи, говорить о задаче в целом, говорить о выполнении задачи, социальный разговор, поговорим о камере, без кода).Надежность между экспертами была превосходной (согласие 99,7% и Каппа Коэна 0,97) на втором этапе кодирования после согласования первого шага (обсуждение содержания задачи с учителем и элементы математических дискуссий), а надежность между экспертами была удовлетворительной (согласие 84% и каппа Коэна 0,67) для третьего шага кодирования после согласования второго шага (подробный анализ математических дискуссий в регулирующих и ключевых действиях). Для третьего шага Каппа Коэна оказалась удовлетворительной, но ниже, чем можно было ожидать, из-за артефакта при вычислении Каппы Коэна.Поскольку подкатегории говорят / показывают работу чаще всего, а другие — редко, распределение диагонали матрицы, используемой при вычислении Каппы Коэна, неравномерно, что приводит к более низкому значению Каппы Коэна, чем было бы в противном случае (Birt et al.
Межэкспертная надежность была хорошей (согласие 82% и каппа Коэна 0,76) для кодирования на первом этапе (говорить о содержании задачи, думать вслух о содержании задачи, говорить о задаче в целом, говорить о выполнении задачи, социальный разговор, поговорим о камере, без кода).Надежность между экспертами была превосходной (согласие 99,7% и Каппа Коэна 0,97) на втором этапе кодирования после согласования первого шага (обсуждение содержания задачи с учителем и элементы математических дискуссий), а надежность между экспертами была удовлетворительной (согласие 84% и каппа Коэна 0,67) для третьего шага кодирования после согласования второго шага (подробный анализ математических дискуссий в регулирующих и ключевых действиях). Для третьего шага Каппа Коэна оказалась удовлетворительной, но ниже, чем можно было ожидать, из-за артефакта при вычислении Каппы Коэна.Поскольку подкатегории говорят / показывают работу чаще всего, а другие — редко, распределение диагонали матрицы, используемой при вычислении Каппы Коэна, неравномерно, что приводит к более низкому значению Каппы Коэна, чем было бы в противном случае (Birt et al. др. 1993). Ассистент-исследователь независимо закодировал данные двух групп в экспериментальных условиях, а первый автор закодировал остальные данные.
др. 1993). Ассистент-исследователь независимо закодировал данные двух групп в экспериментальных условиях, а первый автор закодировал остальные данные.
Мы сравнили абсолютные частоты категориальных элементов математических дискуссий, чтобы определить, возникает ли больше элементов математических дискуссий в условии задачи о сдвиге, чем в условиях обычного учебника.
Математический уровень
Математический уровень учащихся в начальной алгебре измерялся с помощью теста. Предварительный тест проводился на уроке перед вмешательством, и тот же тест проводился в качестве заключительного теста на уроке после вмешательства. Тест направлен на измерение математического уровня учащихся на основе навыков перевода, полученных от Жанвье (1987). Самый высокий уровень подразумевает способность переводить из формул представления в ситуации представления, таблицы и графики и наоборот.
Тест состоит из шести вопросов и 17 подвопросов, из которых 10 использовались для измерения математического уровня. Они состоят из вопросов, касающихся всех навыков перевода формул представления (Janvier 1987). Остальные семь вопросов были отброшены (не включены в баллы) при определении повышения уровня. Они состоят из основных арифметических вопросов в начальной школе, чтобы учащиеся могли ответить по крайней мере на некоторые вопросы, когда тест проводился в качестве предварительного.Были присвоены баллы 0, 1 и 2; 0 означает низкий математический уровень, 1 означает средний математический уровень и 2 означает высокий математический уровень. Подвопросы теста соответствовали переключениям между представлениями Жанвье с использованием формул. Первый подвопрос касался только менее абстрактного представления формулы; поэтому оценка за этот вопрос была ограничена 1 (средний математический уровень). Сумма баллов составляет максимальное количество в 19 баллов, которые студенты могут набрать за тест.Уровни, которые были присвоены подвопросам, обсуждались со вторым кодировщиком (вторым автором этой статьи).
Они состоят из вопросов, касающихся всех навыков перевода формул представления (Janvier 1987). Остальные семь вопросов были отброшены (не включены в баллы) при определении повышения уровня. Они состоят из основных арифметических вопросов в начальной школе, чтобы учащиеся могли ответить по крайней мере на некоторые вопросы, когда тест проводился в качестве предварительного.Были присвоены баллы 0, 1 и 2; 0 означает низкий математический уровень, 1 означает средний математический уровень и 2 означает высокий математический уровень. Подвопросы теста соответствовали переключениям между представлениями Жанвье с использованием формул. Первый подвопрос касался только менее абстрактного представления формулы; поэтому оценка за этот вопрос была ограничена 1 (средний математический уровень). Сумма баллов составляет максимальное количество в 19 баллов, которые студенты могут набрать за тест.Уровни, которые были присвоены подвопросам, обсуждались со вторым кодировщиком (вторым автором этой статьи). Студенты индивидуально работали над тестом в течение 60 мин. Пример простого арифметического вопроса в начальной школе: «Из одной упаковки смеси для блинов можно испечь шесть блинов. Сколько блинов можно испечь с 12 пакетами блинов? » Пример вопроса, который измеряет математический уровень: «Шейн хочет привести в форму, поэтому он идет плавать. С помощью следующей формулы (слово) вы можете рассчитать затраты Шейна.Количество плаваний × 3 + 30 = затраты. (Здесь 3 означает 3 евро, стоимость одного плавания в бассейне для члена, а 30 означает 30 евро, стоимость годового членства в бассейне.) Нарисуйте график для этой формулы ».
Студенты индивидуально работали над тестом в течение 60 мин. Пример простого арифметического вопроса в начальной школе: «Из одной упаковки смеси для блинов можно испечь шесть блинов. Сколько блинов можно испечь с 12 пакетами блинов? » Пример вопроса, который измеряет математический уровень: «Шейн хочет привести в форму, поэтому он идет плавать. С помощью следующей формулы (слово) вы можете рассчитать затраты Шейна.Количество плаваний × 3 + 30 = затраты. (Здесь 3 означает 3 евро, стоимость одного плавания в бассейне для члена, а 30 означает 30 евро, стоимость годового членства в бассейне.) Нарисуйте график для этой формулы ».
Межэкспертная надежность для предварительного и последующего тестирования между двумя кодировщиками (первым и вторым автором) по 36 произвольно выбранным тестам (10% от общего числа тестов) была превосходной (ICC 0,95). Остальные данные закодировал первый автор.
Многоуровневая модель для повторяющихся наблюдений в фиксированных случаях с неограниченной ковариационной матрицей (Snijders and Bosker 2012) использовалась для проверки дифференциального роста между условием проблемы сдвига и условием обычного учебника. Фиксированные случаи — это измерения (до и после тестирования), вложенные в отдельных учащихся. Измерения (до и после тестирования) — это первый уровень, а отдельные ученики — второй уровень.
Фиксированные случаи — это измерения (до и после тестирования), вложенные в отдельных учащихся. Измерения (до и после тестирования) — это первый уровень, а отдельные ученики — второй уровень.
Ресурсы и ответы CIMT по математике г-на Бартона
arrow_back Вернуться к богатым задачамРесурсы и ответы по математике CIMT
В течение долгого времени я был большим поклонником отличного веб-сайта CIMT.это забиты одними из самых инновационных ресурсов, для всех возрастов и уровней способностей, и многие из них поставляются с выдающийся уровень поддержки учителей. Что ж, я рад сказать что благодаря моему партнерству с TES, полный набор удивительных ресурсов по математике Программа улучшения (MEP) теперь доступна для загрузки в удобном виде тематические области.
Есть действительно исключительные ресурсы, доступные для
весь ключевой этап 3 и 4. Все ресурсы выравниваются, а
Ресурсы «специального» уровня для GCSE, безусловно, подходят для A / S.
Студенты уровня, которым нужны алгебраические и геометрические понятия
армирование.
Все ресурсы выравниваются, а
Ресурсы «специального» уровня для GCSE, безусловно, подходят для A / S.
Студенты уровня, которым нужны алгебраические и геометрические понятия
армирование.
В каждом отряде содержится куча блестящих ресурсов, забитых полный примеров, заметок и практических материалов. Деятельность» разделы особенно полезны для подготовки студентов к требования нового GCSE, предлагая богатые задания и мини-проекты, а разделы «Учебные заметки» содержат фантастические исторические фоны по изучаемым предметам, а также выделение ключевой язык и заблуждения.
Поскольку эти ресурсы размещаются на TES. Вам нужно будет зарегистрироваться с ними, прежде чем вы сможете скачать. Это совершенно бесплатно и занимает около 1 минуты.
Типы ресурсов, которые составляют каждую тематическую область, включают следующее:
Практикум для учеников — упражнения в стиле учебника завершены
с примечаниями, примерами и ответами, подходящими для всех
уровни способностей.
Активности — идеи для сложных задач, проекты, головоломки и групповая работа, которая сопровождается заметками и решениями.
Планы уроков — краткий обзор материала, который может проходить в последовательности уроков, дифференцированных по уровням.
Психологические тесты — серия дифференцированных мысленных вопросов по теме, чтобы быстро проверить и закрепить понимание.
Накладные слайды — фотокопирующие ресурсы, используемые в преподавание темы.
Ревизионные испытания — серия дифференцированных конечных устройств тесты для оценки понимания с ответами и отметками схемы.
Учебные материалы — обзор устройства, включая
Историческая справка и введение, Учебные моменты, Общие
Заблуждения, ключевой язык / обозначения, ключевые концепции и
Приложения. ПРИМЕЧАНИЕ. Учебные заметки также содержат указания относительно
какие части темы подходят для Standard, Academic,
Экспресс и специальные группы.
Уровневые дополнительные упражнения — стиль учебника и экзамена вопросы, нацеленные на Standard / Academic и Express / Special группы с ответами.
Прежде чем вы начнете, я настоятельно рекомендую загрузить некоторые из Общая информация, поскольку это дает обзор того, как конечно работает и уровни сложности.
Наслаждайтесь!
Содержание
Общие
keyboard_arrow_upВ начало
MEP
Краткое содержание проекта (годы с 7 по 9)
год
7 Схема работы
год
8 Схема работы
год
9 Схема работы
GCSE
Схема работы
GCSE
Обзор начального уровня
Год 7
keyboard_arrow_upВ начало
1. Логика
Логика
2.
Значение места
3.
Графики
4.
Сложение и вычитание десятичных знаков
5.
Уголки
6.
Умножение десятичных знаков
7.
Числовые узоры и последовательности
8.
Деление десятичных знаков
9.
Территории и периметры
10.
Дроби
11.
Сбор и представление данных
12.Арифметическая версия
13.
Поиск паттернов
14.
Время и расписание
15.
Отрицательные числа
16.
Линейные уравнения
17.
Дроби, десятичные дроби и проценты
18.
Количественные данные
19.
Чертеж в масштабе
20.
Дроби
21.
Вероятность одного события
22.
Том
Год
7 диагностических тестов
Год 8
keyboard_arrow_upВ начало
1. Математические схемы
Математические схемы
2.
Факторы
3.
Пифагор
4.
Округление и оценка
5.
Анализ данных
6.
Сети и площадь поверхности
7.
Соотношение и пропорции
8.
Алгебра (скобки)
9.
Дроби и проценты
10.
Вероятность двух событий
11.
Углы, пеленг и карты
12.Алгебра — формулы
13.
Деньги и время
14.
Прямолинейные графики
15.
Полигоны
16.
Круги и цилиндры
17.
Единицы измерения
18.
Скорость, расстояние и время
19.
Сходство
20.
Анкеты и анализ
год
8 диагностических тестов
Год 9
keyboard_arrow_upВ начало
1. Основная арифметика
Основная арифметика
2.
Основные операции
3.
Индексы и стандартная форма
4.
Доли и проценты
5.
Линейные графики и уравнения
6.
Вероятность
7.
Преобразования
8.
Статистические диаграммы
9.
Площадь, периметр, объем
10.
Последовательности
11.
Алгебраические манипуляции
12.Строительство и расположение
13.
Графики, уравнения и неравенства
14.
Оценка и приближение
15.
Тригонометрия
16.
Кумулятивная частота
17.
Квадратичные функции
18.
Выборка
год
9 диагностических тестов
GCSE
keyboard_arrow_upВ начало
Обратите внимание: листы курса MEP GCSE разделены на четыре
Уровни способностей: Стандартный, Академический, Экспресс и Специальный.
В общих чертах, Standard эквивалентен уровню Foundation, Академические — это студенты, которые поступили бы по старым Промежуточный уровень и сейчас будет на грани Foundation / Higher, Экспресс эквивалентен Высшему, а Особые — Одаренные и Талантливые математики.
Для исчерпывающей разбивки конкретных частей каждой юнит должен быть покрыт для каждого из этих уровней способностей, пожалуйста просмотреть отдельные файлы учебных заметок, которые были загружены с каждой единицей.
1.
Индексы
2.
Формулы
3.
Угловая геометрия
4.
Тригонометрия
5.
Вероятность
6.
Система счисления
7.
Измерение
8.
Обработка данных
9.
Анализ данных
10.
Уравнения
11.
Дроби и проценты
12. Шаблоны номеров
Шаблоны номеров
13.Графики
14.
Локусы и трансформации
15.
Вариант
16.
Неравенства
17.
Использование графиков
18.
3D геометрия
19.
Векторы
20.
Статистика GCSE
GCSE
Экзаменационные работы
GCSE
Разные упражнения
GCSE
Модульные тесты
GCSE
Факты, которые следует запомнить
GCSE
Статистические экзаменационные документы
Начальный уровень
keyboard_arrow_upВ начало
Этот материал был разработан в рамках демонстрации MEP.
Проект в поддержку сертификата Валлийской экзаменационной комиссии
Образовательные достижения по математике.Этот сертификат сейчас
известный как Сертификат начального уровня по математике.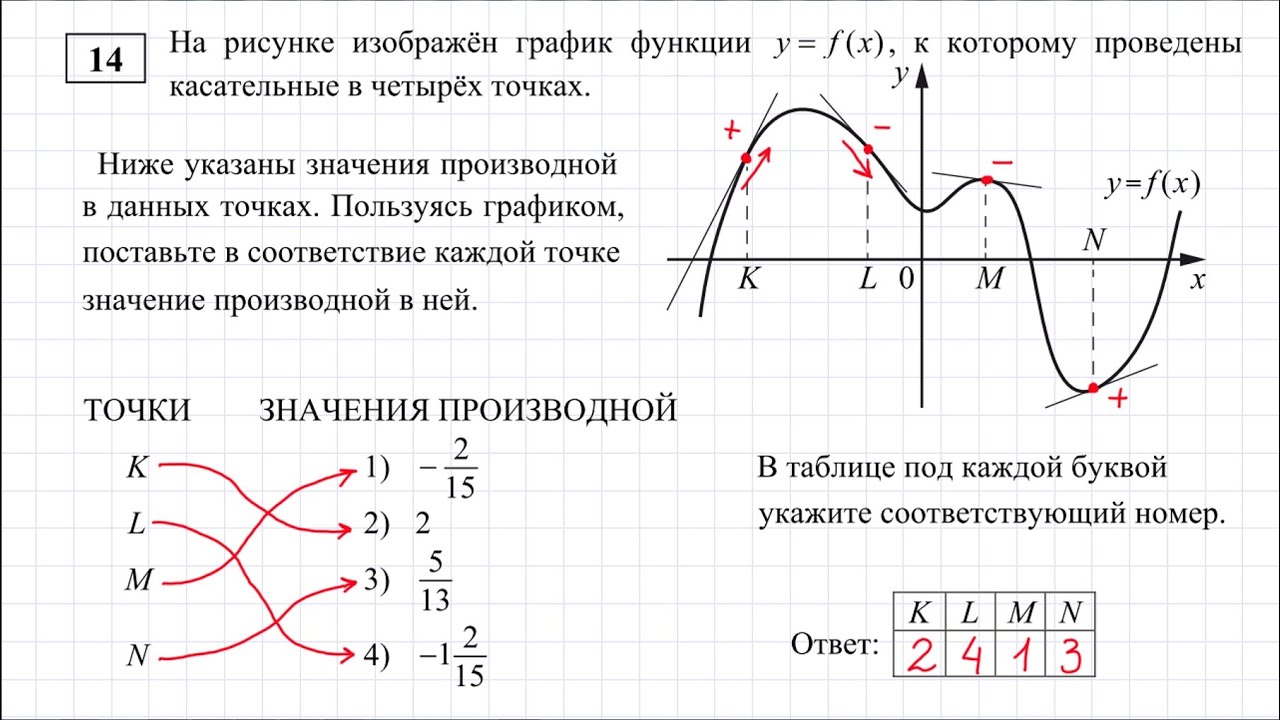 В
Сертификационный курс предназначен для кандидатов 10 и 11 лет, которые
вряд ли получит оценку по математике GCSE.
В
Сертификационный курс предназначен для кандидатов 10 и 11 лет, которые
вряд ли получит оценку по математике GCSE.
Набор ресурсов для этого модуля состоит из следующие:
Схема работы — это подробная схема, показывающая, какие темы должны быть освещены и в каком порядке.
Практикум — эти книги содержат множество упражнений и отработанных примеров на основе содержания Единиц в Схеме Работа.
Примеры из практики — это существенные разделы работы, которые покрывают большую часть содержимого модулей, но не являются обязательными. Они были разработаны для студентов, чтобы получить как мотивацию, так и уверенность и может использоваться в сочетании с более рутинными практика, найденная в Практических книгах.
Накладные слайды — эти мастер-копии могут использоваться как OH
слайды или рабочие листы, скопированные для индивидуального использования с учителем
руководство.
Психологические тесты — эти тесты предназначены для поддержки всех основные затронутые темы, где умственная компетентность и ловкость полезный.
Промежуточные и слуховые тесты — образцы промежуточных и Звуковые тесты для каждого модуля, основанные непосредственно на вопросе framework, используемый в тестах WJEC. Они идут в комплекте с отметкой схемы.
Модуль
1 модуль
2
Модуль
3
Въезд
Уровень Финальный тест
Практические тесты на способность к численному мышлению
Численные тесты — это либо тесты скорости , , либо тесты мощности :
Численные вычисления и численные оценки обычно представляют собой вопросов скорости .Это означает, что тестируемый испытывает давление из-за очень жесткого ограничения по времени.
 Чтобы получить высокие баллы по этим вопросам, вам необходимо уметь делать быстрые и точные вычисления без использования калькулятора. Обычно от вас не ждут, что вы сдадите тест, но вас будут оценивать по количеству полученных вами правильных ответов.
Чтобы получить высокие баллы по этим вопросам, вам необходимо уметь делать быстрые и точные вычисления без использования калькулятора. Обычно от вас не ждут, что вы сдадите тест, но вас будут оценивать по количеству полученных вами правильных ответов.Численное обоснование и интерпретация данных обычно известны как испытания мощности . Здесь, вероятно, не стоит ожидать, что вы получите все правильные ответы, даже если у вас неограниченное время.Обычно вам дается достаточно времени, чтобы ответить на вопросы.
Типы числовых вопросов
Числовые вычисления
Эти вопросы проверяют вашу способность использовать основные принципы арифметики. Например:
Сложение
Вычитание
Умножение
Деление
Они также могут использовать математические термины и методы, такие как:
Десятичные числа
Коэффициенты
Корни
Дроби
Степени
Показатели
Эти вопросы не предназначены для проверки ваших способностей к рассуждению.
Чтобы получить высокие баллы по этим вопросам, вам просто нужно будет произвести быстрые и точные вычисления.
Эти вопросы непосредственно применимы ко многим административным и канцелярским должностям, но также могут появляться в качестве компонента выпускных и управленческих тестов.
Скорость, с которой вы можете ответить на эти вопросы, является критически важным критерием, поскольку большинство людей может набрать очень высокий балл, имея неограниченное время для ответа.
Таким образом, можно ожидать от 25 до 35 вопросов через от 20 до 30 минут .
Примеры вопросов:
1. 139 + 235 =?
A) 372
B) 374
C) 376
D) 437
2. 139 — 235 =?
A) –69
B) 96
C) 98
D) –96
3. 5 x 16 =?
A) 80
B) 86
C) 88
D) 78
Ответы:
1. B
2. D
3. A
Подробнее о как рассчитать дроби и как рассчитать отношения см. Наши специальные статьи.
Наши специальные статьи.
Скачать практические тесты числовых вычислений
Числовые оценки
Эти вопросы проверяют вашу способность быстро оценивать ответы на довольно простые числовые вопросы.
Чтобы получить высокие баллы по этим вопросам, вам нужно будет быстро приблизительно ответить на них.
Вы должны избегать ловушки точного ответа, которая отнимет слишком много времени и помешает вам ответить на достаточно вопросов, чтобы получить хорошую оценку.
Числовая оценка является ключевой во многих ремесленных и технических работах, где важна способность быстро и точно оценить количество материалов.
Тем не менее, способность делать быстрые оценки — полезный навык, которым нужно обладать, даже если вы сдаете выпускной или профессиональный тест, поскольку это позволит вам примерно проверить свои ответы на вопросы интерпретации данных.
Скорость, с которой вы можете ответить на эти вопросы, является критически важным критерием, поскольку большинство людей может набрать очень высокий балл, имея неограниченное время для ответа.
Таким образом, вы можете ожидать 25-35 вопросов через 10 минут или около того .
Несмотря на то, что вопросы численной оценки кажутся простыми, может потребоваться некоторое время, чтобы найти оптимальный компромисс между скоростью и точностью.
Прежде чем вы попытаетесь ответить на каждый вопрос, посмотрите на ряд доступных ответов и спросите себя, насколько точной должна быть ваша оценка.
Например, достаточно ли порядка величины или нужно вычислить ответ до ближайшего целого числа?
Примеры вопросов:
1.347 + 198 =?
A) 650
B) 550
C) 580
D) 590
E) 600
2. 3,509 + 3,492 =?
A) 7,000
B) 7,200
C) 7,100
D) 7,250
E) 6,950
3. 989 + 413 + 498 =?
A) 2,600
B) 900
C) 1,100
D) 1,900
E) 3,200
Ответы:
1. B
2. A
3. D
Практика загрузки Числовые оценочные тесты
Числовые рассуждения
Числовые оценочные тесты позволяют оценить вашу способность использовать числа логически и рационально.
Вам нужно будет интерпретировать предоставленную информацию, а затем применить соответствующую логику, чтобы ответить на вопросы.
Другими словами, вам нужно решить, как получить ответ, а не какие вычисления применить.
Для завершения этих вопросов требуется только базовый уровень образования, и поэтому они измеряют способность к числовому мышлению, а не успеваемость.
Вопросы измеряют ваше понимание числовых рядов, числовых преобразований, взаимосвязей между числами и вашу способность выполнять числовые вычисления.
Они также включают текстовые вопросы, в которых математическая задача сформулирована словами, и ваша задача — применить необходимую логику, чтобы найти ответ.
Иногда вопросы предназначены для того, чтобы приблизиться к типу рассуждений, необходимых на рабочем месте.
Обычно вам разрешается использовать калькулятор для таких вопросов, и неплохо было бы инвестировать в калькулятор, который может обрабатывать дроби и проценты.
Следует ожидать около от 15 до 20 вопросов за от 20 до 30 минут .
Пример вопроса:
1. Анна и Джон едут в свой новый дом за 400 миль. Анна ведет семейный автомобиль со средней скоростью 60 миль в час. Джон водит эвакуатор со средней скоростью 50 миль в час. Во время поездки Анна останавливается в общей сложности на 1 час 20 минут, Джон останавливается на половину этого времени. Какая разница в минутах между их временем прибытия?
A) 60
B) 55
C) 40
D) 90
E) 80
Ответ: C
17 Примеры учебной деятельности на основе проектов STEM
Каждый учитель знает, что обучение на основе STEM — это волна будущего.Многие также знают, что STEM неполноценен без искусства и литературы. Проектное обучение — идеальный способ овладеть навыками STEAM таким образом, чтобы студенты чувствовали себя актуальными. Проекты помогают учащимся овладеть полезными навыками, продолжать учиться весело и позволяют учащимся управлять ходом своего обучения. Это победа для всех. Это также способ получить более высокие баллы за экзамен, не обучая его.
Это победа для всех. Это также способ получить более высокие баллы за экзамен, не обучая его.
Следующие задания могут привлечь в STEAM даже скучающих и разочарованных студентов:
PBL STEAM Мероприятия для детей ясельного и дошкольного возрастаНесколько настроек следующих заданий могут сделать их более или менее сложными, в зависимости от компетенций учащихся, целей учебной программы и подобных факторов.Помогите своим ученикам освоить STEM с помощью этих проектов:
Выращивание хрустального дерева
Постройте дерево из картона или купите его в местном магазине. Подойдет любая форма из картона, поэтому вы можете попробовать шар, цветок или любую другую форму, если учащиеся предпочитают не использовать дерево. Смешайте кристаллический раствор: четыре столовые ложки теплой воды, четыре столовые ложки поваренной соли, две столовые ложки нашатырного спирта и четыре столовые ложки раствора для посинения миссис Стюарт. Раскрасьте картон пищевым красителем, затем нанесите кристаллический раствор. Кристаллы появятся через несколько часов и продолжат развиваться в течение дня или около того.
Кристаллы появятся через несколько часов и продолжат развиваться в течение дня или около того.
Научные эксперименты с конфетами
Дети любят конфеты, и многие родители хотят избавиться от детских конфет. Убейте двух зайцев одним выстрелом, добавив конфеты в школьные проекты. Посмотрите некоторые из этих невероятных экспериментов:
Создание катапульты
Ваши ученики постоянно бросаются друг в друга? Направьте эту энергию на что-то более продуктивное.Помогите им сделать простую катапульту с этим руководством.
PBL Занятия STEAM для старшеклассниковСтаршеклассники на удивление хорошо разбираются в STEM, если у них есть такая возможность. Даже первоклассники и второклассники могут наслаждаться проектами, которые длятся несколько недель и требуют серьезного критического мышления. Попробуйте выполнить одно из следующих действий, при необходимости изменив его в соответствии с потребностями и интересами учащихся.
Проекты по наблюдению за дикой природой
Помогите студентам узнать о диких животных, наблюдая за ними в их естественной среде обитания. Тайная жизнь диких животных — отличный ресурс для начинающих. Некоторые проекты включают:
Тайная жизнь диких животных — отличный ресурс для начинающих. Некоторые проекты включают:
- Разгадайте загадку с животными. Почему некоторые птицы исчезают в холодные месяцы? Куда они идут? Как животные согреваются, когда на улице холодно? Наблюдают ли животные за людьми?
- Понаблюдайте за небольшой экосистемой в течение нескольких недель. Как меняется грязь при переходе к весне? Как муравейники меняются со временем?
Растения
Выращивание растений — это тонкая наука, предлагающая быстрые вознаграждения и возможность узнать о ботанике, кулинарии и даже о геометрии конструкции растений.Попросите учащихся взять сочные черенки и вырастить из них свежие растения, а затем создать сочный рисунок. Или создайте классную траву или огород. Выращивание растений на открытом воздухе — отличный шанс узнать об углеродном цикле. Также подумайте о том, чтобы помочь учащимся найти безопасные и экологически безопасные способы защиты от вредителей и сорняков.
Чтобы получить еще больше от проекта по садоводству, подумайте о том, чтобы каждый учащийся разработал рецепты выращенных им продуктов, а затем создал книгу рецептов для класса.
Чтобы добавить инженерный компонент в ботанический проект, попробуйте спроектировать и построить дождевой сад. Этот проект подходит как для учеников средних, так и для старших классов.
Хотите рассказать ученикам об опылителях и о влиянии небольших изменений окружающей среды на эти жизненно важные ресурсы животных? Ознакомьтесь с этим руководством.
LEGO Механика
LEGO — это весело. Это также отличный способ овладеть пространственным мышлением, геометрией и начальным инженерным делом.Попробуйте некоторые из этих моторизованных проектов LEGO, чтобы помочь своим ученикам превратить любимые игрушки в образование.
Собери робота
Роботы не такие сложные, как кажется. С помощью этого руководства студенты могут построить мини-робота днем. Для еще более увлекательного проекта попробуйте одного из этих роботов. Есть ученик, который предпочитает более старомодный подход к строительству? Помогите им вместо этого сделать этот пропеллерный автомобиль.
Для еще более увлекательного проекта попробуйте одного из этих роботов. Есть ученик, который предпочитает более старомодный подход к строительству? Помогите им вместо этого сделать этот пропеллерный автомобиль.
Создайте свое развлечение
Помогите ученикам создать собственную покадровую анимацию с помощью этого руководства.Затем попросите их включить музыку, создать увлекательную историю и использовать свое воображение, чтобы создать что-нибудь занимательное.
PBL Занятия STEAM для старшеклассниковСтаршеклассников ошеломляют бесконечные испытания и стресс. Однако многие из них считают, что школа не имеет отношения к реальной жизни. Обучение, основанное на проектах, переключает внимание старшеклассников на удовольствие от обучения. Мечтайте масштабно и возлагайте большие надежды. Вы будете удивлены тем, как правильный проект может увлечь даже самых разобщенных учеников.
Создай свой проект
Эффективное обучение вовлекает студентов, побуждая их ставить собственные цели и сроки. Вместо того, чтобы назначать проект, попросите учащихся придумать свои собственные. Установите конкретные правила, а затем запросите ответ. Например, вы можете попросить студентов разработать четырехнедельный эксперимент или разработать решение повседневной проблемы на основе STEM.
Вместо того, чтобы назначать проект, попросите учащихся придумать свои собственные. Установите конкретные правила, а затем запросите ответ. Например, вы можете попросить студентов разработать четырехнедельный эксперимент или разработать решение повседневной проблемы на основе STEM.
Один популярный проект помогает студентам воплотить в реальность шоу с расследованием места преступления.Попробуйте The Cooler and Delivery Truck Evidence.
Видеоигры с физикой
Законы физики видеоигр часто сильно отличаются от законов реального мира. Попросите учащихся выяснить основные законы, которым следуют их любимые видеоигры, используя простые формулы физики. Одна популярная программа использует Angry Birds для лучшего понимания физики.
Выживание зомби
Подростки любят хорошие апокалиптические моменты. Помогите им глубже задуматься о своих любимых фильмах о зомби, размышляя о реальных проблемах выживания.Эта простая головоломка на выживание за рулем глубоко вовлекает учащихся в математику, естественные науки и решение повседневных задач.
Разобраться в реальной проблеме
Ваши ученики могут быть теми, кто решит некоторые из самых сложных задач по математике и естествознанию. Попросите их глубоко изучить современные проблемы, такие как устранение разливов нефти или понимание изменения климата. Некоторые ресурсы для начала работы включают:
Ваше воображение — единственное, что ограничивает ваши возможности для PBL.Цель этого стиля обучения — пробудить в учениках любовь к обучению, а не заставлять их запоминать список фактов. Будь креативным. Спросите студентов, что они хотят узнать. Следуйте своей интуиции и игнорируйте подходы, которые не нравятся вам или вашим ученикам. Находя способы сделать STEM актуальной и интересной, вы можете вызвать новую страсть — и, возможно, даже помочь своим ученикам наметить курс к успешной карьере.
| ’62 Центр театра и танца, ’62 Центр | ||
| касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий / Помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр исследования карьеры, Мирс | 597-2311 | 597-4078 факс |
| Academic Resources, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Прием, Вестон-холл | 597-2211 | 597-4052 факс |
| Affirmative Action, Hopkins Hall | 597-4376 | |
| Africana Studies, Hollander | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art / Лоуренс | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотография Студия, Spencer Studio Art | 597-2030 | |
| Printmaking Studio, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео / фотостудия, Spencer Studio Art | 597-3193 | |
| Asian Studies, Hollander | 597-2391 | 597-3028 факс |
| Астрономия / Астрофизика, Thompson Physics | 597-2482 | 597-3200 факс |
| Департамент легкой атлетики, Физическое воспитание, отдых, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Boat House, Озеро Онота | 443-9851 | |
| Автобусы | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Hockey Rink Ice Line, Lansing Chapman | 597-2433 | |
| Intramurals, Атлетический центр Чандлера | 597-3321 | |
| Физическое воспитание | 597-2141 | |
| Pool Wet Line, Атлетический центр Чандлера | 597-2419 | |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Площадки для игры в сквош | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Thompson Biology | 597-2126 | |
| Биоинформатика, геномика и протеомика, Bronfman | 597-2124 | |
| Биология, Thompson Biology | 597-2126 | 597-3495 факс |
| Охрана и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа / системы сигнализации | 597-4970 / 4033 | |
| Служба сопровождения, Хопкинс-холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Коммутатор | 597-3131 | |
| Центр развития творческих сообществ, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
| Центр экологических исследований, класс 1966 Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория экологических наук, Морли | 597-2380 | |
| Исследования окружающей среды | 597-2346 | |
| Лаборатория ГИС | 597-3183 | |
| Центр иностранных языков, литератур и культур, Холландер | 597-2391 | 597-3028 факс |
| Арабские исследования, Холландер | 597-2391 | 597-3028 факс |
| Сравнительная литература, Холландер | 597-2391 | |
| Критические языки, Hollander | 597-2391 | 597-3028 факс |
| лингафонный кабинет | 597-3260 | |
| Русский, Hollander | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, Стетсон-Корт 24, | 597-2483 | |
| Мусульманская молитвенная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Chemistry, Thompson Chemistry | 597-2323 | 597-4150 факс |
| Классика (греческий и латинский), Hollander | 597-2242 | 597-4222 факс |
| Когнитивная наука, Бронфман | 597-4594 | |
| College Marshal, Thompson Physics | 597-2008 | |
| Отношения с колледжем | 597-4057 | |
| Программа 25-го воссоединения, Фогт | 597-4208 | 597-4039 факс |
| Программа 50-го воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Advancement Operations, Мирс Вест | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Связи с выпускниками, Мирс Вест | 597-4151 | 597-4178 факс |
| Почтовые службы для выпускников / разработчиков, Мирс-Вест | 597-4369 | |
| Разработка, Vogt | 597-4256 | |
| Отношения с донорами, Vogt | 597-3234 | 597-4039 факс |
| Офис по планированию подарков, Vogt | 597-3538 | 597-4039 факс |
| Grants Office, Мирс-Уэст | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Parents Fund, Vogt | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Мирс | 597-4119 | 597-4178 факс |
| Начало занятий и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Коммуникации, Хопкинс Холл | 597-4277 | 597-4158 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Web Team, Southworth Schoolhouse | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Компьютерные науки, Thompson Chemistry | 597-3218 | 597-4250 факс |
| Conferences & Events, Парески | 597-2591 | 597-4748 факс |
Запросы Elm Tree House, Mt. Ферма Надежды, Ферма Надежды, | 597-2591 | |
| Офис контролера, Хопкинс-холл | 597-4412 | 597-4404 факс |
| Счета к оплате и ввод данных, Хопкинс-холл | 597-4453 | |
| Bursar & Cash Receipts, Hopkins Hall | 597-4396 | |
| Financial Information Systems, Hopkins Hall | 597-4023 | |
| Purchasing Cards, Hopkins Hall | 597-4413 | |
| Студенческие ссуды, Хопкинс Холл | 597-4683 | |
| Dance, 62 Центр | 597-2410 | |
| Центр Дэвиса (ранее Мультикультурный центр), Дженнесс | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Jenness House | 597-3344 | |
| Rice House | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета Хопкинс Холл | 597-4351 | 597-3553 факс |
| Столовая, капельницы | 597-2121 | 597-4618 факс |
| ’82 Grill, Парески | 597-4585 | |
| Булочная, Парески | 597-4511 | |
| Общественное питание, факультет | 597-2452 | |
| Driscoll Dining Hall, Дрисколл | 597-2238 | |
| Eco Café, Научный центр | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Lee Snack Bar, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Whitmans ‘, Paresky | 597-2889 | |
| Economics, Schapiro | 597-2476 | 597-4045 факс |
| английский, Hollander | 597-2114 | 597-4032 факс |
| Сооружения, служебное здание | 597-2301 | |
| College Car Request | 597-2302 | |
| Скорая помощь вечером / в выходные дни | 597-4444 | |
| Запросы производственных мощностей | 597-4141 факс | |
| Особые мероприятия | 597-4020 | |
| Кладовая | 597-2143 | 597-4013 факс |
| Клуб преподавателей, Дом факультетов / Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Fellowships Office, Hopkins Hall | 597-3044 | 597-3507 факс |
| Financial Aid, Weston Hall | 597-4181 | 597-2999 факс |
| Geosciences, Clark Hall | 597-2221 | 597-4116 факс |
| Немецко-русский, Hollander | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Программа магистратуры по истории искусств, Кларк | 458-2317 факс | |
| Службы здоровья и благополучия, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Медицинское просвещение | 597-3013 | |
| Услуги интегративного благополучия (консультирование) | 597-2353 | |
| Чрезвычайные ситуации с угрозой жизни | Позвоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Холландер | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Лес Хопкинса | 597-4353 | |
| Розенбург-центр | 458-3080 | |
| Отдел кадров, B&L Building | 597-2681 | 597-3516 факс |
| Услуги няни, корпус B&L | 597-4587 | |
| Льготы | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Заработная плата | 597-4162 | |
| Ресурсы для супруга / партнера | 597-4587 | |
| Занятость студентов | 597-4568 | |
| Weather Line (ICEY) | 597-4239 | |
| Humanities, Schapiro | 597-2076 | |
| Информационные технологии, Jesup | 597-2094 | 597-4103 факс |
| Пакеты для чтения курсов, ящик для сообщений Office | 597-4090 | |
| Центр кредитования оборудования, приложение Додда | 597-4091 | |
| Служба поддержки преподавателей / сотрудников, [адрес электронной почты защищен] | 597-4090 | |
| Медиа-сервисы и справка для класса | 597-2112 | |
| Служба поддержки студентов, [электронная почта] | 597-3088 | |
| Телекоммуникации / Телефоны | 597-4090 | |
| Междисциплинарные исследования, Hollander | 597-2552 | |
| Международное образование и учеба, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс Холл | 597-4447 | |
| Бостонский офис | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Mather | 597-3539 | |
| Справедливость и закон, Холландер | 597-2102 | |
| Latina / o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Thompson Biology | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Hopkins Hall | 597-4376 | 597-4015 факс |
| Управление счетов студентов, Хопкинс-холл | 597-4396 | 597-4404 факс |
| Performance Studies, ’62 Center | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Thompson Physics | 597-2482 | 597-4116 факс |
| Планетарий / Обсерватория Хопкинса | 597-3030 | |
| Театр старой обсерватории Хопкинса | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс-холл | 597-4233 | 597-4015 факс |
| Дом президента | 597-2388 | 597-4848 факс |
| Услуги печати / почты для преподавателей / сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис Провоста, Хопкинс Холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, B&L Building | 597-2195 / 4238 | 597-5031 факс |
| Ипотека для преподавателей / сотрудников | 597-4238 | |
| Жилье для преподавателей / сотрудников | 597-2195 | |
| Офис регистратора, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, Холландер | 597-2076 | 597-4222 факс |
| Romance Languages, Hollander | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 Дом | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Службы доступа | 597-2501 | |
| Приобретения / Серийные номера | 597-2506 | |
| Службы каталогизации / метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные службы | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Шоу, Научный центр | 597-4500 | 597-4600 факс |
| Исследования в области науки и технологий, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Машинно-модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Харди | 597-3747 | 597-4530 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Парески | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Организация студенческих мероприятий | 597-2546 | |
| Студенческий дом, Парески | 597-2555 | |
| Участие студентов | 597-4749 | |
| Программы проживания для старших классов | 597-4625 | |
| Студенческая почта, Паресский почтовый кабинет | 597-2150 | |
| Центр устойчивого развития / Зилха, Харпер | 597-4462 | |
| Коммутатор, Hopkins Hall | 597-3131 | |
| Книжный магазин Williams | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Trust & Estate Administration, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| Вице-президент по кампусной жизни, Хопкинс-холл | 597-2044 | 597-3996 факс |
| Вице-президент по связям с колледжем, Мирс | 597-4057 | 597-4178 факс |
| Вице-президент по финансам и администрированию, Hopkins Hall | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр Williams College, Детский центр Williams | 597-4008 | 597-4889 факс |
| Музей искусств колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Служба безопасности музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Williams International | 597-2161 | |
| Уильямс Outing Club, Парески | 597-2317 | |
| Оборудование / стол для студентов | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Вест | 597-2192 | |
| Williams Record, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Mystic Seaport Museum | 860-572-5359 | 860-572-5329 факс |
| Исследования женщин, гендера и сексуальности, Schapiro | 597-3143 | 597-4620 факс |
| Написание программ, Hopkins Hall | 597-4615 | |
| Центр экологических инициатив «Зилха», Харпер | 597-4462 |
Понимание, диагностика и преодоление медленной скорости обработки
В этой статье Стивен М. Бутник рассматривает несколько вариантов относительно низкой скорости обработки.
Бутник рассматривает несколько вариантов относительно низкой скорости обработки.
Для одаренных учеников нет ничего необычного в низкой скорости обработки информации. Сама по себе низкая скорость обработки данных не является формальным нарушением обучаемости, но ее наличие может расстроить учащихся, учителей и родителей. Как детский клинический психолог, специализирующийся на оценке и лечении учащихся с синдромом дефицита внимания и другими проблемами в обучении, я часто слышу, как родители говорят мне, что их очень умный ребенок не заканчивает уроки или что домашнее задание требует нескольких часов.Через наблюдение или формальную оценку своего ребенка этим родителям сказали, что у ребенка медленная скорость обработки данных .
Важно понимать роль медленной скорости обработки. Одаренные ученики с проблемами скорости обработки информации, которых «упускают», ставят неверный диагноз или неправильно учат, могут впадать в уныние, депрессию, недостаточное образование, неполную занятость или что еще хуже. Напротив, когда этих дважды исключительных (2e) детей понимают и хорошо учат в образовательном процессе, они могут стать сокровищами, сияющими уникальным образом.
Напротив, когда этих дважды исключительных (2e) детей понимают и хорошо учат в образовательном процессе, они могут стать сокровищами, сияющими уникальным образом.
В этой статье я объясню, с какими проблемами сталкиваются дети с низкой скоростью обработки данных; откуда берется низкая скорость обработки; как это можно определить; и что учащиеся, учителя и родители могут сделать, чтобы уменьшить или устранить его влияние.
Признаки медленной скорости обработки данных
Дома родители легко замечают медленную скорость обработки данных за пределами домашней работы. Мама Эйдена попросила его одеться десять минут назад, и когда она проверяет его, он даже не начал — и он должен быть на автобусной остановке через пять минут! Семья Нэнси ждет ее в машине, а она, как обычно, все еще дома в поисках книги.В школе Джек не закончил записывать задание в ежедневнике, когда прозвенел звонок, поэтому он упустил важную информацию, потому что не мог позволить себе снова опоздать к следующему уроку. Когда Эмили не закончила работу в классе, ее учитель отправил незаконченную работу домой, чтобы она была выполнена вместе с ее обычным домашним заданием. У всех этих детей медленный темп работы, что приводит к проблемам в школе и дома. Им нужны понимание и помощь родителей и учителей, чтобы они могли добиться успеха и чтобы их самооценка не пострадала.
Когда Эмили не закончила работу в классе, ее учитель отправил незаконченную работу домой, чтобы она была выполнена вместе с ее обычным домашним заданием. У всех этих детей медленный темп работы, что приводит к проблемам в школе и дома. Им нужны понимание и помощь родителей и учителей, чтобы они могли добиться успеха и чтобы их самооценка не пострадала.
Понимание источника проблемы у таких детей является важной частью понимания того, как им помочь. Необходимы тщательные медицинские и психообразовательные обследования, поскольку есть много источников медленного темпа работы. Это может быть связано с физическим заболеванием или травмой, например с низким уровнем щитовидной железы, эпилепсией или черепно-мозговой травмой. Это может быть связано с другими физическими проблемами, такими как недостаток сна или реакция на лекарства. Это также может быть частью синдрома дефицита внимания и гиперактивности (СДВГ), нарушений обучения и / или эмоциональных факторов.Мы рассмотрим некоторые из этих возможных причин.
Низкая скорость обработки данных, связанная с СДВГ
Дети с преимущественно невнимательным подтипом СДВГ могут иметь вялый когнитивный темп . Обычно они мечтают, смотрят в сторону и кажутся безразличными. Они могут быть умственно затуманенными, малоподвижными, малоподвижными и вялыми. Их работа часто медленная и подвержена ошибкам. Их мозговая активность демонстрирует модели недостаточного возбуждения в той части мозга, которая связана с сосредоточением внимания и планированием.
Кроме того, дети с СДВГ обычно демонстрируют плохие управляющие функции , поведение мозга, которое способствует эффективному функционированию. Полезная модель управляющих функций (см. Рисунок ниже) была разработана Томасом Брауном, доктором философии, психологом из Йельского университета. Согласно Брауну, эти функции нарушены при синдроме дефицита внимания.
Некоторым детям требуется больше времени для выполнения задач из-за проблем с активацией . Учащийся может не приступить к выполнению задания из-за проблем с организацией времени или материалов, а также из-за нежелания, неуверенности, неуверенности или беспокойства. Другим детям может потребоваться больше времени для выполнения заданий из-за проблем с сохранением концентрации. По прошествии времени эти студенты могут отвлекаться или мечтать, привлеченные другими, более интересными стимулами.
Учащийся может не приступить к выполнению задания из-за проблем с организацией времени или материалов, а также из-за нежелания, неуверенности, неуверенности или беспокойства. Другим детям может потребоваться больше времени для выполнения заданий из-за проблем с сохранением концентрации. По прошествии времени эти студенты могут отвлекаться или мечтать, привлеченные другими, более интересными стимулами.
Усилия включают скорость обработки, а также умственную выносливость. Когда усилия являются проблемой, ребенок работает очень медленно, и он может жаловаться, что его «мозг очень устал.С другой стороны, когда проблема носит эмоциональный характер, детям трудно контролировать свои чувства. Они могут растаять, когда приступят к работе или столкнутся с неприятной задачей; или они могут отказаться работать, спорить или впадать в истерику.
Проблемы в рабочей памяти может увеличить время, необходимое ребенку для выполнения задач. Прочитав абзац, ребенок с плохой рабочей памятью может забыть то, что он только что прочитал, и ему нужно будет прочитать это снова; или он может перестать работать над заданием в классе, потому что забыл указания. Наконец, когда действие является проблемой, ребенку сложно сидеть на месте, ерзать с предметами или, возможно, захочется стоять или ходить во время работы.
Наконец, когда действие является проблемой, ребенку сложно сидеть на месте, ерзать с предметами или, возможно, захочется стоять или ходить во время работы.
Еще одна проблема, с которой сталкиваются дети с СДВГ, — плохое чувство времени. Им кажется, что время идет медленнее во время выполнения задач, которые они считают скучными, в то время как время движется быстрее для задач, которые им интересны. Планируя рабочие задачи, ребенок с СДВГ может недооценить, сколько времени займет задача; и во время игры ребенок может не знать, сколько времени прошло.В совокупности плохие управляющие функции и плохое чувство времени могут привести к тому, что выполнение домашнего задания займет часы, и создать серьезный стресс.
Низкая скорость обработки данных, связанная с проблемами когнитивного функционирования и обучения
Скорость обработки данных — это элемент интеллекта, который измеряется многими тестами когнитивных способностей, включая Шкалу интеллекта Векслера для детей (4-е издание). Баллы по подтестам «Рабочая память» и «Скорость обработки» составляют Индекс когнитивной компетентности WISC-IV.Эти способности отделены от индекса общих способностей WISC-IV, показателя основного интеллекта, получаемого на основе индексов вербального понимания и перцептивного мышления (вербальных и невербальных способностей).
Баллы по подтестам «Рабочая память» и «Скорость обработки» составляют Индекс когнитивной компетентности WISC-IV.Эти способности отделены от индекса общих способностей WISC-IV, показателя основного интеллекта, получаемого на основе индексов вербального понимания и перцептивного мышления (вербальных и невербальных способностей).
Многие дети 2e демонстрируют существенные различия между своими вербальными способностями и объемом рабочей памяти и / или между их невербальными способностями и скоростью обработки. У детей 2e часто низкие показатели рабочей памяти и скорости обработки.
Индекс скорости обработки WISC-IV рассчитывается на основе результатов подтестов Coding и Symbol Search .Дополнительный субтест: Отмена . Эти три подтеста, описанные в следующем абзаце, основаны на быстром визуальном / двигательном анализе и результатах. Поскольку на скорость обработки может влиять ряд факторов, это не унифицированная конструкция, как другие части WISC-IV.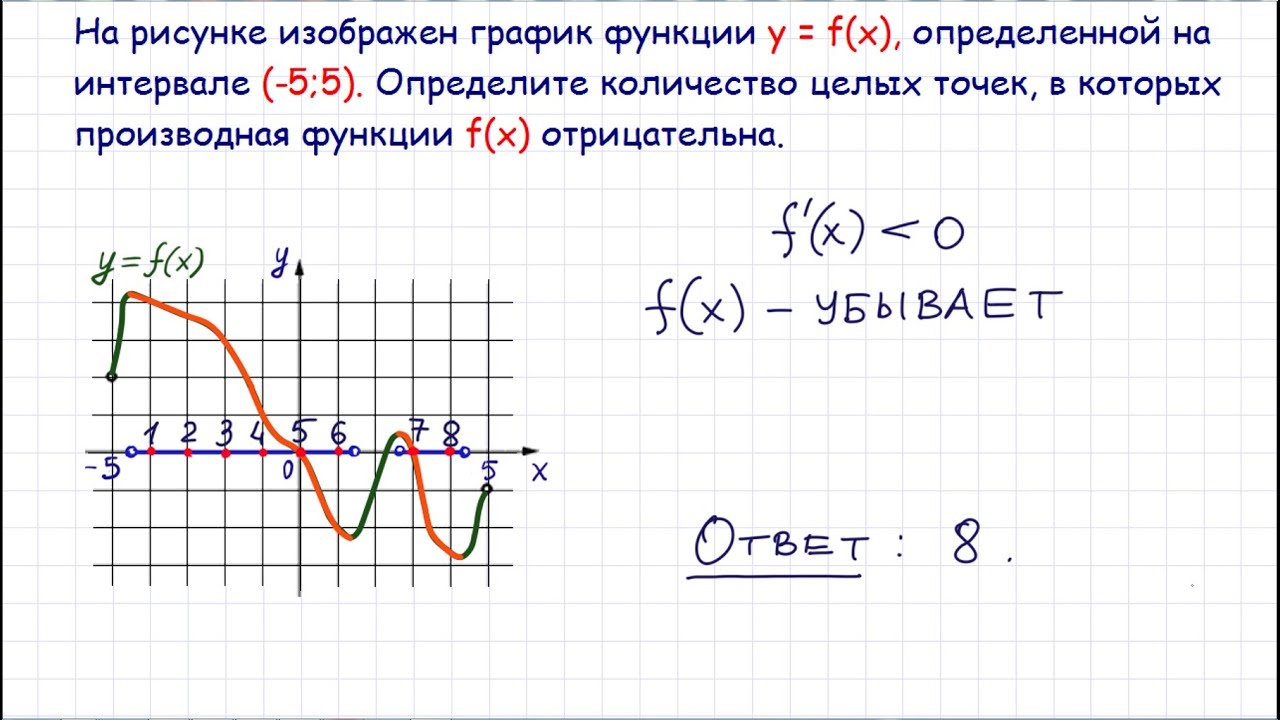 См. Рисунок ниже.
См. Рисунок ниже.
Каждый из этих трех подтестов затрагивает различные способности, которые влияют на оценку скорости обработки. Кодирование, , которое требует, чтобы дети рисовали символы, в значительной степени зависит от требований графомотора.Дети с плохим почерком или дисграфией могут бороться с этой задачей. Поиск символа уделяет меньше внимания мощности двигателя, но требует быстрого различения абстрактных символов. Отмена, дополнительный субтест «Скорость обработки», использует конкретные изображения, а не символы.
В тестах учебных достижений используется скорость обработки субтестов, которые измеряют академическую беглость. Например, Тесты достижений Вудкока-Джонсона включают три субтеста беглости речи:
- Свободное чтение.В течение трех минут ученик быстро читает простые предложения и на каждое отвечает да или нет.
- Свободное владение письмом. Используя три слова и картинку, ученик быстро пишет простые предложения за семь минут.

- Свободное владение математикой. Студент быстро выполняет простые вычисления за три минуты.
2e дети, у которых проблемы с активизацией, невнимательность или медленный познавательный темп, могут с трудом справляться со всеми этими задачами. 2e дети с медленной двигательной активностью будут иметь меньше проблем с беглостью чтения, но хуже будут сдавать тесты по математике и беглому письму.Проблемы с рабочей памятью, вероятно, будут иметь большее влияние на беглость математики, чем на другие задачи беглости речи.
Низкая скорость обработки данных не является нарушением обучения. Чтобы считаться страдающим нарушением обучаемости, студент должен иметь следующее:
- Средний или лучший интеллект
- Образцы существенных различий в обработке
- Значительная разница между способностями и достижениями.
Однако исследования показали, что скорость обработки связана с развитием чтения и скоростью чтения. В частности, скорость обработки может быть фактором в следующих ситуациях:
В частности, скорость обработки может быть фактором в следующих ситуациях:
- Нарушения чтения, такие как дислексия
- Подмножество нарушений чтения, при которых люди демонстрируют выраженные трудности со скоростью вербальной и визуальной обработки.
- Проблемы с графомотором (дисграфия). У людей с дисграфией возникают серьезные проблемы с формированием букв и цифр; их почерк медленный и трудный; у них могут быть проблемы с интервалом между словами; они смешивают буквы верхнего и нижнего регистра; и Т. Д.Поскольку аккуратность приходит только тогда, когда им требуется много времени, их письменная работа может быть очень напряженной и болезненной.
Низкая скорость обработки данных, связанная с эмоциональным вмешательством
Помимо когнитивных переменных и переменных внимания, количество эмоциональных факторов может увеличивать время, необходимое учащимся для выполнения работы. Когда студенты обеспокоены, скорость их обработки может замедлиться из-за неуверенности в себе, неуверенности, сомнений и самосознания.
Обсессивно-компульсивное расстройство (ОКР) может вызвать еще большее замедление.Вот несколько примеров того, как дети с ОКР могут вести себя в этом контексте:
- Один ребенок разработал «правило», согласно которому, если он колеблется при чтении, он «должен» перечитать весь отрывок.
- Другой ребенок тратит слишком много времени на письмо, стараясь составлять буквы и цифры, чтобы они были «идеальными».
Как решить проблему низкой скорости обработки данных
После тщательной психологической и педагогической оценки можно разработать план по уменьшению воздействия низкой скорости обработки.Стратегии вмешательства делятся на три категории: школьные, домашние и детские.
Стратегии на уровне школы
Комитет по обучению детей в государственных школах может провести оценку для определения права учащегося на приспособления и модификации. Если выявлено формальное нарушение обучения, может быть предоставлена индивидуальная образовательная программа (IEP) в соответствии с положениями Закона об улучшении образования для лиц с ограниченными возможностями. Студенты без формальных нарушений обучения, но у которых возникают проблемы с обучением из-за СДВГ, могут получать услуги в соответствии с разделом 504 Закона об американцах с ограниченными возможностями.Школы также могут предоставлять услуги до определения формального права на участие в программе Response to Intervention (RtI). [Информацию для о RtI см. В выпусках 2e: Twice-Exceptional Newsletter за ноябрь 2012 г. и январь 2013 г.]
Студенты без формальных нарушений обучения, но у которых возникают проблемы с обучением из-за СДВГ, могут получать услуги в соответствии с разделом 504 Закона об американцах с ограниченными возможностями.Школы также могут предоставлять услуги до определения формального права на участие в программе Response to Intervention (RtI). [Информацию для о RtI см. В выпусках 2e: Twice-Exceptional Newsletter за ноябрь 2012 г. и январь 2013 г.]
Независимо от категории услуг, на которые может претендовать одаренный ученик, важно не допустить, чтобы медленная обработка информации помешала успеху ребенка. Учителя должны знать, как низкая скорость обработки может повлиять на успеваемость способных учеников, и стремиться дифференцировать их обучение.Одаренным ученикам с медленным темпом работы нельзя отказывать в возможностях получения образования.
Чтобы обеспечить подходящие меры вмешательства, учителю или школе необходимо определить источник проблем и адаптировать меры вмешательства к индивидуальным потребностям учащегося. Справа приведены примеры вмешательств, которые могут их решить.
Справа приведены примеры вмешательств, которые могут их решить.
Другие приспособления или модификации школы могут включать:
- Увеличение времени на выполнение задач, включая викторины, тесты и экзамены
- Способ побудить ученика повысить осведомленность о времени
- Устранение ненужных канцелярских задач (e.g., перевод математических задач из учебника в рабочий лист) и использование форматов кратких ответов
- Устранение временных тестов, таких как тесты «Минута безумной математики».
- Сокращение количества задач, необходимых для демонстрации компетентности (например, 5 математических задач вместо 25)
- Контроль времени, затрачиваемого на домашнее задание, и корректировка заданий по мере необходимости.
Домашние стратегии
Родители должны знать о влиянии медленной скорости обработки информации на повседневную жизнь своего ребенка и разработать планы по снижению этого воздействия. Поскольку у учащихся с медленной скоростью обработки часто возникают серьезные проблемы с домашним заданием, родители должны работать с учителем, чтобы определить, сколько времени ученик должен потратить на каждое домашнее задание и что делать, если это время будет превышено. Цель — избежать битв за домашнее задание. Если почерк мешает работе, некоторые из предложенных в таблице рекомендаций для школы можно применить дома.
Поскольку у учащихся с медленной скоростью обработки часто возникают серьезные проблемы с домашним заданием, родители должны работать с учителем, чтобы определить, сколько времени ученик должен потратить на каждое домашнее задание и что делать, если это время будет превышено. Цель — избежать битв за домашнее задание. Если почерк мешает работе, некоторые из предложенных в таблице рекомендаций для школы можно применить дома.
Родители должны избегать персонализации, наказания и эмоциональной реакции, помня, что медленная скорость обработки не является целенаправленной и может улучшиться.Родители могут помочь, предоставив больше структуры, используя расписания, таймеры, часы, будильники и поощрения. С детьми постарше может быть полезно вовлечь их в процесс решения проблем.
Детям с СДВГ могут помочь стимулирующие препараты, такие как Риталин, Концерта, Аддералл или Виванс. Этот тип лекарств не может напрямую увеличивать фактическую скорость обработки, но часто может помочь с активацией и сосредоточением внимания, увеличивая темпы работы ребенка. После того, как ребенку поставлен правильный диагноз, родители могут обсудить с педиатром или врачом-специалистом вариант лечения.Также важно, чтобы родители отслеживали и решали любые проблемы со сном, которые могут возникнуть, и поощряли правильное питание, а также частые и энергичные упражнения.
После того, как ребенку поставлен правильный диагноз, родители могут обсудить с педиатром или врачом-специалистом вариант лечения.Также важно, чтобы родители отслеживали и решали любые проблемы со сном, которые могут возникнуть, и поощряли правильное питание, а также частые и энергичные упражнения.
Стратегии, ориентированные на детей
Поскольку некоторые очень способные ученики с низкой скоростью обработки информации не считают себя умными, важно помочь им понять природу и структуру своих способностей. Это может помочь напомнить им, что у всех людей есть сильные и слабые стороны, и что более медленный темп не означает, что он не умен.Одному студенту понравилось, что я назвал его интеллектуальным танком — не очень быстрым, но чрезвычайно мощным.
Некоторые учащиеся хорошо используют таймеры и будильники, чтобы отслеживать время. Подросток, с которым я работала, начал использовать будильник в ванной, чтобы напомнить ему выйти из душа. Также может быть полезно провести исследование времени. Родители могут использовать секундомер, чтобы определить, сколько времени у ребенка уходит на выполнение рутинных задач, таких как выполнение работы по дому или подготовка к школе. Это время можно использовать в качестве целей для работы, а награды могут быть предоставлены, когда учащийся выполнит задачу в отведенное время.
Родители могут использовать секундомер, чтобы определить, сколько времени у ребенка уходит на выполнение рутинных задач, таких как выполнение работы по дому или подготовка к школе. Это время можно использовать в качестве целей для работы, а награды могут быть предоставлены, когда учащийся выполнит задачу в отведенное время.
Заключение
Когда они остаются незамеченными и их потребности остаются без внимания, одаренные ученики, обучающиеся медленнее, могут чувствовать себя обескураженными и деморализованными. Однако, как только они будут поняты и будут предприняты усилия, чтобы помочь уменьшить влияние более медленного темпа, лучшие способности этих учеников могут проявиться. Родителям, возможно, потребуется взять на себя инициативу и организовать оценку, обучить тех, кто участвует в жизни их детей, и оказать своему ребенку непоколебимую поддержку и ободрение.
Стивен Бутник, Ph.Д., является лицензированным клиническим психологом и содиректором ADDVANTAGE, PLLC в Ричмонде, Вирджиния, частной практики, посвященной оценке людей с проблемами внимания и другими проблемами обучения.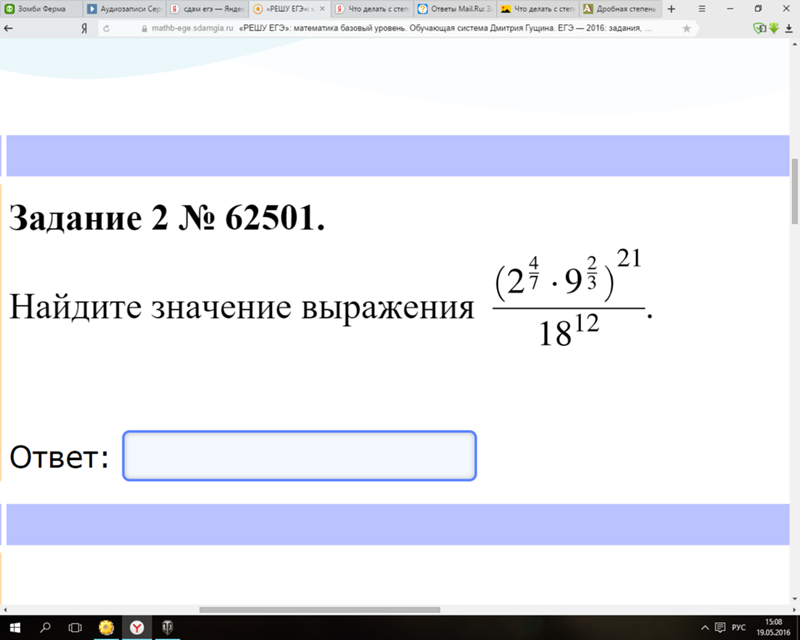

 2013, стр. 148–149)
2013, стр. 148–149)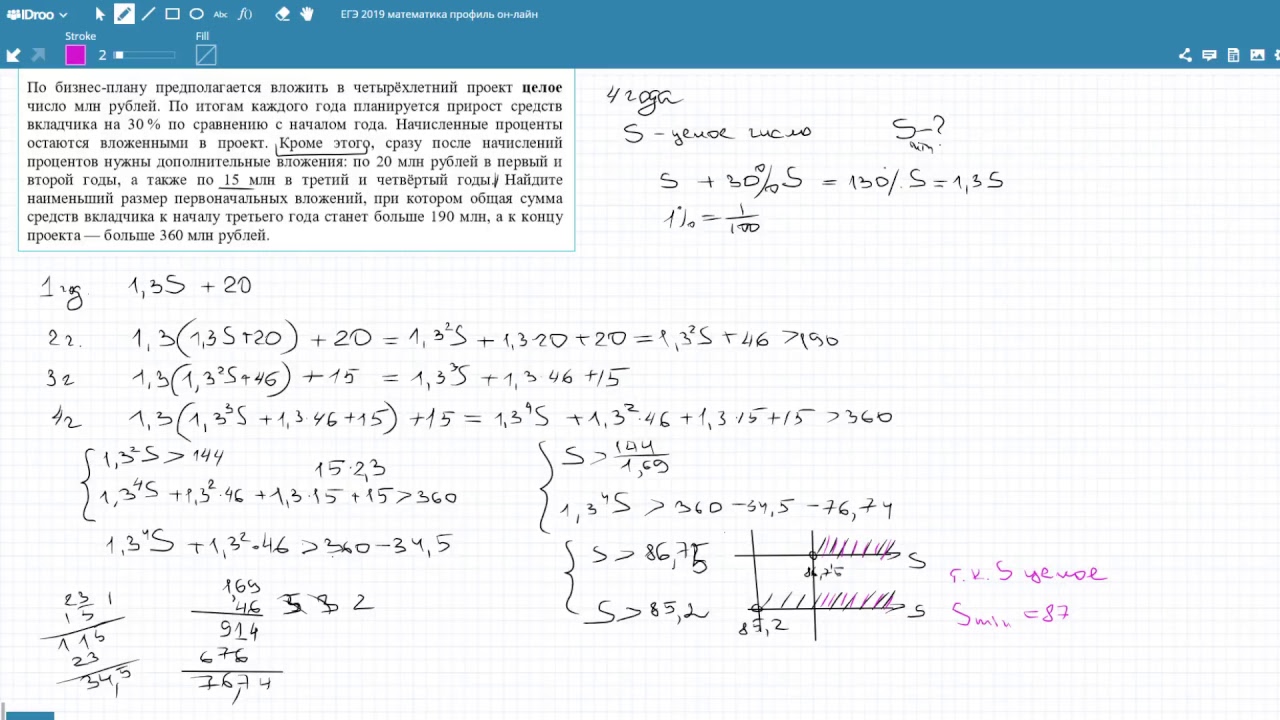 Чтобы получить высокие баллы по этим вопросам, вам необходимо уметь делать быстрые и точные вычисления без использования калькулятора. Обычно от вас не ждут, что вы сдадите тест, но вас будут оценивать по количеству полученных вами правильных ответов.
Чтобы получить высокие баллы по этим вопросам, вам необходимо уметь делать быстрые и точные вычисления без использования калькулятора. Обычно от вас не ждут, что вы сдадите тест, но вас будут оценивать по количеству полученных вами правильных ответов.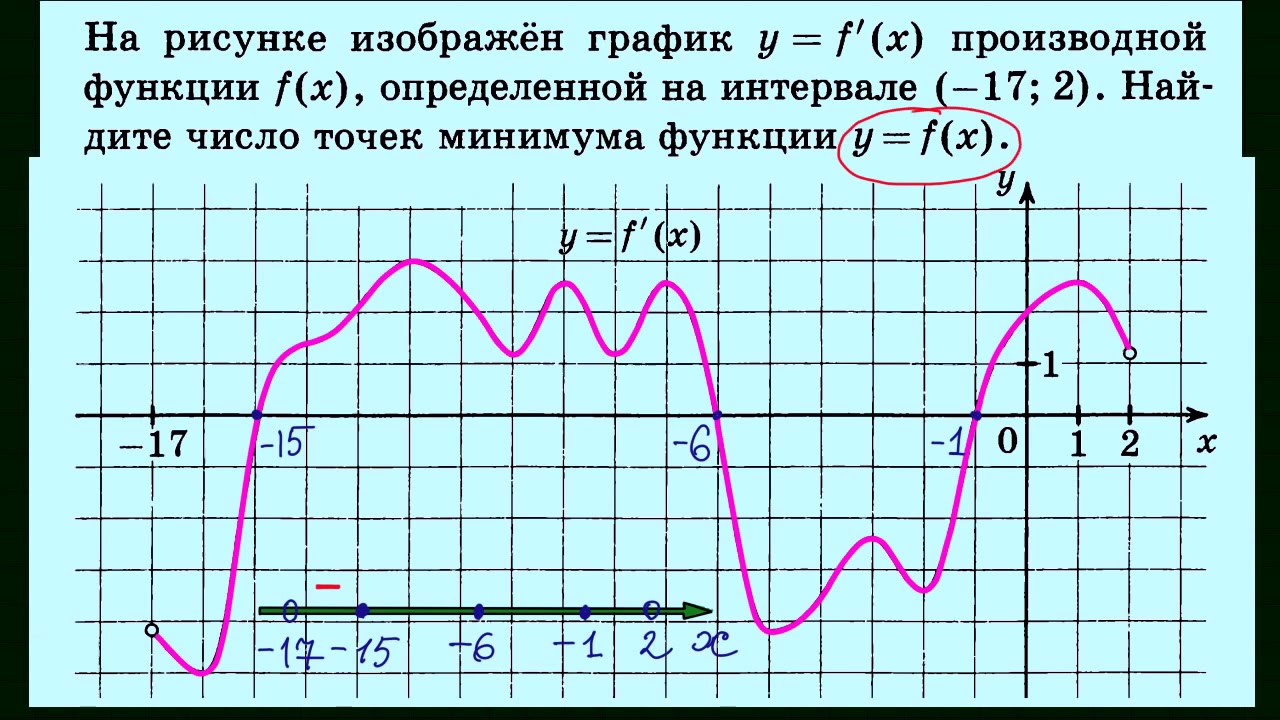
Leave A Comment