Математика ОГЭ 2019 — баллы и оценки
Перевод баллов ОГЭ 2019 по математике (ГИА 9 класс) в оценку можно узнать в рекомендациях, опубликованных на официальном сайте ФИПИ.
Таблица перевода баллов ОГЭ 2019 по математике в оценку
Таблица 1
| Оценка по пятибалльной шкале | Суммарный первичный балл за работу в целом |
| 2 | 0-7 |
| 3 | 8-14, не менее 2 баллов получено за выполнение заданий модуля «Геометрия» |
| 4 | 15-21, не менее 2 баллов получено за выполнение заданий модуля «Геометрия» |
| 5 | 22 — 32, не менее 2 баллов получено за выполнение заданий модуля «Геометрия» |
Максимальное количество баллов, которое может получить участник ОГЭ за выполнение всей экзаменационной работы, — 32 балла.
Из них — за выполнение заданий модуля «Алгебра» — 20 баллов, модуля «Геометрия» — 12 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы — 8 баллов, набранные в сумме за выполнение заданий обоих модулей, при условии, что из них не менее 2 баллов получено по модулю «Геометрия».
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы для обучения по образовательным программам среднего общего образования.
Ориентиром при отборе в профильные классы (проходной балл ОГЭ 2019) могут быть показатели, примеры нижних границ которых соответствуют следующим первичным баллам:
— для естественнонаучного профиля: 18 баллов, из них не менее 6 по геометрии;
— для экономического профиля: 18 баллов, из них не менее 5 по геометрии;
— для физико-математического профиля’. 19 баллов, из них не менее 7 по геометрии.
Разработанные специалистами ФИПИ таблицы перевода первичных баллов в отметки по пятибалльной шкале для проведения ОГЭ носят РЕКОМЕНДАТЕЛЬНЫЙ ХАРАКТЕР. В регионах могут устанавливаться другие пороги.
Смотрите также:
Формат проведения ОГЭ по литературе
Литературу в качестве одного из предметов для сдачи ОГЭ выбирают ученики, планирующие продолжить обучение в классах филологического профиля. Отличительной чертой ОГЭ по литературе в 2019 году от других экзаменационных дисциплин для учеников девятых классов является особенность «начинки» билетов: в них нет тестов с вариантами ответов.
Итоговая аттестация по литературе для девятиклассников проходит на базе школы.
Билет ОГЭ по литературе для 9 класса 2019 года включает следующие блоки:
|
Часть № 1 |
|
|
Часть № 2 |
Написать сочинение на одну их четырёх предложенных тем. |
На выполнение заданий экзамена учащимся предоставляется почти четыре часа — 235 минут.
При выполнении заданий экзаменационного билета следует обратить внимание на следующие важные моменты:
Перед началом работы над анализом текста учащемуся необходимо ознакомиться с двумя предоставленными текстовыми вариантами и выбрать для себя только один текст. Анализировать оба текста нельзя!
При анализе текста лучше всего использовать несложные речевые конструкции. Ответ должен быть ёмким и читабельным, но также он должен чётко отвечать на вопрос и не быть слишком поверхностным.
Для каждого задания в Части № 1 существует определённый объём развёрнутого ответа:
|
Номер задания |
Объём ответа |
|
Задание № 1 |
|
|
Задание № 2 |
3-5 предложений |
|
Задание № 3 |
5-8 предложений |
Для работы над сочинением экзаменующимся разрешено пользоваться полным текстом художественного произведения. Свои мысли и точку зрения следует аргументировать, подкрепляя слова цитатами из художественного текста. Объём сочинения должен быть не менее 150 слов.
Расписание ОГЭ по литературе
Экзаменационный период ОГЭ по литературе состоит из трёх частей: досрочный, основной и дополнительный для пересдачи экзамена осенью.
|
Досрочный период |
|
|
Основной день 29 апреля (пн) |
Резервный день 13 мая (пн) |
|
Основной период |
|
|
Основной день 11 июня (вт) |
Резервные дни 28 июня (пт) 1 июля (пн) 2 июля (вт) |
|
Осенняя пересдача |
|
|
Первая пересдача 11 сентября (ср) |
Вторая пересдача 19 сентября (чт) 21 сентября (сб) |
Досрочный период для сдачи ОГЭ по литературе в 2019 году предусмотрен для:
-
выпускников 2017-2018 учебного года, которые не смогли преодолеть минимум по шкале баллов или решили улучшить свои показатели;
-
выпускников 2018-2019 учебного года (просьба учащегося в разрешении сдавать ОГЭ по литературе досрочно рассматривается педсоветом учебного заведения).
Основной период для сдачи ОГЭ предусмотрен для большей части выпускников.
Дни осенней пересдачи предусмотрены для учащихся, которые не смогли с первого раза преодолеть минимальный порог на сдаче ОГЭ. Однако возможность пересдать неудачный экзамен получат только учащиеся с неудовлетворительными баллами по одному или двум дисциплинам. Ученикам, которые не смогли справиться с б
Резервные дни всех периодов помогут учащимся, которые не смогли присутствовать на сдаче экзамена по уважительной причине.
ОГЭ. Литература. Универсальный справочник
Справочник предназначен для подготовки учащихся к ОГЭ по литературе. Пособие содержит подробный теоретический материал по всем темам, проверяемым экзаменом, а также тренировочные задания в форме ОГЭ. В конце справочника приводятся ответы. Издание будет полезно учителям литературы, так как даёт возможность эффективно организовать учебный процесс и подготовку к экзамену.
Критерии оценивания
Так как экзаменационные билеты по литературе не содержат стандартной для ОГЭ тестовой части, то все работы оцениваются независимыми преподавателями. Как и в прочих экзаменах, ответы оцениваются двумя преподавателями. Если разница в оценивании заданий превысила два балла, работа проверяется третьим, контрольным, учителем. Если же разница менее двух баллов, то выставляется среднее арифметическое двух оценок.
При оценивании экзаменационных работ специалисты опираются на особые критерии, разработанные ФИПИ специально к ОГЭ 2019 по литературе. Изучив требования к экзамену и верно применив свои знания во время сдачи ОГЭ, можно получить максимально высокий результат.
Рассмотрим критерии оценивания для ОГЭ по литературе:
Часть № 1. Критерии оценивания первого и второго заданий
|
Критерий |
Ответ учащегося |
Балл |
Соответствие ответа заданию |
Содержание соотнесено с задачей |
1 |
|
Содержание не соотнесено с задачей |
0 |
|
|
Аргументы и использование текста произведения |
Суждения аргументированы, проанализированы элементы текста |
2 |
|
Суждения аргументированы, но приведены только общие рассуждения по теме или только его пересказ, отсутствует анализ элементов текста |
1 |
|
|
Суждения не аргументированы, текст не использован или существенно искажён |
0 |
|
|
Фактологическая, логическая и речевая точность ответа |
Полностью отсутствуют ошибки |
2 |
|
Допущено не более одной ошибки каждого вида |
1 |
|
|
Допущено две и более ошибок одного вида |
0 |
Часть № 1. Критерии оценивания третьего задания
|
Критерий |
Ответ учащегося |
Балл |
|
Соответствие ответа заданию |
Содержание соотнесено с задачей |
1 |
|
Содержание не соотнесено с задачей или существенно искажено |
0 |
|
|
Сопоставление произведений |
Сопоставлены два произведения, тезисы обоснованы текстом двух произведений |
3 |
|
Сопоставлены два произведения, но тезисы обоснованы текстом одного произведения |
2 |
|
|
Сопоставлены два произведения, но суждения не обоснованы текстом |
1 |
|
|
Нет сопоставления произведения с текстом |
0 |
|
|
Фактологическая, логическая и речевая точность ответа |
Полностью отсутствуют ошибки |
2 |
|
Допущено не более одной ошибки каждого вида |
1 |
|
|
Допущено две и более ошибок одного вида |
0 |
Часть № 2. Критерии оценивания сочинения
|
Критерий |
Ответ учащегося |
Балл |
|
Соответствие сочинения теме |
Сочинение полностью соответствует теме |
1 |
|
Сочинение написано не по теме, тема не раскрыта или существенно искажено содержание |
0 |
|
|
Аргументированность, привлечение текста произведения |
Суждения аргументированы, проанализированы элементы текста |
2 |
|
Суждения аргументированы, но приведены только общие рассуждения по теме или только его пересказ, отсутствует анализ элементов текста |
1 |
|
|
Суждения не аргументированы, недостаточно отсылок к тексту |
0 |
|
|
Опора на теоретико-литературные понятия |
Теоретико-литературные понятия включены, выявлена роль хотя бы одного художественного средства |
2 |
|
Теоретико-литературные понятия включены, но не выявлена роль художественных средств |
1 |
|
|
Теоретико-литературные понятия не включены |
0 |
|
|
Композиционная цельность |
Обладает композиционной цельностью, соблюдены пропорции между частями |
2 |
|
Частично присутствует композиционный замысел, но есть нарушения пропорциональности частей |
1 |
|
|
Почти отсутствует композиционный замысел, нарушения последовательности затрудняют понимание смысла |
0 |
|
|
Логичность |
Ошибки отсутствуют |
2 |
|
Допущена одна ошибка |
1 |
|
|
Допущено две и более ошибок |
0 |
|
|
Фактологическая точность |
Допущено не более одной ошибки |
2 |
|
Допущены две ошибки |
1 |
|
|
Допущено более двух ошибок |
0 |
|
|
Соблюдение речевых норм |
Допущено не более двух ошибок |
2 |
|
Допущено 3-4 ошибки |
1 |
|
|
Допущено 5 и более ошибок |
0 |
Таким образом за каждое задание можно получить следующий максимальный балл:
|
Блок |
Номер задания |
Максимальный балл |
|
Часть № 1 |
Задание № 1 |
5 |
|
Задание № 2 |
5 |
|
|
Задание № 3 |
6 |
|
|
Часть № 2 |
Сочинение |
13 |
Соответственно, максимальный балл ОГЭ по литературе – 2019 теперь составляет 29 баллов.
Что ещё почитать?
Баллы ОГЭ по литературе
Результат ОГЭ по литературе заносится в аттестат учащегося. Для перевода тестового балла ОГЭ в пятибалльную отметку ФИПИ рекомендует пользоваться следующей таблицей соответствия:
|
Отметка |
Баллы |
|
5 |
19-29 |
|
4 |
14-20 |
|
3 |
7-13 |
|
2 |
0-6 |
Таким образом, для сдачи экзамена учащемуся требуется получить за экзамен отметку «удовлетворительно», то есть набрать минимум 7 тестовых баллов. Естественно, что для успешного поступления в другое учебное заведение такого балла будет недостаточно. В 2019 году минимальный порог для поступления в колледж или профильный класс составляет минимум 15 тестовых баллов.
#ADVERTISING_INSERT#
ОГЭ по математике 2019 год
ОГЭ по математике 2019 год — баллы и оценки
Сколько нужно набрать баллов на ОГЭ в 2019 году по математике, что бы получить оценку 3, 4, или 5 можно узнать в рекомендациях, опубликованных на сайте Рособрнадзора.
Максимальное количество баллов, которое может получить участник ОГЭ 2019 за выполнение всей экзаменационной работы, — 32 балла.
Из них — за выполнение заданий модуля «Алгебра» — 20 баллов, модуля «Геометрия» — 12 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы — 8 баллов (оценка 3), набранные в сумме за выполнение заданий обоих модулей, при условии, что из них не менее 2 баллов получено по модулю «Геометрия».
Шкала пересчета суммарного первичного балла за выполнение экзаменационной работы ОГЭ по математике в отметку по пятибалльной шкале
Таблица 1
| Оценка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Суммарный первичный балл за работу в целом | 0-7 | 8-14, не менее 2 баллов получено за выполнение заданий модуля «Геометрия» | 15-21, не менее 2 баллов получено за выполнение заданий модуля «Геометрия» | 22 — 32, не менее 2 баллов получено за выполнение заданий модуля «Геометрия» |
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы для обучения по образовательным программам среднего общего образования.
Ориентиром при отборе в профильные классы (проходной балл ОГЭ 2019) могут быть показатели, примеры нижних границ которых соответствуют следующим первичным баллам:
— для естественнонаучного профиля: 18 баллов, из них не менее 6 по геометрии;
— для экономического профиля: 18 баллов, из них не менее 5 по геометрии;
— для физико-математического профиля’. 19 баллов, из них не менее 7 по геометрии.
Разработанные специалистами Рособнадзора шкалы перевода первичных баллов в отметки по пятибалльной шкале для проведения ОГЭ носят РЕКОМЕНДАТЕЛЬНЫЙ ХАРАКТЕР. В регионах могут устанавливаться другие пороги.
Система оценивания выполнения отдельных заданий и экзаменационной работы ОГЭ 2019 по математике в целом
Для оценивания результатов выполнения работ выпускниками используется общий балл.
В таблице 2 приводится система формирования общего балла. Максимальный балл за работу в целом — 32. Задания, оцениваемые 1 баллом, считаются выполненными верно, если указан номер верного ответа (в заданиях с выбором ответа), или вписан верный ответ (в заданиях с кратким ответом), или правильно соотнесены объекты двух множеств и записана соответствующая последовательность цифр (в заданиях на установление соответствия).
Таблица 2. Система формирования общего балла
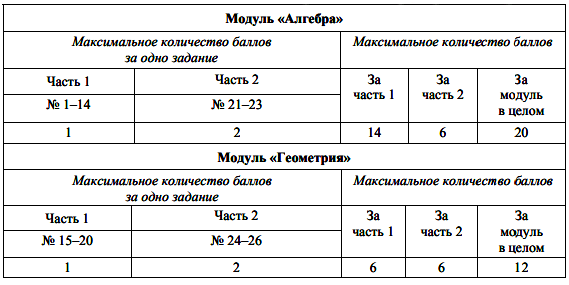

Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику выставляется 1 балл.
Смотрите также:
Перевод баллов ОГЭ 2019 в оценку
- ОГЭ
Сколько баллов нужно набрать на ОГЭ в 2019 году, чтобы получить оценку 3, 4 или 5 интересно для выпускников 9 классов и для учителей.
Рособрнадзор опубликовал рекомендации перевода баллов ОГЭ 2019 в оценки, рекомендации определяющие минимальные баллы ОГЭ, рекомендуемые минимальные баллы ОГЭ 2019 для отбора в профильные классы.
Шкала минимальных баллов ОГЭ 2019
(Сколько баллов нужно набрать чтобы получить оценку 3)
Таблица 1
| Учебный предмет | Первичные баллы, соответствующие минимальному баллу «3» | Дополнительные условия получения минимального первичного балла |
| Русский язык | 15 | |
| Математика | 8 | не менее 2 баллов из 8 получено за выполнение заданий модуля «Геометрия» |
| Физика | 10 | |
| Химия (модель 1, модель 2) | 9 | |
| Биология | 13 | |
| География | 12 | |
| Обществознание | 15 | |
| История | 13 | |
| Литература | 12 | |
| Информатика и ИКТ | 5 | |
| Иностранные языки (английский, немецкий, французский, испанский) | 29 |
Перевод баллов ОГЭ 2019 в оценки
Таблица 2
| Предмет | «2» | «3» | «4» | «5» |
| Русский язык | 0–14 | 15–24 | 25–33 | 34–39 |
| Математика | 0–7 | 8–14 | 15–21 | 22–32 |
| Биология | 0–12 | 13–25 | 26–36 | 37–46 |
| География | 0–11 | 12–19 | 20–26 | 27–32 |
| Информатика и ИКТ | 0–4 | 5–11 | 12–17 | 18–22 |
| История | 0–12 | 13–23 | 24–34 | 35–44 |
| Литература | 0–11 | 12–19 | 20–26 | 27–33 |
| Обществознание | 0–14 | 15–24 | 25–33 | 34–39 |
| Физика | 0–9 | 10–19 | 20–30 | 31–40 |
| Химия (без эксперимента) | 0–8 | 9–17 | 18–26 | 27–34 |
| Химия (с экспериментом) | 0–8 | 9–18 | 19–28 | 29–38 |
| Английский язык | 0–28 | 29–45 | 46–58 | 59–70 |
| Иностранный язык | 0–28 | 29–45 | 46–58 | 59–70 |
В соответствии с пунктом 22 Порядка органы исполнительной власти субъектов Российской Федерации, осуществляющие государственное управление в сфере образования, обеспечивают проведение государственной итоговой аттестации по образовательным программам основного общего образования, в том числе определяют минимальное количество первичных баллов, а также обеспечивают перевод суммы первичных баллов за экзаменационные работы ОГЭ и ГВЭ в пятибалльную систему оценивания.
Смотрите также:
ОГЭ по математике 2019
ОГЭ по математике – один из обязательных экзаменов в 9-м классе. Математику необходимо сдавать для перевода в 10-й класс и получения аттестата об основном среднем образовании. Если вы собираетесь продолжать обучение в физматклассе, то потребуется сдать математику на высокий балл. О дате проведения экзамена и возможных пересдачах можете узнать тут.
Ознакомившись с общей информацией об экзамене, сразу приступайте к подготовке. Экзамен в этом году содержательно не отличается от прошлых лет, поэтому можно готовиться по материалам 2017 и 2018 года. Изменилась лишь структура теста: убрали модуль «Реальная математика», а задания из него распределили по модулям «Алгебра» и «Геометрия».
Структура ОГЭ
Работа состоит из двух частей, в каждой из которых последовательно идут два модуля – «Алгебра» и «Геометрия». В части 1 представлены задания базового уровня сложности, за которые дают по 1 баллу. Это либо задания на выбор правильного ответа или задания, требующие написать краткий ответ в виде цифры, числа или последовательности цифр.
Часть 2 – задания повышенного и высокого уровней сложности, за каждое из которых можно получить 2 балла. В этих заданиях важно не просто дать конечный ответ, но и показать ход решения. Здесь тоже сначала идут задания из модуля «Алгебра», а затем – задания из модуля «Геометрия». Дальше станет яснее:
Часть 1:
- Модуль «Алгебра» состоит из 14 заданий (№ 1-14) – базовый уровень сложности – 1 балл за каждое задание;
- Модуль «Геометрия» состоит из 6 заданий (№ 15-20) – базовый уровень сложности – 1 балл за каждое задание.
Часть 2:
- Модуль «Алгебра» состоит из 3 заданий (№ 21-23) – повышенный и высокий уровень сложности – 2 балла за каждое задание;
- Модуль «Геометрия» состоит из 3 заданий (№ 24-26) – повышенный и высокий уровень сложности – 2 балла за каждое задание.
Оценивание ОГЭ
В отличие от ЕГЭ у ОГЭ нет единого для всех регионов минимального балльного порога по тому или иному предмету. Этот порог определяют местные региональные власти после проведения досрочного этапа проведения экзаменов. Однако у регионов есть эталон, с которым они сверяются и как правило не отходят от него – это ежегодные рекомендации Федерального института педагогических измерений (ФИПИ).
Согласно этим рекомендациям, чтобы сдать ОГЭ по математике хотя бы на тройку, необходимо набрать не менее 8 первичных баллов. Это равносильно правильному выполнению 8 заданий из части 1. Для пятерки необходимо набрать 22-32 первичных балла.
Подготовка к ОГЭ
- На нашем сайте вы можете пройти тесты ОГЭ онлайн бесплатно без регистрации и СМС. На данный момент раздел обновляется, и со временем в нем будут появляться новые тесты за весь период проведения ОГЭ. Представленные тесты по своей сложности и структуре идентичны реальным экзаменам, проводившимся в соответствующие годы.
- Скачайте демонстрационные варианты ОГЭ по математике, которые позволят лучше подготовиться к экзамену и легче его сдать. Все предложенные тесты разработаны и одобрены для подготовки к ОГЭ Федеральным институтом педагогических измерений (ФИПИ). В этом же ФИПИ разрабатываются все официальные варианты ОГЭ.
Задания, которые вы увидите, скорее всего, не встретятся на экзамене, но будут задания, аналогичные демонстрационным, по той же тематике или просто с другими цифрами. - Ознакомьтесь с основными формулами для подготовки к экзамену, они помогут освежить память перед тем, как приступить к выполнению демонстрационных и тестовых вариантов.
Полезные ссылки:
Шкала перевода баллов ОГЭ 2019 года в оценки
Основной Государственный Экзамен (ОГЭ) – испытание, предстоящее каждому девятикласснику! Экзамен является обязательным для всех выпускников средней школы, но особенно старательно к нему готовятся девятиклассники, желающие продолжить обучение в колледжах, ведь для поступления необходимо продемонстрировать высокий уровень знаний и по возможности получить максимально высокий балл.
Самое время для будущих выпускников узнать как можно больше о том, как проверяют экзаменационные работы, и какой будет в 2019 году шкала перевода тестовых баллов ОГЭ в традиционные оценки.
Каким будет ОГЭ в 2019 году?
Если реформа ЕГЭ к 2019 году практически завершится и в КИМах для 11-классников кардинальных изменений не предвидится, то ОГЭ только входит в этап реформирования. В прошлом 20172018 учебном году в очередной раз было увеличено число предметов, выносимых на итоговую аттестацию, и в 2019 году ученикам предстоит сдавать в общей сложности 5 экзаменов:
- 2 обязательных: русский язык и математика;
- 3 на выбор из таких дисциплин, как: физика, химия, история, информатика, иностранный язык, обществознание, биология, география и литература.

Официальной информации о введении 6 экзамена пока нет. Но ранее говорилось, что к 2020 году общее количество сдаваемых предметов достигнет шести.
Выбор профильного предмета должен быть не случайным, ведь результат ОГЭ непосредственно влияет на оценку в аттестате и является основным критерием отбора в профильные классы.
Проверка экзаменационных работ ОГЭ
В 2019 году девятиклассники всех регионов РФ будут выполнять одинаковые задания, ведь в отличие от прежних лет, сегодня активно идет процесс разработки единого банка заданий, которые позволят оценить реальный уровень знаний учащихся.
Как и в 2018 году, писать работы выпускники 9-х классов будут на базе своего учебного заведения, что существенно повышает шансы на хороший результат. Проверкой экзаменационных работ ОГЭ, как и ранее, будут заниматься учителя школ, имеющие достаточную квалификация, что бы стать экспертом ГИА.
По аналогии с ЕГЭ все работы будут проверены двумя экспертами. Если мнения специалистов существенно разойдутся, то к процессу проверки будет привлечен третий эксперт, мнение которого и станет решающим.

Если ученик не согласен с оценкой экспертов, он может подать апелляцию и работу еще раз перепроверят, но уже совсем другие эксперты, входящие в состав апелляционной комиссии.
В ходе проверки за каждое правильно выполненное задание начисляются первичные баллы, которые потом переводят в привычную для школьников 5-тибальную оценку.
Шкала перевода баллов
Хотя в ФГБНУ «ФИПИ» разработали единую стандартизированную шкалу для перевода первичных баллов ОГЭ в оценки, в 2019 году (как и ранее) на местном уровне официально могут быть утверждены другие нормы с учетом региональных особенностей.Так, для 2018 года были утверждены следующие таблицы перевода баллов, которые с большой степенью вероятности будут актуальны и в 2018-2019 учебном году.
Ознакомившись с документом можно увидеть, что при выставлении оценки по русскому языку и математике (всех уровней), во внимание берется не только общий суммарный балл.
Так, в русском языке для получения оценки:
- «4» необходимо набрать не менее 4 баллов за грамотность при 25-33 суммарных баллах;
- «5» – не менее 6 баллов за грамотность при 34-39 суммарных.
Особые требования к оцениванию работ по математике продиктованы тем, что на экзамен выносятся два предмета: алгебра и геометрия. Соответственно, ученик должен не просто набрать минимальный порог, а продемонстрировать определенный уровень знаний по каждой из основных школьных дисциплин по курсу «математика».
Проходной порог для вступления в профильные классы и колледжи также отличается в зависимости от выбранного направления:
Направление | Проходной балл | Примечание |
Естественнонаучный профиль | 18 | 6 баллов по геометрии |
Экономический профиль | 18 | 5 баллов по геометрии |
Физмат профиль | 19 | 7 баллов по геометрии |

Общая шкала рекомендованных минимальных проходных баллов на 2019 год для профильных направлений имеет вид:
Предмет | Баллы |
Русский язык | 31 |
Математика (естественно научный и экономический профиль) | 18 |
Математика (физмат профиль) | 19 |
История | 32 |
Физика | 30 |
Обществознание | 30 |
Информатика | 15 |
Литература | 15 |
Иностранный язык | 56 |
Биология | 33 |
География | 24 |
Химия (с экспериментом) | 25 |
Химия (без эксперимента) | 23 |
Общая таблица для интерпретации тестовых баллов ОГЭ по всем предметам в 2019 году будет иметь вид:
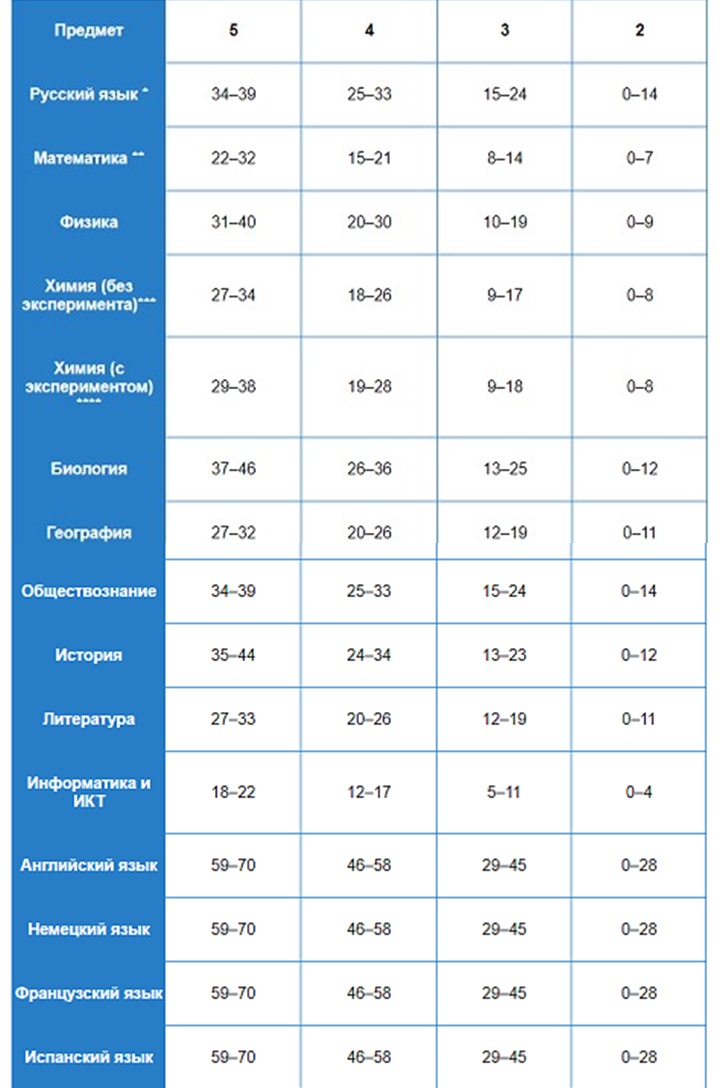
Жители регионов, где в 2019 году при определении результатов ОГЭ за основу берется рекомендованная единая шкала перевода баллов для заканчивающих 9 класс, также могут воспользоваться удобным online калькулятором, который можно найти на сайте 4ege.ru.
Пересдача ОГЭ
В 2018 году ОГЭ сдавали более 1,3 млн. девятиклассников, большинство из которых без проблем справились с испытаниями. Но, как всегда, есть и такие, кто получил оценку «неудовлетворительно». Что ожидает таких девятиклассников? Есть несколько вариантов развития событий:
- Пересдача, к которой допускаются ученики, у которых не более 2 неудовлетворительных результатов.
- Перерыв длиной в учебный год, за время которого ученик получает возможность лучше подготовиться к экзамену (возможно индивидуально занимаясь с преподавателями).

Читайте также:
Заметили опечатку на сайте? Мы будем благодарны вам, если вы выделите ее и нажмете Ctrl + Enter
История. ОГЭ 2019. Перевод баллов в оценки
Перевод баллов ОГЭ 2019 по истории (ГИА 9 класс) в оценку можно узнать в рекомендациях, опубликованных на официальном сайте ФИПИ.
Перевод баллов ОГЭ 2019 по истории в оценку (ГИА 9 класс)
Таблица 1
| Отметка по пятибалльной шкале | Общий балл |
| 2 | 0 – 12 |
| 3 | 13 – 23 |
| 4 | 24 – 34 |
| 5 | 35 – 44 |
Минимальный балл ОГЭ по истории (ГИА 9 класс) в 2019 году (оценка 3) — 13
Проходной балл ОГЭ 2019 по истории в профильные классы — 32
Максимальный балл — 44
Сколько баллов нужно набрать на ОГЭ, чтобы получить 3, 4 или 5 по истории и другим предметам подробно описано в письме Рособрнадзора, которое является официальным документом, хотя и носит рекомендательный характер.
Шкала перевода баллов ОГЭ 2019 в оценки. История (ГИА 9 класс) — рекомендации ФИПИ
Экзаменационные работы ОГЭ по истории проверяются двумя экспертами. По результатам проверки эксперты независимо друг от друга выставляют баллы за каждый ответ на задания экзаменационной работы…
В случае существенного расхождения в баллах, выставленных двумя экспертами, назначается третья проверка. Существенное расхождение в баллах определено в критериях оценивания по соответствующему учебному предмету.
Третий эксперт назначается председателем предметной комиссии из числа экспертов, ранее не проверявших экзаменационную работу.
Третьему эксперту предоставляется информация о баллах, выставленных экспертами, ранее проверявшими экзаменационную работу обучающегося. Баллы, выставленные третьим экспертом, являются окончательными».
Существенным считается расхождение в 2 или более балла за выполнение любого из заданий 31–35. В этом случае третий эксперт проверяет ответы только на те задания, которые вызвали столь существенное расхождение.
На основе баллов, выставленных за выполнение всех заданий работы, подсчитывается общий балл, который переводится в отметку по пятибалльной шкале.
Смотрите также:
90000 Mathematics Cognitive Domains-Fourth and Eighth Grades — TIMSS 2019 ASSESSMENT FRAMEWORKS 90001 90002 Mary Lindquist, Ray Philpot, Ina V.S. Mullis, and Kerry E. Cotter 90003 90002 Download TIMSS 2019 Mathematics Framework (pdf) 90003 90006 Mathematics Cognitive Domains-Fourth and Eighth Grades 90007 90002 In order to respond correctly to TIMSS test items, students need to be familiar with the mathematics content being assessed, but they also need to draw on a range of cognitive skills.Describing these skills plays a crucial role in the development of an assessment like TIMSS 2019, because they are vital in ensuring that the survey covers the appropriate range of cognitive skills across the content domains already outlined. 90003 90002 The first domain, 90011 knowing 90012, covers the facts, concepts, and procedures students need to know, while the second, 90011 applying 90012, focuses on the ability of students to apply knowledge and conceptual understanding to solve problems or answer questions.The third domain, 90011 reasoning 90012, goes beyond the solution of routine problems to encompass unfamiliar situations, complex contexts, and multistep problems. 90003 90002 Knowing, applying, and reasoning are exercised in varying degrees when students display their mathematical competency, which goes beyond content knowledge. These TIMSS cognitive domains encompass the competencies of problem solving, providing a mathematical argument to support a strategy or solution, representing a situation mathematically (e.g., using symbols and graphs), creating mathematical models of a problem situation, and using tools such as a ruler or a calculator to help solve problems. 90003 90002 The three cognitive domains are used for both grades, but the balance of testing time differs, reflecting the difference in age and experience of students in the two grades. For the fourth and eighth grades, each content domain will include items developed to address each of the three cognitive domains. For example, the number domain will include knowing, applying, and reasoning items as will the other content domains.90003 90002 Exhibit 1.4 shows the target percentages of testing time devoted to each cognitive domain for the fourth and eighth grade assessments. 90003 90002 90025 Exhibit 1.4: Target Percentages of the TIMSS 2019 Mathematics Assessment Devoted to Cognitive Domains at the Fourth and Eighth Grades 90026 90003 90028 90029 90030 90031 Cognitive Domains 90032 90033 Percentages 90032 90035 90030 90037 90038 Fourth Grade 90032 90038 Eighth Grade 90032 90035 90030 90031 Knowing 90032 90038 40% 90032 90038 35% 90032 90035 90030 90031 Applying 90032 90038 40% 90032 90038 40% 90032 90035 90030 90031 Reasoning 90032 90038 20% 90032 90038 25% 90032 90035 90067 90068 90069 Knowing 90070 90002 Facility in applying mathematics, or reasoning about mathematical situations, depends on familiarity with mathematical concepts and fluency in mathematical skills.The more relevant knowledge a student is able to recall and the wider the range of concepts he or she understands, the greater the potential for engaging in a wide range of problem solving situations. 90003 90002 Without access to a knowledge base that enables easy recall of the language and basic facts and conventions of number, symbolic representation, and spatial relations, students would find purposeful mathematical thinking impossible. Facts encompass the knowledge that provides the basic language of mathematics, as well as the essential mathematical concepts and properties that form the foundation for mathematical thought.90003 90002 Procedures form a bridge between more basic knowledge and the use of mathematics for solving problems, especially those encountered by many people in their daily lives. In essence, a fluent use of procedures entails recall of sets of actions and how to carry them out. Students need to be efficient and accurate in using a variety of computational procedures and tools. They need to see that particular procedures can be used to solve entire classes of problems, not just individual problems.90003 90028 90029 90030 90031 Recall 90032 90031 Recall definitions, terminology, number properties, units of measurement, geometric properties, and notation (eg, 90011 a 90012 × 90011 b 90012 = 90011 ab 90012, 90011 a 90012 + 90011 a 90012 + 90011 a 90012 = 3 90011 a 90012) . 90032 90035 90030 90031 Recognize 90032 90031 Recognize numbers, expressions, quantities, and shapes. Recognize entities that are mathematically equivalent (e.g., equivalent familiar fractions, decimals, and percents; different orientations of simple geometric figures).90032 90035 90030 90031 Classify / Order 90032 90031 Classify numbers, expressions, quantities, and shapes by common properties. 90032 90035 90030 90031 Compute 90032 90031 Carry out algorithmic procedures for +, -, ×, ÷, or a combination of these with whole numbers, fractions, decimals, and integers. Carry out straightforward algebraic procedures. 90032 90035 90030 90031 Retrieve 90032 90031 Retrieve information from graphs, tables, texts, or other sources. 90032 90035 90030 90031 Measure 90032 90031 Use measuring instruments; and choose appropriate units of measurement.90032 90035 90067 90068 90069 Applying 90070 90002 The applying domain involves the application of mathematics in a range of contexts. In this domain, the facts, concepts, and procedures as well as the problems should be familiar to the student. In some items aligned with this domain, students need to apply mathematical knowledge of facts, skills, and procedures or understanding of mathematical concepts to create representations. Representation of ideas forms the core of mathematical thinking and communication, and the ability to create equivalent representations is fundamental to success in the subject.90003 90002 Problem solving is central to the applying domain, with an emphasis on more familiar and routine tasks. Problems may be set in real life situations, or may be concerned with purely mathematical questions involving, for example, numeric or algebraic expressions, functions, equations, geometric figures, or statistical data sets. 90003 90028 90029 90030 90031 Determine 90032 90031 Determine efficient / appropriate operations, strategies, and tools for solving problems for which there are commonly used methods of solution.90032 90035 90030 90031 Represent / Model 90032 90031 Display data in tables or graphs; create equations, inequalities, geometric figures, or diagrams that model problem situations; and generate equivalent representations for a given mathematical entity or relationship. 90032 90035 90030 90031 Implement 90032 90031 Implement strategies and operations to solve problems involving familiar mathematical concepts and procedures. 90032 90035 90067 90068 90069 Reasoning 90070 90002 Reasoning mathematically involves logical, systematic thinking.It includes intuitive and inductive reasoning based on patterns and regularities that can be used to arrive at solutions to problems set in novel or unfamiliar situations. Such problems may be purely mathematical or may have real life settings. Both types of items involve transferring knowledge and skills to new situations; and interactions among reasoning skills usually are a feature of such items. 90003 90002 Even though many of the cognitive skills listed in the reasoning domain may be drawn on when thinking about and solving novel or complex problems, each by itself represents a valuable outcome of mathematics education, with the potential to influence learners ‘thinking more generally.For example, reasoning involves the ability to observe and make conjectures. It also involves making logical deductions based on specific assumptions and rules, and justifying results. 90003 90028 90029 90030 90031 Analyze 90032 90031 Determine, describe, or use relationships among numbers, expressions, quantities, and shapes. 90032 90035 90030 90031 Integrate / Synthesize 90032 90031 Link different elements of knowledge, related representations, and procedures to solve problems.90032 90035 90030 90031 Evaluate 90032 90031 Evaluate alternative problem solving strategies and solutions. 90032 90035 90030 90031 Draw Conclusions 90032 90031 Make valid inferences on the basis of information and evidence. 90032 90035 90030 90031 Generalize 90032 90031 Make statements that represent relationships in more general and more widely applicable terms. 90032 90035 90030 90031 Justify 90032 90031 Provide mathematical arguments to support a strategy or solution.90032 90035 90067 90068 90002 ‘; numbers.forEach (function (val, index) { if ($. isNumeric (val)) {// Is a References number = val; if (ref_var [number-1]! = undefined) { div_text + = ‘90003 90002’; } } else {// Is a Footnote if (foot_var [val]! = undefined) { footnote_obj = foot_var [val]; div_text + = ‘90003.90000 KNEC releases the 2019 Grade 3 learners ‘assessment criteria 90001 90002 2020 registration for KCPE and KCSE candidates. Here are the instructions from KNEC. 90003 The Kenya National Examinations Council, KNEC, has released guidelines to be used in monitoring the grade three learners ‘progress. Here are the guidelines; 90004 90003 KENYA NATIONAL EXAMINATIONS COUNCIL MONITORING LEARNERS ‘PROGRESS 90006 GRADE 3 2019 90004 90003 INTEGRATED LEARNING AREAS INSTRUCTIONS 90006 a) The teacher will guide the learner to carefully read through the performance task, carry out every step as required, and build a portfolio.90006 b) The task will be carried out within a duration of two months. 90006 c) The task involves a clean up of the market place next to the school. 90006 d) The teacher should seek permission from the local authorities to carry out the task 90006 e) The teacher will use the Assessment Rubrics provided for each task to assess the learner’s work. 90006 f) Samples of work that show the learner’s performance on the tasks should be maintained in the assessment portfolio. 90006 g) Samples of work selected for the portfolio should aim at illustrating the learner’s progress and achievement in learning.90006 h) Each learner is required to develop and maintain a portfolio as evidence of learning. 90004 90018 Also read: 90019 90003 THEME: A CLEAN ENVIRONMENT FOR GOOD HEALTH AND WELL BEING 90004 90003 1.0 GENERAL OUTCOMES FOR EARLY YEARS EDUCATION 90006 a) Explore the immediate environment for learning and enjoyment; 90006 b) Practice hygiene, nutrition, sanitation and safety skills to promote health and wellbeing; 90006 c) Apply creativity and critical thinking skills in problem solving; 90006 d) Apply digital literacy skills for learning and enjoyment.90004 90003 2.0 STANDARD 90006 The learner can: 90006 a) Describe ways of keeping the market place clean; 90006 b) Participate in cleaning the market place; 90006 c) Observe safety when disposing waste; 90006 d) Demonstrate appreciation of a clean environment. 90004 90003 3.0 PERFORMANCE TASK 90004 90003 3.1 Learners will be involved in the following activities: 90006 a) Watching video clips / viewing photographs / pictures of a clean-up exercise and identifying 90006 the cleaning activities observed.90006 b) Pre-visit to the nearest marketplace to observe the state of cleanliness. Guided by the teacher, learners to identify specific areas that require cleaning. 90006 c) i) Identification of the cleaning materials / tools that can be used in cleaning the market place. 90006 ii) With the help of their parents / guardians, each learner to improvise at least one relevant material for cleaning the market place. 90006 d) Learners to visit the marketplace for a clean-up exercise. 90006 (Before the actual cleanup exercise, the teacher should put learners in groups of 4 — 6 and assign cleaning areas to each group).90004 90003 e) Guided by the group leaders, learners to do stretch up exercises to warm up before carrying out the cleaning activity. 90004 90003 f) Learners to carry out the cleaning exercise in their assigned areas while observing safety measures. 90004 90003 g) Learners to safely sort and dispose off the collected waste. 90006 h) Mwanafunzi aandike njia mbalimbali za kutunza usafi sokoni. 90006 i) Learn and sing a song of their choice on cleaning the environment (individually and in groups).90006 j) Individually draw any two objects used in cleaning the market place (such as litter bins, brooms, brushes etc.). Mount the completed drawings in the learner’s assessment portfolio. 90004 90003 3.2 Targeted Learning areas Reference 90006 a) Environmental Activities Vol. 2, G3, Pg. 126, S2.0, ss 2.1.1 Vol. 2, G3, Pg 134, S3.0, ss 3.3 90006 b) Movement and Creative Activities Vol. 4, G3, Pg. 340, S1.0, ss 1.1 Vol. 4, G2, S1.0, ss 1.1, G1 pg. 13, S1.0 ss 2.1 90006 c) Religious Activities Vol.3, G3, Pg. 132, S6.0, ss 6.3 90006 d) English Activities Vol. 1, G3, Pg. 287, S1.0, ss 1.3 90006 e) Kiswahili Activities Vol. 1, G3, Pg. 98, S6.0, ss 6.4 90006 f) Mathematics Activities Vol. 2, G1, Pg. 4, S1.0, ss 1.1 90006 g) Hygiene and Nutrition Activities Vol. 2, G3, Pg. 200, S1.0, ss 1.4 90004 90003 3.3 Core Competencies Targeted 90006 a) Communication and collaboration as they work in groups. 90006 b) Critical thinking and problem solving as they improvise cleaning materials, 90006 c) Imagination and Creativity as they draw, label and mount objects.90006 d) Digital literacy as they watch video clips and take photos of the cleaning activities. 90006 e) Self-efficacy as they sing individually. 90006 f) Learning to learn as they clean the market place. 90004 90018 More reading on TSC matters; 90019 90074 90075 New, latest TSC Teachers recruitment guidelines 90076 90075 TSC: Wealth declaration guide for teachers, staff 90076 90075 A TSC teacher’s payslip details and how to get yours online 90076 90075 TSC posting, employment, letters for newly recruited teachers 90076 90075 TSC adds another new teacher registration, employment requirement; read the details 90076 90075 All TSC online services: the TSC website, online services and how to easily access them 90076 90075 New list of TSC County Directors 90076 90075 Updated TSC recruitment guidelines for teachers 90076 90075 TSC: Process of handing-taking over by new school heads and other administrators 90076 90075 New academic and professional requirements for registration of teachers 90076 90075 How to check the status of TSC number application online 90076 90075 Get the latest TSC news on these official Social Media links (Facebook, Twitter, WhatsApp, Telegram and online) 90076 90075 How to apply online for the vacant administrative positions at the Teachers Service Commission-tsc 90076 90075 TSC: Most marketable subject combinations 90076 90075 TSC: Revised, new, service charter 90076 90075 TSC: Download all the TSC forms, circulars, regulations and Memos here 90076 90075 TSC: How to easily get the retirement, pension, benefits 90076 90075 TSC: Full process of interdicting, disciplining and dismissing teachers 90076 90075 New, updated, list of offences that can lead to a teacher’s removal from the TSC register 90076 90075 TSC: All teachers ‘leaves explained 90076 90075 TSC: List of all allowances paid to teachers and to get them 90076 90075 Latest Career Progression Guidelines, CPG, for teachers 90076 90075 TSC: Answers to all the Frequently asked questions by teachers 90076 90075 TSC: A list of all the TSC contacts 90076 90075 TSC: How a teacher should claim the medical expenses costs from TSC 90076 90075 TSC: How to best apply for a teacher transfer 90076 90075 How to easily apply for a TSC number 90076 90075 Applying for a TSC number? This is all you need to know.90076 90075 All what you are required to have in order to apply for a TSC number 90076 90133 90003 3.4 Link to Values 90006 Responsibility, love, unity, honesty, cooperation and respect as they work in groups. 90004 90003 3.5 Link to PCIs 90006 a) Citizenship, Environmental education, Health Education, Life Skills, 90006 b) Community Service Learning as they clean the market. 90006 c) Education for Sustainable Development. 90004 90003 90143 90004 90003 90146 Other related news; 90147 90004 90149 90003 2019 KNEC Grade 3 Exams- How to register learners for the 2019 Kenya Early Years Assessment; Requirements 90004 90152 .90000 2019 KEYA Assessment Criteria for Grade 3 Learners by KNEC 90001 90002 The following are the 2019 instructional guidelines to teachers in assessing the Grade 3 Learners. The guidelines have been issued by the Kenya National Examination Council, KNEC. 90003 90002 The guidelines are meant to help in monitoring the 2019 Grade 3 learners as part of the Kenya Early Years Assessment, KENYA. 90003 90002 The Grade 3 teacher’s role has been outlined and integrated learning areas Instructions issued.90003 90008 90009 Monitoring Learners ‘Progress Grade 3 2019 90010 90011 90012 Integrated Learning Areas Instructions 90013 90002 a) The teacher will guide the learner to carefully read through the performance task, carry out every step as required, and build a portfolio. 90003 90002 b) The task will be carried out within a duration of two months. 90003 90002 c) The task involves a clean up of the market place next to the school. 90003 90002 d) The teacher should seek permission from the local authorities to carry out the task.90003 90002 e) The teacher will use the Assessment Rubrics provided for each task to assess the learner’s work. 90003 90002 f) Samples of work that show the learner’s performance on the tasks should be maintained in the assessment portfolio. 90003 90002 g) Samples of work selected for the portfolio should aim at illustrating the learner’s progress and achievement in learning. 90003 90002 h) Each learner is required to develop and maintain a portfolio as evidence of learning. 90003 90012 THEME: A Clean Environment for Good Health and Well Being 90013 90032 1.0 General Outcomes for Early Years Education 90033 90002 a) Explore the immediate environment for learning and enjoyment; 90003 90002 b) Practice hygiene, nutrition, sanitation and safety skills to promote health and wellbeing; 90003 90002 c) Apply creativity and critical thinking skills in problem solving; 90003 90002 d) Apply digital literacy skills for learning and enjoyment. 90003 90032 2.0 Standard 90033 90002 The learner can: 90003 90002 a) Describe ways of keeping the market place clean; 90003 90002 b) Participate in cleaning the market place; 90003 90002 c) Observe safety when disposing waste; 90003 90002 d) Demonstrate appreciation of a clean environment.90003 90032 3.0 Performance Task 90033 90032 3.1 Learners will be involved in the following activities: 90033 90002 a) Watching video clips / viewing photographs / pictures of a clean-up exercise and identifying 90059 the cleaning activities observed. 90003 90002 b) Pre-visit to the nearest marketplace to observe the state of cleanliness. Guided by the teacher, learners to identify specific areas that require cleaning. 90003 90002 c) i) Identification of the cleaning materials / tools that can be used in cleaning the market place.90003 90002 ii) With the help of their parents / guardians, each learner to improvise at least one relevant material for cleaning the market place. 90003 90002 d) Learners to visit the marketplace for a clean-up exercise. 90059 (Before the actual cleanup exercise, the teacher should put learners in groups of 4 — 6 and assign cleaning areas to each group). 90003 90002 e) Guided by the group leaders, learners to do stretch up exercises to warm up before carrying out the cleaning activity. 90003 90002 f) Learners to carry out the cleaning exercise in their assigned areas while observing safety measures.90003 90002 g) Learners to safely sort and dispose off the collected waste. 90003 90002 h) Mwanafunzi aandike njia mbalimbali za kutunza usafi sokoni. 90003 90002 i) Learn and sing a song of their choice on cleaning the environment (individually and in groups). 90003 90002 j) Individually draw any two objects used in cleaning the market place (such as litter bins, brooms, brushes etc.). Mount the completed drawings in the learner’s assessment portfolio. 90003 90032 3.2 Targeted Learning areas Reference 90033 90002 a) Environmental Activities Vol.2, G3, Pg. 126, S2.0, ss 2.1.1 Vol. 2, G3, Pg 134, S3.0, ss 3.3 90003 90002 b) Movement and Creative Activities Vol. 4, G3, Pg. 340, S1.0, ss 1.1 Vol. 4, G2, S1.0, ss 1.1, G1 pg. 13, S1.0 ss 2.1 90003 90002 c) Religious Activities Vol. 3, G3, Pg. 132, S6.0, ss 6.3 90003 90002 d) English Activities Vol. 1, G3, Pg. 287, S1.0, ss 1.3 90003 90002 e) Kiswahili Activities Vol. 1, G3, Pg. 98, S6.0, ss 6.4 90003 90002 f) Mathematics Activities Vol. 2, G1, Pg. 4, S1.0, ss 1.1 90003 90002 g) Hygiene and Nutrition Activities Vol.2, G3, Pg. 200, S1.0, ss 1.4 90003 90032 3.3 Core Competencies Targeted 90033 90002 a) Communication and collaboration as they work in groups. 90003 90002 b) Critical thinking and problem solving as they improvise cleaning materials. 90003 90002 c) Imagination and Creativity as they draw, label and mount objects. 90003 90002 d) Digital literacy as they watch video clips and take photos of the cleaning activities. 90003 90002 e) Self-efficacy as they sing individually. 90003 90002 f) Learning to learn as they clean the market place.90003 90032 3.4 Link to Values 90033 90002 Responsibility, love, unity, honesty, cooperation and respect as they work in groups. 90003 90032 3.5 Link to PCIs 90033 90002 a) Citizenship, Environmental education, Health Education, Life Skills. 90003 90002 b) Community Service Learning as they clean the market. 90003 90002 c) Education for Sustainable Development. 90003 90012 Below is the PDF preview of the KNEC Guidelines on Assessment of Grade 3 Learners in 2019 90013 .90000 Mathematics Content Domains-Eighth Grade — TIMSS 2019 ASSESSMENT FRAMEWORKS 90001 90002 Mary Lindquist, Ray Philpot, Ina V.S. Mullis, and Kerry E. Cotter 90003 90002 Download TIMSS 2019 Mathematics Framework (pdf) 90003 90006 Mathematics Content Domains-Eighth Grade 90007 90002 Exhibit 1.3 shows the TIMSS Mathematics-Eighth Grade content domains and the target percentages of assessment score points devoted to each. Each content domain consists of topic areas, and each topic area in turn includes several topics.Across the eighth grade mathematics assessment, each topic receives approximately equal weight. 90003 90002 90011 Exhibit 1.3: Target Percentages of the TIMSS 2019 Mathematics Assessment Devoted to Content Domains at the Eighth Grade 90012 90003 90014 90015 90016 90017 Eighth Grade Content Domains 90018 90019 Percentages 90018 90021 90016 90017 Number 90018 90019 30% 90018 90021 90016 90017 Algebra 90018 90019 30% 90018 90021 90016 90017 Geometry 90018 90019 20% 90018 90021 90016 90017 Data and Probability 90018 90019 20% 90018 90021 90046 90047 90048 Number 90049 90002 At the eighth grade, the thirty percent of the assessment devoted to number consists of three topic areas: 90003 90052 90053 Integers (10%) 90054 90053 Fractions and decimals (10%) 90054 90053 Ratio, proportion, and percent (10%) 90054 90059 90002 Building on the number content domain at the fourth grade, eighth grade students should have developed proficiency with more advanced whole number concepts and procedures as well as extended their mathematical understanding of rational numbers (integers, fractions, and decimals).Students also should understand and be able to compute with integers. Fractions and decimals are an important part of daily life and being able to compute with them requires an understanding of the quantities the symbols represent. Students should understand that fractions and decimals are single entities like whole numbers. A single rational number can be represented with many different written symbols, and students need to be able to recognize the distinctions among interpretations of rational numbers, convert between them, and reason with them.Students should be able to solve problems involving ratios, proportions, and percents. 90003 90062 Integers 90063 90064 90053 Demonstrate understanding of properties of numbers and operations; find and use multiples and factors, identify prime numbers, evaluate positive integer powers of numbers, evaluate square roots of perfect squares up to 144, and solve problems involving square roots of whole numbers. 90054 90053 Compute and solve problems with positive and negative numbers, including through movement on the number line or various models (e.g., losses and gains, thermometers). 90054 90069 90062 Fractions and Decimals 90063 90064 90053 Using various models and representations, compare and order fractions and decimals, and identify equivalent fractions and decimals. 90054 90053 Compute with fractions and decimals, including those set in problem situations. 90054 90069 90062 Ratio, Proportion, and Percent 90063 90064 90053 Identify and find equivalent ratios; model a given situation by using a ratio; divide a quantity according to a given ratio.90054 90053 Solve problems involving proportions or percents, including converting between percents and fractions or decimals. 90054 90069 90048 Algebra 90049 90002 The thirty percent of the assessment devoted to algebra is comprised of two topic areas: 90003 90052 90053 Expressions, operations, and equations (20%) 90054 90053 Relationships and functions (10%) 90054 90059 90002 Patterns and relationships are pervasive in the world around us and algebra enables us to express these mathematically.Students should be able to solve real world problems using algebraic models and explain relationships involving algebraic concepts. They need to understand that when there is a formula involving two quantities, if they know one quantity, they can find the other either algebraically or by substitution. This conceptual understanding can extend to linear equations for calculations about things that expand at constant rates (e.g., slope). Functions can be used to describe what will happen to a variable when a related variable changes.90003 90062 Expressions, Operations, and Equations 90063 90064 90053 Find the value of an expression or a formula given values of the variables. 90054 90053 Simplify algebraic expressions involving sums, products, and powers; compare expressions to determine if they are equivalent. 90054 90053 Write expressions, equations, or inequalities to represent problem situations. 90054 90053 Solve linear equations, linear inequalities, and simultaneous linear equations in two variables, including those that model real life situations.90054 90069 90062 Relationships and Functions 90063 90064 90053 Interpret, relate and generate representations of linear functions in tables, graphs, or words; identify properties of linear functions including slope and intercepts. 90054 90053 Interpret, relate and generate representations of simple non-linear functions (e.g., quadratic) in tables, graphs, or words; generalize pattern relationships in a sequence using numbers, words, or algebraic expressions. 90054 90069 90048 Geometry 90049 90002 Extending the understanding of shapes and measures assessed at the fourth grade, eighth grade students should be able to analyze the properties of a variety of two- and three-dimensional figures and calculate perimeters, areas, and volumes.They should be able to solve problems and provide explanations based on geometric relationships, such as congruence, similarity, and the Pythagorean theorem. 90003 90002 The geometry content domain at the eighth grade consists of one topic area: 90003 90052 90053 Geometric shapes and measurements (20%) 90054 90059 90062 Geometric Shapes and Measurements 90063 90002 At eighth grade, geometric shapes include circles; scalene, isosceles, equilateral, and right-angled triangles; trapezoids, parallelograms, rectangles, rhombuses, and other quadrilaterals; as well as other polygons including pentagons, hexagons, octagons, and decagons.They also include three-dimensional shapes-prisms, pyramids, cones, cylinders, and spheres. One- and two-dimensional figures can be presented in the Cartesian plane. 90003 90064 90053 Identify and draw types of angles and pairs of lines and use the relationships between angles on lines and in geometric figures to solve problems, including those involving the measures of angles and line segments; solve problems involving points in the Cartesian plane. 90054 90053 Identify two-dimensional shapes and use their geometric properties to solve problems, including those involving perimeter, circumference, area, and the Pythagorean Theorem.90054 90053 Recognize and draw images of geometric transformations (translations, reflections, and rotations) in the plane; identify congruent and similar triangles and rectangles and solve related problems. 90054 90053 Identify three-dimensional shapes and use their geometric properties to solve problems, including those involving surface area and volume; relate three-dimensional shapes with their two-dimensional representations. 90054 90069 90048 Data and Probability 90049 90002 Increasingly, the more traditional forms of data display (e.g., bar graphs, line graphs, pie graphs, pictographs) are being supplemented by an array of new graphic forms (e.g., infographics). By the eighth grade, students should to be able to read and extract the important meaning from a variety of visual displays. It is also important for eighth grade students to be familiar with the statistics underlying data distributions and how these relate to the shape of data graphs. Students should know how to collect, organize, and represent data. Students also should have an initial grasp of some concepts related to probability.90003 90002 The data and probability content domain contains two topic areas: 90003 90052 90053 Data (15%) 90054 90053 Probability (5%) 90054 90059 90062 Data 90063 90064 90053 Read and interpret data from one or more sources to solve problems (e.g., interpolate and extrapolate, make comparisons, draw conclusions). 90054 90053 Identify appropriate procedures for collecting data; organize and represent data to help answer questions. 90054 90053 Calculate, use, or interpret statistics (i.e., mean, median, mode, range) summarizing data distributions; recognize the effect of spread and outliers. 90054 90069 90062 Probability 90063 90064 90053 For simple and compound events: a) determine theoretical probability (based on equally likely outcomes, e.g., rolling a fair die) or b) estimate the empirical probability (based on experimental outcomes). 90054 90069 90048 Calculator Use at the Eighth Grade 90049 90002 Continuing the practice of previous TIMSS assessments, at the fourth grade students will not be permitted to use calculators.This includes both paperTIMSS and eTIMSS. At the eighth grade, students will be permitted to use calculators, although the mathematics items are developed to be calculator neutral-do not advantage or disadvantage students whether or not they have calculators. In paperTIMSS, consistent with past TIMSS assessments, students at the eighth grade may bring their own calculators to the assessment. In eTIMSS, students at the eighth grade will have access to a calculator provided as part of the on-screen interface and will not be permitted to bring their own calculators.The on-screen calculator includes the four basic functions (+, -, ×, ÷) and a square root key. The eventual transition to eTIMSS will result in calculators being standardized. 90003 90002 ‘; numbers.forEach (function (val, index) { if ($. isNumeric (val)) {// Is a References number = val; if (ref_var [number-1]! = undefined) { div_text + = ‘90003 90002’; } } else {// Is a Footnote if (foot_var [val]! = undefined) { footnote_obj = foot_var [val]; div_text + = ‘90003.

Leave A Comment