«Числа и их свойства. Задание №19 ЕГЭ по математике»
Числа и их свойства.
Задание №19 ЕГЭ по математике
Оглавление
1. Введение 2
2. Теория чисел 3
2.1. Множества чисел, иерархия множеств 3
2.2. Определение делимости 4
2.2.1. Делимость целых чисел, простые числа, НОД, свойства делимости 4
2.2.2. Чётные и нечётные числа 5
2.2.3. Основная теорема арифметики 6
2.2.4. Признаки делимости целых чисел. 6
2.3. Среднее арифметическое и среднее геометрическое 7
2.4. Прогрессии и их свойства, формулы 8
2.4.1 Арифметическая прогрессия 8
2.4.2 Геометрическая прогрессия 8
3. Методы решения задания № 19 10
3.1. Построение математической модели 10
3.2. Метод кругов Эйлера 10
3.3. Метод математической индукции 10
3.4. Принцип Дирихле 12
3.5. Перебор значений по заданным условиям 12
4. Заключение 13
Заключение 13
Источники информации 14
Приложение 15
- Введение
Понятие числа возникло ещё в древности из практической потребности людей, когда людям были необходимы меры счёта и измерения. Пифагорейцы считали числа «причиной и началом» вещей. Со временем понятие числа стало основным понятием математики.
Свойства чисел — одна из интереснейших тем для изучения. Задание №19 единого государственного экзамена «Числа и их свойства» — одно из самых интересных и сложных заданий второй части. Знания, необходимые для решения данной задачи, ученики получают ещё в средней школе.
Целью работы является
Объект исследования: задание №19 профильного ЕГЭ по математике
Методы исследования:
Изучение теоретического материала;
Решение задач ЕГЭ прошлых лет.
Поставлены следующие задачи:
Изучить теоретический материал для решения задания №19;
Научиться решать задание №19 ЕГЭ по математике профильного уровня, изучить основные методы решения;
Разобрать задания №19 из вариантов ЕГЭ прошлых лет;
Решить и оформить несколько заданий №19 ЕГЭ;
- Теория чисел
2. 1. Множества чисел, иерархия множеств
1. Множества чисел, иерархия множеств
Число — основное понятие математики, которое используется для количественной характеристики, сравнения, нумерации объектов и их частей. Выделяют следующие множества чисел:
Натуральные числа — числа, используемые при счете (перечислении) предметов:
N = {1 ,2, 3, …}
Целые числа — включают в себя натуральные числа, числа противоположные натуральным (т.е. с отрицательным знаком) и ноль.
Z = {…, -2, -1, 0, 1, 2, …}
Рациональные числа — числа, представляемые в виде обыкновенной дроби a / b, где a ∈ b, ∈ N, b ≠0
Q = {m / n, m ∈ Z, n ∈ N}
При переводе в десятичную дробь рациональное число представляется конечной или бесконечной периодической дробью.
Иррациональные числа — числа, которые представляются в виде бесконечной непериодической десятичной дроби. Обозначается как I. Типичным примером является π.
Обозначается как I. Типичным примером является π.
Действительные (вещественные) числа — объединение рациональных и иррациональных чисел. Обозначается R = {I + Q}
Комплексные числа – множество чисел C.
C = {x + iy, где x ∈ R и y ∈ R}, где i − мнимая единица.
Рис. 1 Иерархия множеств
2.2. Определение делимости 2.2.1. Делимость целых чисел, простые числа, НОД, свойства делимости
Опр. Пусть n – целое число (n ∈ Z), m – натуральное число (m ∈ N). Говорят, что n делится нацело на m, если существует такое целое число p ∈ Z, такое, что
n = mp
m называют делителем числа n, n называют делимым, а p называют частным от деления n на m
Любое целое число n можно представить в виде n = mp + q, где m называют делителем числа n, n называют делимым, а p называют частным от деления n на m, а q – остатком от деления n на m. qm называют делителем числа n, n называют делимым, а p называют частным от деления n на m.
qm называют делителем числа n, n называют делимым, а p называют частным от деления n на m.
Число q находится на отрезке от 0 до m – 1.
Опр. Натуральное число a1 называется простым, если оно имеет ровно два натуральных делителя: 1 и само себя. Простых чисел бесконечное множество.
Множество простых чисел: 2, 3, 5, 7, 11, 13, …
Опр. Наибольшее натуральное число, являющееся натуральным делителем каждого из натуральных чисел m и n, называют наибольшим общим делителем этих чисел и обозначают НОД (m, n).
Например, если m = 36 и n = 84, то НОД (36, 84) = 12.
Опр. Два числа называются взаимно простыми, если их НОД равен 1.
Например: 14 и 25, так как НОД (14, 25) = 1
Пусть a ∈ Z, b ∈ Z, m ∈ N, то справедливы следующие свойства делимости:
1. Если a и b делятся на m, то числа a — b и a + b также делятся на m.
Если a и b делятся на m, то числа a — b и a + b также делятся на m.
2. Если a и b делятся на m, то при любых целых числах k и l число ak + bl также делится на m.
3. Если a делится на m, а b не делится на m, то числа a + b и a — b также не делятся на m.
4. Если a делится на m, а m делится на k ∈ N, то число a также делится на k.
5. Если a делится на m, а b не делится на m, то число ab делится на m.
6. Если a делится на каждое из чисел m и k, причем НОД (m, k) = 1, то a делится на произведение mk.
7. Если a делится на m, то ak делится на mk при любом k ∈N.
8. Если ab делится на m и b взаимно просто с m, то a делится на m.
9. В ряде из n подряд идущих целых чисел хотя бы одно делится на n нацело.
2.2.2. Чётные и нечётные числа
Опр. Целое число называется чётным, если оно делится на 2 без остатка
a – чётное число, если a = 2n, где n ∈ Z {…, -4, -2, 0, 2, 4, …}
Опр. Целое число называется нечётным, если при делении на 2 оно даёт остаток 1
Целое число называется нечётным, если при делении на 2 оно даёт остаток 1
a – нечётное число, если a = 2n – 1, где n ∈ Z {…, -3, -1, 1, 3, …}
2.2.3. Основная теорема арифметики
Для каждого натурального числа n 1 существует единственное разложение на простые множители. Это значит, что для любого натурального числа два разложения на простые множители могут отличаться только порядком этих множителей.
2.2.4. Признаки делимости целых чисел.
Признак делимости на 2.
Число делится на 2 тогда и только тогда, когда его последняя цифра чётна.
Признак делимости на 10.
Число делится на 10 тогда и только тогда, когда его последняя цифра равна 0.
Признак делимости на 5.
Число делится на 5 тогда и только тогда, когда его последняя цифра равна 0 или 5.
Признак делимости на 3.
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
Признак делимости на 9.
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 9.
Признак делимости на 4.
Число делится на 4 тогда и только тогда, когда двузначное число, образованное двумя его последними цифрами (в том же порядке), делится на 4.
Признак делимости на 8.
Число делится на 8 тогда и только тогда, когда трёхзначное число, образованное тремя его последними цифрами (в том же порядке), делится на 8.
Признак делимости на 11.
У данного числа найдём сумму цифр, стоящих на чётных местах, и сумму цифр, стоящих на нечётных местах.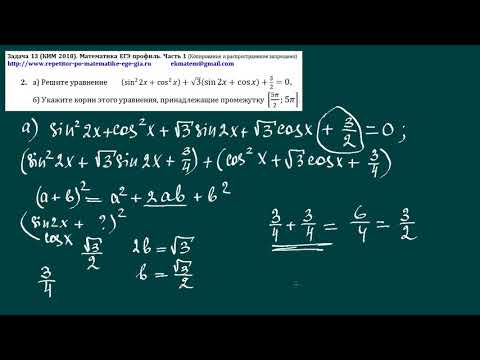 Число делится на 11 тогда и только тогда, когда разность этих сумм делится на 11 (в частности, равна нулю).
Число делится на 11 тогда и только тогда, когда разность этих сумм делится на 11 (в частности, равна нулю).
Признак делимости на 13.
Число делится на 13, если знакочередующаяся сумма его трёхзначных граней делится на 13.
2.3. Среднее арифметическое и среднее геометрическое
Опр. Среднее арифметическое множества чисел — число, равное сумме всех чисел множества, делённой на их количество.
Пусть задано множество чисел A = {a1, a2, a3, …, an}, тогда среднее арифметическое этого множества (Q) равно Q = (a1 + a2 + a3 + … + an) / n
Среднее арифметическое множества, в котором все числа равны, является каждое число этого множества.
Опр. Средним геометрическое нескольких положительных вещественных чисел – такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось
Пусть задано множество чисел B= {b1, b2, b3, …, bn}, тогда среднее арифметическое этого множества (M) равно M =
Опр. Среднее геометрическое двух чисел называется их средним пропорциональным.
Среднее геометрическое двух чисел называется их средним пропорциональным.
2.4. Прогрессии и их свойства, формулы
Опр. Прогрессия — последовательность величин, каждая следующая из которых находится в некой, общей для всей прогрессии, зависимости от предыдущей.
2.4.1 Арифметическая прогрессия
Опр. Арифметическая прогрессия — прогрессия, каждый следующий член которой равен предыдущему, увеличенному на фиксированное для прогрессии число.
Общий вид арифметической прогрессии:
a1, a1 + d, a1 + 2d, …, a1 + (n — 1)d
Рекуррентная формула n – го члена арифметической прогрессии:
an= an-1 + d
Формула n – го члена арифметической прогрессии:
an= a1 + (n – 1)d
Заметим, что если d0, то прогрессия возрастает, если d
d = an – an-1
Сумма n первых членов арифметической прогрессии (Sn):
Sn =
Sn =
2. 4.2 Геометрическая прогрессия
4.2 Геометрическая прогрессия
Опр. Геометрическая прогрессия – прогрессия, в которой каждый следующий член больше предыдущего в фиксированное количество раз.
Общий вид геометрической прогрессии: b1, b1q, b1q2, b1q3, …, b1qn-1
Рекуррентная формула n члена геометрической прогрессии:
bn = bn-1q
Формула n члена геометрической прогрессии: bn =b1qn-1
Если b1 0 и q 0, то прогрессия является возрастающей, если 0qqq = 0 – стационарной
q =
Характеристическое свойство геометрической прогрессии:
Сумма n первых членов геометрической прогрессии (Sn):
Sn =
Сумма всех членов бесконечно убывающей прогрессии: (S):
S =
- Методы решения задания № 19
3. 1. Построение математической модели
1. Построение математической модели
Опр. Метод построения математической модели – главная составляющая решения любой математической задачи. Суть метода заключается в переходе от бытового языка (например, русского) к языку математическому. Так, например, запись «у Пети было 12 яблок» можно представить, как «П = 12». То есть мы переходим к уравнениям, системам уравнений, решение которых приводит к решению данной задачи.
3.2. Метод кругов Эйлера
Опр. Диаграмма Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Первое их использование приписывают Леонарду Эйлеру. Используется в математике, логике, менеджменте и других прикладных направлениях.
Диаграммы Эйлера используются при решении задач на множества.
Рис 2. Диаграмма Эйлера
Диаграмма Эйлера
3.3. Метод математической индукции
Опр. Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — базис индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n +1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Докажем формулу суммы натуральных чисел от 1 до n, обозначим её как S(n):
Базовый случай n = 1, сумма чисел от 1 до 1 равна 1, проверим формулу подставив в неё n = 1:
Значит, наше утверждение верно для базового случая n.
Докажем истинность для утверждения n +1:
Подставим n + 1 в исходную формулу:
Заметим, что:
Тогда:
Мы доказали истинность формулы для n + 1, а значит она верна для любого натурального числа n.
3.4. Принцип Дирихле
Опр. Принцип Дирихле — утверждение, сформулированное немецким математиком Дирихле в 1834 году, устанавливающее связь между объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий.
Формулировка принципа Дирихле также может пригодиться при решении задачи № 19 ЕГЭ по математике:
Если кролики рассажены в клетки, причём число кроликов больше числа клеток, то хотя бы в одной из клеток находится более одного кролика.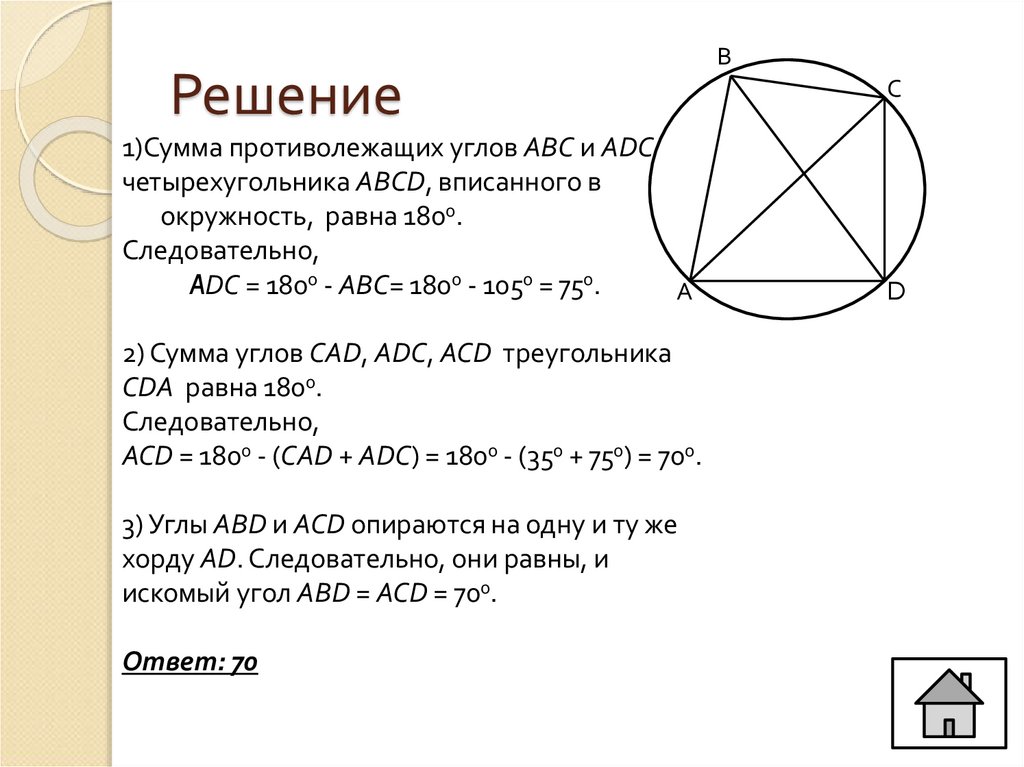
3.5. Перебор значений по заданным условиям
Перебор значений по заданным условиям также является методом решения задачи. Иногда задание №19 можно решить подбором, пункты «а» и «б» можно доказать, попросту приведя примеры и дав ответ «да» / «нет».
- Заключение
Результатом работы стала собранная в одном месте теория, необходимая для решения задания №19 профильного ЕГЭ по математике. Также были решены задания ЕГЭ прошлых лет, задания с сайта РЕШУ ЕГЭ и сборника ЕГЭ по профильной математике 2020 года. Всего было решено10 задач №19 второй части профильного ЕГЭ по математике.
Поставленные задачи работы выполнены: теория для решения задания изучена, задания №19 ЕГЭ прошлых лет разобраны и оформлены в соответствии с требованиями экзамена.
Источники информации
«Задачи на целые числа» Корянов А. Г., Прокофьев А.А. — Р. на Д.: 2016. — 272 с.
Г., Прокофьев А.А. — Р. на Д.: 2016. — 272 с.
«Математика абитуриенту», В. В. Ткачук 4-е изд., испр. и доп. — М.: МЦНМО, 2007. — 976с.
«Математика. Профильный уровень. Типовые экзаменационные варианты 2020», И. В. Ященко М.: Издательство «Национальное образование», 2020 – 256 с. – (ЕГЭ.ФИПИ – школе)
«Математика: Новый полный справочник школьника для подготовки к ЕГЭ», А. Г. Мордкович, В. И. Глизбург, Н. Ю. Лаврентьева – Москва: Издательство АСТ, 2018 – 351 с.
Борис Трушин [Электронный ресурс], URL: https://www.youtube.com/user/trushinbv
Википедия – свободная энциклопедия [Электронный ресурс], URL: https://ru.wikipedia.org/ (дата обращения: 19.01.2020)
Высшая математика [Электронный ресурс], URL: http://www.math34.ru/ (дата обращения: 19.01.2020)
Подготовка к олимпиадам и ЕГЭ по математике и физике [Электронный ресурс], URL: http://mathus. ru/ (дата обращения 06.01.2020)
ru/ (дата обращения 06.01.2020)
Публичная страница канала «Wild Mathing» «ВКонтакте» [Электронный ресурс], URL: https://vk.com/wildmathing (дата обращения 08.01.2020)
Сдам ГИА: РЕШУ ЕГЭ [Электронный ресурс], URL: https://ege.sdamgia.ru/
Приложение
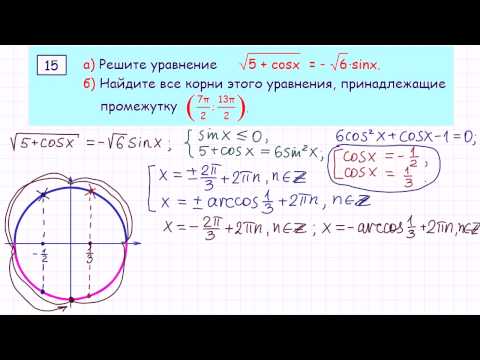
З адание №19 демоверсии ЕГЭ 2020 года
Задание №19 реального ЕГЭ 2017 года
З адание №19 реального ЕГЭ 2018 года
Задание №19 реального ЕГЭ 2018 года
Тренировочный вариант Ларина №42 с сайта РЕШУ ЕГЭ.
Тренировочный вариант Ларина №42 с сайта РЕШУ ЕГЭ.
З адание №19 из сборника И. В. Ященко 2020 год (вар. 35).
В. Ященко 2020 год (вар. 35).
Задание №19 из сборника И. В. Ященко (вар. 20)
Задание №19 из демоверсии ЕГЭ 2018 года.
Задание №19 с сайта РЕШУ ЕГЭ № 514744
Как распределить время на ЕГЭ по математике
Как часто вы слышите от учителей: «Сначала делайте все простые задания и откладывайте сложные напоследок, тогда вы сможете успеть все сделать быстро!»? Но действительно ли нужно следовать этому совету?
Давайте разбираться.
Сколько времени нам дают на ЕГЭ по математике?
Надо понимать, что на ЕГЭ у нас на самом деле не так много времени. К тому же стоит отметить, что базовая и профильная математика совершенно разные вещи.
Сколько времени нам дается на ЕГЭ по базовой математике?
Поскольку базовая математика не такой сложный предмет, который нужен лишь для оценки в аттестат, на него выделяется 3 часа.
Сколько времени нам дается на ЕГЭ по профильной математике?
На все про все дается всего лишь 3 часа 55 минут, за которые нужно не только успеть решить все задания, но и переписать их в бланки ответов. А ЕГЭ по профильной математике по статистике является одним из самых сложных предметов, на котором ученики зачастую не успевают решить все за такой короткий промежуток времени. Именно поэтому так важно правильно разделить время и четко понимать за каким баллом ты гонишься.
Сколько баллов вы можете получить на ЕГЭ?
Всего мы можем получить 32 первичных балла. Получается, что 1 первичный балл равен 4-5 вторичным. Далее мы будем разбираться уже во вторичных баллах.
Эта статья не даст вам знания на 100 баллов, однако, мы постараемся помочь вам грамотно распределить время на экзамене для того, чтобы вы не столкнулись с проблемой, когда вы можете решить все идеально, но просто не успеваете.
Для начала задайте себе вопрос: «За каким баллом я гонюсь?»
Цель менее 70 баллов
Если ваша цель набрать средний балл, не стоит сдавать свою работу уже через час. Спешка и невнимательность – наши главные враги, поэтому даже для невысокого балла нужно грамотное распределение времени. Чтобы набрать 70 или менее вторичных баллов, вам большую часть внимания нужно сосредоточить на первой части.
Спешка и невнимательность – наши главные враги, поэтому даже для невысокого балла нужно грамотное распределение времени. Чтобы набрать 70 или менее вторичных баллов, вам большую часть внимания нужно сосредоточить на первой части.
С 10:00 до 11:20 полностью решаем первую часть.
Далее даем себе передохнуть пару минут (можете попить воды или скушать шоколадку – это отвлечет вас и приведет вашу мозговую активность в норму).
С 11:30 до 12:10 проверяем свои решения на наличие ошибок и переносим ответы в КИМы.
И после этого, ни в коем случае не стоит все сдавать сразу! У вас еще есть время, которое можно потратить с пользой.
Оставшиеся 1,5 часа вы можете потратить на задания с подробным ответом. Вам вполне может повести с заданиями №13,15,17, которые являются самыми легкими. А также, иногда задание №19 можно решить исходя из логики. Таким образом вы сможете подстраховаться, если вдруг в первой части у вас окажутся ошибки.
Цель 70-85 баллов
Вот здесь уже начинаются трудности. Если вы хотите получить балл выше 70, вы уже не будете иметь право на ошибку в заданиях с кратким ответом.
Если вы хотите получить балл выше 70, вы уже не будете иметь право на ошибку в заданиях с кратким ответом.
С 10:00 до 10:40 полностью решаем задания из 1 части и переносим их в бланки ответов.
Немного отдыхаем, пьем воды и приступаем к заданиям с развернутым ответом.
С 10:50 до 12:00 решаем самые легкие задания из второй части (это задания № 13,15,17) и так же сразу переносим все в бланки, чтобы потом не путаться в ответах.
Если вы решите все эти задания правильно или же с парой ошибок, вы уже получите желаемый балл. Однако всегда стоит, как это говорится, «держать туз в рукаве». Поэтому, после того как выполните задания №13,15,17, внимательно посмотрите на остальные задания второй части. Если вам показалось что-то относительно простым – стоит попробовать решить. Лишние баллы никому еще не мешали!
Цель 85-95 баллов
Тем, кто хочет набрать выше 85 баллов придется очень сильно постараться, ведь им придется играть не только с удачей, но и в гонку со временем. Первую часть в данном случае и вовсе нужно решать «с закрытыми глазами».
Первую часть в данном случае и вовсе нужно решать «с закрытыми глазами».
Итак, с 10:00 до 10:20 решаем все тестовые задания. С ними у вас не должно возникать никаких трудностей, если ваша цель – высочайший балл.
С 10:20 до 11:30 решаем уже в чистовике задания №13,15,17. Опять-таки, если ваша цель – 90 баллов, эти задания вы должны «щелкать как орешки».
С 11:30 до 12:30 пытаемся решить задания №14 и №16. Решаем в порядке сложности, от самого легкого.
С 12:30 до 12:35 даем себе наконец передохнуть, чтобы подготовить свой мозг к последним заданиям.
С 12:35 и до конца экзамена решаем задания №18,19. Сначала быстро пробегаемся глазами, определяем самое легкое задания и уже только после этого решаем в порядке возрастания сложности.
Цель 95-100 баллов
И последнее, самое сложное и почти нереальное. То, что снится школьникам в хороших снах.
В данном случае надо понимать, что у вас в принципе нет права на ошибку (разве что на одну или две незначительные). Вы должны быть идеально подготовленными для этого и вот здесь уже без очень четкого распределения времени – никуда.
Вы должны быть идеально подготовленными для этого и вот здесь уже без очень четкого распределения времени – никуда.
С 10:00 до 10:20 не останавливаясь ни на чем, решаем задания первой части.
С 10:20 до 11:10 решаем простейшие для вас номера 13,15,17. Они, как и тестовая часть, у вас должны быть готовы как по шаблону, быстро и четко.
С 11:10 до 11:20 дам себе немного отдохнуть, иначе от такого огромного количества информации за короткое время мозг начинает просто «закипать», а вам ведь нужно еще решить самое сложное!
С 11:20 до 12:30 решаем задачи с чертежами. Важно! В черновике нужно только нарисовать чертеж и записать очень кратко все, что нужно, а само подробное решение нужно писать сразу в чистовик. В противном случае у вас не останется времени на остальные задания, а мы ведь целимся на успешный балл.
С 12:30 до 12:35 даем себе еще немного передохнуть. Попейте воды и немного настройтесь на выполнение следующих, не менее сложных задач.
С 12:35 до 13:40 решаем оставшиеся задачи №18 и №19. Для начала выбираем самую легкую из них. Решаем так же в основном в чистовике, в черновике лишь делаем изначально заметки и рисунки, если нужно.
Для начала выбираем самую легкую из них. Решаем так же в основном в чистовике, в черновике лишь делаем изначально заметки и рисунки, если нужно.
Оставляем себе 15 минут в конце, чтобы спокойно вздохнуть и еще раз все перепроверить и ничего не забыть.
Важно! За каким бы вы баллом ни стремились, переписывайте сразу все ответы в бланки! Так вы не будете нервничать о том, что в конце в спешке могли что-то неправильно написать.
Не ленитесь и усердно готовьтесь! Удачи вам на экзаменах!
Инструкция по математике для изучающих английский язык
Изучение сложных тем в классе: советы преподавателям ELL
Узнайте, как сделать уроки математики более доступными для изучающих английский язык путем накопления базовых знаний, расширения языковых навыков учащихся и явного обучения академическому языку.
На этой странице
- Важность обучения академической лексике
- Важность чтения и понимания письменных математических задач
- Важность накопления фоновых знаний
- Важность повышения языковой продуктивности учащихся в предметной области
- Использование технологий
- Горячие ссылки
Мой папа дал мне однодолларовую купюру
Потому что я его самый умный сын,
И я поменял его на две блестящие монетки
Потому что два больше, чем один!— Отрывок из книги Шела Сильверстайна «Умный»
Будучи студентом, у меня были проблемы с математикой. Я не понимал, почему это было так естественно для некоторых студентов, но не для меня. Однако, оглядываясь назад, я понимаю, что у меня было преимущество, о котором я даже не подозревал — я понимал язык, на котором написаны задачи, даже если не понимал, как их решать! Хотя легко предположить, что многие изучающие английский язык (ELL) будут преуспевать в математике, потому что математика является «универсальным языком» и учащиеся могут иметь предыдущий образовательный опыт, включающий математические инструкции, это предположение может ввести преподавателей в заблуждение.
Я не понимал, почему это было так естественно для некоторых студентов, но не для меня. Однако, оглядываясь назад, я понимаю, что у меня было преимущество, о котором я даже не подозревал — я понимал язык, на котором написаны задачи, даже если не понимал, как их решать! Хотя легко предположить, что многие изучающие английский язык (ELL) будут преуспевать в математике, потому что математика является «универсальным языком» и учащиеся могут иметь предыдущий образовательный опыт, включающий математические инструкции, это предположение может ввести преподавателей в заблуждение.
Когда я разговаривал с учителями и проводил исследования для этой статьи, стало совершенно ясно, что очень важно убедиться, что учащиеся понимают математический словарь и имеют широкие возможности для его использования. Решение текстовых задач, следование инструкциям, понимание и правильное использование математической лексики — все эти навыки требуют владения языком, которое иногда превосходит наши ожидания. Мы склонны думать о математике как о предмете, который не требует сильного владения языком. В действительности, однако, математическое мышление и решение задач тесно связаны с языком и зависят от твердого понимания базовой математической лексики (Dale & Cuevas, 19).92; Джаррет, 1999).
В действительности, однако, математическое мышление и решение задач тесно связаны с языком и зависят от твердого понимания базовой математической лексики (Dale & Cuevas, 19).92; Джаррет, 1999).
Для многих педагогов задача объединения обучения языку и математике является относительно новой. Учителей ELL, которые ранее не преподавали предметные области, теперь просят вести или поддерживать обучение в классе математики, и многие учителя математики, которые не считают себя инструкторами по языку, теперь несут ответственность за обеспечение эффективного обучения математике для ELL.
Учитель математики средней школы Хиллари Хансен узнала, насколько большую роль играет язык в обучении математике, когда в прошлом году она преподавала свой первый базовый курс математики для ELL. Ей так хотелось дать ученикам хорошую основу, в которой они нуждались, но она чувствовала, что не может достучаться до учеников или вовлечь их в свои уроки, и к концу года она была измотана и расстроена.
Тем летом у нее была возможность присоединиться к когорте округа Sheltered Instruction Observation Protocol (SIOP), чтобы получить профессиональное развитие и поддержку для удовлетворения потребностей ELL в предметных классах. Она узнала о важности овладения языком, накопления фоновых знаний, повышения языковой продуктивности учащихся и явного обучения академическому языку. Она начала этот учебный год с нового набора инструментов и более глубокого понимания учебных пособий, необходимых ELL для изучения содержания, одновременно изучая английский язык. Я рад сообщить, что, хотя Хиллари все еще испытывает трудности и очень усердно работает, этот год был намного более успешным для нее и ее учеников.
В результате более эффективного обучения ее ученики:
- лучше понимают содержание и вместе работают над поиском творческих способов изучения
- больше обсуждают математику и знают, как использовать учебные пособия, которые есть у учителя
- легко разбираются в математике и задают вопросы, чтобы получить необходимую им помощь.

Хиллари считает, что дает им основу, необходимую не только для понимания математических понятий, но и для успешного взаимодействия в математическом классе, чтобы продолжить изучение более сложных понятий.
Ниже приведены некоторые стратегии, которые Хиллари и некоторые другие учителя, с которыми я разговаривал, сочли полезными в этом году и которые они рекомендуют в качестве передового опыта при обучении математике учащихся ELL.
Важность обучения академической лексике
Обучение словарному запасу необходимо для эффективного обучения математике. Он включает не только обучение математическим терминам, таким как «процент» или «десятичный», но также включает понимание разницы между математическим определением слова и другими определениями этого слова.
Следующий пример, использованный в презентации доктором Юдит Мошкович из Калифорнийского университета в Санта-Круз, показывает, почему словарный запас должен быть введен в контексте содержания (Moschkovich, 2008): задача, ученику предлагается «найти x». Студент, очевидно, знал значение слова «найти», потому что он «нашел» его на странице и обвел. Ученик даже оставил на странице заметку, чтобы помочь учителю найти потерянный «x». Студент понял значение слова «найти» в одном контексте, но не в соответствующем математическом контексте.
Студент, очевидно, знал значение слова «найти», потому что он «нашел» его на странице и обвел. Ученик даже оставил на странице заметку, чтобы помочь учителю найти потерянный «x». Студент понял значение слова «найти» в одном контексте, но не в соответствующем математическом контексте.
Недавно я помогал учителю математики провести урок в защищенном помещении и с удивлением обнаружил, что в нем есть слова, которые я не понимаю. Мое незнание слов мешало мне решить математическую задачу и дало мне более глубокое сочувствие к ELL, которые так же борются со словарным запасом и пониманием математических заданий. Ниже приведен список советов по явному преподаванию математической академической лексики:
- Продемонстрируйте, что лексика может иметь несколько значений. Помогите учащимся понять различные значения таких слов, как «стол» и «четверть», а также как правильно их использовать в математическом контексте.
- Поощряйте студентов предлагать двуязычную поддержку друг другу.
 Учащиеся лучше поймут материал, если объяснят его другому учащемуся, а новому учащемуся будет полезно услышать объяснение на своем родном языке. (Проверьте горячие ссылки для получения списка двуязычных переводов математической лексики на нескольких языках).
Учащиеся лучше поймут материал, если объяснят его другому учащемуся, а новому учащемуся будет полезно услышать объяснение на своем родном языке. (Проверьте горячие ссылки для получения списка двуязычных переводов математической лексики на нескольких языках). - Визуальные подсказки, графические представления, жесты, реалии и изображения. Предложите учащимся поработать с объектами и изображениями, чтобы расширить словарный запас. Если предметов недостаточно для каждого учащегося, используйте манипулятивные изображения на надписях или развесьте по всему классу и продемонстрируйте словарный запас перед учащимися. Например, Хиллари создала стену математических слов, состоящую из трех частей: ключевой словарь, определения «своими словами» и различные способы изображения функции. Например, умножение обозначается следующими символами: x, * и ( ).
- Определите ключевые фразы или новый словарный запас для предварительного обучения. Эта стратегия поможет учащимся решить, какую математическую функцию им следует применить.
 Пример: «больше чем» означает «добавить». (См. горячие ссылки для получения дополнительных ссылок на математический словарь.)
Пример: «больше чем» означает «добавить». (См. горячие ссылки для получения дополнительных ссылок на математический словарь.)
Важность чтения и понимания письменных математических задач
Письменные задачи представляют собой уникальную проблему как для учащихся ELL, так и для учителей. В книге «Чтение и понимание письменных математических задач» Бренда Крик-Моралес пишет: «Задачи со словами в математике часто представляют собой проблему, потому что они требуют, чтобы учащиеся прочитали и поняли текст задачи, определили вопрос, на который нужно ответить, и, наконец, создали и решить числовое уравнение — ELL, которые получили формальное образование в своих странах, как правило, не имеют математических трудностей; следовательно, их трудности начинаются, когда они сталкиваются со словесными задачами на втором языке, которым они еще не овладели» (Бернардо, 2005).
Учительница Сяо-линь Инь-Крофт столкнулась с этим явлением в классе двуязычных китайских учеников в Сан-Франциско. Она разработала очень творческий способ использования базовых знаний своих учеников по математике в качестве трамплина для изучения других языков. Она делает это, ускоряя обучение математике в начале учебного года, а затем опираясь на то, что учащиеся изучили по математике в чтении и других предметных областях. В статье «Наведение мостов для будущего» в Colorín Colorado «От всего сердца» Сяо-линь объясняет свою стратегию:
Она разработала очень творческий способ использования базовых знаний своих учеников по математике в качестве трамплина для изучения других языков. Она делает это, ускоряя обучение математике в начале учебного года, а затем опираясь на то, что учащиеся изучили по математике в чтении и других предметных областях. В статье «Наведение мостов для будущего» в Colorín Colorado «От всего сердца» Сяо-линь объясняет свою стратегию:
Сначала мы читаем математические задачи; Я демонстрирую процесс логического мышления при переводе слов в картинки и, наконец, в числовые предложения. Вскоре они начинают объяснять свои мысли после прочтения сложных словесных задач, включающих несколько шагов. Они поправляют друг друга и спорят о том, какие числовые предложения им следует использовать, чтобы получить правильные окончательные результаты. По мере того как они оттачивают свои математические навыки, я использую их энтузиазм, чтобы научить их извлекать самую важную информацию из текстов и продвигать их к устной речи и беглости чтения, которые им необходимы для понимания и обсуждения более сложных текстов.
Даже если вы не ускоряете обучение математике, существует ряд способов помочь учащимся справиться со словесными задачами. Крик-Моралес предлагает предложения в ранее упомянутой статье, такие как подробное обучение ключевой лексике, ежедневная практика решения проблем, многократное чтение слова «проблема» вместе всем классом и практические действия, такие как движение, эксперименты или рисование для помочь учащимся понять проблему. По мере того, как учащиеся лучше знакомятся с математической лексикой, им будет легче решать задачи.
Важность накопления базовых знаний
Как напоминает нам вступительная цитата из стихотворения Шела Сильверстайна, базовые знания играют решающую роль на уроках математики! Моя коллега Хиллари обнаружила, что иногда ее ученики «терялись» в задаче просто потому, что не понимали контекста. Ниже приведены некоторые советы, которые помогут в формировании фоновых знаний учащихся.
- Изменить лингвистическую сложность языка и перефразировать математические задачи.
 Учащиеся лучше поймут задачу, если она будет изложена более короткими предложениями и на понятном им языке.
Учащиеся лучше поймут задачу, если она будет изложена более короткими предложениями и на понятном им языке. - Помогите учащимся вычеркнуть ненужную лексику в текстовых задачах. Это позволяет учащимся сосредоточиться на необходимой математической функции. Например, одна проблема, с которой столкнулись ученики Хиллари, относилась к «школьному собранию». Несмотря на то, что значение этой фразы не имело значения при решении математической задачи, ученики не знали, что это неважно, и непонимание способствовало их замешательству.
- Получите знания на примерах из реального мира. Постарайтесь закрепить концепции примерами, которые учащиеся могут изобразить и рассказать учащимся в ситуации. Например, если вам нужно покрасить комнату, вам нужно знать, какая площадь будет покрыта, чтобы знать, сколько краски нужно купить. Ищите знакомые идеи или реквизиты, которые можно использовать для привлечения учащихся, такие как рецепты, новости об экономике или обсуждение личных привычек в отношении расходов.

- Целенаправленно используйте манипуляторы. Это важно на всех уровнях обучения. Хиллари обнаружила, что математические кубики очень полезны, когда учащиеся представляют числа в задачах, а затем манипулируют кубиками, чтобы получить ответ. Она использовала кубики и термины «горячие» и «холодные» числа при обучении концепции отрицательных чисел. Студенты использовали красные кубики как «горячие» или положительные числа, а синие кубики как «холодные» или отрицательные числа. Когда учащиеся раскладывали количество представленных горячих и холодных кубиков, они могли легко увидеть, будет ли ответ положительным или отрицательным числом, в зависимости от того, какой цвет имеет наибольшее количество кубиков. Такая задача, как -2 + 1 = -1, будет выглядеть так: затем учащийся убирает пары кубиков — один красный, один синий — до тех пор, пока он больше не сможет удалять блоки. Остальные блоки представляют собой ответ.
Важность повышения языковой продуктивности учащихся в предметной области
Когда я работал с учителями предметной области в моем округе над разработкой уроков и мероприятий Shelted Instruction для улучшения обучения ELL, я сказал им: «Если учащийся не говорят этого в вашем классе, они никогда этого не скажут». Это немного драматично, но в какой-то степени это правда. Когда учащиеся изучают новую лексику, возможность ее использования должна быть предоставлена в классе, потому что учащиеся вряд ли будут пробовать ее самостоятельно — особенно такие академические слова, как «параллелограмм» или «функция»!
Это немного драматично, но в какой-то степени это правда. Когда учащиеся изучают новую лексику, возможность ее использования должна быть предоставлена в классе, потому что учащиеся вряд ли будут пробовать ее самостоятельно — особенно такие академические слова, как «параллелограмм» или «функция»!
Вот несколько советов, как улучшить взаимодействие между учащимися с помощью академического языка в классе математики:
- Попросите учащихся перевести символы в слова и написать предложение. Хиллари использовала эту стратегию, чтобы проверить понимание учениками задач перед их решением. Например, 3x + 4 = 16 будет записано: «Три раза X плюс четыре равно шестнадцати». Это помогает учащимся обработать операции, связанные с вопросом, и дает им возможность продумать, как его решить. Это также дает учащимся возможность ознакомиться с важными словарными словами.
- Создайте «рамку предложения» и разместите ее на доске. Напишите формат предложения, который вы хотели бы, чтобы учащиеся использовали в обсуждении, а затем привлеките их к ответственности за его использование.
 Например, «Ответ равен _______ градусам, потому что это треугольник _________».
Например, «Ответ равен _______ градусам, потому что это треугольник _________». - Предложите учащимся поделиться стратегиями решения задач. Это включает в себя простой вопрос, например: «Кто-нибудь еще получил ответ другим способом?» Затем дайте учащимся достаточно времени для ожидания, чтобы они могли обдумать, чем их процесс решения задач был похож или отличался от предложенного.0010
- Позвольте учащимся обсудить, что они думают о математике. Это способ перенаправить урок от учителя к ученику и от ученика к ученику. Например, студент может задать вопрос: «Откуда вы знаете, что это за треугольник?» Вместо того, чтобы учитель отвечал и подходил к доске, указывая имена и разные треугольники, учитель может просто спросить: «У кого-нибудь есть ответ? подумайте о математической концепции и любых советах, которые они могут дать для запоминания информации.
- Включите занятия по письму, такие как математические журналы. Это отличный способ для студентов осмыслить то, что они узнали, и какие вопросы у них остались.
 Дневник можно начать с простых подсказок, таких как: «Одна вещь, которую я сегодня узнал…» «Одна вещь, которую я до сих пор не понимаю…» «Один из способов получить необходимую мне помощь…» «Ответ на эту проблему таков: …» Написание ответа на задачу — очень важный навык, который нужно развивать, потому что многие тесты штата по математике требуют сконструированного ответа на вопросы.
Дневник можно начать с простых подсказок, таких как: «Одна вещь, которую я сегодня узнал…» «Одна вещь, которую я до сих пор не понимаю…» «Один из способов получить необходимую мне помощь…» «Ответ на эту проблему таков: …» Написание ответа на задачу — очень важный навык, который нужно развивать, потому что многие тесты штата по математике требуют сконструированного ответа на вопросы. - Предложите учащимся создать свои собственные математические задачи. Это может быть увлекательным занятием, если учащиеся создают задачу, аналогичную той, которую вы использовали в классе, и обмениваются задачами с партнером. Создавая проблему и проверяя ответ, они укрепляют собственное обучение.
Использование технологий
Технологии также могут быть мощным инструментом обучения математике для ELL. Вот несколько идей, как можно поиграть с технологиями на уроке математики:
- Ищите образовательные ресурсы, которые сопровождают технологические инструменты и программы вашей школы.
 Для учителей могут быть доступны онлайновые или программные программы. Для учителей, у которых в классе есть электронная доска, есть много ресурсов, доступных по ссылкам, к которым можно легко получить доступ и принести в класс.
Для учителей могут быть доступны онлайновые или программные программы. Для учителей, у которых в классе есть электронная доска, есть много ресурсов, доступных по ссылкам, к которым можно легко получить доступ и принести в класс. - Ищите интерактивные игры, которые дают учащимся возможность практиковать свои математические навыки. На Nintendo DS есть образовательная игра Brain Age, которая не зависит от языка. Игра обеспечивает отличную математическую подготовку для чисел и отслеживает результаты, показывая прогресс ученика с течением времени.
- Узнайте, что доступно онлайн. Vital NY (Видеопреподавание и обучение для преподавателей штата Нью-Йорк) на сайте Teachers’ Domain предлагает онлайн-библиотеку бесплатных медиа-ресурсов от лучших представителей общественного телевидения. Ресурсы домена учителей включают в себя видео- и аудиосегменты, интерактивные Flash-материалы, изображения, документы, планы уроков для учителей и мероприятия, ориентированные на учащихся.
 (Требуется бесплатная регистрация.)
(Требуется бесплатная регистрация.) - Если учащиеся используют графический калькулятор, убедитесь, что они научились им пользоваться. В зависимости от фона и предшествующего образовательного опыта учащиеся могут не знать, как пользоваться калькулятором, а также с некоторыми более сложными моделями, например, с графическим калькулятором. Дайте учащимся возможность попрактиковаться в решении задач на своих калькуляторах после того, как вы ознакомитесь с различными функциями. Texas Instruments предлагает многочисленные занятия и руководства по продуктам в своих учебных материалах.
Даже если поначалу это дается нелегко, есть способы заинтересовать ELL математикой. Учитывая их языковые навыки и потребности при планировании обучения математике (и помогая своим коллегам делать то же самое), вы сделаете важные шаги, помогая учащимся овладеть математическими понятиями и навыками — и кто знает? Ваши ученики могут стать экономистами нового поколения, учеными-ракетчиками и учителями математики, которые только и ждут необходимых им инструментов!
Примечание. Я хотел бы поблагодарить моих коллег из Миннесоты, Хиллари Хансен из старшей школы Бернсвилля и Ким Олсон из начальной школы Хидден-Вэлли, а также Сяо-линь Инь-Крофт из Сан-Франциско за предоставление многих полезных советы по обучению математике в этой статье. Вдохновляет знать, что есть талантливые, творческие учителя, которые всегда находят лучшие способы преподавания и готовы делиться знаниями.
Я хотел бы поблагодарить моих коллег из Миннесоты, Хиллари Хансен из старшей школы Бернсвилля и Ким Олсон из начальной школы Хидден-Вэлли, а также Сяо-линь Инь-Крофт из Сан-Франциско за предоставление многих полезных советы по обучению математике в этой статье. Вдохновляет знать, что есть талантливые, творческие учителя, которые всегда находят лучшие способы преподавания и готовы делиться знаниями.
Common Core Math и ELL: сообщения в блоге
Эти сообщения из нашего блога Common Core освещают ресурсы, которые можно использовать в обучении математике Common Core для ELL.
EngageNY: Common Core and Math
Веб-сайт EngageNY содержит материалы, посвященные примерам учебных программ, стандартам математической практики и другим материалам для профессионального развития.
Discovery Education: Puzzlemaker
Puzzlemaker — это бесплатный инструмент для создания головоломок для учителей, учащихся и родителей, в котором пользователи могут создавать и распечатывать индивидуальные головоломки с поиском слов, крест-накрест, математические головоломки и многое другое, используя свои собственные списки слов.
Кэтрин Сноу: Word Generation
Новый веб-сайт Кэтрин Сноу предоставляет информацию и ресурсы для преподавателей, которые хотели бы узнать больше о программе Word Generation и о том, как она реализована. Включает ссылки на исчерпывающий список академических слов, которые учащиеся должны освоить, чтобы понять учебный контент.
Math Tables Dave’s Math Tables: English/Spanish Dictionary
Список слов английского математического словаря с испанским эквивалентом.
Учителя PBS: уроки математики
Учителя PBS предлагают базу данных мультимедийных уроков математики и заданий, которые можно искать по классам или темам.
Учебные занятия SMART Notebook
Просматривайте учебные занятия и материалы для классов с помощью программного обеспечения SMART Notebook. Выберите страну или регион и выполните поиск по стандартам учебной программы, предмету и уровню класса.
Colorín Colorado Веб-трансляция: Изучающие английский язык в средних и старших классах
В этой веб-трансляции с участием доктора Деборы Шорт обсуждаются эффективные учебные стратегии для обучения учащихся, изучающих английский язык в средних и старших классах, такие как модель SIOP.
Перевод текстовых задач
Это отличный сайт для учителей начальных классов, так как он содержит список ключевых слов, по которым вы можете научить своих ELL искать их при чтении текстовых задач. Также включены полезные идеи и приемы, чтобы лучше подготовить учащихся к пониманию письменных математических задач.
Ссылки
Бернардо, А. И., (2005). Язык и моделирование словесных задач по математике среди билингвов. Журнал психологии, 139 (5), 413-425.
Дейл, Т.С. и Куэвас, Г.Дж. (1992). Интеграция математики и изучения языка. В П. А. Ричард-Амато и М. А. Сноу (ред.), Мультикультурный класс: материалы для чтения для учителей предметной области. Уайт-Плейнс, Нью-Йорк: Longman, Inc.
Джаррет, Д. (1999). Инклюзивный класс: преподавание математики и естественных наук изучающим английский язык — это просто хорошее преподавание. Портленд: Северо-западная региональная образовательная лаборатория. Получено 8 марта 2009 г. с http://nwrel.org/msec/just_good/8/9.0027
с http://nwrel.org/msec/just_good/8/9.0027
Мошкович, Дж. Н. (2008 г., декабрь). Помимо слов: язык(и) и обучение математике. Презентация на декабрьском семинаре Математической инициативы Силиконовой долины, Фремонт, Калифорния. Презентация PowerPoint получена 8 марта 2009 г. с сайта www.noycefdn.org/math/documents/MoschkovichPILmtg120308.ppt
Репринты
Вы можете распечатывать копии или переиздавать материалы для некоммерческого использования при условии указания авторства Colorín Colorado. и автор(ы). Для коммерческого использования, пожалуйста, свяжитесь с [email protected].
Другие материалы этого автора
- 20 стратегий для руководителей школ
- Удовлетворение потребностей учащихся ELL в изучении языка и специальном образовании: вопросы и соображения
- Контрольный список для учителя ELL перед поступлением в школу
- Двуязычный семейный вечер для ELL Семьи
- Передача важной информации семьям ELL: стратегии достижения успеха
- Связь с семьями ELL: стратегии достижения успеха
- Создание плана действий для вовлечения семьи ELL
- Дистанционное обучение для ELL: проблемы и возможности
- Дистанционное обучение для ELL: уроки семейного партнерства
- Дистанционное обучение для ELL: инструкция по планированию
- Стратегии дистанционного обучения для ELL: что нужно знать
- Eight English Learner Мифы для администраторов
- ELL в дошкольном образовании: набор семей иммигрантов
- Поощрение и поддержка участия родителей ELL
- Привлечение семей ELL посредством партнерства с местным населением
- Привлечение родителей ELL в качестве лидеров
- Основные действия: 15 исследовательских практик для повышения успеваемости ELL учащих Год!
- Подготовка к колледжу: что нужно знать учащимся ELL
- Как соединить базовые знания ELL с содержанием
- Как поддержать учащихся ELL с прерванным формальным образованием (SIFE)
- Как поддержать учащихся-беженцев в вашем школьном сообществе
- Улучшение навыков письма: ELL и удовольствие от письма
- Расширение взаимодействия учащихся с помощью «Думай, пари, делись» и «Круговые чаты»
- Повышение академического уровня владения английским языком Успех учащегося
- Повышение уровня понимания прочитанного учащимися ELL с помощью документального текста
- Введение: стратегии вовлечения семей ELL
- Овладение языком: обзор
- Мотивация читателей ELL
- Изучение музыки и языка
- Ни один ребенок не останется без внимания и оценка учащихся, изучающих английский язык
- Обучение фонетике для учащихся ELL средних и старших классов
- Подготовка увлекательного урока обществознания для изучающих английский язык 9001 0
- Подготовка ELL будут учащимися 21-го века
- Театр чтения: обогащение устной речи и развитие грамотности для ELL
- Reading 101 для изучающих английский язык
- Успешные экскурсии с учащимися, изучающими английский язык
- Успешные встречи родителей и учителей с двуязычными семьями
- Летнее чтение: изучающие английский язык в библиотеке
- Поддержка ELL в обычном классе: 12 стратегий обучения языку
- Tal Эс четвертого Падение успеваемости: как помочь учащимся ELL достичь успеха
- Преподавание и чтение стихов с учащимися, изучающими английский язык
- Советы по проведению успешных родительских собраний с учителями в двуязычных семьях
- Двенадцать вещей, которые учителя могут сделать, чтобы поддержать успех ELL в Новом году
- Стратегии визуального мышления для улучшения понимания
- Написание победившего эссе
- Письменные стихи с изучающими английский язык
Федерация учителей, AFL-CIO.
При щедрой поддержке Национальной ассоциации образования.
РЕКЛАМА
Самые популярные
10 Стратегии построения отношений с ELL
Обучение праздникам и религиозным праздникам с учетом культурных особенностей
Языковые задачи: ключ к эффективному обучению предметной области для изучающих английский язык
900 03Поддержка ELL в основном классе: 12 Стратегии обучения языку
Твиты @ColorinColorado


 Учащиеся лучше поймут материал, если объяснят его другому учащемуся, а новому учащемуся будет полезно услышать объяснение на своем родном языке. (Проверьте горячие ссылки для получения списка двуязычных переводов математической лексики на нескольких языках).
Учащиеся лучше поймут материал, если объяснят его другому учащемуся, а новому учащемуся будет полезно услышать объяснение на своем родном языке. (Проверьте горячие ссылки для получения списка двуязычных переводов математической лексики на нескольких языках). Пример: «больше чем» означает «добавить». (См. горячие ссылки для получения дополнительных ссылок на математический словарь.)
Пример: «больше чем» означает «добавить». (См. горячие ссылки для получения дополнительных ссылок на математический словарь.)
 Учащиеся лучше поймут задачу, если она будет изложена более короткими предложениями и на понятном им языке.
Учащиеся лучше поймут задачу, если она будет изложена более короткими предложениями и на понятном им языке.
 Например, «Ответ равен _______ градусам, потому что это треугольник _________».
Например, «Ответ равен _______ градусам, потому что это треугольник _________». Дневник можно начать с простых подсказок, таких как: «Одна вещь, которую я сегодня узнал…» «Одна вещь, которую я до сих пор не понимаю…» «Один из способов получить необходимую мне помощь…» «Ответ на эту проблему таков: …» Написание ответа на задачу — очень важный навык, который нужно развивать, потому что многие тесты штата по математике требуют сконструированного ответа на вопросы.
Дневник можно начать с простых подсказок, таких как: «Одна вещь, которую я сегодня узнал…» «Одна вещь, которую я до сих пор не понимаю…» «Один из способов получить необходимую мне помощь…» «Ответ на эту проблему таков: …» Написание ответа на задачу — очень важный навык, который нужно развивать, потому что многие тесты штата по математике требуют сконструированного ответа на вопросы. Для учителей могут быть доступны онлайновые или программные программы. Для учителей, у которых в классе есть электронная доска, есть много ресурсов, доступных по ссылкам, к которым можно легко получить доступ и принести в класс.
Для учителей могут быть доступны онлайновые или программные программы. Для учителей, у которых в классе есть электронная доска, есть много ресурсов, доступных по ссылкам, к которым можно легко получить доступ и принести в класс. (Требуется бесплатная регистрация.)
(Требуется бесплатная регистрация.)





 Примечание. Слова допустимы, но не обязательны.
Примечание. Слова допустимы, но не обязательны. 

Leave A Comment