Формулы математика для егэ: школьные формулы по алгебре и геометрии

Формулы к ЕГЭ по математике

Полный сборник красиво оформленных школьных формул по алгебре и геометрии.

В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.

Смотреть в PDF: Скачайте pdf файл.

Можете записаться на занятия к репетитору математики, если что-то не понятно.

По разделам:

Степени и корни:

Сокращенное умножение:

Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители:

Логарифмы:

Формулы тригонометрии, тождества:

Тригонометрические уравнения:

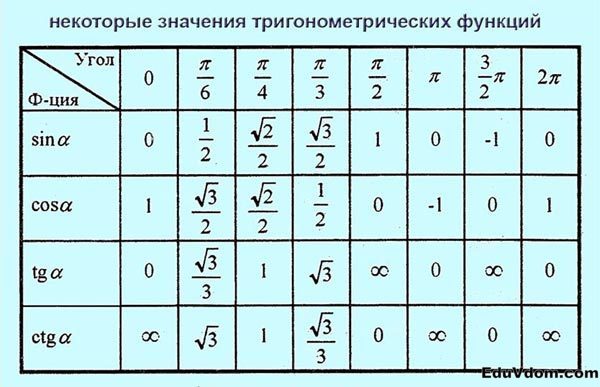
Значения тригонометрических функций:

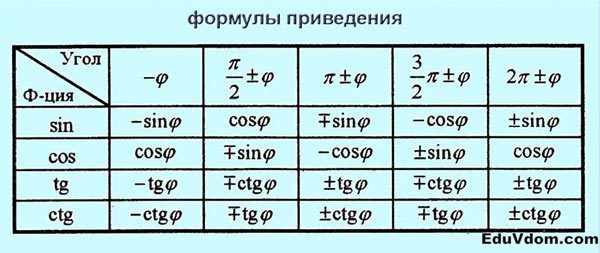
Формулы приведения:

Сумма и разность углов:

Формулы двойного и тройного аргумента:

Формулы половинного аргумента:

Сумма и разность тригонометрических функций:

Произведение тригонометрических функций:

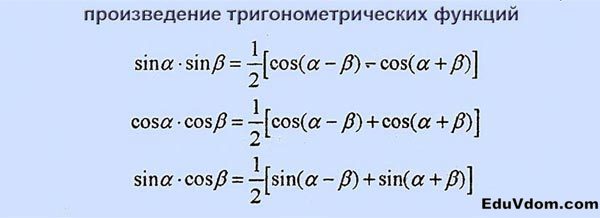
Производная: признаки возрастания, убывания, минимума функции:

Дифференциальное исчисление:

Геометрия: формулы площадей. Прямоугольники, окружности, трапеции:

Стереометрия: объёмы, площади поверхностей:

Обратиться к репетитору по математике.

Теория, пособие для подготовки к ЕГЭ по математике

Факт 1.
$\bullet$ Множество натуральных чисел $\mathbb{N}$ – это числа $1, \ 2, \ 3, \ 4 \ $ и т.д.
$\bullet$ Множество целых чисел $\mathbb{Z}$ состоит из натуральных чисел, противоположных им ($-1, \ -2, \ -3 $ и т.д.) и нуля $0$.
$\bullet$ Рациональные числа $\mathbb{Q}$ – числа вида $\dfrac ab$, где $a\in \mathbb{Z}$, $b\in \mathbb{N}$. Таким образом, существует включение: $\mathbb{N}$ содержится в $\mathbb{Z}$, а $\mathbb{Z}$ содержится в $\mathbb{Q}$.

Факт 2.
$\bullet$ Правила сложения дробей: \[\begin{aligned} &\dfrac ab+\dfrac cb=\dfrac{a+c}b\\[2ex] &\dfrac ab+\dfrac cd=\dfrac{ad+bc}{bd}\end{aligned}\] Пример: $\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6$ $\bullet$ Правила умножения дробей: \[\dfrac ab\cdot \dfrac cd=\dfrac{ac}{bd}\] Пример: $\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}$ $\bullet$ Правила деления дробей: \[\dfrac ab: \dfrac cd=\dfrac ab\cdot \dfrac dc\] Пример: $\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76$

Факт 2.
$\bullet$ Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример: $\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot 2\llap{/}}{3\cdot 2\llap{/}}=\dfrac{49}3\\[2ex] &\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot 7\llap{/}}{7\llap{/}\cdot 5}=\dfrac 85\\[2ex] &\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot 3\cdot 2\llap{/}}=\dfrac{14}{15}\end{aligned}$ $\bullet$ Если $\dfrac ab$ – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель $b$ делится только на числа $2$ и $5$.

Пример: дробь $\dfrac2{65}$ нельзя представить в виде конечной десятичной дроби, так как $65=5\cdot 13$, то есть $\dfrac2{65}=0,0307…$
дробь $\dfrac3{160}$ можно представить в виде конечной десятичной дроби, так как $160=2^5\cdot 5$, то есть $\dfrac3{160}=0,01875$.

Факт 3.
$\bullet$ Формулы сокращенного умножения:
$\blacktriangleright$ Квадрат суммы и квадрат разности: \[(a+b)^2=a^2+2ab+b^2\] \[(a-b)^2=a^2-2ab+b^2\]

$\blacktriangleright$ Куб суммы и куб разности: \[(a+b)^3=a^3+3a^2b+3ab^2+b^3\quad {\small{\text{или}}}\quad (a+b)^3=a^3+b^3+3ab(a+b)\] \[(a-b)^3=a^3-3a^2b+3ab^2-b^3\quad {\small{\text{или}}}\quad (a-b)^3=a^3-b^3-3ab(a-b)\]

Заметим, что применение данных формул справа налево часто помогает упростить вычисления:
$13^3+3\cdot 13^2\cdot 7+3\cdot 13\cdot 49+7^3=(13+7)^3=20^3=8000$

$\blacktriangleright$ Разность квадратов: \[a^2-b^2=(a-b)(a+b)\]

$\blacktriangleright$ Сумма кубов и разность кубов: \[a^3+b^3=(a+b)(a^2-ab+b^2)\] \[a^3-b^3=(a-b)(a^2+ab+b^2)\]

Заметим, что не существует формулы суммы квадратов $a^2+b^2$.
Заметим, что применение данных формул слева направо часто помогает упростить вычисления:

$\dfrac{7^6-2^6}{7^4+14^2+16}= \dfrac{(7^2-2^2)(7^4+7^2\cdot2^2+2^4)} {7^4+(7\cdot2)^2+2^4}=7^2-2^2=45$

Факт 4.
$\bullet$ Квадрат суммы нескольких слагаемых равен сумме квадратов этих слагаемых и удвоенных попарных произведений: \[\begin{aligned} &(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc\\[2ex] &(a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd\\[2ex] &{\small{\text{и т.д.}}}\end{aligned}\]

Справочные материалы ЕГЭ по математике / Блог :: Бингоскул

Для подготовки к ЕГЭ по математике базового и профильного уровней ФИПИ добавил в демоверсию справочные материалы. Ниже рассмотрим:

справочные материалы к базовому уровню;
справочные материалы к профильному уровню.

Справочные материалы к базовому уровню

Алгебра

Таблица квадратов целых чисел от 0 до 99

Свойства арифметического квадратного корня

\sqrt{ab}=\sqrt{a} \cdot \sqrt{b} при a \ge0, b \ge 0

\sqrt\frac{a}{b}=\frac {\sqrt{a}}{\sqrt{b}} при a \ge0, b > 0

Корни квадратного уравнения

ax^2+bx+c=0, a \not = 0

x_1= \frac{-b-\sqrt{b^2-4ac}}{2a}, x_2= \frac{-b+\sqrt{b^2-4ac}}{2a} при b^2-4ac > 0

x=- \frac{b}{2a} при b^2-4ac = 0

Формулы сокращённого умножения

(a + b)^2= a^2 + 2ab + b^2
(a — b)^2= a^2 — 2ab + b^2
a^2 — b^2 = (a + b)(a — b)

Степень и логарифм

Свойства степени

Свойства логарифма

при a>0, b>0

a^{-n}=\frac{1}{a^n}
a^n \cdot a^m=a^{n+m}
\frac{a^n}{a^m}=a^{n-m}
(a^n)^m=a^{nm}
(ab)^n=a^n \cdot b^n
(\frac{a}{b})^n=\frac{a^n}{b^n}

при a>0, a \not =1, b>0, x>0, y>0

a^{\log_{a}b} = b
\log_{a}a=1
\log_{a}1=0
\log_{a}(xy) =\log_{a}x + \log_{a}y
\log_{a}(\frac{x}{y}) =\log_{a}x- \log_{a}y
\log_{a}b^k = k*\log_{a}b

Геометрия

Площади фигур

Площади поверхностей и объёмы тел

Тригонометрические функции

Основное тригонометрическое тождество:

sin²a + cos²a = 1

Функции

Справочные материалы к профильному уровню

sin² α + cos² α = 1
sin 2α = 2sinα * cosα
cos2α = cos²α — sin²α
sin (α + β) = sinα *cosβ + cosα *sinβ
cos (α + β) = cosα * cosβ — sinα * sinβ

Смотри также:

Решай:

Математические формулы по алгебре и геометрии для ЕГЭ

Как выучить все формулы по математике к ЕГЭ

Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.

Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.

Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.

Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.

Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.

Математические формулы школьного курса алгебры

Степени и корни

Формулы сокращенного умножения

Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители

Логарифмические формулы

Формулы тригонометрии

Основные формулы тригонометрии

Тригонометрические уравнения

Значения тригонометрических функций

Формулы приведения

Сумма и разность углов

Формулы двойного и тройного аргумента

Формулы половинного аргумента

Сумма и разность тригонометрических функций

Произведение тригонометрических функций

Формулы дифференциального исчисления

Формулы векторной алгебры из школьного курса математики

Формулы арифметической и геометрической прогрессии

Геометрические формулы школьного курса математики для ЕГЭ

Планиметрия

Стереометрия

Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ. Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.

Учите формулы по математике и сдавайте ЕГЭ на максимальные баллы!

Основные формулы для подготовки к ЕГЭ по математике

Формулы дифференцирования

Правила дифференцирования

Таблица некоторых значений тригонометрических функций

Таблица первообразных и интегралов

Таблица степеней чисел

Законы степеней чисел:

Свойства корня n-ой степени

Координаты точек

Формулы приведения

Формулы сокращённого умножения:

Применение производной:

Прогрессии:

Вернуться в меню выбора предмета

Какие математические формулы запоминать не стоит

Вы считаете, что чем больше формул знаете, тем спокойнее на экзамене? Так-то оно так, но в случае, если вы дейтвительно понимаете суть формул.

Но если вы коллекционируете формулы, не особо разбираясь в них, не видя связей, следствий, то вряд ли это вас спасет…

Давайте вот прямо сейчас выкинем ряд «лишних» формул из ваших шпаргалок!

Выкидываем из шпаргалки формулу площади правильного треугольника

Наверняка в вашей коллекции есть формула площади правильного треугольника $S=\frac{a^2\sqrt3}{4}.$ Если вы ее знаете, – рада за вас, если нет, – давайте поймем как ее в два счета вывести.

Вы обязаны знать формулу площади $S=\frac{1}{2}absin\gamma$ для треугольника со сторонами $a,\;b$ и углом между ними $\gamma.$

А в правильном треугольнике a=b и $sin\gamma=sin60^{\circ}=\frac{\sqrt3}{2}.$ Вот и получаем требуемую формулу: $S=\frac{a^2\sqrt3}{4}.$

Много времени занял вывод формулы?

Выкидываем из шпаргалки формулу площади сектора

$S_{sektor}=\frac{\alpha \pi R^2}{360^{\circ}}$

Составим пропорцию

Площадь сектора в $360^{\circ}$ (круга) – $\pi R^2$ , какая площадь будет у сектора в $\alpha$ градусов находим через пропорцию. Отсюда сразу и получаем формулу.

А в принципе, она и не нужна вовсе… Просто в каждой конкретной задаче вы составляете свою пропорцию.

Например, нужно решить следующую задачу: –> + показать

Найдите центральный угол сектора круга радиуса $\frac{24}{\sqrt{\pi}}$ , площадь которого равна 96. Ответ дайте в градусах.

Решение:

Составляем пропорцию:

Откуда градусная мера центрального угла сектора – $\frac{360^{\circ}\cdot 96}{24^2}=60^{\circ}.$

Ответ: 60.

Больше задач – смотрите здесь.

Выкидываем пару формул из таблицы производных

Наверняка, в таблице производных у вас есть такие две строки:

Вы знаете формулу $(x^{\alpha})$ , где $\alpha$ – действительное число.

Так разве $\sqrt{x}$ – это не $x^{\frac{1}{2}}$ ?

$(x^{\frac{1}{2}})$

Аналогично $(\frac{1}{x})$

Кстати, + показать

некоторые абитуриенты, встречая задание, например, $(\sqrt[3]{x+2})$ , говорят: “не, нас производную от корней не учили брать…”

Но мы же должны понимать, что

$(\sqrt[3]{x+2})$

Выкидываем из шпаргалки формулу боковой поверхности цилиндра

Формула боковой поверхности цилиндра

$S=2\pi RH$

(где $R,\;H$ – радиус и высота цилиндра соответственно)

вполне может встретиться в задачах ЕГЭ по математике.

Но ведь что есть боковая поверхность цилиндра в развертке?

Это прямоугольник с одной стороной – , второй стороной, равной длине окружности основания, то есть $2\pi R.$

Потому и получаем

$S=2\pi RH.$

Выкидываем теорему Пифагора

Шучу, конечно, – кто не знает теорему Пифагора? Но может быть, вам сложно выучить теорему косинусов? Вы подозревали раньше, что теорема Пифагора – частный случай теоремы косинусов?

$c^2=a^2+b^2-2abcos\gamma$

А ведь в случае прямого угла косинус его будет равен 0, а следовательно, мы и получим теорему Пифагора:

Выкидываем из шпаргалок несколько тригонометрических формул

Не обойтись на ЕГЭ по математике без формул двойного угла для косинуса:

$cos2\alpha=cos^2\alpha-sin^2\alpha$

$cos2\alpha=2cos^2\alpha-1$

$cos2\alpha=1-2sin^2\alpha$

Так вот две последние формулы запоминать нет никакой необходимости. Посмотрите, как быстро выводится, например, средняя формула:

$cos2\alpha=cos^2\alpha-sin^2\alpha=cos^2\alpha-(1-cos^2\alpha)=2cos^2\alpha-1.$

С третьей формулой – аналогично.

Анализируем формулу площади четырехугольника через диагонали

Хорошо бы знать формулу площади четырехугольника с диагоналями $d_1,\;d_2$ и углом между ними $\alpha$ …

$S=\frac{d_1d_2sin\alpha}{2}$

Тогда набор формул

$S=\frac{d^2}{2}$ для квадрата с диагональю ,

$S=\frac{d^2sin\alpha}{2}$ для прямоугольника с диагоналями и углом $\alpha$ между ними,

$S=\frac{d_1d_2}{2}$ для ромба с диагоналями $d_1,\;d_2$

не придется запоминать!

Становится ясно, что это всего лишь частные случаи формулы $S=\frac{d_1d_2sin\alpha}{2}$ (например, в квадрате d_1=d_2 и $\sin\alpha=1$ , так как $\alpha=90^{\circ}$ ).

Рада, если описанные случаи для вас очевидны –> 😉 + показать

89д

Значит, вы хорошо подготовлены к ЕГЭ по математике (по крайней мере, к части В)!

Можно продолжать и далее…

Но пока все! Вам есть что сказать/спросить? Пишите в комментариях.

Формулы тригонометрии. Основные тригонометрические формулы для ЕГЭ

Для того чтобы сдать ЕГЭ по математике, вам понадобится около 20 формул тригонометрии. Это не много. Но их надо знать наизусть!

Вот таблица, в которой собраны основные тригонометрические формулы. Здесь все самое необходимое. Их легко выучить и применять.

Ты нашел то, что искал? Поделись с друзьями!

Кроме того, надо знать определения синуса, косинуса и тангенса, а также значения этих функций для основных углов.

Как же выучить тригонометрические формулы?

1. Учите формулы сразу. Не рассказывайте себе сказки о том, что в последнюю ночь перед ЕГЭ все выучите. Каждый день – один блок, то есть три-четыре формулы из нашей таблицы.

2. Тренируйтесь. Выучить иностранный язык проще всего тому, кто вынужден постоянно на нем говорить. Так и здесь. Для тренировки можно из классического задачника Сканави выбрать 20-50 заданий на преобразование тригонометрических выражений и доказательство тождеств.

3. Универсальный способ: ежедневно, садясь за уроки, берите чистый листок и выписывайте наизусть все тригонометрические формулы, какие помните. Когда всё готово — сверяете. И к экзамену вы будете помнить всё.

4. Еще один отличный способ. Вырежьте из плотной бумаги карточки. На одной пишете левую часть формулы. На другой – правую. Перемешиваете. И собираете. Любые формулы запоминаются легко и быстро!

Список математических формул

Тригонометрические отношения		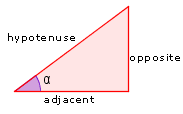sin alpha = (opp.) / (Hip.) `	« opp. »: Напротив « hip. »: Гипотенуза
		`cos alpha = (прил.) / (Бедро)`	`прил .`: смежный ` бедро`: гипотенуза
		`tan alpha = (opp.) / (Прилаг.)`	`opp.`: противоположный ` adj.`: смежный
Фундаментальные тождества	`sin ^ 2 alpha + cos ^ 2 alpha = 1`	` tan alpha = (sin alpha) / (cos alpha) `	` tan ^ 2 alpha + 1 = 1 / (cos ^ 2 альфа) `
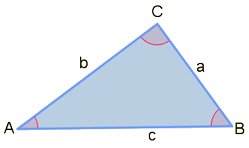		Закон синуса (также известный как правило синуса)	`(sin A) / a = (sin B) / b = (sin C) / c`
		Закон косинусов (также известный как правило косинусов)	`a ^ 2 = b ^ 2 + c ^ 2-2bc cos A`
		Формула Герона	`A = sqrt (s (s-a) (s-b) (s-c))` `s = (a + b + c) / 2`
Точные значения	`sin (pi / 6) = 1 / 2`	` cos (pi / 6) = sqrt (3) / 2`	`tan (pi / 6) = sqrt (3) / 3`
	`sin (pi / 4) = sqrt (2) / 2`	` cos (pi / 4) = sqrt (2) / 2`	`tan (pi / 4) = 1`
	`sin (pi / 3) = sqrt (3) / 2`	` cos (pi / 3) = 1 / 2`	`tan (pi / 3) = sqrt (3)`
Угловые отношения	`sin (-alpha) = — sin alpha`	` cos (- alpha) = cos alpha`	`tan (-alpha) = — tan alpha`
	`sin (pi — alpha) = sin alpha`	` cos (pi — alpha) = — cos alpha`	`tan (pi — alpha) = — tan alpha`
	`sin (pi + alpha) = — sin alpha`	` cos (pi + alpha) = — cos alpha`	`tan (pi + alpha) = tan alpha`
	`sin (pi / 2 — alpha) = cos alpha`	` cos (pi / 2 — alpha) = sin alpha`	`tan (pi / 2 — alpha) = 1 / (tan alpha)`
	`sin (pi / 2 + alpha) = cos alpha`	` cos (pi / 2 + alpha) = — sin alpha`	`tan (pi / 2 + alpha) = — 1 / (tan alpha) `
	`sin ((3pi) / 2 — alpha) = — cos alpha`	` cos ((3pi) / 2 — alpha) = — sin alpha`	`tan ((3pi) / 2 — alpha) = 1 / (тангенциальный альфа) `
	`sin ((3pi) / 2 + alpha) = — cos alpha`	` cos ((3pi) / 2 + alpha) = sin alpha`	`tan ((3pi) / 2 + alpha) = — 1 / (тангенциальный альфа) `
Тригонометрические уравнения	`sin x = sin alpha hArr x = alpha + 2kpi vv x = pi — alpha + 2kpi, k in ZZ`
	`cos x = cos alpha hArr x = alpha + 2kpi vv x = — alpha + 2kpi, k in ZZ`
	`tan x = tan alpha hArr x = alpha + kpi, k в ZZ`
Формулы суммирования	`sin (a + b) = sin a xx cos b + sin b xx cos a`
	`cos (a + b) = cos a xx cos b — sin a xx sin b`
	`tan (a + b) = (tan a + tan b) / (1 — tan a xx tan b)`
Формулы разности	`sin (a-b) = sin a xx cos b — sin b xx cos a`
	`cos (a-b) = cos a xx cos b + sin a xx sin b`
	`tan (a-b) = (tan a — tan b) / (1 + tan a xx tan b)`
Формулы двойного угла	`sin (2a) = 2xxsin a xx cos a`
	`cos (2a) = cos ^ 2 a — sin ^ 2 a`
	`tan (2a) = (2 xx tan a) / (1 — tan ^ 2 a)`

математических формул | Основные математические формулы для классов 6–12 CBSE с файлами PDF

- Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
  BNAT 000 NC
  000 NC Книги
  Книги NCERT для класса 5
  Книги NCERT для класса 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  Книги NCERT для класса 11
  Книги NCERT для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT 9000 9000
  NCERT Exemplar Class
  Решения RS Aggarwal, класс 12
  Решения RS Aggarwal, класс 11
  Решения RS Aggarwal, класс 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  RD Sharma Class 6 Решения
  Решения RD Sharma
  Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Теорема Пифагора
  0004
  000300030004
  9000
  Простые числа
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Деление фракций
  000
  000
  000
  000
  000
  000 Microology
  000
  000 Microology
  000 BIOG3000
  FORMULAS
  Математические формулы
  Алгебраические формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000 PBS4000
  000300030002 Примеры калькуляторов химии
  Класс 6
  Образцы бумаги CBSE для класса 7
  Образцы бумаги CBSE для класса 8
  Образцы бумаги CBSE для класса 9
  Образцы бумаги CBSE для класса 10
  Образцы бумаги CBSE для класса 11
  Образцы бумаги CBSE чел для класса 12
  CBSE Контрольный документ за предыдущий год
  CBSE Контрольный документ за предыдущий год Класс 10
  Контрольный документ за предыдущий год CBSE, класс 12
  HC Verma Solutions
  HC Verma Solutions Class 11 Physics
  Решения HC Verma, класс 12, физика
  Решения Лакмира Сингха
  Решения Лакмира Сингха, класс 9
  Решения Лакмира Сингха, класс 10
  Решения Лакмира Сингха, класс 8
  Заметки CBSE
  CBSE Notes
  Примечания CBSE класса 7
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания CBSE класса 12
  Примечания к редакции CBSE
  Примечания к редакции
  CBSE Class
  Примечания к редакции класса 10 CBSE
  Примечания к редакции класса 11 CBSE 9000 4
  Примечания к редакции класса 12 CBSE
  Дополнительные вопросы CBSE
  Дополнительные вопросы по математике класса 8 CBSE
  Дополнительные вопросы по науке 8 класса CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Дополнительные вопросы по науке класса 9 CBSE
  Дополнительные вопросы по математике для класса 10
  Дополнительные вопросы по науке, класс 10 по CBSE
  CBSE, класс
  , класс 3
  , класс 4
  , класс 5
  , класс 6
  , класс 7
  , класс 8
  , класс 9 Класс 10
  Класс 11
  Класс 12
  Учебные решения
  Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для класса 11 по физике
  Решения NCERT для класса 11 Химия
  Решения для биологии класса 11
  Решения NCERT для математики класса 11
  9 0003 NCERT Solutions Class 11 Accountancy
  NCERT Solutions Class 11 Business Studies
  NCERT Solutions Class 11 Economics
  NCERT Solutions Class 11 Statistics
  NCERT Solutions Class 11 Commerce
  NCERT Solutions For Class 12
  NCERT Solutions For Класс 12 по физике
  Решения NCERT для химии класса 12
  Решения NCERT для класса 12 по биологии
  Решения NCERT для класса 12 по математике
  Решения NCERT Класс 12 Бухгалтерия
  Решения NCERT, класс 12, бизнес-исследования
  Решения NCERT, класс 12 Экономика
  NCERT Solutions Class 12 Accountancy Part 1
  NCERT Solutions Class 12 Accountancy Part 2
  NCERT Solutions Class 12 Micro-Economics
  NCERT Solutions Class 12 Commerce
  NCERT Solutions Class 12 Macro-Economics
  NCERT Solutions For Класс 4
  Решения NCERT для математики класса 4
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для математики класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для математики класса 6
  Решения NCERT для науки класса 6
  Решения NCERT для социальных наук класса 6
  Решения NCERT для класса 6 Английский
  Решения NCERT для класса 7
  Решения NCERT для класса 7 Математика
  Решения NCERT для класса 7 Наука
  Решения NCERT для класса 7 по социальным наукам
  Решения NCERT для класса 7 Английский
  Решения NCERT для класса 8
  Решения NCERT для класса 8 Математика
  Решения NCERT для класса 8 Science
  Решения NCERT для социальных наук 8 класса
  Решение NCERT ns для класса 8 Английский
  Решения NCERT для класса 9
  Решения NCERT для социальных наук класса 9
  Решения NCERT для математики класса 9
  Решения NCERT для математики класса 9 Глава 1
  Решения NCERT для Математика класса 9 Глава 2
  Решения NCERT для математики класса 9 Глава 3
  Решения NCERT для математики класса 9 Глава 4
  Решения NCERT
  для математики класса 9 Глава 5
  Решения NCERT для математики класса 9 Глава 6
  Решения NCERT для Математика класса 9 Глава 7
  Решения NCERT для математики класса 9 Глава 8
  Решения NCERT
  для математики класса 9 Глава 9
  Решения NCERT
  для математики класса 9 Глава 10
  Решения NCERT для математики класса 9 Глава 11
  Решения NCERT для Математика класса 9 Глава 12
  Решения NCERT для математики класса 9 Глава 13
  Решения
  NCERT для математики класса 9 Глава 14
  Решения NCERT для математики класса 9 Глава 15
  Решения NCERT для науки класса 9
  Решения NCERT для науки класса 9 Глава 1
  Решения NCERT для науки класса 9 Глава 2
  Решения NCERT для класса 9 Наука Глава 3
  Решения NCERT для Науки Класса 9 Глава 4
  Решения NCERT для Науки Класса 9 Глава 5
  
  Решения NCERT для Науки Класса 9 Глава 6
  Решения NCERT для Науки Класса 9 Глава 7
  Решения NCERT для Класса 9 Наука Глава 8
  Решения NCERT для Науки Класса 9 Глава 9
  Решения NCERT для Науки Класса 9 Глава 10
  Решения NCERT для Науки Класса 9 Глава 12
  Решения NCERT для Науки Класса 9 Глава 11
  Решения NCERT для Класса 9 Наука Глава 13
  Решения NCERT для класса 9 Наука Глава 14
  Решения NCERT для класса 9 по науке Глава 15
  Решения NCERT для класса 10
  Решения NCERT для класса 10 по социальным наукам
  Решения NCERT для математики класса 10
  
  Решения NCERT для математики класса 10 Глава 1
  Решения NCERT для математики класса 10 Глава 2
  Решения NCERT для математики класса 10 Глава 3
  Решения NCERT для математики класса 10 Глава 4
  Решения NCERT для математики класса 10 Глава 5
  Решения NCERT для математики класса 10 Глава 6
  Решения NCERT для математики класса 10 Глава 7
  Решения NCERT для математики класса 10 Глава 8
  Решения NCERT для математики класса 10 Глава 9
  Решения NCERT
  для математики класса 10 Глава 10
  Решения
  NCERT для математики класса 10 Глава 11
  Решения NCERT для математики класса 10 Глава 12
  
  Решения NCERT для математики класса 10 Глава 13
  NCERT Sol Решения NCERT для математики класса 10 Глава 14
  Решения NCERT для математики класса 10 Глава 15
  Решения NCERT для науки класса 10
  Решения NCERT для науки класса 10 Глава 1
  Решения NCERT для науки класса 10 Глава 2
  Решения NCERT для науки класса 10, глава 3
  Решения NCERT для науки класса 10, глава 4
  Решения NCERT для науки класса 10, глава 5
  Решения NCERT для науки класса 10, глава 6
  Решения NCERT для науки класса 10, глава 7
  Решения NCERT для науки 10 класса, глава 8
  Решения NCERT для науки класса 10 Глава 9
  
  Решения NCERT для науки класса 10 Глава 10
  Решения NCERT для науки класса 10 Глава 11
  Решения NCERT для науки класса 10 Глава 12
  Решения NCERT для науки 10 класса Глава 13
  Решения NCERT для науки 10 класса Глава 14
  Решения NCERT для науки класса 10 Глава 15
  Решения NCERT
  для науки класса 10 Глава 16
  Учебный план NCERT
  NCERT
  Commerce
  Class 11 Commerce Syllabus
  ancy Account
  Учебный план по бизнесу, класс 11
  Учебный план по экономике, класс 11
  Учебный план по коммерции, класс 12
  Учебный план по бухгалтерии, класс 12
  
  Учебный план по бизнесу, класс 12
  Учебный план по экономике, класс 12 9000 9000
  Образцы документов по коммерции класса 11
  Образцы документов по коммерции класса 12
  TS Grewal Solutions
  TS Grewal Solutions Class 12 Accountancy
  TS Grewal Solutions Class 11 Accountancy
  Отчет о движении денежных средств
  Что такое Entry eurship
  Защита прав потребителей
  Что такое основной актив
  Что такое баланс
  Формат баланса
  Что такое акции
  Разница между продажей и маркетингом
  ICSE
  Документы ICSE
  
  Вопросы ICSE
  ML Aggarwal Solutions
  ML Aggarwal Solutions Class 10 Maths
  ML Aggarwal Solutions Class 9 Maths
  ML Aggarwal Solutions Class 8 Maths
  ML Aggarwal Solutions Class 7 Maths
  ML 6 Maths
  ML Aggarwal Solutions Class 6 Maths
  ML Aggarwal Solutions Class
  Selina Solutions
  Selina Solutions для класса 8
  Selina Solutions для Class 10
  Selina Solutions для Class 9
  Frank Solutions
  Frank Solutions для математики класса 10
  Frank Solutions для математики класса 9
  Класс ICSE 9000 2
  ICSE Class 6
  ICSE Class 7
  ICSE Class 8
  ICSE Class 9
  ICSE Class 10
  ISC Class 11
  ISC Class 12
  IAS
  Exam
  IAS
  Civil
  Сервисный экзамен
  Программа UPSC
  Бесплатная подготовка к IAS
  Текущие события
  Список статей IAS
  Пробный тест IAS 2019
  Пробный тест IAS 2019 1
  Пробный тест IAS 2019 2
  
  Экзамен KPSC KAS
  Экзамен UPPSC PCS
  Экзамен MPSC
  Экзамен RPSC RAS 
  TNPSC Group 1
  APPSC Group 1
  Экзамен BPSC
  WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
  Вопросник UPSC 2019
  Ключ ответов UPSC 2019
  Коучинг IAS
  IA S Coaching Бангалор
  IAS Coaching Дели
  IAS Coaching Ченнаи
  IAS Coaching Хайдарабад
  IAS Coaching Mumbai
  JEE
  BYJU’SEE
  9000 JEE 9000 Основной документ JEE 9000 JEE 9000
  Вопросник JEE
  Биномиальная теорема
  Статьи JEE
  Квадратичное уравнение
  NEET
  Программа BYJU NEET
  NEET 2020
  NEET Приемлемость 9000 Критерии 9000 NEET4 9000 NEET 9000 Пример 9000 9000 NEET
  Поддержка
  Разрешение жалоб
  Служба поддержки
  Центр поддержки
  Государственные советы
  GSEB
  GSEB Syllabus
  GSEB4
  GSEB3 Образец статьи
  GSEB3 004
  MSBSHSE
  MSBSHSE Syllabus
  MSBSHSE Учебники
  Образцы статей MSBSHSE
  Вопросники MSBSHSE
  AP Board
  APSCERT
  Syll
  AP 9000SC4
  Syll
  AP
  Syll 9000SC4
  Syll
  Syll
  MP Board
  MP Board Syllabus
  MP Board Образцы документов
  Учебники MP Board
  Assam Board
  Assam Board Syllabus
  Assam Board Учебники 9000 9000 Board4 BSEB
  Bihar Board Syllabus
  Bihar Board Учебники
  Bihar Board Question Papers
  Bihar Board Model Papers
  BSE Odisha
  Odisha Board Syllabus
  Odisha Board Syllabus
  Odisha Board Syllabus
  Программа PSEB
  Учебники PSEB
  Вопросники PSEB
  RBSE
  Rajasthan Board Syllabus
  RBSE Учебники
  RBSE Question Papers
  HPBOSE
  000 HPBOSE
  HPBOSE
  JKBOSE
  Программа обучения JKBOSE
  Образцы документов JKBOSE
  Шаблон экзамена JKBOSE
  TN Board
  TN Board Syllabus
  TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 9000 Paper Papers 9000 TN Board 9000 4 JAC
  Программа JAC
  Учебники JAC
  Вопросники JAC
  Telangana Board
  Telangana Board Syllabus
  Telangana Board Учебники
  Papers Telangana Board Учебники
  Учебный план KSEEB
  Типовой вопросник KSEEB
  KBPE
  Учебный план KBPE
  Учебники KBPE
  Документы по KBPE
  9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000
  Совет по Западной Бенгалии
  Учебный план Совета по Западной Бенгалии
  Учебники для Совета по Западной Бенгалии
  Вопросы для Совета по Западной Бенгалии
  UBSE
  TBSE
  Гоа Совет
  000
  NBSE0003 Board
  Manipur Board
  Haryana Board
  Государственные экзамены
  Банковские экзамены
  Экзамены SBI
  Экзамены IBPS
  Экзамены RBI
  IBPS
  03
  Экзамены SSC
  9SC2
  SSC GD
  SSC CPO 900 04
  SSC CHSL
  SSC CGL
  Экзамены RRB
  RRB JE
  RRB NTPC
  RRB ALP
  O Экзамены на страхование
  LIC4
  LIC4
  UPSC CAPF
  Список статей государственных экзаменов
  Обучение детей
  Класс 1
  Класс 2
  Класс 3
  Академические вопросы
  Вопросы по физике
  Вопросы по химии
  Вопросы по химии
  Вопросы
  Вопросы по науке
  Вопросы для общего доступа
  Онлайн-обучение
  Домашнее обучение
  Полные формы
  CAT
  BYJU’S CAT Program
  CAT3 9000 Предварительный курс CAT3
  Экзамен 9000 9000 CAT3 Экзамен Шаблон экзамена CAT 2020
  Обзор приложения Byju по CAT
  КУПИТЬ КУРС
  .
  32 математических формулы на ACT
  {{Privy: Embed campaign = 1309544}}
  В отличие от SAT, ACT не предоставляет вам список основных математических формул, на которые можно положиться в начале теста ACT. Это означает, что вам нужно будет запоминать математические формулы на ACT. Ниже вы найдете списки математических формул ACT, которые необходимо знать, формулы «Полезно знать» и формулы «Бонус», которые необходимо сохранить в памяти для ACT! Выучите их все, а затем просмотрите наш список тем по математике ACT, чтобы начать применять их!
  Математические формулы ACT, которые необходимо знать
  Хотя ACT проверяет разные концепции на каждом экзамене, есть популярные темы, которые возникают снова и снова.Этот список содержит лучшие математические формулы ACT. Для большей практики попробуйте Magoosh ACT Prep.
  Среднее значение
  S / T (Среднее = Сумма / Количество вещей)
  строк
  Форма пересечения откоса:
  y = м x + b (где м — наклон, а b — пересечение по оси Y)
  Наклон:
  Треугольники
  Площадь треугольника:
  1/2 bh (1/2 основания × высота)
  Теорема Пифагора:
  a ² + b ² = c ²
  Четырехугольники
  Периметр прямоугольника:
  2 l + 2 w (где l — длина, а w — ширина)
  Площадь прямоугольника:
  lw (длина × ширина)
  Объем ящика:
  л / ч (длина × ширина × высота)
  Площадь прямоугольного твердого тела:
  2 левый + 2 левый + 2 левый
  Диагональ в сплошном прямоугольнике:
  Примените теорему Пифагора дважды или l ² + w ² + h ² = d ²
  Круги и сферы
  Площадь круга:
  πr ²
  Окружность круга:
  2 πr
  Объем шара:
  4/3 πr ³
  Цилиндры
  Объем цилиндра:
  πr ² ч
  Тригонометрия
  SOHCAHTOA:
  sin x = противоположный / гипотенуза
  cos x = смежный / гипотенуза
  tan x = противоположный / смежный
  Вы также должны знать свои квадранты и где синус, косинус и тангенс положительны или отрицательны:
  Вероятность
  Вероятность:
  Количество желаемых результатов / общее количество результатов
  Факториалы (например,грамм. 8!):
  Чтобы найти факториал любого целого числа, умножьте его на каждое положительное целое число под ним, например:
  8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
  Бонус: математические формулы «Должен знать» в ACT также появляются на уроках математики в старшей школе. Итак, вы действительно учитесь сразу двум вещам. Ницца.
  Бонусный бонус: посмотрите видео ниже, чтобы увидеть, как эксперт ACT Кристин более подробно обсуждает 6 обязательных математических формул ACT:
  
  Полезные формулы ACT
  Объем и площадь
  Объем конуса:
  В = 1/3 πr ² ч
  Объем пирамиды:
  Площадь трапеции:
  
  (сложите основания, разделите на два, затем умножьте на высоту.)
  Логарифмы
  Определение:
  Если log _a b = c , то a ^c = b
  Изменение основного правила:
  Треугольники
  30-60-90 Передаточное число треугольника:
  1:: 2
  45-45-90 Соотношение треугольников:
  1: 1:
  Дополнительные формулы
  Уравнение круга:
  ( x — h ) ² + ( y — k ) ² = r ² (где центр окружности ( h , k ))
  Арифметические последовательности:
  t _n = t ₁ + d ( n -1)
  Геометрические последовательности:
  т _n = т ₁ × r ^{( n — 1)}
  Формула экспоненциального роста:
  Где P = основная сумма (начальная стоимость), r = скорость роста, n = количество месяцев, t = время в годах и A = новая сумма.
  Дополнительная информация
  Квадратное уравнение:
  Часто для решения сложной алгебраической задачи вам будет лучше применить такую стратегию, как обратное решение, но если вам комфортно с квадратным уравнением, держите его в уме.
  Перестановки:
  Комбинации:
  Важное примечание о математических формулах ACT
  Иногда математическая задача ACT может полагаться на более сложную формулу, такую как площадь поверхности сферы.В таких случаях формула, которая вам нужна, обычно задается самим вопросом. Так что не нужно думать, что нужно все запоминать. Однако способность вспоминать основные формулы гарантирует, что вы сможете с уверенностью решать проблемы, не содержащие формулы! В приведенный ниже список включены формулы для концепций, которые ACT проверяет наиболее часто.
  Важные математические формулы ACT (PDF)
  Иногда легче запоминать формулы, ежедневно изучая понемногу. Чтобы упростить задачу, мы создали PDF-файл с математическими формулами Magoosh ACT для печати. Вот ссылка, по которой вы можете получить копию.
  {{Privy: Embed campaign = 1309544}}
  Сообщите нам, если у вас есть какие-либо вопросы об этих формулах ACT. 🙂
  Кредит изображения: hotmath.com и getmathhelp.jimdo.com
  Популярные ресурсы
  О Кристин Фраккиа
  Доктор Кристин Фраккиа в настоящее время занимается подготовкой к экзаменам MCAT и LSAT, но она также имеет опыт проведения широкого спектра стандартизированных тестов, включая ACT, SAT, GRE и GMAT, а также приема в колледжи и аспирантуру.Имея докторскую степень в Калифорнийском университете в Ирвине и степень в области образования и английского языка, она работает в сфере образования с 2004 года. Она наслаждается агонией и блаженством бега на длинные дистанции, пеших прогулок, горячей йоги и эзотерических знаний.
  Политика в отношении комментариев в блоге Magoosh: Чтобы обеспечить максимальное удобство для наших читателей, мы будем одобрять и отвечать на комментарии, относящиеся к статье, достаточно общие, чтобы быть полезными для других студентов, краткие и хорошо написанные! 🙂 Если ваш комментарий не был одобрен, вероятно, он не соответствовал этим правилам.Если вы студент Premium Magoosh и хотите более персонализированное обслуживание, вы можете использовать вкладку «Справка» на панели управления Magoosh. Спасибо!
  .
  Математические формулы, физические формулы и химические формулы проверить онлайн @ Byjus
  Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 11-12
  КОНКУРСНЫЙ ЭКЗАМЕН
  BNAT 000 NC
  000 NC Книги
  Книги NCERT для класса 5
  Книги NCERT для класса 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  Книги NCERT для класса 11
  Книги NCERT для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT 9000 9000
  NCERT Exemplar Class
  Решения RS Aggarwal, класс 12
  Решения RS Aggarwal, класс 11
  Решения RS Aggarwal, класс 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  RD Sharma Class 6 Решения
  Решения RD Sharma
  Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Теорема Пифагора
  0004
  000300030004
  9000
  Простые числа
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Деление фракций
  000
  000
  000
  000
  000
  000 Microology
  000
  000 Microology
  000 BIOG3000
  FORMULAS
  Математические формулы
  Алгебраические формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000 PBS4000
  000300030002 Примеры калькуляторов химии
  Класс 6
  Образцы бумаги CBSE для класса 7
  Образцы бумаги CBSE для класса 8
  Образцы бумаги CBSE для класса 9
  Образцы бумаги CBSE для класса 10
  Образцы бумаги CBSE для класса 11
  Образцы бумаги CBSE чел. для класса 12
  CBSE — вопросник за предыдущий год
  CBSE — вопросник за предыдущий год, класс 10
  CBSE — за предыдущий год — вопросник, класс 12
  HC Verma Solutions
  HC Verma Solutions Class 11 Physics
  Решения HC Verma, класс 12, физика
  Решения Лакмира Сингха
  Решения Лакмира Сингха, класс 9
  Решения Лакмира Сингха, класс 10
  Решения Лакмира Сингха, класс 8
  Заметки CBSE
  , класс
  CBSE Notes
  Примечания CBSE класса 7
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания CBSE класса 12
  
  .

Формулы математика для егэ: школьные формулы по алгебре и геометрии

Формулы к ЕГЭ по математике

Теория, пособие для подготовки к ЕГЭ по математике

Справочные материалы ЕГЭ по математике / Блог :: Бингоскул

Справочные материалы к базовому уровню

Алгебра

Таблица квадратов целых чисел от 0 до 99

Свойства арифметического квадратного корня

Корни квадратного уравнения

Формулы сокращённого умножения

Степень и логарифм

Геометрия

Площади фигур

Площади поверхностей и объёмы тел

Тригонометрические функции

Основное тригонометрическое тождество:

Функции

Справочные материалы к профильному уровню

Математические формулы по алгебре и геометрии для ЕГЭ

Как выучить все формулы по математике к ЕГЭ

Математические формулы школьного курса алгебры

Логарифмические формулы

Формулы тригонометрии

<img decoding="async" src="/800/600/https/ege-paragraf.ru/Произведение тригонометрических функций.jpg" alt="егэ математика в таблицах" />

Формулы векторной алгебры из школьного курса математики

Формулы арифметической и геометрической прогрессии

Геометрические формулы школьного курса математики для ЕГЭ

Основные формулы для подготовки к ЕГЭ по математике

Формулы дифференцирования

Правила дифференцирования

Таблица некоторых значений тригонометрических функций

Таблица первообразных и интегралов

Таблица степеней чисел

Законы степеней чисел:

Свойства корня n-ой степени

Координаты точек

Координаты точек

Формулы приведения

Формулы сокращённого умножения:

Применение производной:

Прогрессии:

Какие математические формулы запоминать не стоит

Выкидываем из шпаргалки формулу площади правильного треугольника

Выкидываем из шпаргалки формулу площади сектора

Выкидываем пару формул из таблицы производных

Выкидываем из шпаргалки формулу боковой поверхности цилиндра

Выкидываем теорему Пифагора

Выкидываем из шпаргалок несколько тригонометрических формул

Анализируем формулу площади четырехугольника через диагонали

Формулы тригонометрии. Основные тригонометрические формулы для ЕГЭ

Список математических формул

математических формул | Основные математические формулы для классов 6–12 CBSE с файлами PDF

03 Экзамены SSC 9SC2

32 математических формулы на ACT

Математические формулы ACT, которые необходимо знать

Среднее значение

строк

Треугольники

Четырехугольники

Круги и сферы

Цилиндры

Тригонометрия

Вероятность

Полезные формулы ACT

Объем и площадь

Логарифмы

Треугольники

Дополнительные формулы

Дополнительная информация

Важное примечание о математических формулах ACT

Важные математические формулы ACT (PDF)

Популярные ресурсы

О Кристин Фраккиа

Математические формулы, физические формулы и химические формулы проверить онлайн @ Byjus

Share This Story, Choose Your Platform!

Related Posts

База егэ математика пробник: Задание 12 ЕГЭ по математике база

Решу егэ профиль математика 2019: Реальный вариант ЕГЭ по математике 2019

Математика 4 класс всероссийская проверочная работа ответы волкова бубнова: ВПР по математике 4 класс 2019 Волкова Вариант 4 с решениями

Решу огэ ответы математика 1 вариант: ОГЭ 2022 математика Ященко 36 вариантов, ответы 1 варианта с решением

03
Экзамены SSC
9SC2