Задание 11 ЕГЭ по математике Профиль. Исследование функций
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции будет при том же , что и точка максимума функции А ее найти легко.
при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при
Ответ: — 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.
Точка — точка минимума функции . Точка не лежит на отрезке Поэтому
и Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то Если , то
Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку если
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции
Мы нашли точку максимума, но это еще не все.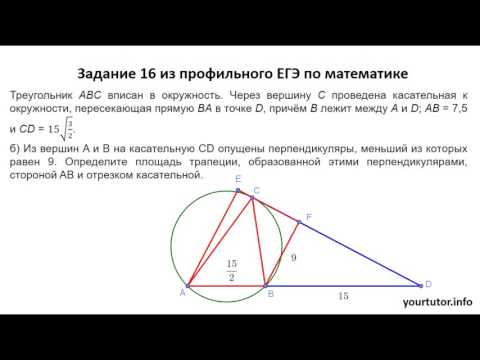 Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если Тогда
При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при
Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что для всех , и функция монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Публикация обновлена: 09.03.2023
Как решать задания на производную в ЕГЭ? 11 задание профиль
По мнению выпускников, задание № 11 — самое сложное в первой части ЕГЭ по математике. Ведь там… производная! На деле не стоит бояться — все задания можно решить, зная только 2 алгоритма. В этой статье я о них расскажу! А еще поделюсь полезным лайфхаком, как решать некоторые задания на производную в ЕГЭ, вообще не используя алгоритм и экономя драгоценное время.
Производная на ЕГЭ по математике. Как решать задание № 11?Хочешь круто подготовится к ЕГЭ по математике? Тебе поможет учебный центр MAXIMUM! Все наши преподаватели сами сдавали этот экзамен на хороший балл. Мы ежегодно изучаем изменения ФИПИ и корректируем курсы, исходя из этого. Читай подробнее про наши курсы и выбирай подходящий!
Почему задания на производную решает только 40% выпускников?
Ни для кого не секрет, что профильный ЕГЭ по математике состоит из частей с кратким и развёрнутым ответом. В первой части всего 11 заданий. В том числе и интересующее нас задание № 11.
В первой части всего 11 заданий. В том числе и интересующее нас задание № 11.
Задание № 11 проверяет, умеют ли выпускники работать с производной. По статистике его решают около 40% всех сдающих экзамен, что для первой части ЕГЭ по математике очень мало.
Проблема этого задания в том, что производную проходят только в середине 11 класса, когда уже активно идет подготовка к ЕГЭ по другим темам. Из-за этого школьники не успевают ее отработать.
Два прототипа задания № 11 ЕГЭ по математике
В этом номере есть всего два типа заданий, которые можно решить с помощью простых алгоритмов. Ученикам нужно лишь запомнить их и выучить таблицу производных.
Два прототипаСначала необходимо понять, что именно от нас хотят в задании — расскажу небольшой лайфхак. Многие ученики путают понятия «точка максимума / минимума» и «наибольшее / наименьшее значение». Дело в том, что точка экстремума – это x, а наибольшее или наименьшее значение – это у. Как не запутаться? Обрати внимание на слово-маркер «точка». Если ты видишь его, то речь идет об х, если этого слова нет, то речь об у.
Если ты видишь его, то речь идет об х, если этого слова нет, то речь об у.
Поиск точек экстремума
Теперь, когда мы разобрались, как не запутаться и понять, что необходимо найти в задаче, приступим к разбору самих заданий и алгоритмов к ним. Начнём с поиска точек экстремума. Чтобы провести анализ функции, необходимо определить основные этапы. У функции есть точки экстремума, в них производная равна нулю. Единственный способ, определить, является ли данная точка точкой максимума или минимума – это определить знаки производной до и после неё, если знак производной меняется с «–» на «+», то это будет точка минимума, а если с «+» на «–», то точка максимума. Таким образом общий порядок действий будет следующим:
Данному алгоритму подчиняются абсолютно все задания, в которых нужно найти точки экстремума.
Поиск наибольшего / наименьшего значения функции
Перейдём ко второму прототипу, в котором нужно найти наибольшее/наименьшее значение функции. Интересно, что второй прототип можно отличить даже визуально, потому что кроме самой функции вам будет дан ещё промежуток, ограничивающий функцию в двух точках [a; b]. Так как мы про эти точки ничего не знаем, их придётся дополнительно учитывать. В остальном начало этого алгоритма будет совпадать с предыдущим. Начинать всегда будем именно с точек экстремума, потом проверим, как ведёт себя функция в каждой точке экстремума, а также в начале и конце заданного промежутка, и в итоге запишем в ответ нужное значение функции.
Интересно, что второй прототип можно отличить даже визуально, потому что кроме самой функции вам будет дан ещё промежуток, ограничивающий функцию в двух точках [a; b]. Так как мы про эти точки ничего не знаем, их придётся дополнительно учитывать. В остальном начало этого алгоритма будет совпадать с предыдущим. Начинать всегда будем именно с точек экстремума, потом проверим, как ведёт себя функция в каждой точке экстремума, а также в начале и конце заданного промежутка, и в итоге запишем в ответ нужное значение функции.
Лайфак, чтобы решать задания на производную в ЕГЭ
Давайте посмотрим на некоторые задания, которые можно решить гораздо быстрее, не прибегая к использованию алгоритмов. Лайфхаки не работают на абсолютно всех заданиях, поэтому будьте аккуратны, применяя их!
Лайфхак, которые мы рассмотрим сегодня, будет опираться на знание формата экзамена. № 11 – задание из части с кратким ответом, ответ на который мы пишем в клеточки на бланке, а чего в этих клеточках не может быть? Очевидно, что бесконечную дробь, буквы 𝑒, ln(…), log(…), 𝜋, sin𝑥, бесконечность и прочие знаки мы не сможем записать, и это очень сильно упрощает нам задачу.
Разбираем лайфхак на примере
Чтобы выполнить данное задание, необходимо знать таблицу производных и немного порассуждать логически. Если мы пойдём по алгоритму, нам придётся брать производную от e в степени (x-9), а производная от данной функции будет равна тому же самому. И получается, что мы никак не можем избавиться от символа, которого просто не может быть в ответе.
Или можем? Есть замечательная степень, которая абсолютно любое основание может превратить в единицу — это 0. Таким образом, мы можем избавиться от е, если представим её степень (х – 9) равной нулю. Получается х – 9 = 0, тогда х = 9.
Но единственный ли это способ избавиться от «е»? На самом деле нет, так как есть ещё один множитель – скобка. Ее можно занулить, тогда занулится и всё произведение. Получим 10 – х = 0, тогда х = 10. Но не стоит забывать, что найти нас просят наименьшее значение ФУНЦИИ, поэтому теперь подставим найденные х в исходную функцию.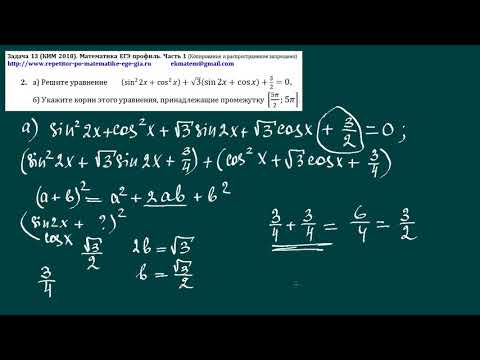
При х = 9 получаем 1, а при х = 10 получаем 0. Видим, что значение 0 меньше, чем 1, а значит именно его мы запишем в ответ. Обратите внимание, что оно достигается при х = 10, поэтому критично важно учитывать как степень экспоненты, так и множитель-скобку.
В этой статье мы рассмотрели два алгоритма, с помощью которых можно решить абсолютно любое задание № 11 ЕГЭ по математике. А еще вы узнали лайфхак, как можно выполнить задание на производную в ЕГЭ, не прибегая к использованию алгоритма, и сэкономить время!
- Учите производную
- Пользуйтесь алгоритмами
- Не забывайте про крутые лайфхаки, но будьте внимательны, применяя их!
Если хочешь разобраться в остальных темах по математике и не только, почитай другие статьи в блоге и обрати внимание на наши онлайн-курсы. Уже более 150 тысяч выпускников подготовились с нами к ЕГЭ. Кстати, у меня на курсах MAXIMUM тоже можно поучиться!
TABE 11 и 12 Оценка взрослых
TABE® работает на основе DRC INSIGHT™, ведущей в отрасли онлайн-системы оценки, которая уже предоставляет надежные оценки более чем половине США. С помощью DRC INSIGHT вы можете повысить гибкость и надежность своей программы тестирования, с той же мерой успеваемости, которую вы знаете и доверяете TABE.
С помощью DRC INSIGHT вы можете повысить гибкость и надежность своей программы тестирования, с той же мерой успеваемости, которую вы знаете и доверяете TABE.
ТАБЛИЦА 11 и 12
- Сокращенное время тестирования для ТАБЛИЦЫ 11 и 12.
- Согласование с новыми стандартами готовности к колледжу и карьере и дескрипторами NRS.
- Соответствует современным строгим положениям Закона об инновациях и возможностях для рабочей силы (WIOA).
- Веб-инструмент для сканирования поддерживает отчеты и передачу данных, устраняя необходимость ручного ввода данных.
- Улучшенный локатор готовит учащихся к тестированию.
- Связь TABE 11 и 12 с эквивалентом средней школы и поступлением в высшие учебные заведения.
ТАБЛИЦА 11 и 12 Грамотность
Содержание подчеркивает интеграцию и применение учебных навыков в контекстах, значимых для взрослых испытуемых. Грамотность является ключевым фактором для взрослых учащихся, и TABE 11 и 12 измеряет ее по этим трем ключевым типам.
- Базовые навыки
- Литературные тексты
- Информационные тексты
ТАБЛИЦА 11 и 12 Чтение
Содержание отражает зрелые, жизненные и рабочие ситуации и подчеркивает пересекающиеся цели, от навыков понимания слов до навыков критического мышления.
ТАБЛИЦА 11 и 12 Язык
Целью обучения взрослых языку является развитие коммуникативных навыков, необходимых для эффективного функционирования на работе и в повседневной жизни.
TABE 11 и 12 Математика
Содержание отражает применение математики, особенно рутинные задачи, такие как оценка величин и выполнение вычислений, связанных со временем, расстоянием, весом и т. д.
TABE 11 и 12 Чтение образцов элементов 11 и 12 Образцы элементов чтения M
TABE 11 и 12 Образцы элементов чтения D
TABE 11 и 12 Образцы элементов чтения A
TABE 11 и 12 Образцы элементов языка
Tabe 11 и 12 Языков. Образец элементов E
Образец элементов E
Tabe 11 и 12 Языковые образцы. Образец языка M
Tabe 11 и 12 Язык. Образец. Элементы M
TABE 11&12 Math Sample Items D
TABE 11&12 Math Sample Items A
TABE 11&12 Blueprints
Уровень A
Уровень D
Уровень E
Уровень L
Уровень M
Tabe 11 и 12 Blueprints математики
Уровень A
Уровень D
Уровень E
Level
Level M
.
Уровень D
Уровень E
Уровень L
Уровень M
Tabe 11 и 12 Письмо.0003 Нажмите здесь для онлайн-инструментов. Нажмите здесь , чтобы узнать, почему специалисты в области образования взрослых полагаются на TABE больше, чем на любую другую систему оценивания взрослых в стране. Оценка по математике и счету — это больше, чем формирование суждений о способностях учащегося. Он отслеживает понимание учащимся математического языка, концепций и навыков, а также того, что им нужно делать, чтобы добиться успеха. Для этого требуется: Подготовить обучение учащихся по математике является основной задачей учителей. Учителям нужна точная информация о том, что каждый ученик уже знает, и при поддержке, что может быть в пределах досягаемости ученика. Прогресс обучения математике Викторианской эпохи описывает последовательность наблюдаемых показателей все более сложного понимания и навыков в 15 ключевых концепциях арифметики. Прогрессии: Прогресс обучения счету не является учебным планом. См. Викторианскую учебную программу: математика для описания содержания и стандартов успеваемости. Каждый этап обучения включает в себя ряд шагов развития, предусмотренных в промежутке. Каждый шаг иллюстрирует наблюдаемую прогрессию обучения. Например, количественная оценка чисел включает 12 шагов в диапазоне от основания до уровня 6, а работа с десятичными дробями состоит из четырех шагов в диапазоне от уровня 4 до уровня 7. Чтобы помочь учителям понять и использовать прогресс в обучении арифметике, каждый прогресс был сопоставлен с викторианской учебной программой F – 10: Континуум математики. Каждая строка показывает количество шагов в процессе обучения и их отношение к каждому уровню. Для арифметики подзаголовок каждого шага также был включен для поддержки использования учителем. Платформа оценки знаний – это помощь учителям в оценке успеваемости всех учащихся и поддержка более целенаправленных методов обучения. Доступ к этой онлайн-платформе могут получить учителя государственных школ. Ресурсы, поддержка и инструменты на платформе поддерживают высококачественные методы оценки и предоставляют учителям информацию, которую они могут использовать для удовлетворения учебных потребностей учащихся по мере их продвижения по континууму обучения. Цифровая библиотека оценивания (DAL) предоставляет ряд онлайн-инструментов оценивания в классе по математике. Эти оценки предназначены для предоставления значимой и своевременной информации о навыках, знаниях и понимании учащихся по трем направлениям математики. Ресурс Scaffolding numeracy in the Middle Years (SNMY) позволяет практикам получить доступ к оценочным материалам, системе обучения и оценки для мультипликативного мышления (LAF), планам обучения, аутентичным задачам и результатам исследований из проект, в котором исследовался новый подход к улучшению навыков счета учащихся с 4 по 8 классы, основанный на оценивании. Система обучения и оценки мультипликативного мышления (LAF) была разработана на основе исследований, проведенных в рамках проекта SNMY. LAF помогает объединить все ключевые идеи, стратегии и представления умножения и деления, необходимые для уверенной работы с целыми числами, дробями, десятичными дробями и процентами в широком диапазоне контекстов. Он связан с обширными оценочными заданиями, используемыми для оценки мультипликативного мышления, и содержит подробные рекомендации по применению в обучении. Инструменты Оценки распространенных недоразумений (ACM) основаны на серии тестовых заданий, разработанных в учебных целях для определения потребностей в обучении в Number. Руководство по зондированию включает в себя ряд задач и ресурсов, организованных для устранения распространенных недоразумений.
Оценка по математике и счету


Платформа оценки знаний

Цифровая библиотека оценивания
Scaffolding numeracy in the Middle Years

Система обучения и оценки мультипликативного мышления
Оценка распространенных недоразумений


Leave A Comment