Формула проекции перемещения при прямолинейном равноускоренном движении: Прямолинейное равноускоренное движение. Ускорение — урок. Физика, 9 класс.

Перемещение при прямолинейном равноускоренном движении – формула

4

Средняя оценка: 4

Всего получено оценок: 155.

4

Средняя оценка: 4

Всего получено оценок: 155.

Движение, при котором траектория представляет собой прямую линию, называется прямолинейным. Если при таком движении скорость равномерно изменяется, то изменение скорости за единицу времени называется ускорением, а такое движение называется равноускоренным. Рассмотрим перемещение при прямолинейном равноускоренном движении.

Прямолинейное равноускоренное движение

Наиболее удобным для изучения примером равноускоренного прямолинейного движения является свободное падение тел в первые секунды полета, когда сопротивление воздуха пренебрежительно мало. Скорость падения тела при этом равномерно увеличивается, и за одинаковые промежутки времени изменение составляет одну и ту же величину.

Рис. 1. Свободное падение тел.

Для Земли на средних широтах каждую секунду скорость падения увеличится приблизительно на 9. 81 м/с. Данная величина называется ускорением свободного падения.

Если бы движение было равномерным, то материальная точка каждую секунду проходила бы одно и то же расстояние. Однако для равноускоренного движения это не так.

Найдем формулу перемещения тела при прямолинейном равноускоренном движении.

Вывод формулы перемещения

Наиболее просто найти формулу перемещения из графика скорости. Перемещение материальной точки равно площади фигуры, лежащей под графиком скорости.

Например, для равномерного движения график скорости представляет горизонтальную прямую, а значит, площадь под этим графиком является прямоугольником, высота которого равна скорости, а ширина – времени. Для нахождения его площади необходимо перемножить эти величины, получив известную формулу «расстояние равно произведению скорости на время пути».

При равноускоренном движении скорость равномерно меняется, а значит, ее график представляет собой наклонную прямую:

Рис. 2. График скорости при равноускоренном движении.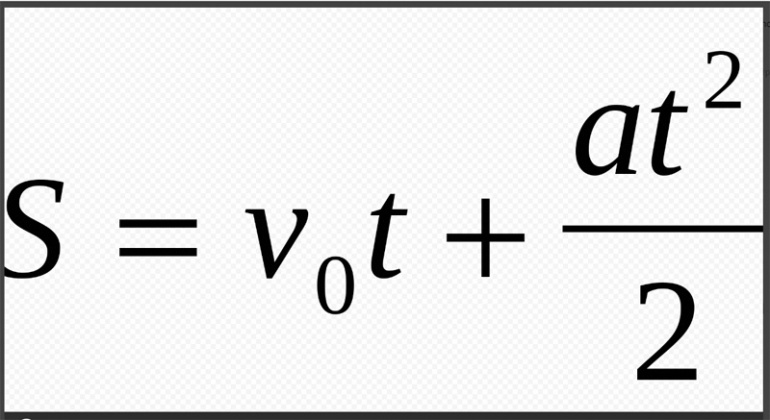

Найдем площадь фигуры под этой прямой.

Фигура является четырехугольником, одна сторона является отрезком оси абсцисс длинной $Δt=t_2-t_1$, две соседние стороны – вертикальные отрезки, длина каждого равна значению скорости в соответствующий момент времени: $v_1$ и $v_2$. То есть, фигура является трапецией, площадь которой, как известно из геометрии, равна произведению полусуммы оснований на высоту. Высота равна промежутку времени, основания – скоростям вначале и в конце пути. То есть, если начальный момент времени нулевой ($t_1=0$), а скорость в начальный момент обозначить $v_0$ то рассматриваемое перемещение равно:

$$x(t)={v+ v_0\over 2}t$$

Поскольку при равноускоренном движении скорость за единицу времени увеличивается на величину ускорения, то скорость в момент $t$ будет равна сумме начальной скорости и произведению ускорения на время пути:

$$v(t)= v_0 + at$$

Подставив значение скорости в предыдущую формулу, и приняв, что перемещение в начальный момент времени было равно $x_0$, получим окончательную формулу перемещения тела при прямолинейном равноускоренном движении:

$$x(t)=x_0+v_0t+{at^2\over 2}$$

Из вида формулы можно заключить, что график перемещения при равноускоренном движении является параболой. 2\over 2a}$$

Парабола имеет, как правило, два корня. А значит, задачи о перемещении тела при равноускоренном движении могут иметь не одно, а два правильных решения. Например, если найти время, когда предмет, брошенный вверх со скоростью 20м/с достигнет высоты 9 м, мы получим два ответа: через 0.52 с и 3.56 с. Оба эти ответы правильны. Предмет будет на высоте 9 м дважды – первый раз при полете вверх, второй раз в момент падения.

Что мы узнали?

Наиболее частый пример прямолинейного равноускоренного движения – это свободное падение тел, пока сопротивление воздуха пренебрежительно мало. Перемещение при равноускоренном прямолинейном движении является квадратичной функцией, ее график является параболой.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4

Средняя оценка: 4

Всего получено оценок: 155.

---

А какая ваша оценка?

Перемещение и путь при равноускоренном прямолинейном движении

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Формула перемещения

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

v = v₀ ± at

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

t₁ = t – t₂

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

0 = v₀₁ – at₁

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

t₂ = t – t₁

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

v = at₂

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

s = |s₁ – s₂|

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

l = s₁ + s₂

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с². Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

v₀₂ = v₀₁ + a₁t₁ = a₁t₁ (так как v₀₁ = 0)

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с^2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с². Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (

v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени

t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Задание EF18553

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t²(все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

---

Алгоритм решения

1.Записать исходные данные и перевести их единицы измерения величин в СИ.

2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.

3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.

4.Определить перемещение тела и его кинетическую энергию.

5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x(t)=x0+v0t+at22..

Теперь мы можем выделить кинематические характеристики движения тела:

• x₀ = 10 (м).

• v₀ = 5 (м/с).

• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).

Перемещение тела определяется формулой:

s=v0t+at22..

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x(t)=v0t+at22..=5t−3t2

Кинетическая энергия тела определяется формулой:

Ek=mv22..

Скорость при прямолинейном равноускоренном движении равна:

v=v0+at=5−6t

Поэтому кинетическая энергия тела равна:

Ek=m(5−6t)22.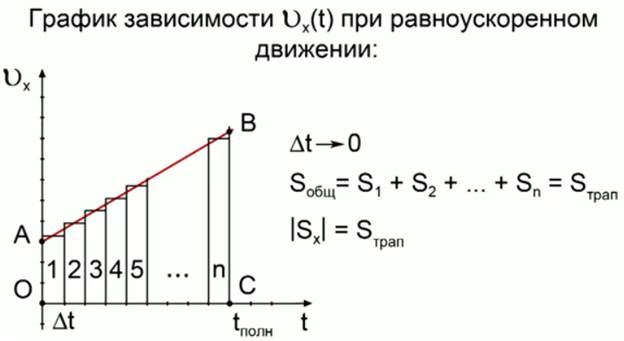 .=0,22..(5−6t)2=0,1(5−6t)2

Следовательно, правильная последовательность цифр в ответе будет: 34.

.

.

Ответ: 34

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

---

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

• перемещение и путь;
• скорость;
• ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17957 За 10 секунд скорость автомобиля, движущегося равноускоренно по прямой дороге, увеличилась от 0 до 20 м/с. Пройденный автомобилем путь равен…

---

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения пути при равноускоренном прямолинейном движении.
3. Определить недостающие исходные данные.
4. Найти искомую величину.

Решение Запишем исходные данные:

• Начальная скорость v₀ = 0 м/с.
• Конечная скорость v = 20 м/с.
• Время изменения скорости t = 10 с.

Формула для вычисления пути при равноускоренном прямолинейном движении: Так как начальная скорость равна нулю, формула принимает вид: Нам неизвестно ускорение, но его можно вычислить по формуле: Вычисляем путь:  Ответ: 100

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18831 На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t₁=20 с до t₂=50 с.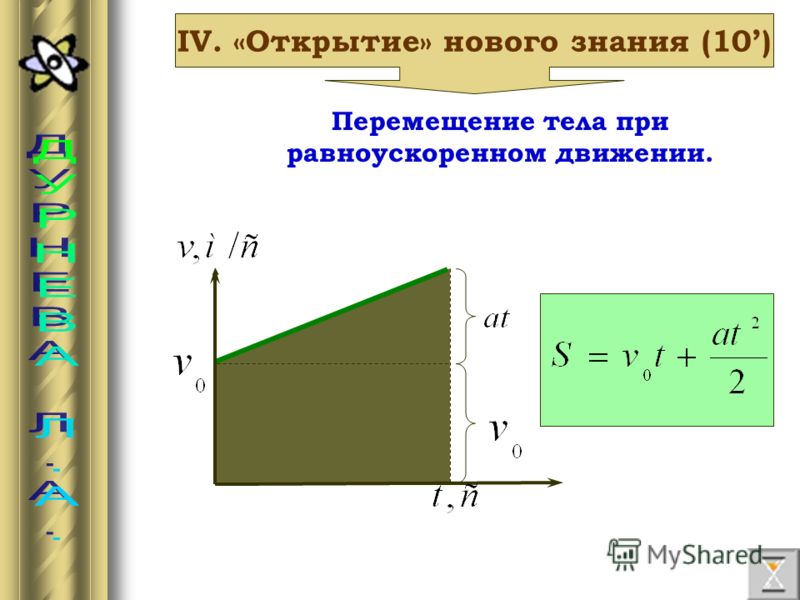

---

Алгоритм решения

1. Охарактеризовать движение тела на различных участках графика.
2. Выделить участки движения, над которыми нужно работать по условию задачи.
3. Записать исходные данные.
4. Записать формулу определения искомой величины.
5. Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

1. От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
2. От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
3. От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

1. От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
2. От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

Исходные данные:

• Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
• Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s = s₁ + s₂

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

s₁+ s₂= 100 + 100 = 200 (м)

Ответ: 200

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 24. 1k

Как рассчитать путь для прямолинейного равноускоренного движения. Равноускоренное прямолинейное движение

Это движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, т. е. ускорение постоянно.

Примерами такого движения являются свободное падение тел у поверхности Земли и движение под действием постоянной силы.

При равноускоренном прямолинейном движении координата тела изменяется во времени в соответствии с законом движения:

где x 0 – начальная координата материальной точки, 0 x – проекция начальной скорости и a x – проекция ускорения точки на ось 0 X .

Проекция скорости материальной точки на ось 0 X в этом случае изменяется по следующему закону:

В этом случае проекции скорости и ускорения могут принимать различные значения, в том числе и отрицательные те.

Графики зависимостей х ( t ) и х ( t ) представляют собой прямую и параболу соответственно и, как и в алгебре, можно судить о расположении графика функции относительно оси координат коэффициентами в уравнениях прямой и параболы.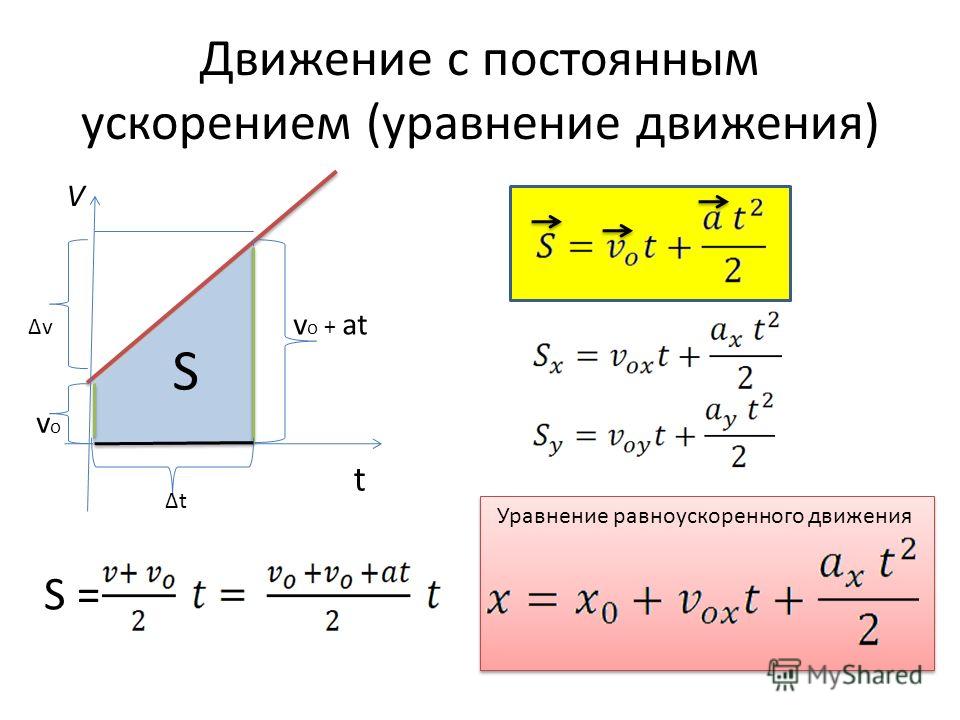

На рис. 6 показаны графики для x ( t ), x ( t ), s ( t ) когда x 0 > 0, 0 x > 0, a x t) имеет отрицательный наклон (tg  = a x

3. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.

Равномерное круговое движение происходит с постоянной скоростью по модулю, т.е. = const (рис. 7). Однако направление скорости при таком движении постоянно меняется, поэтому равномерное движение тела по окружности есть движение с ускорением.

Для описания равномерного движения тела по окружности вводятся следующие физические величины: период , частота обращения , линейная скорость , угловая скорость И центростремительное ускорение .

Период обращения T – время, необходимое для совершения одного полного оборота.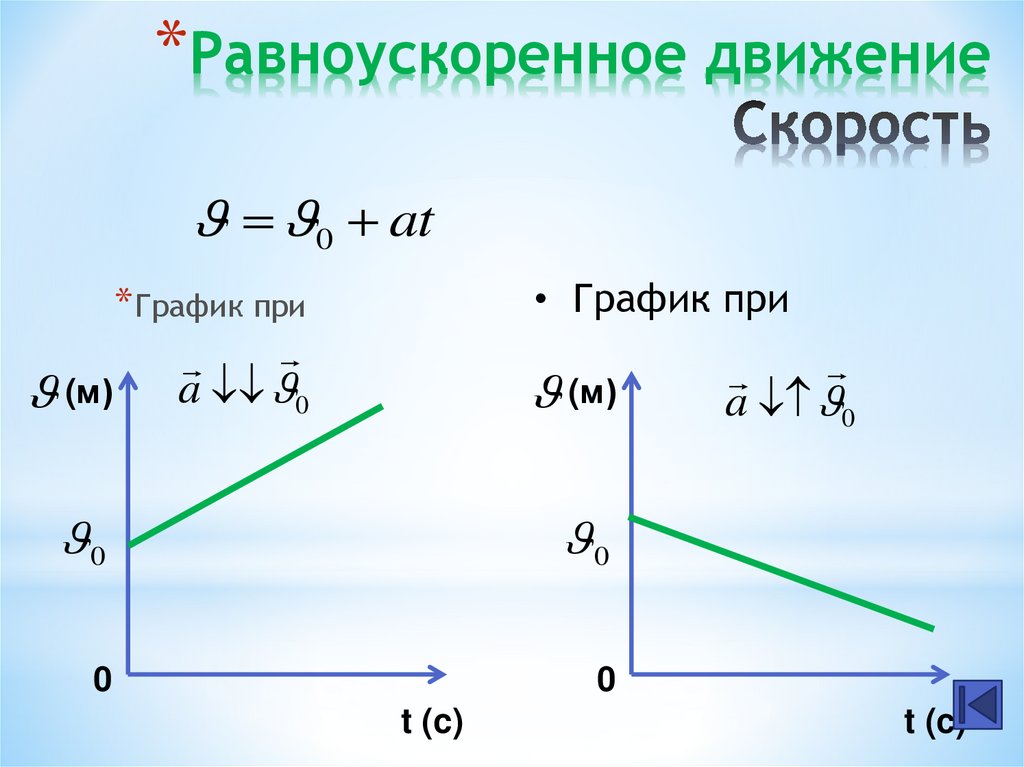

Частота обращения  — число оборотов, совершаемых телом за 1 с. Единицей частоты в системе СИ является с-1.

Частота и период обращения связаны между собой соотношением .

Вектор скорости при движении точки по окружности постоянно меняет свое направление (рис. 8).

При равномерном движении тела по окружности отрезок пути  с проходит за время  t , длина дуги окружности. Отношение является постоянным во времени и называется модулем линейной скорости . На время, равное периоду обращения T , точка проходит расстояние, равное длине окружности 2 R , поэтому

Скорость вращения твердых тел обычно характеризуют физической величиной, называемой угловой скоростью , модуль которого равен отношению угла поворота тела  к интервалу времени, за который этот поворот совершается (рис. 8):

Единицей угловой скорости в СИ является с -1 .

Поскольку ориентация твердого тела одинакова во всех системах отсчета, движущихся поступательно друг относительно друга, угловая скорость твердого тела будет одинаковой во всех системах отсчета, движущихся поступательно друг относительно друга.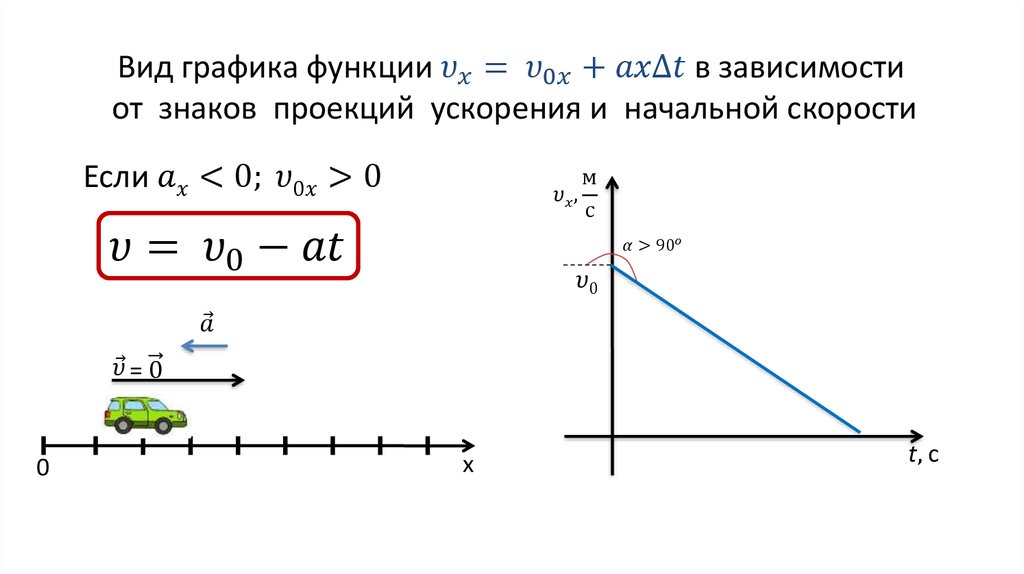

При равномерном вращении твердого тела вокруг некоторой оси любая точка этого тела движется вокруг этой же оси по окружности радиусом R с линейной скоростью, равной

Если начальные координаты точки ( R ; 0), затем его координаты изменяются в соответствии с законом x ( T ) = R COS 15 T и Y ( T ) = R SINC T .

Как, зная тормозной путь, определить начальную скорость автомобиля и как, зная характеристики движения, такие как начальная скорость, ускорение, время, определить движение автомобиля? Ответы мы получим после ознакомления с темой сегодняшнего урока: «Перемещение при равноускоренном движении, зависимость координат от времени при равноускоренном движении»

При равномерно ускоренном движении график выглядит как прямая, идущая вверх, так как ее проекция ускорения больше нуля.

При равномерном прямолинейном движении площадь будет численно равна модулю проекции перемещения тела.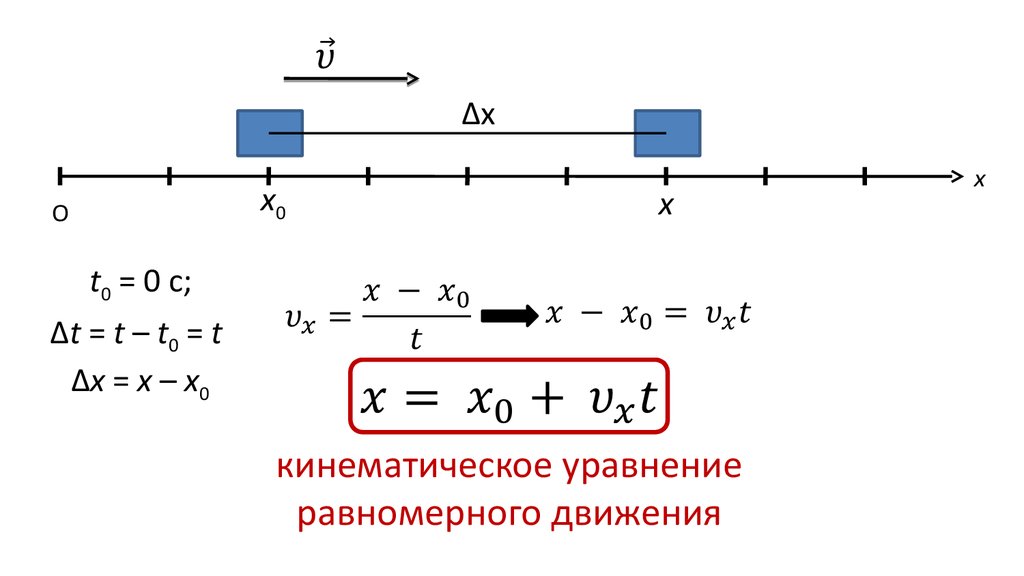 Оказывается, этот факт можно обобщить на случай не только равномерного движения, но и любого движения, т. е. показать, что площадь под графиком численно равна модулю проекции смещения. Делается это строго математически, но мы воспользуемся графическим методом.

Рис. 2. График зависимости скорости от времени при равноускоренном движении ()

Разобьем график проекции скорости от времени при равноускоренном движении на малые интервалы времени Δt. Предположим, что они настолько малы, что на протяжении их длины скорость практически не менялась, то есть условно превратим график линейной зависимости на рисунке в лесенку. На каждом его шаге считаем, что скорость не сильно изменилась. Представьте, что мы делаем интервалы времени Δt бесконечно малыми. В математике говорят: совершаем предельный переход. В этом случае площадь такой лестницы будет бесконечно близко совпадать с площадью трапеции, которая ограничена графиком V x (t). А это значит, что для случая равноускоренного движения можно сказать, что модуль проекции перемещений численно равен площади, ограниченной графиком V x (t): осями абсцисс и ординат и перпендикуляром, опущенным на ось абсцисс, то есть площадь трапеции OABS, которую мы видим на рис. 2.

Задача из физической превращается в математическую — нахождение площади трапеции. Это стандартная ситуация, когда физики строят модель, описывающую то или иное явление, а потом в дело вступает математика, которая обогащает эту модель уравнениями, законами — что превращает модель в теорию.

Находим площадь трапеции: трапеция прямоугольная, так как угол между осями равен 90 0 , делим трапецию на две фигуры — прямоугольник и треугольник. Очевидно, что общая площадь будет равна сумме площадей этих фигур (рис. 3). Найдем их площади: площадь прямоугольника равна произведению сторон, то есть V 0x t, площадь прямоугольного треугольника будет равна половине произведения катетов — 1/2AD BD, подставив проекционные значения, получим: 1/2t (V x — V 0x), а, памятуя о законе изменения скорости от времени при равноускоренном движении: V x (t) = V 0x + a x t, получим совершенно очевидно, что разность проекций скоростей равна произведению проекции ускорения а х на время t, т. е. V х — V 0x = а х t.

Рис. 3. Определение площади трапеции (А источник)

С учетом того, что площадь трапеции численно равна модулю проекции смещения, получаем:

S x (t) = V 0 x t + a x t 2 / 2

Получили закон зависимости проекции смещения от времени при равноускоренном движении в скалярной форме, в векторной форме это будет выглядеть так:

(t) = t + t 2 / 2

Выведем еще одну формулу для проекции смещения, которая не будет включать время как переменную. Решаем систему уравнений, исключив из нее время:

S x (t) = V 0 x + a x t 2 / 2

V x (t) = V 0 x + a x t

Представим, что мы не знаем время, то выразим время из второго уравнения:

t = V x — V 0x / a x

Подставляем полученное значение в первое уравнение:

Получаем такое громоздкое выражение, возводим его в квадрат и дайте похожие:

Мы получили очень удобное выражение проекции смещения для случая, когда мы не знаем время движения.

Пусть начальная скорость автомобиля, когда началось торможение, V 0 = 72 км/ч, конечная скорость V = 0, ускорение a = 4 м/с 2. Узнать длину торможения расстояние. Преобразовав километры в метры и подставив значения в формулу, получим, что тормозной путь будет равен:

S x = 0 — 400 (м/с) 2/-2 4 м/с 2 = 50 м

Разберем следующую формулу:

S х = (V 0 х + V х) / 2 t

Проекция движения равна половине суммы проекций начальной и конечной скоростей, умноженных на время движение. Напомним формулу смещения для средней скорости

S х = V ср t

В случае равноускоренного движения средняя скорость будет: вплотную подошли к решению основной проблемы механики равноускоренного движения, т. е. к получению закона изменения координаты со временем:

x(t) = x 0 + V 0 x t + a x t 2 / 2

Чтобы научиться пользоваться этим законом, разберем типичную задачу.

Автомобиль, двигаясь из состояния покоя, приобретает ускорение 2 м/с 2. Найти расстояние, пройденное автомобилем за 3 секунды и за третью секунду.

Дано: V 0 x = 0

Запишем закон, по которому перемещение изменяется со временем при

равноускоренном движении: S x = V 0 x t + a x t 2 /2. 2 с

На первый вопрос задачи мы можем ответить, подставив данные:

t 1 = 3 c S 1x = a x t 2 / 2 = 2 3 2 / 2 = 9 (m) — это путь который прошел

c машиной за 3 секунды.

Узнать, какое расстояние он проехал за 2 секунды:

S x (2 с) = a x t 2 / 2 = 2 2 2 / 2 = 4 (м)

Итак, мы с вами знаем, что за два секунд машина проехала 4 метра.

Теперь, зная эти два расстояния, мы можем найти путь, который он прошел за третью секунду:

S 2x = S 1x + S x (2 s) = 9 — 4 = 5 (м)

Один из самых распространенных видов движения объектов в пространстве, с которым человек сталкивается каждый день, это равномерно ускоренное прямолинейное движение. В 9 классе общеобразовательной школы в курсе физики подробно изучается этот вид движения. Рассмотрим это в статье.

Кинематические характеристики движения

Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, характеризующие его.

Прежде всего, это выбранный путь. Обозначим его буквой S. Согласно определению, путь – это расстояние, которое прошло тело по траектории движения. В случае прямолинейного движения траектория представляет собой прямую линию. Соответственно, путь S — это длина прямого отрезка на этой прямой. Измеряется в метрах (м) в системе физических единиц СИ.

Скорость, или как ее часто называют линейная скорость, это скорость изменения положения тела в пространстве по траектории его движения. Обозначим скорость как v. Она измеряется в метрах в секунду (м/с).

Ускорение — третья важная величина для описания прямолинейного равноускоренного движения. Она показывает, как быстро изменяется скорость тела во времени. Обозначьте ускорение символом а и определите его в метрах в секунду в квадрате (м/с 2 ).

Путь S и скорость v являются переменными характеристиками для прямолинейного равноускоренного движения. Ускорение является постоянной величиной.

Зависимость между скоростью и ускорением

Представим себе, что некий автомобиль движется по прямой дороге, не изменяя своей скорости v 0 .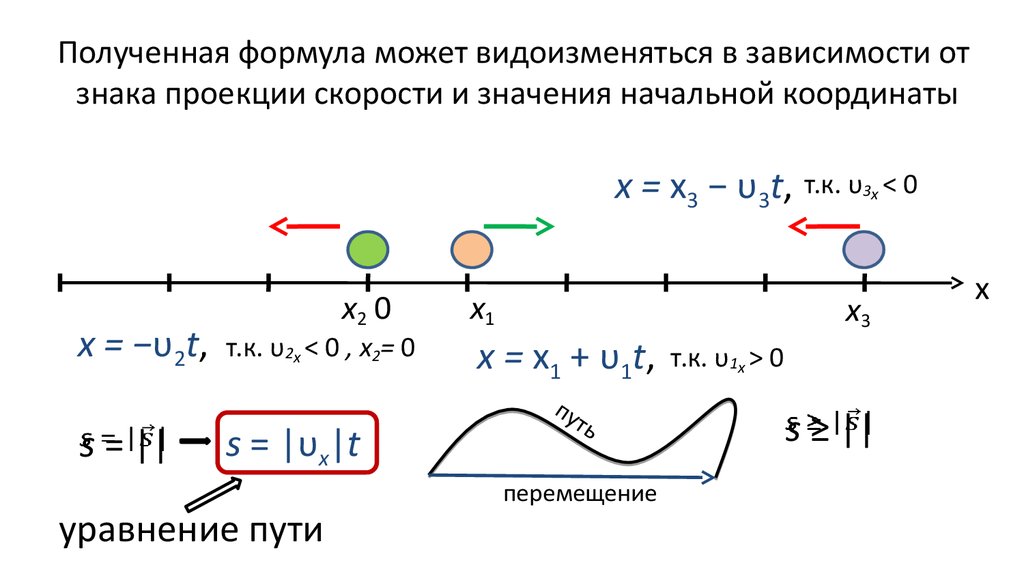 Это движение называется равномерным. В какой-то момент водитель начал нажимать на педаль газа, и машина начала увеличивать скорость, приобретая ускорение a. Если начать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, то уравнение зависимости скорости от времени примет вид:

Здесь второй член описывает увеличение скорости за каждый период времени. Так как v 0 и a — постоянные величины, а v и t — переменные параметры, то график функции v будет представлять собой прямую, пересекающую ось ординат в точке (0; v 0), и имеющую некоторый угол наклон к оси абсцисс (тангенс этого угла равен величине ускорения а).

На рисунке показаны два графика. Единственное различие между ними состоит в том, что верхний график соответствует скорости при наличии некоторого начального значения v 0 , а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начинает разгоняться из состояния покоя (например, стартующий автомобиль ).

Заметим, что если бы в приведенном выше примере водитель нажимал педаль тормоза вместо педали газа, то торможение описывалось бы следующей формулой:

Такой тип движения называется прямолинейным равномедленным.

Формулы расстояний

На практике часто бывает важно знать не только ускорение, но и величину пути, который проходит тело за заданный промежуток времени. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:

S = v 0 * t + a * t 2 / 2.

Первый член соответствует равномерному движению без ускорения. Второй член — это вклад в расстояние, пройденное чистым ускоренным движением.

В случае торможения движущегося объекта выражение для пути примет вид:

S = v 0 * t — a * t 2 / 2.

В отличие от предыдущего случая, здесь ускорение направлено против скорости движения, что приводит к тому, что последняя через некоторое время после начала торможения обращается в нуль.

Нетрудно догадаться, что графики функций S(t) будут ветвями параболы. На рисунке ниже эти графики представлены в схематическом виде.

Параболы 1 и 3 соответствуют ускоренному движению тела, парабола 2 описывает процесс торможения.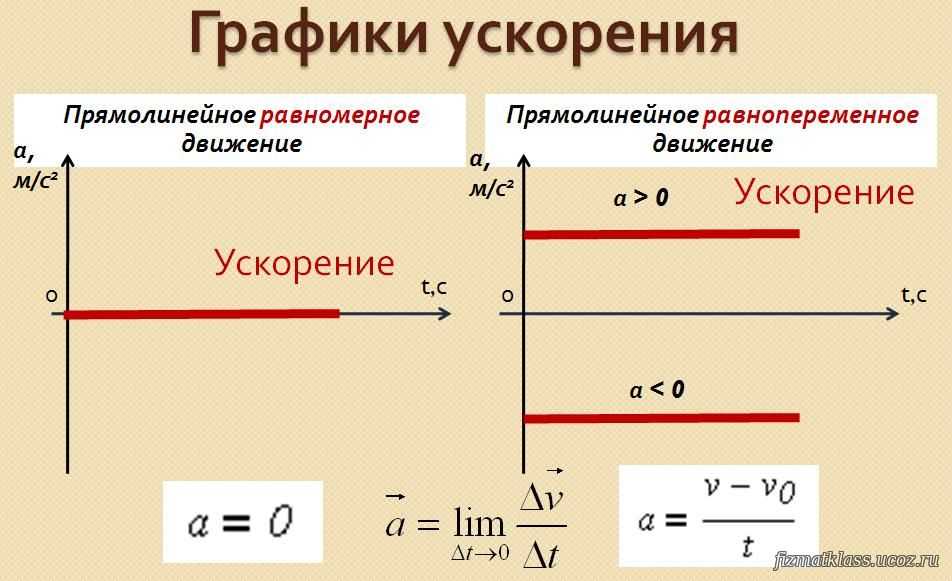 Видно, что пройденное расстояние для 1 и 3 постоянно увеличивается, а для 2 достигает некоторого постоянного значения. Последнее означает, что тело прекратило свое движение.

Задача на определение времени движения

Автомобиль должен доставить пассажира из пункта А в пункт Б. Расстояние между ними 30 км. Известно, что автомобиль движется с ускорением 1 м/с 2 в течение 20 секунд. Тогда его скорость не изменится. За какое время автомобиль довезет пассажира до точки В?

Расстояние, которое автомобиль проедет за 20 секунд, будет равно:

При этом скорость, которую он наберет за 20 секунд, будет равна:

Тогда искомое время в пути t можно рассчитать по следующей формуле:

t = (S — S 1) / v + t 1 = (S — a * t 1 2 / 2) / (a ​​​​* т 1) + т 1.

Здесь S — расстояние между А и В.

Переведите все известные данные в систему СИ и подставьте в написанное выражение. Получаем ответ: t = 1510 секунд, или примерно 25 минут.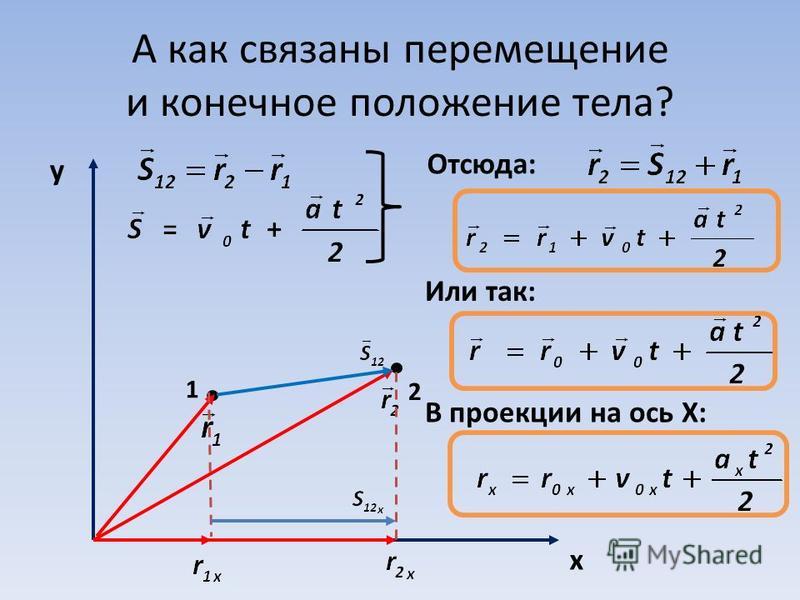

Задача расчета тормозного пути

Теперь решим задачу равномерно замедленного движения. Предположим, что грузовик движется со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь автомобиля, если он остановился за 15 с.

S = v 0 *t — a *t 2 / 2.

Время торможения t и начальная скорость v 0 известны. Ускорение а можно найти из выражения для скорости, учитывая, что его конечное значение равно нулю. Имеем:

Подставляя полученное выражение в уравнение, приходим к окончательной формуле пути S:

S = v 0 * t — v 0 * t / 2 = v 0 * t / 2.

Подставляем значения из условия и записываем ответ: S = 145,8 метра.

Задача определения скорости свободного падения

Пожалуй, самым распространенным прямолинейным равноускоренным движением в природе является свободное падение тел в гравитационном поле планет. Решим следующую задачу: тело брошено с высоты 30 метров. Какую скорость он будет иметь в момент удара о землю?

Где g = 9,81 м/с 2.

Время падения тела определяется из соответствующего выражения для пути S:

S = г * т 2 / 2;

t = √(2 * S/g).

Подставляем время t в формулу для v, получаем:

v = g * √(2 * S/g) = √(2 * S * g).

Значение пути S, пройденного телом, известно из условия, подставляем его в уравнение, получаем: v = 24,26 м/с или около 87 км/ч.

Графическое изображение равномерного прямолинейного движения

Механический механизм представлен графически. Зависимость физических величин выражается с помощью функций. Обозначение:

В (t) — изменение скорости во времени

a(t) — изменение ускорения во времени

За ускорение во времени . Так как при равномерном движении ускорение равно нулю, то зависимость a(t) представляет собой прямую линию, лежащую на оси времени.

Скорость в зависимости от времени . Так как тело движется прямолинейно и равномерно (v = const ), т. е. скорость не меняется со временем, то график зависимости скорости от времени v(t) представляет собой прямую, параллельную оси времени.

Проекция смещения тела численно равна площади прямоугольника AOBC под графиком, так как модуль вектора смещения равен произведению вектора скорости на время, в течение которого совершалось движение сделал.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора смещения равен площади прямоугольника под графиком скорости.

Зависимость перемещения от времени. График s(t) — наклонная линия :

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, можно сказать, что чем больше угол, тем быстрее движется тело и проходит большее расстояние за меньшее время.

Правило определения скорости по графику s(t): Тангенс наклона графика к оси времени равен скорости движения.

Неравномерное линейное движение.

Равномерное движение – это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело совершает неравные движения через равные промежутки времени, называется неравномерным или переменным движением .

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой, к интервалу времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, ​​а мгновенная скорость , который определяется как предел, к которому стремится средняя скорость за бесконечно малый интервал времени Δ t :

мгновенная скорость переменным движением называется скорость тела в данный момент времени или в данной точке траектории .

Мгновенная скорость тела в любой точке криволинейной траектории направлена ​​по касательной к траектории в этой точке.

Разница между средней и мгновенной скоростями показана на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называется равноускоренным или равноускоренным движением .

Ускорение — это векторная физическая величина, характеризующая скорость изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково на протяжении всего времени движения, то ускорение можно рассчитать по формуле:

Обозначения:

V x — Скорость тела при равноускоренном прямолинейном движении

V x o — Начальная скорость кузова

a x — Ускорение тела

t — время движения тела

Ускорение показывает, как быстро изменяется скорость тела. Если ускорение положительно, то скорость тела увеличивается, движение ускоряется. Если ускорение отрицательное, то скорость уменьшается, движение медленное.

Единица ускорения в системе СИ [м/с 2 ].

Ускорение измеряется Акселерометр

Уравнение скорости для равноускоренного движения: v x = v xo + a x t

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

Обозначения:

S x — Движение тела при равноускоренном прямолинейном движении

V x o — Начальная скорость тела

V x — Скорость тела при равноускоренном прямолинейном движении

a x — Ускорение тела

t — время движения тела

Еще формулы для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

Если известны начальная, конечная скорость и ускорение.

Если известны начальная, конечная скорости движения и время всего движения

Графическое изображение неравномерного прямолинейного движения

Механический механизм представлен графически.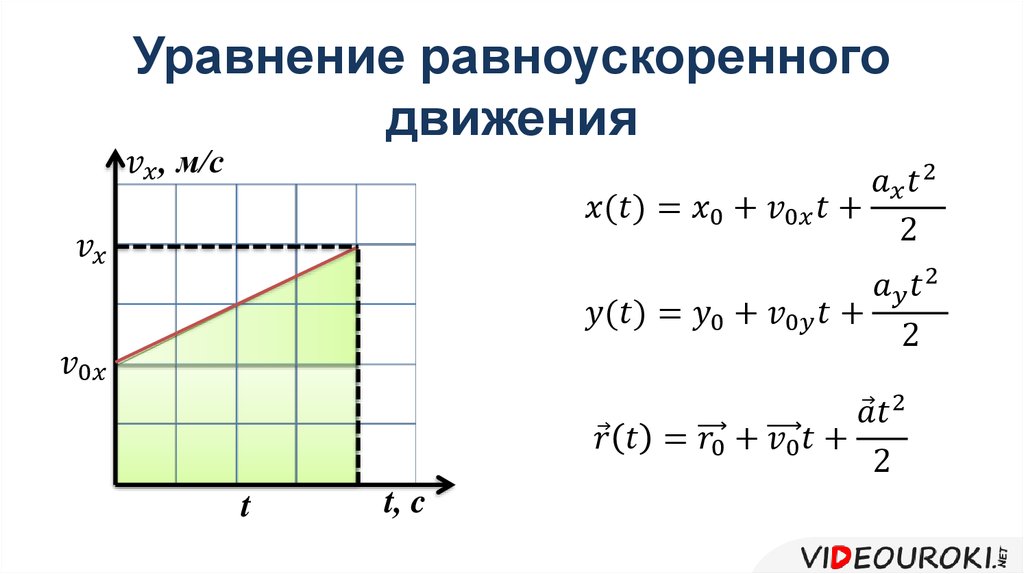 Зависимость физических величин выражается с помощью функций. Обозначение:

V(t) — изменение скорости во времени

S(t) — изменение перемещения (пути) во времени

При прямолинейном равноускоренном движении тела

1. движется по условной прямой,
2. его скорость постепенно увеличивается или уменьшается,
3. через равные промежутки времени скорость изменяется на одинаковую величину.

Например, автомобиль из состояния покоя начинает движение по прямой дороге, и до скорости, скажем, 72 км/ч движется с равномерным ускорением. При достижении заданной скорости автомобиль движется без изменения скорости, т.е. равномерно. При равноускоренном движении его скорость увеличивалась от 0 до 72 км/ч. И пусть скорость увеличивается на 3,6 км/ч за каждую секунду движения. Тогда время равноускоренного движения автомобиля будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах в секунду в квадрате, ускорение 3,6 км/ч в секунду необходимо перевести в соответствующие единицы измерения.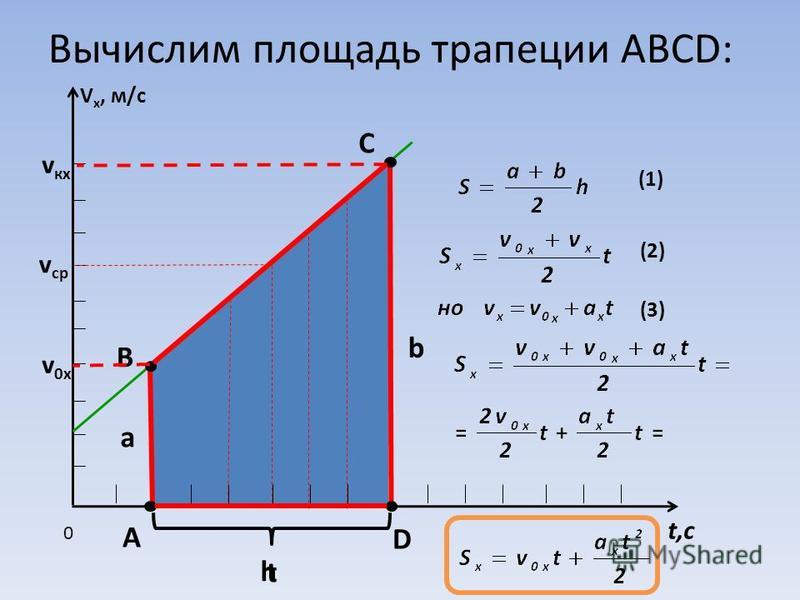 Он будет равен (3,6*1000 м)/(3600 с*1 с)=1 м/с 2,

Допустим, после некоторого времени движения с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении также было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В этом случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательное.

Итак, если начальная скорость тела равна нулю, то его скорость через время t секунд будет равна произведению ускорения к этому времени:

При падении тела «срабатывает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:

Если знать текущую скорость тела и время потребовалось развить такую ​​скорость из состояния покоя, то можно определить ускорение (т.е. как быстро изменилась скорость) путем деления скорости на время:

Однако тело могло начать равноускоренное движение не из состояния покоя , но уже обладающий некоторой скоростью (или ему была задана начальная скорость). Допустим, вы с силой бросаете камень вертикально вниз с башни. На такое тело действует ускорение свободного падения, равное 90,8 м/с 2. Однако ваша сила придала камню еще большую скорость. Таким образом, конечная скорость (в момент касания земли) будет суммой скорости, развиваемой в результате разгона, и начальной скорости. Таким образом, конечная скорость будет найдена по формуле:

Однако если камень подбросили вверх. Тогда его начальная скорость направлена ​​вверх, а ускорение свободного падения — вниз. То есть векторы скорости направлены в противоположные стороны. В этом случае (а также при торможении) из начальной скорости нужно вычесть произведение ускорения на время:

Из этих формул получаем формулы ускорения. При разгоне:

при = v – v0
а = (v – v 0)/t

При торможении:

при = v 0 – v
а = (v 0 – v)/ t

В случае, когда тело останавливается с равноускорением, то в момент остановки его скорость равна 0. Тогда формула приводится к следующему виду:

Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:

Теперь выведем формулы для пути, который проходит тело при прямолинейном равноускоренном движении . График зависимости скорости от времени при прямолинейном равномерном движении представляет собой отрезок, параллельный оси времени (обычно берется ось абсцисс). Путь рассчитывается как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении график прямой, но не параллельный оси времени. Эта прямая либо увеличивается в случае ускорения, либо уменьшается в случае замедления. Однако путь также определяется как площадь фигуры под графиком.

При прямолинейном равноускоренном движении эта фигура является трапецией. Его основаниями являются отрезок на оси у (скорости) и отрезок, соединяющий конечную точку графика с его проекцией на ось абсцисс. Стороны — это сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось абсцисс является не только стороной, но и высотой трапеции, так как она перпендикулярна ее основаниям.

Как известно, площадь трапеции равна половине суммы оснований, умноженных на высоту. Длина первого основания равна начальной скорости (v 0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом, мы получаем:

с = ½ * (v 0 + v) * t

Выше была приведена формула зависимости конечной скорости от начальной и ускорения (v = v 0 + at). Поэтому в формуле пути мы можем заменить v:

s = ½ * (v 0 + v 0 + at) * t = ½ * (2v 0 + at) * t = ½ * t * 2v 0 + ½ * t * at = v 0 t + 1/2at 2

Итак, пройденный путь определяется по формуле:

s = v 0 t + at 2 /2

(эта формула может быть получена, если учесть не площадь трапеции, а суммированием площадей прямоугольника и прямоугольного треугольника, на которые разбита трапеция.)

Если тело начало двигаться равномерно ускоренно из состояния покоя (v 0 = 0), то формула пути упрощается до s = at 2/2.

Если вектор ускорения был противоположен скорости, то произведение 2/2 необходимо вычесть. Ясно, что в этом случае разница между v 0 t и at 2/2 не должна становиться отрицательной. Когда он станет равным нулю, тело остановится. Тормозной путь будет найден. Выше была формула времени до полной остановки (t = v 0 /a). Если в формулу пути подставить значение t, то путь торможения сводится к такой формуле.

Прямолинейное и нелинейное движение: важные понятия

Движение — это процесс, посредством которого объект меняет свое положение во времени. Эта концепция неразрывно связана с изучением физики, поэтому важно понимать, что представляют собой различные типы движения. Существует несколько типов движения, но все их можно разделить на две большие категории — прямолинейное движение и нелинейное движение.

Прямолинейное движение

Прямолинейное движение относится к движению, которое происходит по прямой линии и поэтому может быть описано как имеющее только одну ось координат. Другими словами, он не меняет направление непрерывно. Этот тип движения может относиться как к движению частицы, так и тела. Движение тела называется прямолинейным, если две частицы в теле проходят одинаковое расстояние по параллельным прямым.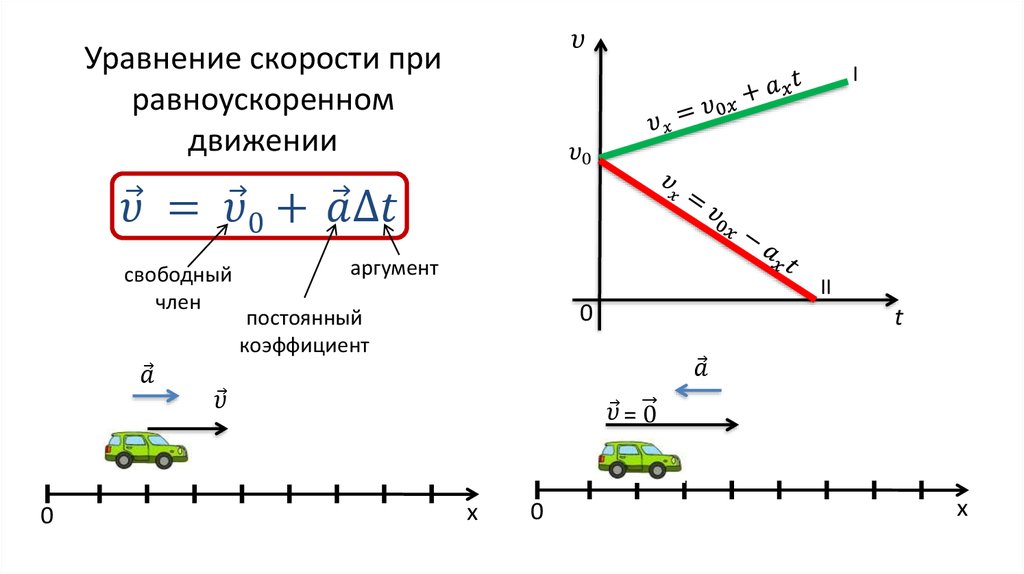 Некоторые примеры прямолинейного движения включают автомобиль или поезд, движущийся по прямой линии, или движение лифтов.

Существует три основных типа прямолинейного движения.

1. Равномерное прямолинейное движение : Это происходит, когда частица или тело движется с постоянной скоростью. то есть без ускорения.

2. Равноускоренное прямолинейное движение : Это происходит, когда объект движется с постоянным ускорением.

3. Прямолинейное движение с неравномерным ускорением : Это происходит, когда объект движется с неравномерной скоростью и ускорением.

Источник: https://www.real-world-physics-problems.com/rectilinear-motion.html

Прямолинейное движение тела.

В случае прямолинейного движения вычислить его перемещение, скорость и ускорение относительно просто. На рисунке x(t) относится к конечному положению частиц как функции времени t , где направление движения вдоль оси x.

Зная положение частиц вдоль направления движения, мы можем определить смещение, скорость и ускорение. В этих случаях мы часто предполагаем, что ускорение является постоянным, чтобы получить и использовать уравнения, которые помогают нам вычислить значения, упомянутые выше. Вот уравнения для скорости и положения в случае прямолинейного движения.

v(t) = v(0) + at

х(t) = х(0) + v(0)t + 1/2at , v(t) и x(t) относятся к скорости и положению объекта во времени и x(0) относятся к скорости и положению в момент времени t =0 соответственно.

С водоизмещением ( d ) определяется как x(t) – x(0) ,

d = v(0)t + 1/2at ²

900 только смещение, ускорение и начальная скорость, исключая время как переменную, используя это уравнение: ускорение известно и постоянно, вам просто нужно подставить соответствующие значения в уравнения, чтобы найти смещение, скорость и ускорение объекта. В случае, когда ускорение непостоянно, для получения соответствующего уравнения необходимо использовать расчет.

Например, если ускорение задано как функция времени, вам потребуется проинтегрировать его один раз, чтобы найти уравнение для скорости, и два раза — для смещения. И наоборот, если дано уравнение смещения, вам придется один раз продифференцировать его для скорости и дважды для уравнения ускорения.

Нелинейное движение

Нелинейное движение — это движение, которое не происходит по прямой линии. То есть его скорость постоянно меняется. Есть, опять же, несколько типов нелинейного движения. Вот лишь несколько примеров:

1. Движение снаряда : Это происходит, когда объект отбрасывается от земли, двигаясь по воздуху под действием силы тяжести. Это означает, что он движется по параболе. Некоторые примеры этого типа движения включают футбольный мяч или стрелу, летящую по воздуху после запуска.

2. Круговое движение : Это происходит, когда объект движется по кругу. Даже если скорость постоянна, ее скорость постоянно меняется, потому что ее направление постоянно меняется, что делает движение нелинейным. Этому изменению скорости способствует центростремительная сила, представляющая собой результирующую силу, направленную перпендикулярно направлению скорости к центру окружности. Примеры кругового движения включают воду, вращающуюся внутри ведра, или спутник, вращающийся вокруг Земли.

Работать с этими типами движения несколько сложнее, так как они уже не являются одномерными, как прямолинейное движение. В случае движения снаряда вам придется иметь дело с вертикальной и горизонтальной составляющими движения. Для круговых движений вместо этого вам нужно будет иметь дело с такими понятиями, как угловое смещение и угловая скорость.

Эти понятия может быть трудно понять самостоятельно, поэтому не стесняйтесь обращаться за помощью. Независимо от того, изучаете ли вы физику уровня O или уровня A, здесь, в Best Physics Tuition, мы можем помочь упростить эти концепции, чтобы сделать их более удобоваримыми.