Решение задачи №19 ЕГЭ по математике. Советы репетитора
Анна Малкова
Задача 18 на профильном ЕГЭ по математике. Когда-то ее называли С6, позже она была в вариантах под номером 19. Самая страшная и загадочная. Самая нестандартная. Ни на что не похожая.
Конечно, не совсем… Она похожа на задачи олимпиад по математике. Но в школьных учебниках нет даже намека на эту задачу!
Уравнения в целых числах с несколькими неизвестными. Действия в неопределенной ситуации. Метод «Оценка плюс пример» (а многие о нем даже не слышали). И конечно, культура математических рассуждений. В школе такому не учат! И немногие репетиторы умеют решать задачу 18 профильного ЕГЭ по математике.
Зато она оценивается в целых 4 первичных балла, которые пересчитываются в 9-10 тестовых!
Есть хорошая новость. Можно научиться решать эту загадочную задачу! Более того – это нужно сделать, если вы хотите сдать ЕГЭ по математике на достойные баллы. Или если вы участвуете в олимпиадах по математике.
Или если вы участвуете в олимпиадах по математике.
Многим выпускникам ЕГЭ-Студии эта задача дала необходимые для поступления баллы.
Откроем секрет. Оказывается, что один-два из четырех баллов за задачу 18 профильного ЕГЭ по математике буквально лежат у вас под ногами, и вам надо только нагнуться, чтобы взять их! Как это может быть? Смотрите видео! Учитесь строить оценки и находить нужные примеры. Без этого решить эту странную задачу невозможно. Вы узнаете также, как правильно оформлять решение задачи 18 на профильном ЕГЭ по математике.
Вот задача 18 из варианта ЕГЭ по математике. Рассказывает Анна Малкова:
На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6.
б) Может ли ровно одно число на доске оканчивается на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?
Ну как, сможете решить хотя бы первый пункт задачи 18 на профильном ЕГЭ по математике? Стоит попробовать!
Чтобы научиться решать задачу 18 профильного ЕГЭ по математике, читайте книгу Анны Малковой «Математика. Авторский курс подготовки к ЕГЭ» и смотрите видеокурс Анны Малковой по задачам на числа и их свойства (№18 ЕГЭ).
Удачи на ЕГЭ по математике!
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «ЕГЭ по математике u0026#8212; профильный уровень, задача №18» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
06. 02.2023
02.2023
Задание №19 ЕГЭ по математике профильного уровня с решением
19 задание в профильном уровне ЕГЭ по математике направлено на выявление у учеников способности оперировать числами, а именно их свойствами. Это задание наиболее сложное и требует нестандартного подхода и хорошего знания свойств чисел. Перейдем к рассмотрению типового задания.
Разбор типовых вариантов заданий №19 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно –3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно –8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Алгоритм решения:
- Вводим переменные k, l, m.

- Находим сумму набора чисел.
- Отвечаем на пункт а).
- Определяем, каких чисел больше (пункт б)).
- Определяем, сколько положительных чисел.
Решение:
1. Пусть среди записанных на доске чисел положительных k. Отрицательных чисел l и нулевых m.
2. Сумма выписанных чисел равна их количеству в данной записи на доске, умноженному на среднее арифметическое. Определяем сумму:
4k −8l + 0⋅m = − 3(k + l +m)
3. Заметим, что слева в приведенном только что равенстве каждое из слагаемых делится на 4, потому сумма количества каждого типа чисел k + l + m тоже делится на 4. По условию общее число записанных чисел удовлетворяет неравенству:
40 < k + l + m < 48
Тогда k + l + m = 44, потому что 44 единственное между 40 и 48 натуральное число, которое делится на 4.
Значит, написано на доске всего 44 числа.
4. Определяем, чисел какого вида больше: положительных или отрицательных. Для этого приведем равенство 4k −8l = − 3(k + l +m) к более упрощенному виду: 5l = 7k + 3m.
Для этого приведем равенство 4k −8l = − 3(k + l +m) к более упрощенному виду: 5l = 7k + 3m.
5. m≥ 0. Отсюда вытекает: 5l ≥ 7k, l > k. Получается, что отрицательных чисел записано больше положительных. Подставляем вместо k + l + m число 44 в равенство
4k −8l = − 3(k + l + m).
Имеем
4k − 8l = −132, k = 2l − 33
k + l ≤ 44, тогда получается: 3l − 33 ≤ 44; 3l ≤ 77; l ≤ 25; k = 2l − 33 ≤17. Отсюда приходим к выводу, что положительных чисел не более 17.
Если же положительных чисел всего 17, то на доске 17 раз записано число 4, 25 раз – число −8 и 2 раза записано число 0. Такой набор отвечает всем требованиям задачи.
Ответ: а) 44; б) отрицательных; в) 17.
Второй вариант 1 (из Ященко, №1)
На доске написано 35 различных натуральных чисел, каждое из которых либо чётное, либо его десятичная запись оканчивается на цифру 3. Сумма написанных чисел равна 1062.
Сумма написанных чисел равна 1062.
а) Может ли на доске быть ровно 27 чётных чисел?
б) Могут ли ровно два числа на доске оканчиваться на 3?
в) Какое наименьшее количество чисел, оканчивающихся на 3, может быть на доске?
Алгоритм решения:
- Приведем пример набора чисел, который удовлетворяет условию (Это подтверждает возможность набора чисел).
- Проверяем вероятность второго условия.
- Ищем ответ на третий вопрос, введя переменную n.
- Записываем ответы.
Решение:
1. Такой примерный перечень чисел на доске соответствует заданным условиям:
3,13,23,33,43,53,63,73,2,4,6,…,50,52,56
Это дает положительный ответ на вопрос а.
2. Пусть на доске написано ровно два числа, у которых последняя цифра 3. Тогда там записано 33 чётных числа. Их сумма:
Это противоречит тому, что сумма написанных чисел равна 1062, то есть, утвердительного ответа на вопрос б нет.
3. Полагаем, что на доске записано n чисел, которые оканчиваются на 3, и (35 – n)из выписанных чётные. Тогда сумма чисел, которые оканчиваются на 3, равна
Полагаем, что на доске записано n чисел, которые оканчиваются на 3, и (35 – n)из выписанных чётные. Тогда сумма чисел, которые оканчиваются на 3, равна
а сумма чётных:
2+4+…+2(35 – n)=(35 – n)(36 – n)= n2-71 n+1260.
Тогда из условия:
Решаем получившееся неравенство:
Получается, что . Отсюда, зная, что n — натуральное, получаем .
3. Наименьшее число чисел, оканчивающихся на 3, может быть только 5. И добавлено 30 чётных чисел, тогда сумма всех чисел нечётна. Значит, чисел, которые оканчиваются на 3, больше. чем пять, поскольку сумма по условию равна четному числу. Попробуем взять 6 чисел, с последней цифрой 3.
Приведём пример, когда 6 чисел, оканчиваются на три, и 29 чётных чисел. Сумма их равна 1062. Получается такой список:
3, 13, 23, 33, 43, 53, 2, 4, …, 54, 56, 82.
Ответ: а) да; б) нет; в) 6.
Третий вариант (из Ященко, №4)
Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа — n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1173 фотографии больше, чем Маша, и что фотографировали они больше одного дня.
В первый день Маша сделала m фотографий, а Наташа — n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1173 фотографии больше, чем Маша, и что фотографировали они больше одного дня.
а) Могли ли они фотографировать в течение 17 дней?
б) Могли ли они фотографировать в течение 18 дней?
в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 45 фотографий?
Алгоритм решения:
- Ответим на вопрос а).
- Найдем ответ на вопрос б).
- Найдем суммарное количество фотографий, сделанных Наташей.
- Запишем ответ.
Решение:
1. Если Маша сделала m фотографий в 1-й день, то за 17 дней она сфотографировала снимков.
Наташа, за 1-й день сделала n фотографий, тогда за оставшиеся 17 дней она сделала
кадров.
Найдем такие m и n, чтобы выполнялось равенство:
Возьмем, к примеру, n=70 и m=1. Это ответ на вопрос а).
2. Если фотографировали девочки всего 18 дней, получается:
1173 на 18 не разделится, следовательно, выбрать такие n и m нельзя. Это ответ на вопрос б.
3. Поищем ответ на последний вопрос. Допускаем, что девочки делали фотографии x дней. Тогда Маша сделала бы в последний день снимков
То есть . А согласно условию
число x является делителем 1173. Тогда возможны только варианты: x = 23, 17 или 3.
Вычисляем наибольшее число фотографий, которые могла сделать Маша. Получаем:
Для числа x=3:
При x=17:
А при x=23:
Самое большое количество снимков, которые сделала Наташа:
759+1173=1932.
Ответ: а) да; б) нет; в) 1932.
заданий, решений и пояснений ЕГЭ профильные тесты
Программа ЕГЭ, как и в предыдущие годы, составлена из материалов основных математических дисциплин. Билеты будут включать в себя математические, геометрические и алгебраические задачи.
Билеты будут включать в себя математические, геометрические и алгебраические задачи.
В КИМ ЕГЭ 2020 по математике на профильном уровне изменений нет.
Особенности заданий ЕГЭ по математике-2020- При подготовке к ЕГЭ по математике (профильному) обратите внимание на основные требования программы ЕГЭ. Он предназначен для проверки знаний продвинутой программы: векторных и математических моделей, функций и логарифмов, алгебраических уравнений и неравенств.
- Отдельно потренируйтесь решать задачи на.
- Важно проявить нестандартное мышление.
Задания ЕГЭ по профилю математики разделены на два блока.
- Часть — краткие ответы , включает 8 заданий, проверяющих базовую математическую подготовку и умение применять знания по математике в повседневной жизни.
- Часть — краткое и подробные ответы . Он состоит из 11 заданий, 4 из которых требуют краткого ответа, а 7 — развернутого с аргументацией выполняемых действий.

- Повышенной сложности — задания 9-17 второй части КИМ.
- Высокий уровень сложности — задания 18-19 –. В этой части экзаменационных заданий проверяется не только уровень математических знаний, но и наличие или отсутствие творческого подхода к решению сухих «цифровых» задач, а также эффективность умения использовать знания и умения в качестве профессионального инструмента. .
Важно! Поэтому при подготовке к экзамену всегда подкрепляйте теорию по математике решением практических задач.
Как будут распределяться баллы?Задания первой части КИМ по математике близки к ЕГЭ базового уровня, поэтому набрать по ним высокий балл невозможно.
Баллы за каждое задание по математике на профильном уровне распределились следующим образом:
- за правильные ответы на задания №№ 1-12 — по 1 баллу;
- №13-15 — по 2 шт.;
- №16-17 — по 3 шт.;
- №18-19 — по 4 штуки.

До сдачи экзамена -2020 студенту назначено 3 часа 55 минут (235 минут).
В это время учащийся не должен:
- шуметь;
- пользоваться гаджетами и другими техническими средствами;
- списание;
- попробуй помочь другим или попроси помощи для себя.
За такие действия экзаменатор может быть исключен из аудитории.
На госэкзамен по математике разрешено принести с собой только линейку, остальные материалы вам выдадут непосредственно перед экзаменом. выдается на месте.
Эффективная подготовка — решение онлайн-тестов по математике 2020. Выбирайте и получайте наивысший балл!
Оценка
две части , в том числе 19 заданий . Часть 1 Часть 2
3 часа 55 минут (235 минут).
Ответы
Но можно сделать компас Калькуляторы на экзамене

паспорт ), пропуск и капилляр или! Разрешено брать с собой воду (в прозрачной бутылке) и еду
Экзаменационная работа состоит из две части , в том числе 19 задач . Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного уровня сложности с развернутым ответом.
На выполнение экзаменационной работы по математике дается 3 часа 55 минут (235 минут).
Ответы на задания 1–12 записываются
При выполнении работы можно использовать выданные вместе с работой. Можно использовать только линейку , но можно сделать циркуль своими руками. Запрещается использовать инструменты с напечатанными на них справочными материалами. Калькуляторы на экзамене не используются .
Калькуляторы на экзамене не используются .
На экзамен необходимо иметь при себе документ, удостоверяющий личность. 9паспорт 0006 ), пропуск и ручка капиллярная или гелевая
USE 2017 Пробная версия
Уровень профиля
Условия задачи с
Экзаменационная работа состоит из двух частей, включающих 19 заданий. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут. Ответы на задания 1-12 записываются в виде целого числа или конечной десятичной дроби. При выполнении заданий 13–19, вам нужно записать полное решение.
Часть 1
Ответ на задания 1- 12 является целым числом или конечным десятичным числом. Ответ записывается в бланк ответов №1 справа от номера соответствующего задания,
 Каждую цифру, знак минус и десятичную точку числа запишите в отдельную ячейку в соответствии с образцами, приведенными в бланке. Единицы измерения не требуются.
Каждую цифру, знак минус и десятичную точку числа запишите в отдельную ячейку в соответствии с образцами, приведенными в бланке. Единицы измерения не требуются. 1 . На заправке литр бензина стоит 33 рубля. 20 коп. Водитель залил в бак 10 литров бензина и купил бутылку воды за 41 рубль. Сколько рублей сдачи он получит из 1000 рублей?
2 . На рисунке представлен график осадков в Калининграде с 4 по 10 февраля 1974 г. По оси абсцисс отложены дни, по оси ординат — количество осадков в мм. Определите по рисунку, за сколько дней из этого периода выпало от 2 до 8 мм осадков.
3 . На клетчатой бумаге два круга. Площадь внутреннего круга равна 2. Найдите площадь заштрихованной фигуры.
4 . Вероятность того, что студент Петя правильно решит более 8 задач на контрольной по истории, равна 0,76. Вероятность того, что Петя правильно решит более 7 задач, равна 0,88. Найти вероятность того, что Петя правильно решит ровно 8 задач.
5 . Решите уравнение. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
6 . Окружность, вписанная в равнобедренный треугольник, делит одну из сторон в точке касания на два отрезка, длины которых равны 10 и 1, считая от вершины, противоположной основанию. Найдите периметр треугольника.
7 . На рисунке показан график производной функции , определено на интервале (–8; 9). Найдите количество точек минимума функции , , принадлежащий интервалу [–4; 8].
8 . Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна .
9 . Найдите значение выражения
10 . Расстояние от наблюдателя, находящегося на высоте ч м над землей, выраженное в километрах, до линии горизонта, которую он видит, рассчитывается по формуле, где R = 6400 км — радиус Земли. Человек, стоящий на берегу, видит горизонт на расстоянии 4,8 километра. К пляжу ведет лестница, каждая ступенька которой имеет высоту 10 см. Какое наименьшее количество ступеней нужно пройти человеку, чтобы он мог видеть горизонт на расстоянии не менее 6,4 километра?
Человек, стоящий на берегу, видит горизонт на расстоянии 4,8 километра. К пляжу ведет лестница, каждая ступенька которой имеет высоту 10 см. Какое наименьшее количество ступеней нужно пройти человеку, чтобы он мог видеть горизонт на расстоянии не менее 6,4 километра?
11 . Два человека выходят из одного дома на прогулку на опушку леса, расположенную в 1,1 км от дома. Один идет со скоростью 2,5 км/ч, а другой – со скоростью 3 км/ч. Дойдя до края, второй возвращается с той же скоростью. На каком расстоянии от точки старта они встретятся? Дайте ответ в километрах.
12 . Найдите точку минимума функции, принадлежащую интервалу .
Для записи решений и ответов на задания 13- 19 используйте лист ответов № 2. Сначала запишите номер выполняемого задания, а затем полное мотивированное решение и ответ.
13 . а) Решите уравнение. б) Определите, какие из его корней принадлежат отрезку.
14 . В параллелепипеде ABCDA 1 B 1 C 1 D 1 точка M среднее ребро C 1 D 1 и точка K делит ребро AA 1 против AK:KA= 1:3. Через точки К А М проведена плоскость α, параллельная прямой BD и пересекающая диагональ А 1 С в точке О .
В параллелепипеде ABCDA 1 B 1 C 1 D 1 точка M среднее ребро C 1 D 1 и точка K делит ребро AA 1 против AK:KA= 1:3. Через точки К А М проведена плоскость α, параллельная прямой BD и пересекающая диагональ А 1 С в точке О .
а) Докажите, что плоскость α делит диагональ A 1 C в соотношении A 1 O: OC = 3:5.
б) Найдите угол между плоскостью α и плоскостью ( ABC ), если известно, что ABCDA 1 B 1 C 1 D 1 — куб.
15 . Решите неравенство.
16 . Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности CD и является хордой, а стороны D A и BC пересекают окружность в точках P И Q соответственно .
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ , если известно, что AP = a , BC = b , BQ = c .
17 . Вася взял кредит в банке на сумму 270 200 руб. Схема погашения кредита такова: в конце каждого года банк увеличивает оставшуюся сумму долга на 10%, после чего Вася перечисляет банку свой очередной платеж. Известно, что Вася погасил кредит за три года, и каждый его последующий платеж был ровно в три раза больше предыдущего. Сколько Вася заплатил в первый раз? Дайте ответ в рублях.
18 . Найти все такие значения параметра , при каждом из которых уравнение имеет решения на отрезке ..
Серия «ЕГЭ. ФИПИ — Школа» подготовлен разработчиками контрольно-измерительных материалов (КИМ) единого государственного экзамена. Сборник содержит:
36 типовых вариантов ЕГЭ, составленных в соответствии с проектом демо-версии КИМ ЕГЭ по математике профильного уровня в 2017;
инструкция по выполнению экзаменационной работы;
ответов на все задания;
решений и критериев оценки задач 13-19.
Выполнение заданий типовых вариантов экзамена предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки.
Учителя могут использовать стандартные экзаменационные варианты для организации контроля результатов освоения учащимися образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.
Примеры.
В чемпионате по прыжкам в воду соревнуются 30 спортсменов, среди которых 3 дайвера из Голландии и 9 дайверов из Колумбии. Порядок выступлений определяется жеребьевкой. Найти вероятность того, что прыгун из Голландии будет восьмым.
Путем смешивания 25% и 95% растворов кислот и добавления 20 кг чистой воды был получен 40% раствор кислоты. Если вместо 20 кг воды добавить 20 кг 30% раствора той же кислоты, то получится 50% раствор кислоты. Сколько килограммов 25% раствора ушло на приготовление смеси?
В чемпионате по прыжкам в воду соревнуются 20 спортсменов, в том числе 7 дайверов из Голландии и 10 дайверов из Колумбии. Порядок выступлений определяется жеребьевкой. Найти вероятность того, что прыгун из Голландии будет восьмым.
Содержание
Введение
Карта индивидуальных достижений обучающегося
Рабочая инструкция
Стандартные бланки ответов ЕГЭ
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Опция 7
Опция 8
Опция 9
Опция 10
Опция 11
Опция 12
Опция 13
Опция 14
Опция 15
Опция 16
Опция 17
Опция 2 2 2 210196 2 210196 2 21019. Опция 2196 2 210196 2 21019. Опция 2196 2 210196 2196 2 21019 2 210196 2 210196 2 210196 2196 2196 210196 2 210196 2 210196 2 210196 2 210196 2 210196 2 210196 2 210196 2 210196. 23
Опция 24
Опция 25
Опция 26
Опция 27
Опция 28
Опция 29
Опция 30
Опция 31
Опция 32
Опция 9 60196 Ответы
Решения и критерии оценивания заданий 13-19.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ, Математика, Профильный уровень, Типовые варианты ЕГЭ, 36 вариантов, Ященко И. В., 2017 — fileskachat.com, скачать быстро и бесплатно.
В., 2017 — fileskachat.com, скачать быстро и бесплатно.
- Сдам ЕГЭ, Математика, Самостоятельный курс, Технология решения задач, Профильный уровень, Часть 3, Геометрия, Ященко И.В., Шестаков С.А., 2018
- Сдам ЕГЭ, Математика, Самостоятельный курс, Технология решения задач, Профильный уровень, Часть 2, Алгебра и начало математического анализа, Ященко И.В., Шестаков С.А., 2018
- Сдам ЕГЭ , Математика, Самостоятельный курс, Технология решения задач, Базовый уровень, Часть 3, Геометрия, Ященко И.В., Шестаков С.А., 2018
- Сдам ЕГЭ, Математика, Профильный уровень, Часть 3, Геометрия, Ященко И.В., Шестаков С.А. , 2018
Следующие учебники и книги.
Среднее общее образование
Линия УМК Г.К. Муравина. Алгебра и начала математического анализа (10-11) (углубленный)
Линия УМК Мерзляк. Алгебра и начало анализа (10-11) (У)
Математика
Разбираем задачи и решаем примеры с учителем Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут).
Минимальный порог — 27 баллов.
Экзаменационная работа состоит из двух частей, различающихся по содержанию, сложности и количеству заданий.
Отличительной чертой каждой части работы является форма заданий:
- часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целой или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13-19) с развернутым ответом (полная запись решения с обоснованием выполняемые действия).
Панова Светлана Анатольевна , учитель математики высшей категории школы, стаж работы 20 лет:
«Для получения школьного аттестата выпускник должен сдать два обязательных экзамена в форме ЕГЭ Экзамен, одним из которых является математика. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике делится на два уровня: базовый и специализированный. Сегодня мы рассмотрим варианты профильного уровня.
Сегодня мы рассмотрим варианты профильного уровня.
Задание №1 — проверяет умение участников ЕГЭ применять навыки, полученные в ходе 5-9 классов по элементарной математике, в практической деятельности. Участник должен иметь вычислительные навыки, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.
Пример 1 В квартире, где проживает Петр, установлен счетчик (счетчик) холодной воды. Первого мая счетчик показывал расход 172 куб. м воды, а на первое июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды 34 рубля 17 копеек? Дайте ответ в рублях.
Решение:
1) Найдите количество расходуемой воды в месяц:
177 — 172 = 5 (м3)
2) Найдите, сколько денег заплатят за израсходованную воду:
34,17 5 = 170,85 (руб.)
Ответ: 170,85.
Задание №2 — это одно из самых простых заданий ЕГЭ. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований – это задание на использование полученных знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит в описании с помощью функций различных реальных отношений между величинами и интерпретации их графиков. Задание №2 проверяет умение извлекать информацию, представленную в таблицах, схемах, графиках. Выпускники должны уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по ее графику. Также необходимо уметь находить наибольшее или наименьшее значение по графику функции и строить графики исследуемых функций. Допущенные ошибки носят случайный характер при чтении условий задачи, чтении схемы.
С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований – это задание на использование полученных знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит в описании с помощью функций различных реальных отношений между величинами и интерпретации их графиков. Задание №2 проверяет умение извлекать информацию, представленную в таблицах, схемах, графиках. Выпускники должны уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по ее графику. Также необходимо уметь находить наибольшее или наименьшее значение по графику функции и строить графики исследуемых функций. Допущенные ошибки носят случайный характер при чтении условий задачи, чтении схемы.
#РЕКЛАМА_ВСТАВИТЬ#
Пример 2 На рисунке показано изменение курсовой стоимости одной акции горнодобывающей компании в первой половине апреля 2017 года. 7 апреля предприниматель приобрел 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько бизнесмен потерял в результате этих операций?
7 апреля предприниматель приобрел 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько бизнесмен потерял в результате этих операций?
Решение:
2) 1000 3/4 = 750 (акций) — составляют 3/4 всех купленных акций.
6) 247500 + 77500 = 325000 (рублей) — получил бизнесмен после продажи 1000 акций.
7) 340 000 — 325 000 = 15 000 (рублей) — бизнесмен потерял в результате всех операций.
математических навыков в США потерпели самый большой спад во время COVID-19
- Результаты Национального табеля успеваемости выявили резкое снижение успеваемости по математике у учащихся четвертого и восьмого классов.
- Только 26% восьмиклассников хорошо владеют математикой, по сравнению с 34% в 2019 году.
- Раздел образования.
 Кардона сказал, что, хотя отчасти виновата пандемия, основным фактором являются годы отказа от инвестиций в образование.
Кардона сказал, что, хотя отчасти виновата пандемия, основным фактором являются годы отказа от инвестиций в образование.
Спасибо за регистрацию!
Получайте доступ к своим любимым темам в персонализированной ленте, пока вы в пути.
В настоящее время у страны есть конкретные данные о экстремальных потерях в обучении, которые понесли учащиеся во время пандемии.
В понедельник была опубликована Национальная оценка образовательного прогресса, известная как Национальный табель успеваемости, в которой оценивалась успеваемость учащихся четвертого и восьмого классов с 2019 года.. Результаты были ошеломляющими: баллы по математике восьмиклассников упали почти во всех штатах, и только 26% из них владеют этим предметом, по сравнению с 34% в 2019 году. Средний балл четвероклассников по математике упал на пять баллов, а баллы по чтению по обоим сортам упал на три балла. Министр образования Мигель Кардона заявил в своем выступлении в понедельник, что эти выводы должны стать «срочным призывом к действию».
Средний балл четвероклассников по математике упал на пять баллов, а баллы по чтению по обоим сортам упал на три балла. Министр образования Мигель Кардона заявил в своем выступлении в понедельник, что эти выводы должны стать «срочным призывом к действию».
«Результаты Национальной оценки прогресса в образовании, опубликованные сегодня, ужасны, неприемлемы и напоминают о влиянии этой пандемии на наших учащихся», — говорится в заявлении Кардоны. «Эти данные также представляют собой призыв к важной работе, которую мы должны сделать сейчас для наших студентов, особенно для тех, кто больше всего пострадал во время пандемии».
«Этот вирус, появляющийся раз в поколение, перевернул нашу страну во многих отношениях — и наши ученики не могут быть теми, кто больше всего жертвует сейчас или в долгосрочной перспективе», — добавил он. «Мы должны подходить к задаче наверстать упущенное у наших детей в чтении и математике с той срочностью, которой требует этот момент».
Согласно отчету, Юта была единственным штатом, где снижение успеваемости по математике не было статистически значимым, а в таких штатах, как Мэриленд и Вашингтон, округ Колумбия, наблюдалось наибольшее снижение успеваемости по этому предмету. Комиссар Национального центра статистики образования Пегги Карр заявила журналистам в понедельник, что это «самое большое снижение в математике, которое мы наблюдали за всю историю этой оценки».
Комиссар Национального центра статистики образования Пегги Карр заявила журналистам в понедельник, что это «самое большое снижение в математике, которое мы наблюдали за всю историю этой оценки».
Но, как отметил Кардона в своем выступлении в понедельник, эти результаты нельзя отнести исключительно к пандемии, заявив, что «данные до пандемии не отражали систему образования, которая была на правильном пути. Пандемия просто усугубила ситуацию». . Это привело к снижению производительности и еще больше снизило ее».
Он назвал нехватку инвестиций в образование при предыдущих администрациях. Кардона сказал, что в ближайшие дни его отдел проинформирует преподавателей о том, как они могут использовать финансирование школ из пакета стимулов Американского плана спасения 2021 года для решения проблемы потери обучения, и запустит серию инструментов для ускорения обучения учащихся математике и чтению.
Законодатели как от республиканцев, так и от демократов выразили обеспокоенность этими результатами.


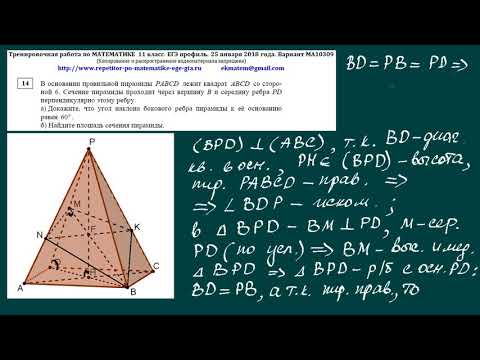
 Кардона сказал, что, хотя отчасти виновата пандемия, основным фактором являются годы отказа от инвестиций в образование.
Кардона сказал, что, хотя отчасти виновата пандемия, основным фактором являются годы отказа от инвестиций в образование.
Leave A Comment