Период полураспада | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Период полураспада — время, за которое первоначальное количество радиоактивных ядер уменьшится в два раза
![Rendered by QuickLaTeX.com \[\Large T_{1/2} = \tau \ln 2 = \frac{\ln 2}{\lambda}=0,693 \tau \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0f31a658bccf10a299546644b6f83838_l3.png)
Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время
![Rendered by QuickLaTeX.com \[2T_{1/2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-66bac2f8def84efc4679b5fa7a54a415_l3.png)
останется четверть от начального числа частиц, за
![Rendered by QuickLaTeX.com \[3T_{1/2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a302de9d7ea62cacfc0815c94e79dce9_l3.png)
— одна восьмая и так далее…
В формуле мы использовали среднее время жизни радиоактивного атома
![Rendered by QuickLaTeX.com \[\large \tau = -\frac{1}{N_0}\int_{N_0}^0 tdN = \lambda \int_0^\infty t e^{-\lambda t}dt = \frac{1}{\lambda}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bda6fa3dfe0216ee62544cb7f7f79ab5_l3.png)
В Формуле мы использовали :
![Rendered by QuickLaTeX.com \[T_{1/2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-4f1655c8d30c4dca2da8628ed160987f_l3.png)
— Период полураспада
![Rendered by QuickLaTeX.com \[\tau\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c296a066018607f6f4b9a98c8b47b913_l3.png)
— Среднее время жизни радиоактивного атома
![Rendered by QuickLaTeX.com \[\lambda\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-ab40e408da0bd057cd6a2beecd9fb7c4_l3.png)
— Постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени
Закон радиоактивного распада. Период полураспада
Закон радиоактивного распада. Период полураспада
- Подробности
- Просмотров: 585
«Физика — 11 класс»
Радиоактивный распад подчиняется статистическому закону.
Резерфорд, исследуя превращения радиоактивных веществ, установил опытным путем, что их активность убывает с течением времени.
Об этом говорилось в предыдущем параграфе.
Так, активность радона убывает в 2 раза уже через 1 мин.
Активность таких элементов, как уран, торий и радий, тоже убывает со временем, но гораздо медленнее.
Для каждого радиоактивного вещества существует определенный интервал времени, на протяжении которого активность убывает в 2 раза.
Этот интервал носит название период полураспада.
Период полураспада (Т) — это время, в течение которого распадается половина начального числа радиоактивных атомов.
Спад активности, т. е. числа распадов в секунду, в зависимости от времени для одного из радиоактивных препаратов изображен на рисунке.
Пусть число радиоактивных атомов в начальный момент времени (t = 0) равно N0.
Тогда по истечении периода полураспада это число будет равно
Спустя еще один такой же интервал времени это число станет равным:
По истечении времени t = nТ, т. е. спустя n периодов полураспада Т, радиоактивных атомов останется:
Поскольку
то
Это и есть основной закон радиоактивного распада.
По формуле можно найти число нераспавшихся ядер в любой момент времени.
Период полураспада
Чем меньше период полураспада, тем меньше времени «живут» ядра, тем быстрее происходит распад.
Для разных веществ период полураспада имеет сильно различающиеся значения.
Так, период полураспада урана равен 4,5 млрд лет.
Именно поэтому активность урана на протяжении нескольких лет заметно не меняется.
Период полураспада радия значительно меньше — он равен 1600 лет.
Поэтому активность радия значительно больше активности урана.
Есть радиоактивные элементы с периодом полураспада в миллионные доли секунды.
Чтобы определить период полураспада, надо знать число атомов
Сам закон радиоактивного распада довольно прост.
Но физический смысл этого закона уяснить себе нелегко.
Действительно, согласно этому закону за любой интервал времени распадается одна и та же доля имеющихся атомов (за период полураспада половина атомов).
Значит, с течением времени скорость распада нисколько не меняется?
Радиоактивные ядра «не стареют»..
Так, ядра радона, возникающие при распаде радия, претерпевают радиоактивный распад как сразу же после своего образования, так и спустя 10 мин после этого.
Для радиоактивных ядер не существует понятия возраста.
Можно определить лишь их среднее время жизни τ.
Время существования отдельных ядер может варьироваться от долей секунды до миллиардов лет.
Атом урана, например, может спокойно пролежать в земле миллиарды лет и внезапно взорваться, тогда как его соседи благополучно продолжают оставаться в прежнем состоянии. Среднее время жизни τ — это просто среднее арифметическое времени жизни достаточно большого количества атомов данного вида.
Предсказать, когда произойдет распад ядра данного атома, невозможно.
Смысл имеют только утверждения о поведении в среднем большой совокупности атомов.
Закон радиоактивного распада определяет среднее число ядер атомов, распадающихся за определенный интервал времени.
Но всегда имеются неизбежные отклонения от среднего значения, и, чем меньше количество радиоактивных ядер в препарате, тем больше эти отклонения.
Закон радиоактивного распада является статистическим законом.
Говорить об определенном законе радиоактивного распада для малого числа ядер атомов не имеет смысла.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Физика атомного ядра. Физика, учебник для 11 класса — Класс!ная физика
Методы наблюдения и регистрации элементарных частиц — Открытие радиоактивности. Альфа-, бета- и гамма-излучения — Радиоактивные превращения — Закон радиоактивного распада. Период полураспада — Открытие нейтрона — Строение атомного ядра. Ядерные силы. Изотопы — Энергия связи атомных ядер — Ядерные реакции — Деление ядер урана — Цепные ядерные реакции — Ядерный реактор — Термоядерные реакции. Применение ядерной энергии — Получение радиоактивных изотопов и их применение — Биологическое действие радиоактивных излучений — Краткие итоги главы — Три этапа в развитии физики элементарных частиц — Открытие позитрона. Античастицы
Период полураспада — Википедия
Пери́од полураспа́да квантовомеханической системы (частицы, ядра, атома, энергетического уровня и т. д.) — время T 1 / 2 {\displaystyle T_{1/2}} , в течение которого система распадается в примерном отношении 1/2. Если рассматривается ансамбль независимых частиц, то в течение одного периода полураспада количество выживших частиц уменьшится в среднем в 2 раза. Термин применим только к экспоненциально распадающимся системам.
Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время 2 T 1 / 2 {\displaystyle 2T_{1/2}} останется четверть от начального числа частиц, за 3 T 1 / 2 {\displaystyle 3T_{1/2}} — одна восьмая и т. д. Вообще, доля выживших частиц (или, точнее, вероятность выживания p {\displaystyle p} для данной частицы) зависит от времени t {\displaystyle t} следующим образом:
- N ( t ) N 0 ≈ p ( t ) = 2 − t / T 1 / 2 . {\displaystyle {\frac {N(t)}{N_{0}}}\approx p(t)=2^{-t/T_{1/2}}.}
Период полураспада, среднее время жизни τ {\displaystyle \tau } и постоянная распада λ {\displaystyle \lambda } связаны следующими соотношениями, полученными из закона радиоактивного распада:
- T 1 / 2 = τ ln 2 = ln 2 λ . {\displaystyle T_{1/2}=\tau \ln 2={\frac {\ln 2}{\lambda }}.}
Поскольку ln 2 = 0 , 693 … {\displaystyle \ln 2=0,693\dots } , период полураспада примерно на 30,7 % короче, чем среднее время жизни.
На практике период полураспада определяют, измеряя активность исследуемого препарата через определённые промежутки времени. Учитывая, что активность препарата пропорциональна количеству атомов распадающегося вещества, и воспользовавшись законом радиоактивного распада, можно вычислить период полураспада данного вещества[1].
Примеры
Пример 1
Если обозначить для данного момента времени число ядер, способных к радиоактивному превращению, через N {\displaystyle N} , а промежуток времени через t 2 − t 1 {\displaystyle t_{2}-t_{1}} , где t 1 {\displaystyle t_{1}} и t 2 {\displaystyle t_{2}} — достаточно близкие моменты времени ( t 1 < t 2 ) {\displaystyle (t_{1}<t_{2})} , и число разлагающихся атомных ядер в этот отрезок времени через n {\displaystyle n} , то n = K N ( t 2 − t 1 ) {\displaystyle n=KN(t_{2}-t_{1})} , где коэффициент пропорциональности K = 0 , 693 T 1 / 2 {\displaystyle K={0,693 \over T_{1/2}}} носит название константы распада. Если принять разность ( t 2 − t 1 {\displaystyle t_{2}-t_{1}} ) равной единице, то есть интервал времени наблюдения равным единице, то K = n / N {\displaystyle K=n/N} и, следовательно, константа распада показывает долю от наличного числа атомных ядер, испытывающих распад в единицу времени. Следовательно, распад совершается так, что в единицу времени распадается одна и та же доля от наличного числа атомных ядер, что определяет закон экспоненциального распада.
Величины периодов полураспада для различных изотопов различны; для некоторых, особенно быстро распадающихся, период полураспада может быть равным миллионным долям секунды, а для некоторых изотопов, как уран-238 и торий-232, он соответственно равен 4,498·109 и 1,389·1010 лет. Легко подсчитать число атомов урана-238, испытывающих превращение в данном количестве урана, например, в одном килограмме в течение одной секунды. Количество любого элемента в граммах, численно равное атомному весу, содержит, как известно, 6,02·1023 атомов. Поэтому согласно приведённой выше формуле n = K N ( t 2 − t 1 ) {\displaystyle n=KN(t_{2}-t_{1})} найдём число атомов урана, распадающихся в одном килограмме в одну секунду, имея в виду, что в году 365*24*60*60 секунд,
- 0 , 693 4 , 498 ⋅ 10 9 ⋅ 365 ⋅ 24 ⋅ 60 ⋅ 60 6 , 02 ⋅ 10 23 238 ⋅ 1000 = 12 ⋅ 10 6 . {\displaystyle {\frac {0,693}{4,498\cdot 10^{9}\cdot 365\cdot 24\cdot 60\cdot 60}}{\frac {6,02\cdot 10^{23}}{238}}\cdot 1000=12\cdot 10^{6}.}
Вычисления приводят к тому, что в одном килограмме урана в течение одной секунды распадается двенадцать миллионов атомов. Несмотря на такое огромное число, всё же скорость превращения ничтожно мала. Действительно, в секунду распадается следующая часть урана:
- 12 ⋅ 10 6 ⋅ 238 6 , 02 ⋅ 10 23 ⋅ 1000 = 47 ⋅ 10 − 19 . {\displaystyle {\frac {12\cdot 10^{6}\cdot 238}{6,02\cdot 10^{23}\cdot 1000}}=47\cdot 10^{-19}.}
Таким образом, из наличного количества урана в одну секунду распадается его доля, равная
- 47 10000000000000000000. {\displaystyle 47 \over 10000000000000000000.}
Обращаясь опять к основному закону радиоактивного распада KN(t2 — t1), то есть к тому факту, что из наличного числа атомных ядер в единицу времени распадается всего одна и та же их доля и, имея к тому же ввиду полную независимость атомных ядер в каком-либо веществе друг от друга, можно сказать, что этот закон является статистическим в том смысле, что он не указывает какие именно атомные ядра подвергнутся распаду в данный отрезок времени, а лишь говорит об их числе. Несомненно, этот закон сохраняет силу лишь для того случая, когда наличное число ядер очень велико. Некоторые из атомных ядер распадутся в ближайший момент, в то время как другие ядра будут претерпевать превращения значительно позднее, поэтому когда наличное число радиоактивных атомных ядер сравнительно невелико, закон радиоактивного распада может и не выполняться во всей строгости.
Пример 2
Образец содержит 10 г изотопа плутония Pu-239 с периодом полураспада 24 400 лет. Сколько атомов плутония распадается ежесекундно?
- N ( t ) = N 0 ⋅ 2 − t / T 1 / 2 . {\displaystyle N(t)=N_{0}\cdot 2^{-t/T_{1/2}}.}
- d N d t = − N 0 ln 2 T 1 / 2 ⋅ 2 − t / T 1 / 2 = − N ln 2 T 1 / 2 . {\displaystyle {\frac {dN}{dt}}=-{\frac {N_{0}\ln 2}{T_{1/2}}}\cdot 2^{-t/T_{1/2}}=-{\frac {N\ln 2}{T_{1/2}}}.}
- N = m μ N A = 10 239 ⋅ 6 ⋅ 10 23 = 2.5 ⋅ 10 22 . {\displaystyle N={\frac {m}{\mu }}N_{A}={\frac {10}{239}}\cdot 6\cdot 10^{23}=2.5\cdot 10^{22}.}
- T 1 / 2 = 24400 ⋅ 365.24 ⋅ 24 ⋅ 3600 = 7.7 ⋅ 10 11 s . {\displaystyle T_{1/2}=24400\cdot 365.24\cdot 24\cdot 3600=7.7\cdot 10^{11}s.}
- d N d t = N ln 2 T 1 / 2 = 2.5 ⋅ 10 22 ⋅ 0.693 7.7 ⋅ 10 11 = 2.25 ⋅ 10 10 s − 1 . {\displaystyle {\frac {dN}{dt}}={\frac {N\ln 2}{T_{1/2}}}={\frac {2.5\cdot 10^{22}\cdot 0.693}{7.7\cdot 10^{11}}}=2.25\cdot 10^{10}~s^{-1}.}
Мы вычислили мгновенную скорость распада. Количество распавшихся атомов вычислим по формуле
- Δ N = Δ t ⋅ d N d t = 1 ⋅ 2.25 ⋅ 10 10 = 2.25 ⋅ 10 10 . {\displaystyle \Delta N=\Delta t\cdot {\frac {dN}{dt}}=1\cdot 2.25\cdot 10^{10}=2.25\cdot 10^{10}.}
Последняя формула действительна только тогда, когда рассматриваемый период времени (в данном случае — 1 секунда) значительно меньше, чем период полураспада. Когда рассматриваемый период времени сравним с периодом полураспада, следует пользоваться формулой
- Δ N = N 0 − N ( t ) = N 0 ( 1 − 2 − t / T 1 / 2 ) . {\displaystyle \Delta N=N_{0}-N(t)=N_{0}\left(1-2^{-t/T_{1/2}}\right).}
Эта формула пригодна в любом случае, однако для малых периодов времени требует вычислений с очень большой точностью. Для данной задачи:
- Δ N = N 0 ( 1 − 2 − t / T 1 / 2 ) = 2.5 ⋅ 10 22 ( 1 − 2 − 1 / 7.7 ⋅ 10 11 ) = 2.5 ⋅ 10 22 ( 1 − 0.99999999999910 ) = 2.25 ⋅ 10 10 . {\displaystyle \Delta N=N_{0}\left(1-2^{-t/T_{1/2}}\right)=2.5\cdot 10^{22}\left(1-2^{-1/7.7\cdot 10^{11}}\right)=2.5\cdot 10^{22}\left(1-0.99999999999910\right)=2.25\cdot 10^{10}.}
Парциальный период полураспада
Если система с периодом полураспада T 1 / 2 {\displaystyle T_{1/2}} может распадаться по нескольким каналам, для каждого из них можно определить парциальный период полураспада. Пусть вероятность распада по i-му каналу (коэффициент ветвления) равна p i {\displaystyle p_{i}} . Тогда парциальный период полураспада по i-му каналу равен
- T 1 / 2 ( i ) = T 1 / 2 p i . {\displaystyle T_{1/2}^{(i)}={\frac {T_{1/2}}{p_{i}}}.}
Парциальный T 1 / 2 ( i ) {\displaystyle T_{1/2}^{(i)}} имеет смысл периода полураспада, который был бы у данной системы, если «выключить» все каналы распада, кроме i-го. Так как по определению p i ≤ 1 {\displaystyle p_{i}\leq 1} , то T 1 / 2 ( i ) ≥ T 1 / 2 {\displaystyle T_{1/2}^{(i)}\geq T_{1/2}} для любого канала распада.
Стабильность периода полураспада
Во всех наблюдавшихся случаях (кроме некоторых изотопов, распадающихся путём электронного захвата) период полураспада был постоянным (отдельные сообщения об изменении периода были вызваны недостаточной точностью эксперимента, в частности, неполной очисткой от высокоактивных изотопов). В связи с этим период полураспада считается неизменным. На этом основании строится определение абсолютного геологического возраста горных пород, а также радиоуглеродный метод определения возраста биологических останков.
Предположение об изменяемости периода полураспада используется креационистами, а также представителями т. н. «альтернативной науки» для опровержения научной датировки горных пород, остатков живых существ и исторических находок, с целью дальнейшего опровержения научных теорий, построенных с использованием такой датировки. (См., например, статьи Креационизм, Научный креационизм, Критика эволюционизма, Туринская плащаница).
Вариабельность постоянной распада для электронного захвата наблюдалась в эксперименте, но она лежит в пределах процента во всём доступном в лаборатории диапазоне давлений и температур. Период полураспада в этом случае изменяется в связи с некоторой (довольно слабой) зависимостью плотности волновой функции орбитальных электронов в окрестности ядра от давления и температуры. Существенные изменения постоянной распада наблюдались также для сильно ионизованных атомов (так, в предельном случае полностью ионизованного ядра электронный захват может происходить только при взаимодействии ядра со свободными электронами плазмы; кроме того, распад, разрешённый для нейтральных атомов, в некоторых случаях для сильно ионизованных атомов может быть запрещён кинематически). Все эти варианты изменения постоянных распада, очевидно, не могут быть привлечены для «опровержения» радиохронологических датировок, поскольку погрешность самого радиохронометрического метода для большинства изотопов-хронометров составляет более процента, а высокоионизованные атомы в природных объектах на Земле не могут существовать сколько-нибудь длительное время.
Поиск возможных вариаций периодов полураспада радиоактивных изотопов, как в настоящее время, так и в течение миллиардов лет, интересен в связи с гипотезой о вариациях значений фундаментальных констант в физике (постоянной тонкой структуры, константы Ферми и т. д.). Однако тщательные измерения пока не принесли результата — в пределах погрешности эксперимента изменения периодов полураспада не были найдены. Так, было показано, что за 4,6 млрд лет константа α-распада самария-147 изменилась не более чем на 0,75 %, а для β-распада рения-187 изменение за это же время не превышает 0,5 %[2]; в обоих случаях результаты совместимы с отсутствием таких изменений вообще.
См. также
Примечания
- ↑ Фиалков Ю. Я. Применение изотопов в химии и химической промышленности. — К.: Техніка, 1975. — С. 52. — 240 с. — 2000 экз.
- ↑ Jean-Philippe Uzan. The fundamental constants and their variation: observational status and theoretical motivations. Rev.Mod.Phys. 75(2003)403. arXiv: hep-ph/0205340.
Период полураспада | Все формулы
Период полураспада — время, за которое первоначальное количество радиоактивных ядер уменьшится в два раза
Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время останется четверть от начального числа частиц, за — одна восьмая и так далее…
В формуле мы использовали среднее время жизни радиоактивного атома
Таблица значений периода полураспада для некоторых значений:
В Формуле мы использовали :
— Период полураспада
— Среднее время жизни радиоактивного атома
— Постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени
Период полураспада — Википедия
Пери́од полураспа́да квантовомеханической системы (частицы, ядра, атома, энергетического уровня и т. д.) — время T 1 / 2 {\displaystyle T_{1/2}} , в течение которого система распадается в примерном отношении 1/2. Если рассматривается ансамбль независимых частиц, то в течение одного периода полураспада количество выживших частиц уменьшится в среднем в 2 раза. Термин применим только к экспоненциально распадающимся системам.
Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время 2 T 1 / 2 {\displaystyle 2T_{1/2}} останется четверть от начального числа частиц, за 3 T 1 / 2 {\displaystyle 3T_{1/2}} — одна восьмая и т. д. Вообще, доля выживших частиц (или, точнее, вероятность выживания p {\displaystyle p} для данной частицы) зависит от времени t {\displaystyle t} следующим образом:
- N ( t ) N 0 ≈ p ( t ) = 2 − t / T 1 / 2 . {\displaystyle {\frac {N(t)}{N_{0}}}\approx p(t)=2^{-t/T_{1/2}}.}
Период полураспада, среднее время жизни τ {\displaystyle \tau } и постоянная распада λ {\displaystyle \lambda } связаны следующими соотношениями, полученными из закона радиоактивного распада:
- T 1 / 2 = τ ln 2 = ln 2 λ . {\displaystyle T_{1/2}=\tau \ln 2={\frac {\ln 2}{\lambda }}.}
Поскольку ln 2 = 0 , 693 … {\displaystyle \ln 2=0,693\dots } , период полураспада примерно на 30,7 % короче, чем среднее время жизни.
На практике период полураспада определяют, измеряя активность исследуемого препарата через определённые промежутки времени. Учитывая, что активность препарата пропорциональна количеству атомов распадающегося вещества, и воспользовавшись законом радиоактивного распада, можно вычислить период полураспада данного вещества[1].
Примеры
Пример 1
Если обозначить для данного момента времени число ядер, способных к радиоактивному превращению, через N {\displaystyle N} , а промежуток времени через t 2 − t 1 {\displaystyle t_{2}-t_{1}} , где t 1 {\displaystyle t_{1}} и t 2 {\displaystyle t_{2}} — достаточно близкие моменты времени ( t 1 < t 2 ) {\displaystyle (t_{1}<t_{2})} , и число разлагающихся атомных ядер в этот отрезок времени через n {\displaystyle n} , то n = K N ( t 2 − t 1 ) {\displaystyle n=KN(t_{2}-t_{1})} , где коэффициент пропорциональности K = 0 , 693 T 1 / 2 {\displaystyle K={0,693 \over T_{1/2}}} носит название константы распада. Если принять разность ( t 2 − t 1 {\displaystyle t_{2}-t_{1}} ) равной единице, то есть интервал времени наблюдения равным единице, то K = n / N {\displaystyle K=n/N} и, следовательно, константа распада показывает долю от наличного числа атомных ядер, испытывающих распад в единицу времени. Следовательно, распад совершается так, что в единицу времени распадается одна и та же доля от наличного числа атомных ядер, что определяет закон экспоненциального распада.
Величины периодов полураспада для различных изотопов различны; для некоторых, особенно быстро распадающихся, период полураспада может быть равным миллионным долям секунды, а для некоторых изотопов, как уран-238 и торий-232, он соответственно равен 4,498·109 и 1,389·1010 лет. Легко подсчитать число атомов урана-238, испытывающих превращение в данном количестве урана, например, в одном килограмме в течение одной секунды. Количество любого элемента в граммах, численно равное атомному весу, содержит, как известно, 6,02·1023 атомов. Поэтому согласно приведённой выше формуле n = K N ( t 2 − t 1 ) {\displaystyle n=KN(t_{2}-t_{1})} найдём число атомов урана, распадающихся в одном килограмме в одну секунду, имея в виду, что в году 365*24*60*60 секунд,
- 0 , 693 4 , 498 ⋅ 10 9 ⋅ 365 ⋅ 24 ⋅ 60 ⋅ 60 6 , 02 ⋅ 10 23 238 ⋅ 1000 = 12 ⋅ 10 6 . {\displaystyle {\frac {0,693}{4,498\cdot 10^{9}\cdot 365\cdot 24\cdot 60\cdot 60}}{\frac {6,02\cdot 10^{23}}{238}}\cdot 1000=12\cdot 10^{6}.}
Вычисления приводят к тому, что в одном килограмме урана в течение одной секунды распадается двенадцать миллионов атомов. Несмотря на такое огромное число, всё же скорость превращения ничтожно мала. Действительно, в секунду распадается следующая часть урана:
- 12 ⋅ 10 6 ⋅ 238 6 , 02 ⋅ 10 23 ⋅ 1000 = 47 ⋅ 10 − 19 . {\displaystyle {\frac {12\cdot 10^{6}\cdot 238}{6,02\cdot 10^{23}\cdot 1000}}=47\cdot 10^{-19}.}
Таким образом, из наличного количества урана в одну секунду распадается его доля, равная
- 47 10000000000000000000. {\displaystyle 47 \over 10000000000000000000.}
Обращаясь опять к основному закону радиоактивного распада KN(t2 — t1), то есть к тому факту, что из наличного числа атомных ядер в единицу времени распадается всего одна и та же их доля и, имея к тому же ввиду полную независимость атомных ядер в каком-либо веществе друг от друга, можно сказать, что этот закон является статистическим в том смысле, что он не указывает какие именно атомные ядра подвергнутся распаду в данный отрезок времени, а лишь говорит об их числе. Несомненно, этот закон сохраняет силу лишь для того случая, когда наличное число ядер очень велико. Некоторые из атомных ядер распадутся в ближайший момент, в то время как другие ядра будут претерпевать превращения значительно позднее, поэтому когда наличное число радиоактивных атомных ядер сравнительно невелико, закон радиоактивного распада может и не выполняться во всей строгости.
Пример 2
Образец содержит 10 г изотопа плутония Pu-239 с периодом полураспада 24 400 лет. Сколько атомов плутония распадается ежесекундно?
- N ( t ) = N 0 ⋅ 2 − t / T 1 / 2 . {\displaystyle N(t)=N_{0}\cdot 2^{-t/T_{1/2}}.}
- d N d t = − N 0 ln 2 T 1 / 2 ⋅ 2 − t / T 1 / 2 = − N ln 2 T 1 / 2 . {\displaystyle {\frac {dN}{dt}}=-{\frac {N_{0}\ln 2}{T_{1/2}}}\cdot 2^{-t/T_{1/2}}=-{\frac {N\ln 2}{T_{1/2}}}.}
- N = m μ N A = 10 239 ⋅ 6 ⋅ 10 23 = 2.5 ⋅ 10 22 . {\displaystyle N={\frac {m}{\mu }}N_{A}={\frac {10}{239}}\cdot 6\cdot 10^{23}=2.5\cdot 10^{22}.}
- T 1 / 2 = 24400 ⋅ 365.24 ⋅ 24 ⋅ 3600 = 7.7 ⋅ 10 11 s . {\displaystyle T_{1/2}=24400\cdot 365.24\cdot 24\cdot 3600=7.7\cdot 10^{11}s.}
- d N d t = N ln 2 T 1 / 2 = 2.5 ⋅ 10 22 ⋅ 0.693 7.7 ⋅ 10 11 = 2.25 ⋅ 10 10 s − 1 . {\displaystyle {\frac {dN}{dt}}={\frac {N\ln 2}{T_{1/2}}}={\frac {2.5\cdot 10^{22}\cdot 0.693}{7.7\cdot 10^{11}}}=2.25\cdot 10^{10}~s^{-1}.}
Мы вычислили мгновенную скорость распада. Количество распавшихся атомов вычислим по формуле
- Δ N = Δ t ⋅ d N d t = 1 ⋅ 2.25 ⋅ 10 10 = 2.25 ⋅ 10 10 . {\displaystyle \Delta N=\Delta t\cdot {\frac {dN}{dt}}=1\cdot 2.25\cdot 10^{10}=2.25\cdot 10^{10}.}
Последняя формула действительна только тогда, когда рассматриваемый период времени (в данном случае — 1 секунда) значительно меньше, чем период полураспада. Когда рассматриваемый период времени сравним с периодом полураспада, следует пользоваться формулой
- Δ N = N 0 − N ( t ) = N 0 ( 1 − 2 − t / T 1 / 2 ) . {\displaystyle \Delta N=N_{0}-N(t)=N_{0}\left(1-2^{-t/T_{1/2}}\right).}
Эта формула пригодна в любом случае, однако для малых периодов времени требует вычислений с очень большой точностью. Для данной задачи:
- Δ N = N 0 ( 1 − 2 − t / T 1 / 2 ) = 2.5 ⋅ 10 22 ( 1 − 2 − 1 / 7.7 ⋅ 10 11 ) = 2.5 ⋅ 10 22 ( 1 − 0.99999999999910 ) = 2.25 ⋅ 10 10 . {\displaystyle \Delta N=N_{0}\left(1-2^{-t/T_{1/2}}\right)=2.5\cdot 10^{22}\left(1-2^{-1/7.7\cdot 10^{11}}\right)=2.5\cdot 10^{22}\left(1-0.99999999999910\right)=2.25\cdot 10^{10}.}
Парциальный период полураспада
Если система с периодом полураспада T 1 / 2 {\displaystyle T_{1/2}} может распадаться по нескольким каналам, для каждого из них можно определить парциальный период полураспада. Пусть вероятность распада по i-му каналу (коэффициент ветвления) равна p i {\displaystyle p_{i}} . Тогда парциальный период полураспада по i-му каналу равен
- T 1 / 2 ( i ) = T 1 / 2 p i . {\displaystyle T_{1/2}^{(i)}={\frac {T_{1/2}}{p_{i}}}.}
Парциальный T 1 / 2 ( i ) {\displaystyle T_{1/2}^{(i)}} имеет смысл периода полураспада, который был бы у данной системы, если «выключить» все каналы распада, кроме i-го. Так как по определению p i ≤ 1 {\displaystyle p_{i}\leq 1} , то T 1 / 2 ( i ) ≥ T 1 / 2 {\displaystyle T_{1/2}^{(i)}\geq T_{1/2}} для любого канала распада.
Стабильность периода полураспада
Во всех наблюдавшихся случаях (кроме некоторых изотопов, распадающихся путём электронного захвата) период полураспада был постоянным (отдельные сообщения об изменении периода были вызваны недостаточной точностью эксперимента, в частности, неполной очисткой от высокоактивных изотопов). В связи с этим период полураспада считается неизменным. На этом основании строится определение абсолютного геологического возраста горных пород, а также радиоуглеродный метод определения возраста биологических останков.
Предположение об изменяемости периода полураспада используется креационистами, а также представителями т. н. «альтернативной науки» для опровержения научной датировки горных пород, остатков живых существ и исторических находок, с целью дальнейшего опровержения научных теорий, построенных с использованием такой датировки. (См., например, статьи Креационизм, Научный креационизм, Критика эволюционизма, Туринская плащаница).
Вариабельность постоянной распада для электронного захвата наблюдалась в эксперименте, но она лежит в пределах процента во всём доступном в лаборатории диапазоне давлений и температур. Период полураспада в этом случае изменяется в связи с некоторой (довольно слабой) зависимостью плотности волновой функции орбитальных электронов в окрестности ядра от давления и температуры. Существенные изменения постоянной распада наблюдались также для сильно ионизованных атомов (так, в предельном случае полностью ионизованного ядра электронный захват может происходить только при взаимодействии ядра со свободными электронами плазмы; кроме того, распад, разрешённый для нейтральных атомов, в некоторых случаях для сильно ионизованных атомов может быть запрещён кинематически). Все эти варианты изменения постоянных распада, очевидно, не могут быть привлечены для «опровержения» радиохронологических датировок, поскольку погрешность самого радиохронометрического метода для большинства изотопов-хронометров составляет более процента, а высокоионизованные атомы в природных объектах на Земле не могут существовать сколько-нибудь длительное время.
Поиск возможных вариаций периодов полураспада радиоактивных изотопов, как в настоящее время, так и в течение миллиардов лет, интересен в связи с гипотезой о вариациях значений фундаментальных констант в физике (постоянной тонкой структуры, константы Ферми и т. д.). Однако тщательные измерения пока не принесли результата — в пределах погрешности эксперимента изменения периодов полураспада не были найдены. Так, было показано, что за 4,6 млрд лет константа α-распада самария-147 изменилась не более чем на 0,75 %, а для β-распада рения-187 изменение за это же время не превышает 0,5 %[2]; в обоих случаях результаты совместимы с отсутствием таких изменений вообще.
См. также
Примечания
- ↑ Фиалков Ю. Я. Применение изотопов в химии и химической промышленности. — К.: Техніка, 1975. — С. 52. — 240 с. — 2000 экз.
- ↑ Jean-Philippe Uzan. The fundamental constants and their variation: observational status and theoretical motivations. Rev.Mod.Phys. 75(2003)403. arXiv: hep-ph/0205340.
Период полураспада – формула для радиоактивных веществ и частиц
Одним из важнейших параметров радиоактивного распада является параметр, называемый периодом полураспада. Рассмотрим это понятие более подробно.


Закон радиоактивного распада
Радиоактивность – это способность атомов некоторых веществ превращаться в атомы других веществ с испусканием γ-лучей, а также α- и β- частиц. Такой способностью обладают все элементы с номером 84 и более.


Рис. 1. Радиоактивность.
Распад атомов – это случайный процесс, но, если взять большое число атомов, то можно заметить, что скорость распада зависит только от количества атомов в пробе. Например, количество атомов Калия-42 (цифра означает массовое число изотопа) в пробе равно:
Часы | Количество,% |
0 | 100 |
6 | 70.7 |
12 | 50.0 |
18 | 35.4 |
24 | 25.0 |
30 | 17.7 |
36 | 12.5 |
42 | 8.8 |
48 | 6.3 |
То есть, если массовая доля Калия-42 в пробе изначально была 100г, то за первые шесть часов она уменьшилась на 30г, а за восьмой шестичасовый период – только на 2,5г. Произошло это потому, что в пробе к этому времени стало значительно меньше атомов, скорость распада уменьшилась.
Если взять другое вещество, с другой скоростью распада, например, Йод-124, и замерить массовую долю Йода в пробе в те же моменты, получим следующую таблицу:
Часы | Количество,% |
0 | 100 |
6 | 95.8 |
12 | 91.7 |
18 | 87.8 |
24 | 84.1 |
30 | 80.5 |
36 | 77.1 |
42 | 73.8 |
48 | 70.7 |
Сравнивая ее с предыдущей, можно отметить, что скорость распада у Йода-124 гораздо меньше, чем у Калия-42, однако, и для этого элемента за первый период распадается большее количество атомов, в последующие периоды – меньшее.
Таким образом, количество нераспавшегося вещества представляет собой бесконечно убывающую геометрическую прогрессию:


Рис. 2. График радиоактивного распада.
Это степенная функция с отрицательным показателем. В качестве основания функции удобно принять число 2. В результате закон, радиоактивного распада, выражающий, сколько атомов остается в пробе спустя время $t$, выражается формулой:
$$N=N_0×2^{-{1over T}t},$$
где:
- $t$ – прошедшее время,c;
- $N$ – оставшееся количество атомов;
- $N_0$ – начальное количество атомов в момент $t=0$.
- T – параметр интенсивности (период полураспада),c.
Период полураспада
В представленной формуле есть важный параметр $T$. Его физический смысл можно понять, если в принять $T=t$. В этом случае:
$$N=N_0×2^{-{1over T}t}=N_0×2^{-{Tover T}}={N_0over 2}$$
То есть, этот параметр представляет собой время, за которое распадется половина атомов исходного вещества. Он называется периодом полураспада. Подставляя в формулу период полураспада и текущее время, можно получать количество оставшихся атомов в данный момент времени.
Все природные радиоактивные вещества – это изотопы с большими периодами полураспада, превышающими время жизни Солнечной системы. Изотопы с более короткими периодами к настоящему времени уже распались, и образуются только в результате распада более долгоживущих изотопов или в результате специальных реакций в ядерных реакторах. Наиболее длительный измеренный период полураспада имеет Теллур-128 – более $2×10^{24}$ лет, что намного больше больше, чем возраст Вселенной ($1.4×10^{10}$ лет).


Рис. 3. Периоды полураспада элементов.
Что мы узнали?
Доля атомов любых радиоактивных веществ, распадающихся за единицу времени постоянна (для каждого вещества – своя). Период полураспада – это время, за которое распадается половину исходных атомов.
Предыдущая
ФизикаРеактивное движение – формула, теория, принцип
СледующаяФизикаЗакон радиоактивного распада – формула
Период полураспада — Википедия. Что такое Период полураспада
Пери́од полураспа́да квантовомеханической системы (частицы, ядра, атома, энергетического уровня и т. д.) — время T 1 / 2 {\displaystyle T_{1/2}} , в течение которого система распадается в примерном отношении 1/2. Если рассматривается ансамбль независимых частиц, то в течение одного периода полураспада количество выживших частиц уменьшится в среднем в 2 раза. Термин применим только к экспоненциально распадающимся системам.
Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время 2 T 1 / 2 {\displaystyle 2T_{1/2}} останется четверть от начального числа частиц, за 3 T 1 / 2 {\displaystyle 3T_{1/2}} — одна восьмая и т. д. Вообще, доля выживших частиц (или, точнее, вероятность выживания p {\displaystyle p} для данной частицы) зависит от времени t {\displaystyle t} следующим образом:
- N ( t ) N 0 ≈ p ( t ) = 2 − t / T 1 / 2 . {\displaystyle {\frac {N(t)}{N_{0}}}\approx p(t)=2^{-t/T_{1/2}}.}
Период полураспада, среднее время жизни τ {\displaystyle \tau } и постоянная распада λ {\displaystyle \lambda } связаны следующими соотношениями, полученными из закона радиоактивного распада:
- T 1 / 2 = τ ln 2 = ln 2 λ . {\displaystyle T_{1/2}=\tau \ln 2={\frac {\ln 2}{\lambda }}.}
Поскольку ln 2 = 0 , 693 … {\displaystyle \ln 2=0,693\dots } , период полураспада примерно на 30,7 % короче, чем среднее время жизни.
На практике период полураспада определяют, измеряя активность исследуемого препарата через определённые промежутки времени. Учитывая, что активность препарата пропорциональна количеству атомов распадающегося вещества, и воспользовавшись законом радиоактивного распада, можно вычислить период полураспада данного вещества[1].
Примеры
Пример 1
Если обозначить для данного момента времени число ядер, способных к радиоактивному превращению, через N {\displaystyle N} , а промежуток времени через t 2 − t 1 {\displaystyle t_{2}-t_{1}} , где t 1 {\displaystyle t_{1}} и t 2 {\displaystyle t_{2}} — достаточно близкие моменты времени ( t 1 < t 2 ) {\displaystyle (t_{1}<t_{2})} , и число разлагающихся атомных ядер в этот отрезок времени через n {\displaystyle n} , то n = K N ( t 2 − t 1 ) {\displaystyle n=KN(t_{2}-t_{1})} , где коэффициент пропорциональности K = 0 , 693 T 1 / 2 {\displaystyle K={0,693 \over T_{1/2}}} носит название константы распада. Если принять разность ( t 2 − t 1 {\displaystyle t_{2}-t_{1}} ) равной единице, то есть интервал времени наблюдения равным единице, то K = n / N {\displaystyle K=n/N} и, следовательно, константа распада показывает долю от наличного числа атомных ядер, испытывающих распад в единицу времени. Следовательно, распад совершается так, что в единицу времени распадается одна и та же доля от наличного числа атомных ядер, что определяет закон экспоненциального распада.
Величины периодов полураспада для различных изотопов различны; для некоторых, особенно быстро распадающихся, период полураспада может быть равным миллионным долям секунды, а для некоторых изотопов, как уран-238 и торий-232, он соответственно равен 4,498·109 и 1,389·1010 лет. Легко подсчитать число атомов урана-238, испытывающих превращение в данном количестве урана, например, в одном килограмме в течение одной секунды. Количество любого элемента в граммах, численно равное атомному весу, содержит, как известно, 6,02·1023 атомов. Поэтому согласно приведённой выше формуле n = K N ( t 2 − t 1 ) {\displaystyle n=KN(t_{2}-t_{1})} найдём число атомов урана, распадающихся в одном килограмме в одну секунду, имея в виду, что в году 365*24*60*60 секунд,
- 0 , 693 4 , 498 ⋅ 10 9 ⋅ 365 ⋅ 24 ⋅ 60 ⋅ 60 6 , 02 ⋅ 10 23 238 ⋅ 1000 = 12 ⋅ 10 6 . {\displaystyle {\frac {0,693}{4,498\cdot 10^{9}\cdot 365\cdot 24\cdot 60\cdot 60}}{\frac {6,02\cdot 10^{23}}{238}}\cdot 1000=12\cdot 10^{6}.}
Вычисления приводят к тому, что в одном килограмме урана в течение одной секунды распадается двенадцать миллионов атомов. Несмотря на такое огромное число, всё же скорость превращения ничтожно мала. Действительно, в секунду распадается следующая часть урана:
- 12 ⋅ 10 6 ⋅ 238 6 , 02 ⋅ 10 23 ⋅ 1000 = 47 ⋅ 10 − 19 . {\displaystyle {\frac {12\cdot 10^{6}\cdot 238}{6,02\cdot 10^{23}\cdot 1000}}=47\cdot 10^{-19}.}
Таким образом, из наличного количества урана в одну секунду распадается его доля, равная
- 47 10000000000000000000. {\displaystyle 47 \over 10000000000000000000.}
Обращаясь опять к основному закону радиоактивного распада KN(t2 — t1), то есть к тому факту, что из наличного числа атомных ядер в единицу времени распадается всего одна и та же их доля и, имея к тому же ввиду полную независимость атомных ядер в каком-либо веществе друг от друга, можно сказать, что этот закон является статистическим в том смысле, что он не указывает какие именно атомные ядра подвергнутся распаду в данный отрезок времени, а лишь говорит об их числе. Несомненно, этот закон сохраняет силу лишь для того случая, когда наличное число ядер очень велико. Некоторые из атомных ядер распадутся в ближайший момент, в то время как другие ядра будут претерпевать превращения значительно позднее, поэтому когда наличное число радиоактивных атомных ядер сравнительно невелико, закон радиоактивного распада может и не выполняться во всей строгости.
Пример 2
Образец содержит 10 г изотопа плутония Pu-239 с периодом полураспада 24 400 лет. Сколько атомов плутония распадается ежесекундно?
- N ( t ) = N 0 ⋅ 2 − t / T 1 / 2 . {\displaystyle N(t)=N_{0}\cdot 2^{-t/T_{1/2}}.}
- d N d t = − N 0 ln 2 T 1 / 2 ⋅ 2 − t / T 1 / 2 = − N ln 2 T 1 / 2 . {\displaystyle {\frac {dN}{dt}}=-{\frac {N_{0}\ln 2}{T_{1/2}}}\cdot 2^{-t/T_{1/2}}=-{\frac {N\ln 2}{T_{1/2}}}.}
- N = m μ N A = 10 239 ⋅ 6 ⋅ 10 23 = 2.5 ⋅ 10 22 . {\displaystyle N={\frac {m}{\mu }}N_{A}={\frac {10}{239}}\cdot 6\cdot 10^{23}=2.5\cdot 10^{22}.}
- T 1 / 2 = 24400 ⋅ 365.24 ⋅ 24 ⋅ 3600 = 7.7 ⋅ 10 11 s . {\displaystyle T_{1/2}=24400\cdot 365.24\cdot 24\cdot 3600=7.7\cdot 10^{11}s.}
- d N d t = N ln 2 T 1 / 2 = 2.5 ⋅ 10 22 ⋅ 0.693 7.7 ⋅ 10 11 = 2.25 ⋅ 10 10 s − 1 . {\displaystyle {\frac {dN}{dt}}={\frac {N\ln 2}{T_{1/2}}}={\frac {2.5\cdot 10^{22}\cdot 0.693}{7.7\cdot 10^{11}}}=2.25\cdot 10^{10}~s^{-1}.}
Мы вычислили мгновенную скорость распада. Количество распавшихся атомов вычислим по формуле
- Δ N = Δ t ⋅ d N d t = 1 ⋅ 2.25 ⋅ 10 10 = 2.25 ⋅ 10 10 . {\displaystyle \Delta N=\Delta t\cdot {\frac {dN}{dt}}=1\cdot 2.25\cdot 10^{10}=2.25\cdot 10^{10}.}
Последняя формула действительна только тогда, когда рассматриваемый период времени (в данном случае — 1 секунда) значительно меньше, чем период полураспада. Когда рассматриваемый период времени сравним с периодом полураспада, следует пользоваться формулой
- Δ N = N 0 − N ( t ) = N 0 ( 1 − 2 − t / T 1 / 2 ) . {\displaystyle \Delta N=N_{0}-N(t)=N_{0}\left(1-2^{-t/T_{1/2}}\right).}
Эта формула пригодна в любом случае, однако для малых периодов времени требует вычислений с очень большой точностью. Для данной задачи:
- Δ N = N 0 ( 1 − 2 − t / T 1 / 2 ) = 2.5 ⋅ 10 22 ( 1 − 2 − 1 / 7.7 ⋅ 10 11 ) = 2.5 ⋅ 10 22 ( 1 − 0.99999999999910 ) = 2.25 ⋅ 10 10 . {\displaystyle \Delta N=N_{0}\left(1-2^{-t/T_{1/2}}\right)=2.5\cdot 10^{22}\left(1-2^{-1/7.7\cdot 10^{11}}\right)=2.5\cdot 10^{22}\left(1-0.99999999999910\right)=2.25\cdot 10^{10}.}
Парциальный период полураспада
Если система с периодом полураспада T 1 / 2 {\displaystyle T_{1/2}} может распадаться по нескольким каналам, для каждого из них можно определить парциальный период полураспада. Пусть вероятность распада по i-му каналу (коэффициент ветвления) равна p i {\displaystyle p_{i}} . Тогда парциальный период полураспада по i-му каналу равен
- T 1 / 2 ( i ) = T 1 / 2 p i . {\displaystyle T_{1/2}^{(i)}={\frac {T_{1/2}}{p_{i}}}.}
Парциальный T 1 / 2 ( i ) {\displaystyle T_{1/2}^{(i)}} имеет смысл периода полураспада, который был бы у данной системы, если «выключить» все каналы распада, кроме i-го. Так как по определению p i ≤ 1 {\displaystyle p_{i}\leq 1} , то T 1 / 2 ( i ) ≥ T 1 / 2 {\displaystyle T_{1/2}^{(i)}\geq T_{1/2}} для любого канала распада.
Стабильность периода полураспада
Во всех наблюдавшихся случаях (кроме некоторых изотопов, распадающихся путём электронного захвата) период полураспада был постоянным (отдельные сообщения об изменении периода были вызваны недостаточной точностью эксперимента, в частности, неполной очисткой от высокоактивных изотопов). В связи с этим период полураспада считается неизменным. На этом основании строится определение абсолютного геологического возраста горных пород, а также радиоуглеродный метод определения возраста биологических останков.
Предположение об изменяемости периода полураспада используется креационистами, а также представителями т. н. «альтернативной науки» для опровержения научной датировки горных пород, остатков живых существ и исторических находок, с целью дальнейшего опровержения научных теорий, построенных с использованием такой датировки. (См., например, статьи Креационизм, Научный креационизм, Критика эволюционизма, Туринская плащаница).
Вариабельность постоянной распада для электронного захвата наблюдалась в эксперименте, но она лежит в пределах процента во всём доступном в лаборатории диапазоне давлений и температур. Период полураспада в этом случае изменяется в связи с некоторой (довольно слабой) зависимостью плотности волновой функции орбитальных электронов в окрестности ядра от давления и температуры. Существенные изменения постоянной распада наблюдались также для сильно ионизованных атомов (так, в предельном случае полностью ионизованного ядра электронный захват может происходить только при взаимодействии ядра со свободными электронами плазмы; кроме того, распад, разрешённый для нейтральных атомов, в некоторых случаях для сильно ионизованных атомов может быть запрещён кинематически). Все эти варианты изменения постоянных распада, очевидно, не могут быть привлечены для «опровержения» радиохронологических датировок, поскольку погрешность самого радиохронометрического метода для большинства изотопов-хронометров составляет более процента, а высокоионизованные атомы в природных объектах на Земле не могут существовать сколько-нибудь длительное время.
Поиск возможных вариаций периодов полураспада радиоактивных изотопов, как в настоящее время, так и в течение миллиардов лет, интересен в связи с гипотезой о вариациях значений фундаментальных констант в физике (постоянной тонкой структуры, константы Ферми и т. д.). Однако тщательные измерения пока не принесли результата — в пределах погрешности эксперимента изменения периодов полураспада не были найдены. Так, было показано, что за 4,6 млрд лет константа α-распада самария-147 изменилась не более чем на 0,75 %, а для β-распада рения-187 изменение за это же время не превышает 0,5 %[2]; в обоих случаях результаты совместимы с отсутствием таких изменений вообще.
См. также
Примечания
- ↑ Фиалков Ю. Я. Применение изотопов в химии и химической промышленности. — К.: Техніка, 1975. — С. 52. — 240 с. — 2000 экз.
- ↑ Jean-Philippe Uzan. The fundamental constants and their variation: observational status and theoretical motivations. Rev.Mod.Phys. 75(2003)403. arXiv: hep-ph/0205340.
Формула Half Life с примерами и ответами
Что такое Half Life?
«Время, в течение которого распадается половина нестабильных радиоактивных ядер, называется периодом полураспада образца радиоактивного элемента». Здесь также представлена формула периода полураспада.
Продолжайте читать ..
Мы видели, что всякий раз, когда α- или β-частица испускается радиоактивным элементом, она превращается в какой-то другой элемент. Этот процесс радиоактивного распада довольно случайен и не подвержен какой-либо симметрии.Это означает, что мы не можем предсказать для какого-либо конкретного атома, когда он распадется. Он может сразу распасться или может оставаться неизменным в течение миллионов лет. Таким образом, мы не можем ничего сказать о жизни какого-либо конкретного атома радиоактивного элемента.
Давайте возьмем пример города с населением в один миллион человек, и мы знали, что в среднем каждый день умирает десять человек. Даже имея это знание, мы не можем с уверенностью сказать, какой именно человек умрет в какой день.Мы можем только сказать, что в целом умрут десять человек. Чем больше население города, тем точнее такие прогнозы.
Как население города нельзя говорить об атоме радиоактивного элемента. Для получения более точных результатов мы всегда говорим о больших группах атомов и о законах статистики, которые применяются к ним. Предположим, что мы рассматриваем группу из 100000 атомов и ждем, пока половина из них, то есть 50000, распадется на дочерний элемент.Это время называется периодом полураспада T 1/2 этого элемента. Если период полураспада указанного элемента составляет одни сутки, то через сутки останется только 25000 атомов. То есть по прошествии каждого дня количество оставшихся атомов становится половиной от числа уже имеющихся.
Помимо определения периода полураспада, из этого примера мы можем сделать еще два вывода. Это, во-первых, ни один радиоактивный элемент не может полностью распасться. Это связано с тем, что за любой период полураспада распадается только половина ядер, и, таким образом, для распада всех атомов требуется бесконечное время.
Во-вторых, количество атомов, распадающихся за определенный период, пропорционально количеству атомов, присутствующих в начале периода. Если количество атомов вначале велико, тогда большое количество атомов будет распадаться за период, а если количество атомов, присутствующих вначале, мало, то будет распадаться меньшее количество атомов.
Эти результаты можно представить в виде уравнения. Если в любой конкретный момент времени количество радиоактивных атомов равно N. Тогда в интервале Δt число распадающихся атомов ΔN пропорционально интервалу времени Δt и количеству атомов N, i.е.,
ΔN ∝ — NΔt
или ΔN = — λ N Δt ……… .. (1)
Где λ — константа пропорциональности и называется константой затухания. В уравнении показано, что если константа распада любого элемента велика, тогда в определенном интервале распадется большее количество его атомов, а если константа λ мала, то в этом самом интервале будет распадаться меньшее количество атомов. Из уравнения (1) мы можем определить константу распада λ, как указано ниже: 
здесь ΔN / N — доля распадающихся атомов.Таким образом, константа распада любого элемента равна доле распадающегося атома в единицу времени. Единица постоянной спада s -1 . Отрицательный знак в уравнении (1) указывает на уменьшение количества атомов N.
Распадную способность любого радиоактивного элемента можно также показать графическим методом:

Мы знали, что каждый радиоактивный элемент распадается при определенная скорость со временем. Если мы построим график между количеством атомов в образце радиоактивных элементов, присутствующих в разное время, и временем, тогда будет получена кривая.Этот график показывает, что вначале количество атомов, присутствующих в образце радиоактивного элемента, было N ° , с течением времени количество этих атомов уменьшалось из-за их распада. Этот график называется кривой спада.
После периода полураспада N 0 /2 количество атомов этого радиоактивного элемента остается позади. Если подождать еще один полупериод, тогда половина оставшихся атомов N 0 /2 распадется и 1/2 × N o /2 = (1/2) 2 N o атомы остаются позади.По истечении следующего периода полураспада половина оставшихся (1/2) 2 N ° атомов распадается. Число нераспавшихся атомов составляет 1/2 × (1/2) 2 N o = ((1/2) 3 N o . Из этого примера можно сделать вывод, что если у нас есть N ° число любого радиоактивного элемента, тогда после периода полураспада n число атомов позади будет (1/2) n N o .
Было обнаружено, что оценка распада каждого радиоактивного элемента соответствует графику, но период полураспада каждого радиоактивного элемента разный.Например, период полураспада урана-238 составляет 4,5 × 10 9 лет, а половина радия-226 — 1620 лет. Период полураспада некоторых радиоактивных элементов очень мал, например, период полураспада радона составляет 3,8 дня, а урана-239 — 23,5 минуты.
Из приведенного выше обсуждения установлено, что оценка любого радиоактивного элемента может быть сделана по его периоду полураспада или путем определения его постоянной распада λ. С помощью расчетов можно доказать, что существуют следующие соотношения между постоянной распада λ и периодом полураспада T 1/2 .
λ T 1/2 = 0,693 …………… .. (2)
Уравнение (2) показывает, что, если известна постоянная распада λ любого радиоактивного элемента, можно определить его период полураспада.
Любой стабильный элемент, кроме встречающегося в природе радиоактивного элемента, можно сделать радиоактивным. Для этого стабильный элемент бомбардируют частицами очень высокой энергии. Эта бомбардировка возбуждает ядра, и ядра, становясь нестабильными, становятся радиоактивными элементами. Такие радиоактивные элементы называют искусственными радиоактивными элементами.
Формула периода полураспада радиоактивного вещества и примеры (видео)
.
Калькулятор периодов полураспада
Следующие инструменты могут генерировать любое из значений из трех других в формуле периода полураспада для вещества, подвергающегося распаду, для уменьшения вдвое.

Калькулятор периодов полураспада
Для расчета четвертого значения укажите любые три из следующих значений.
Период полураспада, среднее время жизни и постоянная конверсия распада
Пожалуйста, предоставьте одно из следующих, чтобы получить два других.
Определение и формула
Период полураспада определяется как количество времени, которое требуется данному количеству, чтобы уменьшиться до половины его первоначального значения.Этот термин чаще всего используется в отношении атомов, подвергающихся радиоактивному распаду, но может быть использован для описания других типов распада, экспоненциального или нет. Одно из самых известных применений периода полураспада — датирование углерода-14. Период полураспада углерода-14 составляет приблизительно 5730 лет, и его можно надежно использовать для измерения дат примерно 50 000 лет назад. Процесс датирования углерода-14 был разработан Уильямом Либби и основан на том факте, что углерод-14 постоянно образуется в атмосфере.Он попадает в растения через фотосинтез, а затем в животных, когда они потребляют растения. Углерод-14 подвергается радиоактивному распаду после смерти растения или животного, и измерение количества углерода-14 в образце дает информацию о том, когда погибло растение или животное.
Ниже показаны три эквивалентные формулы, описывающие экспоненциальный распад:
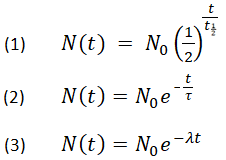
- где
N 0 — начальное количество
N т — оставшееся количество по истечении времени, т
т 1/2 — период полураспада
τ — средний срок службы
λ — постоянная затухания
Если археолог обнаружит образец окаменелости, содержащий 25% углерода-14 по сравнению с живым образцом, время смерти образца окаменелости можно определить, переставив уравнение 1, поскольку N t , N 0 и t 1/2 известны.
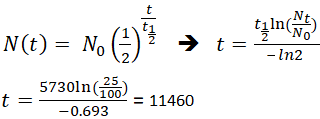
Это означает, что возраст окаменелости 11460 лет.
Вывод связи между константами периода полураспада
Используя приведенные выше уравнения, также можно вывести соотношение между t 1/2 , τ и λ . Эта связь позволяет определять все значения, если известно хотя бы одно.

Вывод формулы полураспада | Фармакокинетика формулы полужизни
- Классы
- Класс 1–3
- Класс 4–5
- Класс 6–10
- Класс 11–12
- КОНКУРЕНТНЫЙ ЭКЗАМЕН
- BNAT 000 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma класса 8
- Решения RD Sharma класса 9
- Решения RD Sharma класса 10
- Решения RD Sharma класса 11
- Решения RD Sharma класса 12
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел для класса 12
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- CBSE Notes
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции CBSE
- Примечания к редакции
- CBSE Class
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE Дополнительные вопросы по математике для класса 10
- Дополнительные вопросы по науке, класс 10 по CBSE
- CBSE, класс
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Учебные решения
- CBSE Class
- Решения NCERT
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions Class 11 Business Studies
- NCERT Solutions Class 11 Economics
- NCERT Solutions Class 11 Statistics
- NCERT Solutions Class 11 Commerce
- NCERT Solutions For Class 12
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- NCERT Solutions For Класс 4
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 11
- Примечания к редакции
- Примечания CBSE класса 7
900 .
Half-Life — Концепция — Физика Видео от Brightstorm
Итак, давайте возьмем, к примеру, стронций 90, это наш радиоактивный изотоп, его период полураспада составляет 29 лет, поэтому, если у меня изначально, если у меня нет времени, нет года, так что нет периода полураспада, у меня есть мои 10 граммов стронция 90 Хорошо, проходит один период полураспада, и это 29 лет, поэтому 29 лет спустя я [IB] мои 10 граммов, которые у меня были изначально, половина из них осталась в качестве определения состояний полураспада, так что это означает, что у меня осталось 5 граммов стронция 90 Ладно.После 2 периодов полураспада через 58 лет мой оригинальный образец в 10 граммов прошел 2 периода полураспада. Половина его ушла через первые 29 лет, и снова другая половина через вторые 29 лет дала мне 2,5 грамма, оставшихся после 58 лет и так далее, и так далее, пока фактически не останется никаких атомов стронция 90, так что мы могли бы сделать это внутри диаграммы. и проделайте это шаг за шагом, и это займет много времени, или мы можем перевести это в формулу. И формула в основном говорит, что оставшаяся сумма равна начальной сумме, которая [IB] — это то, что вы сделали 10 умножить на половину, а это именно то, что мы сделали раз в n-й степени, поэтому n — это число половины. жизни, которые мы прошли, мы прошли, поэтому первую половину я сказал, что одна вторая жизнь имеет половину умноженную на два, которая возведена в квадрат, умноженная на половину, умноженную на половину, которая возведена в квадрат, так что число полураспада равно n.Хорошо, поэтому мы можем фактически разбить это n, потому что мы можем не пойти, мы могли бы захотеть узнать, например, долю периода полураспада, хотя вещи, у которых нет периода полураспада, поэтому я ожидаю этого и даже больше и сказал количество полураспада, которое мы собираемся обозначить это n равно маленькому t, которое представляет собой время, которое прошло, разделенное на большое T, которое представляет собой длину периода полураспада, хорошо, поэтому давайте фактически объединим эту и эту проблему.
Хорошо, допустим, у нас есть железо 59, радиоактивный изотоп железа используется в медицине для диагностики нарушений кровообращения, хорошо.Период полураспада железа 59 составляет 44 с половиной дня. Какая часть 2-граммовой пробы остается через 133,5 дня. Хорошо, давайте на самом деле посмотрим на нашу формулу и подключим все, чтобы оставшееся количество — это то, что мы ищем, так что это x, изначально у нас было 2 грамма, которые мы собираемся умножить на половину до какой степени? Мы не сказали нам, сколько периодов полураспада мы должны разбить по истекшему времени, а это 44 с половиной дня, о нет, извините, на самом деле прошло 133 с половиной дня, а период полураспада составлял 44 с половиной дня, убедитесь, когда вы делаете это, время, прошедшее время, и на этот раз единицы времени для этих двух одинаковые, поэтому у вас не может быть секунд сверху и дней снизу, поэтому убедитесь, что они на самом деле одинаковы и когда вы [IB], когда вы 2 раза умножаете половину на 30, 133 на 5, это на самом деле, если вы сделали это по математике, это на самом деле равняется 3 полураспадам, это даст мне x равно 0.25, 0,25 грамма остатка Fe59, что имеет смысл, это меньше половины, потому что на самом деле прошло более одного периода полураспада, на самом деле прошло 3 периода полураспада, так что на самом деле должно быть намного меньше, чем 2 грамма, поэтому большая часть его разлагается и превращается в что-то другое.
Давайте сделаем что-нибудь посложнее, вы можете увидеть проблему, которая немного сложнее, и это так, давайте предположим, что мы говорим об углероде 14, а углерод 14 является радиоактивным изотопом углерода 12, я имею в виду, что его на самом деле [IB] атмосфера с атмосферой много, и это всегда происходит.В атмосфере всегда присутствует определенное радиоактивное соотношение этого изотопа, поэтому в этой атмосфере он действительно используется, что очень полезно для растений для фотосинтеза, растения затем берут его и используют для фотосинтеза, животные затем едят растения и так далее. на самом деле у всех живых существ есть некоторое соотношение углерода 14, равное всему, что находится в атмосфере, так что все живые объекты имеют это в своей системе, и это совершенно нормально. Происходит то, что со временем он разлагается, поэтому у нас есть углерод-14, и он разлагается, потому что он радиоактивен, и он пройдет через бета-распад, и он превратится в азот, нет ничего страшного, и на это уйдет 5730 лет на самом деле это не происходит при нашей жизни, но что происходит, когда вы умираете? Он начнет разрушаться, поэтому мы не собираемся больше регулировать этот углерод 14, и мы собираемся начать, он перестанет разрушаться и разлагаться на этот азот.
Итак, если соотношение C-14 в ископаемом составляет одну шестнадцатую, чем в атмосфере. Сколько лет окаменелости? Итак, мы собираемся фактически сказать, что оставшаяся сумма составляет одну шестнадцатую от первоначального соотношения, поэтому мы собираемся сказать одну шестнадцатую. Первоначальное количество равнялось 1, а соотношение было таким же, как и у атмосферы, хорошо, умножаем на половину, мы хотим вычислить, сколько времени прошло, поэтому мы ищем маленькое t и знаем, что период полураспада составляет 5730 лет. Теперь я собираюсь перейти к логарифмам. Я не собираюсь объяснять логарифмы, если вы хотите узнать больше о логарифмах, вы, возможно, захотите проверить видео по математике, но я просто предполагаю, что вы знаете логарифмы, и скажу, потому что я Я ищу показатель степени. Я возьму натуральный логарифм по основанию 5, поэтому я скажу, что ln натурального логарифма одной шестнадцатой равняется натуральному логарифму 1 и половине, потому что натуральный логарифм 1 равно 1.Натуральный логарифм, умноженный на половину 2, до 5730, и когда натуральные логарифмы с натуральными логарифмами, я могу взять этот показатель и поставить его впереди, так что теперь он становится, теперь он больше не экспонент, поэтому я собираюсь сказать хорошо, натуральный логарифм единицы шестнадцатое равно t, позвольте мне увидеть, t более чем в 5730 раз больше натурального логарифма 2, так что извините, одна половина, я собираюсь разделить на натуральный логарифм половины и, таким образом, натуральный логарифм одной шестнадцатой на натуральный логарифм половины, мне придется принести свой калькулятор, чтобы сделать это, это 4 равно t более 5730, поэтому я собираюсь просто умножить базовую алгебру 4 на 5730, и это дает мне 22 920 лет. по.
Это хорошо, это называется углеродным датированием, и на самом деле это хороший способ выяснить, сколько лет окаменелости, и вот какое соотношение они используют и на самом деле используют период полураспада, поэтому период полураспада — отличный способ выяснить, сколько лет чему-то или сколько вы собираетесь иметь через определенный период времени.
.
- BNAT 000 000 NC Книги
- Классы

Leave A Comment