Движение по окружности, теория и онлайн калькуляторы
Движение по окружности, теория и онлайн калькуляторыЗначимым частным случаем перемещения материальной точки по заданной траектории служит движение по окружности. Местоположение точки на окружности можно задавать не при помощи расстояния от некоторой начальной точки (допустим A), а с помощью угла $\varphi $, который образуют радиусы, которые провели из центра окружности (O) к рассматриваемой частице (точка M) и из О в точку начала отсчета (A) (рис.1).
Скорость при движении по окружности
При движении по окружности вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($\omega $), которая характеризует быстроту изменения угла $\varphi $:
\[\omega =\frac{d\varphi }{dt}\left(1\right).\]
Определим, какова связь между линейной и угловой скоростями. Длину дуги АМ ($s$) (рис.1) можно найти как:
\[s=R\varphi \left(2\right),\]
тогда изменение длины дуги за время$\ \Delta t$ равно$\ \Delta s$:
\[\Delta s=R\Delta \varphi \ \left(3\right). \]
\]
Найдем отношение $\frac{\Delta s}{\Delta t}$, разделив обе части выражения (3) на $\Delta t$:
\[\frac{\Delta s}{\Delta t}=R\frac{\Delta \varphi }{\Delta t}\ \left(4\right).\]
Перейдем к пределу в правой и левой частях равенства (4) при $\Delta t\to 0$, получим:
Ускорение материальной точки при движении по окружности
При движении по окружности (как при любом неравномерном криволинейном движении) ускорение можно разложить на две составляющие: тангенциальное ускорение (${\overline{a}}_{\tau }$), которое направлено по касательной к траектории движения точки и характеризующее быстроту изменения модуля скорости $v$ и центростремительной ускорение (${\overline{a}}_n$), направленное к центру кривизны траектории, определяющее быстроту изменения направления скорости.
При равномерном перемещении по окружности величина центростремительного ускорения постоянна ($a_n=const).\ $Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Тангенциальное ускорение при движении по окружности вычисляют, как и при любом криволинейном движении:
\[{\overline{a}}_{\tau }=\frac{d\overline{v}}{dt}\left(7\right).\]
Период и частота — характеристики равномерного движения по окружности
Равномерное движение по окружности можно характеризовать при помощи такой физической величины как период обращения ($T$), который определяют как время совершения материальной точкой полного оборота. Используют и частоту ($\nu$) обращения, которую определяют как величину обратную периоду, равную количеству оборотов за единицу времени:
\[\nu =\frac{1}{T}\left(8\right).\]
При равномерном движении по окружности угловая скорость, частота и период связаны как:
\[\omega =\frac{2\pi }{T}=2\pi \nu \left(9\right).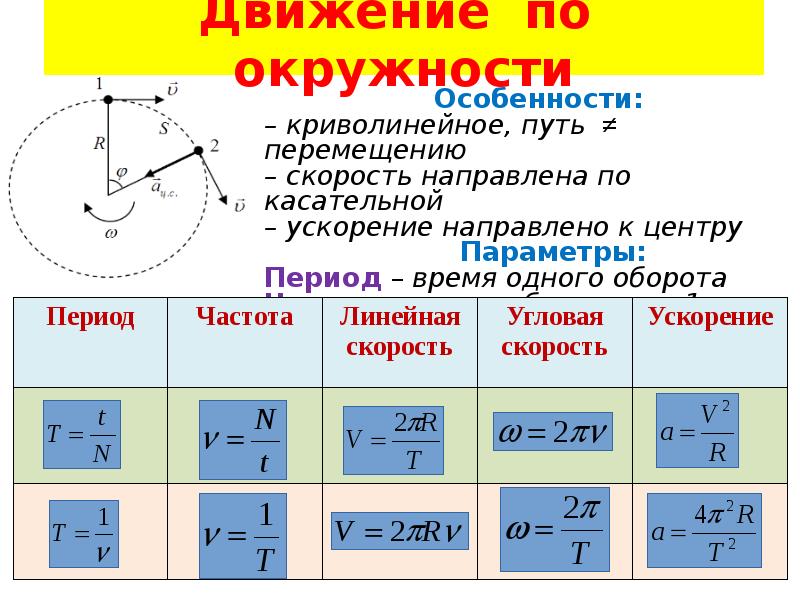 2\right)$
2\right)$
Читать дальше: жесткость пружины.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
На главную Теория Задачи Учёные Интересные статьи Шкала скоростей |
Сила и круговое движение | Университетская физика
Имя: _________________________________________
Дата: ____________________________
Партнеры:____________________________________________________________
Оборудование
0- Интерфейс LabPro
- Аппарат центростремительной силы (CFA)
- Датчик силы
- Центростремительная сила файл программного обеспечения
- Программный файл для построения графиков
- По две гири массой 5, 10 и 20 г
Введение
Согласно первому закону Ньютона, движущееся тело будет двигаться с постоянной скоростью, если результирующая сила, действующая на него, равна нулю. Постоянная скорость означает, что ни скорость, ни направление не меняются. Объект, движущийся по круговой траектории с постоянной скоростью, не имеет постоянной скорости, потому что направление скорости постоянно меняется. Это означает, что объект, движущийся с постоянной скоростью по круговой траектории, ускоряется.
Постоянная скорость означает, что ни скорость, ни направление не меняются. Объект, движущийся по круговой траектории с постоянной скоростью, не имеет постоянной скорости, потому что направление скорости постоянно меняется. Это означает, что объект, движущийся с постоянной скоростью по круговой траектории, ускоряется.
Согласно второму закону Ньютона, необходима ненулевая результирующая сила, чтобы вызвать ускорение. В случае движения объекта по круговой траектории ускорение направлено к центру окружности. Следовательно, результирующая сила также направлена к центру. Эту результирующую силу часто называют центростремительной силой .
Поскольку ускорение объекта, совершающего равномерное круговое движение, равно v 2 /R, результирующая сила, необходимая для удержания массы на круговой траектории, равна F = m (v 2 /R). В этой лабораторной работе вы исследуете, как изменения m, v и R влияют на результирующую силу F, необходимую для удержания массы на круговой траектории.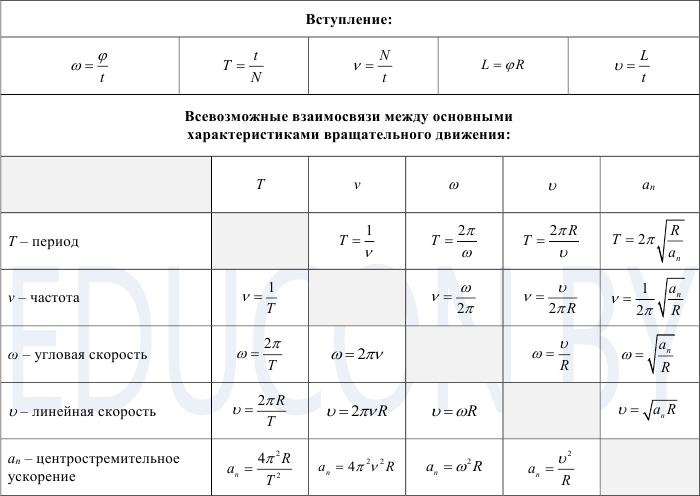
I. Замена массы
1. Внимательно наблюдайте за тем, как ваш инструктор или лаборант демонстрирует правильное использование прибора центростремительной силы. Ни при каких обстоятельствах не подавайте на двигатель напряжение более 12 вольт или 0,40 А, иначе двигатель сгорит!
2. Откройте файл Центростремительная Сила .
3. Откалибруйте датчик силы, выбрав Experiment/Calibrate . Во всплывающем меню выберите датчик силы и выберите Calibrate Now . Теперь вы выполните двухточечную калибровку датчиков силы:
- Для первой точки калибровки не применяйте силу к датчику, введите 0 Н и нажмите Сохранить.
- Для второй точки калибровки подвесьте к датчику груз массой 500 г. Введите вес этой массы (4,90 N) и нажмите Keep.
Примечание: Вы несете ответственность за постоянную проверку калибровки датчика силы, сначала сняв все грузы и проверив, показывает ли датчик 0 Н, а затем подвесив 500 граммов на датчик и проверяя, он читает 4. 9N. Если вы не видите этих значений, вам необходимо либо повторно обнулить, либо повторно откалибровать датчик.
9N. Если вы не видите этих значений, вам необходимо либо повторно обнулить, либо повторно откалибровать датчик.
4. Поместите груз массой 5 г с каждой стороны аппарата на отметке 70 мм. Подвижная масса должна быть расположена так, чтобы один партнер удерживал центр массы на расстоянии 70 мм, в то время как второй партнер перемещал датчик силы вверх, пока тетива не натянулась. Затем датчик усилия должен быть зафиксирован в этом положении.
5. Значения m и R могут быть измерены непосредственно с помощью прибора для измерения центростремительной силы (CFA). Тангенциальная скорость определяется с помощью таймера фотозатвора и вычислений, выполненных в LoggerPro. Фотозатвор измеряет время (T), за которое масса совершает один полный оборот. Таким образом, тангенциальная скорость:
v = 2πR/T
Эту формулу можно найти в Logger Pro в разделе Data/Column Options, , а затем выберите Velocity. По умолчанию используется значение радиуса 0,07 м. «Время импульса» — это время одного оборота массы.
Примечание: Эта формула вычисляет правильную тангенциальную скорость только при радиусе окружности 0,07 м. Когда используются другие радиусы, пользователь должен изменить эту формулу, введя текущий радиус вместо 0,07.
6. Установите напряжение на 8,0 В и наблюдайте за прибором, чтобы убедиться, что струна, ведущая к датчику силы, расположена вертикально и точно выровнена со шкивом под ним.
7. Нажмите Соберите и контролируйте скорость и силу в течение примерно 10 секунд, затем отключите питание.
8. Выделите область графика, которая показывает наиболее постоянные значения скорости и силы. Запишите средние значения скорости и силы в приведенную ниже таблицу вместе с соответствующими погрешностями.
9. Повторите описанные выше шаги, чтобы заполнить таблицу. Убедитесь, что скорость такая же, как в первом испытании. Если нет, отрегулируйте напряжение на блоке питания.
Влияние изменения массы на силу (R = 0,070 м)
Масса (кг) | Скорость (м/с) | Сила (С) |
0,005 | ± | ± |
0,010 | ± | ± |
0,015 | ± | ± |
0,020 | ± | ± |
0,025 | ± | ± |
0,030 | ± | ± |
0,035 | ± | ± |
II. Изменение скорости
Изменение скорости
1. Поместите груз массой 20 г с центром на отметке 70 мм с каждой стороны аппарата.
2. Проверьте калибровку датчика силы с 0 Н и 4,9 Н. Обнулите или выполните повторную калибровку, если необходимо.
3. Установите напряжение на 4,0 вольта и наблюдайте за прибором, чтобы убедиться, что струна, ведущая к датчику усилия, расположена вертикально и точно выровнена со шкивом под ним.
4. Нажмите . Соберите и отслеживайте скорость и силу в течение примерно 10 секунд, затем отключите питание.
5. Выделите область графика, которая показывает наиболее постоянные значения скорости и силы. Запишите средние значения скорости и силы в приведенную ниже таблицу вместе с соответствующими погрешностями.
6. Повторите описанные выше шаги, чтобы заполнить таблицу.
Влияние изменения скорости на силу (m = 0,020 кг и R = 0,070 м)
Напряжение (В) | Скорость (м/с) | Сила (Н) |
4,0 | ± | ± |
5,0 | ± | ± |
6,0 | ± | ± |
7,0 | ± | ± |
8,0 | ± | ± |
9,0 | ± | ± |
10,0 | ± | ± |
11,0 | ± | ± |
12,0 | ± | ± |
III. Изменение радиуса
Изменение радиуса
1. Поместите 20-граммовый груз с центром на отметке 50 мм с каждой стороны аппарата.
2. Нажмите Параметры данных/столбцов и затем выберите Скорость . Поскольку наш радиус теперь равен 0,05 м, отредактируйте выражение для массовой скорости на 2*pi*(0,05)/»Время импульса».
3. Проверьте калибровку датчика силы с 0 Н и 4,9 Н. При необходимости выполните повторную калибровку или повторную калибровку.
4. Установите напряжение на 12,0 В и наблюдайте за прибором, чтобы убедиться, что струна, ведущая к датчику усилия, расположена вертикально и точно выровнена со шкивом под ним.
5. Нажмите . Соберите и отслеживайте скорость и силу в течение примерно 10 секунд, затем отключите питание.
6. Выделите область графика, которая показывает наиболее постоянные значения скорости и силы. Запишите средние значения скорости и силы в приведенную ниже таблицу вместе с соответствующими погрешностями.
7. Повторите описанные выше шаги, чтобы заполнить таблицу. Для каждого нового радиуса нужно:
Повторите описанные выше шаги, чтобы заполнить таблицу. Для каждого нового радиуса нужно:
а. Отредактируйте уравнение скорости, введя текущий радиус
b. Отрегулируйте напряжение, чтобы поддерживать постоянную скорость для каждого испытания.
Радиус
(м)
Скорость
(м/с)
Сила
(С)
0,050
±
±
0,060
±
±
0,070
±
±
0,080
±
±
0,090
±
±
0,100
±
±
IV. Анализ данных
Анализ данных
A. Сила и масса
Откройте файл График . Этот файл позволяет вам вводить свои данные и неопределенности и создавать наиболее подходящий график.
- Введите свои данные в соответствующую колонку. (Сила по оси Y, масса по оси X и погрешности в соответствующих столбцах.)
- Дважды щелкните заголовок каждого столбца, чтобы изменить метку и единицы измерения для каждого столбца.
- Выберите подходящую функцию наилучшего соответствия (в данном случае Analyze/Linear Fit ) и отобразите ее на графике. Чтобы определить неопределенности в параметрах линейной аппроксимации, щелкните правой кнопкой мыши поле Linear Fit и выберите Linear Fit Options . Отображает стандартное отклонение наклона и точки пересечения по оси Y.
- Завершите подготовку диаграммы, затем распечатайте ее и прикрепите в конце этого задания.
Вопрос: Сравните общую форму линейной функции, Y =AX + B , с теоретической формулой F = m (v 2 /R) . Чему должны быть равны значения A и B, если теория верна? Подсказка: если переменная изображена на оси X или Y, она не может быть частью А или В. ваша наиболее подходящая функция. Согласуется ли ваше экспериментальное значение А с единицами измерения и неопределенностями с этим известным значением?
Чему должны быть равны значения A и B, если теория верна? Подсказка: если переменная изображена на оси X или Y, она не может быть частью А или В. ваша наиболее подходящая функция. Согласуется ли ваше экспериментальное значение А с единицами измерения и неопределенностями с этим известным значением?
B. Сила и скорость
Создайте график силы и скорости, как описано выше. Сопоставьте ваши данные со степенной функцией и прикрепите ее к концу этого действия.
Вопрос: Сравните общую форму степенной функции Y =AX B , с теоретической формулой F = m (v 2 /R) . Чему должны быть равны значения A и B, если теория верна?
Вопрос: Является ли мощность вашей функции наилучшего соответствия равной 2 в пределах вашей неопределенности? Если нет, подумайте о конкретных источниках возможных ошибок и о том, как бы вы исправили эти ошибки, если бы повторили эксперимент.
Вопрос: Вычислите известное значение констант, составляющих A, в вашей функции наилучшего соответствия. Согласуется ли ваше экспериментальное значение А с единицами измерения и неопределенностями с этим известным значением?
Согласуется ли ваше экспериментальное значение А с единицами измерения и неопределенностями с этим известным значением?
C. Сила и радиус
Создайте график силы и радиуса, как описано выше. Сопоставьте ваши данные со степенной функцией и прикрепите ее к концу этого действия.
Вопрос: Сравните общую форму степенной функции Y =AX B , с теоретической формулой F = m (v 2 /R) . Чему должны быть равны значения A и B, если теория верна?
Вопрос: Равна ли мощность вашей функции наилучшего соответствия -1 в пределах вашей неопределенности? Если нет, подумайте о конкретных источниках возможных ошибок и о том, как бы вы исправили эти ошибки, если бы повторили эксперимент.
Вопрос: Вычислите известное значение констант, составляющих A, в вашей функции наилучшего соответствия. Согласуется ли ваше экспериментальное значение А с единицами измерения и неопределенностями с этим известным значением?
Использование уравнений кругового движения — физика для старших классов
Все ресурсы по физике для старших классов
6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущий 1 2 3 4 5 Далее →
Справка по физике для старших классов » Движение и механика » Круговое движение » Использование уравнений кругового движения
Мяч катится по краю круга радиусом . Если он катится со скоростью , каково его центростремительное ускорение?
Если он катится со скоростью , каково его центростремительное ускорение?
Возможные ответы:
Правильный ответ:
Объяснение:
Центростремительное ускорение — это ускорение, направленное к центру, когда объект движется по окружности. Хотя скорость может быть постоянной, изменение направления приводит к ненулевому ускорению.
Формула для этого: , где – воспринимаемая тангенциальная скорость, – радиус окружности.
Подставьте данные значения и найдите ускорение.
Сообщить об ошибке
Мяч катится по краю круга радиусом . Если он катится со скоростью, какова центростремительная сила?
Возможные ответы:
Правильный ответ:
Пояснение:
Центростремительная сила — это сила, которая постоянно перемещает объект к центру; это то, что заставляет объект двигаться по кругу, а не лететь по касательной к кругу.
Формула силы: .
Чтобы найти центростремительную силу, нам нужно найти центростремительное ускорение. Мы делаем это с формулой, где воспринимается тангенциальная скорость и является радиусом круга.
Подставьте данные значения и найдите ускорение.
Подставьте это в первое уравнение, чтобы найти силу.
Сообщить об ошибке
Мяч катится по краю круга радиусом . Если он катится со скоростью , каков период полета мяча?
Возможные ответы:
Правильный ответ:
Объяснение:
Период, , объекта, движущегося по кругу, – это количество времени, которое требуется объекту, чтобы совершить один полный цикл по окружности.
Если мы начнем с линейного понимания скорости, мы можем применить ту же концепцию здесь. Наша скорость должна быть изменением расстояния по сравнению с изменением времени. В этом случае у нас нет определенного времени, но у нас есть период с точки зрения одного полного цикла.
В этом случае у нас нет определенного времени, но у нас есть период с точки зрения одного полного цикла.
Мы можем составить уравнение для периода, используя длину окружности в качестве расстояния: .
Подставьте данные значения для расчета периода.
Сообщить об ошибке
Мяч катится по краю круга радиусом . Если он катится со скоростью , каково его центростремительное ускорение?
Возможные ответы:
Правильный ответ:
Объяснение:
Центростремительное ускорение — это ускорение, направленное к центру, когда объект движется по окружности. Хотя скорость может быть постоянной, изменение направления приводит к ненулевому ускорению.
Формула для этого: , где – воспринимаемая тангенциальная скорость, – радиус окружности.
Подставьте данные значения и найдите ускорение.
Сообщить об ошибке
Мяч катится по краю круга радиусом . Если он катится со скоростью, какова центростремительная сила?
Возможные ответы:
Правильный ответ:
Пояснение:
Центростремительная сила — это сила, которая постоянно перемещает объект к центру; это то, что заставляет объект двигаться по кругу, а не лететь по касательной к кругу.
Формула силы: .
Чтобы найти центростремительную силу, нам нужно найти центростремительное ускорение. Мы делаем это с формулой, где воспринимается тангенциальная скорость и является радиусом круга.
Подставьте данные значения и найдите ускорение.
Подставьте ускорение и заданную массу в первое уравнение, чтобы найти силу.
Сообщить об ошибке
Мяч катится по краю круга радиусом . Если он катится со скоростью , каков период полета мяча?
Возможные ответы:
Правильный ответ:
Объяснение:
Период, , объекта, движущегося по кругу, – это количество времени, которое требуется объекту, чтобы совершить один полный цикл по окружности.
Если мы начнем с линейного понимания скорости, мы можем применить ту же концепцию здесь. Наша скорость должна быть изменением расстояния по сравнению с изменением времени. В этом случае у нас нет определенного времени, но у нас есть период с точки зрения одного полного цикла.
Мы можем составить уравнение для периода, используя длину окружности в качестве расстояния: .
Подставьте данные значения для расчета периода.
Сообщить об ошибке
Мяч катится по краю круга радиусом . Если на него действует центростремительная сила, какова его скорость?
Если на него действует центростремительная сила, какова его скорость?
Возможные ответы:
Правильный ответ:
Пояснение:
Центростремительная сила — это сила, которая постоянно перемещает объект к центру; это то, что заставляет объект двигаться по кругу, а не лететь по касательной к кругу.
Формула силы: .
Поскольку мы знаем массу и силу, мы можем найти ускорение.
Центростремительное ускорение определяется по формуле , где – воспринимаемая тангенциальная скорость, а – радиус окружности.
Подставьте данные значения и найдите скорость.
Сообщить об ошибке
Радиус Солнца составляет 696 000 км. Если его период равен 587,28 часа, какова его тангенциальная скорость на экваторе?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение скорости.

 Учитывая, что
|r1| = |r2| = R и |v1| = |v2| = v, из
подобия треугольников находим:
Учитывая, что
|r1| = |r2| = R и |v1| = |v2| = v, из
подобия треугольников находим:

 Например:
Например: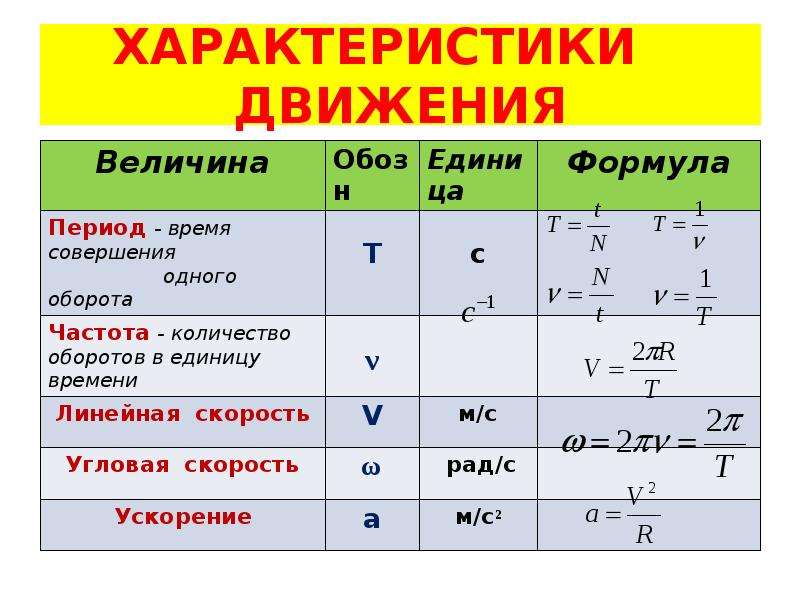
Leave A Comment